Сигнальный процессор, формирователь окон, кодированный медиа-сигнал, способ обработки сигнала и способ формирования окон - RU2616863C2
Код документа: RU2616863C2
Чертежи
Описание
Решения согласно изобретению связаны с сигнальным процессором для того, чтобы обеспечить обработанную версию входного сигнала в зависимости от входного сигнала, с формирователем окна для того, чтобы обеспечить сигнал, обработанный весовыми коэффициентами окна, с кодируемым медиа-сигналом, с способом обработки сигнала и с способом формирования сигнала, обработанного весовой функцией окна.
Решение согласно изобретению связано с устройством для кодирования или декодирования аудио- или видеосигнала, используя различные функции окна. Другое решение согласно изобретению связано с способом для кодирования или декодирования аудио- или видеосигнала, используя различные функции окна.
Решения согласно данному изобретению имеют отношение к способам анализа и обработки сигнала, которые могут использоваться в аудио- или видеокодирующих системах.
Фильтрация с конечной импульсной характеристикой (FIR) дискретных сигналов, особенно в контексте банков фильтров, широко используется в спектральном анализе, обработке, синтезе и сжатии медиа данных. Хорошо известно, что временная (или пространственная) ограниченность FIR фильтра, и, следовательно, ограниченность интервала сигнала, который может быть обработан в один момент времени или в пространстве, может привести к явлению, известному как смещение или утечка. При изменении интервала фильтрации, например, при различных изменениях передачи или квантизации, после операции обратной фильтрации могут появиться блочные или кольцевые артефакты. Было найдено, что причина этих артефактов может быть вызвана разрывами между конечными точками формы волны сигнала и его производных на обработанном интервале (в дальнейшем именуемом сегмент). Таким образом, было обнаружено, что для уменьшения таких нежелательных эффектов смещения полезно или даже необходимо минимизировать разрывы сигнала и некоторых его производных на краях сегмента. Это может быть достигнуто умножением каждого семпла s(n), n=0, 1…, N-1, сегмента длиной N на определенный вес w(n) до фильтрования, и в случае манипуляции с сигналом в фильтрованной области, также после обратного фильтрования, так, что разрывы между конечными точками сигнала сегмента и его производных сведены к нулю. Эквивалентным подходом является применение веса к каждому базисному фильтру банка фильтров (См., например, ссылку [2]). Так как весовые коэффициенты часто описываются аналитическим выражением, набор коэффициентов обычно известен как функция веса или функция окна.
В типичных аудио- и видеокодирующих системах, исходная форма волны сегментирована как указано выше, и каждый сегмент квантуется к более грубому представлению, чтобы достигнуть высокого сжатия данных, то есть низкого битрейта, необходимого для хранения или передачи сигнала. При попытке получить выгоду от кодирования путем энергетического уплотнения в меньшее, чем N число семплов (или, другими словами, увеличить перцепционное качество закодированного сигнала для данного битрейта), стали популярными фильтр банк преобразования сегментов до квантизации. В недавно разработанных системах используется ортогональное преобразование от времени к частоте с перекрытиями в виде модифицированного дискретного косинусного преобразования (MDCT), банк фильтров, позволяющий накладываться смежным сегментам, обеспечивает минимальную частоту дискретизации. Для улучшенной работы прямые и обратные операции MDCT объединены с применением весовых коэффициентов для каждого сегмента: на центральной стороне применяется аналитическое окно wa(n) перед прямым MDCT и на стороне приемника, окно ws(n) используется после обратного MDCT. К сожалению, не все функции весовых коэффициентов подходят для использования с MDCT. Принимая предопределенные окна (инвариантные во времени/пространстве), для всех архитектур было найдено, что для осуществления совершенной реконструкции входного сигнала при отсутствии ошибок квантизации или передачи, wa(n) и ws(n) должны быть выбраны следующим образом:
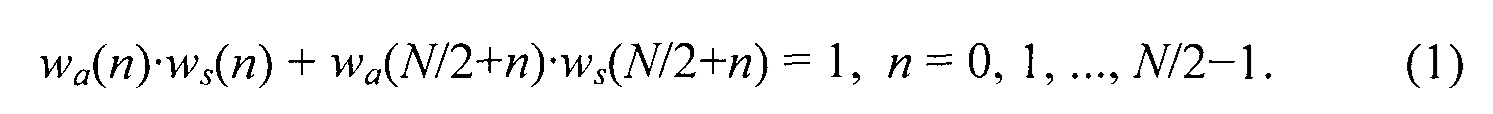
Если wa(n) и ws(n) являются идентичными, т.е. wa(n)=ws(n)=w(n), уравнение. (1) сокращается к более известной форме
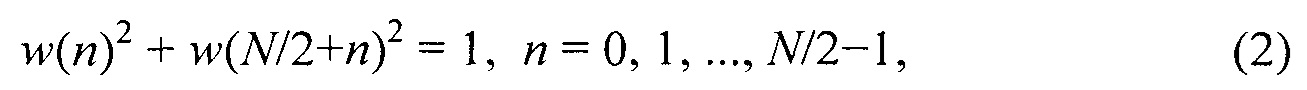
опубликованной в [7]. Для большей энергетической компактности, w(n) является симметричной относительно n=N/2-1/2, т.е. обычно используется выражение
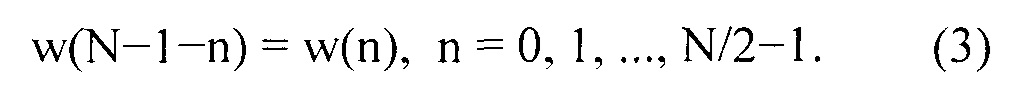
В стандарте улучшенного аудиокодирования (ААС) [8] возможны две оконных функции. Одна - синусоидальное окно, даваемое выражением
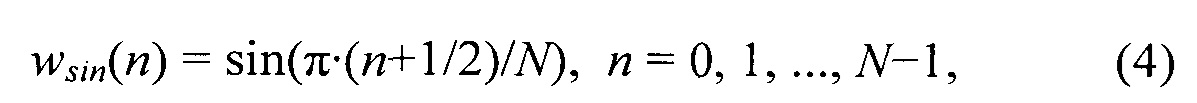
другая – окно Кайзера-Бесселя (KBD), описанное в патентах Филдера и Давидсона с названием, ʺLowbitratetransformcoder, decoder, andencoder/decoderforhigh-qualityaudio,ʺ патенты США 5109417 и 5142656. Последнее окно используется в стандарте кодирования AC-3 (Dolby Digital) (ATSC, Inc., ʺDigital Audio Compression Standard (AC-3, E-AC-3), RevisionB,ʺ document A/52B, June 2005), хотя и в другой конфигурации (α=5). Vorbis Спецификация Ворбиса [9] определяет окно
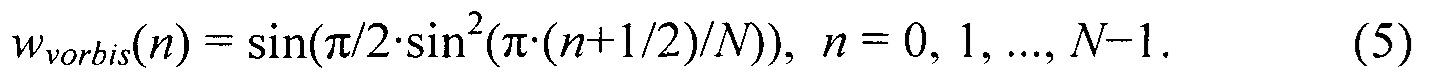
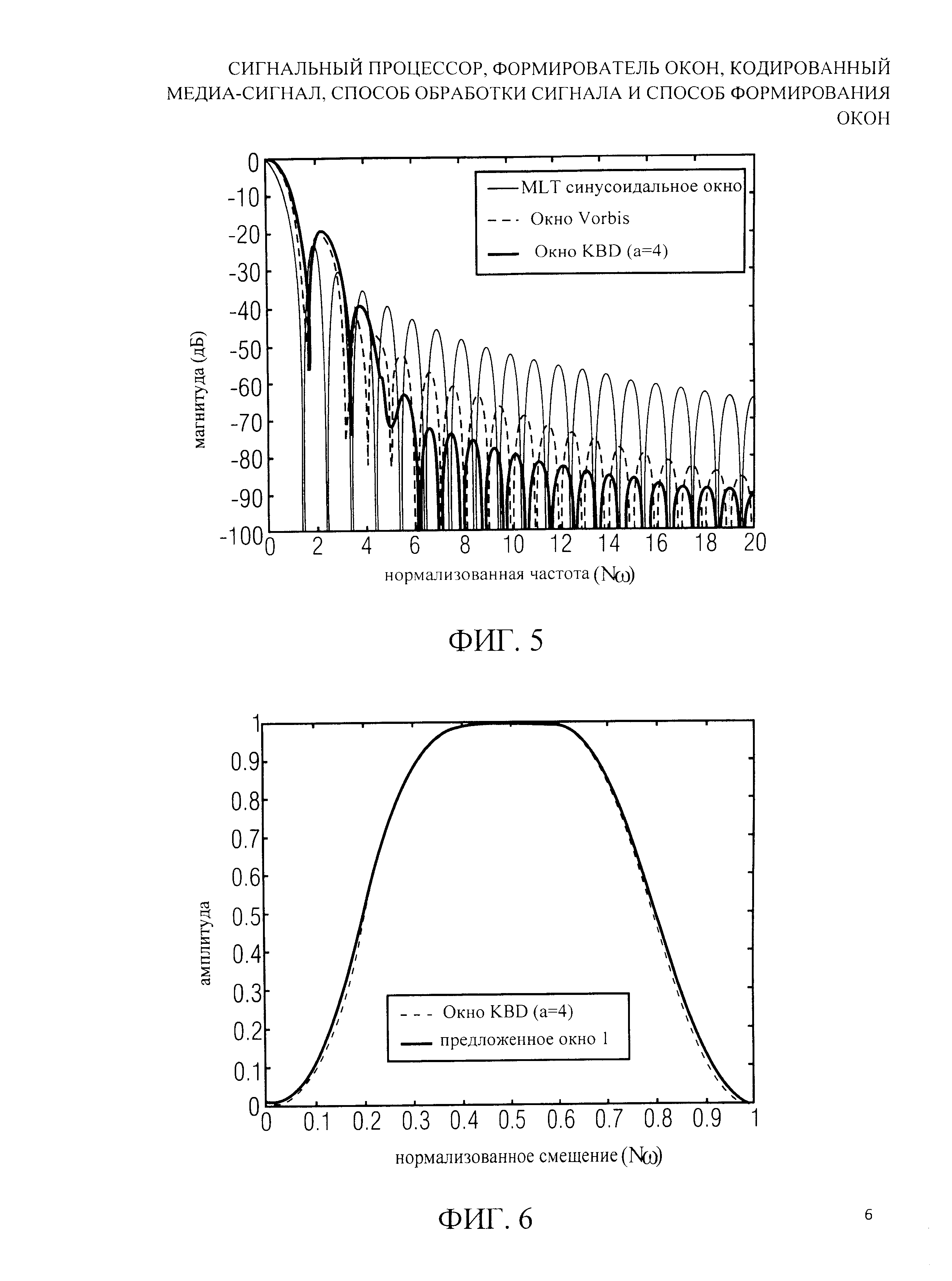
На фиг.5 показаны частотные характеристики функций окна ААС и Vorbis, полученных путем Фурье преобразований, согласно [4]. Можно заметить, что у синусоидального окна есть относительно высокая частотная селективность по соседним частотам (узкий главный лепесток) и относительно низкое внеполосное подавление (низкое ослабление бокового лепестка). У окна KBD, напротив, есть высокое внеполосное подавление и низкая частотная селективность по соседним частотам. Окно Vorbis имеет промежуточные характеристики между рассмотренными двумя окнами.
Было найдено, что для некоторых решений, может быть желательно осуществить более совершенный контроль над селективностью в полосе пропускания и внеполосным подавлением функции весовых коэффициентов, удовлетворяющей (2). Более определенно было найдено, что для повышения эффективности кодирования, параметр окна можно непрерывно приспосабливать характеристики окна к характеристикам входного спектра. Из всех трех функций, обсужденных выше, только функция KBD предлагает такой параметр α, который может быть различен для достижения различных соотношений селективности/ослабления. Эта функция, однако, включает в вычислительном отношении сложную математику (функция Бесселя, гиперболический синус, квадратный корень и деление), что потенциально запрещает ее перевычисление для каждого сегмента сигнала на устройствах с низкой производительности или в системах, работающих в режиме реального времени. То же самое относится к классу функций окна, представленных в статье Синхи и Феррейры с названием ʺA New Class of Smooth Power Complementary Windows and their Application to Audio Signal Processing,ʺ AES 119thConvention, Oct. 2005, paper 6604, требуя операций с комплексными числами, спектрального разложения на множители и преобразования Фурье. Также было найдено, для управления частотной характеристикой может использоваться интерполяция между двумя функциями (например, KBD и синус), которая наиболее эффективно может быть выполнена взвешенным суммированием, но этот подход имеет ограниченную гибкость.
Множество функций окна, оптимизированных к различным критериям, было описано, например, в [1], [2], [3], [4], [5]. Возможно сегодня три самых популярных в использовании функции - это те, о которых сообщают Ханн, Хамминг и Блекман.
Далее будут описаны некоторые классические функции окна. Другими словами, далее будут описаны вышеупомянутые функции окна (например, Ханна, Хемминга и Блекмана), и будет определено основное общее уравнение для разработки.
Для последовательности и сравнимости с оригинальными исследованиями функций окна в данном обсуждении должны быть приняты способология и нотация Наттола (см., например, [4]). В частности будем обозначать через L продолжительность (длину) окна, t местоположение (время) в диапазоне применения весовых коэффициентов и f частота в пределах спектральной плотности мощности, полученной преобразованием Фурье функции окна. Дополнительно, все функции окна должны быть нормализованы к пиковой амплитуде. Здесь будут рассмотрены только симметричные, колоколообразные окна, это подразумевает w (L/2)=1. Первая рассматриваемая весовая функция, известная как функция Ханна (или Хеннинга), определена в [2] для приложений цифровой обработки сигнала (DSP), как
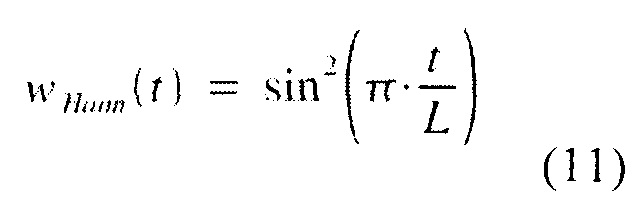
где t - неотрицательные значения. Как показано в [2] и следует из (11), функция Ханна является специальным случаем класса функций синуса в степени a:
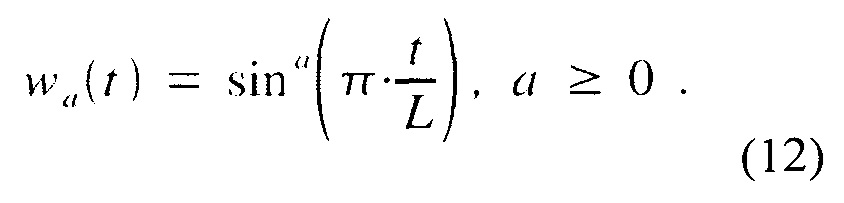
Обычно на практике, a - положительные целые числа. Заметим, что (12) может быть также записано как сумма со сдвинутым и масштабированным косинусом:
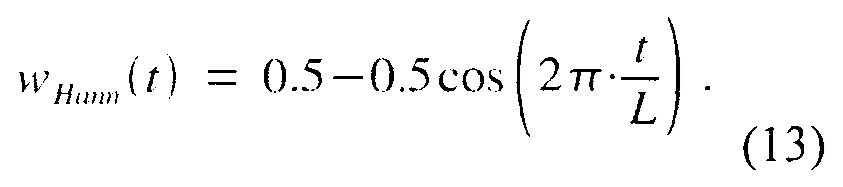
Эта формулировка допускает частичную спектральную оптимизацию окна Ханна (см. ниже дискуссию в отношении вычисления и оптимизации) путем изменения смещения и коэффициента масштабирования. Результатом является функция Ханна, для которой точные параметры даны в [4] как
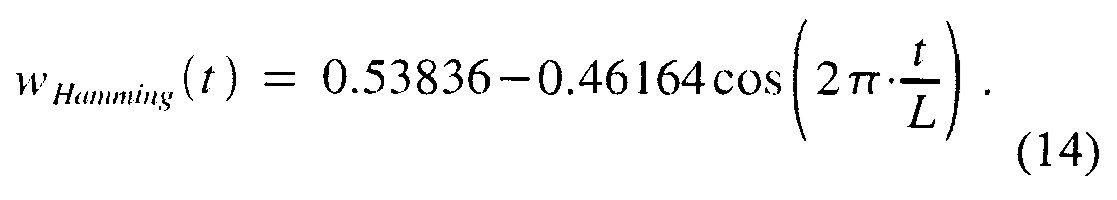
Как замечено Натталом (см. например, [4]), окна Ханна и Хеннинга - это двухэлементной реализацией класса (K+1) - элементных функций, которые могут быть описаны как сумма косинусоидальных функций. Упрощая запись Наттола, они могут быть записаны как
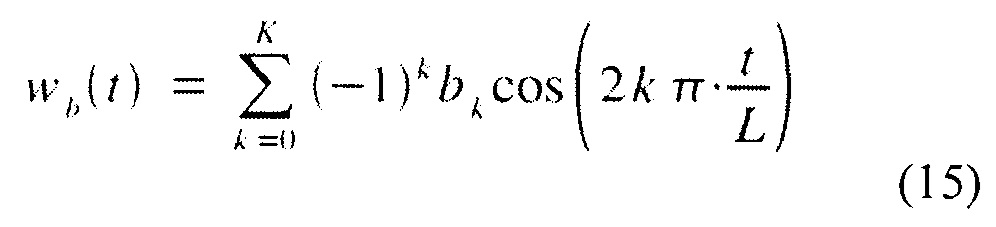
для использования в DSP приложениях. Это совпадает с уравнением (11) [4] с опущенным скаляром 1/L. Трехэлементные применения также общеприняты. Простейшим является случай (15) с K=2 и коэффициентами
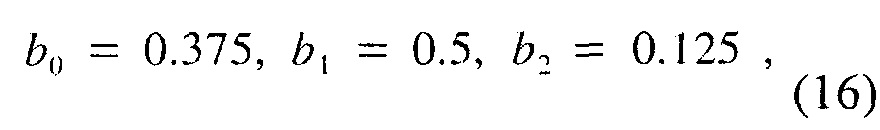
который эквивалентен (12) с a=4. Аналогично подходу Хемминга, Блекман, (см., например, [1]) выводит следующие оптимальные bk:
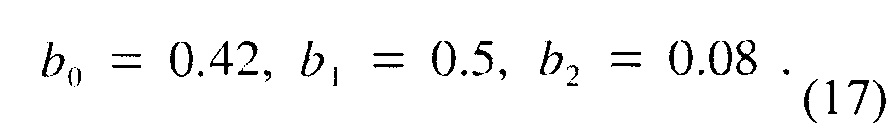
Наттол (см., например, [4]) далее улучшает параметры Блекмана для лучшего спектрального разрешения в окрестности (см. ниже дискуссию в отношении вычисления и оптимизации):
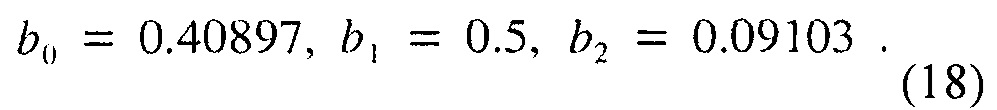
Заинтересованному читателю следует изучить [4] для других оптимизированных окон с тремя и четырьмя элементными суммами косинусов.
Ввиду вышеизложенного есть необходимость в альтернативной оконной функции, имеющей умеренную вычислительную сложность, но обеспечивающей хорошую гибкость в разработке.
Соответственно, целью данного изобретения является создание концепции получения оконных функций с умеренной вычислительной сложностью и хорошей гибкостью в разработке для обработки сигналов.
Решение согласно изобретению создает сигнальный процессор для того, чтобы обеспечить обработанную версию входного сигнала в зависимости от входного сигнала. Чтобы получить обработанную версию входного сигнала, сигнальный процессор включает оконный обработчик, формирующий часть входного сигнала, или его предварительно обработанной версии, в зависимости от окна обработки сигнала, описанного весовыми величинами окна обработки сигнала для множества значений индекса весовых величин окна. Сигнальный процессор также включает формирователь окна для того, чтобы обеспечить весовые величины окна сигнала для множества значений индекса окна в зависимости от одного или более параметров формы окна. Формирователь окна выполнен с возможностью вычислить функцию синуса для множества величин аргумента, связанных со значениями индекса величин окна, чтобы получить сигнал, обработанный величинами окна. Формирователь окна выполнен с возможностью вычислить взвешенную сумму линейных слагаемых, которые линейно зависят от значений индекса величин окна, и значений одной или более функций формы, где одна или более функций формы отображают индексы величин окна на соответствующие значения функции, чтобы получить величины аргумента, и где одна или более функций формы симметричны относительно центра огибающей окна.
Это решение согласно изобретению основано на открытии того, что оконная обработка входного сигнала может быть достигнута легко приспосабливаемым способом, путем определения величин окна обработки сигнала в вышеописанной манере, так как взвешенное суммирование линейных слагаемых и одной или более функций формы может быть выполнено с очень низкими вычислительными затратами. Кроме этого, было обнаружено, что точка симметрии одной или большего количества функций формы и вычисление функции синуса для множества величин аргумента вносит с собой особенно хорошие свойства окна, такие как, например, хорошие характеристики сохранения энергии между двумя последующими огибающими окна. Кроме того, можно легко приспособить характеристики окна, определенные величинами окна обработки сигнала, изменяя вес одной или большего количества функций формы в зависимости от одного или большего количества параметров формы окна, так что окна с различными характеристиками доступны со сравнительно небольшими вычислительными затратами. Например, определенный здесь способ позволяет получать большое количество различных форм окна, имеющих упомянутые хорошие характеристики, изменяя вес одной или большего количества функций формы.
Кроме того, необходимо отметить, что, используя вышеупомянутый способ вычисления окон, имеющих различные характеристики, которые могут быть приспособлены с очень высокой степенью детализации, не требует особенно трудных вычислений, а просто требует формирования взвешенной суммы, чтобы получить величины аргумента и вычислить функцию синуса, используя величины аргумента.
Другое решение согласно изобретению создает сигнальный процессор для того, чтобы обеспечить обработанную версию входного сигнала в зависимости от входного сигнала. Сигнальный процессор включает оконный обработчик, формирующий часть входного сигнала, или его предварительно обработанной версии, в зависимости от окна обработки сигнала, описанного весовыми величинами окна обработки сигнала для множества значений индекса весовых величин окна, чтобы получить обработанную версию входного сигнала. Величины окна обработки сигнала, являются величинами результата вычисления функции синуса для множества величин аргумента, связанных со значениями индекса величин окна, где величины аргумента - взвешенные суммы линейного выражения, которое линейно зависит от значений индекса величин окна и величин одной или более синусоидальной функции формы, где одна или более синусоидальная функция формы отображает значения индекса величин окна на соответствующие величины одной или более синусоидальной функции формы с точкой симметрии относительно центра огибающей окна. Это решение согласно изобретению основано на тех же самых ключевых идеях как ранее обсужденное решение. Кроме того, было найдено, что использование синусоидальных функций формы создает окна обработки сигнала, имеющие особенно хорошие характеристики.
Другое решение согласно изобретению создает формирователь окна для того, чтобы обеспечить величины окна обработки сигнала для множества значений индекса величин окна в зависимости от одного или более параметров формы окна. Формирователь окна выполнен с возможностью вычислить функцию синуса для множества значений аргумента, связанных со значениями индекса величин окна, чтобы получить величины окна обработки сигнала. Формирователь окна выполнен с возможностью вычислить взвешенную сумму линейных членов, которые линейно зависят от значений индекса величин окна и значений одной или более функций формирования, чтобы получить значения аргумента. Одно или больше значений функции формы отображают значения индекса значений окна на соответствующие значения функции, и одна или больше функций формы с точкой симметрии относительно центра огибающей окна.
Это решение согласно изобретению основано на тех же самых идеях как вышеупомянутые решения.
Другое решение согласно изобретению создает сигнальный процессор для того, чтобы обеспечить обработанную версию входного сигнала в зависимости от входного сигнала. Сигнальный процессор включает оконный обработчик, формирующий часть входного сигнала, или его предварительно обработанной версии, в зависимости от окна обработки сигнала, описанного весовыми величинами окна обработки сигнала для множества значений индекса весовых величин окна, чтобы получить обработанную версию входного сигнала. Сигнальный процессор также включает формирователь окна для того, чтобы обеспечить величины окна обработки сигнала для множества значений индекса величин окна в зависимости от одного или более параметров формы окна. Формирователь окна выполнен с возможностью вычислить взвешенную сумму величин функции множества синусоидальных функций формы, которые отображают значения индекса величин функции окна на соответствующие значения функции, чтобы получить величины окна сигнала обработки сигнала. Вес величин функции определен параметрами формы окна. Это решение согласно изобретению основано на открытии, того, что с хорошей вычислительной эффективностью и гибкостью могут быть получены формы окна, имеющие достаточно хорошие характеристики для многих решений, чтобы приспособить характеристики окна, используя параметры формы окна и описанное правило вычисления.
Другое решение согласно изобретению создает сигнальный процессор для того, чтобы обеспечить обработанную версию входного сигнала в зависимости от входного сигнала. Сигнальный процессор включает оконный обработчик, формирующий часть входного сигнала, или его предварительно обработанной версии, в зависимости от окна обработки сигнала, описанного весовыми величинами окна обработки сигнала для множества значений индекса весовых величин окна, чтобы получить обработанную версию входного сигнала. Значения окна обработки сигнала являются результатом функции взвешенного суммирования величин множества синусоидальных функций формы, которые отображают значения индекса величин функции окна на соответствующие значения функции. Это решение согласно изобретению основано на тех же самых идеях как ранее обсужденное решение.
Другое решение согласно изобретению создает кодированный медиа-сигнал. Кодированный медиа-сигнал включает закодированное представление мультимедийного контента и один или более параметров формы окна. Один или более параметров формы окна определяют форму окна, которое будет применено в расшифровке закодированного представления мультимедийного контента. Один или более параметров формы окна описывают веса для того, чтобы вычислить взвешенную сумму линейного выражения, которое линейно зависит от значения индекса величин окна и величин функции одной или более функций формы, чтобы получить значение аргумента для того, чтобы вывести значения окна обработки сигнала для множества величин индекса величин окна, вычисляя функцию синуса для множества значений аргумента. Этот вложенный медиа- сигнал обеспечивает высокую гибкость для индикации оконной обработки, потому что может описать большое количество различных типов окон, которые могут быть эффективно получены декодером, используя параметры формы окна.
Краткое описание иллюстраций.
Решения согласно изобретению будут впоследствии описаны, в соответствии с чертежами, где:
На фиг.1a показана блок-схема сигнального процессора, согласно решению изобретения;
На фиг.1b показана блок-схема сигнального процессора, согласно другому решению изобретения;
На фиг.2 показана блок-схема сигнального процессора, согласно другому решению изобретения;
На фиг.3 показана блок-схема формирователя окна, согласно решению изобретения;
На фиг.4 показано схематическое представление кодируемого медиа-сигнала, согласно решению изобретения;
На фиг.5 показано графическое представление в децибелах амплитуд частот образов окон ААС и Vorbis;
На фиг.6 показано графическое представление амплитуд частот образа функции окна ААС KBD и одного варианта изобретенной функции;
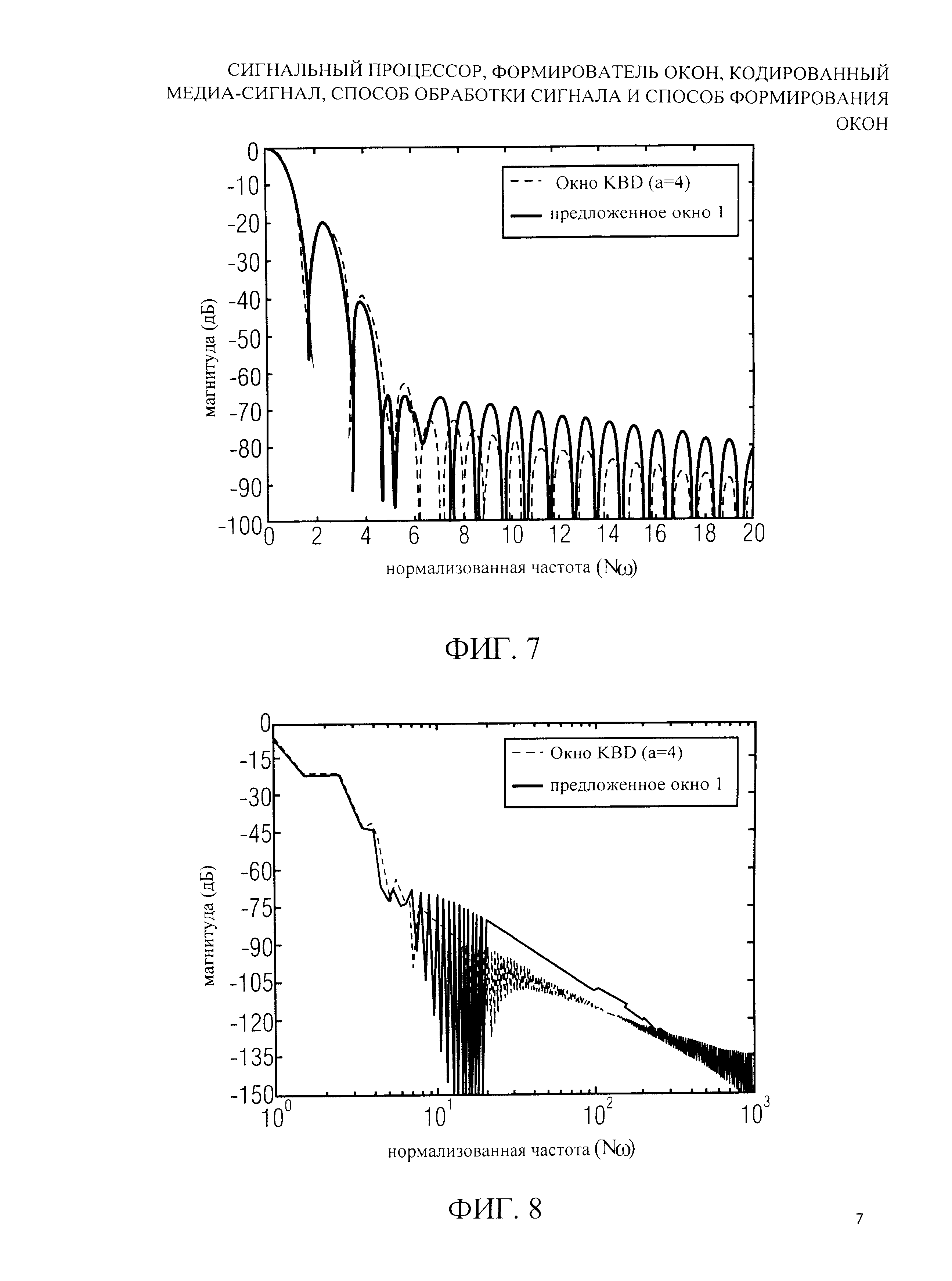
На фиг.7 показано графическое представление величин частот для указанного варианта изобретенной функции окна по сравнению с функцией окна ААС KBD при линейном масштабе абсциссы и дБ (децибельном) масштабе ординаты;
На фиг.8 показано графическое представление величин частот для указанного варианта изобретенной функции окна по сравнению с функцией окна ААС KBD при логарифмическом масштабе абсциссы и dB масштабе ординаты;
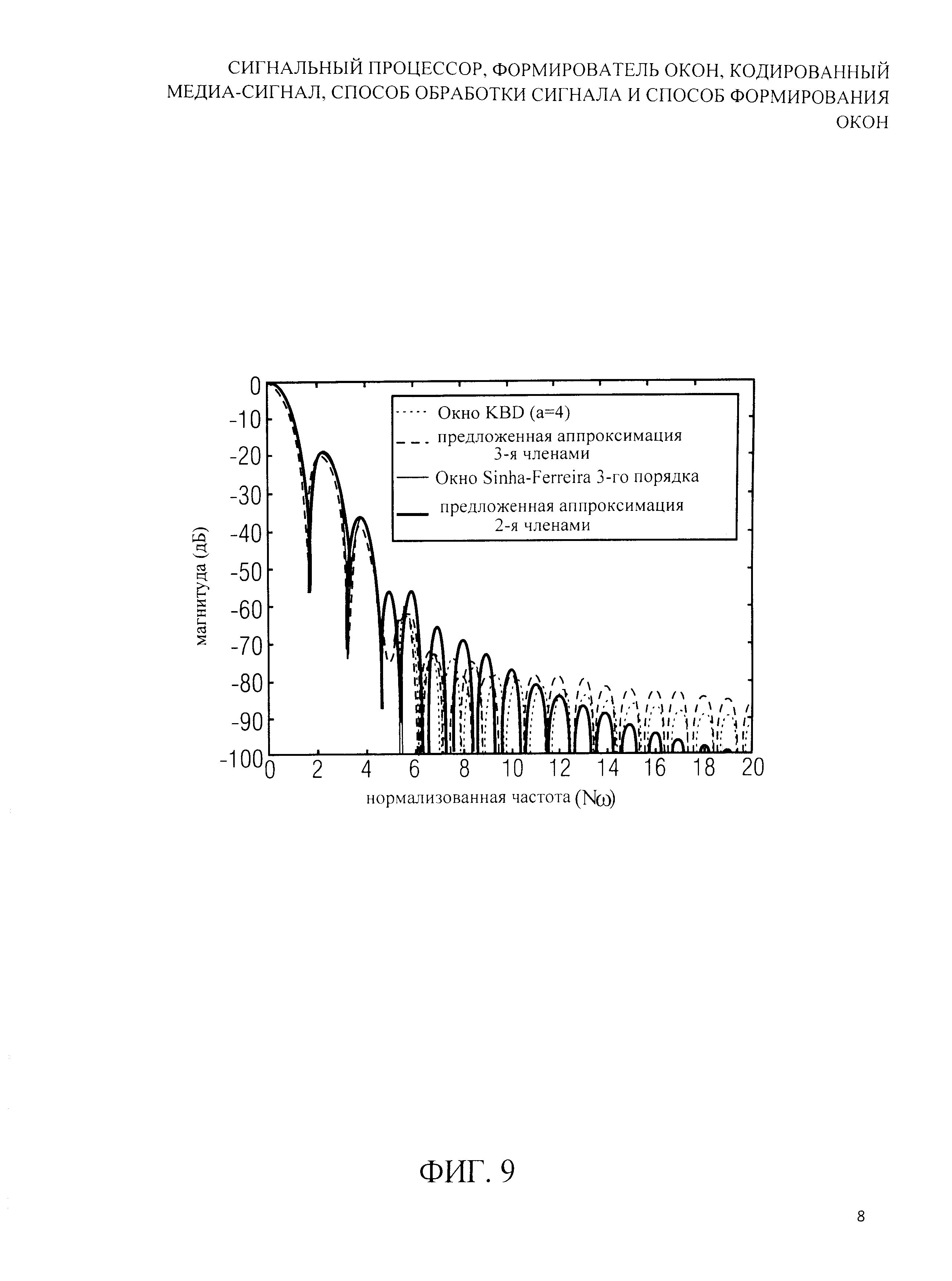
На фиг.9 показано графическое представление величин частот еще для двух вариантов изобретенной функции окна по сравнению с функцией окна AACKBD и окна Сина-Феррейры (Sinha-Ferreira) третьего порядка;
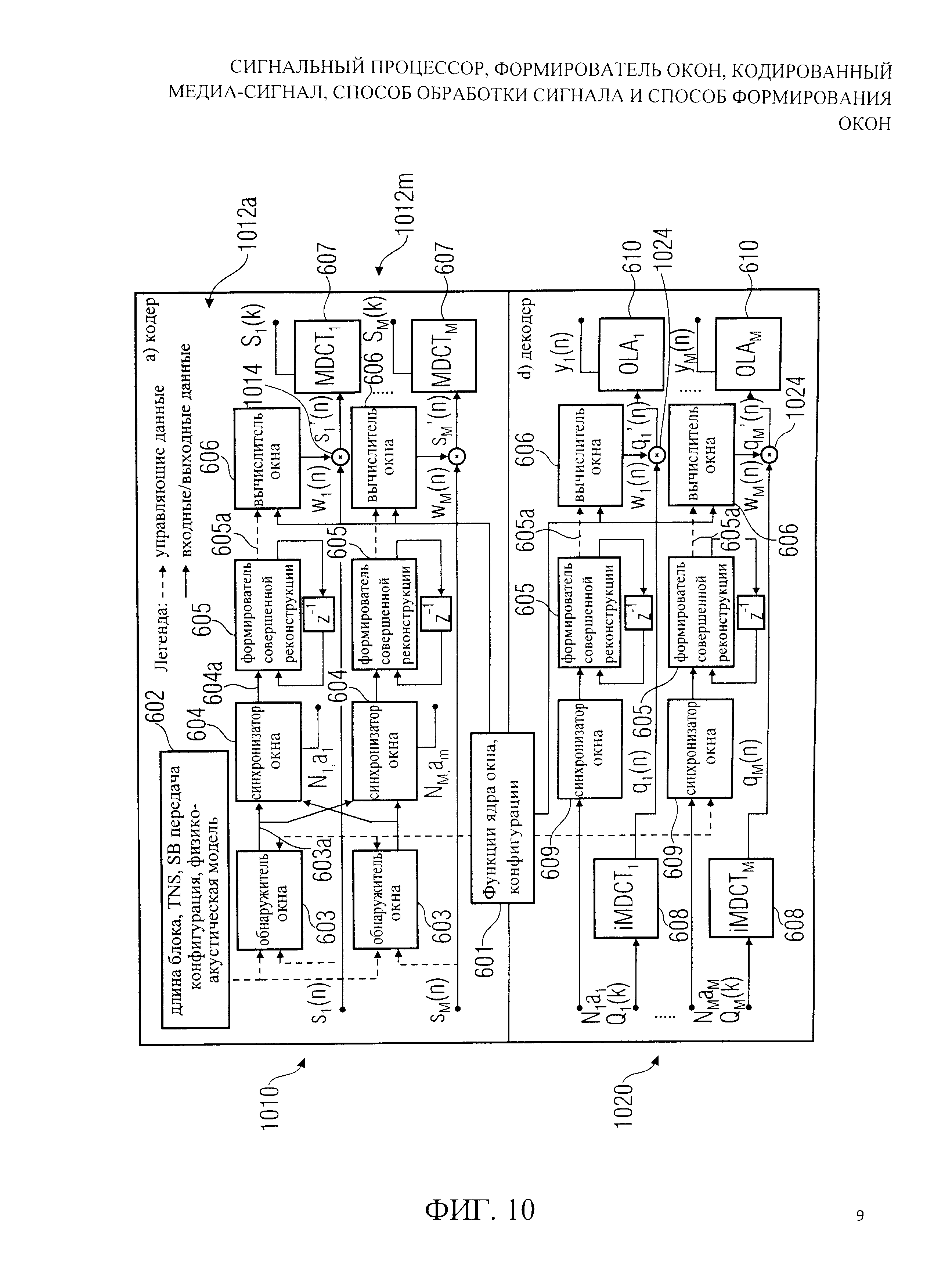
На фиг.10, показана блок-диаграмма, процесса адаптации сигнала для изобретенных и аналогичных функций окна;
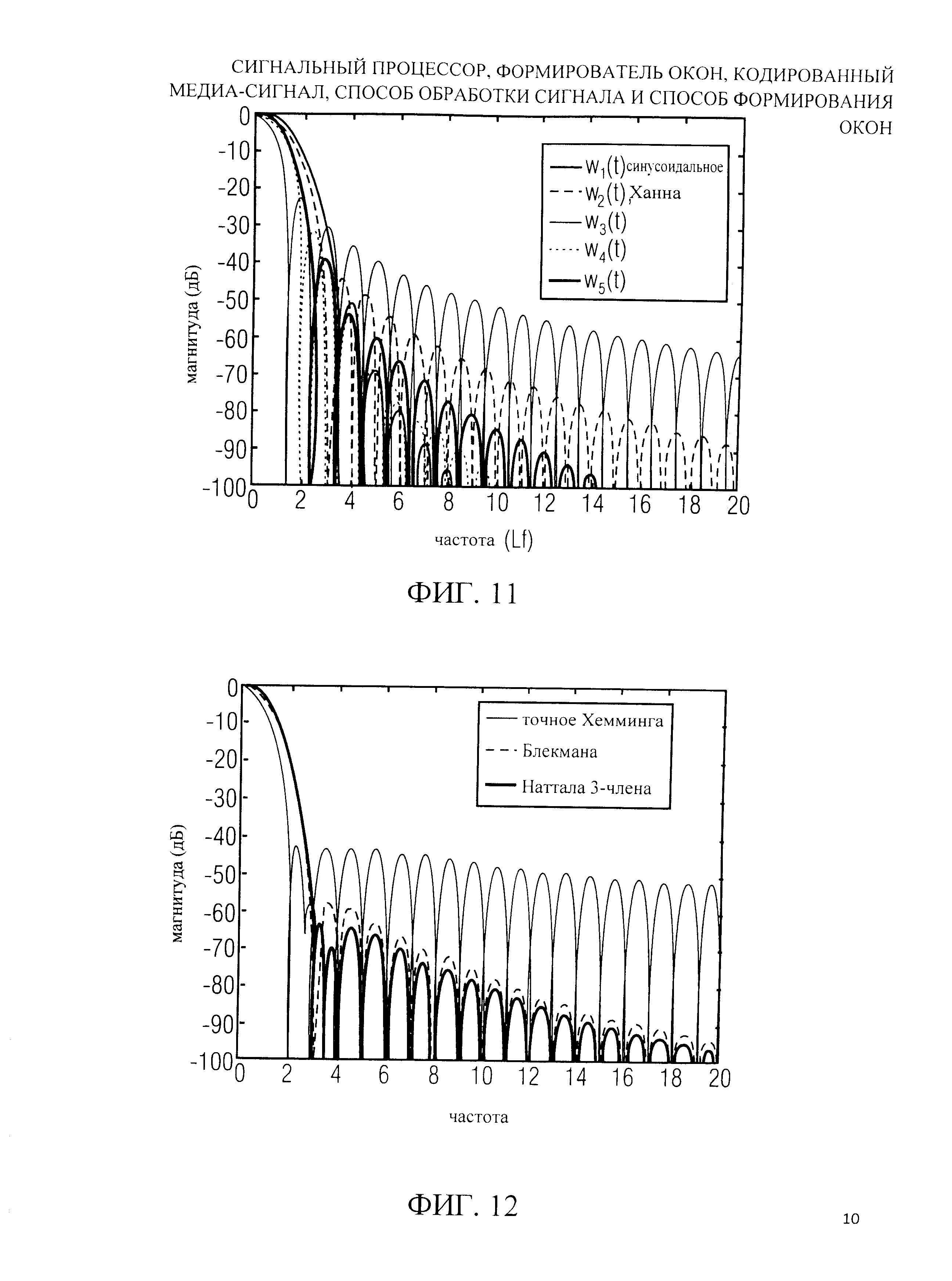
На фиг.11 показано графическое представление спектров некоторых функций степени синуса согласно уравнению (12);
На фиг.12 показано графическое представление спектров оптимизированных функций суммы косинусов согласно уравнению (15);
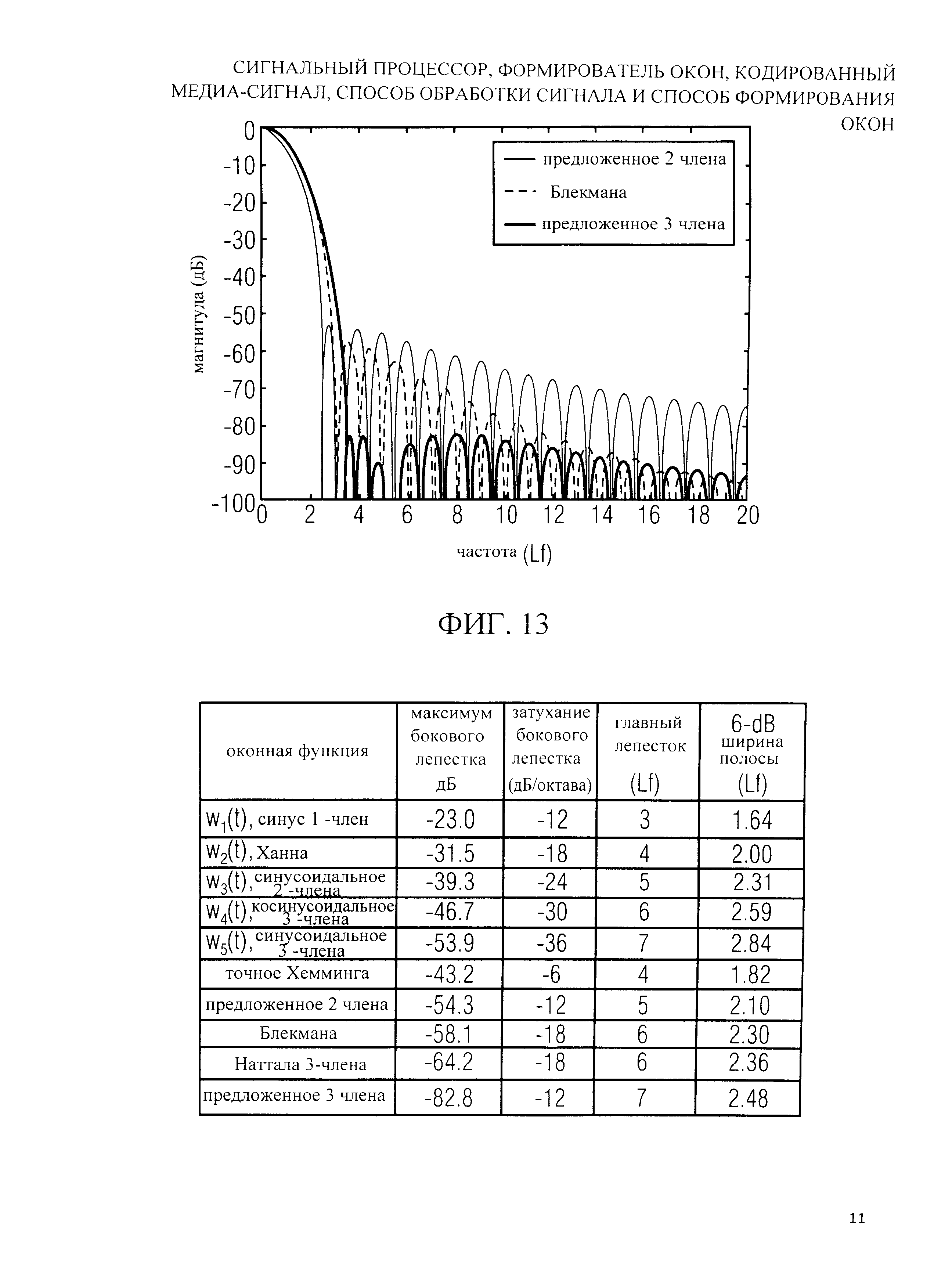
На фиг.13 показано графическое представление предложенных оптимизированных окон суммы синусов согласно уравнению (19);
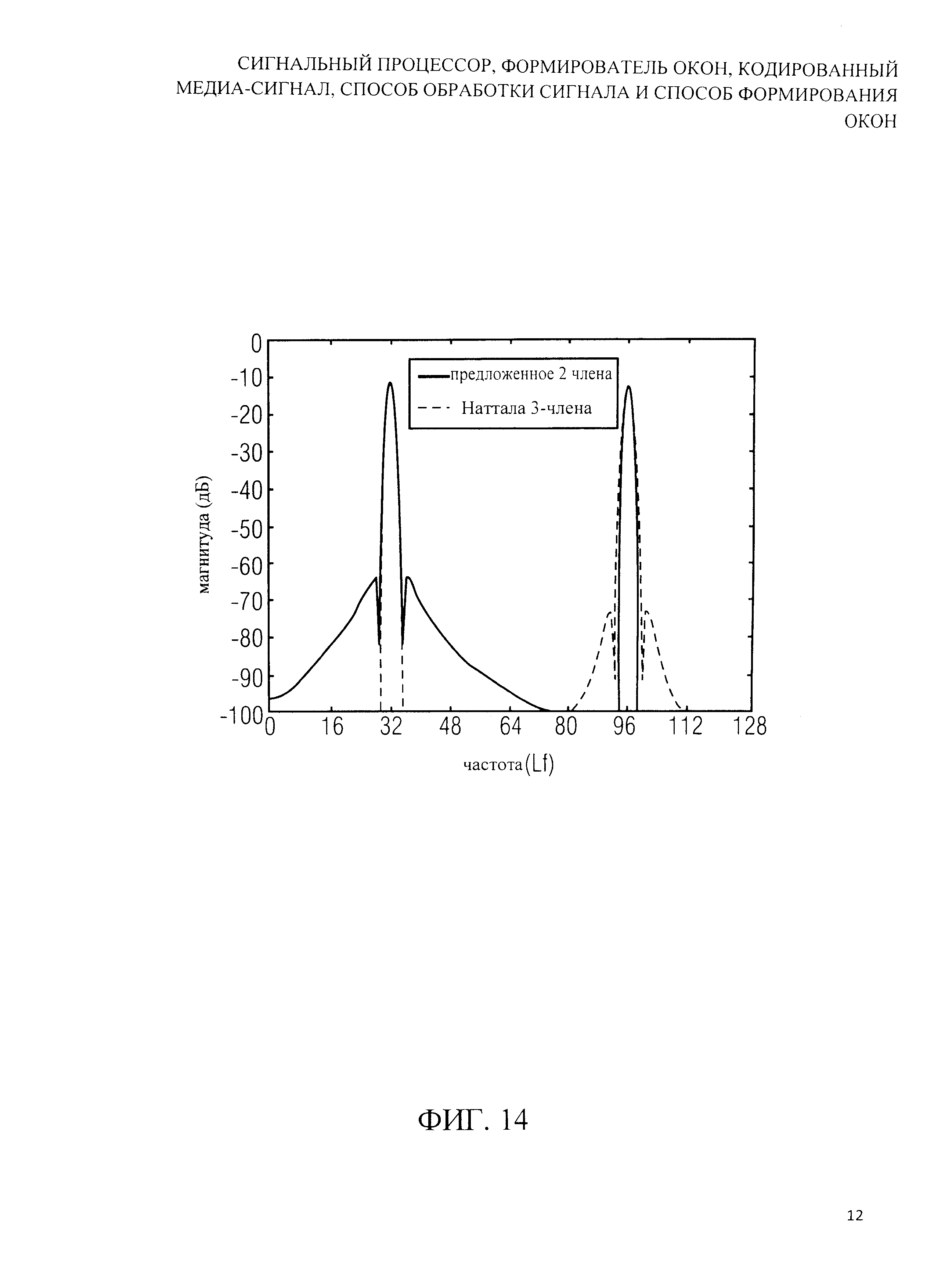
На фиг.14 показано графическое представление спектров DFT двух синусоид с частотами Lf=32 и 96.5 после применения различных функций окна; и
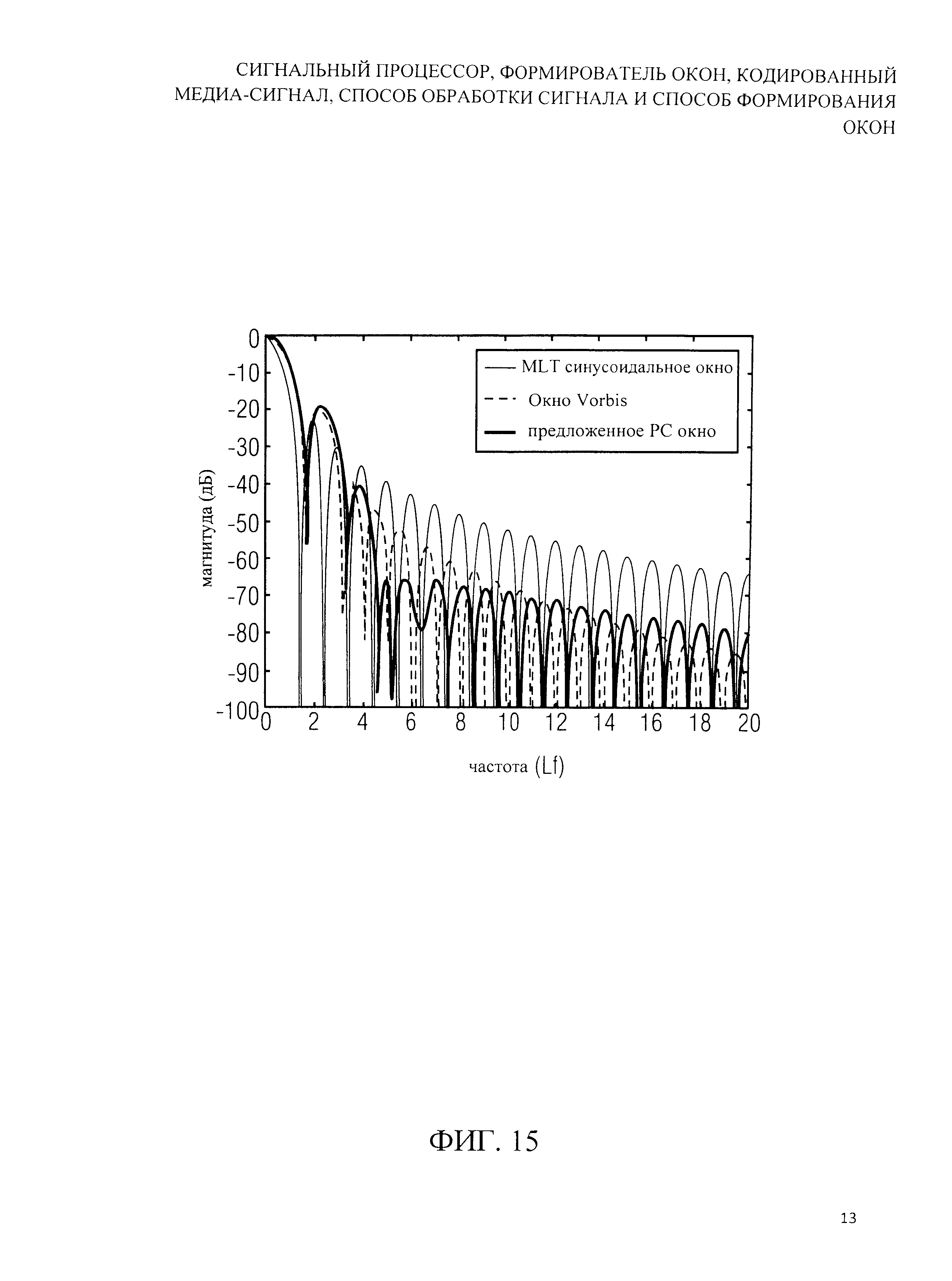
На фиг.15 показано графическое представление спектров двух окон PC и предложенного окна.
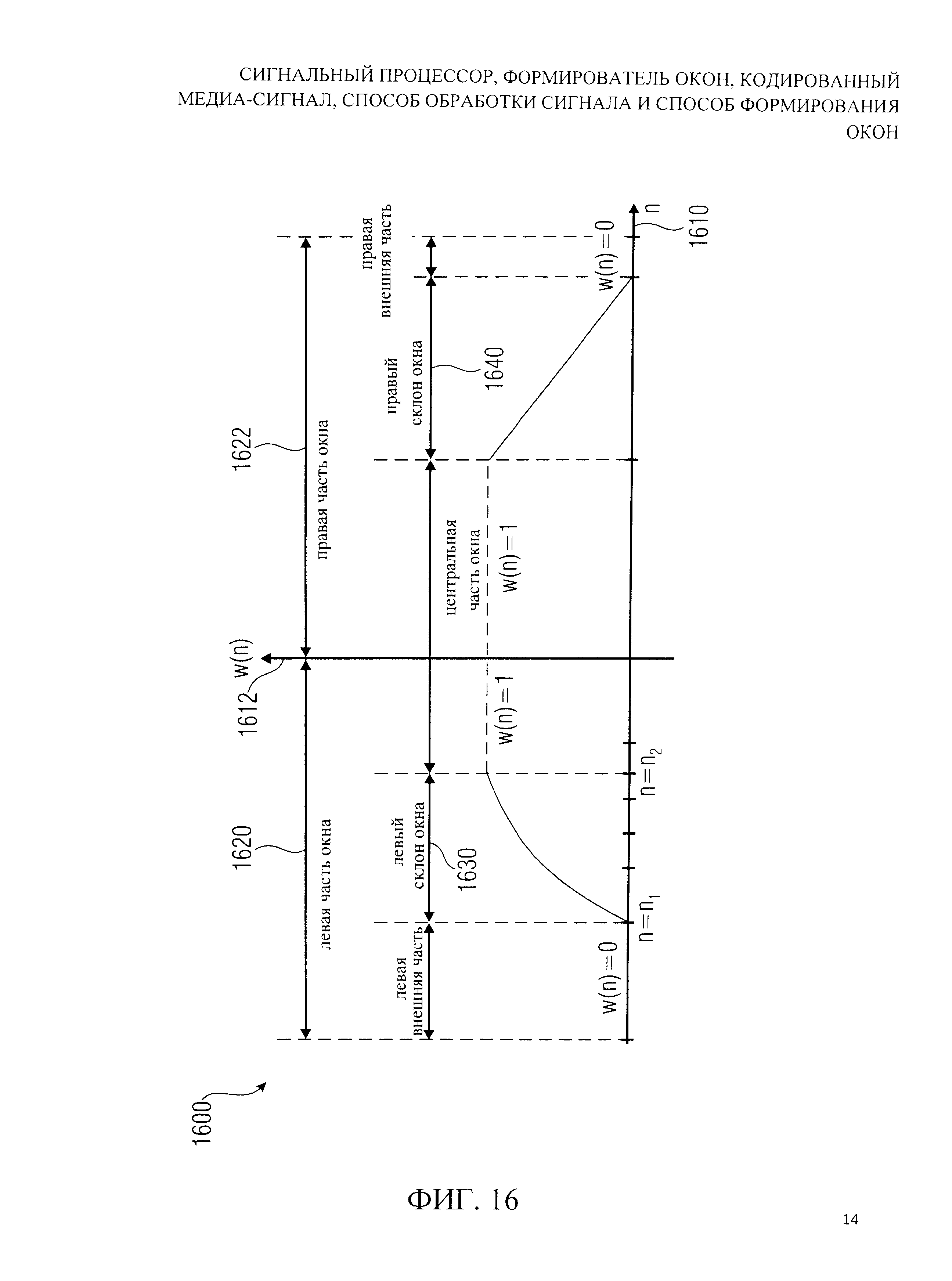
На фиг.16 показано схематическое представление окна.
Подробное описание решений
1. Сигнальный процессор согласно фиг.1a.
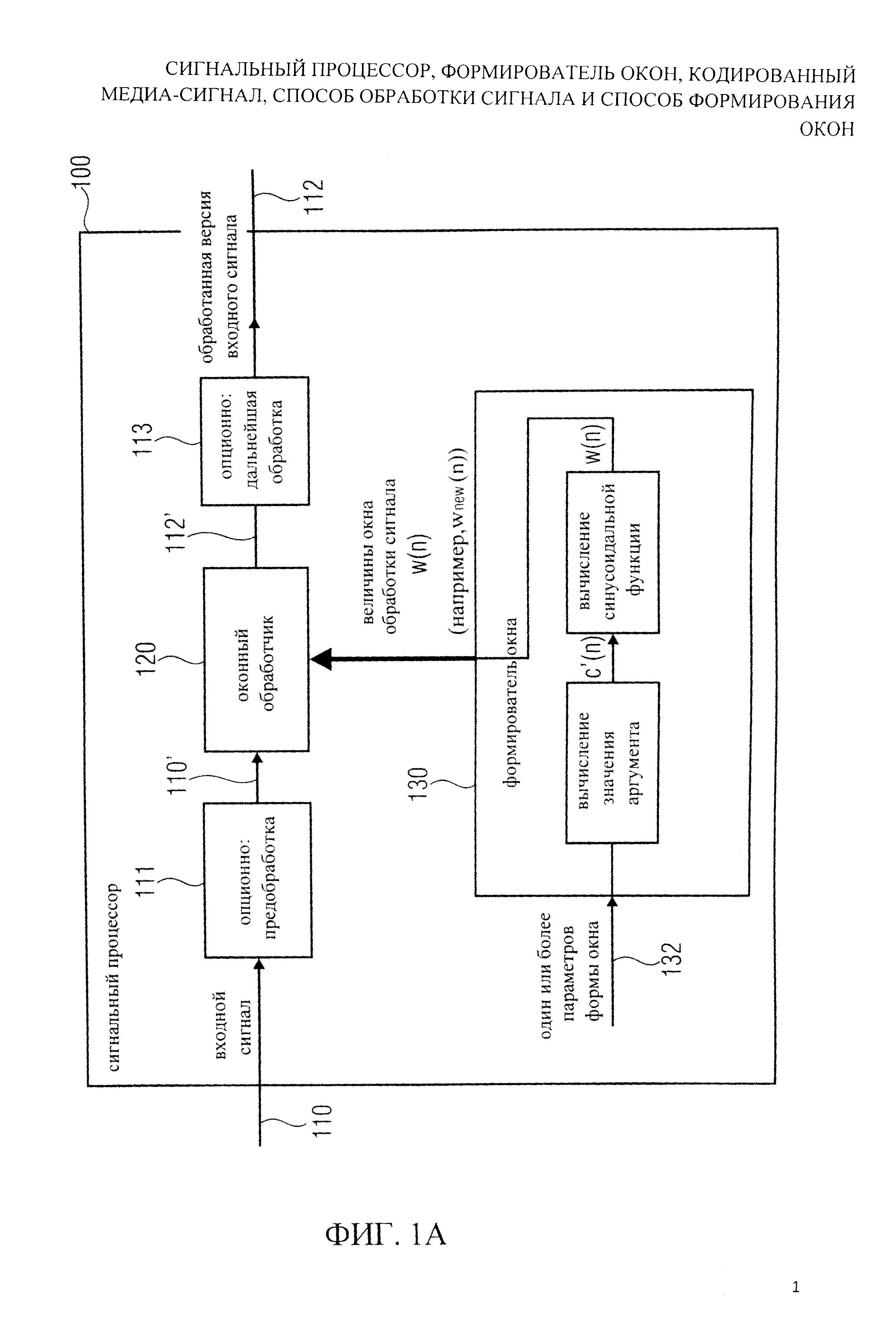
На фиг.1 показана блок-схема сигнального процессора 100 согласно первому решению изобретения. Сигнальный процессор 100 выполнен с возможностью получить входной сигнал 110 и обеспечить, на его основе, обработанную версию 112 входного сигнала. Сигнальный процессор 100 включает оконный обработчик 120, формирующий часть входного сигнала, или его предварительно обработанной версии 110' (которая может быть получена дополнительной предварительной обработкой 111) в зависимости от окна обработки сигнала, описанного весовыми величинами окна обработки сигнала 122 для множества значений индекса n весовых величин окна, чтобы получить обработанную версию 112 входного сигнала (или версию 112' входного сигнала, которая испытывает последующую обработку в дополнительном постпроцессоре 130).
С этой целью оконный обработчик 120 получает величины окна обработки сигнала w(n) от формирователя окна 130, который является, как правило, также частью сигнального процессора 100. Формирователь окна 130 выполнен с возможностью обеспечить величины окна обработки сигнала w(n) для множества n значений индекса величин окна в зависимости от одного или более параметров формы окна 132. Формирователь окна выполнен с возможностью вычислить функцию синуса для множества значений аргумента c'(n), ассоциируемых с n значениями индекса величин окна, чтобы получить величины окна обработки сигнала w(n). Формирователь окна 130 также выполнен с возможностью вычислить взвешенную сумму линейного выражения, например, определяемого c(n), которое линейно зависит от значений индекса величин окна n и значения функции одной или более функций формы. Одна или более функций формы отображают значения индекса величин окна n на соответствующие значения функции. Одна или более функций формы симметричны относительно центра огибающей окна. Вычисление взвешенной суммы выполняется, чтобы получить величины аргумента c'(n).
Соответственно, формирователь окна 130 обеспечивает, величины окна обработки сигнала w(n), которые описывают окна, имеющие особенно хорошие характеристики. Применение вычисления функции синуса в формирователе окна, чтобы получить величины окна обработки сигнала w(n), позволяет получать окна, у которых есть хорошие характеристики сохранения энергии для случая перекрытия двух соответствующих огибающих окна. Кроме того, с использованием значений аргумента c'(n) при вычислении функции синуса, которая не является линейной функцией значений индекса величин окна (также кратко определяемых как ʺзначения индексаʺ), а скорее суперпозиции линейного выражения, которое линейно зависит от значений индекса и значений функции одной или более функций формы, которые являются нелинейными и симметричными относительно центра огибающей окна возможно подстроить форму окна обработки сигнала, описанного величинами окна обработки сигнала w(n).
Например, возможно приспособить вклады одного или более функций формы в значения аргумента c'(n) так, что различные изменения значения аргумента (как функции значения индекса n) могут быть получены в зависимости от одного или большего количества параметров формы окна 132. Соответственно, характеристики окна обработки сигнала, описанные величинами окна обработки сигнала, могут быть приспособлены к особым потребностям в зависимости от одного или большего количества параметров формы окна 132. Кроме того было найдено, что выбор одной или более функций формы, которые являются симметричными относительно центра огибающей окна, помогает гарантировать хорошее сохранение энергии и характеристики уплотнения окна обработки сигнала и также обеспечивает шанс уменьшить вычислительные затраты для того, чтобы вычислить значения аргумента.
Детали относительно вычисления величин окна обработки сигнала wnew(n), которые могут иметь место для вычисления величин окна обработки сигнала wnew(n), будут описаны ниже.
2. Сигнальный процессор согласно фиг.1b
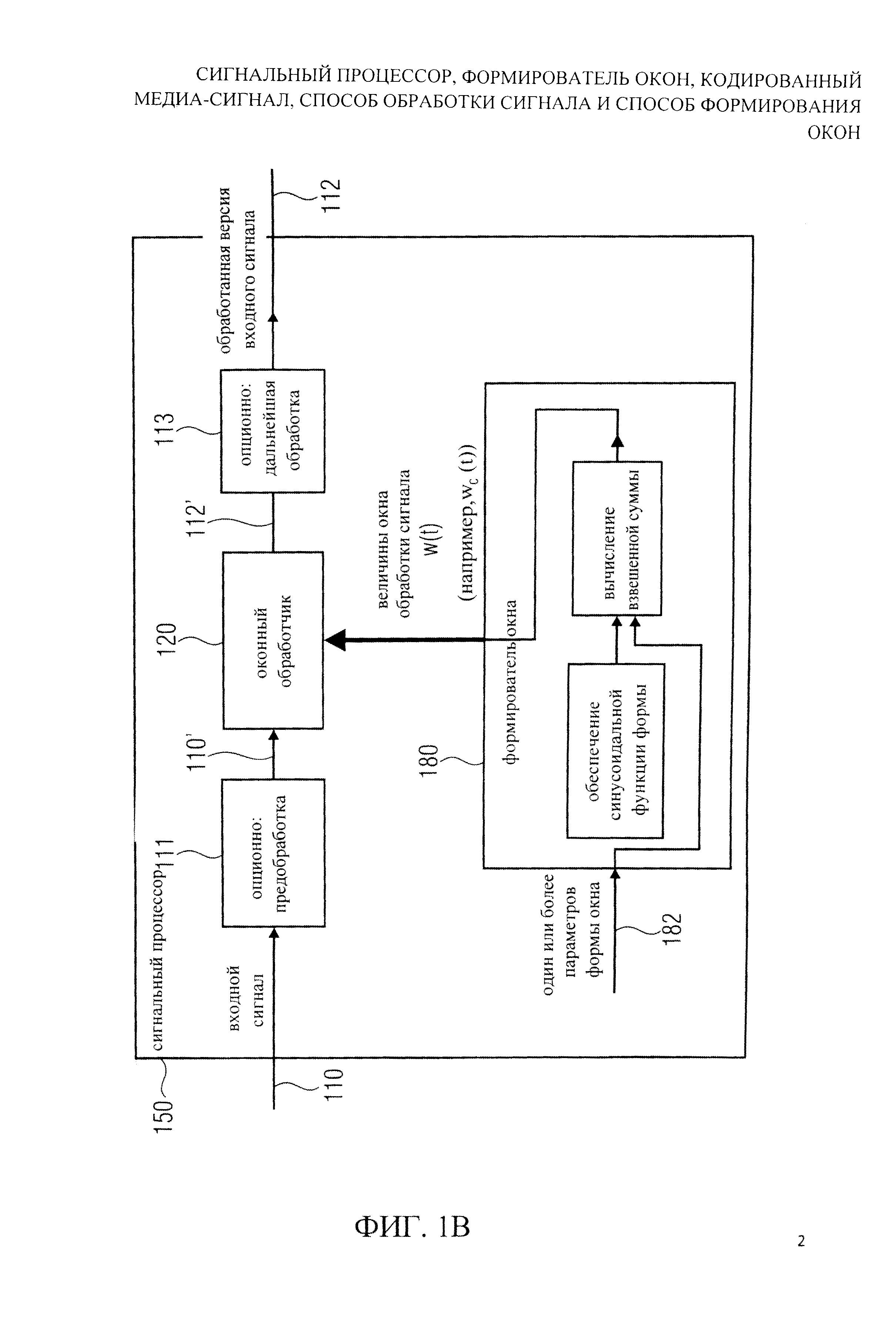
На фиг.1b показана блок-схема сигнального процессора 150, который подобен сигнальному процессору 100. Соответственно, идентичные средства и сигналы определяются идентичными справочными цифрами. Однако сигнальный процессор 150 включает формирователь окна 180, который отличается от формирователя окна 130. Формирователь окна 180 получает один или более параметров формы ck' 182 и обеспечивает на их основе, величины окна обработки сигнала w(t), которые определяются, например, как wc(t). Здесь надо отметить, что переменная t является значением индекса величины окна и также кратко определяется как ʺзначение индексаʺ.
Формирователь окна 180 выполнен с возможностью обеспечить величины окна обработки сигнала w(t) на множестве t значений индекса величин окна в зависимости от одного или более параметров формы окна ck. Формирователь окна 180 выполнен с возможностью вычислить взвешенную сумму значений функции множества синусоидальных функций формы, которые отображают значения индекса величин окна на соответствующие значения функции, чтобы получить величины окна обработки сигнала w(t). Весовой коэффициент величин функции определен параметрами формы окна ck.
Обеспечивая величины окна обработки сигнала с использованием формирователя окна 180 величин окна обработки сигнала, могут быть сформированы так, что они во многих случаях имеют достаточно хорошие характеристики. Кроме того, возможно приспособить определенные характеристики, используя один или более параметров формы окна ck так, что различные окна обработки сигнала доступны для различного выбора одного или более параметров формы окна.
Как будет обсуждено подробно ниже, при помощи синусоидальных функций формы и формирования взвешенной суммы значений функции указанных синусоидальных весовых функций получены окна, имеющие хорошие характеристики.
Кроме того необходимо отметить, что детали относительно вычисления величин окна обработки сигнала w(t), которые обеспечены формирователем окна 180, будут обсуждены ниже.
3. Сигнальный процессор согласно фиг.2.
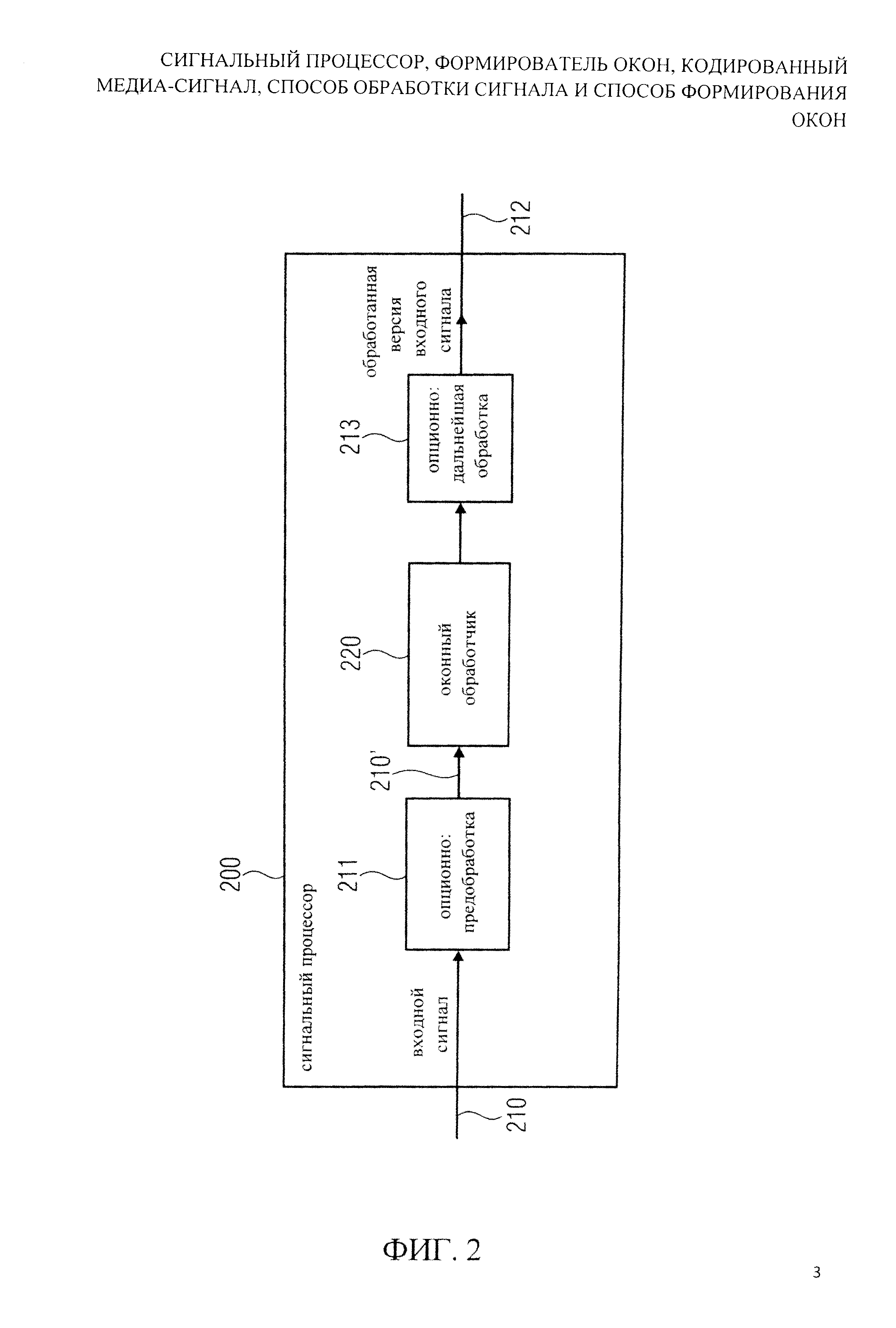
На фиг.2 показана блок-схема сигнального процессора 200 согласно решению изобретения. Сигнальный процессор 200 выполнен с возможностью получить входной сигнал 210 и обеспечить на его основе обработанную версию 212 входного сигнала.
Сигнальный процессор 200 включает оконный обработчик 220, формирующий часть входного сигнала 210, или его предварительно обработанной версии 210, в зависимости от окна обработки сигнала, описанного величинами окна обработки сигнала для множества значений индекса величин окна (кратко определяемых как ʺзначения индексаʺ), чтобы получить обработанную версию 212 входного сигнала. Процессор 200 сигнала может включать дополнительную предварительную обработку 211 и дополнительную последующую обработку 213.
Величины окна обработки сигнала являются значениями результата вычисления синусоидальных функций для множества значений аргумента, связанных со значениями индекса величин окна, где значениями аргумента являются взвешенные суммы линейного выражения, которое линейно зависит от значений индекса величин окна и значений функции одной или более синусоидальной функций формы, где одна или более синусоидальные функции формы отображают значения индекса величин окна на соответствующие значения функции. Одна или более синусоидальных функций формы симметричны относительно центра огибающей окна.
Оконный обработчик 220 может, следовательно, выполнить оконную обработку, которая очень подобна оконной обработке, выполняемой оконным обработчиком 120. Например, величины окна обработки сигнала, используемые оконным обработчиком 220, могут быть идентичны величинам окна обработки сигнала, используемым оконным обработчиком 120. Величины окна обработки сигнала, используемые оконным обработчиком 220, могут, например, быть сохранены в справочной таблице или могут быть получены иначе.
В альтернативных решениях могут использоваться различные величины окна обработки сигнала. В альтернативном решении величины окна обработки сигнала, являются значениями функции результата взвешенного суммирования значений множества синусоидальных функций формы, которые отображают значения индекса величин окна на соответствующие значения функции.
Наконец, оконный обработчик 220 может быть, например, выполнен с возможностью применения окна, описанного величинами окна обработки сигнала wnew(n) к входному сигналу 210, или его предварительно обработанной версии 211'. Альтернативно, однако, в оконном обработчике 220 к входному сигналу 210 или его предварительно обработанной версии 210' могут применяться величины окна обработки сигнала wc(t).
Детали относительно окон обработки сигнала, используемых оконным обработчиком 220 описаны ниже.
4. Формирователь окна согласно фиг.3
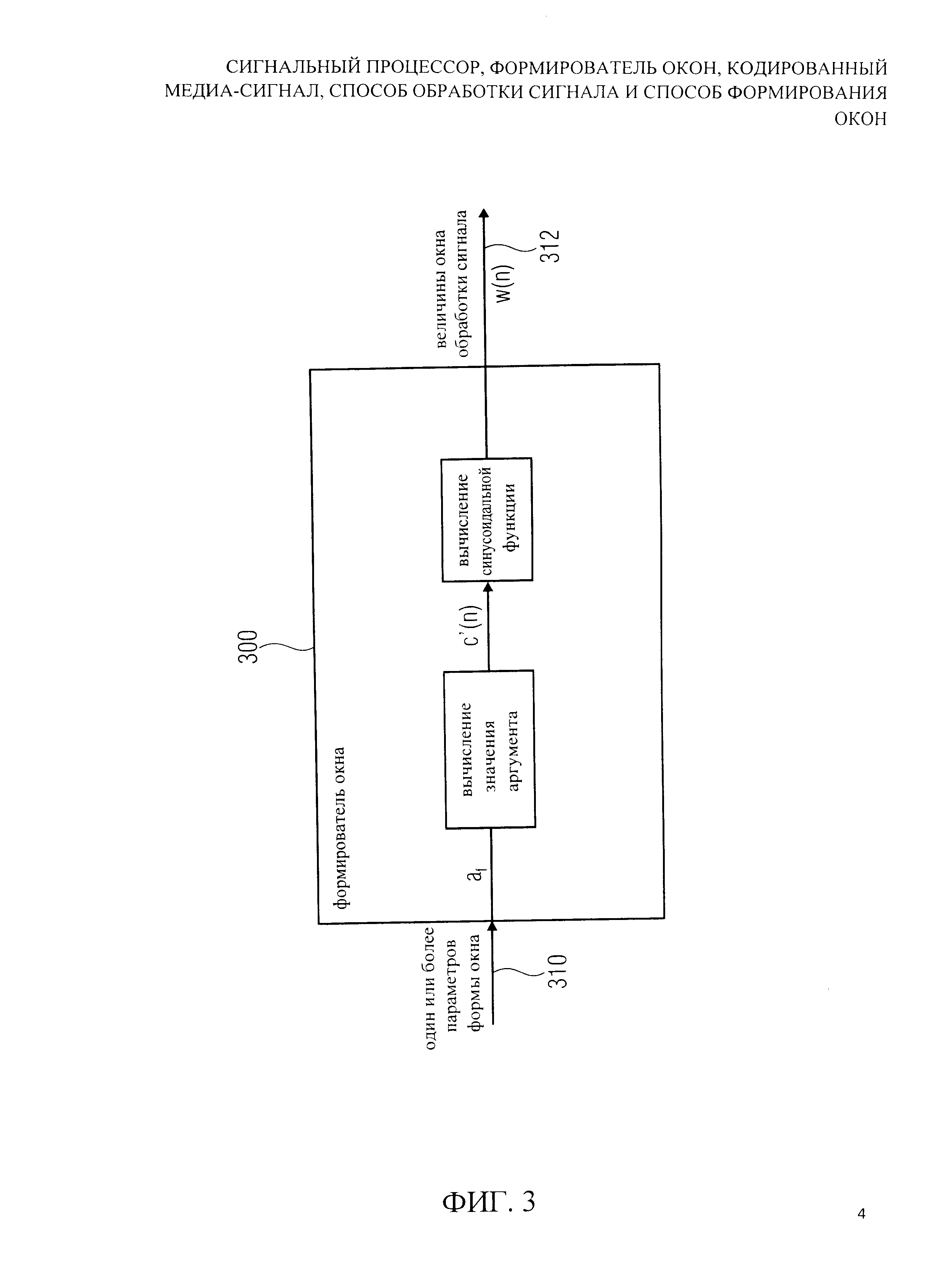
На фиг.3 показана блок-схема формирователя окна 300 согласно решению изобретения. Формирователь окна 300 выполнен с возможностью получить один или более параметров формы окна 310, которые типично являются переменными величинами, и обеспечить, их основе, ряд величин окна обработки сигнала w(n) 312 для множества значений индекса величин окна. Формирователь окна 300 выполнен с возможностью вычислить функцию синуса для множества значений аргумента, связанных со значениями индекса величин окна, чтобы получить величины окна обработки сигнала w(n). Формирователь окна также выполнен с возможностью вычислить взвешенную сумму линейного выражения, иногда определяемого c(n), которое линейно зависит от n значения индекса величины окна и значений функции одной или более функций формы. Одна или более функции формы отображают значения индекса величин окна n на соответствующие значения функции. Одна или более функции формирования симметричны относительно центра огибающей окна.
Соответственно, формирователь окна 300 по существу имеет функциональность формирователя окна 130. Однако, необходимо отметить, что формирователь окна 300 может быть компонентом, который независим от оконного обработчика 130. Альтернативно, однако, формирователь окна 300 может иметь функциональность формирователя окна 180.
5. Кодируемый медиа-сигнал согласно фиг.4
Далее будет описан кодируемый медиа-сигнал. Схематическое представление такого кодируемого медиа-сигнала представлено на фиг.4. Кодированный медиа-сигнал 400 включает кодированное представление мультимедийного контента и параметров формы окна. Сформированные параметры окна, например, приспособлены, чтобы служить одним или более числом параметров формы окна 132 для формирователя окна 130 или служить одним или более числом параметров формы окна 132 для формирователя окна 180. Соответственно, параметры формы окна в закодированном медиа-сигнале 400 выбраны так, чтобы создать величины окна обработки сигнала w(n) или w(t), используя формирователь окна 130 или формирователь окна 180. Кроме того, закодированное представление мультимедийного контента, как правило, кодируется, используя обработку в соответствии с окном, описанным параметрами формы окна.
6. Детали относительно окон, обеспеченных формирователем окна 130 или используемых оконным обработчиком 220
6.1 Краткий обзор и определения
Далее будут описаны некоторые детали относительно окон, обеспеченных формирователем окна 130, эти окна могут также использоваться оконным обработчиком 220. Здесь необходимо отметить, что окна определены здесь величинами окна обработки сигнала w(n). Указанные величины окна обработки сигнала w(n), как правило перемножаются с входным сигналом 110 или его предварительно обработанной версией 110', чтобы получить обработанную окном версию входного сигнала, или его предварительно обработанной версии 110'. Окно, как правило, описывается величинами окна обработки сигнала w(n), где n - значение индекса (например, значения индекса времени) величины окна сигнального процессора.
Кроме того, необходимо отметить, что окно, как правило, включает склон слева окна и склон справа окна. Окно далее возможно может включать постоянную (или приблизительно постоянную) центральную часть так, что ряд величин центральной части окна обработки сигнала имеют общее предопределенное значение. Однако необходимо отметить, что склон слева окна и склон справа окна могут отличаться. Соответственно, необходимо указать, что следующее обсуждение существенно описывает форму одного склона окна, то есть перехода между маленькой величиной окна (например, нулевой величиной окна) и большой величиной окна (например, максимальной величиной окна).
На фиг.16 показано схематическое представление окна, которое будет объяснено более подробно в графическом представлении на фиг.16, где абсцисса 1610 описывает значение индекса n и ордината 1612 описывает величины окна обработки сигнала w(n), связанные со значением индекса n. Как видно, окно 1600 включает левую часть окна 1620 и правую часть окна 1622. Левая часть окна включает, как основной элемент, левый склон окна 1630. Левый склон окна 1630 определен, например, множеством величин окна обработки сигнала w(n) со значением n=n1 до n=n2. Левая часть окна 1620 может, опционно, также включить левую внешнюю часть, в которой величины окна обработки сигнала w(n) имеют малое значение, например, w(n)=0. Левая часть окна опционно также включает часть центральной части окна в которой величины окна обработки сигнала w(n) имеют предопределенное значение, например, w(n)=1. Окно 1600 включает правую часть окна 1622, которая включает, как основной элемент, правый склон окна 1640. Правая часть окна может опционно включать часть центральной части окна, в которой величины окна обработки сигнала имеют предопределенное значение, например, w(n)=1. Правая часть окна может также, опционно, включать правую внешнюю часть, в которой величины окна обработки сигнала w(n) имеют малое значение, например, w(n)=0.
Необходимо отметить, что левую внешнюю часть, центральную часть окна и правую внешнюю часть окна надо рассматривать как дополнительные части. Кроме того, необходимо отметить, что окно 1600 может быть симметричным или асимметричным. Таким образом, левый склон окна 1630 и правый склон окна 1640 могут быть одинаковы, или могут существенно отличаться в некоторых решениях.
Здесь необходимо отметить, что следующее обсуждение существенно касается левого склона окна 1630, то есть к переходу между малыми или нулевыми величинами окна и большими или максимальными величинами окна. Однако необходимо отметить, что полное окно 1600 может быть получено из знания левого склона окна 1630 с опционно добавленной левой внешней частью и опционно добавленной центральной частью окна и с добавленным правым склоном окна и опционно добавленной правой внешней частью окна. Необходимо также отметить, что правый склон окна 1640 может быть получен таким же образом как и левый склон окна с использованием простого процесса зеркального отражения, такого как процесс, описываемый уравнением (3).
Здесь необходимо отметить, что в соответствии с дальнейшим обсуждением, левый склон окна должен быть описан величинами w(n) для n в диапазоне от n=0 до n=N/2-1. Однако, использование различных значений индекса естественно возможно.
6.2 Детали окна wnew(n).
Решения согласно изобретению мотивированы нехваткой гибких и в вычислительном отношении эффективных функций окна для решений MDCT, объявляя расширение к синусоидальным функциям окна уравнения (4).
Отметьте, что уравнение (4) можно рассмотреть как синус треугольной функции окна, симметричной относительно n=N/2-1/2. В уравнении (3) подразумевается
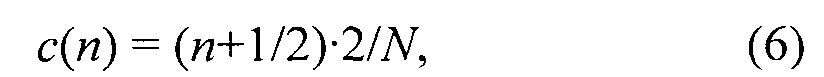
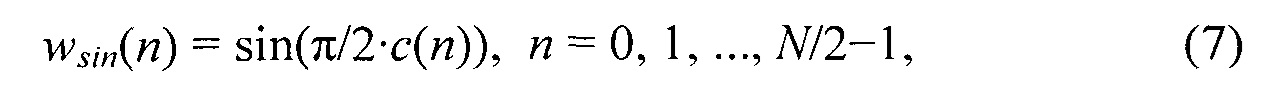
где c(n) обозначает функцию ядра окна, которая может быть вычислена заранее, так как она предопределена. Предложенное расширение необходимо добавить к c(n) в уравнении взвешенных синусоид (7), имеющих угловые частоты, которые являются произведениями целого на 2π:
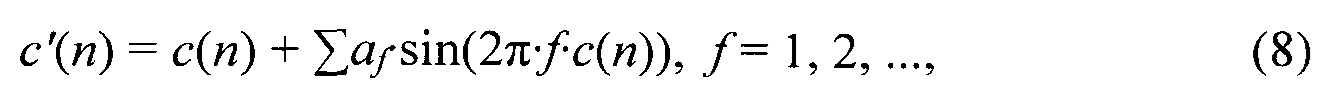
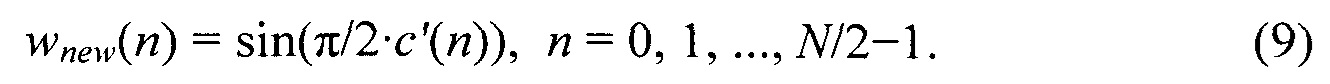
Выражения синуса от c'(n) могут также быть вычислены заранее. Только их вес, определенный коэффициентами af должен быть подстроен. Следовательно, адаптируя (подстраивая) предложенное окно к сигналу на основе преобразования путем преобразования, только уравнение (9) и вес в уравнении (8) должны быть вычислены повторно, что делает эту адаптацию в вычислительном отношении менее сложной, чем для окон Сина-Феррейры и KBD.
Кроме того, стоит упомянуть, что, из-за синусоидальных слагаемых в уравнениях (8) и (9), каждая реализация предложенного класса функций окна полностью сходится к нолю в его конечных точках, что гарантирует уменьшение уровня бокового лепестка по крайней мере на 12 дБ за октаву на частотной характеристике окна. Дело обстоит не так с окном KBD и окнами, предложенными в статье Принсена и Брэдли, ʺAnalysis/SynthesisFilterBankDesignBasedonTimeDomainAliasingCancellation,ʺ IEEETrans. Acoustics, Speech, and Signal Processing, Oct. 1986, pp. 1153-1161 и в статье Феррейры ʺConvolutional Effects in Transform Coding with TDAC: An Optimal Window,ʺ IEEE Trans. Speech and Audio Processing, Mar. 1996, pp. 104-114, где боковые лепестки затухают меньше, чем в 12 дБ за октаву. Для равных главных ширин лепестка это означает, что окно согласно уравнениям (8) и (9) потенциально выигрывает у разработанных ранее в технике окон с точки зрения ослабления бокового лепестка.
Вычисление или адаптация окна согласно данному изобретению включают следующие шаги:
- Выбор ряда слагаемых синусоидальных функций в выражении для c'(n) и соответствующих весовых коэффициентов af основанных на конструктивных соображениях.
- Определение или задание длины окна N и вычисление c'(n) с выбранными аf и рядом слагаемых синусоидальных функций.
- Вычисление wnew(n) в уравнении (9) для n=0, 1…, N/2-1, затем использование уравнения (3), чтобы получить окно длины N.
- Если используется различная параметризация окна для предыдущего и текущего сегментов, удовлетворение любого необходимого ограничения на преобразование путем исправления правой половины окна предыдущего сегмента, или исправления левой половины окна текущего сегмента, или исправления правой половины предыдущего и левой половины окна текущего сегмента.
В предпочтительном решении) относительно вычислительной сложности предложенная функция окна сопоставима с синусоидальным окном и окном Ворбиса (Vorbis), но при этом она обеспечивает, по крайней мере, гибкость дизайна, характерную для окон Сина-Феррейры и KBD.
Относительно вышеупомянутого необходимо отметить, что величины c'(n) можно рассматривать как значения аргумента, связанные с индексами n величин окна. Кроме того, необходимо отметить, что функции sin(2π⋅f⋅c(n)) можно рассматривать как функции формы.
Кроме того, необходимо отметить, что нет необходимости использовать функции синуса в качестве функций формы. Скорее может быть достаточно выбрать функции формы, таким образом, что функции формы будут симметричны относительно центра огибающей окна. Центр огибающей окна определен, например, значением линейного выражения c(n)=0.5. Например, симметричные многочленные функции могут использоваться вместо функций синуса, что может облегчить вычисления в некоторых случаях. Кроме того, функции формы должны предпочтительно иметь значение, которое является достаточно близким к нолю для c(n)=0 и c(n)=1, то есть при крайнем левом значении индекса величины огибающей окна и в крайнем правым значении индекса величины огибающей окна. Другими словами, функции формы должны иметь ноли или должны иметь приблизительно нулевые значения на границах окна с самым левым значением индекса величины окна (например, n=0) и самым правым значением индекса величины окна (например, n=N/2-1).
Кроме того, необходимо отметить, что уравнения (6) и (7) могут быть вычислены, например, путем вычисления значения аргумента в формирователе окна 130, и что уравнение (9) может быть вычислено путем вычисления функции синуса в формирователе окна 130. Соответственно, значения wnew(n), полученные вычислением функции синуса в формирователе окна 130 для n в диапазоне от n=0 до n=N/2-1 могут описать, например, левый склон окна 1630.
Следовательно, формирователь окна 130 может быть выполнен с возможностью собрать все окно 1610 на основе указанных величин окна обработки сигнала связанных с левым склоном окна. С этой целью формирователь окна может добавить левую внешнюю часть, центральную часть окна, правый склон окна и внешнюю правую часть окна, как показано на фиг.16. Для случая симметричного окна правый склон окна может быть получен отражением левого склона окна. Альтернативно, однако, правый склон окна может отличаться от левого склона окна и может быть получен отражением склона окна, полученного для параметров формы окна отличных от параметров левого склона окна.
Кроме того, необходимо отметить, что процессором сигнала может быть обеспечено устранение разрывов между склоном перехода с правой стороны, связанным с предыдущем сегментом входного сигнала, и склоном перехода с левой стороны, связанным с последующим сегментом входного сигнала. С этой целью левый склон окна, связанный с последующим сегментом входного сигнала, может быть получен, используя те же самые параметры, которые были применены для того, чтобы получить правый склон окна, связанный с предыдущим сегментом входного сигнала.
Кроме того, необходимо отметить, что алгоритм, определенный уравнениями (6), (8) и (9) подходит для онлайн вычисления функций окна в устройстве, имеющем ограниченную вычислительную мощность.
Однако, окна, определенные в соответствии с уравнениями (6), (8) и (9) могут быть рассчитаны однократно, и результаты расчета могут быть сохранены в справочной таблице для более позднего использования в некоторых решениях.
6.3. Комментарии к дизайну окна.
Далее будут обсуждены некоторые условия, которые приводят к окнам, имеющим особенно хорошие характеристики. Однако, необходимо отметить, что неопределенность обсужденных далее условий нельзя считать существенными.
Как было упомянуто ранее, кодеры сигнала, использующие MDCT, должны наложить определенные условия на функцию окна, относящегося к сигналу, чтобы позволить всей системе быть полностью обратимой, то есть обеспечить совершенную реконструкцию входного сигнала, когда никакие манипуляции с сигналом не выполнены. Функции, соответствующие уравнению (2), представляют подходящую категорию. Любая реализация данного класса окон принадлежит этой категории. Однако, можно показать, что реализация с неотрицательным c'(n) для всех n,
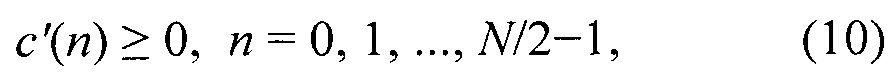
приводит одновременно к особенно хорошей селективности полосы пропускания и заграждения вне полосы пропускания. Дальнейшее обсуждение поэтому сосредоточится на этом подмножестве класса окон. В некоторых случаях только реализация с неотрицательными c'(n) для всех n приводят к удовлетворительной селективности полосы пропускания и заграждения вне полосы пропускания одновременно.
Вообще, в то время как можно использовать произвольное число синусоидальных слагаемых в уравнении (8), чтобы проектировать частотные характеристики окна, приспособленные к данному случаю использования, было обнаружено, что два синусоидальных слагаемых (f=1, 2) обеспечивают соответствующий компромисс между гибкостью, сложностью и использованием памяти. В частности, используя два синусоидальных слагаемых, могут быть получены параметры, которые
- минимизируют ширину главного лепестка, то есть максимизируют частотную селективность,
- минимизируют максимальный уровень бокового лепестка выше определенной нормализованной частоты,
- максимизируют уровень затухания бокового лепестка, то есть ослабления дальней частоты вне полосы пропускания,
- минимизируют максимальное различие данной эталонной реализации окна от всех реализации окна.
Каждое из этих соображений будет исследовано ниже с помощью определенных примеров.
6.3.1 Окна с максимальной селективностью полосы пропускания.
Хотя условие баланса мощности в уравнении (2) ограничивает диапазон достижимых частотных характеристик, особенно относительно ширины и уровня нескольких первых боковых лепестков, функция окна, приводящая к самому узкому главному лепестку, может быть получена, путем установки всех коэффициентов af в выражении для c'(n) в ноль. Получающееся окно, как очевидно, является ААС синусоидальным окном уравнения (4). Его спектр изображен на фиг.5 наряду со спектрами окон KBD (α=4) и Vorbis.
Короче говоря, необходимо отметить, что предпочтительно, чтобы, по крайней мере, один из параметров формы окна af был установлен в ненулевое значение. Однако вышеописанная структура формирователя окна 113 дает гибкость, чтобы получить даже ААС синусоидальное окно без любого особенного сигнала, просто устанавливая параметров формы окнаaf.
6.3.2 Окна с минимальным максимумом бокового лепестка
Конфигурации уравнения (9), которые минимизируют максимальный уровень бокового лепестка, могут быть получены, путем совместной оптимизации параметров af или полным перебором или способом, основанным на градиентных способах поиска. Однако, вследствие уравнения (2), желательно определить более низкую границу частоты Nω0>1.5, выше которой должна быть выполнена минимаксная оптимизация. Было найдено, что значение Nω0=4.5 создает параметры a1=0.1224 и a2=0.00523. Формируемая таким образом функция окна показана на фиг.6. Подобие с AACKBD функцией окна, которая также изображена, очевидно. Соответствующие спектры окна показаны на фиг.7. Стоит отметить более низкий уровень первых двух боковых лепестков предложенного окна по сравнению с окном KBD, так же как сокращение максимального уровня бокового лепестка Nω0≈5 (у первых трех боковых лепестков предложенного окна выше этой частоты есть уровень -66.8 дБ, тогда как окно KBD достигает несколько более высокого уровня -63.0 дБ).
Из-за использования синусоидальных слагаемых в c'(n), каждая реализация существующего класса окна непрерывна и, следовательно, гарантируемо гладко приближается к нолю в его конечных точках. Это преимущество иллюстрировано на фиг.8. Как видно, боковые лепестки ранее полученного окна уменьшаются при на 12 дБ за октаву. Окно KBD, напротив, показывает меньший уровень уменьшения, причиной чего являются небольшие неоднородности в конечных точках весовой функции KBD. В результате с использованием предложенного окна достигается более высокое заграждение, чем с использованием окна KBD выше Nω≈250 даже при том, что оно лучше в диапазоне между Nω≈250 и Nω≈7. В некоторых приложениях анализа или синтеза эта особенность может иметь выгоду.
6.3.3 Окна с максимальным затуханием бокового лепестка
В некоторых случаях может быть желательно использовать окна, боковые лепестки которых затухают при ставках более, чем на 12 дБ за октаву. Данное изобретение учитывает, например, создание окна с затуханием боковых лепестков на 24 дБ за октаву. Это достигнуто требованием непрерывности первого дифференциала весовой функции, то есть исчезающего дифференциала на краях окна. Самое интуитивное решение этой проблемы - конфигурация a1=0.1591, a2=0. Получающаяся частная характеристика окна изображена на фиг.9 рядом с тремя другими характеристиками, которые обсуждены далее.
6.3.4 Окна, приближающиеся к эталонному окну
Чтобы закончить демонстрацию гибкости предложенного класса окон, предпринята попытка создать две реализации окон, которые хорошо напоминают два существующих окна. Из-за их разнообразия в качестве эталонов выбраны функции KBD (α=4) и Сина-Феррейры третьего порядка. Реконструкция через c'(n) и уравнение (9) приближается к эталону в смысле наименьших квадратов, то есть минимизации квадратов разностей между эталоном и приближением (отметьте, что другие способы также возможны). На фиг.9 показан результат. Можно заметить, что предложенные окна почти идентичны своим предшествующим решениям, и что существенные различия происходят только на очень низких уровнях. Поэтому в критичных к сложности или памяти системах эталонные окна могут быть заменены устройством, использующим предложенный класс окон, поддерживая высокую степень обратной совместимости и, если необходимо, возможность почти совершенной реконструкции.
7. Применение системы адаптивной к сигналу
Дополнительное преимущество представленного класса окон возникает, когда система обрабатывает сегменты сигнала с отличающимися длинами, связанными с целыми числами, равными степени числа 2. В ААС, например, эта процедура, также известна как переключение блоков, реализуется применением MDCT (модифицированное дискретное косинусное преобразование) или однажды по 2048 (1920) или 8 раз по 256 (240) семплам за фрейм. Здесь, подмножества отдельных слагаемых в уравнении (8), например n=0, 1…, N/8-1, могут быть снова использованы как функции ядра для окон меньшей длины или, в случае синусоидальных слагаемых, как сами функции окна. Это может использоваться, если приемлема уменьшенная гибкость дизайна для окон малой длины, чтобы далее уменьшить объем памяти, требуемый для того, чтобы сохранить функции ядра.
8. Дальнейшие применения изобретения
Такие как рассмотренные здесь оконные функции со сбалансированной мощностью, могут быть довольно привлекательным для нескольких прикладных сценариев кроме аудио- или видеокодирования. Как отмечено ранее, оконные функции со сбалансированной мощностью могут использоваться при перекрытиях с сохранением мгновенной энергии или при переключении системы, когда устройства анализа сигнала и обработки, работающие на основе техники «блок за блоком» с наложением между последовательными блоками. Более широко говоря, любые устройства, выполняющие задачи фильтрации одно- или многомерного сигнала могут использовать предложенные в данном изобретении окна при построении ядра (ер) фильтрования, включая, но не ограничиваясь,
- фильтры высоких частот (дифференцирование), фильтры низких частот (интеграция) и полосовые фильтры,
- уменьшители частоты выборки (децимальные фильтры) и увеличители частоты выборки (фильтры интерполяции),
- одно- или многополосные эквалайзеры, компрессоры, расширители и ограничители,
- алгоритмы для шумоподавления и связанного улучшения или инструменты эффектов.
Принимая в таких системах представленную здесь предлагаемую функцию окна и подстраивая ее спектральные характеристики к эксплуатационным характеристикам, предпочтительно в адаптивной к сигналу сегмента манере, можно надеяться, что может быть достигнуто улучшение восприятия.
9. Кодирующее устройство медиа-сигнала декодер медиа-сигнала согласно фиг.10.
На фиг.10 показана блок-схема устройства, кодирующего медиа-сигнал (кодер медиа-сигнала) и декодера медиа-сигнала. Кодер медиа-сигнала 1010 выполнен с возможностью получить один или более канальных сигналов от s1(n) до sM(n) и обеспечить, на их основе закодированное представление. Закодированное представление входных медиа-сигналов может иметь форму коэффициентов MDCT от S1(k) до SM(k) или может быть закодированным представлением таких коэффициентов MDCT. Кодер сигнала 1010 включает, например, множество идентичных путей обработки сигнала 1012a-1012m, которые могут работать независимо или которые могут быть соединены. Кроме того, кодер сигнала 1010 также включает вычислитель параметров кодирования 602, который определяет один или более параметров кодирования, таких как, например, размер блока, параметр сглаживания переходных шумов во временной области (TNS), параметр компенсации передачи полосы частот, информацию о конфигурации и/или о физико-акустической модели. Далее будут обсужден путь обработки сигнала 1012a, но это обсуждение также применимо к другим путям обработки сигнала, например, к пути обработки сигнала 1012m.
Путь обработки сигнала 1012a включает обнаружитель окна 603, который получает входной сигнал s1(n) соответствующего канала и информацию о параметрах кодирования от определителя параметров кодирования 602. Обнаружитель окна 603 может предоставить, например, информацию о форме окна 603а, которая описывает форму желаемого окна.
Информация о форме окна может, например, быть определена из входного сигнала обнаружителя окна 603 таким образом, чтобы объективная работа (кодированный коэффициент передачи, частотная селективность или энергетическое уплотнение, сжатие данных, количество введенного совмещения) или субъективная работа (перцепционное качество выходного кода после безошибочной или ошибочной передачи и декодирования) кодирующего устройства 1010 были оптимизированы или улучшены.
Путь 1012а также включает синхронизатор окна 604, который необходимо рассматривать как дополнительный, и который может объединить информацию о форме окна, предоставленную обнаружением окна 603 из пути 1012а с информацией о форме окна, предоставленной обнаружителями окна различных путей. Соответственно, синхронизированная информация о форме окна 604а может быть, как опция, предоставлена синхронизатором окна 604. Путь прохождения сигнала 1012а также включает формирователь совершенной реконструкции 605, который выполнен с возможностью получить информацию о форме окна 603 а или синхронизированную информацию о форме окна 604а, и обеспечить на их основе приспособленную информацию о форме окна 605а. Например, формирователь совершенной реконструкции 605 может гарантировать, что склон перехода правой стороны окна (также определяемый как склон окна), связанного с предыдущей частью входного сигнала, является зеркальным вариантом огибающей окна, связанного с последующей частью входного сигнала. Например, может быть обеспечено такое окно, что склоны окон, связанных с последующими частями входного сигнала, определены идентичными параметрами формы окна. Путь обработки сигнала 1012а также включает вычислитель окна 606, который выполнен с возможностью обеспечить величины окна обработки сигнала w1(n) для оконного обработчика 1014. Оконный обработчик 1014 выполнен с возможностью умножить семплы входного сигнала s1(n) на соответствующие величины окна обработки сигнала w1(n), чтобы получить обработанный окном сигнал , который поступает в модифицированный дискретный косинусный преобразователь 607, чтобы получить MDCT коэффициенты S1(k).
Здесь необходимо отметить, что вычислитель окна 606 может иметь функциональность формирователя окна 130 или формирователя окна 180, так что величины окна обработки сигнала w1(n), эквивалентны величинам окна обработки сигнала w(n), или величинам окна обработки сигнала w(t). Кроме того, оконный обработчик 1014 может иметь функциональность оконного обработчика 120.
Соответственно, кодер 1010 выполнен с возможностью применить множество различных окон для обработки входного сигнала s1(n) в зависимости от приспособленных параметров формы окна 605а, где вычислитель окна 606 обеспечивает сигнал, обрабатывающий величины окна.
Кодер 1010 может произвольно включать дальнейшие стадии кодирования для того, чтобы эффективно закодировать спектральные величины от S1(k) до SM(k), обеспеченные модифицированным дискретным косинусным преобразователем 607.
Декодер сигнала 1020 выполнен с возможностью получить декодированные спектральные величины от Q1(k) до QM(k). Декодированные спектральные величины от Q1(k) до QM(k) могут быть извлечены из битового потока, который может быть обеспечен кодером 1010, кодирующим спектральные величины от S1(k) до SM(k). Другими словами декодированные спектральные величины от Q1(k) до QM(k) могут быть идентичным, за исключением ошибок квантизации, спектральным величинам от S1(k) до SM(k). Здесь, k - индекс частоты, и M≥1 определяет число каналов (где одному пути предоставлен канал).
Декодер 1020 также выполнен с возможностью получить значения длины окна от N1 до NM (которые являются функцией от N как описано выше), и один или более параметров формы окна от a1 до aM (например, один на путь или канал). Декодер 1020 включает обратный модифицированный дискретный косинусный преобразователь 608, который выполнен с возможностью получить декодированные спектральные величины от Q1(k) до QM(k) и обеспечить на их основе сигналы обратного преобразования от q1(n) до qM(n). Декодер 1020 также включает выборщик окна 609, который работает в сочетании с формирователем совершенной реконструкции 605, чтобы получить приспособленные параметры формы окна 605а из входных параметров формы окна от a1 до aM, где входные параметры формы окна от a1 до aM могут быть извлечены или получены из битового потока представляющего мультимедийный контент. Например, и входные параметры формы окна от a1 до aM и декодированные спектральные величины от Q1(k) до QM(k) могут быть представлен в кодируемом медиа-сигнале.
Декодер 1020 далее включает вычислитель окна 606, который получает приспособленные параметры формы окна 605а (или, альтернативно, входные параметры формы окна от a1 до aM), и обеспечивает на их основе величины окна обработки сигнала от w1(n) до wM(n). Вычислитель окна 606 может иметь функциональность формирователя окна 130 или формирователя окна 180, где приспособленные параметры формы окна 605а могут соответствовать одному или более числу параметров формы окна 132 или к одному или более числу параметров формы окна 182. Аналогично, величины окна обработки сигнала от w1(n) до wM(n) могут быть эквивалентны величинам окна обработки сигнала w(n), или величинам окна обработки сигнала w(t).
Соответственно, вычислитель окна 606 может обеспечить окна различных форм в соответствии с приспособленными параметрами формы окна 605а, или входные параметры формы окна от a1 до aM.
Величины окна обработки сигнала от w1(n) до wM(n), обеспеченные вычислителем окна 606 из декодера 1020, могут быть использованы, например, путем операции умножения, выполняемой умножителем 1024, с сигналами обратного преобразования от q1(n) до qM(n), обеспеченными обратным модифицированным дискретным косинусным преобразователем 608, чтобы получить обработанную окном версию от до величин от q1(n) до qM(n).
Декодер 1020 далее включает блок добавления и перекрытия 610, который выполнен с возможностью получить последовательность обработанных окном версий от до сигналов обратного преобразования от q1(n) до qM(n), добавить с перекрытиями указанные обработанные окном версии последовательности, чтобы получить восстановленные сигналы от y1(n) до yM(n). Работа блока добавления и перекрытия 610 предпочтительно скоординирована с оконным обработчиком 1024 таким образом, что последовательность обработанных окном версий от до , которая перекрыта в блоке добавления и перекрытия 610, обработана ʺкомплементарнымиʺ окнами так, что правый склон первого окна накладывается на левый склон последующего окна, где накладывающиеся склоны окна обеспечивают обсужденные выше сохранение энергии и/или совершенную реконструкцию входного сигнала.
Таким образом, кодер 1010 и декодер 1020 выполнены с возможностью кодирования и декодирования медиа-сигналов, таких как, например, аудиосигналы, речевые сигналы, видеосигналы, сигналы изображения, и т.д.
Наконец, вышеупомянутые решения согласно данному изобретению могут быть осуществлены с использованием программного обеспечения, аппаратурных модулей и цифровых сигнальных процессоров (DSP) для различных видов аналоговых или цифровых систем хранения или передачи сигналов.
Чтобы подвести итог, на фиг.10 иллюстрируется, как предложенная техника оконной обработки может использоваться в адаптивном к сигналу подобном ААС аудио кодере-декодере или другом типе устройства кодера или декодера сигнала. Функции ядра окна 601 для построения c'(n) сохранены в памяти наряду с определением доступных конфигураций параметров. Эти данные разделены между кодером и декодером. Для каждого фрейма сегменты показанного на фиг.10а кодера 1010 образуют M входных каналов, и для каждого из M сегментов s(n) данные от спектрально-временной физико-акустической модели 602, анализируются в обнаружителе окна 603, чтобы определить подходящую форму окна и если необходимо длину и номер. Соответствующее окно выбирается на основе критериев, таких как частотная селективность (энергетическая компактность), или низкое перекрытие фреймов (устранение алиасинга, используя TNS или компенсацию передачи в полосе частот (SB)).
Другими словами, кодер 1010 (или любой другой сигнальный процессор) может быть выполнен с возможностью определения изменение или подстройку одного или более параметров формы окна af, адаптивных к сигналу способом так, что объективная работа или субъективная работа сигнального процессора оптимизируются или улучшаются. Соответственно, один или более параметров формы окна могут быть изменены или подстроены способом адаптивным к входному сигналу, таким образом, что объективная (то есть числовая) или субъективная (то есть перцепционная) работа сигнального процессора (например, аудиокодирующего устройства 1010) оптимизируется или улучшается.
После обеспечения дополнительного соответствия параметров формы окна для каналов с использованием синхронизатора окна 604, совершенная реконструкция (PR) выполненных преобразований с использованием выбранных функций окна обеспечивается формирователем совершенной реконструкции 605 путем подстройки параметров накладывающихся половин окон текущего и предыдущего фрейма. Основанные на подстроенных параметрах формы окна с использованием уравнений (8) и (9) фактические коэффициенты, определенные в вычислителе окна 606, перемножаются с соответствующим аудио сегментом, формируя обработанный окном сегмент s'(n), который, наконец, преобразуется в частотную область путем MDCT 607 для последующей квантизации, кодирования и передачи. В декодере 1020, показанном на фиг.10b, полученные параметры формы окна для каждого фрейма и канала декодируются и подаются на выборщик окна 609, который отображает их на соответствующую конфигурацию окна для использования после обратного MDCT 608 от деквантизированных спектров Q(k). После осуществления совершенной реконструкции (PR) оконных последовательностей и вычисления коэффициентов окна, аналогично кодирующему устройству, выходные сегменты q(n) следующие из обратного MDCT являются обработанными окном, и с использованием блока добавления и перекрытия 610 восстанавливаются отдельные сигналы канала y(n).
10. Альтернативное вычисление окна
10.1. Краткий обзор по вычислению функции окна из альтернативного класса окон
Далее будет описан альтернативный класс функций окон, который может использоваться формирователем окна (например, формирователем окна 180 или формирователем окна 300 или вычислителем окна 606) для того, чтобы обеспечить величины окна обработки сигнала.
Другими словами, далее будут даны детали относительно определения альтернативного класса окон, которые основаны на существенной модификации некоторых вышеупомянутых уравнений.
В одном из предыдущих разделов было отмечено, что уравнение (12) с a=2, так что w2(t) эквивалентно уравнению (15) с K=1, b0=0.5, b1=0.5. Кроме того, была установлена эквивалентность между w4(t) и (15) с K=2 and bk из (16). Было установлено, что bk формируют w1(t), w3(t), или в более общем случае любой wa(t) с нечетным a. Из уравнений (12) и (15) было найдено, что невозможно построить окно в виде суммы косинусов, которое эквивалентно синусоидальному окну в нечетной степени. Однако в некоторых решениях, где требуются wa(t) с нечетным a, может быть желательно использовать формулировку, подобную уравнению (15), чтобы учесть спектральную оптимизацию смещения, как выполнено Хеммингом, Блекманом и Натталом.
Было найдено, что сумма синусов
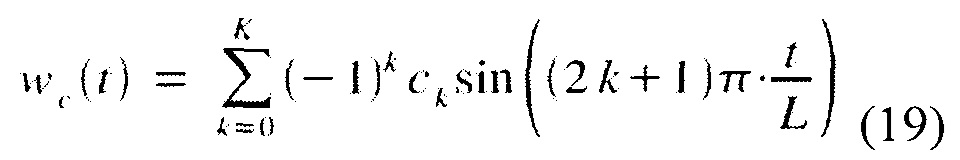
обеспечивает необходимые средства для оптимизации. Как видно, величины окна обработки сигнала wc(t) могут быть получены формированием взвешенной суммы синусоидальных функций формы sin((2k+1)π⋅t/L). Склон окна сигнала может быть получен для значений t между 0 и L/2.
Необходимо также отметить, что предпочтительно, чтобы суммировались функции синуса, частоты которых являются произведениями фундаментальной частоты на нечетное число. Например, нормализованные угловые частоты могут быть определены как (2k+1)π/L. Можно заметить, что вышеприведенные нормализованные частоты являются произведением фундаментальной нормализованной частоты π/L на нечетное число.
Необходимо также отметить, что функции формы переменно нагружены с положительными и отрицательными весами (-1)kck с увеличивающимся индексом частоты k (для k между нолем, и максимальным значением индекса частоты K).
Выбирая константы ck соответствующим образом, могут быть достигнуты две возможности.
Во-первых, может быть построено окно, соответствующее окну синуса в нечетной степени (2). Здесь должны быть определены значения ck для wa(t) для трех нечетных а нижнего порядка. Классическое синусоидальное окно w1(t) тривиально для построения с использованием (19), устанавливая
K=0 и c0=1. Для w3(t), K увеличено до K=1, и

Пятый порядок w5(t) окончательно получается с использованием K=2 и
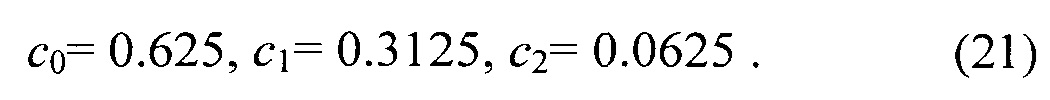
Во-вторых, аналогично bk в (15), ck могут быть определены так, что спектральные характеристики будут подобны спектральным характеристикам окон Блекмана, Хемминга и Наттала. Тем не менее, прежде чем получить соответствующий ck для K=1 и K=2, важно оценить точно, какой аспект спектрального образа окна должен быть оптимизирован. С этой целью необходимы объективные меры спектральных характеристик окна. В следующей секции проводится анализ всех функций окна, упомянутых к настоящему времени, посредством некоторых популярных мер.
10.2. Оценка и оптимизация
Далее будут оценены качество вариантов этого класса окон с 2-я и с 3-я членами по сравнению с другими окнами, используя некоторые показатели качества, описанные в [2]. Будет описана оптимизированная реализация, мотивированная результатом.
Далее будут обсуждены различные наборы параметров формы окна ck. Будет показано, что комбинация величин окна обработки сигнала согласно уравнению (19), позволяет создавать большое разнообразие различных окон, имеющих различные характеристики. Соответственно в итоге может быть получено, что формирователь окон, выполненный с возможностью сформировать окна обработки сигнала wc(t) согласно уравнению (19), очень гибко конфигурируем и реализует алгоритмы с очень низкой вычислительной сложностью, потому что функции формы sin((2k+1)π⋅t/L) могут быть вычислены предварительно, в то время как взвешенное суммирование имеет сравнительно небольшую вычислительную сложность.
Хорошо известно, что умножение сигнала во времени на другой сигнал соответствует преобразованию свертки частот двух сигналов. Следовательно, применением весовой функции к сигналу осуществляется свертка спектра сигнала со спектром весовой функции. Поэтому, чтобы оценить эффект оконной функции, достаточно изучить ее спектр, например, используя преобразование Фурье.
На фиг.11 и 12 иллюстрируются спектры мощности вышеупомянутых окон, нормализованных по частоте и амплитуде аналогично [4]. Из-за повторяющихся спектральных нолей все окна показывают главный лепесток на нулевой частоте и боковые лепестки с затухающей амплитудой с увеличением частоты. Уровень затухания боковых лепестков определяют неоднородности на краях функции окна и ее производных; чем больше производных младших порядков непрерывны, тем быстрее окно затухает к нолю с ростом f. См. также [2] и [4].
Для синуса в степени wa(t) на фиг.11 можно заявить, что асимптотический спад в дБ за октаву пропорционален (см., например, [6]):
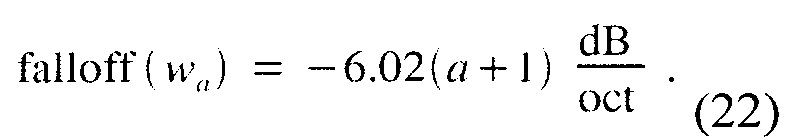
Это имеет место для всего любого неотрицательного реального a, не только для целых чисел. Для оптимизированных окон фиг.12 может наблюдаться различное поведение боковых лепестков. Окно Хемминга, ширина главного лепестка которого равняется ширине w2(t)=wHann(t), уменьшается только на 6 дБ за октаву, потому что весовая функция не непрерывна. Точно так же окна Блекмана и Наттола, у которых ширина главного лепестка такая же как w4(t), показывают затухание только 18 дБ за октаву; первые производные их весовой функции непрерывны, но их третьи производные не непрерывны. Однако эти окна демонстрируют пониженные максимальные уровни бокового лепестка, чем wa(t). Это может привести к особенно уменьшенному спектральному смещению в некоторых решениях и является причиной развития этих оптимизированных окон.
Так как было найдено, что процедура оптимизации, используемая для окон суммы косинусов на фиг.12, может также быть применена к сумме функций синусов (19), возможно изменить окно с 2 членами в (20), и окно с 3 членами в (21) для обеспечения самого низкого максимального уровня бокового лепестка (окно синуса с одним членом с c0=1 не может быть оптимизировано таким образом). Было найдено, что из-за использования синусоид любая реализация (15) приближается к нулевой амплитуде в ее конечных точках; поэтому гарантируется величина затухания бокового лепестка 12 дБ за октаву (1/f2, см. [2]). Если позволить производным быть разрывными, появляются дополнительные степени свободы для того, чтобы определить ck, которые могут использоваться, чтобы минимизировать пиковую величину бокового лепестка (см., например, [4]).
Для окна суммы синусов с двумя слагаемыми (членами) (K=1), допуск разрыва первой производной приводит к одной дополнительной степени свободы в выборе c0 аи c1. Было обнаружено, что значения
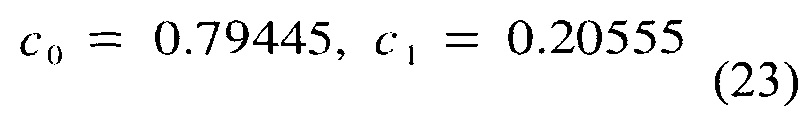
приводят к самому низкому максимуму бокового лепестка -54.3 дБ (первый и третий боковые лепестки). Окно с 3 членами (K=2) создает две дополнительных степени свободы в выборе ck. Минимальный пиковый уровень бокового лепестка -82.8 дБ достигнут, используя
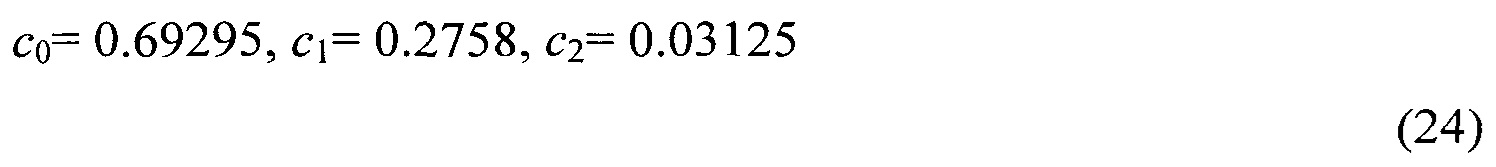
На фиг.13 показаны спектры мощности окон (23) и (24). Для всех десяти представленных окон максимальный уровень бокового лепестка, асимптотический спада, ширина главного лепестка (как определяется местоположением первого ноля), и 6 дБ полоса пропускания (мера разрешения окна, см. [2]) перечислены в таблице 1. Отметьте, что с точки зрения всех спектральных свойств, окно (23) находится прямо между окнами Хемминга с 2 членами и окном Наттала с 3 членами. Кроме того, достигая пика бокового лепестка, подобного этому пику для окна Блекмана, у окна (23) более узкий главный лепесток. У окна (24) самый низкий максимум бокового лепестка из всех рассмотренных окон, но аналогично w5(t), оно также имеет самый широкий главный лепесток.
В заключение, вычисление величин окна обработки сигнала согласно уравнению (19) создает возможность получить окна с сильно различными характеристиками путем изменения только параметров ck, не изменяя основное правило вычисления. Это уменьшает вычислительные затраты и затраты на реализацию решений. Кроме того, в некоторых решениях может использоваться один или более количество различных наборов параметров (20), (21), (23) или (24). Величины окна обработки сигнала могут быть вычислены и сохранены в справочной таблице или могут быть вычислены онлайн (всякий раз, когда требуется), в зависимости от фактического исполнения.
10.3. Окна суммы синусов и дискретное преобразование Фурье (DFT) или модифицированное дискретное преобразование Фурье (MDCT).
Далее будет описана интересная особенность предложенного класса окон, использующаяся в дискретном преобразовании Фурье.
Наблюдательный читатель заметит различие местоположениях нулей между спектрами окон суммы синусов и суммы косинусов. Как видно на рисунках, для последних окон, большинство или все нули возникают в точках, являющихся произведением Lf на целое число, тогда как для окон суммы синусов нули находятся на полпути между произведением Lf на целое число. Далее эта особенность должна быть освещена относительно анализа спектров гармонических сигналов, обработанных окном, используя DFT.
Как отмечено ранее, преобразование Фурье (FT) на интервале сигнала s(t), умноженного на весовые коэффициенты w(t) эквивалентно свертке FT от функций s(t) и w(t). FT окна w1(t) синуса и окна Ханна w2(t) дают
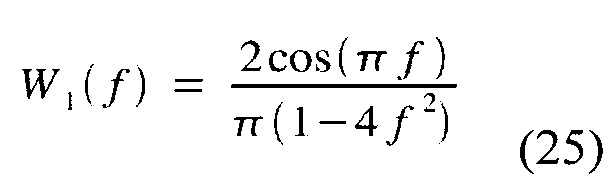
и
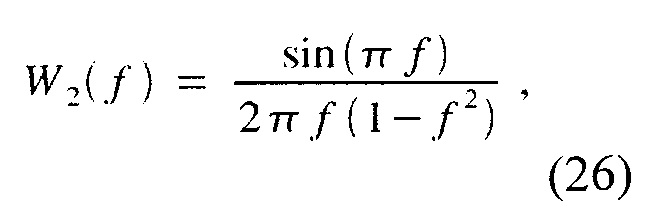
соответственно (см., например, [3]). Таким образом, W1(f)=0 для f=n+0.5, , и W2(f)=0 для f=n, , с целым числом n. FT оптимизированных окон высшего порядка, приведенных в таблице 1, отличаются от (25) и (26), но соответствующий тригонометрическая функция в знаменателе (cos() для окна суммы синусов, sin() для окна суммы косинусов) характерна для всех окон. В контексте дискретного преобразования Фурье максимальное спектральное смещение при использовании окна суммы косинусов совпадает с минимальным смещением при использовании окна суммы синусов, и наоборот. Пример дан на фиг.14 для предложенного окна (23) с 2 членами и окна (18) Наттола с 3 членами с использованием DFT длиной 256 точек.
В современных аудио- или видеокодерах реализация сигнала разделена на сегменты, и каждый сегмент квантуется к более грубому представлению, чтобы получить высокое сжатие данных, то есть низкий битрейт, требуемый для хранения или передачи сигнала. В попытке достигнуть выгоды при кодировании посредством энергетического уплотнения (или другими словами, увеличить перцепционное качество закодированного сигнала для данного битрейта), стали популярными преобразования с использованием банка фильтров (например, MDCT-преобразование 607) сегментов до квантизации. Последние разработанные системы используют преобразование от времени к частоте в форме модифицированного дискретного косинусного преобразования (MDCT), банка фильтров, разрешая смежным сегментам накладываться, обеспечивая критическое осуществление выборки.
Для лучшего результата прямые и обратные операции MDCT (например, MDCT преобразование 607 и обратное MDCT преобразование 608), сопровождаются оконной обработкой каждого сегмента: перед MDCT на стороне кодирующего устройства используется аналитическое окно (например, окно w1(n)), и на стороне декодера окно синтеза (например, окно синтеза w1(n)) применяется после обратного MDCT.
К сожалению, не каждая весовая функция подходит для использования с MDCT. Будем использовать идентичные, симметричные функции для окон анализа и синтеза,
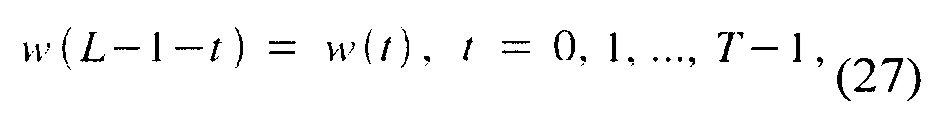
Вся система может осуществлять совершенную реконструкцию входного сигнала при отсутствии ошибок квантизации и передачи если только
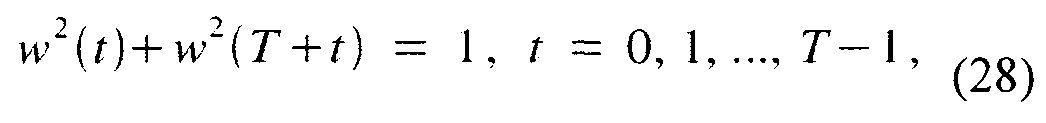
с T=L/2. Это так называемые условия Принсона-Брадли (Princen-Bradley) или комплементарности мощности (PC) описанные в [7]. Общеизвестными PC окнами являются синусоидальные и KBD окна, используемые в стандарте MPEG-2/-4 ААС (см., например, ссылки [6] и [8]), с формулой
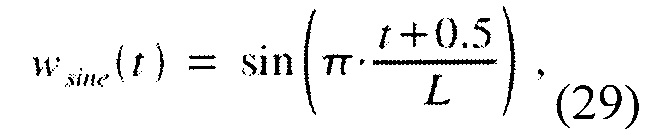
также как окно в спецификации кодека Vorbis (см., например, [9]), дается формулой
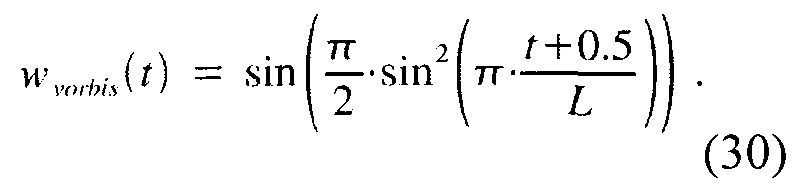
Чтобы исследовать, может ли уравнение (19) быть использовано для создания окна суммы синусов, удовлетворяющего (28), мы заметим, что, учитывая (27), функция wsine(t) может быть получена как синус от треугольной функции:
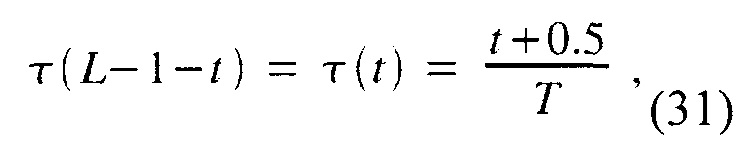
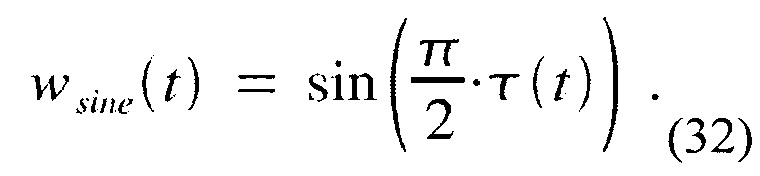
Аналогично, функция wvorbis(t) может быть записана как (32) с элементом τ(t) замененным на
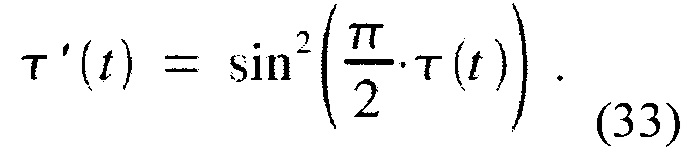
Амплитуднаякомплементарность уравнений (31) и (33) (или 31') относительно Т=L/4,
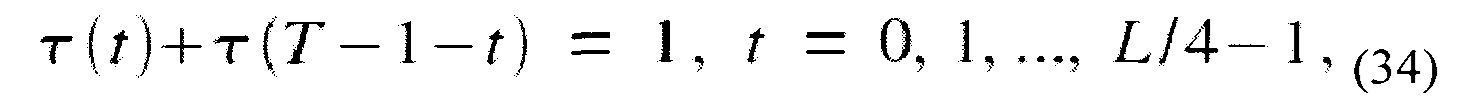
означает, что могут быть разработаны функции, альтернативные этим функциям, чтобы оптимизировать частотную характеристику функции окна без удовлетворения PC свойства. Фактически, поддерживая (27),
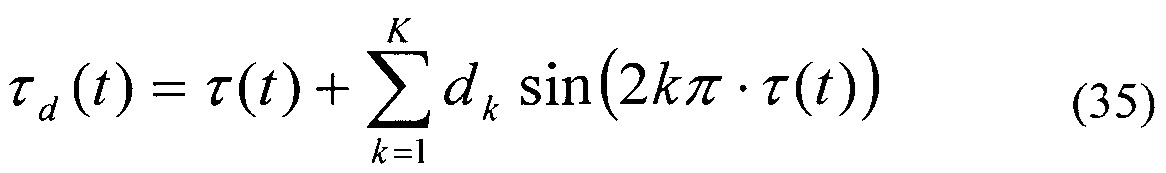
является расширением (31) удовлетворяющим (34), которое использует модификацию функции суммы синусов (19); знакопеременный член опущен, и вместо нечетных множителей числа π, рассматриваются четные множители. Неформальные эксперименты, выполненные автором, указывают, что, хотя PC имеет место даже с dk, производимым τd(t)<0 для некоторых t, только реализация с неотрицательным τd(t) для всех t приводит к удовлетворительной селективности полосы пропускания и заграждению вне полосы пропускания одновременно.
Более того, в разделе, названном ʺОценка и Оптимизацияʺ, коэффициенты ck в уравнении (19) были выбраны таким образом, чтобы максимальный уровень бокового лепестка получающегося окна минимизирован. Подобная процедура может быть выполнена здесь. Однако вследствие ограничения PC (28), спектральные возможности дизайна более ограничены, особенно относительно первых двух или трех боковых лепестков. Вообще, необходимо определить нижнюю частотную границу Lf0>1.5 (или альтернативно, начальный боковой лепесток), выше которой максимум бокового лепестка может быть минимизирован к разумной величине. Чтобы привести пример, был осуществлен неформальный исчерпывающий поиск (перебором) с Lf0=4.5 давший параметры
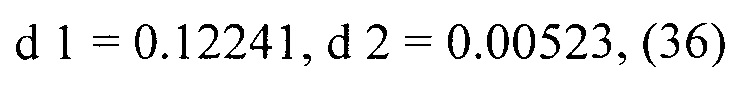
которые создают окно, у которого все три первых боковых лепестка выше Lf0 имеют уровень -66.8 дБ. Боковые лепестки на более высоких частотах затухают от этой величины на -12 дБ за октаву,
точно так же, как боковые лепестки оптимизированных окон (23) и (24), рассмотренных в предыдущих разделах. Частотная характеристика весовой функции, построенная с использованием (27), (32), (35) и (36), показана на фиг.15 наряду с частотными характеристиками wsine(t) and wvorbis(t). Ясно, что в предложенном окне по сравнению с синусоидальным окном достигнуто существенное увеличение заграждения у бокового лепестка. Из-за ограничения (28), это преимущество возникает за счет немного более широкого главного лепестка и более высокого первого бокового лепестка. Сравнение с окном Vorbis показывает почти идентичные ширину главного лепестка и максимумы первых двух боковых лепестков. Для 4.5
11. Альтернативная реализация.
Хотя некоторые аспекты были описаны в контексте устройства, ясно, что эти аспекты также представляют описание соответствующего способа, где блок или устройство соответствуют шагу способа или характеристике шага способа. Аналогично, аспекты, описанные в контексте шага способа также, представляют описание соответствующего блока или модуля или характеристики соответствующего устройства.
Некоторые или все шаги способа могут быть выполнены (или использованы) аппаратурными средствами, такими как, например, микропроцессор, программируемый компьютер или электронная схема. В некоторых решениях, один или большее количество самых важных шагов способа может быть выполнено таким устройством.
Кодируемый медиа-сигнал, которым может быть кодируемый аудио- или видеосигнал или последовательность функций окна, может быть сохранен на цифровом носителе данных или может быть передан в среде передачи, такой как беспроводная среда передачи или проводная среда передачи, такая как Интернет.
В зависимости от определенных требований применения решения изобретения могут быть осуществлены в аппаратурных средствах или в программном обеспечении. Применение может быть выполнено, используя цифровой носитель данных, например, дискету, DVD, диск blu-ray, CD, ROM, PROM, EPROM (стираемая программируемая постоянная память), EEPROM или Флэш-память, путем сохранения в электронном виде удобочитаемых управляющих сигналов, которые далее взаимодействуют (или способны к взаимодействию) с программируемой компьютерной системой, таким образом, что выполняется соответствующий способ. Поэтому, цифровой носитель данных может быть читаемым компьютером.
Некоторые решения согласно изобретению включают носитель информации, имеющий в электронном виде удобочитаемые управляющие сигналы, которые способны к взаимодействуют с программируемой компьютерной системой так, что выполняется один из описанных здесь способов.
Вообще, решения данного изобретения могут быть осуществлены как программный продукт с кодом программы, кодом программы, чтобы выполнить один из способов, когда программный продукт выполняется на компьютере. Код программы может, например, быть сохранен на машиночитаемом носителе.
Другие решения включают компьютерную программу, сохраненную на машиночитаемом носителе, для того чтобы выполнить один из описанных здесь способов.
Другими словами, реализацией изобретенного является, компьютерная программа, имеющая код программы для того, чтобы выполнить один из описанных здесь способов, когда компьютерная программа выполняется на компьютере.
Дальнейшей реализацией изобретенных способов является носитель информации (или цифровой носитель данных или удобочитаемая компьютером среда), включающий записанную на нем компьютерную программу для того, чтобы выполнить один из описанных здесь способов. Носитель информации, цифровой носитель данных или записанная среда типично материальны и/или не промежуточны (не изменяемы).
Дальнейшей реализацией изобретенных способов является поток данных или последовательность сигналов, представляющих компьютерную программу для того, чтобы выполнить один из описанных здесь способов. Поток данных или последовательность сигналов могут, например, быть переданными через сеть передачи данных, например, через Интернет.
Дальнейшее решение включает средство обработки, например компьютер или программируемое логическое устройство, выполненное с возможностью выполнить один из описанных здесь способов.
Дальнейшее решение включает компьютер с установленной компьютерной программой для того, чтобы выполнить один из описанных здесь способов.
Дальнейшее решение согласно изобретению включает устройство или систему, выполненную с возможностью передать к приемнику (например, в электронном виде или оптически) компьютерную программу для того, чтобы выполнить один из описанных здесь способов. Приемник может, например, быть компьютером, мобильным устройством, устройством памяти и т.п. Устройство или система могут, например, включать файловый сервер для того, чтобы передать компьютерную программу приемнику.
В некоторых решениях может использоваться программируемое логическое устройство (например, программируемая логическая интегральная схема), чтобы выполнить некоторые или все описанные здесь способы. В некоторых решениях программируемое логическое устройство может взаимодействовать с микропроцессором, чтобы выполнить один из описанных здесь способов. Вообще, способы предпочтительно выполняются любым аппаратным устройством.
Вышеупомянутые описанные решения - просто иллюстрации для принципов данного изобретения. Подразумевается, что модификации и изменения описанных здесь мероприятий и деталей будут очевидны для квалифицированных специалистов. Поэтому ограничимся только областью формулы изобретения, а не определенными деталями, представленными здесь посредством описания и объяснения решений.
12. Заключения
Из вышеописанного можно заключить, что вычисление функции окна, как описано в уравнениях (6), (8) и (9), создает функцию окна, имеющую особенно хорошие характеристики.
Кроме того, можно прийти к заключению, что вычисление функции окна, как описано уравнением (19), создает функцию окна, имеющую хорошие характеристики.
Суммируя вышесказанное, решения согласно данному изобретению вообще имеют отношение к анализу сигнала и способам обработки, которые могут использоваться в аудио- или видеокодирующих системах. Некоторые решения согласно изобретению относятся к применениям, требующим энергетического уплотнения сигнала посредством инвариантных или адаптивных к сигналу источника различных преобразований банком фильтров. Они могут быть использованы, чтобы улучшить работу энергетическую уплотнения, обеспечивая совершенную инверсию указанного преобразования. Решения согласно данному изобретению поэтому составляют решение проблемы необходимости в альтернативной функции окна, имеющей умеренную вычислительную сложность, но обеспечивающей хорошую гибкость дизайна.
Некоторые решения согласно данному изобретению, которые определены формулой изобретения или данным описанием, относятся к нехватке гибких и эффективных в вычислительном отношении функций окна для приложений MDCT, объявляя расширение к функции синусоидального окна уравнения (4).
Однако другие решения согласно изобретению создают улучшенные функции окна, которые обеспечивают увеличенную гибкость, но не обеспечивают возможность для совершенной реконструкции в приложениях MDCT. Однако такие функции окна полезны во многих приложениях.
Необходимо также указать, что для облегчения понимания изобретение было описано путем иллюстративных примеров, не ограничивая область или дух изобретения в отношении сопровождающих рисунков. Другими словами, описанные здесь решения, просто иллюстрации принципов данного изобретения для более гибкой оконной обработки и/или улучшенного энергетического уплотнения сигнала в приложениях, связанных с фильтрацией. Подразумевается, что изменения и модификации описанных здесь устройств и деталей, будут очевидны для специалистов, квалифицированных в технике. Поэтому ограничимся только областью формулы изобретения патента, а не особыми деталями, раскрытыми здесь путем описания и объяснения решений.
Вообще говоря, оконная обработка дискретных сигналов во времени с использованием весовых коэффициентов является важным инструментом для спектрального анализа при обработке, чтобы уменьшить эффекты смещения. Много популярных весовых функций (например, Ханна, Хемминга, Блекмана), основаны на сумме масштабированных косинусов.
Решения согласно изобретению представляют альтернативный класс окон, построенных использую суммы синусов и демонстрирующих измененные (или даже уникальные) спектральные характеристики относительно местоположения нулей и затухания бокового лепестка по крайней мере на -12 дБ/октава из-за гарантируемой непрерывности весовой функции окна. Параметры для 2 и 3-членных реализаций обеспечены с минимальным пиковым уровнем бокового лепестка. Некоторые решения согласно изобретению связаны с использованием окон суммы синусов с дискретным преобразованием Фурье, и их адаптацией к преобразованиям с перекрытиями, таким как модифицированное косинусное преобразование (MDCT).
Другими словами, решения согласно изобретению предлагают альтернативы обычным функциям окна (например, Ханна, Хемминга, Блекмана), одинаково легко вычисляются с подобными или даже уникальными свойствами с точки зрения сокращения смещения.
Вообще говоря, решения согласно изобретению создают устройство, способ или компьютерную программу для кодирования или декодирования или обработки аудио- или видеосигнала, используя различные функции окна.
Некоторые решения согласно изобретению создают устройство, способ или компьютерную программу для того, чтобы вычислить последовательность различных функций окна для аудиосигнала или видеосигнала.
Дальнейшие решения согласно изобретению создают кодированный аудио- или видеосигнал, включающий закодированный аудио- или видеоконтент и параметрическую информацию об окне, касающуюся переменных окон, используемых для того, чтобы кодировать аудио- или видеосигнал, чтобы получить кодированный аудио- или видеосигнал.
Дальнейшие решения согласно изобретению создают последовательность различных функций окна, определяемых адаптивным к сигналу способом.
Дальнейшие решения согласно изобретению создают устройство, способы, компьютерные программы, кодированные сигналы и последовательности различных функций окна, в которых окно (wnew) получено на основе
c(n)=(n+1/2)⋅2/N,
wsin(n)=sin(π/2⋅c(n)), n=0, 1, … N/2-1,
где c(n) обозначает функцию ядра окна, которая может быть вычислена заранее, так как ядро предопределено. Предложенное расширение добавляется к c(n) в уравнении взвешенных синусоид (7), имеющих угловые частоты, являющиеся произведением целого числа на 2π:
c'(n)=c(n)+Σafsin(2π⋅f⋅c(n)), f=1, 2, …,
wnew(n)=sin(π/2⋅c'(n)), n=0, 1, … N/2-1.
Таким образом, были представлены математически простые альтернативы окнам Хемминга, Блекмана и подобным, формируемым с использованием сумм взвешенных синусов. Подход с использованием суммы синусов приводит к уникальным свойствам, таким как гарантируемая непрерывность функции окна, этот подход может также быть применен при создании окон, комплиментарных по мощности, например, для аудиокодирования.
Литература
[1] R.В. Blackman and J.W. Tukey, The Measurement of Power Spectra from the Point of View of Communications Engineering, New York, NY, USA:Dover Publications, 1958.
[2] F.J. Harris, ʺOn the Use of Окна for Harmonic Analysis with the Discrete Fourier Transform,ʺ Proc. IEEE, vol. 66, no. 1, pp. 51-83, Jan. 1978.
[3] N.С. Geçkinli and D. Yavuz, ʺSome Novel Окна and a Concise Tutorial Comparison of Window Families,ʺ IEEE Trans. Acoustics, Speech, and Signal Processing, vol. ASSP-26, no. 6, pp. 501-507, Dec. 1978.
[4] A.H. Nuttall, ʺSome Окна with Very Good Sidelobe Behavior,ʺ IEEE Trans. Acoustics, Speech, and Signal Processing, vol. ASSP-29, no. 1, pp. 84-91, Feb. 1981.
[5] S.W.A. Bergen and A. Antoniou, ʺDesign of Ultraspherical Window Functions with Prescribed Spectral Characteristics,ʺ EURASIP Journal on Applied Signal Processing, vol. 2004, no. 13, pp. 2053-2065, 2004. Available on-line at http://www.hindawi.com/GetArticle.aspx?doi=10.1155/S1110865704403114.
[6] J.O. Smith III, Spectral Audio Signal Processing, Mar. 2009 Draft, Center for Computer Research in Music and Acoustics (CCRMA), Stanford University, CA, USA. Available on-line at http://ccrma.stanford.edu/~jos/sasp/ (accessed Mar. 2010).
[7] J.P. Princen, A.W. Johnson, and A.B. Bradley, ʺSubband / Transform Coding Using Filter Bank Designs Based on Time Domain Aliasing Cancellation,ʺ Proc. IEEE 1987 ICASSP-12, pp. 2161-2164, May 1987.
[8] ISO/IEC 14496-3:2009, ʺInformation technology - Coding of audio-visual objects - Part 3: Audio,ʺ Geneva, Aug. 2009.
[9] Xiph. org Foundation, ʺVorbis I specification,ʺ Feb. 2010. Online at http://www.xiph.org/vorbis/doc/Vorbis_I_spec.html.
Реферат
Изобретение относится к передаче данных и предназначено для обработки входного сигнала весовыми коэффициентами окна. Технический результат – повышение эффективности кодирования путем адаптации характеристик окна к характеристикам входного спектра сигнала. Сигнальный процессор для того, чтобы обеспечить обработанную версию входного сигнала в зависимости от входного сигнала, включает оконный обработчик, формирующий часть входного сигнала, или его предварительно обработанной версии, в зависимости от окна обработки сигнала, описанного величинами окна обработки сигнала для множества значений индекса величин окна, чтобы получить обработанную версию входного сигнала. Сигнальный процессор также включает формирователь окна для того, чтобы обеспечить величины окна обработки сигнала для множества значений индекса величин окна в зависимости от одного или более параметров формы окна. 13 н. и 22 з.п.ф-лы, 17 ил.
Формула
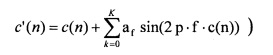
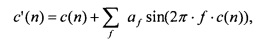
Документы, цитированные в отчёте о поиске
Способ и устройство для векторного квантования с надежным предсказанием параметров линейного предсказания в кодировании речи с переменной битовой скоростью

Комментарии