Способ сопровождения воздушной цели из класса "самолёт с турбореактивным двигателем" при воздействии уводящих по дальности и скорости помех - RU2764781C1

Чертежи

Описание

Предлагаемое изобретение относится к области цифровой обработки радиолокационных сигналов и может быть использовано в радиолокационной станции (РЛС) для формирования при сопровождении воздушной цели (ВЦ) из класса «самолет с турбореактивным двигателем (ТРД)» достоверной идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех или отсутствия их воздействия и оценки радиальных функционально-связанных координат (ФСК) взаимного перемещения ВЦ и носителя РЛС при различных вариантах воздействия таких помех.

Известен способ сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех [1], заключающийся в том, что сигнал, отраженный от цели, подвергается узкополосной доплеровской фильтрации на основе процедуры быстрого преобразования Фурье (БПФ) и преобразуется в амплитудно-частотный спектр, составляющие которого обусловлены отражениями сигнала от планера сопровождаемой ВЦ и вращающихся лопаток рабочего колеса компрессора низкого давления (КНД) ее силовой установки, определяются отсчет доплеровской частоты, соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, который соответствует его отражениям от планера ВЦ, и отсчет доплеровской частоты, соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, находящийся справа по доплеровской частоте относительно спектральной составляющей сигнала, отраженного от планера ВЦ, которые поступают на вход фильтра совместного сопровождения ВЦ и первой компрессорной составляющей спектра сигнала, функционирующего в соответствии с процедурой (1а)-(6а) многомерной линейной дискретной калмановской фильтрации в соответствии с уравнениями [1]

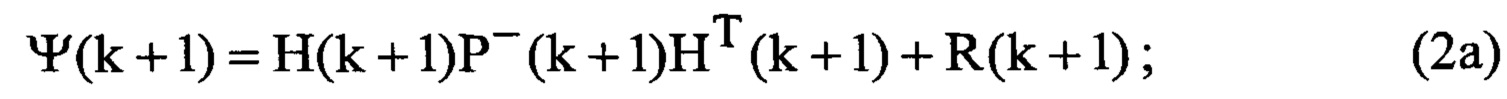
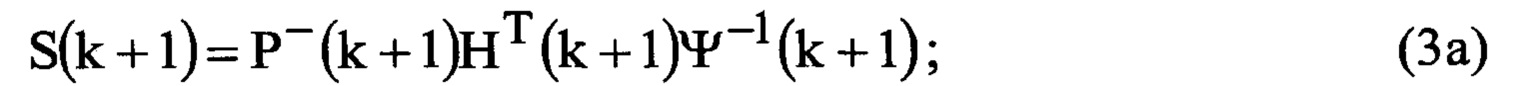
где

k=0,1, …, К, …, - номер такта работы фильтра;

и Р(k+1) - ковариационные матрицы (КМ) ошибок экстраполяции и фильтрации соответственно;

Φ(k) - переходная матрица состояния;

Q(k+1) и R(k+1) - КМ шумов возбуждения и наблюдения соответственно;

S(k+1) - матрица весовых коэффициентов; I - единичная матрица;

и - вектор текущих и экстраполированных оценок радиальных ФСК взаимного перемещения носителя РЛС и ВЦ;

Н(k+1) - матрица наблюдения;

Y(k) - вектор наблюдения;

Z(k+1) - матрица невязок измерения;

Ψ(k+l) - матрица априорных ошибок фильтрации;

"-1" - операция вычисления обратной матрицы;

"т" - операция транспонирования матрицы,

определяется оценка разности

между оцененными значениями доплеровских частот, обусловленных отражениями от планера и лопаток рабочего колеса первой ступени КНД силовой установки ВЦ, вычисляется модуль производной оценки разности между оцененными значениями доплеровских частот, который сравнивается с пороговым значением 8, близким к нулю, выполнение или невыполнение условия

свидетельствует соответственно об отсутствии или воздействии уводящей по скорости помехи, измеряется дальность до ВЦ, в соответствии с процедурой (1а)-(6а) осуществляется формирование оценки дальности,

вычисляется производная оценки дальности , вычисляется дальность Д*(k+1) на основе динамической модели радиальных ФСК взаимного перемещения носителя РЛС и ВЦ, вычисляется модуль разности между оценкой производной дальности и оценкой скорости , величина которого сравнивается с порогом ε₁,

где

- оценка скорости, сформированная на основе измерения скорости Y(k+1) = [V(k+1)]^T и динамической модели радиальных ФСК, вычисляется модуль разности между оценкой дальностью и вычисленной дальностью Д*(k+1) на основе динамической модели радиальных ФСК, величина которого сравнивается с порогом ε₂,

одновременное выполнение условий (8а) и (10а) свидетельствует об отсутствии уводящих по скорости и дальности помех, в этом случае оценки дальности

и скорости формируются в соответствии с процедурой (1а)-(6а) на основе наблюдения Y(k+1) = [Д(k+1), V(k+1)]^T и динамической модели радиальных ФСК, одновременное выполнение условия (8а) и невыполнение условия (10а) свидетельствует о воздействии только уводящей по дальности помехи, в этом случае оценка скорости формируется в соответствии с процедурой (1а)-(6а) на основе наблюдения Y(k+1)=[V(k+1)] и динамической модели радиальных ФСК, а оценка дальности вычисляется без учета измерения дальности путем интегрирования оценки скорости одновременное невыполнение условия (8а) и выполнение условия (10а) свидетельствует о воздействии уводящих по дальности и скорости помех с функционально-связанным законом увода, в этом случае оценки дальности и скорости вычисляются в соответствии с процедурой (1а)-(6а) без учета измерений дальности и скорости Y(k+1) = 0 и только на основе динамической модели радиальных ФСК, одновременное невыполнение условий (9а) и (10а) свидетельствует о воздействии уводящих по дальности и скорости помех без функционально-связанного закона увода, в этом случае оценки дальности и скорости также вычисляются в соответствии с процедурой (1а)-(6а) без учета измерений дальности и скорости Y(k+1) = 0 и только на основе динамической модели радиальных ФСК, одновременное невыполнение условия (8а) и выполнение условия (10а) свидетельствует о воздействии только уводящей по скорости помехи, в этом случае оценки дальности и скорости формируются в соответствии с процедурой (1а)-(6а) на основе измерения только дальности Y(k+1) = [Д(k+1)] и динамической модели радиальных ФСК.

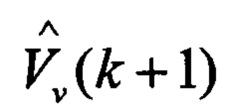
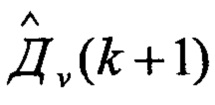
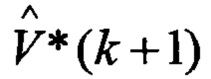
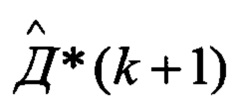
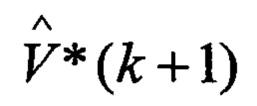
Недостатком данного способа сопровождения ВЦ является низкая достоверность идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех или отсутствия такого воздействия и оценки радиальных ФСК взаимного перемещения ВЦ и носителя РЛС при различных вариантах воздействия таких помех вследствие:

1. Допущения о линейном характере зависимости ФСК от времени, в то время как фактически динамика ФСК носит нелинейный характер.

2. Не оптимальности, определяемых на его основе оценок ФСК, так как они находятся при условии справедливости гипотезы о фактическом варианте воздействия уводящих помех, которая носит вероятностный характер, а значит, оценки являются условно-оптимальными.

3. Отсутствия возможности комплексирования информации РЛС, измеряющей ФСК, и индикатора (обнаружителя) варианта воздействия уводящих помех.

4. Отсутствия возможности учитывать априорные данные о смене варианта воздействия уводящих помех.

5. Отсутствия адаптации системы наблюдения к различным вариантам воздействия уводящих помех.

Известен способ сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех [2], заключающийся в том, что сигнал, отраженный от цели, подвергается узкополосной доплеровской фильтрации на основе процедуры БПФ и преобразуется в амплитудно-частотный спектр, составляющие которого обусловлены отражениями сигнала от планера сопровождаемой ВЦ и вращающихся лопаток рабочего колеса КНД ее силовой установки, определяются отсчет доплеровской частоты, соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, который соответствует его отражениям от планера ВЦ, и отсчет доплеровской частоты, соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, находящийся справа по доплеровской частоте относительно спектральной составляющей сигнала, отраженного от планера ВЦ, выделенные отсчеты доплеровских частот поступают на вход многоканального фильтра совместного сопровождения ВЦ и первой компрессорной составляющей спектра сигнала, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния марковской структуры линейной стохастической динамической системы

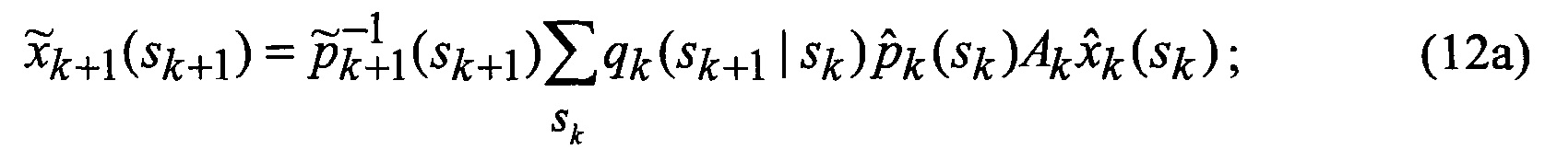
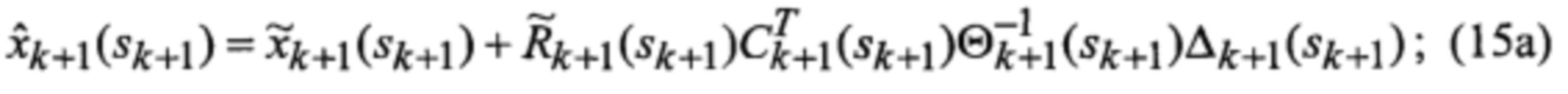
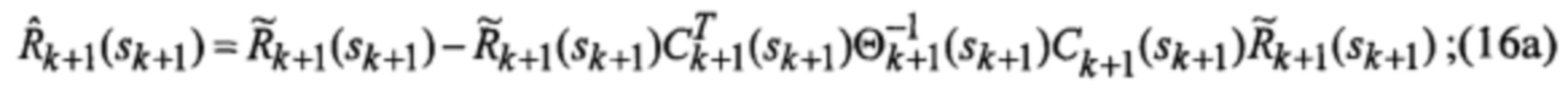
основанной на априорных данных в виде математической модели (ММ) системы «ВЦ - РЛС - индикатор» со случайной скачкообразной структурой (ССС), включающей модели линейной динамики радиальных ФСК взаимного перемещения носителя РЛС и ВЦ

их измерений в РЛС

смены варианта воздействия уводящих помех

индикатора варианта воздействия уводящих помех

неуправляемых случайных возмущений и помех

при начальных условиях

где

k - дискретный момент времени;

x_k - вектор радиальных ФСК взаимного перемещения носителя РЛС и ВЦ;

- вариант воздействия уводящих помех (1 - отсутствие помех; 2 - воздействие только уводящей по скорости помехи; 3 - воздействие только уводящей по дальности помехи; 4 - воздействие уводящих как по скорости, так и по дальности помех);

z_k - вектор измерений РЛС;

- выходные показания индикатора варианта воздействия уводящих помех;

- условные вероятности смены варианта воздействия уводящих помех;

- условные вероятности смены показаний индикатора варианта воздействия уводящих помех;

- прогнозируемые на один шаг дискретности вперед и апостериорные соответственно вероятности воздействия уводящих помех по s_k+1 варианту, условные математические ожидания ФСК при фиксированном варианте воздействия уводящих помех, условные КМ ошибок оценивания ФСК при фиксированном варианте воздействия уводящих помех;

- квазиоптимальная по критерию максимума апостериорной вероятности оценка варианта воздействия уводящих помех;

- апостериорное безусловное математическое ожидание ФСК;

- апостериорная безусловная КМ ошибок оценивания ФСК;

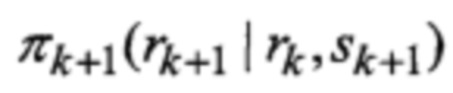
G_k, Q_k - КМ соответственно векторов шумов возбуждения F_kξ_k и помех E_k(s_k)ζ_k;

ξ_k, ζ_k - стандартные дискретные векторные белые шумы;

Θ_k(s_k) - условная КМ измерения при фиксированном варианте воздействия уводящих помех;

A_k, F_k - известные матрицы коэффициентов;

C_k(s_k), E_k(s_k) - известные матрицы детерминированных функций от варианта воздействия уводящих помех s_k;

- обратная матрица по отношению к матрице Θ_k(s_k);

Т - операция транспонирования матрицы;

detΘ_k(s_k) - определитель матрицы Θ_k(s_k);

ехр[⋅] - экспоненциальная функция,

определяется оценка

варианта воздействия уводящих помех, определяется оценка безусловного математического ожидания ФСК, определяется оценка безусловной КМ ошибок оценивания ФСК, на основе ММ (24а) динамики радиальных ФСК, включающих дальность до цели, планерные и компрессорные составляющие радиальных скоростей и ускорений взаимного перемещения носителя РЛС и ВЦ, в непрерывном времени

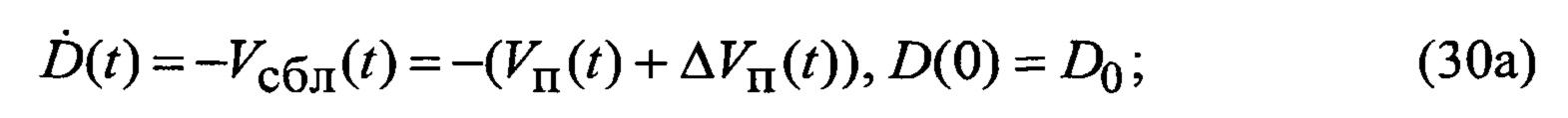
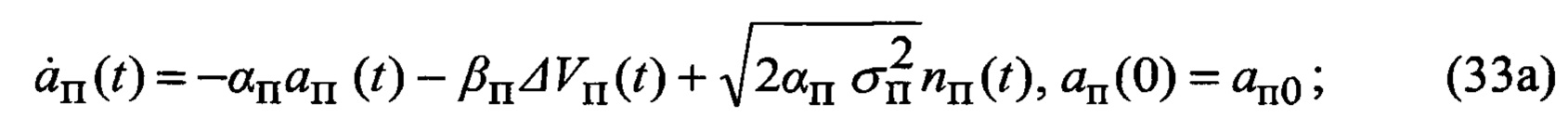
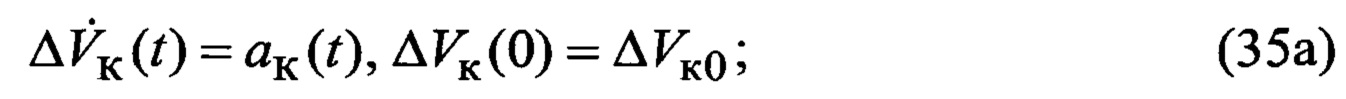
где индексы «п» и «к» относятся соответственно к планерной и первой компрессорной составляющим спектра, отраженного от ВЦ сигнала;

D(t), V_сбл(t), a_п(t) - радиальные ФСК соответственно дальность, скорость и ускорение сближения носителя РЛС с ВЦ;

V_п(t), V_к(t) - детерминированные составляющие радиальных скоростей сближения носителя РЛС с ВЦ;

ΔV_п(t), ΔV_к(t) - флюктуационные составляющие радиальных скоростей сближения носителя РЛС с ВЦ;

a_п(t), a_к(t) - флюктуационные составляющие радиальных ускорений;

α_п, α_к, - величины, обратные времени корреляции скоростных флюктуации взаимного перемещения носителя РЛС и ВЦ;

β_п, β_к - квадраты собственных частот скоростных флюктуации взаимного перемещения носителя РЛС и ВЦ;

σ_п, σ_к - среднеквадратические отклонения (СКО) флюктуации ускорения взаимного перемещения носителя РЛС и ВЦ;

n_п(t), n_к(t) - формирующие нормированные белые гауссовские шумы;

D₀, V_п0, V_к0, ΔV_п0, Δ_к0, а_п0, а_к0 - начальные значения соответственно дальности до ВЦ, детерминированных и флюктуационных составляющих радиальных скоростей, флюктуационных составляющих радиальных ускорений,

представляемой в процедуре (11а)-(23а) матрицами A_k и F_k, размерностями 7×7, ненулевыми элементами которых являются соответственно a₁₁=a₂₂=a₃₃=а₅₅=а₆₆=1; a₁₂=a₁₃=-Δt; a₃₄=a₆₇=Δt; a₄₄=1-a_nΔt; a₇₇=1-a_кΔt; a₄₃=-βпΔt; a₇₆=-β_кΔt;

где Δt - период дискретизации, и на основе ММ (25а) измерений в РЛС функционально-связанных координат, представляемой в процедуре (11а)-(23а) матрицами C_k(s_k) и E_k(s_k), размерностями 7×7, ненулевыми элементами которых являются соответственно c₁₁(s_k); c₂₂(s_k); c₃₃(s_k); с₅₅; с₆₆; e₁₁(s_k); e₂₂(s_k); e₃₃(s_k); e₅₅; e_66, при отсутствии помех спрогнозированные на основе априорных данных (30а)-(36а) ФСК корректируются по результатам измерений D(t), V_п(t), ΔV_п(t), V_к(t), ΔV_к(t) и с₁₁(1)=с₁₁, c₂₂(1)=c₂₂, С₃₃(1)=с₃₃; е₁₁(1)=e₁₁, е₂₂(1)=e₂₂, е₃₃(1)=е₃₃, при воздействии только уводящей по скорости помехи корректируются по результатам измерений D(t), , , V_к(t), ΔV_к(t) и с₁₁(2)=с₁₁, ; е₁₁(2)=е₁₁, , при воздействии только уводящей по дальности помехи корректируются по результатам измерений D*(t), V_n(t), ΔV_n(t), V_к(t), ΔV_к(t) и , c₂₂(3)=c₂₂, с₃₃(3)=с₃₃; , e₂₂(3)=e₂₂, е₃₃(3)=е₃₃, при воздействии уводящих как по скорости, так и по дальности помех корректируются по результатам измерений D*(t), , , V_к(t), ΔV_к(t) и , , ; , , , где символом «*» отмечены компоненты вектора ФСК, на искажение которых направлено воздействие уводящих помех, а также измененные элементы матриц C_k(s_k) и E_k(s_k), компенсирующие в РЛС соответствующие воздействия.

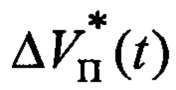
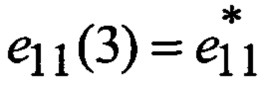
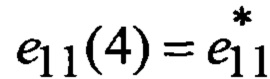
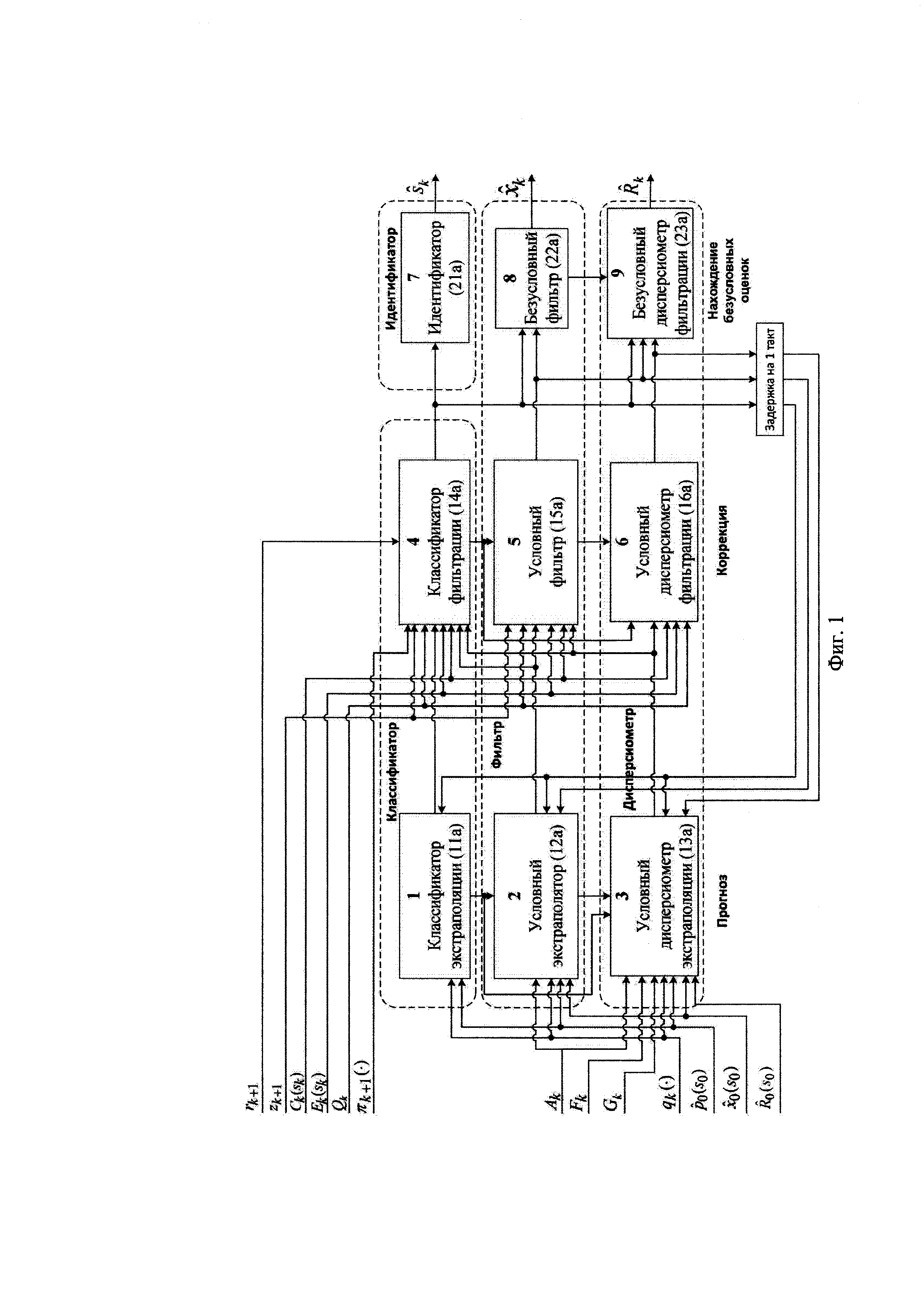
На фиг. 1 приведена блок-схема, поясняющая реализацию известного способа сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех [2].

Недостатком данного способа сопровождения ВЦ является низкая достоверность идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех или отсутствия такого воздействия и оценки радиальных ФСК взаимного перемещения ВЦ и носителя РЛС при различных вариантах воздействия таких помех вследствие:

1. Допущения о линейном характере зависимости ФСК от времени, в то время как фактически динамика ФСК носит нелинейный характер.

2. Допущения о статистической независимости смены вариантов воздействия уводящих помех от ФСК, в то время как фактически вероятности смены таких вариантов зависят от фазовых координат, в частности, с сокращением дальности до цели возрастают вероятности переходов к варианту совместного воздействия уводящих по дальности и скорости помех.

3. Допущения о нормальности аппроксимирующей условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех - значительное отличие вида фактической плотности вероятности ФСК от нормального вида аппроксимирующей плотности приводит к возрастанию ошибок оценивания.

Цель изобретения - повышение достоверности идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех или отсутствия их воздействия и оценки радиальных функционально-связанных дальности до ВЦ и скорости сближения носителя РЛС с нею путем адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности ФСК смесью априорно задаваемых аппроксимирующих функций и приближением получаемых оценок к их оптимальным значениям за счет учета нелинейностей в динамике ФСК и их измерений, учета статистической зависимости вероятностей смены вариантов воздействия уводящих помех от ФСК, комплексирования информации РЛС и индикатора варианта воздействия уводящих помех, учета априорных данных о смене этих вариантов и адаптации системы наблюдения к ним.

Для достижения цели в способе сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех [2], заключающемся в том, что сигнал, отраженный от цели, подвергается узкополосной доплеровской фильтрации на основе процедуры БПФ и преобразуется в амплитудно-частотный спектр, составляющие которого обусловлены отражениями сигнала от планера сопровождаемой ВЦ и вращающихся лопаток рабочего колеса КНД ее силовой установки, определяются отсчет доплеровской частоты, соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, который соответствует его отражениям от планера ВЦ, и отсчет доплеровской частоты, соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, находящийся справа по доплеровской частоте относительно спектральной составляющей сигнала, отраженного от планера ВЦ, выделенные отсчеты доплеровских частот дополнительно поступают на вход многоканального фильтра совместного сопровождения ВЦ и первой компрессорной составляющей спектра сигнала и идентификации варианта воздействия уводящих помех, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания [3] в соответствии с функциональными интегральными рекуррентными уравнениями

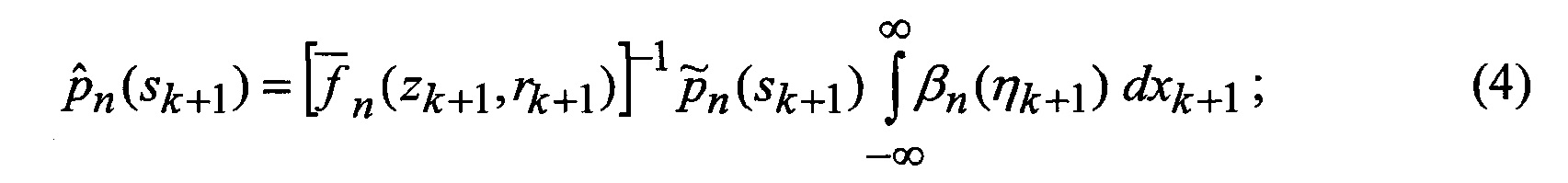
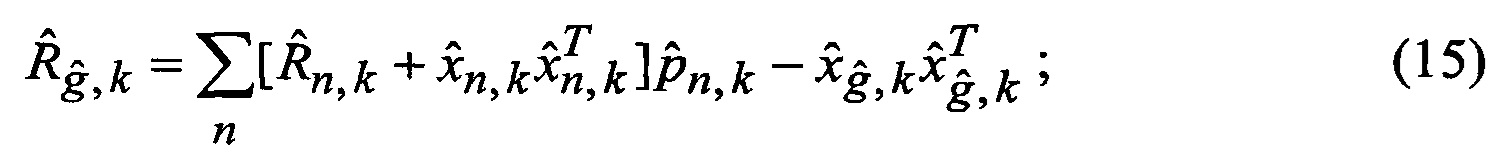
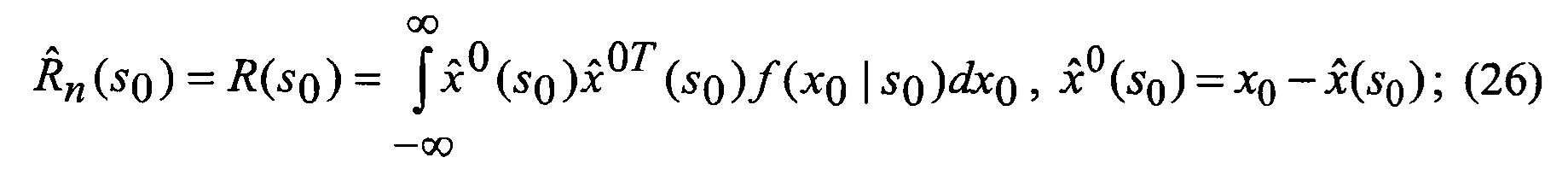
которые после выполнения процедуры аппроксимации (выдвижения гипотезы относительно видов аппроксимирующих функций) в соответствии с выражениями

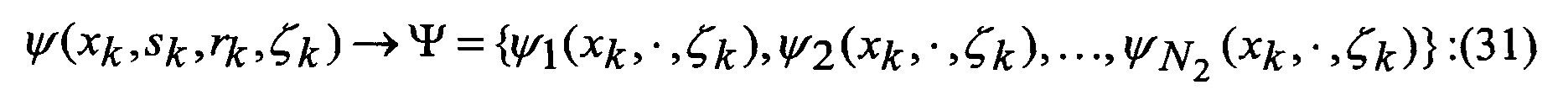
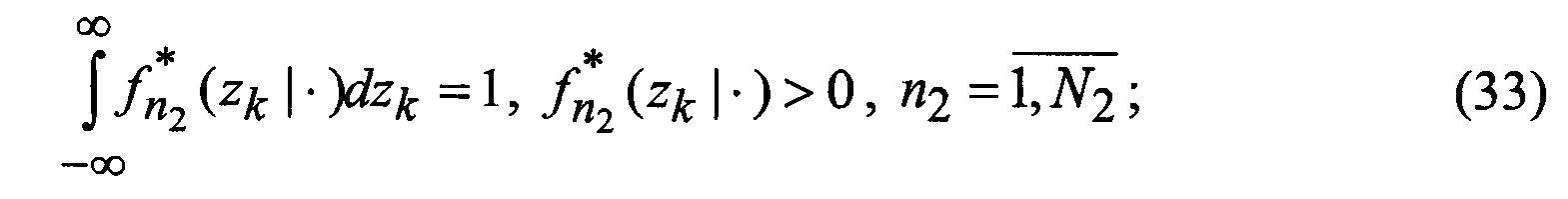
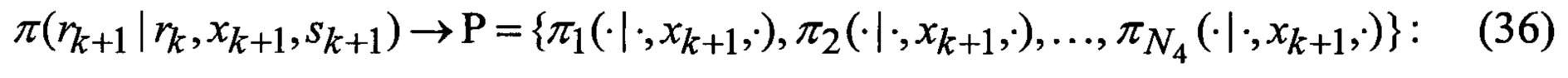
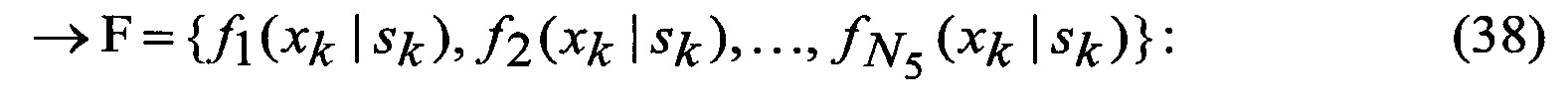
замыкаются (число неизвестных становится равным числу уравнений), интегралы в правых частях уравнений выражаются через элементарные или табулированные функции, а сами уравнения вырождаются в следующие обыкновенные рекуррентные уравнения относительно условных вероятностей воздействия уводящих помех в различных вариантах (состояний структуры) при фиксированном наборе аппроксимирующих функций, условных МО функционально-связанных координат и КМ ошибок их оценивания при фиксированных варианте набора аппроксимирующих функций и варианте воздействия уводящих помех:

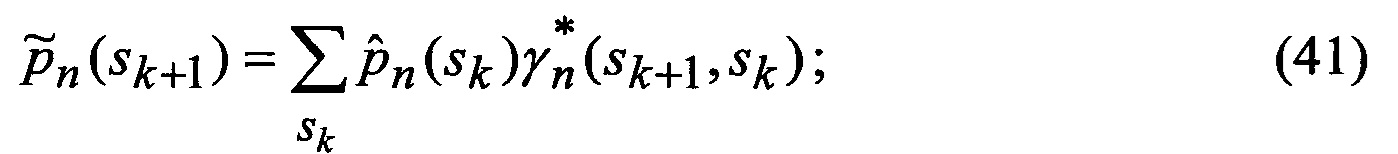
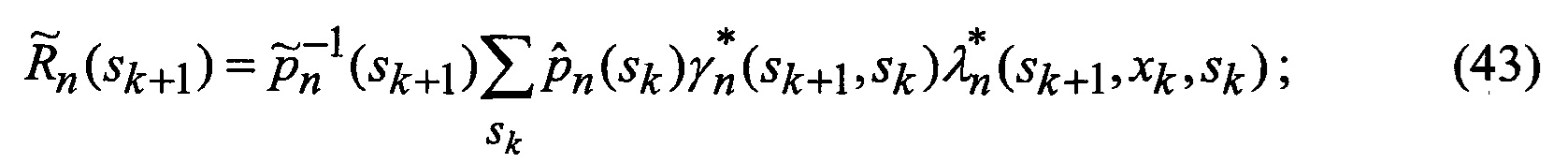
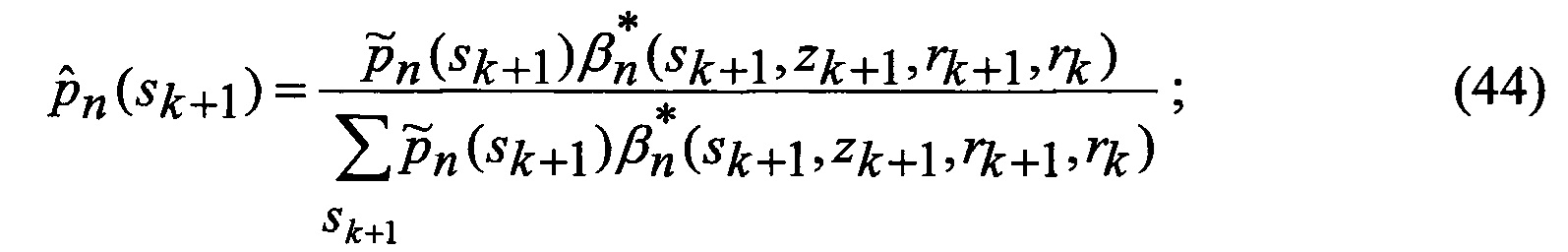
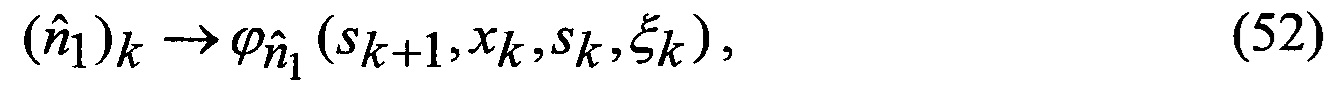
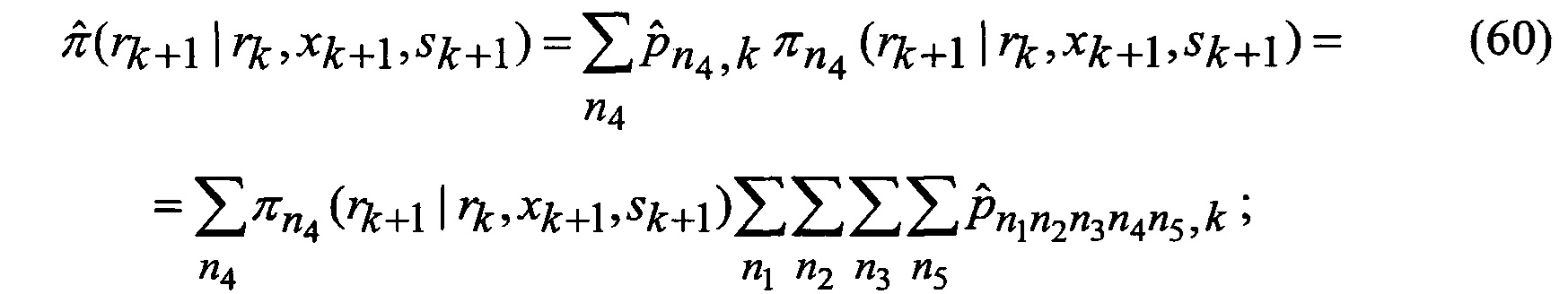
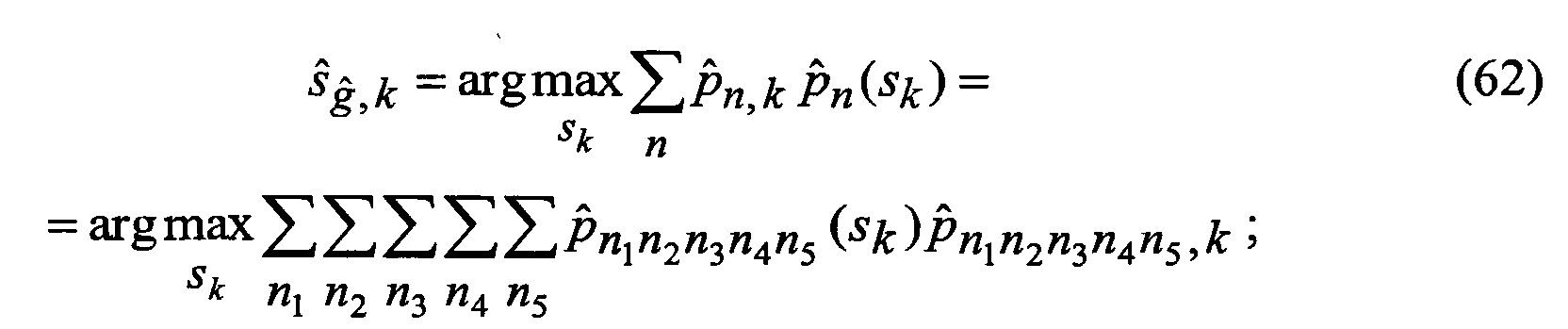
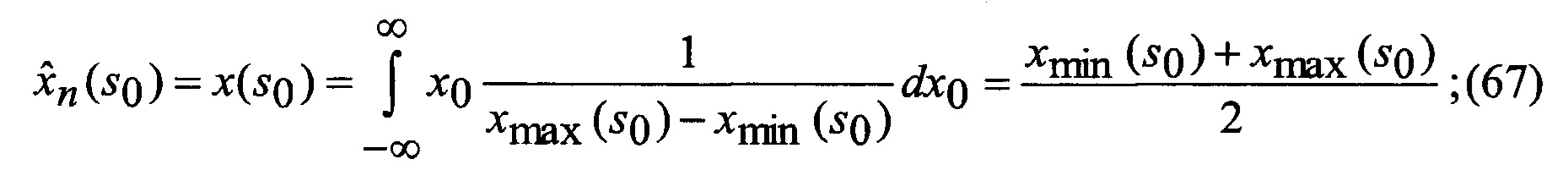
основанной на априорных данных в виде ММ системы «ВЦ - РЛС - индикатор» со ССС, включающей, в общем виде, нелинейную модель динамики радиальных ФСК - дальности до цели, планерных и компрессорных составляющих радиальных скоростей и ускорений взаимного перемещения носителя РЛС и ВЦ

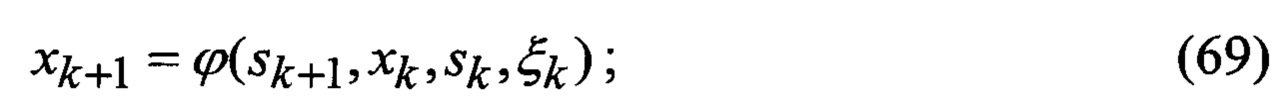
нелинейную модель измерений этих ФСК в РЛС

условно-марковскую модель смены варианта воздействия уводящих помех

условно-марковскую модель индикатора варианта воздействия уводящих помех

модель неуправляемых случайных возмущений и помех

при начальных условиях

где

n = (n₁, n₂, n₃, n₄, n₅) - вектор порядковых номеров видов аппроксимирующих функций, определяет вариант набора аппроксимирующих функций;

- порядковый номер функции, аппроксимирующей модель динамики ФСК, из конечного множества таких функций ;

- порядковый номер функции, аппроксимирующей модель измерения ФСК, из конечного множества таких функций ;

- порядковый номер функции, аппроксимирующей зависимость вероятностей смены вариантов воздействия уводящих помех от значений ФСК, из конечного множества таких функций ;

- порядковый номер функции, аппроксимирующей зависимость вероятностей смены показаний индикатора варианта воздействия уводящих помех от значений ФСК, из конечного множества таких функций ;

- порядковый номер вида аппроксимирующей условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех, из априорно задаваемого конечного множества таких функций;

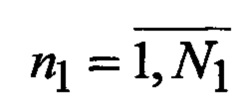
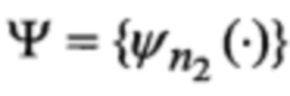
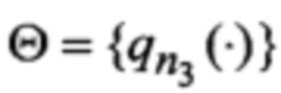
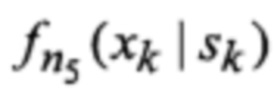
N - число альтернативных наборов видов аппроксимирующих функций;

N₁, N₂, N₃, N₄ и N₅ - число элементов множеств соответственно Φ, Ψ, Θ, P и F;

k - дискретный момент времени;

x_k = (D, V_п,k, ΔV_п,k, а_п,k, V_к,k, ΔV_к,k, а_к,k)^Т - вектор радиальных ФСК, включающих радиальные дальность до ВЦ, планерные и компрессорные составляющие радиальных скорости и ускорения взаимного перемещения носителя РЛС и цели;

- номер варианта воздействия уводящих помех (1 - отсутствие помех; 2 - воздействие только уводящей по скорости помехи; 3 - воздействие только уводящей по дальности помехи; 4 - воздействие уводящих как по скорости, так и по дальности помех);

- вектор измерений в РЛС функционально-связанных координат;

- выходные показания индикатора (обнаружителя) варианта воздействия уводящих помех;

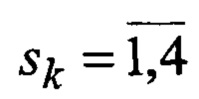
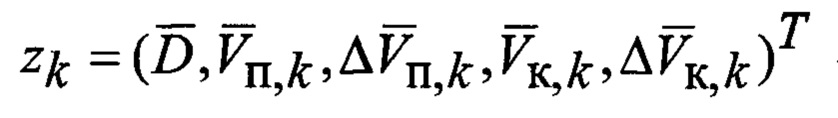
ξ_k, ζ_k - векторы соответственно случайных возмущений, действующих на ВЦ, и помех, воздействующих на РЛС;

ϕ(⋅) и ψ(⋅) - известные, в общем виде, нелинейные векторные детерменированные функции случайных аргументов;

- известные условные вероятности смены вариантов воздействия уводящих помех;

- известные условные вероятности смены показаний индикатора варианта воздействия уводящих помех;

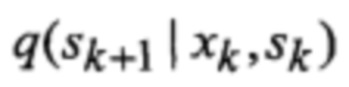
Φ(ξ_k, ζ_k) - совместная функция распределения возмущений и помех;

- условная функция распределения помех при фиксированных возмущениях;

Φ(ξ_k) - функция распределения возмущений;

ƒ(x_k,s_k) - совместная плотность вероятности ФСК и варианта воздействия уводящих помех;

- условная плотность вероятности ФСК при фиксированном варианте воздействия уводящих помех;

- условная плотность вероятности ФСК при фиксированном варианте воздействия уводящих помех и фиксированном варианте набора аппроксимирующих функций;

- прогнозируемая на один шаг дискретности вперед условная плотность вероятности ФСК при фиксированном варианте воздействия уводящих помех и фиксированном варианте набора аппроксимирующих функций;

- апостериорная условная плотность вероятности ФСК при фиксированном варианте воздействия уводящих помех и фиксированном варианте набора аппроксимирующих функций;

- n₅-й ВИД функции, аппроксимирующей условную плотность вероятности ФСК при фиксированном варианте воздействия уводящих помех;

- n₅-й вид функции, аппроксимирующей прогнозируемую на один шаг дискретности вперед условную плотность вероятности ФСК при фиксированном варианте воздействия уводящих помех;

- n₅-й вид функции, аппроксимирующей апостериорную условную плотность вероятности фазовых координат ФСК при фиксированном варианте воздействия уводящих помех;

- прогнозируемые на один шаг дискретности вперед и апостериорные соответственно вероятности воздействия уводящих помех по s_k+1-му варианту при фиксированном n-м варианте набора аппроксимирующих функций, условные МО функционально-связанных координат при фиксированном варианте воздействия уводящих помех и фиксированном n-м варианте набора аппроксимирующих функций, условные КМ ошибок оценивания ФСК при фиксированном варианте воздействия уводящих помех и фиксированном n-м варианте набора аппроксимирующих функций;

- начальные условия;

^_ условные плотности вероятности соответственно ФСК и их измерений в РЛС при фиксированных {s_k+1, x_k, s_k} и {х_k, s_k, r_k};

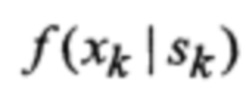
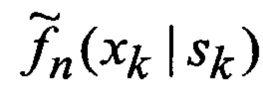
n_x, n_z - размерности соответственно векторов ФСК и их измерений;

- нормировочный коэффициент при фиксированном варианте набора аппроксимирующих функций;

- апостериорные условные квазиоптимальные оценки соответственно варианта воздействия уводящих помех (по критерию максимума апостериорной вероятности), математического ожидания ФСК и КМ ошибок их оценивания при фиксированном варианте набора аппроксимирующих функций;

- апостериорная вероятность соответствия варианта набора аппроксимирующих функций фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ, воздействия со стороны цели на РЛС помех, измерения в радиолокационной станции ФСК и идентификации в индикаторе помеховой обстановки варианта воздействия уводящих помех (далее фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ);

- квазиоптимальная по критерию максимума апостериорной вероятности идентификация моделей соответственно динамики ФСК , их измерений , смены варианта воздействия уводящих помех , индикатора (обнаружителя) варианта воздействия уводящих помех и условной плотности вероятности фазовых координат при фиксированном варианте воздействия уводящих помех , из вариантов набора аппроксимирующих функций задаваемых множествами Φ, Ψ, Θ, Р и F;

- квазиоптимальная по критерию максимума апостериорной вероятности оценка условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех смесью аппроксимирующих функций из множества F;

- апостериорные условные квазиоптимальные оценки соответственно варианта воздействия уводящих помех (по критерию максимума апостериорной вероятности), математического ожидания ФСК и КМ ошибок их оценивания при квазиоптимальном наборе аппроксимирующих смесей ;

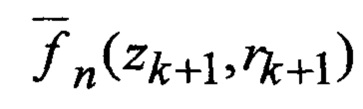
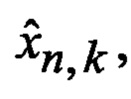
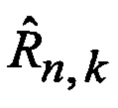
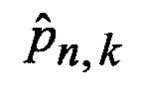
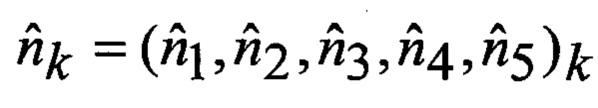
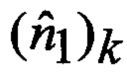
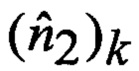
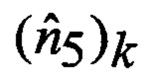
Т - операция транспонирования матрицы;

ехр{⋅} - экспоненциальная функция;

i - мнимая единица;

ω - частота;

Г: - статистическая гипотеза, заключающаяся в том, что …;

ϕ(s_k+1, x_k, s_k, ξ_k) → Φ: - в (28), выбор для заданной функции ϕ(s_k+1, x_k, s_k, ξ_k) множества Φ видов аппроксимирующих функций

, таких, что … (по аналогии в (31), (34), (36));

- n₁-й вид аппроксимирующей функции из множества Φ таких функций (по аналогии для функций ψ_n2 (⋅), q_n3 (⋅), π_n4 (⋅), f_n5 (⋅) из множеств Ψ, Θ, Р, F);

- функция, состоящая только из элементарных или табулированных функций (по аналогии для функций );

и - n₁-й и n₂-й виды функций, аппроксимирующих условные плотности вероятности соответственно ФСК и их измерений при фиксированных {s_k+1, x_k, s_k}, и {x_k, s_k, r_k},

- квантор всеобщности [( а,b)с - для любых а и b выполняется с];

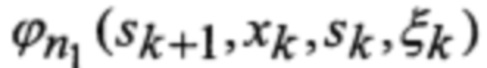
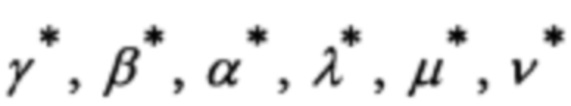
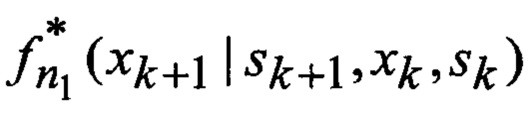
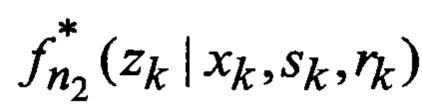
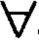
→ F - выбор множества F видов аппроксимирующих функций

,

и - условные соответственно МО функционально-связанных координат и КМ (для одномерного случая - дисперсия) ошибок их оценивания при фиксированной варианте воздействия уводящих помех s_k;

{Φ, Ψ, Θ, P, F}: - совокупность множеств видов аппроксимирующих функций таких, что …;

- функция правдоподобия;

- идентификация квазиоптимального вида аппроксимирующей функции модели динамики ФСК ϕ(s_k+1, х_k, s_k, ξ_k) по его порядковому номеру n₁ в множестве Φ видов таких функций (по аналогии для функций ϕ(⋅), q(⋅), π(⋅), ƒ(⋅) в множествах Ψ, Θ, Р, F);

- квазиоптимальная по критерию максимума апостериорной вероятности оценка модели динамики ФСК смесью аппроксимирующих функций из множества Φ;

- квазиоптимальная по критерию максимума апостериорной вероятности оценка модели измерения ФСК, смесью аппроксимирующих функций из множества Ψ;

- квазиоптимальная по критерию максимума апостериорной вероятности оценка модели смены варианта воздействия уводящих помех, смесью аппроксимирующих функций из множества Θ;

- квазиоптимальная по критерию максимума апостериорной вероятности оценка модели индикатора варианта воздействия уводящих помех, смесью аппроксимирующих функций из множества Р;

- квазиоптимальная по критерию максимума апостериорной вероятности оценка набора моделей соответственно динамики ФСК , их измерений , смены варианта воздействия уводящих помех , индикатора варианта воздействия уводящих помех и условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех , смесью априорно выбираемых аппроксимирующих функций из множеств Φ, Ψ, Θ, Р и F;

- апостериорные условные квазиоптимальные оценки соответственно варианта воздействия уводящих помех (по критерию максимума апостериорной вероятности), МО функционально-связанных координат и КМ ошибок их оценивания при квазиоптимальном наборе аппроксимирующих смесей ;

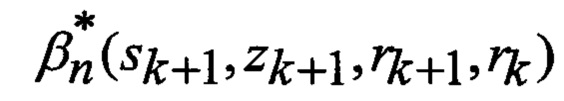
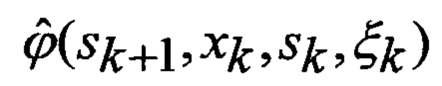
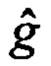
n^(s) - мощность (число элементов) множества вариантов воздействия уводящих помех;

x_min(s₀) и x_mах(s₀) - вектора соответственно минимальных и максимальных значений ФСК при фиксированном варианте воздействия уводящих помех в начальный момент времени;

x_{min i}(s₀) и x_{mах i}(s₀) - i-e компоненты векторов соответственно минимальных и максимальных значений ФСК при фиксированном варианте воздействия уводящих помех в начальный момент времени,

определяется оценка

варианта воздействия уводящих помех при оптимальном наборе аппроксимирующих смесей из априорно выбираемого множества функций, определяется оценка безусловного по отношению к вариантам воздействия уводящих помех математического ожидания ФСК при оптимальном наборе аппроксимирующих смесей, определяется оценка безусловной по отношению к вариантам воздействия уводящих помех ковариационной матрицы ошибок оценивания фазовых координат при оптимальном наборе аппроксимирующих смесей, на основе ММ (69)-(74) системы «ВЦ - РЛС - индикатор» со ССС, включающей, в общем виде, нелинейные и условно-марковские модели.

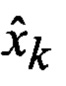
При этом, в качестве аппроксимирующих распределений предлагаются четырех-параметрические распределения Пирсона при известности (заданности) любых двух из его параметров [его частные случаи: гауссовское, усеченное гауссовское, бета-распределение (и его частные случаи: закон арксинуса, равномерное и степенное распределения), гамма-распределение (и его частные случаи: показательное и показательно-степенное распределения, χ² - распределение, закон Эрланга), Т-распределение Стьюдента], а также такие двухпараметрические распределения, как закон Симпсона, Релея, Максвелла, Парето, логистическое распределение и F-распределение Фишера [3].

Новыми признаками, обладающими существенными отличиями, являются:

1. Применение многоканального, как по числу вариантов воздействия уводящих помех, так и по числу вариантов набора аппроксимирующих функций, фильтра совместных оценивания радиальной дальности до цели, планерной и первой компрессорной составляющих радиальных скорости и ускорения взаимного перемещения носителя РЛС и цели, и распознавания варианта воздействия уводящих помех, функционирующего в соответствии с процедурой (1)-(74) квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания вместо одноканального, по числу вариантов набора аппроксимирующих функций, фильтра, функционирующего в соответствии с процедурой многомерной линейной дискретной калмановской фильтрации [1], и вместо одноканального, по числу вариантов набора аппроксимирующих функций, фильтра, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния марковской структуры линейной стохастической динамической системы при наблюдении без запаздывания на основе двухмоментной параметрической аппроксимации нормальным законом распределения [2, 3].

2. Автоматический выбор (51)-(56)набора видов аппроксимирующих функций из априорно задаваемых множеств (28), (31), (34), (36), (38) таких функций непосредственно в процессе функционирования фильтра.

3. Автоматическое формирование (57)-(61) набора смесей аппроксимирующих функций из априорно задаваемых множеств таких функций непосредственно в процессе функционирования фильтра.

4. Совместное оценивание ФСК (42), (43), (45), (46), (48), (49), (63), (64) и распознавание варианта воздействия уводящих помех (41), (44), (47), (62) на основе двухмоментной параметрической аппроксимации [3] в N многоканальных, по числу вариантов воздействия уводящих помех, квазиоптимальных фильтрах, отличающихся набором видов аппроксимирующих функций

, , , и в (41)-(49), на основе априорных данных о смене варианта воздействия уводящих помех и динамике ФСК, представленных соответственно начальными (74), (66) и переходными (71) вероятностями условной цепи Маркова и моделью (69), по результатам измерений в (19), (32), (44)-(46), (50) и показаниям индикатора варианта воздействия уводящих помех в (18), (36), (44)-(46), (50) с альтернативными моделями измерений (70), соответствующими различным вариантам воздействия уводящих помех, и моделью индикатора (72).

5. Комплексирование измерений РЛС с моделью (70) и показаний индикатора варианта воздействия уводящих помех с моделью (72).

6. Адаптация фильтра к различным вариантам воздействия уводящих помех с одновременным уточнением используемых математических моделей.

7. Прогнозирование (41) вероятностей

воздействия уводящих помех по каждому варианту на один шаг дискретности вперед в каждом фильтре при фиксированном варианте набора аппроксимирующих функций, на основе априорных данных о смене варианта воздействия уводящих помех, представленных соответственно начальными (74), (66) и переходными (71) вероятностями условной цепи Маркова.

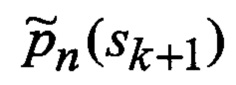
8. Прогнозирование (42) условных математических ожиданий

ФСК на один шаг дискретности вперед в каждом фильтре при фиксированных варианте набора аппроксимирующих функций и варианте воздействия уводящих помех, с учетом найденных вероятностей (41) на основе априорных данных о смене этих вариантов (71) и динамике ФСК взаимного перемещения носителя РЛС и ВЦ (69), с учетом найденной, как обратное преобразование Фурье от характеристической функции ФСК, в (20), (29) условной плотности вероятности и ее аппроксимирующей функции

9. Прогнозирование (43) условных КМ

ошибок оценивания ФСК на один шаг дискретности вперед в каждом фильтре при фиксированных варианте набора аппроксимирующих функций и варианте воздействия уводящих помех, с учетом найденных вероятностей (41) и математических ожиданий (42).

10. Оценивание (44) апостериорных вероятностей

воздействия уводящих помех по каждому варианту, в каждом фильтре при фиксированном варианте набора аппроксимирующих функций, по степени согласованности, представленной функцией правдоподобия, спрогнозированных вероятностей (41), математических ожиданий (42) ФСК и КМ (43) ошибок их оценивания с результатами измерений в (19), (32), (44)-(46), (50) и показаниями индикатора в (18), (36), (44)-(46), (50), с учетом найденной, как обратное преобразование Фурье от характеристической функции измерений, в (19), (32) условной плотности вероятности и ее аппроксимирующей функции

11. Оценивание (45) условных апостериорных математических ожиданий

ФСК взаимного перемещения носителя РЛС и ВЦ в каждом фильтре при фиксированном варианте набора аппроксимирующих функций, для каждой альтернативной модели измерения (70), соответствующей различным вариантам воздействия уводящих помех, на основе спрогнозированных математических ожиданий (42) и КМ (43) ошибок прогноза с учетом результатов измерения в (19), (32), (44)-(46), (50) и показаний индикатора в (18), (36), (44)-(46), (50).

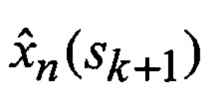
12. Оценивание (46) условных апостериорных КМ

ошибок фильтрации ФСК в каждом фильтре при фиксированном варианте набора аппроксимирующих функций, для каждой альтернативной модели измерения (70), соответствующей различным вариантам воздействия уводящих помех, на основе спрогнозированных математических ожиданий (42) и КМ (43) ошибок прогноза с учетом результатов измерения в (19), (32), (44)-(46), (50) и показаний индикатора в (18), (36), (44)-(46), (50).

13. Идентификация (47) такого

варианта воздействия уводящих помех в каждом фильтре при фиксированном варианте набора аппроксимирующих функций, для которого найденная апостериорная вероятность (44) окажется больше.

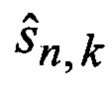
14. Нахождение (48) безусловной, по отношению к вариантам воздействия уводящих помех, оценки ФСК

в каждом фильтре при фиксированном варианте набора аппроксимирующих функций на основе апостериорных вероятностей (44) воздействия уводящих помех по каждому варианту и условных апостериорных оценок (45) ФСК, как безусловного математического ожидания.

15. Нахождение (49) безусловной по отношению к вариантам воздействия уводящих помех КМ

ошибок оценивания ФСК в каждом фильтре при фиксированном варианте набора аппроксимирующих функций с учетом найденных апостериорных вероятностей (44) воздействия уводящих помех по каждому варианту, условных математических ожиданий ФСК (45), условных КМ (46) ошибок их оценивания и безусловных оценок ФСК (48).

16. Коррекция (50) апостериорных вероятностей

соответствия наборов видов аппроксимирующих функций из задаваемых множеств таких функций фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ, для каждого фильтра на (k+1) -м шаге дискретности, по степени согласованности, представленной функцией правдоподобия, спрогнозированных вероятностей (41), математических ожиданий (42) ФСК и КМ (43) ошибок их оценивания с результатами очередных измерений в (19), (32), (44)-(46), (50) и показаний индикатора в (18), (36), (44)-(46), (50), с учетом найденной, как обратное преобразование Фурье от характеристической функции измерений, в (19), (31) условной плотности вероятности и ее аппроксимирующей функции

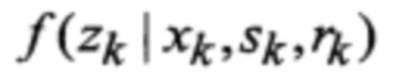
17. Идентификация (51)-(56)такого варианта набора аппроксимирующих функций (моделей)

из их множеств Φ, Ψ, Θ, Р и F, для которого найденная вероятность (50) окажется больше.

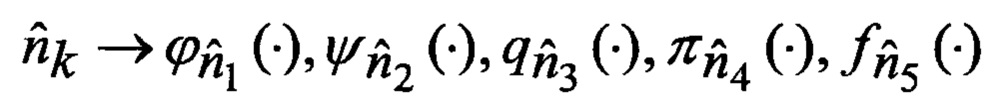
18. Оценивание (57)-(61) набора моделей соответственно динамики ФСК ϕ(⋅) их измерений в РЛС ψ(⋅), смены варианта воздействия уводящих помех q(⋅), индикатора воздействия уводящих помех и условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех

, набором смесей аппроксимирующих функций из априорно задаваемых множеств Φ, Ψ, Θ, Р и F, взятых с весовыми коэффициентами, пропорциональными вероятностям соответствия видов этих функций фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ.

19. Идентификация (62) варианта

воздействия уводящих помех с учетом оценок вероятностей (50) соответствия наборов видов аппроксимирующих функций фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ, и апостериорных условных вероятностей (44) воздействия уводящих помех по каждому варианту при фиксированном варианте набора аппроксимирующих функций.

20. Оценивание (63) ФСК

с учетом найденных условных оценок функционально-связанных координат (48) при фиксированном варианте набора аппроксимирующих функций и вероятностей (44), как безусловного, по отношению к вариантам набора аппроксимирующих функций, математического ожидания.

21. Оценивание (64) безусловной по отношению к вариантам набора аппроксимирующих функций КМ

ошибок оценивания ФСК с учетом найденных апостериорных вероятностей (50) соответствия вариантов набора аппроксимирующих функций фактическим видам закономерностей, условных математических ожиданий ФСК (48) и КМ (49) ошибок их оценивания при фиксированном варианте набора аппроксимирующих функций, и безусловных оценок ФСК (63).

22. Принятие равновероятными (66) и равномерными (67), (68), начальных условий (74), при отсутствии дополнительных априорных данных, соответственно для варианта воздействия уводящих помех и ФСК взаимного перемещения носителя РЛС и цели, как обладающих наибольшей мерой неопределенности (энтропией) соответственно среди дискретных и непрерывных законов распределения.

Данные признаки являются существенными и в известных технических решениях не обнаружены.

Применение всех новых существенных признаков позволит достоверно идентифицировать совместное или раздельное воздействие уводящих по дальности и скорости помех с одновременным формированием достоверных безусловных оценок дальности до ВЦ и скорости сближения носителя РЛС с нею путем адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности ФСК набором смесей априорно задаваемых видов функций за счет учета нелинейностей в динамике ФСК и их измерений, учета статистической зависимости вероятностей смены вариантов воздействия уводящих помех от ФСК, комплексирования информации РЛС и индикатора (обнаружителя) варианта воздействия уводящих помех, учета априорных данных о смене этих вариантов и адаптации системы наблюдения к ним.

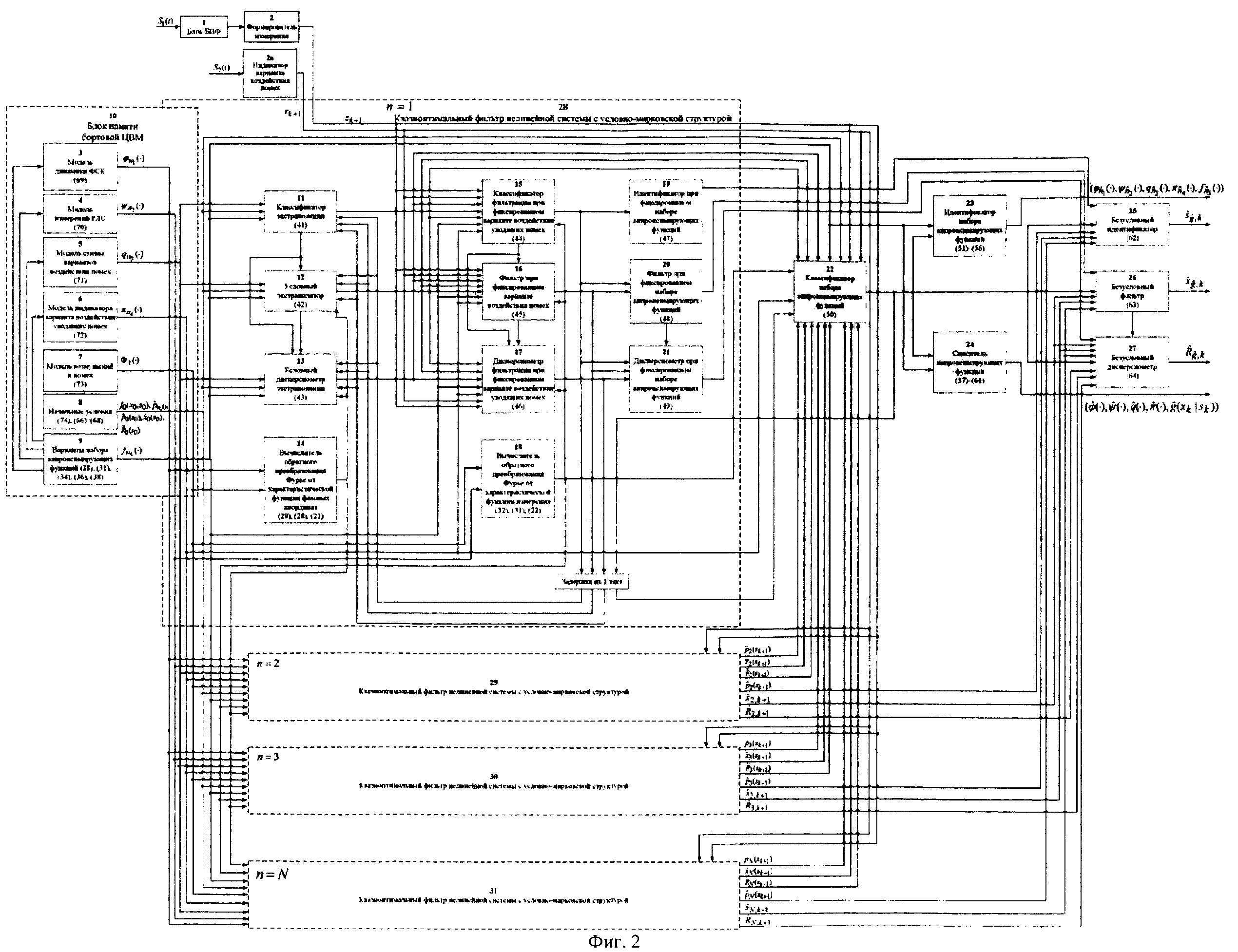
На фиг. 2 приведена блок-схема, поясняющая реализацию предлагаемого способа сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех.

Способ сопровождения ВЦ из класса «самолет с ТРД» и идентификации уводящих по дальности и скорости помех осуществляется следующим образом.

На вход известного блока 1 БПФ, используемого в [1], на промежуточной частоте с выхода приемника РЛС поступает сигнал S₁(t), отраженный от ВЦ, который подвергается узкополосной доплеровской фильтрации на основе процедуры БПФ и преобразуется в амплитудно-частотный спектр, составляющие которого обусловлены отражениями сигнала от планера сопровождаемой ВЦ и вращающихся частей КНД ее силовой установки.

В известном формирователе 2 измерения, используемом в [1], во-первых, определяется отсчет доплеровской частоты F_п(k+1), соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, который соответствует его отражениям от планера ВЦ, во-вторых, данный отсчет доплеровской частоты преобразуется в значение скорости, как V_п(k+1) = λF_п(k+1)/2 (где λ - рабочая длина волны РЛС), в-третьих, поступающее на вход измерение дальности в непрерывном времени D(t) преобразуется в дискретные отсчеты дальности D(k+1), в-четвертых, определяется отсчет доплеровской частоты F_к(k+1), соответствующий максимальной амплитуде спектральной составляющей спектра сигнала, находящейся справа по доплеровской частоте относительно спектральной составляющей сигнала, отраженного от планера ВЦ, в-пятых, данный отсчет доплеровской частоты преобразуется в значение скорости, как V_к (k+1) = λF_к(k+1) / 2.

В результате на выходе блока 2 формируется измерение z_k+1 = (D(k+1), V_п(k+1), V_к(k+1))^Т которое совместно с выходными показаниями индикатора 2а поступают на вход нового многоканального фильтра 28, 29, 30, 31 совместного оценивания радиальных дальности до ВЦ, планерных и компрессорных составляющих радиальных скорости и ускорения взаимного перемещения носителя РЛС и цели, фильтра, каждый канал которого функционирует в соответствии с известной процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания, структурная схема которой и описание приводятся в [3], и отличается только вариантом набора аппроксимирующих функций, положенным в основу этой процедуры. Многоканальный фильтр работает на основе априорных данных (69)-(74) в виде ММ системы «ВЦ -РЛС - индикатор» со ССС, включающей (блок 10 памяти бортовой ЦВМ) нелинейную модель динамики радиальных ФСК 3 взаимного перемещения носителя РЛС и ВЦ, представленную функцией модель их измерений в РЛС 4, представленную функцией ϕ_k(⋅), модель смены варианта воздействия уводящих помех 5, представленную переходными вероятностями q_k(⋅), модель индикатора варианта воздействия уводящих помех 6, представленную переходными вероятностями π_k+1(⋅), модель неуправляемых случайных возмущений и помех 7, представленную совместной функцией распределения Φ_k(⋅), при начальных ƒ₀(x₀, s₀),

, , условиях 8 и множестве (Φ, Ψ, Θ, P, F) наборов видов аппроксимирующих функций 9, также поступающих на вход многоканального фильтра 28, 29, 30, 31.

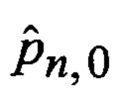
Сформированные на выходе многоканального фильтра 28, 29, 30, 31 прогнозируемые на один шаг дискретности вперед вероятности

, , воздействия уводящих помех по каждому варианту при фиксированном варианте набора аппроксимирующих функций, условные математические ожидания ФСК , , , при фиксированных варианте набора аппроксимирующих функций и варианте воздействия уводящих помех, условные КМ ошибок оценивания ФСК , , , при фиксированных варианте набора аппроксимирующих функций и варианте воздействия уводящих помех, поступают на вход нового классификатора варианта набора аппроксимирующих функций 22, функционирующего в соответствии с (50), на вход которого также с блока 10 памяти бортовой ЦВМ поступают априорные данные в виде аппроксимированной модели индикатора варианта воздействия уводящих помех 6, множества наборов видов аппроксимирующих функций 9 и начальных вероятностей 8 соответствия вариантов набора аппроксимирующих функций фактическим видам, с вычислителя обратного преобразования Фурье от характеристической функции измерения 18 поступает условная плотность вероятности , с формирователя 2 поступают результаты измерения ФСК z_k+1, с индикатора 2а варианта воздействия уводящих помех поступают его выходные показания r_k+1, а также поступают вероятности соответствия вариантов набора аппроксимирующих функций фактическим видам закономерностей, рассчитанные для предыдущего шага дискретности.

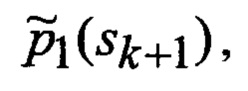
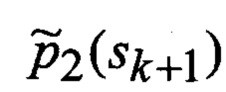
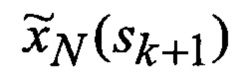
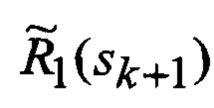
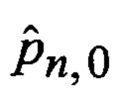
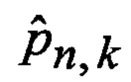
В результате на выходе блока 22 формируются вероятности

соответствия вариантов набора аппроксимирующих функций фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ, которые поступают на вход нового идентификатора варианта набора аппроксимирующих функций 23, функционирующего в соответствии с (51)-(56), нового смесителя аппроксимирующих функций 24, функционирующего в соответствии с (57)-(61), нового безусловного по отношению к вариантам набора аппроксимирующих функций идентификатора 25 варианта воздействия уводящих помех, функционирующего в соответствии с (62), нового безусловного по отношению к вариантам набора аппроксимирующих функций фильтра ФСК 26, функционирующего в соответствии с (63), и нового безусловного по отношению к вариантам набора аппроксимирующих функций дисперсиометра ФСК 27, функционирующего в соответствии с (64).

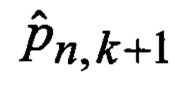
Помимо этого на вход идентификатора 23 и смесителя 24 поступают множества Φ, Ψ, Θ, Р и F видов аппроксимирующих функций 9, а на входы идентификатора 25, фильтра 26 и дисперсиометра 27 с выходов многоканального фильтра 28, 29, 30, 31 поступают соответственно апостериорные вероятности

, , , воздействия уводящих помех по каждому варианту при фиксированном варианте набора аппроксимирующих функций, условные математические ожидания ФСК , , , при фиксированном варианте набора аппроксимирующих функций и условные КМ ошибок оценивания ФСК , , , при фиксированном варианте набора аппроксимирующих функций. Также на вход дисперсиометра 27 поступают апостериорные условные математические ожидания ФСК , , при фиксированном варианте набора аппроксимирующих функций и найденное в безусловном фильтре 26 математическое ожидание ФСК .

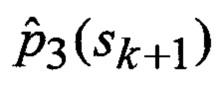
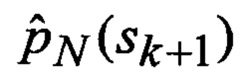
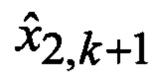
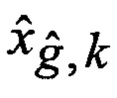
Сформированные на выходе идентификатора 23 оценка

варианта набора аппроксимирующих функций, на выходе смесителя 24 оценка варианта набора аппроксимирующих смесей, на выходе идентификатора 25 оценка варианта воздействия уводящих помех, на выходе фильтра 26 оценка математического ожидания ФСК, на выходе дисперсиометра 27 оценка КМ ошибок оценивания ФСК поступают на выход канала сопровождения ВЦ в РЛС.

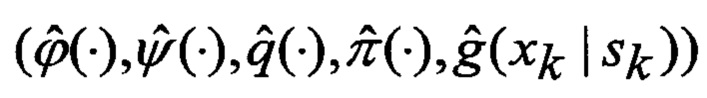
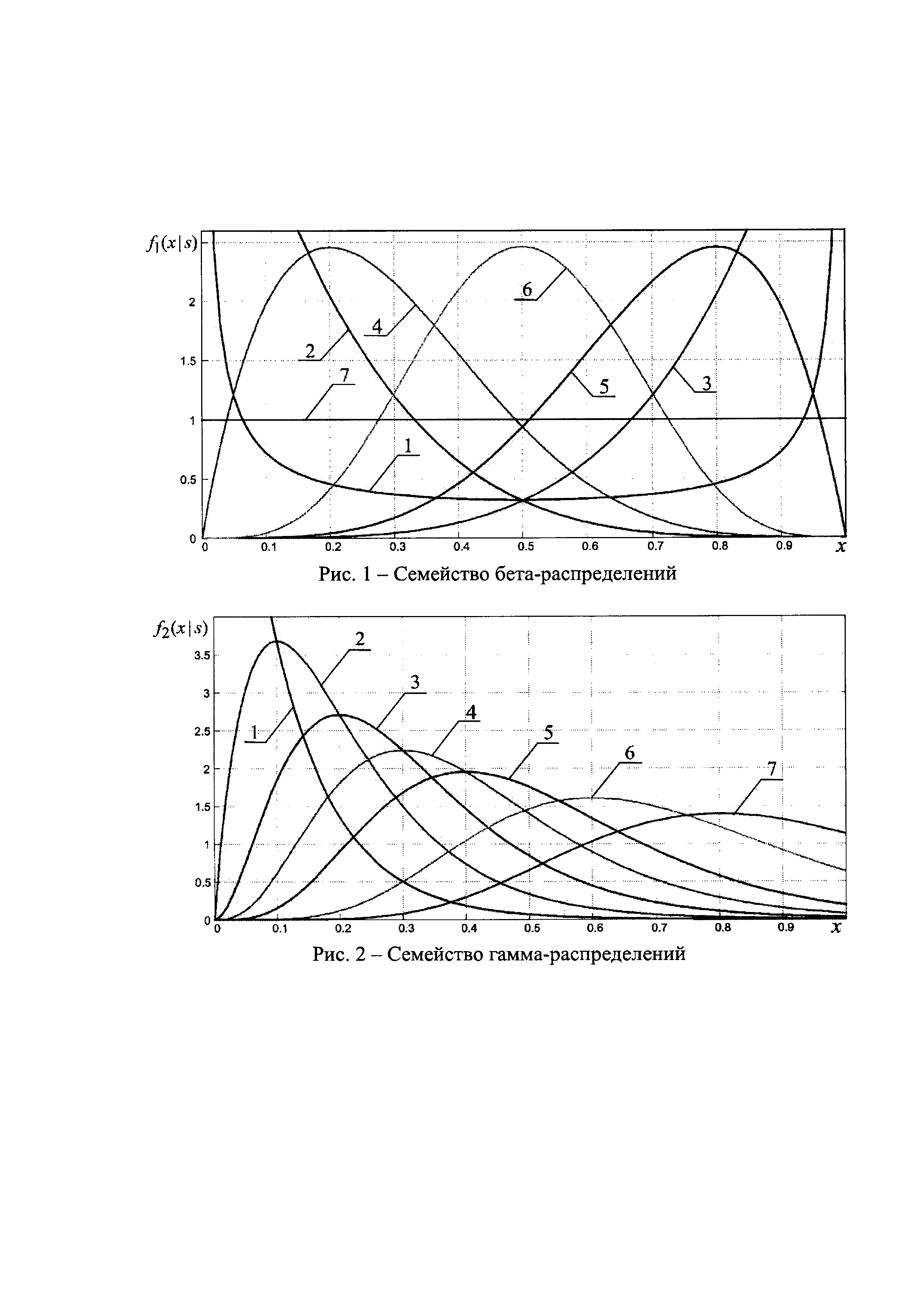
На фиг. 3 приведен пример семейства плотностей вероятности бета- (рис. 1) и гамма- (рис. 2) распределений (значения параметров распределений представлены соответственно в табл. 1 и 2), которые рассматриваются в качестве элементов множества F альтернативных условных плотностей вероятности ФСК при фиксированном варианте воздействия уводящих помех (38), а также конкретных реализаций этих альтернативных аппроксимирующих плотностей (рис. 3, 5, 7, 9) и соответствующих им семейств смесей (87 г) из этих плотностей (рис. 4, 6, 8, 10) при различных значениях вероятностей

, построенных по исходным данным табл. 3.

Плотность вероятности бета-распределения, обобщенная на случай произвольного отрезка [c;d], с необходимыми выражениями параметров распределения через условное МО и дисперсию, определяются соотношениями

а плотность вероятности гамма-распределения имеет вид

где

a{s_k) и b(s_k) - параметры бета-распределения, зависящие от условного МО компоненты

вектора ФСК и дисперсии ошибки ее оценивания при фиксированном варианте s_k воздействия уводящих помех;

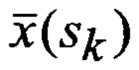
c и d - соответственно левая и правая границы, возможных значений рассматриваемой компоненты вектора ФСК;

B(a(s_k),b(s_k)) - бета-функция;

α(s_k) и β(s_k) - параметры гамма-распределения, зависящие от условного МО компоненты

вектора ФСК и дисперсии ошибки ее оценивания при фиксированном варианте воздействия уводящих помех s_k;

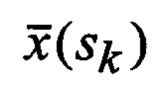
Г(α(s_k)) - гамма-функция.

При этом сущность процедуры квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы заключается в следующем.

1. На основании априорных данных, представленных ММ системы «ВЦ - РЛС - индикатор» (69)-(74), выдвигается (28), (31), (34), (36), (38) гипотеза Г об альтернативных видах

, аппроксимирующих функций, удовлетворяющих условиям нормировки (30), (33), (35), (37) и обеспечивающих (40) при их подстановке в (1)-(6), (10), (17)-(20) выражение интегралов алгоритма через элементарные или табулированные функции. При этом для аппроксимации условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех выбираются такие функции , параметры которых зависят не более чем от первых двух вероятностных моментов - вектора условных МО фазовых координат и условных КМ ошибок их оценивания, и связаны с ними простыми алгебраическими соотношениями, например бета- и гамма- распределения (75), (76), представленные на фиг. 3, рис. 1, 2.

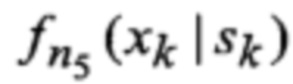
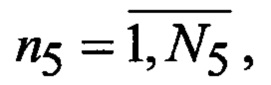
2. Система уравнений замыкается и сложные интегральные рекуррентные уравнения (1)-(27) вырождаются в новые обыкновенные рекуррентные уравнения (41)-(65) относительно условных вероятностей

воздействия уводящих помех по каждому варианту при фиксированном варианте набора аппроксимирующих функций, условных МО функционально-связанных координат и КМ ошибок их оценивания при фиксированных варианте набора аппроксимирующих функций и варианте воздействия уводящих помех.

3. В соответствии с выражениями (41)-(49) находятся условные квазиоптимальные по критерию максимума апостериорной вероятности оценки варианта

воздействия уводящих помех, МО функционально-связанных координат и КМ ошибок их оценивания при фиксированном варианте набора аппроксимирующих функций.

4. С учетом выдвинутой гипотезы в соответствии с (50) находятся апостериорные вероятности

соответствия варианта набора аппроксимирующих функций фактическому виду закономерностей взаимного перемещения носителя РЛС и ВЦ.

5. С учетом выдвинутой гипотезы и найденных вероятностей в соответствии с (57)-(61) оценивается набор моделей динамики ФСК, их измерений в РЛС, смены вариантов воздействия уводящих помех, индикатора таких вариантов и условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех, набором

смесей аппроксимирующих функций из априорно задаваемых множеств таких функций, взятых с весовыми коэффициентами, пропорциональными вероятностям соответствия видов этих функций видам фактических закономерностей взаимного перемещения носителя РЛС и ВЦ.

6. С учетом найденных условных оценок

и при фиксированном варианте набора аппроксимирующих функций, и апостериорных вероятностей соответствия наборов видов этих функций видам фактических закономерностей, в соответствии с (62)-(64) находятся безусловные, по отношению к вариантам набора аппроксимирующих функций, квазиоптимальные по критерию максимума апостериорной вероятности оценки варианта воздействия уводящих помех, МО функционально-связанных координат и КМ ошибок их оценивания.

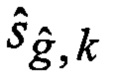
7. При отсутствии дополнительных априорных данных, начальные условия для вероятностей воздействия уводящих помех по фиксированному варианту принимаются равновероятными (66), а для МО функционально-связанных координат и КМ ошибок их оценивания - равномерными (67), (68), как обладающие наибольшей энтропией.

На рис. 4, 6, 8, 10 представлены итоговые аппроксимирующие смеси из бета- и гамма- распределений, взятых с весовыми коэффициентами из табл. 3.

Результаты сравнительного моделирования предлагаемого способа сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех на основе многоканального фильтра совместных оценивания радиальных дальности до цели, планерные и компрессорные составляющие радиальных скорости и ускорения взаимного перемещения носителя РЛС и цели, и распознавания варианта воздействия уводящих помех, функционирующего в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания на основе адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно задаваемых аппроксимирующих функций, и известного способа сопровождения ВЦ из класса «самолет с ТРД» при воздействии уводящих по дальности и скорости помех [2] свидетельствуют с доверительной вероятностью 0,99 о снижении СКО ошибки фильтрации на 9±0,1% и о повышении вероятности правильного распознавания варианта воздействия уводящих помех на 8±0,1%.

Таким образом, применение предлагаемого изобретения позволит повысить достоверность совместного или раздельного воздействия уводящих помех и оценки радиальных функционально-связанных дальности до ВЦ и скорости сближения носителя РЛС с нею путем адаптивной двухмоментной параметрической аппроксимации неизвестных плотностей вероятности смесью априорно задаваемых аппроксимирующих функций и приближением получаемых оценок к их оптимальным значениям за счет учета нелинейностей в динамике ФСК и их измерений, учета статистической зависимости вероятностей смены вариантов воздействия уводящих помех от ФСК, комплексирования информации РЛС и индикатора варианта воздействия уводящих помех, учета априорных данных о смене этих вариантов и адаптации системы наблюдения к ним.

ИСТОЧНИКИ ИНФОРМАЦИИ

1. Богданов А.В., Васильев О.В., Докучаев Я.С. Способ сопровождения воздушной цели из класса «самолет с турбореактивным двигателем» при воздействии уводящих по дальности и скорости помех. Патент на изобретение №2665031, 2018 (аналог).

2. Мужичек С.М., Филонов А.А., Скрынников А.А., Федотов А.Ю., Ткачева О.О., Викулова Ю.М., Корнилов А.А., Макашин С.Л. Способ сопровождения воздушной цели из класса «самолет с турбореактивным двигателем» при воздействии уводящих по дальности и скорости помех. Патент на изобретение №2713635 от 05.02.20 (прототип).

3. Бухалев, В.А. Оптимальное сглаживание в системах со случайной скачкообразной структурой / В.А. Бухалев. М.: ФИЗМАТ ЛИТ, 2013, страницы 115, 116, 117.

Реферат

Изобретение относится к области цифровой обработки радиолокационных сигналов и может быть использовано в радиолокационной станции (РЛС) для формирования при сопровождении воздушной цели (ВЦ) из класса «самолет с турбореактивным двигателем» достоверной идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех или отсутствия их воздействия и оценки радиальных функционально-связанных координат (ФСК) взаимного перемещения ВЦ и носителя РЛС при различных вариантах воздействия таких помех. Технический результат - повышение достоверности идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех и оценки дальности до ВЦ и скорости сближения носителя РЛС с ней. Способ заключается в идентификации совместного или раздельного воздействия уводящих по дальности и скорости помех или отсутствия их воздействия и оценки радиальных функционально-связанных дальности до ВЦ и скорости сближения носителя РЛС с ней путем адаптивной двухмоментной параметрической аппроксимации (АДПА) неизвестных плотностей вероятности фазовых координат смесью априорно задаваемых аппроксимирующих функций и приближением получаемых оценок к их оптимальным значениям за счет учета нелинейностей в динамике ФСК и их измерений, учета статистической зависимости вероятностей смены вариантов воздействия уводящих помех от ФСК, комплексирования информации РЛС и индикатора варианта воздействия уводящих помех, учета априорных данных о смене этих вариантов и адаптации системы наблюдения к ним. В способе проводят узкополосную доплеровскую фильтрацию сигнала, отраженного от цели, с использованием процедуры быстрого преобразования Фурье, формирование отсчетов доплеровских частот, обусловленных отражениями сигнала от планера и лопаток рабочего колеса первой ступени компрессора низкого давления силовой установки ВЦ, и обработку сформированных отсчетов доплеровских частот и выходных показаний индикатора варианта воздействия уводящих помех в многоканальном фильтре совместных сопровождения ВЦ и первой компрессорной составляющей спектра сигнала и идентификации варианта воздействия уводящих помех. Указанный фильтр функционирует в соответствии с процедурой квазиоптимальной совместной фильтрации фазовых координат и распознавания состояния условно-марковской структуры нелинейной стохастической динамической системы при наблюдении без запаздывания. На выходе фильтра формируются оценки условной плотности вероятности ФСК при фиксированном варианте воздействия уводящих помех. 12 ил.

Формула