Способ шифрования двоичной информации - RU2701128C1

Описание

Изобретение относится к области криптографии. Предлагается способ шифрования, обеспечивающий высокую криптозащиту двоичной информации.

Под высокой криптозащитой здесь понимается такое шифрование, при котором:

- единственным способом вскрытия двоичной информации является перебор всех возможных ключей шифрования;

- время полного перебора ключей шифрования превышает срок конфиденциальности зашифрованной информации.

Предлагаемый способ шифрования пригоден для текстовой, графической, речевой и других типов информации, представленных двоичными последовательностями.

Из уровня техники известны различные способы и устройства для шифрования информации, отраженные в патентных документах: RU 2642351 (С1), дата публикации 24.01.2018; KR 20160067992 (А), дата публикации 14.06.2016; GB 1518997 (А), дата публикации 26.07.1978; ЕР 0492325 (А2), дата публикации 01.07.1992; RU 2013802 (А), дата публикации 30.05.1994; SU 1265973 (А1), дата публикации 23.10.1986; US 2018011691 (А1), дата публикации 11.01.2018; ES 2644485 (Т3), дата публикации 29.11.2017; CN 107683502 (А), дата публикации 09.02.2018. Однако указанные технические решения не обеспечивают достаточной криптоустойчивости.

Аналогами предлагаемого способа шифрования являются решения, описанные в патентах RU 2091983, дата публикации 27.09.1997; RU 2032990, дата публикации 10.04.1995; RU 2119260, дата публикации 20.09.1998.

В устройстве по патенту №2091983 сделана попытка для каждой порции текста на основе единственного секретного ключа построить «индивидуальный» поточный шифр с учетом значения самой порции текста. Недостатком этого устройства является использование в его структуре весьма сложного устройства возведения

кода (i-1) группы поточного шифра в степень m по модулю Р, а также использование одного фиксированного секретного ключа с числом бит, равным разрядности одной порции текста.

Известен способ шифрования Вернама [1], в котором двоичная последовательность, представляющая информационные элементы сообщения

шифруется множеством ключей по формуле:

где

а знак обозначает сложение по модулю 2.

Для расшифровки необходимо осуществить операцию:

Такой способ шифрования обеспечивает совершенную секретность шифра только в том случае, если ключ

удовлетворяет следующим требованиям:

- должен быть очень длинным (на все сообщение);

- применяться только один раз;

- состоять из списка случайных равномерно распределенных значений битов.

Удовлетворить этим требованиям на практике достаточно трудно.

Более близким к заявленному способу является техническое решение, приведенное в патенте №2119260, в котором предлагается модифицировать блочный шифр. Информацию блока из 48 бит предлагается разбить на участки, которые преобразуются под управлением случайного двоичного вектора. Затем к преобразованным участкам двоичного кода информации присоединяется псевдослучайный двоичный вектор. После этого выполняется преобразование блока данных под управлением ключа шифрования

Недостатками этого способа являются следующие положения.

1. Генерирование двоичных векторов предлагается выполнять по «случайному (или псевдослучайному) закону путем измерения вероятностного физического процесса или измерения сигнала датчика шума, в качестве которого во многих приложениях используются специально сконструированные электронные устройства». Такие устройства достаточно сложны и не всегда доступны.

2. Для предварительного преобразования кода текста формируется вспомогательный ключ

представляющий собой повторение двоичного вектора V несколько раз. Повторение вспомогательного ключа несколько раз снижает стойкость шифрования.

Достаточно близким аналогом является решение по патенту №2032990, в котором текст разбивается на группы, представляющие собой порции двоичной информации. «При зашифровывании очередной порции двоичной информации применяется новое

функциональное преобразование, выработанное с использованием зависящего от секретного ключа криптографического способа шифрования двоичной информации». функциональное преобразование задается таблицей. «Известным, зависящим от ключа, и нового, например, случайного начального состояния, способом шифрования двоичной информации вырабатывается последовательность псевдослучайных бит достаточной длины». Из этой последовательности «нарезаются» последовательности таблицы, выполняющие функциональное преобразование.

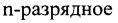
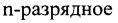
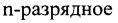
При расшифровке информации надо также предварительно набрать задающую функциональное преобразование таблицу. Для этого нужно знать использованные при зашифровывании для набора таблицы ключ и начальное состояние.

Недостатком этого способа также является то, что для формирования таблицы необходимо формировать псевдослучайную двоичную последовательность достаточной длины. Причем при шифровании и расшифровке текста необходимо знать способ формирования таблицы.

Решения, описанные в патентах №2119260 и №2032990, имеют еще тот недостаток, что знание хотя бы одного текста дает возможность хакеру вычислить ключ шифрования и, тем самым, вскрыть все последующие и предыдущие тексты (недостаточная криптозащита).

Техническим результатом заявленного способа является повышение криптозащиты информации.

Для достижения указанного результата предлагается способ шифрования, при котором двоичное представление текста разбивается на сообщения, каждое сообщение представляется двумя криптограммами, одна из которых получена с помощью зашифрованной одним из двух ключей произвольно выбранной из полного кода последовательности, являющейся таблицей замены символов для этого сообщения, а другая криптограмма представляет собой зашифрованную вторым ключом таблицу замены символов для этого сообщения.

В предлагаемом способе шифрования текст разбивается на сообщения C1, С2, …Ck одинаковой длины. Это позволяет шифровать сообщения ключами одной длины.

Набор символов каждого сообщения С (каждой двоичной последовательности ДП_С) искажается (шифруется) с помощью произвольного набора символов (с помощью произвольной двоичной последовательности ДП_Т), сформированного для этого сообщения. Последовательность ДП_Т шифруется ключом шифрования ДП_К. Шифр сообщения С представляется двумя криптограммами: искаженной последовательностью ДП_С (искаженным сообщением С) и зашифрованной последовательностью ДП_Т. При этом используется одно и то же преобразование последовательностей ДП_С и ДП_Т.

Это реализуется с помощью модифицированного шифра простой замены и модифицированного шифрования, предложенного в патенте RU 2598784, дата публикации 27.09.2016.

В шифре простой замены используется таблица замены символов алфавита. Это приводит к тому, что символы зашифрованного текста имеют ту же статистику, что и исходный текст, но для других символов, т.е. если в исходном сообщении частота встречи какого-либо символа равна f, то в шифрограмме с такой же частотой будет встречаться соответствующий ей символ.

Модификация шифра простой замены заключается в том, что, вместо таблицы замены символов алфавита, предлагается использовать таблицу замены символов сообщения, т.е. для каждого сообщения Cj используется своя таблица замены символов сообщения.

Если таблицу замены символов сообщения выбирать произвольно, то набор символов сообщения Cj будет заменен на произвольный набор символов алфавита (в зашифрованном тексте могут появиться символы, которых не было в сообщении Cj). Вскрыть таким образом зашифрованное сообщение можно будет только методом перебора всех таблиц замены символов сообщения.

Реализация модифицированного шифра простой замены основывается на способе шифрования, предложенном в патенте №2598784, в котором для шифрования информации, представленной двоичными последовательностями, используется преобразование:

где ФУ_j - функции Уолша, используемые как сообщения, ДП_k - ключ шифрования, ДП_jk - криптограмма сообщения ФУ_j.

Показано, что если функции Уолша рассматривать как алфавит равновероятных символов, из которых формируются независимые сообщения, то в соответствии с [2] криптограммы ДП_jk будут строго идеальными (совершенно секретными) шифрами.

Модификация этого способа шифрования состоит в том, что вместо преобразования (1) предлагается использовать обобщенное преобразование:

где ДП_С - сообщения из

битов, ДП_k - ключ шифрования из битов, а ДП_Кр - криптограммы сообщений ДП_С. Очевидно, что последовательности ДП_С, ДП_k и ДП_Кр принадлежат полному коду.

Если последовательности полного кода рассматривать как алфавит равновероятных символов, из которых формируются независимые сообщения, то преобразование (2), как и преобразование (1), формирует совершенно секретные криптограммы ДП_Кр.

В (2) последовательность ДП_k можно рассматривать как таблицу замены символов сообщения ДП_С. Сформируем для каждого сообщения Cj свою таблицу замены символов сообщения ДП_Cj. В этом случае (2) можно записать как:

В качестве последовательностей

будем использовать произвольно выбранные последовательности из полного кода. Каждая из последовательностей будет содержать свой набор символов алфавита. Преобразование символов последовательности ДП_Cj с помощью произвольного набора символов последовательности даст произвольный набор символов в последовательности

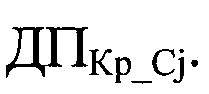
Для расшифровки сообщения ДП_Cj необходимо знать последовательность

следовательно, последовательность необходимо передать расшифровку. Это можно сделать, если вместе с зашифрованным текстом сообщения Cj передать зашифрованную последовательность Шифрование последовательности осуществляется с помощью того же преобразования (2), в котором в качестве сообщения выступает последовательность а в качестве ключа шифрования последовательность ДП_k. Так как последовательность была выбрана из полного кода произвольно и независимо, то криптограмма сообщения будет в соответствии с [2] совершенно секретной.

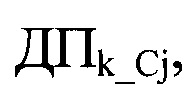
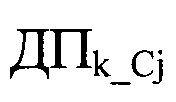
Поясним работу предлагаемого способа шифрования на примере русского алфавита, состоящего из 32 символов (из 31 буквы алфавита и символа «пробел»). Каждый символ представляется двоичным кодом из 5 битов.

Пусть в сеансе j надо передать текст, состоящий из 116 символов. Заменяя символы их кодами, получим последовательность из 580 битов. Эта двоичная последовательность разбивается на сообщения C1, С2, С3, С4, С5 по 120 битов каждая. Сообщение С5 дополняется до 120 бит случайно выбранными значениями «0» или «1». Полученные последовательности обозначим как

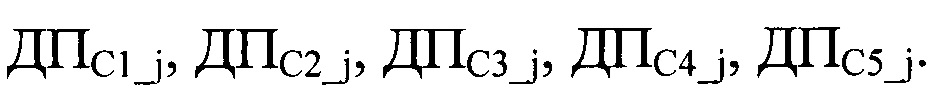
Количество бит в сообщении определяет длину ключей шифрования. Чем больше длина сообщений, тем больше множество возможных ключей, тем больше время перебора.

Шифрование передаваемой двоичной информации осуществляется двумя 120-и битными ключами

и которые постоянны в течение j-го сеанса передачи текста. Ключом шифрования может быть любая последовательность полного кода. Необходимость двух ключей шифрования будет обоснована в разделе «Криптоанализ предлагаемого способа шифрования».

Шифрование текста в j-ом сеансе

Из полного кода случайным образом выбирается количество последовательностей на две единицы больше, чем количество сообщений шифруемого текста (способ и техническая реализация такого выбора последовательностей будет показана в разделе «Криптоанализ предлагаемого способа шифрования»). В нашем примере это будут семь последовательностей

- пять последовательностей, которые используются в качестве таблиц замены символов для сообщений C1, С2, С3, С4, С5, и две последовательности - новые ключи шифрования ДП_К1 и ДП_К2 для сеанса (j+1).

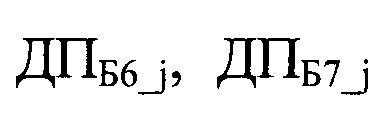
Шифрование последовательности

1. Шифруется таблица замены

для символов сообщения С1:

Необходимость шифрования таблицы замены символов сообщения С1 будет обоснована в разделе «Криптоанализ предлагаемого способа шифрования».

2. Ключом шифрования

шифруется последовательность

Символы сообщения С1 шифруются с помощью последовательности

Последовательность

является зашифрованной таблицей замены для сообщения С1. Так как сформирована с помощью произвольно выбранной последовательности то набор символов в также произволен. Следовательно, набор символов последовательности (набор символов сообщения С1) будет заменен на произвольный набор символов алфавита. Вскрыть таким образом зашифрованное сообщение можно будет только методом перебора всех возможных таблиц замены.

Таким образом, для конфиденциальной передачи сообщения С1, необходимо передать две криптограммы:

и

Шифрование последовательности

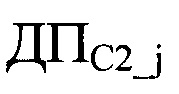
1. Шифруется таблица замены

для сообщения С2:

2. Ключом шифрования

шифруется последовательность

3. Символы сообщения С2 шифруются с помощью зашифрованной таблицы замены

Таким образом, для конфиденциальной передачи сообщения С2, необходимо передать две криптограммы:

и

Аналогично шифруются сообщения С3, С4 и С5. В результате получаются: для сообщения С3 - криптограммы

для сообщения С4 - криптограммы и для сообщения С5 - криптограммы и

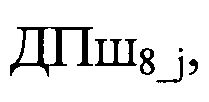
Формирование новых ключей шифрования для сеанса (j+1).

1. Последовательности

и шифруются ключом шифрования

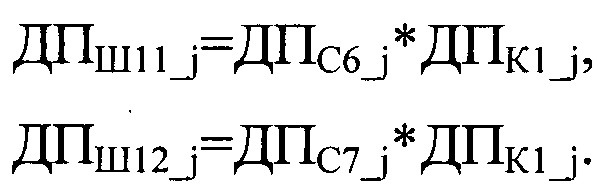
Таким образом, криптограммы последовательностей

будут представлены последовательностями

Расшифровка текста в i-ом сеансе

Расшифровка сообщения С1.

1. С помощью криптограммы

вычисляется последовательность (таблица замены символов для сообщения С1):

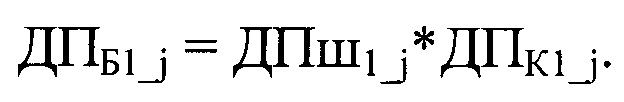
2. С помощью ключа

и последовательности вычисляется последовательность (зашифрованная таблица замены символов для сообщения С1):

3. С помощью криптограммы

вычисляется последовательность

Расшифровка сообщения С2.

1. С помощью криптограммы

вычисляется последовательность

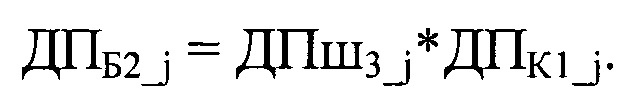
2. С помощью ключа

и последовательности вычисляется последовательность

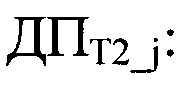
3. С помощью криптограммы

вычисляется последовательность

Аналогичным образом расшифровываются сообщения С₃, С₄, С₅.

Вычисляются последовательности

и

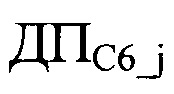
Объединением последовательностей С₁, С₂, С₃, С₄, С₅ формируется двоичная последовательность из 600 символов, которая при разбиении на группы по 5 бит даст исходный текст.

Последовательности

и будут использованы в качестве новых ключей шифрования в сеансе

Криптоанализ предлагаемого способа шифрования

1. Последовательности полного кода рассматриваются как равновероятные символы алфавита. Из полного кода случайно и независимо выбираются последовательности (символы)

В соответствии с [2] криптограммы

будут идеальными шифрами, которые вскрыть нельзя.

Это можно обосновать еще и следующим образом.

Выполним преобразование:

для всех последовательностей полного кода:

где m=2ⁿ.

Преобразуем (3) в вид:

Из (4) видно, что произвольная последовательность ДП_К может быть сформирована

разными парами последовательностей полного кода.

В нашем примере каждая из криптограмм

может быть получена 2¹²⁰ разными парами последовательностей. Зная последовательности хакер не сможет определить те пары, с помощью которых были образованы эти последовательности, т.е. вскрыть криптограммы без знания ключа невозможно.

2. Криптограммы

также получены преобразованием (2), а именно:

Последовательности (сообщения)

нельзя рассматривать в качестве произвольных наборов символов алфавита. Однако, в силу того, что последовательности состоят из произвольных наборов символов, то криптограммы будут представлять собой тексты с произвольными наборами символов. Вскрыть такие сообщения без знания таблицы замены можно только методом перебора всех таблиц замены (всех возможных последовательностей ).

3. Необходимость двух ключей шифрования и шифрования таблиц замены символов.

Последовательности

являются таблицами замены символов сообщений C1, С2, …, С5. Если эти таблицы замены не шифровать, то криптограммы будут уязвимыми. Например, сообщение С1 будет формироваться уравнениями:

Это тоже способ шифрования. Однако в этом случае существенно снижается безопасность шифра. Действительно, если хакер каким-то способом узнал (или ему удалось вскрыть) одно из сообщений, например, сообщение С1, то из второго уравнения он сможет вычислить последовательность

а из первого уравнения ключ шифрования Зная ключ шифрования, хакер вскроет остальные сообщения С2, С3, С4, С5, т.е. весь текст.

Введение второго ключа шифрования, с помощью которого шифруется таблица замены

исключает такую возможность.

Действительно, зашифрованное сообщение С1 представлено двумя криптограммами, полученными из уравнений:

Зная последовательности

и хакер сможет вычислить последовательность (зашифрованную таблицу замены для сообщения С1). Но последовательность образована уравнением:

В этом уравнении хакеру неизвестны ни последовательность

ни последовательность

Таким образом, знание последовательности

не позволит ему вычислить другие ключи шифрования и другие сообщения.

Техническая реализация предлагаемого способа шифрования

В основе технической реализации предлагаемого способа шифрования лежат: способ реализации преобразования (2) и способ выбора случайным образом последовательности из полного кода.

1. Техническая реализация преобразования (2) представляет собой побитное умножение двух последовательностей в соответствии с некоторым правилом. Такая операция выполняется на компьютере просто и быстро. Она просто реализуется и в виде устройства.

2. Выбор случайным образом последовательности из полного кода можно реализовать, используя известные устройства и программы, описанные в [3], [4], [5] и в других источниках.

Один из способов, реализованных автором, состоит в следующем.

Берется

маска, которая заполняется значениями или «1». Эти значения формируются с помощью линейного конгруэнтного генератора псевдослучайных чисел, который задается выражением:

где а, с и

- некоторые коэффициенты.

Коэффициенты а, с и

выбираются таким образом, чтобы период последовательности из случайных чисел превышал

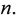
Рассмотрим конкретный пример формирования 120-битной маски.

Пусть а=13, с=7,

=257, Х₀=13. Последовательность псевдослучайных чисел, выданных линейным конгруэнтным генератором при этих значениях коэффициентов, приведена в таблице 1.

Выделим из полученной последовательности 120 первых псевдослучайных чисел. В таблице 2 эти числа представлены двоичными кодами.

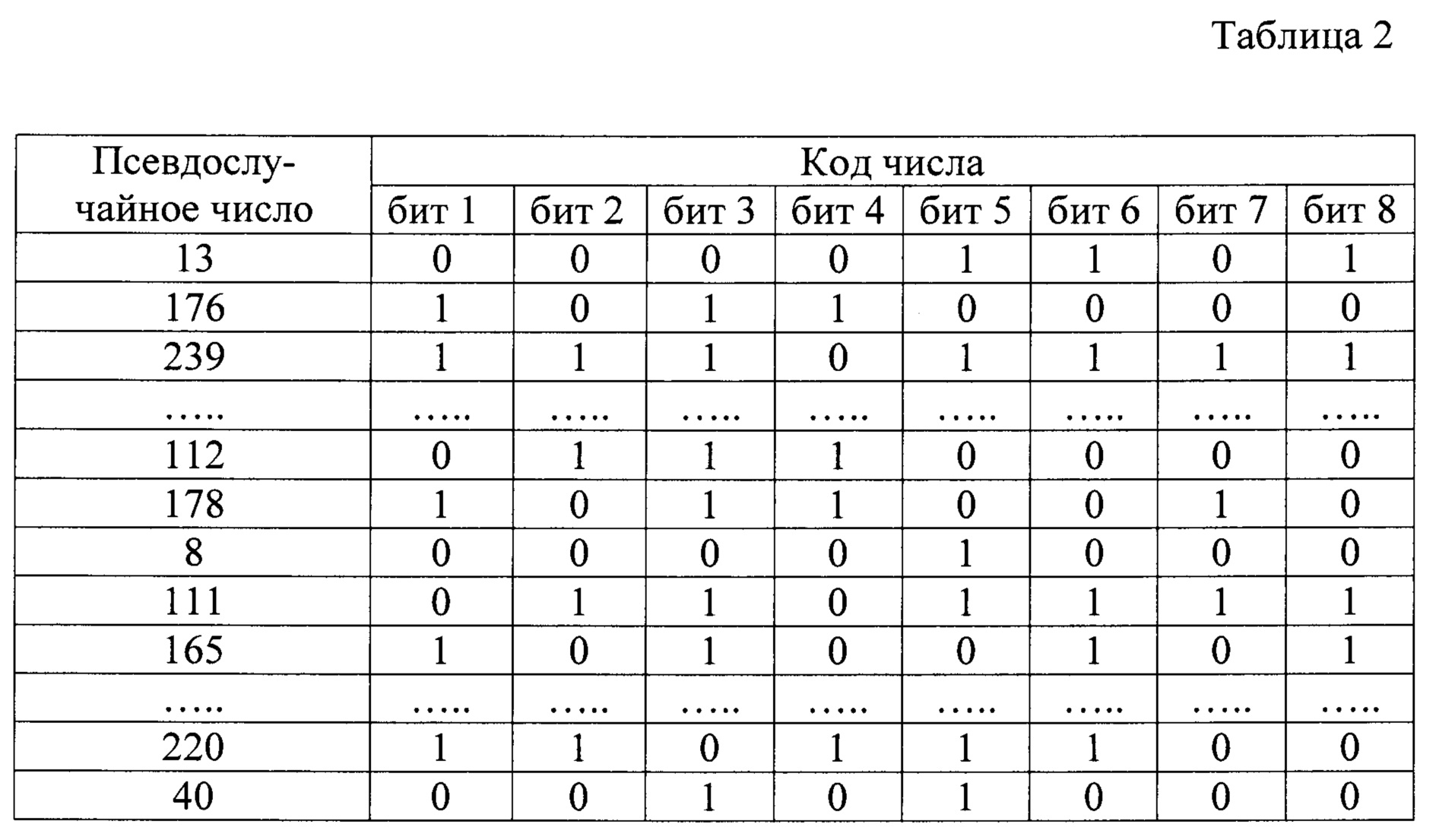
Произвольным образом выбираются, например, пятые биты кодов всех псевдослучайных чисел. Получим последовательность:

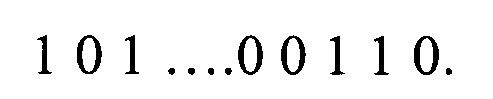
Можно менять коэффициенты а, с и

и получать большое разнообразие псевдослучайных чисел, а, следовательно, большое количество 120-и битных масок.

Можно из одной и той же последовательности псевдослучайных чисел, выбирая разные номера бит или пары бит, получать большое разнообразие 120-и битных масок.

Все полученные последовательности будут принадлежать полному коду последовательностей длиной 120 бит.

Такой способ формирования последовательностей

произволен и непредсказуем. Его нельзя определить по криптограммам.

Предлагаемый способ шифрования не требует псевдослучайности каких-либо последовательностей.

Литература

1. Основы современной криптографии и стенографии, Б.Я. Рябко, А.Н. Фионов, 2-е изд. - М.: Горячая линия-Телеком, 2013 г., стр. 124.

2. Теория связи в секретных системах, К. Шеннон, 1945 г., Раздел 18.

3. Формирование двоичных последовательностей Гордона-Миллса-Велча, Журнал: «Наукоемкие технологии в космических исследованиях земли», Москва, ISSN: 2409-5419eISSN: 2412-1363.

4. Патент RU 2281603 на изобретение «Генератор случайной двоичной последовательности», 10.08.2006 г.

5. Формирование и свойства М-последовательностей, ГОУ ВПО «Уральский государственный технический университет», Екатеринбург, 2007 г.

Реферат

Изобретение относится к области криптографии. Техническим результатом является повышение криптозащиты информации. В способе шифрования двоичное представление текста разбивается на сообщения, каждое сообщение представляется двумя криптограммами, одна из которых получена с помощью зашифрованной одним из двух ключей произвольно выбранной из полного кода последовательности, являющейся таблицей замены символов для этого сообщения, а другая криптограмма представляет собой зашифрованную вторым ключом таблицу замены символов для этого сообщения. 2 табл.

Формула