Способ генерации цифрового белого гауссовского шума по методу уоллеса - RU2723271C1

Чертежи

Описание

Предлагаемый способ относится к области электротехники, в частности к способу моделирования канала связи для проверки модуля помехоустойчивого кодирования.

Естественным путем реализации алгоритма помехоустойчивого кодирования является следующая последовательность действий.

1) Моделирование алгоритма на языке высокого уровня (C – C++, Matlab, Octave, SystemC, OpenCL), причем в целых числах.

2) Реализация алгоритма на ПЛИС (программируемая логическая интегральная схема) [Стешенко В. Б. ПЛИС фирмы Altera: Проектирование устройств обработки сигнала, Москва 2000]. ПЛИС представляет собой набор логических элементов на плате и регистров, состоящих из двоичных чисел заданной разрядности, с возможностью их программно коммутировать. Первое отличие от реализации алгоритма на компьютере состоит в том, что разрядность каждого регистра может быть выбрана произвольно, и она не обусловлена разрядностью центрального процессора, которого нет. Второе отличие состоит в том, что все действия выполняют одновременно и параллельно, но на более низкой тактовой частоте чем в системе центральным процессором. Описание алгоритма в этом случае состоит из статического описания коммутации элементов и динамического описания их взаимодействия (VHDL, Verilog). Здесь уже помимо правильности реализации алгоритма возникают вопросы энергопотребления и физического быстродействия. На каждый структурный блок подается синхроимпульс, обеспечивающий его динамическое взаимодействие с остальными, причем сам элемент имеет емкость и/или индуктивность, коммутирующая линия также имеет активное и реактивное сопротивление, которое растет с размерами схемы, что вынуждает увеличивать напряжение питания с целью предотвратить “размывание” фронтов синхронизирующих импульсов. Все выше изложенные факторы ограничивают тактовую частоту ПЛИС 200 МГц. В настоящее время идут попытки использовать язык высокого уровня для программирования ПЛИС, это осложняется тем фактом, что языки высокого уровня не имеют средств для описания статических связей. Однако, есть библиотечные расширения (SystemC) над языком C/C++, которые позволяют моделировать системное поведение модели посредством описания интерфейсов, очередей, сигналов в статическом и динамическом виде, но подобное моделирование не учитывает реальные физические процессы в микросхеме.

Верификация разрабатываемых алгоритмов достигается за счет последовательного применения тестовых векторов, разработанных на предыдущих стадиях. Тестовый вектор может являться оцифрованной смесью сигнала и шума, бинарной конфигурацией ошибок с заданными свойствами, любым набором тестовых значений, который, будучи поданными на вход разрабатываемого устройства или элемента этого устройства, вызовет предсказанную (на предыдущей стадии) реакцию. Хотелось бы отметить, что алгоритмы помехоустойчивого кодирования исправляют все ошибки, в том числе ошибки разработчика и программиста, поэтому часть тестов не связанная с моделированием Монте-Карло в белом гауссовском шуме, может быть пройдена успешно и при наличии ошибок в реализации. Полную верификацию обеспечивают статистически достоверное моделирование на ПЛИС по методу Монте Карло в канале, где аддитивной помехой является белый гауссовский шум (БГШ). Поэтому весьма актуальной является задача разработки компонентов такой модели, в частности генератора белого гауссовского шума в целых числах для реализации его на ПЛИС.

Известные алгоритмы такие Бокса-Мюллера [G. E. P. Box and M. E. Muller, “A note on the generation of randomnormal deviates,” Ann. Math. Stat., vol. 29, pp. 610–61, 1958.] и полярный [Marsaglia, G.; Bray, T. A. (1964). "A Convenient Method for Generating Normal Variables". SIAM Review. 6 (3): 260–264. doi:10.1137/1006063. JSTOR 2027592., D. E. Knuth, The Art of Computer Programming, Volume 2: Seminumerical Algorithms (second edition). Addison-Wesley, Menlo Park, 1981.] требуют вычисления функций log, sin, cos, что является сложной задачей для реализации в целочисленной арифметике. Уоллес предложил свой метод [C. S. Wallace "Fast Pseudorandom Generators for Normal and Exponential Variates", ACM Transactions on Mathematical Software, Vol. 22, No 1, March 1996, Pages 119-127] не требовавший вычислений с плавающей точкой, по крайней мере на каждом такте.

Способ Уоллеса состоит в следующем:

• заранее заполняют массив из

элементов гауссовскими случайными величинами с нулевым матожиданием и единичной дисперсией;

• формируют

адресов для доступа к массиву, первый из которых равномерно распределенное случайное число от до , а остальные ;

• для

случайных величин выполняют ортогональное линейное преобразование путем умножения на ортогональную матрицу, получая новых отсчетов;

• раз повторяют шаги 2 и 3, формируют новый массив из , перемежают его, записывая по строкам и читая по столбцам в перемежителе , перемеженным массивом заменяют первоначально инициализированный массив;

• вычисляют корректирующий множитель, используя последний элемент из нового массива, умножают на корректирующий нормирующий множитель на

элементов массива, которые являются выходом алгоритма.

В дальнейшем алгоритм для улучшения статистических свойств, в частности снижения корреляции между отсчетами претерпел ряд изменений.

Аналогом является китайская заявка Gaussian white noise generator based FPGA CN201810037910.5A, CN108390648A приоритет 2018/01/16 опубликована 2018/08/10, где приведен генератор белого гауссовского шума, реализованный по алгоритму Уоллеса [C. S. Wallace, Fast Pseudo-Random Generators for Normal and Exponential Variates, ACM Trans. on Mathematical Software 22 (1996), 119–127].

Способ, реализованный в данном устройстве отличается от способа из статьи [Dong-U Lee, Wayne Luk, John D. Villasenor, Guanglie Zhang, Philip H. W. Leong "A Hardware Gaussian Noise Generator Using the Wallace Method" IEEE TRANSACTIONS ON VERY LARGE SCALE INTEGRATION (VLSI) SYSTEMS, VOL. 13, NO. 8, AUGUST 2005] тем, что:

• взят другой генератор равномерных случайных величин (более простой);

• адреса вычисляют по формулам:

Вычисление каждого из адресов займет не больше такта, так как в случае

суммирование с единицей есть просто присоединение дополнительного бита. Однако в [Dong-U Lee, Wayne Luk, John D. Villasenor, Guanglie Zhang, Philip H. W. Leong "A Hardware Gaussian Noise Generator Using the Wallace Method" IEEE TRANSACTIONS ON VERY LARGE SCALE INTEGRATION (VLSI) SYSTEMS, VOL. 13, NO. 8, AUGUST 2005] указывается, что изменение алгоритма генерации адресов весьма критично влияет на статистические свойства результирующей последовательности, поэтому точное выполнение алгоритма Уоллеса в плане генерации псевдослучайных адресов имеет важное значение. В заявке CN108390648A добились сбалансированного вычисления адресов, т. е. каждый адрес вычисляют за одинаковое количество тактов, только за счет изменения оригинального алгоритма.

Наиболее близким к заявляемому является способ, описанный в [Dong-U Lee, Wayne Luk, John D. Villasenor, Guanglie Zhang, Philip H. W. Leong "A Hardware Gaussian Noise Generator Using the Wallace Method" IEEE TRANSACTIONS ON VERY LARGE SCALE INTEGRATION (VLSI) SYSTEMS, VOL. 13, NO. 8, AUGUST 2005], принятый за прототип.

Способ-прототип состоит в следующем:

• заранее заполняют массив из

элементов гауссовскими случайными величинами с нулевым матожиданием и единичной дисперсией;

• каждый такт, используя 32 битный отсчет генератора равномерных случайных чисел, формируют два 10-разрядных числа:

и одно 9-разрядное число путем последовательного взятия бит, с первого по десятый, с одиннадцатого по двадцатый, с двадцать первого по двадцать девяты1;

• в каждый такт формируют 4 адреса:

• считывают по сформированным адресам отсчеты

, формируют 4-х мерный вектор , выполняют ортогональное линейное преобразование ,

• где

,

матрицы

и используют попеременно и меняют через каждые отсчета;

• полученные отсчеты

записывают в массив по новым адресам , полученным за то время, пока выполнялось ортогональное преобразование;

• также отсчеты

поступают на вход блока коррекции, где каждый отсчет умножают на корректирующий множитель , получая отсчеты , которые являются выходом алгоритма;

• каждые

отсчетов производят корректировку корректирующего множителя по формуле , где текущий отсчет предвычисленные константы.

Необходимость корректирующего множителя обусловлена тем, что в случае его отсутствия, сумма квадратов каждых

отсчетов была бы константой, что неприемлемо для моделирования. В качестве генератора 32-битных равномерных случайных чисел используют генератор Таусворта [ P. L’Ecuyer, “Maximally equidistributed combined Tausworthe generators,” Math. Comput., vol. 65, no. 213, pp. 203–213, 1996] с порождающим полиномом . Периодичность такого генератора бит.

Рассмотрим работу блока ортогонального линейного преобразования. Легко видеть, что отсчеты

могут быть получены посредством следующих операций:

для матрицы ,

для матрицы .

Нетрудно видеть, что

. Эти вычисления займут три такта и могут быть выполнены в конвейерном режиме. Матрицы используют поочередно, каждые отсчетов меняя между собой.

Рассмотрим работу блока формирования адресов. Операция суммы с последующим сложением результата по модулю 2 является быстрой операцией, которая может быть выполнена за один такт. Также быстрой является операция умножение на 2, которая, по сути, является битовым сдвигом или перекомпоновкой бит и не требует временных затрат. Однако операция умножения на 3 занимает целый такт и может быть выполнена как сумма

. Таким образом, вычисление займет два такта, а остальных адресов – один такт, что является недостатком блока формирования адресов, так как ограничивает его быстродействие.

Задачу упрощения и повышения быстродействия способа, в частности балансировки вычислений в блоке формирования адреса решает способ аналог [Чен Ён Gaussian white noise generator based FPGA CN201810037910.5A, CN108390648A], однако, при этом адреса формируют иным способом, чем в способе прототипе, что может вызвать ухудшение статистических свойств результирующей последовательности отсчетов белого гауссовского шума.

Наиболее используемой в настоящее время является двухпортовая память, которая позволяет получить доступ для записи или чтения одновременно к двум адресам. Однако известны разработки [Kevin R. Townsend, Osama G. Attia, Phillip H. Jones, and Joseph Zambreno "A Scalable Unsegmented Multiport Memory for FPGA-Based Systems", International Journal of Reconfigurable Computing Volume 2015, Article ID 826283, 12 pages], позволяющие организовать эффективный многопортовый доступ к памяти. Таким образом, видно, что эффективность и быстродействие генератора цифрового белого шума может быть значительно повышена за счет балансировки вычислений и применения многопортовой памяти.

Задача, на решение которой направлено заявляемое техническое решение – повышение эффективности испытания радиоэлектронной аппаратуры, в частности, системы моделирования помехоустойчивых кодов.

Для решения поставленной задачи в способе формирования отсчетов цифрового белого гауссовского шума, заключающемся в том, что заполняют массив из

элементов гауссовскими случайными величинами с нулевым матожиданием и единичной дисперсией; в каждый такт, используя 32-разрядный отсчет генератора равномерных случайных чисел, формируют 2 10-разрядных числа: и одно 9-разрядное двоичное число путем последовательного взятия бит с первого по десятый, с одиннадцатого по двадцатый, с двадцать первого по двадцать девятый; в каждый такт формируют четыре адреса, считывают по сформированным адресам отсчеты , формируют 4-х мерный вектор , выполняют ортогональное линейное преобразование , где

путем выполнения следующих операций:

,

,

полученные отсчеты

записывают в массив по новым адресам , полученным за то время, пока выполнялось ортогональное преобразование; также отсчеты поступают на вход блока коррекции, где каждый отсчет умножают на корректирующий множитель , получая отсчеты , которые являются результатом алгоритма; каждые отсчетов производят корректировку корректирующего множителя по формуле , где текущий отсчет предвычисленные константы, которые определяются по следующим формулам: ,

согласно изобретению, формируют однобитный сигнал

из тридцатого бита генератора равномерных случайных чисел; адреса формируют по формулам:

при этом если

, то изменяют знак отсчетов на противоположный.

Заявляемый способ решает техническую задачу повышения быстродействия за счет балансирования вычислений в блоке формирования адресов, не изменяя при этом исходного алгоритма без ухудшения статистических свойств результирующей последовательности отсчетов белого гауссовского шума.

Графические материалы, используемые в описании:

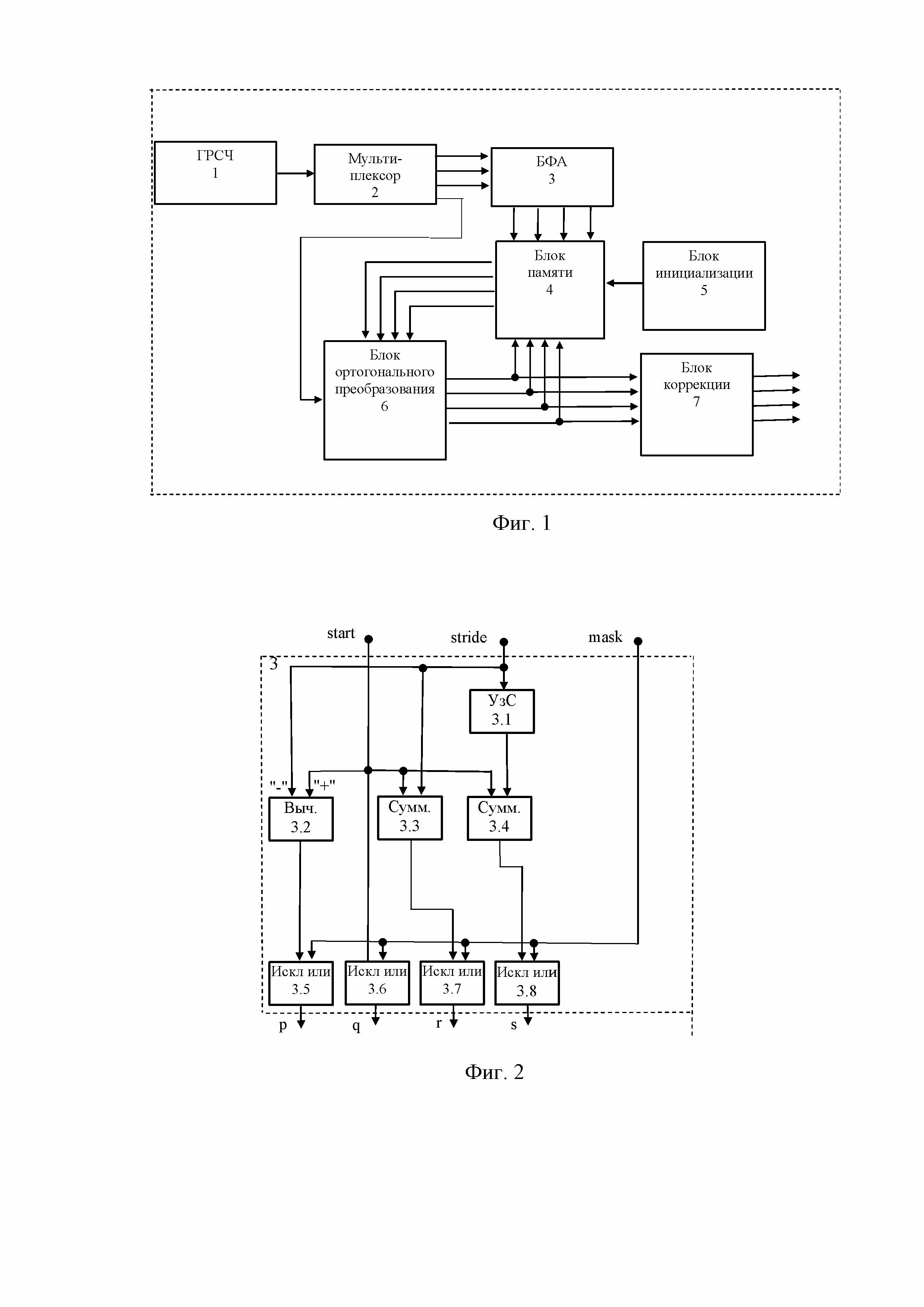
фиг. 1 – схема устройства, реализующего заявляемый способ;

фиг. 2 – схема блока формирования адреса.

Заявляемый способ заключается в следующем.

Заполняют массив из

элементов гауссовскими случайными величинами с нулевым матожиданием и единичной дисперсией;

каждый такт, используя 32-разрядный отсчет генератора равномерных случайных чисел, формируют два 10-разрядные числа:

и одно 9-разрядное путем последовательного взятия бит, с первого по десятый, с одиннадцатого по двадцатый, с двадцать первого по двадцать девятый, а также формируют однобитный сигнал из тридцатого бита;

каждый такт формируют 4 адреса:

считывают по сформированным адресам отсчеты

, формируют 4-х мерный вектор , выполняют ортогональное линейное преобразование , где

путем выполнения следующих операций:

,

,

если

то изменяют знак отсчетов на противоположный;

полученные отсчеты

записывают в массив по новым адресам , полученным за то время, пока выполнялось ортогональное преобразование;

отсчеты

также поступают на вход блока коррекции, где каждый отсчет умножают на корректирующий множитель , получая отсчеты , которые являются выходом алгоритма;

каждые

отсчетов производят корректировку корректирующего множителя по формуле , где текущий отсчет предвычисленные константы, которые определяются по следующим формулам: .

Новыми отличительными признаками способа являются:

-формирование однобитного сигнал

из тридцатого бита;

-если

то изменяют знак отсчетов на противоположный;

-формирование четырех адресов по формулам:

Устройство, реализующее заявляемый способ, представлено на фиг. 1, где обозначено:

1 – генератор равномерных случайных чисел (ГРСЧ);

2 – мультиплексор;

3 – блок формирования адресов (БФА);

4 – блок памяти;

5 – блок инициализации;

6 – блок ортогонального преобразования;

7 – блок коррекции.

Устройство содержит последовательно соединенные генератор равномерных случайных чисел 1 и мультиплексор 2, три выхода которого соединены с соответствующими входами блока формирования адресов 3 и соответствуют сигналам

. Выходы блока формирования адресов 3 соединены с соответствующими входами блока памяти 4, четыре выхода которого соединены с соответствующими входами блока ортогонального преобразования 6, выходы которого соединены с соответствующими входами блока памяти 4 и блока коррекции 7, выходы которого являются выходами устройства. Выход блока инициализации 5 соединен с соответствующим входом блока памяти 4. Четвертый выход мультиплексора 2, соответствующий сигналу , подключен к пятому входу блока ортогонального преобразования 6.

На фиг. 2 представлена схема блока формирования адресов, где обозначено:

3.1 – узел сдвига;

3.2 – вычитатель;

3.3, 3.4 – первый и второй сумматоры;

3.5, 3.6, 3.7, 3.8 – первый, второй, третий и четвертый узлы "исключающее или".

Блок формирования адресов 3 содержит узел сдвига 1, вычитатель 3.2, первый 3.3 и второй 3.4 сумматоры, а также первый 3.5, второй 3.6, третий 3.7 и четвертый 3.8 узлы "исключающее или". При этом вход узла сдвига 1, первые входы вычитателя 3.2 и первого сумматора 3.3 объединены и являются вторым входом блока формирования адресов 3 и соответствуют сигналу

Выход узла сдвига 1 через второй сумматор 3.4 соединен с первым входом четвертого узла "исключающее или" 3.8. Выход вычитателя 3.2 соединен с первым входом первого узла "исключающее или" 3.5. Выход первого сумматора 3.3 соединен с первым входом третьего узла "исключающее или" 3.7. Первый вход второго узла "исключающее или" 3.6 соединен со вторыми входами вычитателя 3.2, первого 3.3 и второго 3.4 сумматоров и является первым входом блока формирования адресов 3 и соответствует сигналу . Кроме того, вторые входы первого 3.5, второго 3.6, третьего 3.7 и четвертого 3.8 узлов "исключающее или" объединены и являются входом блока формирования адресов 3, соответствующий сигналу . Выходы узлов "исключающее или" являются выходами блока формирования адресов 3, соответствующие сигналам .

Устройство, реализующее предлагаемый способ работает следующим образом. В генераторе равномерных случайных чисел (ГРСЧ) 1 формируют 32-разрядное равномерное случайное число из которого в мультиплексоре 2 формируют два 10-разрядных сигнала:

и и один 9-разрядный сигнал stride для блока формирования адресов 3, а также однобитный сигнал для блока ортогонального преобразования 6. В блоке формирования адресов 3 параллельно формируют четыре адреса по формуле:

по которым проводят считывание отсчетов

для блока ортогонального преобразования 6, а также запись текущих отсчетов с выхода блока ортогонального преобразования 6, в блоке ортогонального преобразования проводят преобразования входных сигналов по формулам:

,

,

а также изменяют знак

на противоположный, если , отсчеты поступают на вход блока коррекции 7 где получают выходные отсчеты алгоритма в виде

где после каждых

отсчетов производят обновление по формуле , где текущий отсчет белого гауссовского шума предвычисленные константы, которые определяются по следующим формулам: .

Технический результат заключается в увеличении быстродействия способа и достигается за счет балансировки вычислений в блоке формирования адресов 6, для чего предлагается формировать псевдослучайные адреса следующим образом:

Операция вычитания эквивалентна операции сложения при использовании двоично-дополнительного кода, и в совокупности занимает также один такт. Таким образом, все 4 случайные адреса могут быть получены за один такт и переданы на блок памяти. Следует отметить, что вычитание здесь выполняют по модулю

, т. е. число -1 эквивалентно числу 1023. Таким образом, заявляемый способ позволяет достичь двукратного повышения производительности блока формирования адресов. Производительность генератора цифрового белого гауссовского шума по методу Уоллеса при условии применения четырех портового блока алгоритма доступа к блоку памяти также повысится в два раза при этом генератор равномерных случайных величин используют такой же как и в способе прототипе. Таким образом, выигрыш в производительности достигнут без ухудшения статистических свойств получаемых отсчетов белого шума.

Реферат

Изобретение относится к области электротехники и может быть использовано для моделирования канала связи для проверки модуля помехоустойчивого кодирования. Техническим результатом является увеличение быстродействия генератора цифрового белого гауссовского шума. Для этого в способе предлагается формировать псевдослучайные адреса следующим образом:Операция вычитания эквивалентна операции сложения при использовании двоично-дополнительного кода и в совокупности занимает также один такт. Таким образом, все четыре адреса могут быть получены за один такт и переданы на блок памяти. Причем эти адреса получены в точном соответствии с алгоритмом Уоллеса. Следует отметить, что вычитание здесь выполняют по модулю, т.е. число -1 эквивалентно числу 1023. При этом снижена корреляция выходных отсчетов при использовании только одной матрицыза счет использования одного из оставшихся битов от 32-разрядного отсчета генератора равномерных случайных чисел для изменения знака отсчетов. 1 з.п. ф-лы, 2 ил.

Формула