Устройство и способ кодирования-декодирования блоковых кодов низкой плотности с контролем на четность в системе мобильной связи - RU2316111C2
Код документа: RU2316111C2
Чертежи
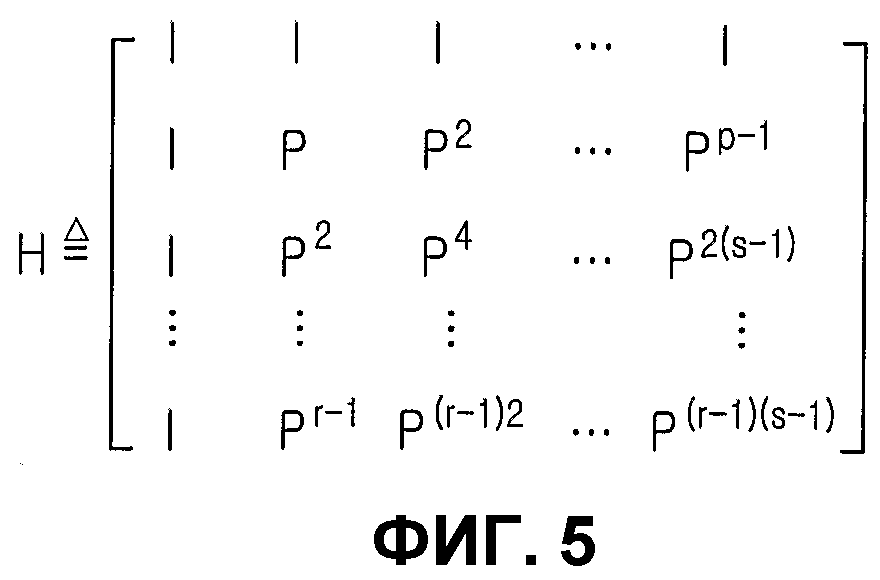
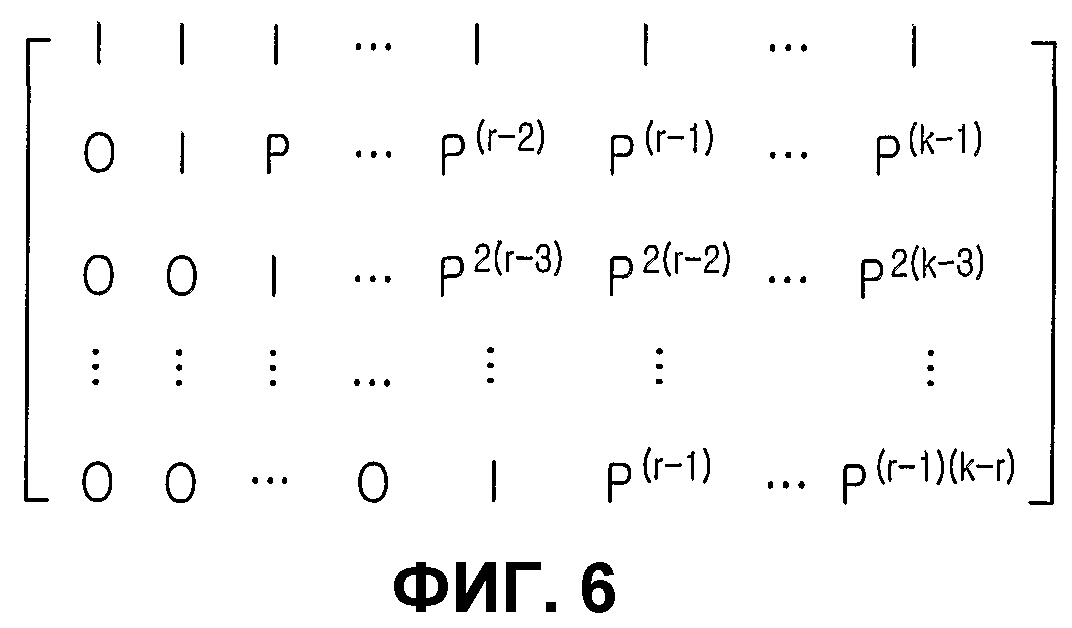
Описание
Область изобретения
Настоящее изобретение относится в общем к системам мобильной связи, а в частности к устройству и способу кодирования-декодирования блоковых кодов низкой плотности с проверкой на четность (НППЧ) (LDPC).
Уровень техники
С введением сотовой системы мобильной связи в Соединенных Штатах в конце 1970-х годов Южная Корея начала предоставлять услугу речевой связи в системе усовершенствованной услуги мобильного телефона (УУМТ) (AMPS) - аналоговой системе мобильной связи первого поколения (1G). В середине 1990-х годов Южная Корея коммерциализировала систему множественного доступа с кодовым разделением каналов (МДКР) (CDMA) - систему мобильной связи второго поколения (2G), чтобы предоставлять речевую услугу и услугу низкоскоростной передачи данных.
В конце 1990-х годов Южная Корея частично развернула международную мобильную телекоммуникационную систему IMT-2000 - систему мобильной связи третьего поколения (3G), нацеленную на усовершенствованные беспроводные мультимедийные услуги, глобальный роуминг и услугу высокоскоростной передачи данных. Эта система мобильной связи третьего поколения специально разрабатывалась для передачи данных с высокой скоростью согласно быстрому возрастанию в объемах обслуживаемых данных. То есть система мобильной связи третьего поколения превратилась в систему связи с услугой пакетной передачи, и эта система связи с услугой пакетной передачи передает пакеты данных ко множеству мобильных станций и сконструирована для передачи массовых данных. Система связи с услугой пакетной передачи разрабатывается для услуги высокоскоростной пакетной передачи.
Система мобильной связи третьего поколения развивается в систему мобильной связи четвертого поколения (4G). Система мобильной связи четвертого поколения находится в процессе стандартизации для стандартизации взаимодействия и интеграции между сетью проводной связи и сетью беспроводной связи вне простой услуги беспроводной связи, которую предоставляли предыдущие системы мобильной связи. Для беспроводной сети связи должна разрабатываться технология для передачи больших объемов данных вплоть до уровня пропускной способности, доступного в сети проводной связи.
Т.к. требуется высокоскоростная и с высокой пропускной способностью система связи, способная обрабатывать и передавать такие данные как изображение и радиоданные, а также такие простые как данные услуги речевой связи, необходимо увеличить эффективность передачи системы с помощью подходящей схемы канального кодирования, чтобы улучшить рабочие характеристики системы. Система мобильной связи неизбежно проявляет ошибки вследствие шумов, интерференции и затухания в соответствии с канальными условиями в течение передачи данных. Появление ошибок вызывает потерю информационных данных.
Чтобы снизить потерю информационных данных из-за появления ошибок, можно улучшить надежность системы мобильной связи за счет использования различных методов обнаружения ошибок. Один метод, использующий исправляющий ошибки код, является наиболее популярным методом обнаружения ошибок. Ниже приводится описание турбокода и кода низкой плотности с проверкой на четность (НППЧ), которые являются типичными обнаруживающими ошибки кодами.
Турбокод
Турбокод представляет собой обнаруживающий ошибки код, используемый как в синхронной системе мобильной связи третьего поколения, так и в асинхронной системе мобильной связи третьего поколения. Общеизвестно, что при высокоскоростной передаче данных турбокод превосходит по выигрышу в рабочих характеристиках сверточный код, ранее использовавшийся в качестве основного исправляющего ошибки кода. Помимо этого, турбокод является выгодным в том, что он может эффективно исправлять ошибку, вызванную шумами, генерируемыми в канале связи, тем самым увеличивая надежность передачи данных.
Код НППЧ
Код НППЧ может быть декодирован с помощью алгоритма итеративного декодирования на основании алгоритма суммирования-перемножения графа коэффициентов. Вследствие того, что декодер кода НППЧ использует основанный на алгоритме суммирования-перемножения алгоритм итеративного декодирования, он является менее сложным, чем декодер для турбокода. Помимо этого декодер для кода НППЧ легко воплотить с помощью декодера параллельной обработки в сравнении с декодером для турбокода. Когда код НППЧ выражается через граф коэффициентов, на графе коэффициентов кода НППЧ имеются циклы. Общеизвестно, что итеративное декодирование на графе коэффициентов кода НППЧ, где имеются циклы, является менее чем оптимизированным (субоптимальным). Кроме того, экспериментально доказано, что код НППЧ имеет превосходные рабочие характеристики при итеративном декодировании. Однако, когда на графе коэффициентов кода НППЧ имеется много циклов короткой длины, код НППЧ страдает от ухудшения рабочих характеристик. Поэтому постоянно проводятся исследования для разработки метода конструирования такого кода НППЧ, чтобы на графе коэффициентов кода НППЧ не имелось циклов короткой длины.
Процесс кодирования кода НППЧ превращается в процесс кодирования, который использует матрицу проверки на четность, имеющую низкую плотность весов вследствие характеристики порождающей матрицы, обычно имеющей высокую плотность весов. «Вес» представляет элемент с ненулевым значением среди элементов, составляющих порождающую матрицу и матрицу проверки на четность. В частности, если частичная матрица, соответствующая проверке на четность в матрице проверки на четность, имеет регулярный формат, возможно более эффективное кодирование.
Поскольку код НППЧ включает в себя различные коды с ненулевым значением, очень важно разработать алгоритм эффективного кодирования и алгоритм эффективного декодирования для различных типов кодов НППЧ, чтобы ввести код НППЧ в практическое использование. Помимо этого, поскольку матрица проверки на четность кода НППЧ определяет рабочие характеристики кода НППЧ, очень важно сконструировать матрицу проверки на четность с превосходными рабочими характеристиками. То есть, эффективная матрица проверки на четность с превосходными рабочими характеристиками, алгоритм эффективного кодирования и алгоритм эффективного декодирования должны учитываться одновременно, чтобы выработать высокопроизводительный код НППЧ.
Один код НППЧ определяется матрицей проверки на четность, в которой главные элементы имеют значение 0, а минорные элементы за исключением элементов, имеющих значение 0, имеют значение 1. Например, код НППЧ (N, j, k) является линейным блоковым кодом, имеющим блоковую длину N, и определяется неплотной матрицей проверки на четность, в которой каждый столбец имеет j элементов со значением 1, каждая строка имеет k элементов со значением 1, и все элементы, за исключением элементов, имеющих значение 1, имеют значение 0.
Код НППЧ, в котором весовое значение каждого столбца в матрице проверки на четность фиксируется на «j», а весовое значение каждой строки в матрице проверки на четность фиксируется на «k», как изложено выше, называется «регулярным кодом НППЧ». Здесь весовое значение представляет число весов. В отличие от регулярного кода НППЧ, код НППЧ, в котором весовое значение каждого столбца в матрице проверки на четность и весовое значение каждой строки в матрице проверки на четность не фиксируются, называется «нерегулярным кодом НППЧ». Общеизвестно, что нерегулярный код НППЧ лучше по рабочим характеристикам, чем регулярный код НППЧ. Однако в случае нерегулярного кода НППЧ из-за того, что весовое значение каждого столбца и весовое значение каждой строки в матрице проверки на четность не фиксируются, т.е. являются нерегулярными, весовое значение каждого столбца в матрице проверки на четность и весовое значение каждой строки в матрице проверки на четность должны соответственно регулироваться, чтобы гарантировать превосходные рабочие характеристики.
Теперь, со ссылкой на фиг.1, будет описана матрица проверки на четность кода НППЧ (8, 2, 4) в качестве примера кода НППЧ (N, j, k).
Фиг.1 является схемой, иллюстрирующей матрицу проверки на четность обычного кода НППЧ (8, 2, 4). На фиг.1 матрица Н проверки на четность кода НППЧ (8, 2, 4) состоит из 8 столбцов и 4 строк, причем весовое значение каждого столбца фиксируется на 2, а весовое значение каждой строки фиксируется на 4. Из-за того, что весовое значение каждого столбца и весовое значение каждой строки в матрице проверки на четность являются регулярными, как изложено выше, код НППЧ (8, 2, 4), показанный на фиг.1, становится регулярным кодом НППЧ.
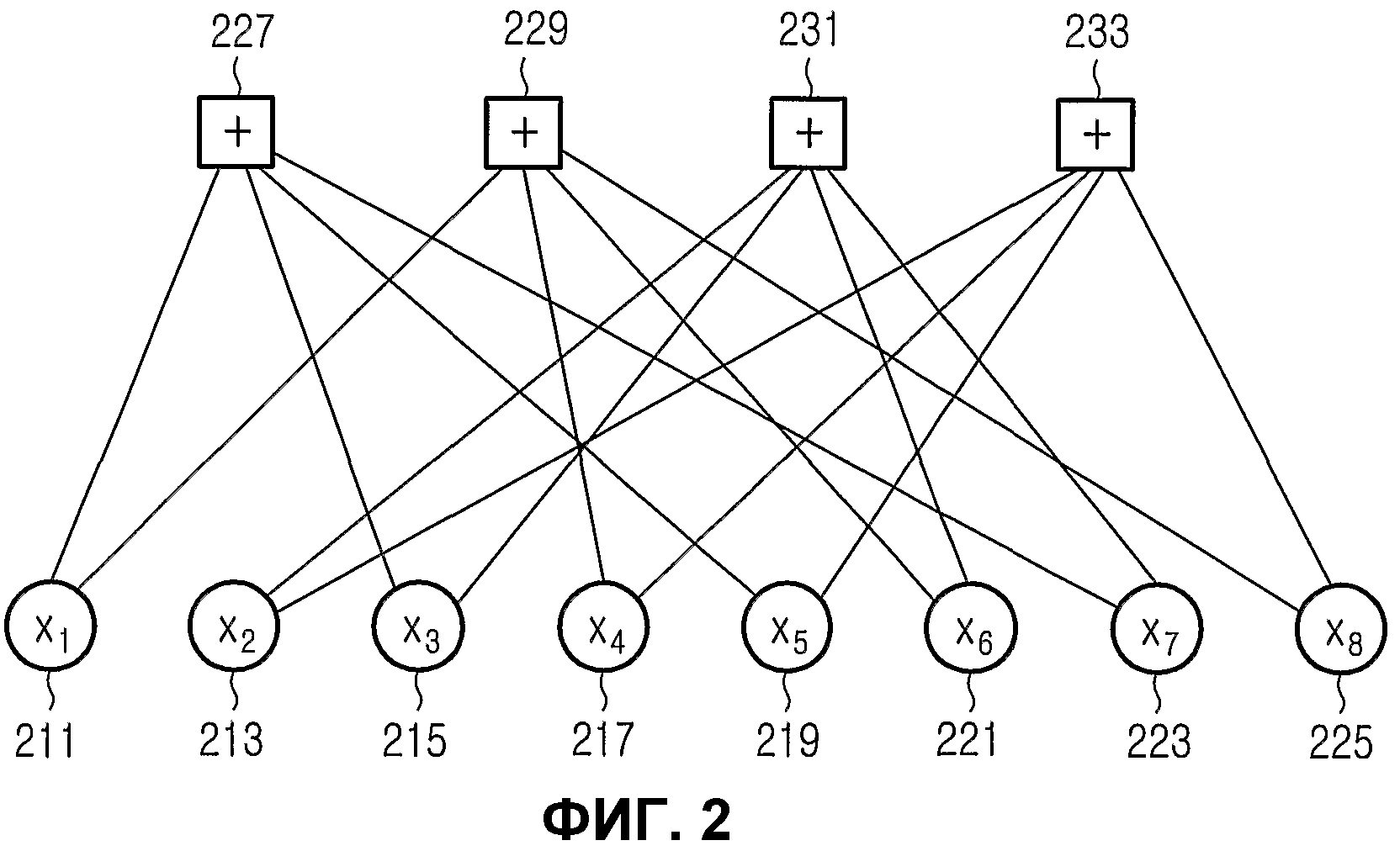
Граф коэффициентов кода НППЧ (8, 2, 4), описанного в связи с фиг.1, будет теперь описан ниже со ссылкой на фиг.2.
Фиг.2 представляет собой схему, иллюстрирующую граф коэффициентов кода НППЧ (8, 2, 4) по фиг.1. На фиг.2 граф коэффициентов кода НППЧ (8, 2, 4) состоит из 8 узлов переменных х1 211, х2 213, х3 215, х4 217, х5 219, х6 221, х7 223 и х8 225, и 4 проверочных узлов 227, 229, 231 и 233. Когда элемент с весом, т.е. со значением 1, существует в точке, где i-я строка и j-й столбец матрицы проверки на четность кода НППЧ (8, 2, 4) пересекаются друг с другом, образуется ветвь между узлом xj и i-м проверочным узлом.
Поскольку матрица проверки на четность кода НППЧ имеет малое весовое значение, как описывается выше, возможно выполнить декодирование посредством процесса итеративного декодирования, даже в блоковом коде с относительно большой длиной, который проявляет производительность, приближающуюся к пределу пропускной способности шенноновского канала, такую как турбокод, при непрерывном повышении блоковой длины блокового кода. Доказано, что процесс итеративного декодирования кода НППЧ с помощью метода переноса потока является почти полным приближением к процессу итеративного декодирования турбокода по производительности.
Чтобы генерировать высокопроизводительный код НППЧ, должны удовлетворяться следующие условия.
(1) Следует учитывать циклы на графе коэффициентов кода НППЧ
«Цикл» относится к петле, образованной гранями, соединяющими узлы переменных с проверочными узлами на графе коэффициентов кода НППЧ, а длина цикла определяется как число граней, составляющих петлю. Цикл, имеющий большую длину, означает, что число граней, соединяющих узлы переменных с проверочными узлами и составляющих петлю на графе коэффициентов кода НППЧ, велико. В противоположность этому, цикл, имеющий малую длину, означает, что число граней, соединяющих узлы переменных с проверочными узлами и составляющих петлю на графе коэффициентов кода НППЧ, мало.
По мере того, как циклы на графе коэффициентов кода НППЧ становятся длиннее, эффективность рабочих характеристик кода НППЧ возрастает по следующим причинам. То есть, когда на графе коэффициентов кода НППЧ генерируются длинные циклы, возможно предотвратить такое ухудшение рабочих характеристик как нижний предел ошибок, появляющийся, когда слишком много циклов малой длины существуют на графе коэффициентов кода НППЧ.
(2) Следует учитывать эффективное кодирование кода НППЧ
Трудно подвергать код НППЧ кодированию в реальном времени по сравнению со сверточным кодом или турбокодом из-за его высокой сложности кодирования. Чтобы снизить сложность кодирования кода НППЧ, предложен код с повторным накоплением (ПН) (RA). Код ПН также имеет ограничение в снижении сложности кодирования кода НППЧ. Поэтому следует учитывать эффективное кодирование кода НППЧ.
(3) Следует учитывать распределение рангов графа коэффициентов кода НППЧ
Обычно нерегулярный код НППЧ превосходит по рабочим характеристикам регулярный код НППЧ, потому что граф коэффициентов нерегулярного кода НППЧ имеет разные ранги. «Ранг» относится к числу граней, соединенных с узлами переменных и проверочными узлами в графе коэффициентов кода НППЧ. Далее, «распределение рангов» на графе коэффициентов кода НППЧ относится к отношению числа узлов, имеющих конкретный ранг, к общему числу узлов. Доказано, что код НППЧ, имеющий конкретное распределение рангов, является превосходным по рабочим характеристикам.
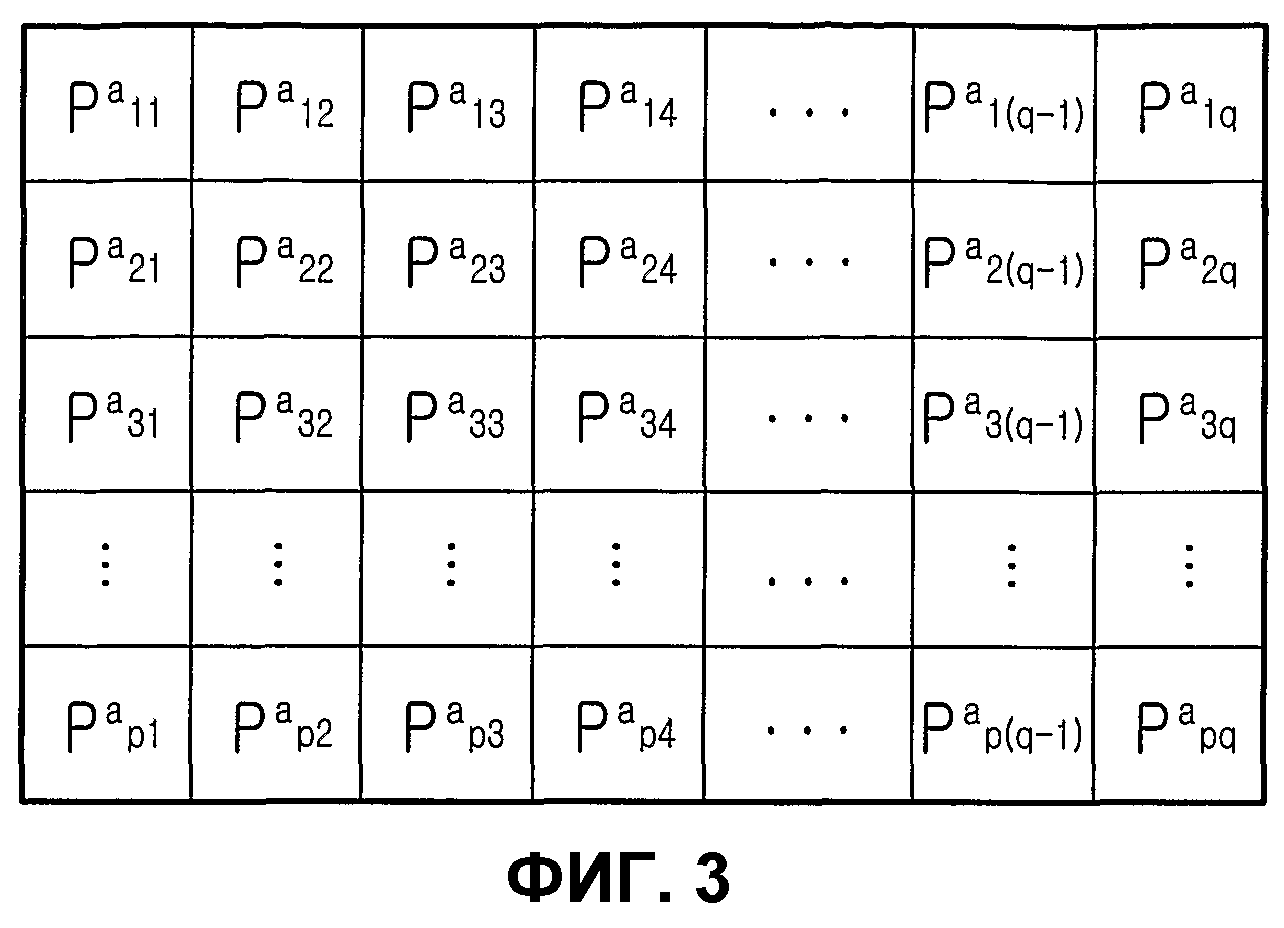
Фиг.3 представляет собой схему, иллюстрирующую матрицу проверки на четность обычного блокового кода НППЧ. Перед тем, как дать описание фиг.3, следует отметить, что блоковый код НППЧ является новым кодом НППЧ, для которого учитывались не только эффективное кодирование, но также эффективное хранение и улучшение рабочих характеристик матрицы проверки на четность, и что блоковый код НППЧ является кодом НППЧ, расширенным путем обобщения структуры регулярного кода НППЧ. На фиг.3 матрица проверки на четность блокового кода НППЧ разделена на множество частичных блоков, и матрица перестановок отображается в каждый из этих частичных блоков. На фиг.3 «Р» представляет матрицу перестановок размером NS×NS, а верхний индекс (или экспонента) aij матрицы перестановок Р равна либо 0≤aij≤NS-1, либо aij=∞. На фиг.3 р представляет число строк частичных блоков, а q представляет число столбцов частичных блоков. «i» означает, что соответствующая матрица перестановок располагается в i-й строке частичных блоков матрицы проверки на четность, а «j» означает, что соответствующая матрица перестановок располагается в j-м столбце частичных блоков матрицы проверки на четность. То есть,
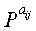
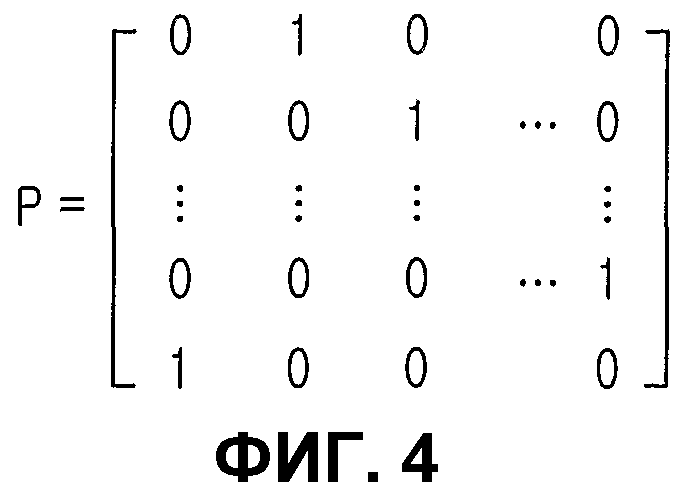
Теперь со ссылкой на фиг.4 будет описана матрица перестановок.
Фиг.4 представляет собой схему, иллюстрирующую матрицу перестановок Р по фиг.3. Как показано на фиг.4, матрица перестановок Р является квадратной матрицей размером NS×NS, и каждый из NS столбцов, составляющих матрицу перестановок Р, имеет вес 1, а каждая из NS строк, составляющих матрицу перестановок Р, также имеет вес 1.
На фиг.3 матрица перестановок с верхним индексом aij=0, т.е. матрица Р0 перестановок представляет единичную матрицу
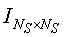
В полной матрице проверки на четность блокового кода НППЧ, показанной на фиг.3, вследствие того, что общее число строк составляет NS×p, а общее число столбцов составляет NS×q (для p≤q), когда полная матрица проверки на четность кода НППЧ имеет полный ранг, скорость кодирования может быть выражена как уравнение (1) независимо от размера частичных блоков.
Если aij≠∞ для всех i и j, матрицы перестановок, соответствующие частичным блокам, не являются нулевыми матрицами, и частичные блоки составляют регулярный код НППЧ, в котором весовое значение каждого столбца и весовое значение каждой строки в каждой из матриц перестановок, соответствующих частичным блокам, равны p и q, соответственно. Здесь каждая из матриц перестановок, соответствующих частичным блокам, будет именоваться «частичными матрицами».
Из-за того, что в полной матрице проверки на четность имеется (р-1) зависимых строк, скорость кодирования выше, чем скорость кодирования, вычисленная с помощью уравнения (1). В случае блокового кода НППЧ, если находится весовая позиция первой строки каждой из частичных матриц, составляющих полную матрицу проверки на четность, находятся и весовые позиции остальных (NS-1) строк. Поэтому требуемый размер памяти снижается до 1/NS по сравнению со случаем, где веса выбираются нерегулярно, чтобы хранить информацию во всей полной матрице проверки на четность.
Фиг.5 является схемой, иллюстрирующей матрицу проверки на четность обычного регулярного блокового кода НППЧ. Показанная на фиг.5 матрица проверки на четность представляет собой матрицу проверки на четность кода массива (s, r), т.е. регулярного блокового кода НППЧ. Предложенный код массива (s, r) является типичным регулярным блоковым кодом НППЧ, и этот код массива (s, r) соответствует блоковому коду НППЧ для NS=s и q=s и p=r на фиг.3. Здесь «s» является нечетным простым числом, а «r» всегда удовлетворяет условию r≤s.
Матрица проверки на четность кода массива (s, r) имеет s2 столбцов и r×s строк, а ее ранг становится r×(s-1). Причина, по которой ранг матрицы проверки на четность кода массива (s, r) становится r×(s-1), состоит в том, что в случае, где r частичных матриц в направлении строк матрицы проверки на четность кода массива (s, r), если s строк в каждой из частичных матриц суммируются, генерируется матрица, в которой все элементы имеют значение 1. То есть, из-за того, что генерируются r строк, в которых все элементы имеют значение 1, можно понять, что имеется r зависимых строк. Поэтому скорость Rмассив кодирования кода массива (s, r) можно выразить уравнением (2):
Как описано выше, можно отметить, что в случае кода массива (s, r) в графе коэффициентов не имеется цикла длиной 4 из-за его алгебраической характеристики, и можно также снизить емкость памяти, как изложено выше.
Однако, поскольку код массива (s, r) является регулярным кодом НППЧ, он стоит ниже нерегулярного кода НППЧ в ухудшении рабочих характеристик. Далее, блоковый код НППЧ не может гарантировать превосходных рабочих характеристик, потому что его случайность ниже. То есть, код массива (s, r), хотя учитывалось эффективное кодирование, все же имеет высокую сложность кодирования, и в коде массива (s, r), хотя имеется цикл длиной 4, имеется также цикл длиной 6. Далее, поскольку распределение рангов не учитывается, происходит ухудшение рабочих характеристик.
Фиг.6 является схемой, иллюстрирующей матрицу проверки на четность обычного блокового кода НППЧ. Перед тем, как дается описание фиг.6, следует отметить, что нерегулярный блоковый код НППЧ является блоковым кодом НППЧ, заданным путем модификации кода массива, описанного в связи с фиг.5, при учете эффективного кодирования. В матрице проверки на четность нерегулярного блокового кода НППЧ, показанного на фиг.6, «I» отмечает единичную матрицу размера s× s, а «0» отмечает нулевую матрицу размером s×s. Матрица проверки на четность нерегулярного блокового кода НППЧ, показанная на фиг.6, соответствует матрице проверки на четность блокового кода НППЧ для NS=s, q=k и p=r на фиг.3.
Для эффективного кодирования кода НППЧ кодирование разрешается в линейном времени за счет формирования частичной матрицы, соответствующей проверке на четность полной матрицы проверки на четность как полной нижней треугольной матрицы, как показано на фиг.6. Структура полной матрицы проверки на четность, т.е. структура частичной матрицы, соответствующей информационному слову, и частичной матрицы, соответствующей проверке на четность, будут описаны здесь ниже. Когда частичная матрица, соответствующая проверке на четность, формируется таким путем как полная нижняя треугольная матрица, матрица проверки на четность всегда имеет полный ранг из-за своих структурных характеристик. Поэтому длина блока модифицированного кода массива, т.е. нерегулярного кода НППЧ, становится ks, а скорость R кодирования может быть выражена уравнением (3):
Однако нерегулярный код НППЧ по фиг.6, имеющий матрицу проверки на четность, в которой частичная матрица, соответствующая проверке на четность, имеет форму полной нижней треугольной матрицы, является более эффективным, нежели код массива, но не учитывался ранг распределения на графе коэффициентов, который должен учитываться во время генерирования кода НППЧ, и не учитывалось также удаление циклов короткой длины. Поэтому он имеет более низкую, чем нерегулярный код НППЧ, имеющий случайный характер, исправляющую способность. Соответственно, имеется необходимость в нерегулярном коде НППЧ, который максимизирует исправляющую способность.
Сущность изобретения
Таким образом, цель настоящего изобретения состоит в обеспечении устройства и способа кодирования-декодирования кода НППЧ с максимизированной исправляющей способностью в системе мобильной связи.
Другая цель настоящего изобретения состоит в обеспечении устройства и способа кодирования-декодирования кода НППЧ с максимизированной минимальной длиной цикла в системе мобильной связи.
Еще одна цель настоящего изобретения состоит в обеспечении устройства и способа кодирования-декодирования кода НППЧ с минимизированной сложностью кодирования в системе мобильной связи.
Первым объектом настоящего изобретения является способ генерирования матрицы проверки на четность блокового кода низкой плотности с проверкой на четность (НППЧ), чтобы улучшить исправляющую способность, причем матрица проверки на четность имеет информационную часть, соответствующую информационному слову, и первую проверочную часть, соответствующую проверке на четность, и вторую проверочную часть, соответствующую проверке на четность. Этот способ включает в себя шаги, в которых: находят размер матрицы проверки на четность на основании скорости кодирования, примененной при кодировании информационного слова блоковым кодом НППЧ, и длины кодового слова; разделяют матрицу проверки на четность, имеющую найденный размер, на заранее заданное число блоков; классифицируют блоки на блоки, соответствующие информационной части, блоки, соответствующие первой проверочной части, и блоки, соответствующие второй проверочной части; размещают матрицы перестановки в заранее заданных блоках среди блоков, классифицированных как первая проверочная часть, и размещают единичные матрицы в полной нижней треугольной форме в заранее заданных блоках среди блоков, классифицированных как вторая проверочная часть; и размещают матрицы перестановки в блоках, классифицированных как информационная часть, так что минимальная длина цикла максимизируется, а веса являются нерегулярными на графе коэффициентов блокового кода НППЧ.
Вторым объектом настоящего изобретения является способ кодирования блокового кода низкой плотности с проверкой на четность (НППЧ). Этот способ включает в себя следующие шаги: генерируют матрицу проверки на четность, состоящую из информационной части, соответствующей информационному слову, и первой проверочной части и второй проверочной части, каждая из которых соответствует проверке на четность, и определяют метод деперемежения и метод перемежения согласно матрице проверки на четность; находят значения вероятности приема сигнала; генерируют первый сигнал в текущем процессе декодирования путем вычитания сигнала, генерированного в предыдущем процессе декодирования, из значений вероятности принятого сигнала; деперемежают первый сигнал с помощью метода деперемежения; находят значения вероятности путем приема деперемеженного сигнала; генерируют второй сигнал путем вычитания деперемеженного сигнала из значений вероятности деперемеженного сигнала; и перемежают второй сигнал с помощью метода перемежения и итеративно декодируют перемеженный сигнал.
Третьим объектом настоящего изобретения является способ кодирования блокового кода низкой плотности с проверкой на четность (НППЧ). Этот способ включает в себя следующие шаги: генерируют первый сигнал путем перемножения информационного слова на первую частичную матрицу ранее генерированной матрицы проверки на четность, состоящей из информационной части, соответствующей информационному слову, и первой проверочной части и второй проверочной части, каждая из которых соответствует проверке на четность; генерируют второй сигнал путем перемножения информационного слова на вторую частичную матрицу матрицы проверки на четность; генерируют третий сигнал путем перемножения первого сигнала на матричное произведение третьей частичной матрицы и обратной матрицы от четвертой частичной матрицы из матрицы проверки на четность; генерируют четвертый сигнал путем сложения второго сигнала и третьего сигнала; генерируют пятый сигнал путем перемножения четвертого сигнала на пятую частичную матрицу матрицы проверки на четность; генерируют шестой сигнал путем сложения второго сигнала и пятого сигнала; генерируют седьмой сигнал путем перемножения шестого сигнала на матричное произведение третьей частичной матрицы и обратной матрицы от четвертой частичной матрицы из матрицы проверки на четность; и мультиплексируют информационное слово, четвертый сигнал в качестве первой проверочной части и седьмой сигнал в качестве второй проверочной части согласно формату блокового кода НППЧ.
Четвертым объектом настоящего изобретения является способ генерирования матрицы проверки на четность, чтобы улучшить исправляющую способность, причем эта матрица проверки на четность размещается в матрице строк и столбцов множества информационных частичных блоков и множества проверочных частичных блоков, матрица проверки на четность разделяется на информационную часть, состоящую из матриц информационных частичных блоков, и проверочную часть, состоящую из матриц проверочных частичных блоков, причем каждый из информационных частичных блоков состоит из матрицы, представляющей множество информационных битов, каждый из проверочных частичных блоков состоит из матрицы, представляющей множество битов проверки на четность, каждый из информационных частичных блоков и проверочных частичных блоков существуют во множестве строк в матрице проверки на четность, разделенной на первую информационную матрицу, первую проверочную матрицу и вторую проверочную матрицу, каждый из информационных частичных блоков и проверочных частичных блоков существуют во множестве остальных строк за исключением множества строк, разделенных на вторую информационную матрицу, третью проверочную матрицу и четвертую проверочную матрицу; и первая и вторая информационные матрицы, первая и третья проверочные матрицы, и вторая и четвертая проверочные матрицы размещены в одних и тех столбцах, соответственно. Способ включает в себя следующие шаги: суммируют третью проверочную матрицу и произведение четвертой проверочной матрицы, обратной матрицы от второй проверочной матрицы и первой проверочной матрицы так, что сумма является единичной матрицей; находят транспонированный вектор первого проверочного вектора, соответствующего первой проверочной матрице и третьей проверочной матрице, путем перемножения суммы второй информационной матрицы и произведения четвертой проверочной матрицы, обратной матрицы от второй проверочной матрицы и первой информационной матрицы на информационный вектор, соответствующий первой информационной матрице и второй информационной матрице; и находят транспонированный вектор второго проверочного вектора, соответствующего второй проверочной матрице и четвертой проверочной матрице, путем перемножения обратной матрицы от второй проверочной матрицы на сумму произведения первой информационной матрицы и транспонированного вектора информационного вектора и произведения первой проверочной матрицы и транспонированного вектора первого проверочного вектора.
Пятым объектом настоящего изобретения является способ генерирования матрицы проверки на четность блокового кода низкой плотности с проверкой на четность (НППЧ), чтобы улучшить исправляющую способность, при этом матрица проверки на четность размещена в матрице строк и столбцов из множества частичных блоков, а матрицы перестановки, генерированные путем сдвига единичной матрицы размером NS×NS на заранее заданную экспоненту согласно каждому из частичных блоков, размещены в каждом из частичных блоков. Способ включает в себя следующие шаги: находят блоковый цикл блокового кода НППЧ в качестве первого значения; и находят второе значение путем перемножения второго значения на значение, определенное вычитанием суммы экспонент матриц перестановки с нечетной экспонентой среди матриц перестановки, размещенных в каждом из частичных блоков, из суммы экспонент перестановок с четной экспонентой среди матриц перестановки, размещенных в каждом из частичных блоков; и выполняют контрольную операцию так, что каждый из частичных блоков имеет цикл, соответствующий произведению первого значения и второго значения.
Шестым объектом настоящего изобретения является устройство для декодирования блокового кода низкой плотности с проверкой на четность (НППЧ). Это устройство включает в себя декодер узлов переменных для соединения узлов переменных согласно весу каждого столбца, составляющего матрицу проверки на четность, состоящую из информационной части, соответствующей информационному слову, и первой проверочной части и второй проверочной части, каждая из которых соответствует проверке на четность согласно заранее заданному контрольному сигналу, и для нахождения значений вероятности принятого сигнала; первый сумматор для вычитания сигнала, генерированного в предыдущем процессе декодирования, из сигнала, выданного из декодера узлов переменных в текущем процессе декодирования; деперемежитель для деперемежения сигнала, выданного из первого сумматора, с помощью метода деперемежения, установленного согласно матрице проверки на четность; декодер узлов проверки для соединения узлов проверки согласно весу каждой строки, составляющей матрицу проверки на четность, и для нахождения значений вероятности сигнала, выданного из деперемежителя, согласно заранее заданному контрольному сигналу; второй сумматор для вычитания сигнала, выданного из деперемежителя, из сигнала, выданного из декодера узлов проверки; перемежитель для перемежения сигнала, выданного из второго сумматора, с помощью метода перемежения, установленного согласно матрице проверки на четность, и для выведения перемеженного сигнала на декодер узлов переменных и первый сумматор; и контроллер для генерирования матрицы проверки на четность и управления методом деперемежения и методом перемежения согласно матрице проверки на четность.
Седьмым объектом настоящего изобретения является устройство для кодирования блокового кода низкой плотности с проверкой на четность (НППЧ). Это устройство включает в себя первый матричный перемножитель для перемножения принятого информационного слова на первую частичную матрицу матрицы проверки на четность, состоящей из информационной части, соответствующей информационному слову, и первой проверочной части и второй проверочной части, каждая из которых соответствует проверке на четность; второй матричный перемножитель для перемножения информационного слова на вторую частичную матрицу матрицы проверки на четность; третий матричный перемножитель для перемножения сигнала, выданного из первого матричного перемножителя, на матричное произведение из третьей частичной матрицы и обратной матрицы от четвертой частичной матрицы из матрицы проверки на четность; первый сумматор для сложения сигнала, выданного из второго матричного перемножителя, и сигнала, выданного из третьего матричного перемножителя; четвертый матричный перемножитель для перемножения сигнала, выданного из первого сумматора, на пятую частичную матрицу матрицы проверки на четность; второй сумматор для сложения сигнала, выданного из второго матричного перемножителя, и сигнала, выданного из четвертого матричного перемножителя; пятый матричный перемножитель для перемножения сигнала, выданного из второго сумматора, на матричное произведение третьей частичной матрицы и обратной матрицы от четвертой частичной матрицы из матрицы проверки на четность; и переключатели для мультиплексирования информационного слова, выходного сигнала первого сумматора в качестве первой проверочной части и выходного сигнала пятого перемножителя в качестве второй проверочной части согласно формату блокового кода НППЧ.
Краткое описание чертежей
Вышеуказанные и иные цели, признаки и преимущества настоящего изобретения станут яснее из нижеследующего подробного описания вместе с сопровождающими чертежами, на которых:
Фиг.1 является схемой, иллюстрирующей матрицу проверки на четность обычного кода НППЧ (8, 2, 4);
Фиг.2 является схемой, иллюстрирующей граф коэффициентов кода НППЧ (8, 2, 4) по фиг.1;
Фиг.3 является схемой, иллюстрирующей матрицу проверки на четность обычного блокового кода НППЧ;
Фиг.4 является схемой, иллюстрирующей матрицу Р перестановок по фиг.3;
Фиг.5 является схемой, иллюстрирующей матрицу проверки на четность обычного регулярного блокового кода НППЧ;
Фиг.6 является схемой, иллюстрирующей матрицу проверки на четность обычного нерегулярного блокового кода НППЧ;
Фиг.7 является схемой, иллюстрирующей структуру цикла блокового кода НППЧ, матрица проверки на четность которого состоит из 4 частичных матриц;
Фиг.8 является схемой, иллюстрирующей структуру цикла блокового кода НППЧ, матрица проверки на четность которого состоит из 6 частичных матриц;
Фиг.9 является схемой, иллюстрирующей структуру блокового цикла блокового кода НППЧ;
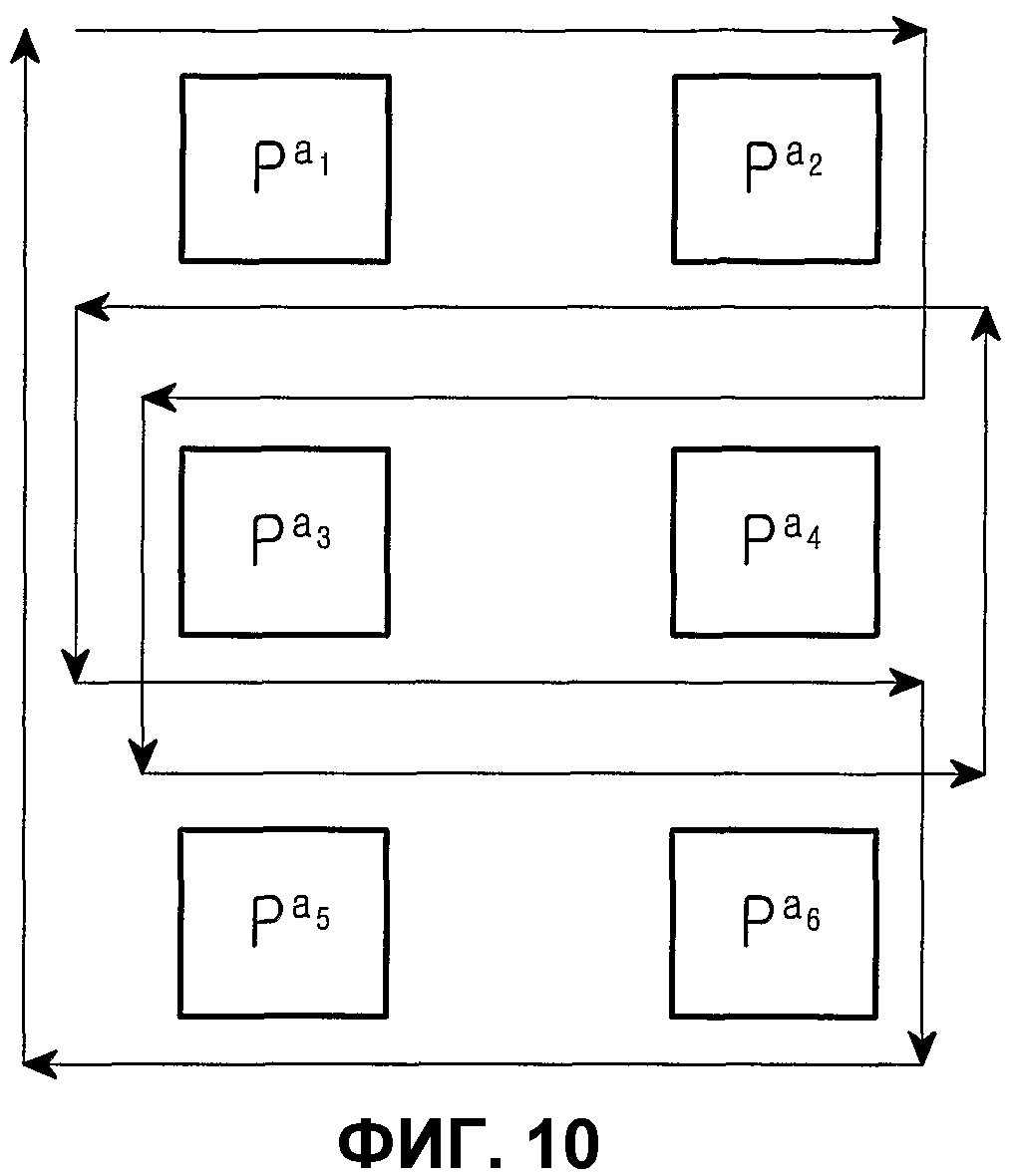
Фиг.10 является схемой, иллюстрирующей структуру блокового цикла блокового кода НППЧ, в котором дублируются 6 частичных матриц из матрицы проверки на четность;
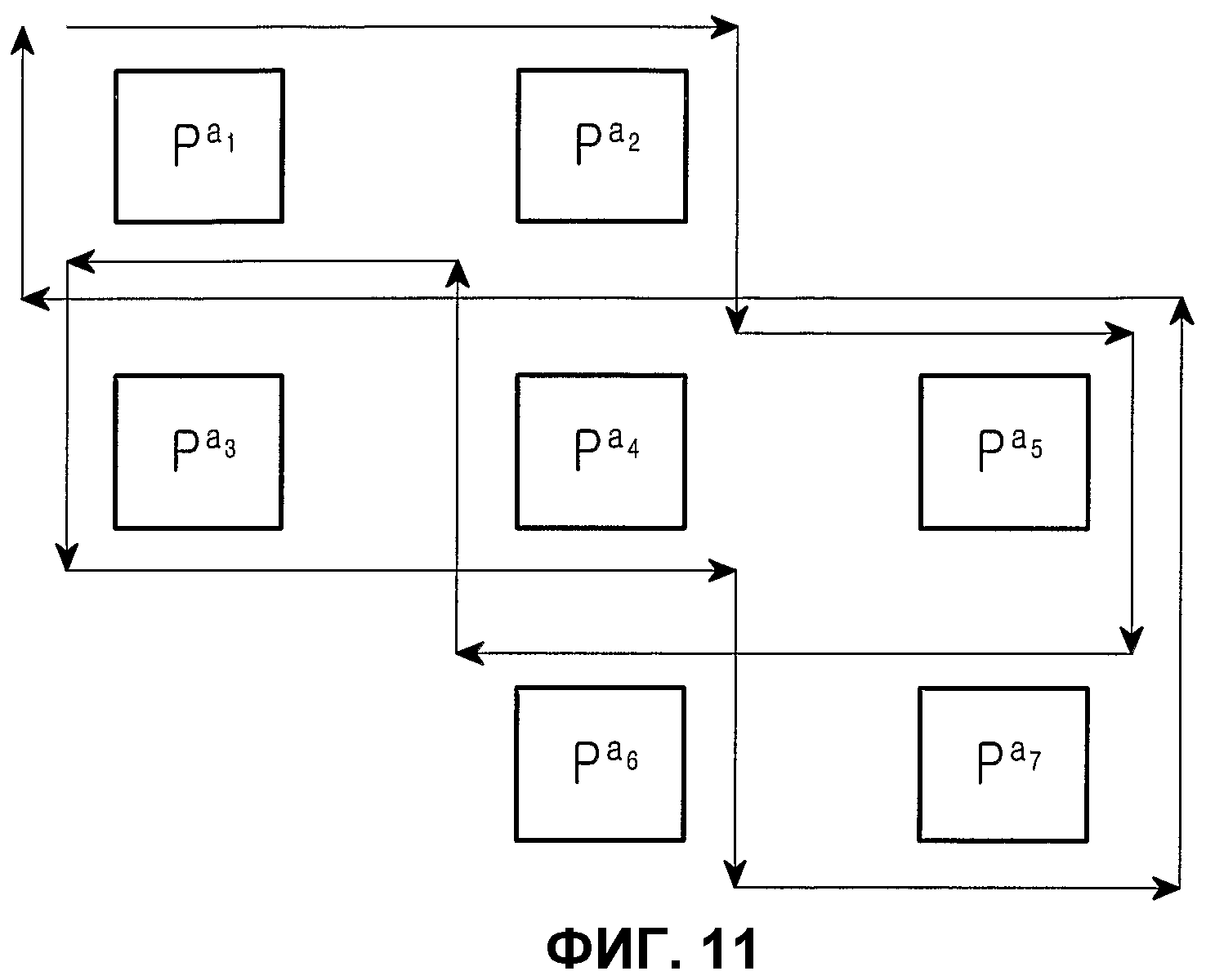
Фиг.11 является схемой, иллюстрирующей структуру блокового цикла блокового кода НППЧ, в котором дублируются 7 частичных блоков из матрицы проверки на четность;
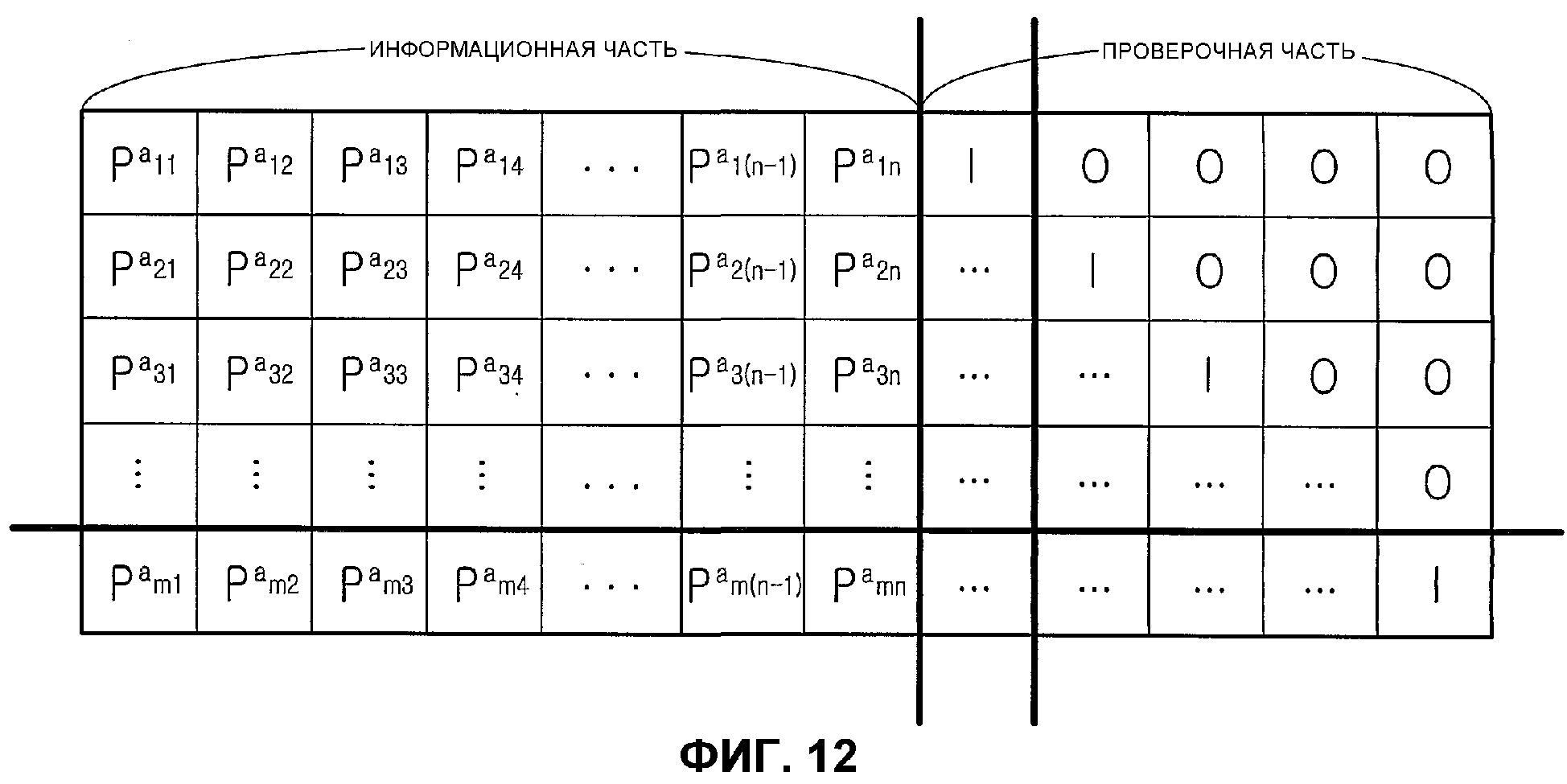
Фиг.12 является схемой, иллюстрирующей матрицу проверки на четность, имеющую форму полной нижней треугольной матрицы;
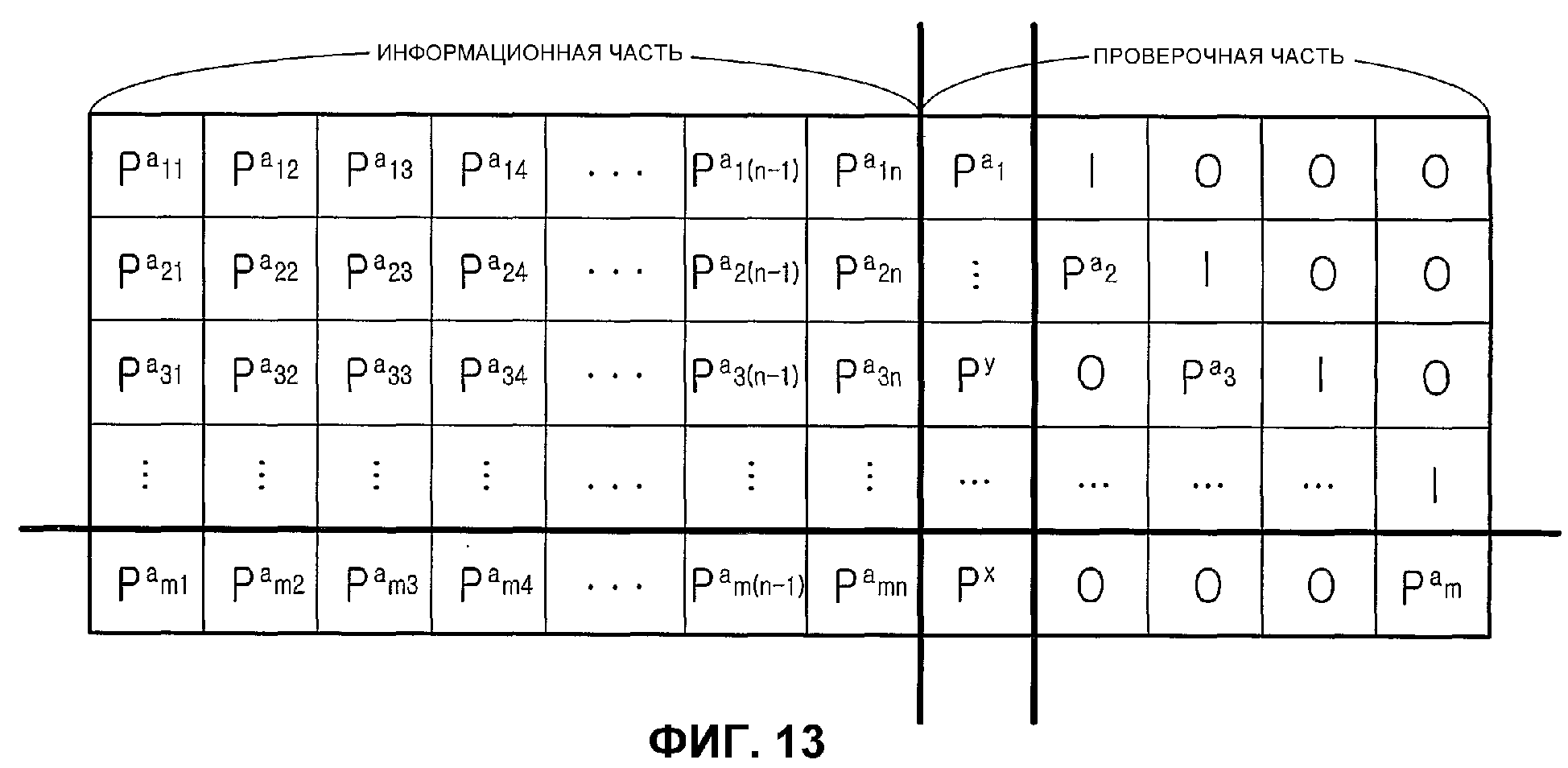
Фиг.13 является схемой, иллюстрирующей матрицу проверки на четность, имеющую форму, подобную форме полной нижней треугольной матрицы;
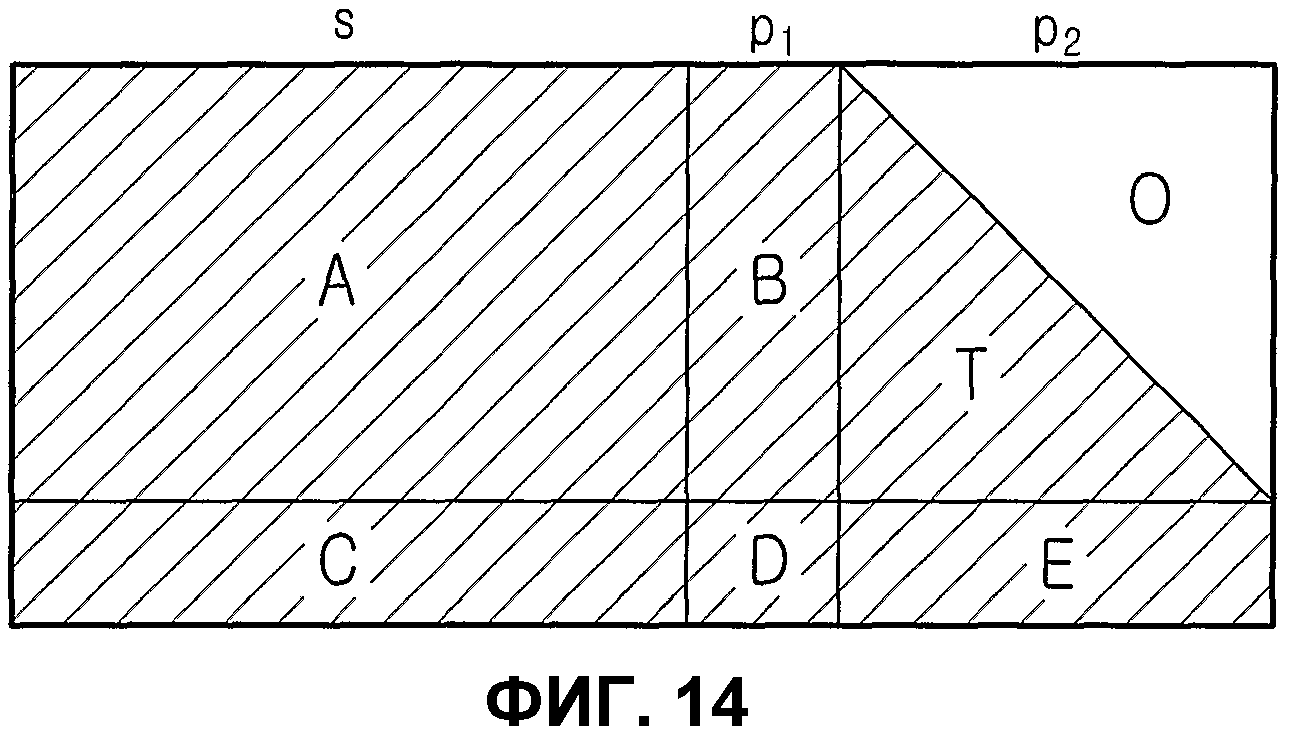
Фиг.14 является схемой, иллюстрирующей матрицу проверки на четность по фиг.13, которая разделяется на 6 частичных блоков;
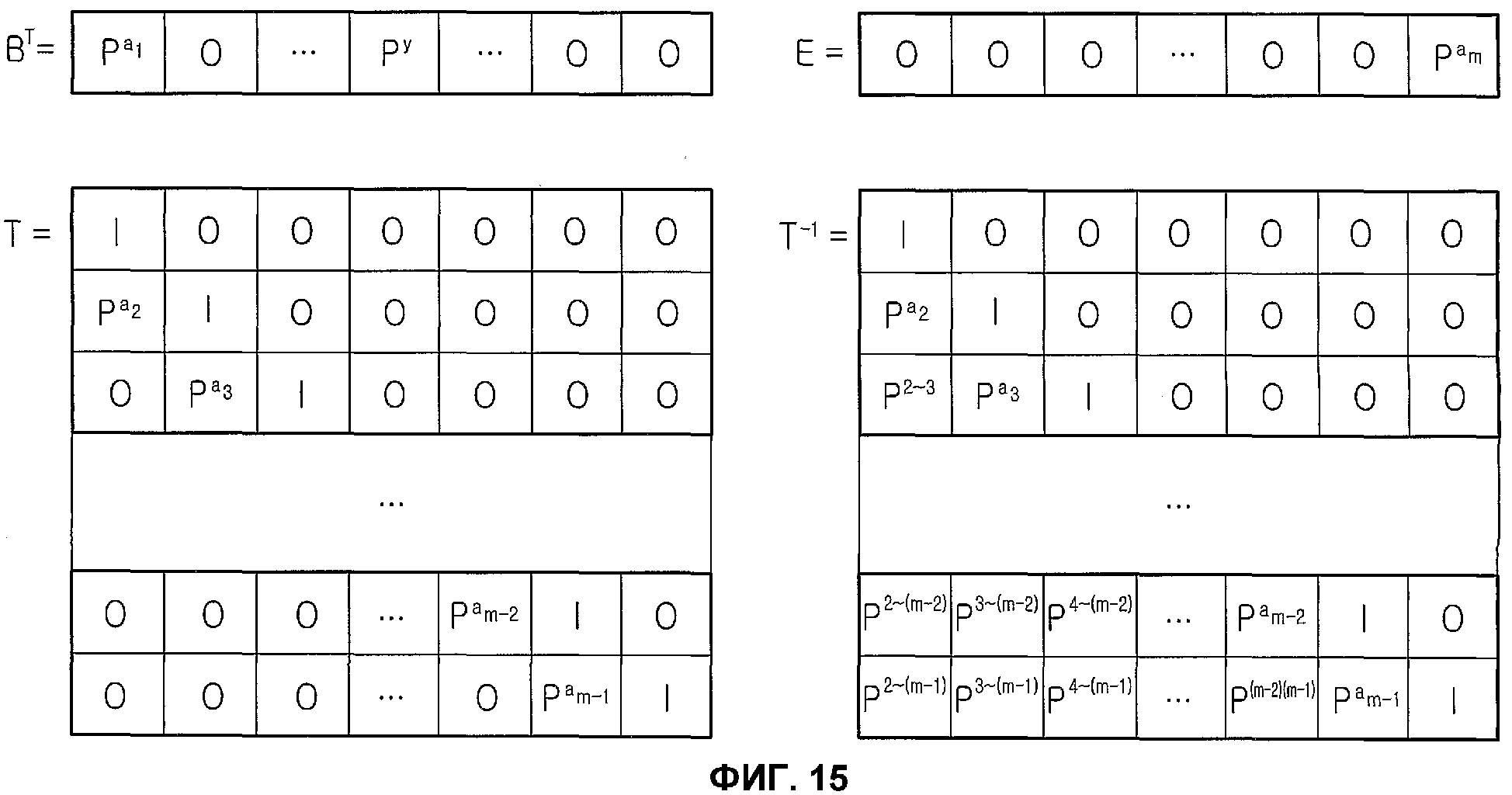
Фиг.15 является схемой, иллюстрирующей транспонированную матрицу частичной матрицы В, показанной на фиг.14, частичной матрицы Е, частичной матрицы Т и обратной матрицы от частичной матрицы Т;
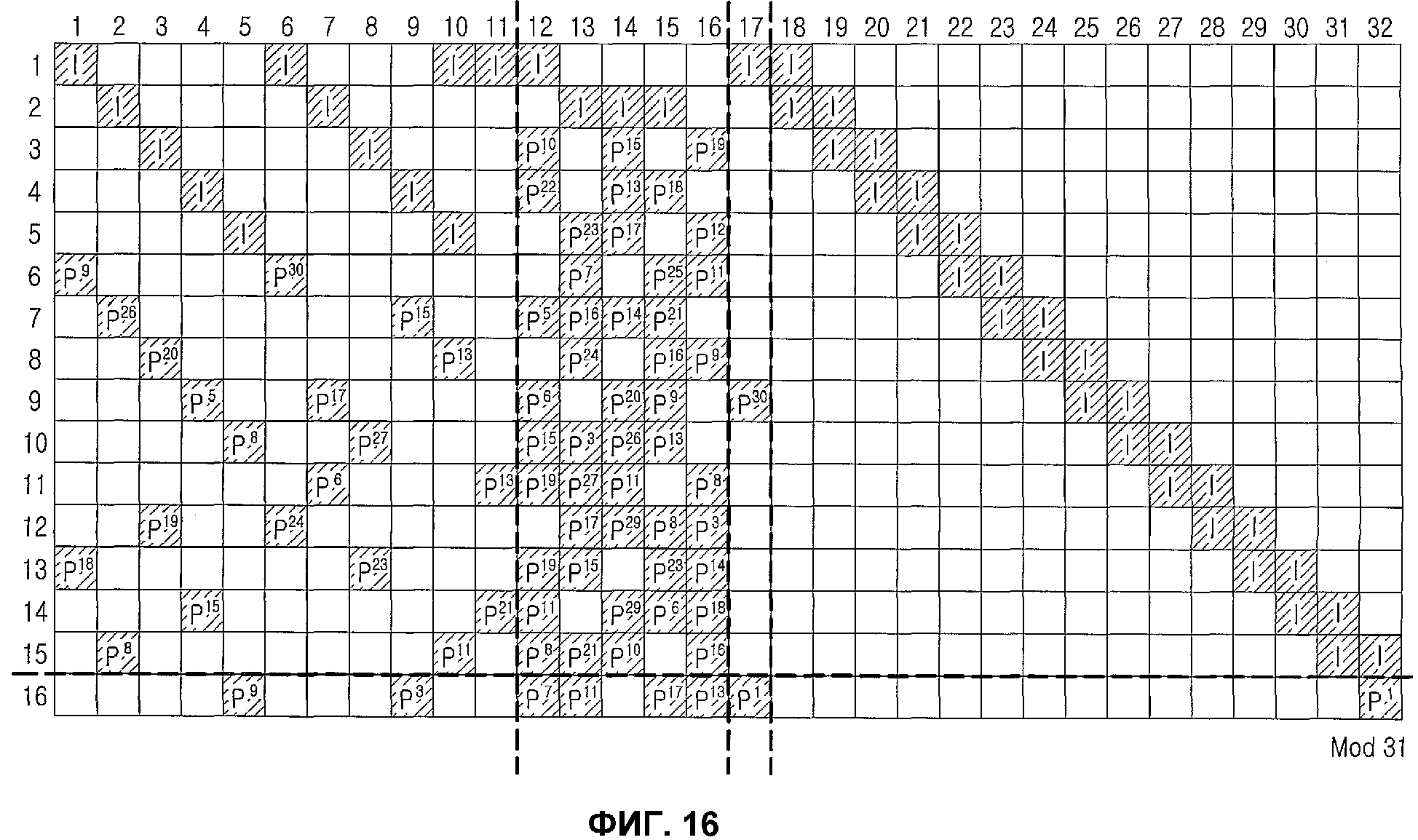
Фиг.16 является схемой, иллюстрирующей матрицу проверки на четность блокового кода НППЧ согласно варианту осуществления настоящего изобретения;
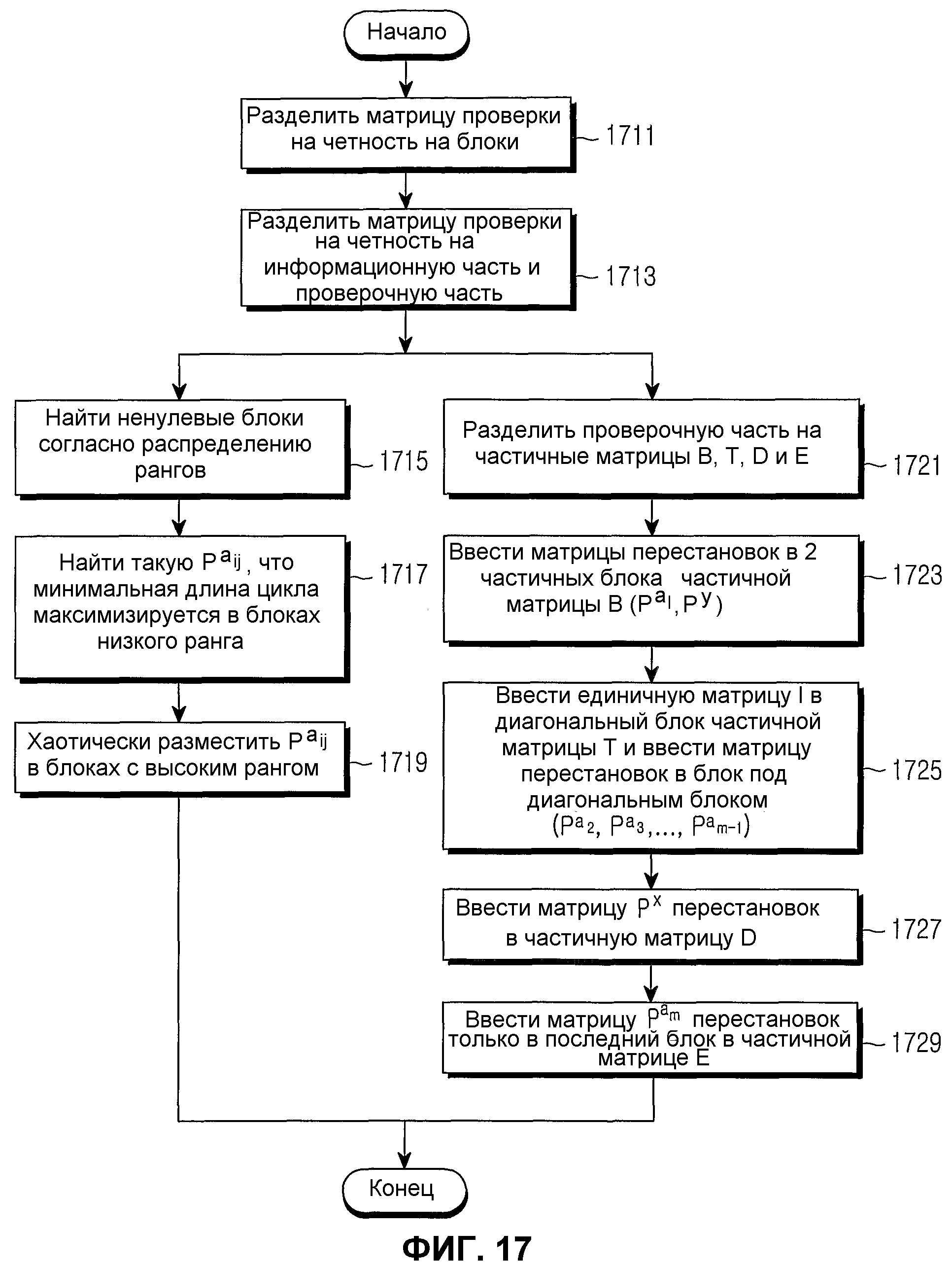
Фиг.17 является блок-схемой алгоритма, иллюстрирующей процедуру генерирования матрицы проверки на четность блокового кода НППЧ согласно варианту осуществления настоящего изобретения;
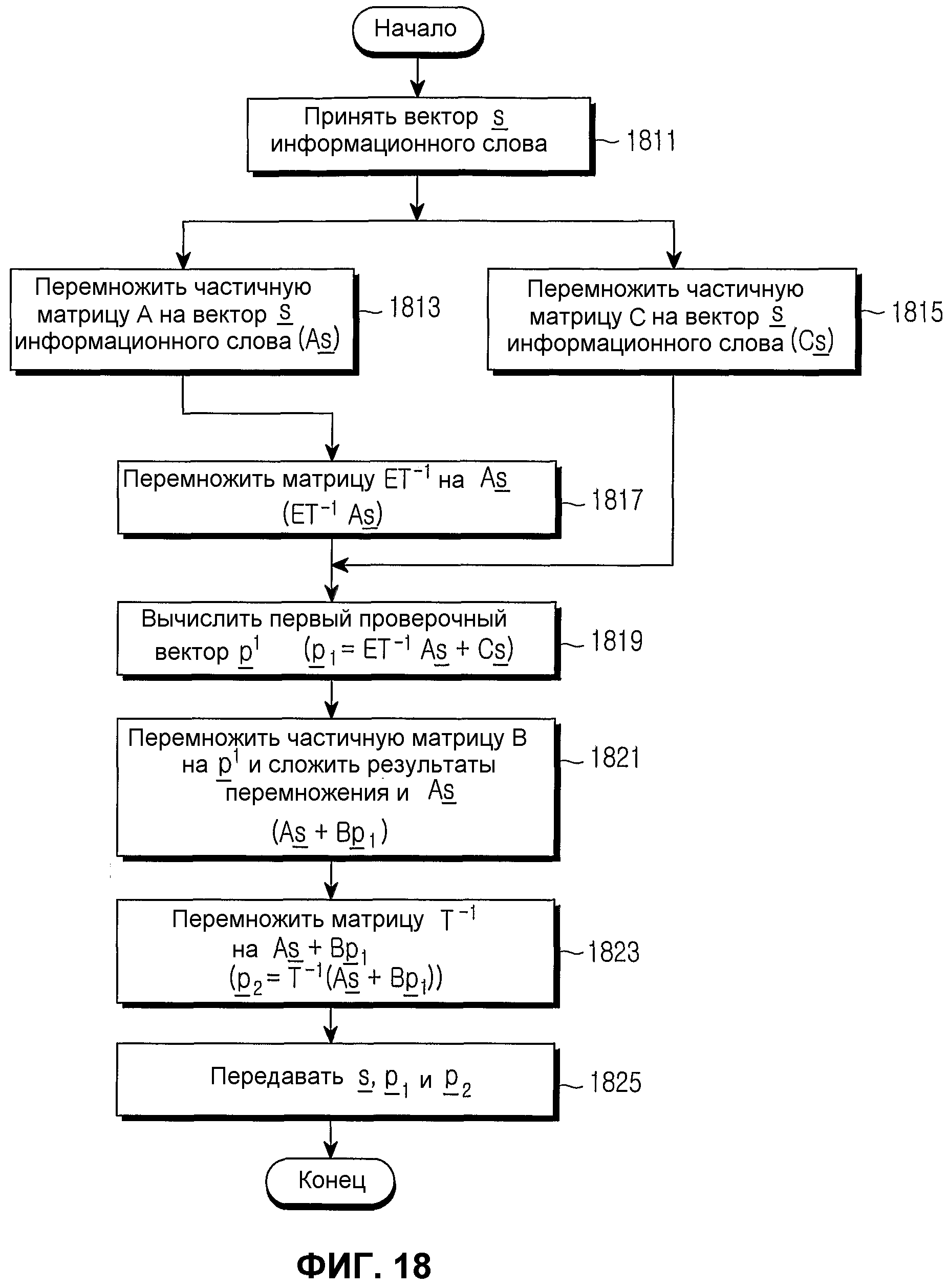
Фиг.18 является блок-схемой алгоритма, иллюстрирующей процедуру кодирования блокового кода НППЧ согласно варианту осуществления настоящего изобретения;
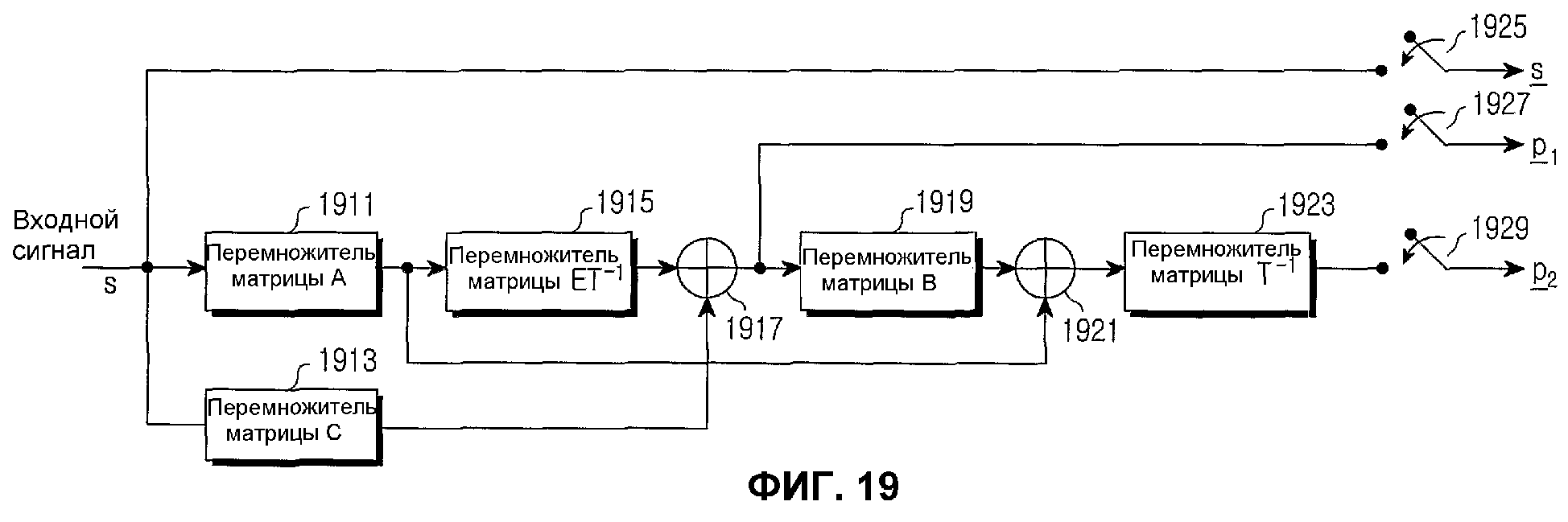
Фиг.19 является блок-схемой, иллюстрирующей внутреннее строение кодирующего устройства для блокового кода НППЧ согласно варианту осуществления настоящего изобретения; и
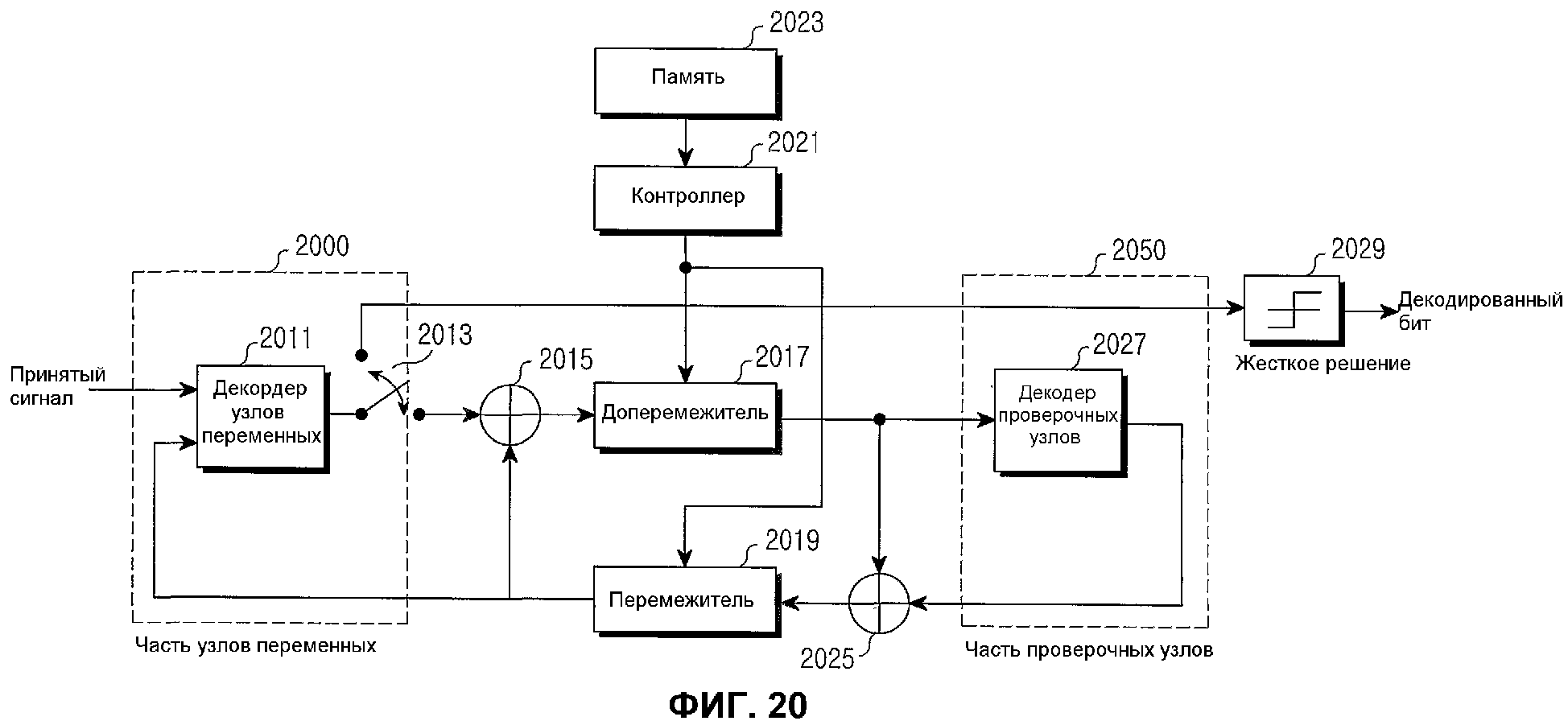
Фиг.20 является блок-схемой, иллюстрирующей внутреннее строение декодирующего устройства для блокового кода НППЧ согласно варианту осуществления настоящего изобретения.
Подробное описание предпочтительного варианта осуществления
Теперь будет подробно описан предпочтительный вариант осуществления настоящего изобретения со ссылкой на приложенные чертежи. В нижеследующем описании подробное изложение известных функций и конфигураций, включенных сюда, опущено для краткости.
Настоящее изобретение предлагает схему для кодирования и декодирования высокопроизводительного нерегулярного кода низкой плотности с проверкой на четность (НППЧ). Настоящее изобретение предлагает схему для кодирования и декодирования нерегулярного кода НППЧ, в которой максимизируется минимальная длина цикла на графе коэффициентов, минимизируется сложность кодирования и оптимизируется распределение рангов на графе коэффициентов.
Термин «цикл», раз он связан с графом коэффициентов кода НППЧ, относится к петле, образованной гранями, соединяющими узлы переменных с узлами проверок в графе коэффициентов, а длина цикла определяется как число граней, составляющих эту петлю. Цикл, который имеет большую длину, означает, что число граней, соединяющих узлы переменных с узлами проверок, составляющих эту петлю в графе коэффициентов, велико. По мере того, как циклы на графе коэффициентов генерируются все более длинными, рабочие характеристики кода НППЧ становятся лучше. Наоборот, когда на графе коэффициентов имеется много циклов с короткой длиной, код НППЧ ухудшается в его исправляющей способности, потому что происходит такое ухудшение рабочих характеристик как нижний предел ошибок. То есть, когда много циклов с короткой длиной существуют на графе коэффициентов, информация о конкретном узле, принадлежащем циклу с короткой длиной, начинающаяся из него, возвращается после малого числа итераций. По мере того, как увеличивается число итераций, информация возвращается к соответствующему узлу чаще, так что информация не может обновляться правильно, что и вызывает ухудшение исправляющей способности кода НППЧ.
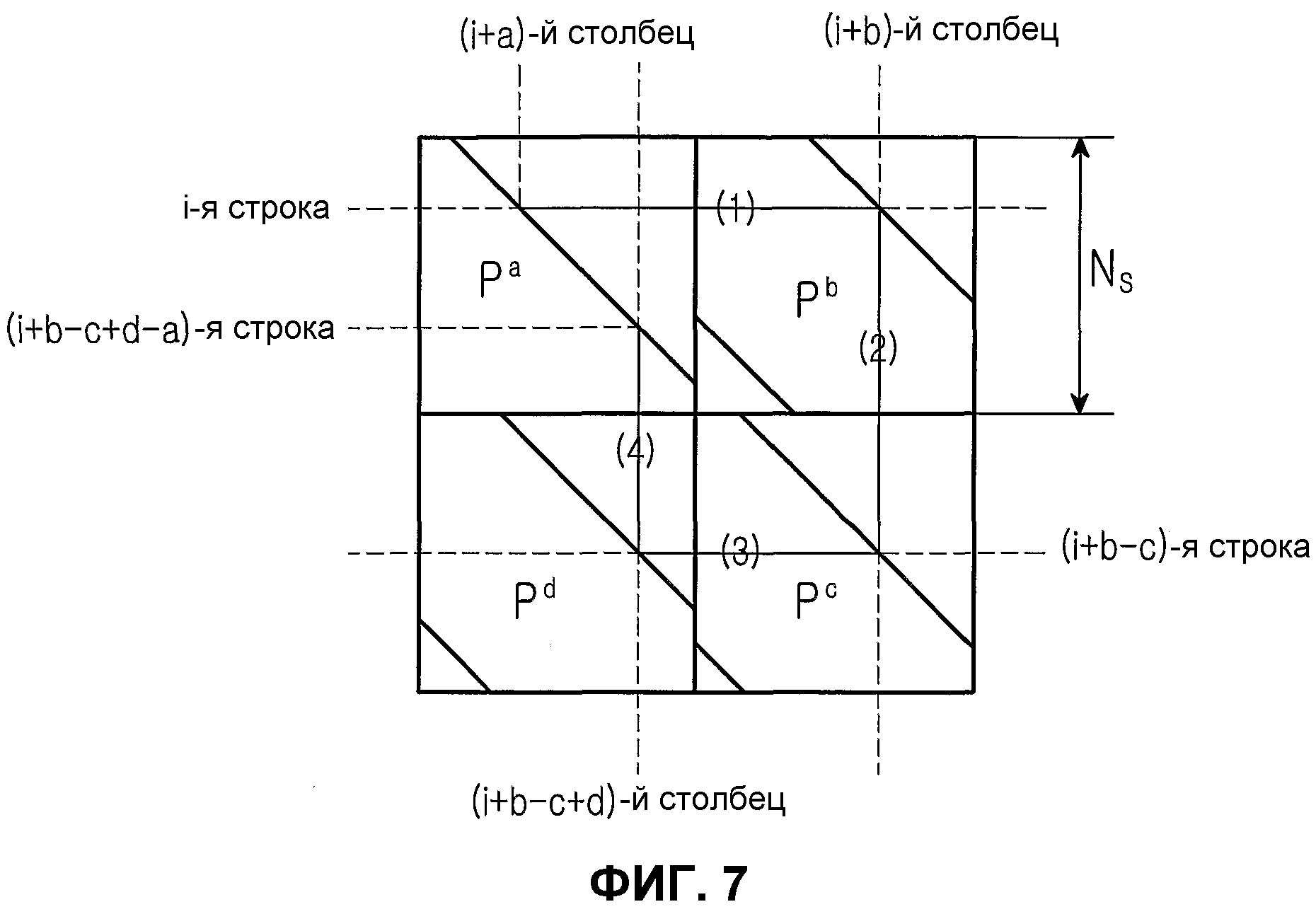
Фиг.7 является схемой, иллюстрирующей структуру цикла блокового кода НППЧ, матрица проверки на четность которого состоит из 4 частичных матриц. Перед тем, как дать описание фиг.7, следует отметить, что блоковый код НППЧ является новым кодом НППЧ, для которого учитывались не только эффективное кодирование, но также и эффективное хранение и улучшение рабочих характеристик матрицы проверки на четность. Блоковый код НППЧ является также кодом НППЧ, расширенным путем обобщения структуры регулярного кода НППЧ. Матрица проверки на четность блокового кода НППЧ, показанного на фиг.7, разделяется на 4 частичных блока, наклонная линия представляет позицию, где располагаются элементы со значением 1, а части, отличные от наклонных частей, представляют позиции, где располагаются элементы со значением 0. Помимо этого, «Р» представляет такую же матрицу перестановки, что и матрица перестановки, описанная в связи с фиг.4. Здесь матрица Р перестановки, как описано в связи с фиг.4, является квадратной матрицей размером NS×NS, в которой каждый из NS столбцов, составляющих матрицу Р перестановки, имеет вес 1, и каждая из NS строк, составляющих матрицу Р перестановки, имеет вес 1. Здесь «вес» представляет элемент с ненулевым значением среди элементов, составляющих матрицу проверки на четность.
Для того чтобы анализировать структуру цикла блокового кода НППЧ, показанного на фиг.7, элемент со значением 1, расположенный в i-й строке частичной матрицы Ра, определяется как эталонный элемент, а элемент со значением 1, расположенный в i-й строке, будет обозначаться как «0-точка». Здесь «частичная матрица» будет относиться к матрице, соответствующей частичному блоку. 0-точка располагается в (i+a)-м столбце частичной матрицы Ра.
Элемент со значением 1 в частичной матрице Pb, расположенный в той же самой строке, что и 0-точка, будет именоваться как «1-точка». По той же самой причине, что и 0-точка, 1-точка располагается в (i+b)-м столбце частичной матрицы Pb.
Далее, элемент со значением 1 в частичной матрице Рс, расположенный в том же самом столбце, что и 1-точка, будет именоваться как «2-точка». Поскольку частичная матрица Рс является матрицей, получаемой путем сдвига соответствующих столбцов единичной матрицы I вправо по модулю NS на с, 2-точка располагается в (i+b-c)-й строке частичной матрицы Рс.
Помимо этого, элемент со значением 1 в частичной матрице Pd, расположенный в той же самой строке, что и 2-точка, будет именоваться как «3-точка». 3-точка располагается в (i+b-c+d)-м столбце частичной матрицы Pd.
Наконец, элемент со значением 1 в частичной матрице Ра, расположенный в том же самом столбце, что и 3-точка, будет именоваться как «4-точка». 4-точка располагается в (i+b-c+d-a)-й строке частичной матрицы Ра.
В структуре цикла кода НППЧ, показанного на фиг.7, если цикл длиной 4 существует, 0-точка и 4-точка располагаются в одной и той же позиции. То есть, соотношение между 0-точкой и 4-точкой определяется уравнением (4):
Уравнение (4) можно переписать в уравнение (5):
В результате, когда удовлетворяется соотношение в уравнении (5), генерируется цикл длиной 4. В общем, когда 0-точка и 4-точка идентичны друг другу, задается соотношение i≡i+m(b-c+d-a)(mod NS) и удовлетворяется нижеследующее соотношение в уравнении (6):
Иными словами, если положительное целое число с минимальным значением среди положительных целых чисел, удовлетворяющих уравнению (6) для заданных a, b, c и d, определяется как «m», цикл длиной 4m становится циклом с минимальной длиной в структуре цикла блокового кода НППЧ, показанного на фиг.7.
В заключение, как описано выше, для (a-b+c-d)≠0, если удовлетворяется НОД(NS, a-b+c-d)=1, то m=NS. Здесь НОД(NS, a-b+c-d) есть функция для вычисления наибольшего общего делителя целых чисел NS и a-b+c-d. Поэтому цикл длиной 4NS становится циклом минимальной длины.
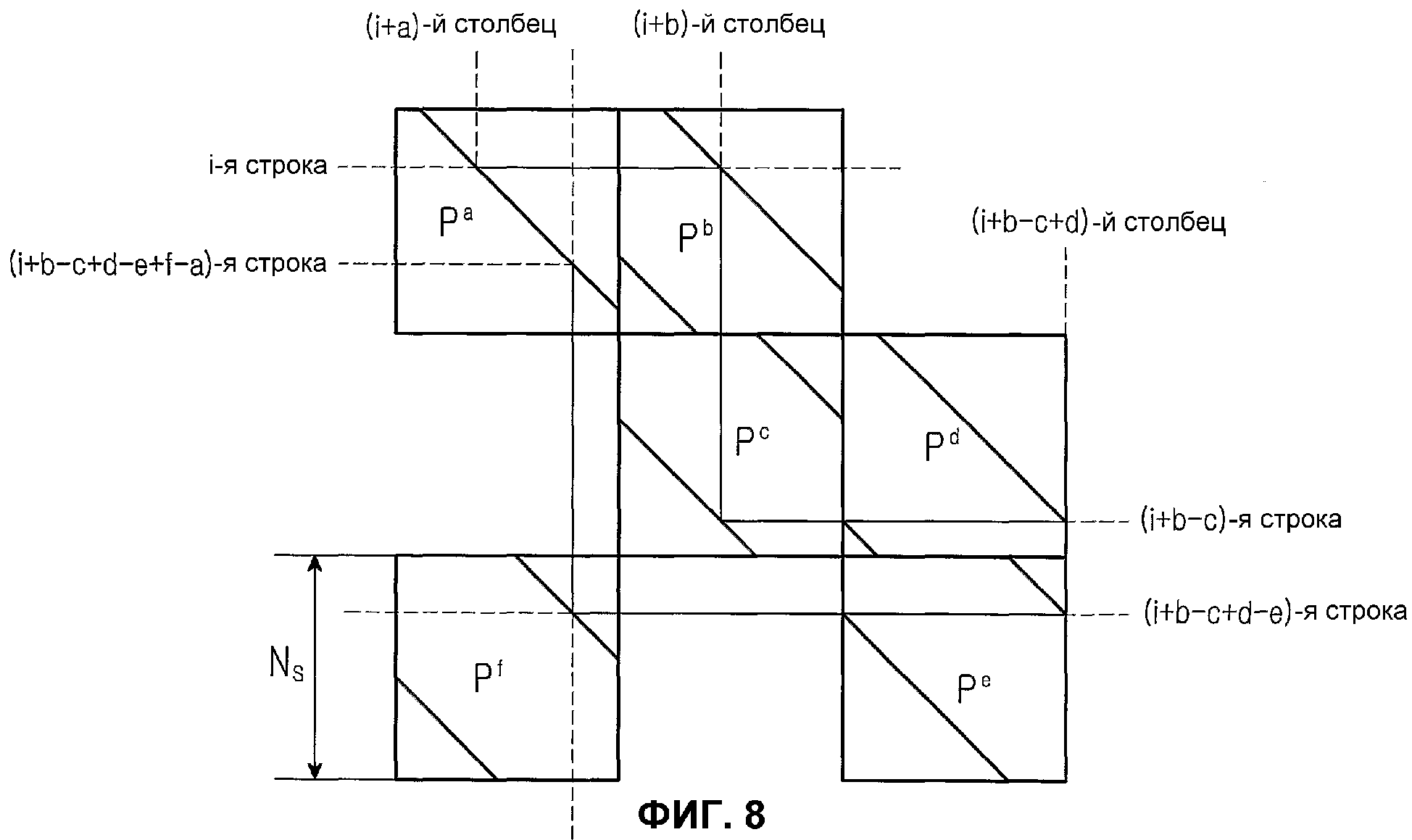
Описанный в связи с фиг.7 анализ цикла блокового кода НППЧ можно применять даже когда число блоков, составляющих матрицу проверки на четность блокового кода НППЧ, превышает 4, т.е. когда число частичных матриц, составляющих матрицу проверки на четность, превышает 4. Теперь, со ссылкой на фиг.8, будет дано описание структуры циклов кода НППЧ, в котором число частичных матриц, составляющих матрицу проверки на четность, превышает 4.
Фиг.8 является схемой, иллюстрирующей структуру циклов блокового кода НППЧ, матрица проверки на четность которого состоит из 6 частичных матриц. Матрица проверки на четность блокового кода НППЧ, показанная на фиг.8, состоит из 6 частичных матриц. Как показано на фиг.8, наклонная линия представляет позицию, где располагаются элементы со значением 1, а части, отличные от частей наклонной линии, представляют позиции, где располагаются элементы со значением 0. Помимо этого, «Р» представляет ту же самую матрицу перестановок, что и матрица перестановок, описанная в связи с фиг.4. Когда структура циклов кода НППЧ, показанная на фиг.8, анализируется способом, описанным в связи с фиг.7, цикл длиной 6m становится циклом минимальной длины.
В общем, когда 0-точка и 6m-точка, во-первых, идентичны друг другу, задано соотношение i≡i+m(b-c+d-e+f-a)(mod NS), и удовлетворяется нижеследующее соотношение, показанное в уравнении (7):
Иными словами, если положительное целое число с минимальным значением среди положительных целых чисел, удовлетворяющих уравнению (7) для заданных a, b, c, d, e и f определяется как «m», цикл длиной 6m становится циклом с минимальной длиной в структуре цикла блокового кода НППЧ, показанного на фиг.8.
В заключение, как описано выше, для (a-b+c-d+e-f)≠0, если удовлетворяется НОД(NS, a-b+c-d+e-f)=1, то m=NS. Поэтому цикл длиной 6NS становится циклом минимальной длины.
Для описанного выше блокового кода НППЧ можно вывести следующие правила.
Правило 1
Если цикл длиной 2l существует в блоковом коде НППЧ, должно удовлетворяться условие уравнения (8):
В уравнении (8) ai (i=1, 2, ..., 2l) представляет экспоненты матриц перестановки, через которые последовательно проходит цикл длиной 2l. То есть, цикл длиной 2l проходит через частичные блоки, составляющие код проверки на четность блокового кода НППЧ в порядке
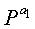
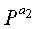
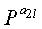
Правило 2
«m» будет определяться как минимальное положительное целое число, удовлетворяющее уравнению (9).
В уравнении (9) ai представляет экспоненты матриц перестановки, выбранных так, что основанный на блоках цикл формируется во всей матрице проверки на четность. Как описано в Правиле 1, не все значения ai должны обязательно отличаться друг от друга, и соответствующий цикл может проходить повторно через одни и те же частичные блоки. В результате частичные матрицы
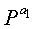
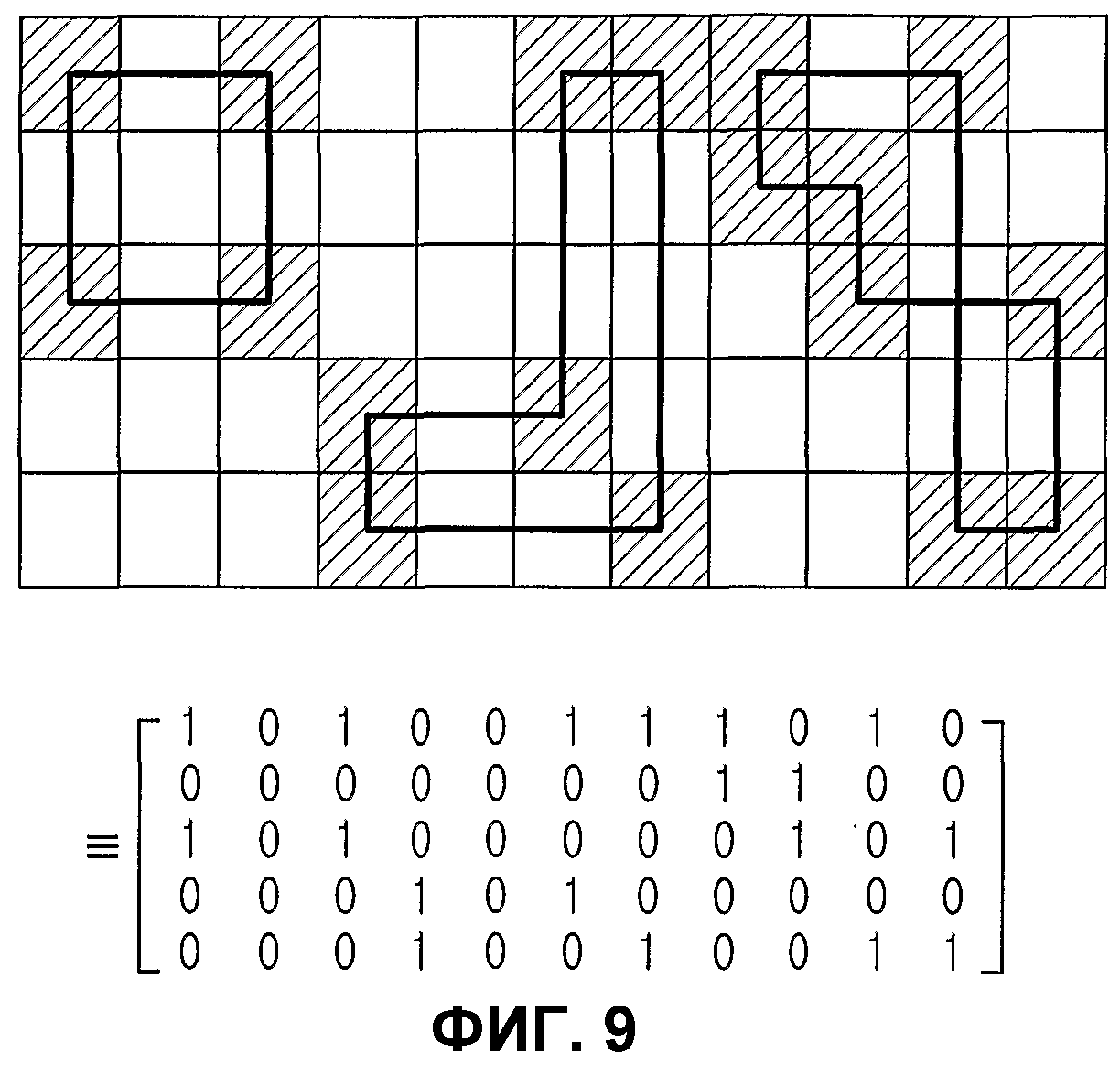
Характеристику структуры циклов блокового кода НППЧ можно легко анализировать с помощью Правила 1 и Правила 2. Например, при использовании Правила 1 и Правила 2 можно не только правильно определить, сколько циклов минимальной длины 6 распределены в коде массива, но также легко анализировать характеристику структуры основанного на блоках цикла («блокового цикла») блокового кода НППЧ, который будет описан здесь ниже. Блоковый цикл является важным фактором, используемым для регулировки длины цикла для формирования матрицы проверки на четность, и блоковый цикл будет описан со ссылкой на фиг.9, Правило 1 и Правило 2.
Фиг.9 является схемой, иллюстрирующей структуру блокового цикла блокового кода НППЧ. На фиг.9 предполагается, что каждый из блоков, составляющих блоковый код НППЧ, имеет вес 1, и когда блоки образуют цикл, говорится, что «блоковый цикл сформирован». Фиг.9 иллюстрирует слева блоковый цикл, образованный из 4 блоков, блоковый цикл, образованный из 6 блоков, и блоковый цикл, образованный из 8 блоков. Как описано в Правиле 1 и Правиле 2, хотя образуется блоковый цикл с короткой длиной, если частичные матрицы, соответствующие блокам, составляющим блоковый цикл, выбраны соответствующим образом, можно выполнять контрольную операцию, так что цикл с короткой длиной не генерируется в реальной матрице проверки на четность. Однако, когда множество блоковых циклов дублируются в блоковом коде НППЧ, минимальная длина реальных циклов в блоковых циклах снижается. В результате циклы с короткой длиной нежелательно генерируются в реальной матрице проверки на четность.
Теперь, со ссылкой на фиг.10, Правило 1 и Правило 2, будет дано описание проблемы, когда множество блоковых циклов дублируются в блоковом коде НППЧ, и причины, почему следует избегать дублированных блоковых циклов при генерировании матрицы проверки на четность кода НППЧ.
Фиг.10 является схемой, иллюстрирующей структуру блоковых циклов блокового кода НППЧ, в котором дублируются 6 частичных матриц в матрице проверки на четность. Нижеследующий последовательный порядок блоков можно рассматривать по стрелкам, показанным на фиг.10.
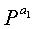
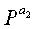
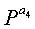
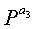
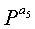
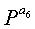
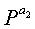
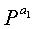
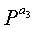
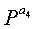
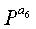
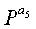
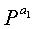
Экспоненты частичных матриц, следующие вышеприведенному последовательному порядку блоков, удовлетворяют уравнению (10) независимо от значений NS.
Если уравнение (10) прикладывается к уравнению (9), описанному в Правиле 2, то m=1. Поэтому в случае блокового кода НППЧ, показанного на фиг.10, где имеется блоковый цикл, в котором дублируются 6 частичных матриц, даже если выбирается любая частичная матрица, составляющая полную матрицу проверки на четность, выбранная частичная матрица всегда включает в себя структуру циклов длиной 12. То есть, в случае блокового кода НППЧ, показанного на фиг.10, где имеется блоковый цикл, в котором дублируются 6 частичных матриц, минимальная длина цикла матрицы проверки на четность ограничивается до максимума в 12.
Фиг.11 является схемой, иллюстрирующей структуру блоковых циклов блокового кода НППЧ, в котором дублируются 7 частичных блоков матрицы проверки на четность.
На фиг.11 показана структура блоковых циклов блокового кода НППЧ, где дублируются 7 частичных блоков матрицы проверки на четность, и нижеследующий последовательный порядок блоков можно рассматривать по стрелкам, показанным на фиг.11.
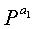
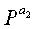
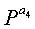
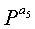
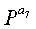
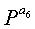
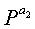
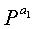
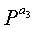
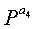
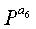
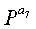
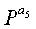
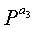
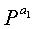
Экспоненты частичных матриц, следующие вышеприведенному последовательному порядку блоков, удовлетворяют уравнению (11) независимо от значений NS.
Если уравнение (11) прикладывается к уравнению (9), описанному в Правиле 2, то m=1. Поэтому в случае блокового кода НППЧ, показанного на фиг.11, где имеется блоковый цикл, в котором дублируются 7 частичных матриц, даже если выбирается любая частичная матрица, составляющая полную матрицу проверки на четность, выбранная частичная матрица всегда включает в себя структуру циклов длиной 14. То есть, в случае блокового кода НППЧ, показанного на фиг.11, где имеется блоковый цикл, в котором дублируются 7 частичных матриц, минимальная длина цикла матрицы проверки на четность ограничивается до максимума в 14.
Как описано выше, если слишком много циклов дублируются между блоками, составляющими матрицу проверки на четность в блоковом коде НППЧ, то имеется ограничение при максимизации минимальной длины цикла независимо от того, как выбрать частичную матрицу матрицы проверки на четность, что вызывает ухудшение в рабочих характеристиках блокового кода НППЧ. Поэтому матрица проверки на четность генерируется в блоковом коде НППЧ так, что генерируются как можно меньше блоковых циклов, посредством чего предотвращается генерирование дублированных блоковых циклов.
Далее будет приведено описание способа генерирования матрицы проверки на четность блокового кода НППЧ с учетом эффективного кодирования кроме блокового цикла.
В настоящем изобретении в качестве метода кодирования блокового кода НППЧ будет использоваться метод Ричардсона-Урбанке. Поскольку в качестве метода кодирования используется метод Ричардсона-Урбанке, сложность кодирования можно минимизировать, так что форма матрицы проверки на четность может быть подобна форме полной нижней треугольной матрицы.
Фиг.12 является схемой, иллюстрирующей матрицу проверки на четность, имеющую форму полной нижней треугольной матрицы. Матрица проверки на четность, показанная на фиг.12, имеет форму полной нижней треугольной матрицы и состоит из информационной части и проверочной части. Информационная часть представляет часть матрицы проверки на четность, отображенную на реальное информационное слово в процессе кодирования блокового кода НППЧ, а проверочная часть представляет часть матрицы проверки на четность, отображенную на реальную проверку на четность в процессе кодирования блокового кода НППЧ. В проверочной части, как показано на фиг.12, нулевые матрицы и частичные матрицы существуют с единичными матрицами I в качестве их начальных точек, и частичные матрицы имеют полную нижнюю треугольную форму.
Фиг.13 является схемой, иллюстрирующей матрицу проверки на четность, имеющую форму, подобную форме полной нижней треугольной матрицы. Матрица проверки на четность, показанная на фиг.13, отличается от матрицы проверки на четность, имеющей форму полной нижней треугольной матрицы, показанной на фиг.12, в проверочной части. На фиг.13 верхний индекс (или экспонента) aij матрицы Р перестановок составляет либо 0≤aij≤NS-1, либо aij=∞. Матрица перестановок с верхним индексом aij=0, т.е. матрица Р0 перестановок представляет единичную матрицу
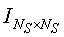
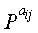
Кроме того, верхние индексы ai, x, y в матрицах перестановки, отображающихся на проверочную часть, представляют верхние индексы матриц перестановки, однако для удобства пояснения эти верхние индексы ai, x, y представляются ссылочными буквами отличного формата для отличия от информационной части. То есть, на фиг.13 Pa1-Pam также являются матрицами перестановки, эти матрицы Pa1-Pam перестановки располагаются в диагональной части проверочной части. Верхние индексы a1-am индексированы последовательно. Матрицы PX и PY также является матрицами перестановок, однако, для удобства пояснения, матрицы PX и PY перестановок представляются ссылочными буквами отличного формата для отличия от информационной части.
Если предполагается, что длина блока блокового кода НППЧ, имеющего матрицу проверки на четность, показанную на фиг.13, составляет N, сложность кодирования блокового кода НППЧ линейно возрастает относительно длины N блока.
Наибольшая проблема кода НППЧ, имеющего матрицу проверки на четность по фиг.13, состоит в том, что если длина частичного блока определяется как NS, генерируются NS проверочных узлов, ранги которых всегда равны 1 на графе коэффициентов блокового кода НППЧ. Здесь ранги проверочных узлов не могут воздействовать на улучшение рабочих характеристик на основании итеративного декодирования. Поэтому стандартный код НППЧ на основании метода Ричардсона-Урбанке не включает в себя узла проверки с рангом 1. Поэтому матрица проверки на четность по фиг.13 будет предполагаться в качестве основной матрицы проверки на четность для конструирования такой матрицы проверки на четность, чтобы она обеспечивала эффективное кодирование, не включая в себя узла проверки с рангом 1. В матрице проверки на четность по фиг.13, состоящей из частичных матриц, выбор частичной матрицы представляет собой очень важный фактор для улучшения рабочих характеристик блокового кода НППЧ, так что нахождение приемлемого критерия выбора для частичной матрицы также становится очень важным фактором.
Поэтому, когда генерируется блоковый код НППЧ, матрица проверки на четность формируется с учетом нижеследующего критерия разработки.
Критерий разработки для матрицы проверки на четность блокового кода НППЧ
(1) Проверочная часть формируется так, чтобы она имела фиксированную форму.
Тот факт, что проверочная часть имеет фиксированную форму, означает, что она имеет конфигурацию, в которой единичные матрицы располагаются, как показано на фиг.16, которая будет описана здесь ниже.
(2) Частичные матрицы с более низким рангом выбираются последовательно первыми.
В настоящем изобретении «ранг» частичной матрицы относится к рангу между 3 и 5. Помимо этого, частичные матрицы размещаются так, что когда частичные матрицы с низким рангом выбираются последовательно первыми, генерируются как можно меньше блоковых циклов, и цикл с минимальной длиной среди частичных матриц с низким рангом формируется как можно дольше.
(3) Частичные матрицы с высоким рангом формируются последовательно после того, как формируются частичные матрицы с низким рангом. Когда размещены частичные матрицы с высоким рангом, цикл минимальной длины формируется как можно дольше.
Теперь будет описан способ разработки матрицы проверки на четность блокового кода НППЧ на основании вышеописанного критерия разработки для матрицы проверки на четность блокового кода НППЧ.
Чтобы облегчить способ разработки матрицы проверки на четность блокового кода НППЧ и способ кодирования блокового кода НППЧ, предполагается, что матрица проверки на четность, показанная на фиг.13, формируется шестью частными матрицами, как показано на фиг.14.
Фиг.14 является схемой, иллюстрирующей матрицу проверки на четность по фиг.13, которая разделяется на 6 частичных блоков. На фиг.14 матрица проверки на четность блокового кода НППЧ, показанная на фиг.14, разделяется на информационную часть s, первую проверочную часть р1 и вторую проверочную часть р2. Информационная часть s представляет часть матрицы проверки на четность, отображенной на реальное информационное слово в процессе кодирования блокового кода НППЧ, как и информационная часть, описанная в связи с фиг. 12 и 13, и однако, для удобства пояснения, информационная часть s представляется отличными ссылочными буквами. Первая проверочная часть р1 и вторая проверочная часть р2 представляют часть матрицы проверки на четность, отображенную на реальную проверку на четность в процессе кодирования блокового кода НППЧ, аналогично проверочной части, описанной в связи с фиг. 12 и 13, и проверочная часть разделяется на две части.
Частичные матрицы А и С соответствуют частичным блокам А и С информационной части s, частичные матрицы В и D соответствуют частичным блокам В и D первой проверочной части р1, а частичные матрицы Т и Е соответствуют частичным блокам Т и Е второй проверочной части р2. Хотя матрица проверки на четность разделяется на 7 частичных блоков на фиг.14, следует отметить, что «0» не является отдельным частичным блоком, а потому частичная матрица Т, соответствующая частичному блоку Т, имеет полную нижнюю треугольную форму, область же, где нулевые матрицы размещаются на основе диагонали, представляется посредством «0». Процесс упрощения способа кодирования с помощью частичных матриц информационной части s, первой проверочной части р1 и второй проверочной части р2 будет описан позже со ссылкой на фиг.17.
Частичные матрицы на фиг.14 будут теперь описаны здесь ниже со ссылкой на фиг.15.
Фиг.15 является схемой, иллюстрирующей транспонированную матрицу частичной матрицы В, показанной на фиг.14, частичную матрицу Е, частичную матрицу Т и обратную матрицу частичной матрицы Т. На фиг.15 частичная матрица ВТ представляет транспонированную матрицу частичной матрицы В, а частичная матрица Т-1 представляет обратную матрицу частичной матрицы Т.
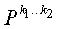
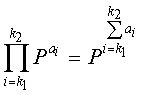
Матрицы перестановок, показанные на фиг.15, к примеру Ра1 будет единичной матрицей. Как описано выше, если верхний индекс матрицы перестановки, т.е. а1 равен 0, Ра1 будет единичной матрицей. Также, если верхний индекс матрицы перестановки, т.е. а1 увеличивается согласно заранее заданному значению, эта матрица перестановки является циклическим сдвигом согласно заранее заданному значению, так что матрица Ра1 будет единичной матрицей.
Фиг.17 является блок-схемой алгоритма, иллюстрирующей процедуру генерирования матрицы проверки на четность блокового кода НППЧ согласно варианту осуществления настоящего изобретения. Перед тем, как дать описание фиг.17, следует отметить, что для генерирования блокового кода НППЧ нужно найти размер кодовых слов и скорость кодирования блокового кода НППЧ, подлежащего генерированию, а размер матрицы проверки на четность должен быть определен согласно найденным размеру кодовых слов и скорости кодирования. Если размер кодовых слов блокового кода НППЧ представляется как N, а кодовая скорость представляется как R, размер матрицы проверки на четность становится равным N(1-R)×N. Фактически процедура генерирования матрицы проверки на четность блокового кода НППЧ, показанного на фиг.17, выполняется лишь единожды, потому что матрица проверки на четность генерируется вначале, и генерированная матрица проверки на четность используется все время работы системы связи.
На фиг.17 на шаге 1711 контроллер разделяет матрицу проверки на четность размером N(1-R)×N на общее число из p×q блоков, в том числе р блоков по горизонтальной оси и q блоков по вертикальной оси, а затем переходит к шагу 1713. Поскольку каждый из блоков имеет размер NS×NS, матрица проверки на четность состоит из NS×p столбцов и NS×q строк. На шаге 1713 контроллер классифицирует р×q блоков, отделенных от матрицы проверки на четность, на информационную часть s, первую проверочную часть р1 и вторую проверочную часть р2, а затем переходит к шагам 1715 и 1721.
На шаге 1715 контроллер разделяет информационную часть на ненулевые блоки, или ненулевые матрицы, и нулевые блоки, или нулевые матрицы, согласно распределению рангов, чтобы гарантировать хорошие рабочие характеристики блокового кода НППЧ, а затем переходит к шагу 1717. Поскольку распределение рангов, чтобы гарантировать хорошие рабочие характеристики блокового кода НППЧ, описано выше, его подробное описание здесь опущено. На шаге 1717 контроллер находит такие матрицы
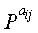
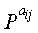
На шаге 1719 контроллер случайным образом находит матрицы
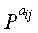
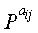
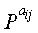
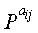
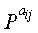
На шаге 1721 контроллер разделяет первую проверочную часть р1 и вторую проверочную часть р2 на 4 частичных матрицы В, Т, D и Е, а затем переходит к шагу 1723. На шаге 1723 контроллер не вводит нулевых матриц, но вводит матрицы РY и
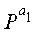
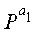
На шаге 1725 контроллер вводит единичные матрицы I в диагональные частичные блоки частичной матрицы Т, вводит конкретные матрицы
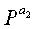
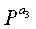
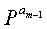
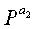
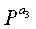
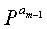
На шаге 1727 контроллер вводит частичную матрицу РХ в частичную матрицу D, а затем переходит к шагу 1729. На шаге 1729 контроллер вводит матрицу
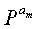
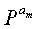
Если частичная матрица В, частичная матрица D и частичная матрица Е соответственно сформированы в матрице проверки на четность блокового кода НППЧ, процессом кодирования для блокового кода НППЧ можно легко управлять. Теперь будет дано описание процесса формирования частичной матрицы В, частичной матрицы D и частичной матрицы Е матрицы проверки на четность, чтобы легко управлять процессом кодирования для блокового кода НППЧ.
Когда матрица проверки на четность по фиг.13 разделяется на частичные матрицы, описанные в связи с фиг.14 вышеприведенным образом, можно рассмотреть фиг.15.
Когда вектор с кодового слова разделяется на информационную часть s, первую проверочную часть р1 и вторую проверочную часть р2, как показано на фиг.14, этот вектор с кодового слова можно разделить на вектор s информационного слова, первый проверочный вектор р1 и второй проверочный вектор р2. В этом случае произведение матрицы проверки на четность и вектора с кодового слова можно выразить как уравнение (12) и уравнение (13):
В уравнении (12) Т обозначает операцию транспонирования, а в уравнении (13) часть р1Т, относящаяся к первому проверочному вектору р1, может быть вычислена так:
В уравнении (14), поскольку сложность кодирования блокового кода НППЧ пропорциональна квадрату размера матрицы φ, настоящее изобретение устанавливает матрицу φ, используемую для вычисления первого проверочного вектора р1, как единичную матрицу I. За счет установки матрицы φ как единичной матрицы I таким образом, сложность кодирования блокового кода НППЧ минимизируется. Со ссылкой на фиг.15 будет дано описание процесса установки матрицы φ как единичной матрицы I.
Матрица
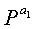
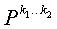
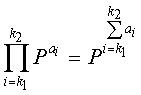
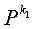
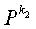
Сначала, на фиг.15, поскольку частичная матрица Е включает в себя все нулевые матрицы кроме одного частичного блока, произведение частичной матрицы Е и обратной матрицы Т-1 частичной матрицы Т можно выразить как произведение последней строки обратной матрицы Т-1 частичной матрицы Т и последнего блока частичной матрицы Е, как показано в уравнении (15):
Если произведение частичной матрицы Е и обратной матрицы Т-1 частичной матрицы Т перемножается на частичную матрицу В, результат можно выразить, как показано в уравнении (16):
где k есть конкретное натуральное число, найденное согласно позиции РY.
Когда произведение частичной матрицы Е и обратной матрицы Т-1 частичной матрицы Т перемножается на частичную матрицу В, как показано в уравнении (16), поскольку частичная матрица В включает в себя все нулевые матрицы кроме двух частичных блоков, перемножение выполняется только на двух частичных блоках в частичной матрице В, посредством чего упрощаются вычисления.
Если D=PX=
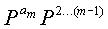
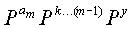
Как описано выше со ссылкой на уравнения (15)-(17), если матрица φ устанавливается как единичная матрица I, процесс кодирования для блокового кода НППЧ можно упростить в его сложности.
Далее, со ссылкой на фиг.18, будет дано описание процедуры кодирования блокового кода НППЧ с помощью матрицы проверки на четность, разработанной в настоящем изобретении.
Фиг.18 является блок-схемой алгоритма, иллюстрирующей процедуру кодирования блокового кода НППЧ согласно варианту осуществления настоящего изобретения. На фиг.18 на шаге 1811 контроллер принимает вектор s информационного слова, а затем переходит к шагам 1813 и 1815. Здесь предполагается, что длина вектора s информационного слова, принятого для кодирования блокового кода НППЧ, равна k. На шаге 1813 контроллер матрично перемножает вектор s информационного слова на матрицу (As) проверки на четность, а затем переходит к шагу 1817. Поскольку число элементов со значением 1, имеющихся в частичной матрице А, намного меньше, чем число элементов со значением 0, имеющихся в частичной матрице А, матричное перемножение вектора s информационного слова и частичной матрицы А матрицы проверки на четность можно осуществить с относительно малым числом вычислений сумм-произведений. Помимо этого, поскольку позиции элементов со значением 1 в частичной матрице А можно выразить позицией ненулевого блока и экспонентой матрицы перестановки для ее блока, матричное перемножение можно выполнять с помощью простых вычислений по сравнению с конкретной матрицей проверки на четность. На шаге 1815 контроллер матрично перемножает частичную матрицу С матрицы проверки на четность на вектор s информационного слова (Cs), а затем переходит к шагу 1819.
На шаге 1817 контроллер матрично перемножает матрицу ЕТ-1 на результат матричного перемножения вектора s информационного слова и частичной матрицы А для матрицы проверки на четность (ЕТ-1Аs), а затем переходит к шагу 1819. Как описано выше, поскольку число элементов со значением 1 в матрице ЕТ-1 очень мало, если только известна экспонента матрицы перестановки соответствующего блока, матричное перемножение можно осуществить легко. На шаге 1819 контроллер вычисляет первый проверочный вектор р1 путем сложения ЕТ-1Аs и Cs(р1=ЕТ-1Аs+Cs), а затем переходит к шагу 1821. Здесь вычисление сложения является вычислением Исключительного ИЛИ (XOR), в котором когда складываются одинаковые биты, результат сложения становится «0», а когда складываются различные биты, результат сложения становится «1». То есть, в процессе до шага 1819 вычисляется первый проверочный вектор р1 из уравнения (14).
На шаге 1821 контроллер перемножает частичную матрицу В матрицы проверки на четность на первый проверочный вектор р1 (Вр1), складывает Вр1 и As (As+Bp1), а затем переходит к шагу 1823. Как описано в связи с уравнением (12), если вектор s информационного слова и первый проверочный вектор р1 известны, обратная матрица Т-1 частичной матрицы Т в матрице проверки на четность должна перемножаться, чтобы вычислить второй проверочный вектор р2. Поэтому на шаге 1823 контроллер перемножает вектор (As+Bp1), вычисленный на шаге 1821, на обратную матрицу Т-1 частичной матрицы Т, чтобы вычислить второй проверочный вектор р2 (р2=Т-1(As+Bp1)), а затем переходит к шагу 1825. Как описано выше, если известен только вектор s информационного слова блокового кода НППЧ, можно вычислить первый проверочный вектор р1 и второй проверочный вектор р2. В результате можно получить вектор кодового слова. На шаге 1825 контроллер передает вектор с информационного слова, генерированный вектором s информационного слова, первым проверочным вектором р1 и вторым проверочным вектором р2, и заканчивает процедуру.
Фиг.19 является блок-схемой, иллюстрирующей внутреннее строение кодирующего устройства для блокового кода НППЧ согласно варианту осуществления настоящего изобретения. На фиг.19 кодирующее устройство для блокового кода НППЧ состоит из перемножителя 1911 матрицы А, перемножителя 1913 матрицы С, перемножителя 1915 матрицы ЕТ-1, первого сумматора 1917, перемножителя 1919 матрицы В, второго сумматора 1921, перемножителя 1923 матрицы Т-1 и переключателей 1925, 1927 и 1929.
Когда принимается входной сигнал, т.е. вектор s информационного слова длиной k, подлежащий кодированию блоковым кодом НППЧ, принятый вектор s информационного слова вводится в каждый из переключателя 1925, перемножителя 1911 матрицы А и перемножителя 1913 матрицы С. Перемножитель 1911 матрицы А перемножает вектор s информационного слова на частичную матрицу А полной матрицы проверки на четность и выводит результат перемножения на перемножитель 1915 матрицы ЕТ-1 и второй сумматор 1921. Перемножитель 1913 матрицы С перемножает вектор s информационного слова на частичную матрицу С полной матрицы проверки на четность и выводит результат перемножения на первый сумматор 1917. Перемножитель 1915 матрицы ЕТ-1 перемножает сигнал, выведенный из перемножителя 1911 матрицы А, на частичную матрицу ЕТ-1 полной матрицы проверки на четность и выводит результат перемножения на первый сумматор 1917.
Первый сумматор 1917 складывает сигнал, выведенный из перемножителя 1915 матрицы ЕТ-1, и сигнал, выведенный из перемножителя 1913 матрицы С, и выводит результат сложения на перемножитель 1919 матрицы В и переключатель 1927. Здесь первый сумматор 1917 выполняет вычисление Исключительного ИЛИ на побитовой основе. Например, когда принимаются вектор длины 3 х=(х1, х2, х3) и вектор длины 3 у=(у1, у2, у3), первый сумматор 1917 осуществляет операцию Исключительное ИЛИ над вектором длины 3 х=(х1, х2, х3) и вектором длины 3 у=(у1, у2, у3) и выводит вектор длины 3 z=(x1⊕y1, x2⊕y2, x3⊕y3). Здесь вычисление ⊕ представляет вычисление Исключительного ИЛИ, в котором когда складываются одинаковые биты, результат сложения становится «0», а когда складываются различные биты, результат сложения становится «1». То есть, сигнал, выводимый из первого сумматора 1917, становится первым проверочным вектором р1.
Перемножитель 1919 матрицы В перемножает сигнал или первый проверочный вектор р1, выводимый из первого сумматора 1917, на частичную матрицу В полной матрицы проверки на четность и выводит результат перемножения на второй сумматор 1921. Второй сумматор 1921 складывает сигнал, выводимый из перемножителя 1919 матрицы В, и сигнал, выводимый из перемножителя 1911 матрицы А, и выводит результат перемножения на перемножитель 1923 матрицы Т-1. Второй сумматор 1921, как и сумматор 1917, осуществляет операцию Исключительное ИЛИ над сигналом, выводимым из перемножителя 1919 матрицы В, и сигналом, выводимым из перемножителя 1911 матрицы А, и выводит результат на перемножитель 1923 матрицы Т-1.
Перемножитель 1923 матрицы Т-1 перемножает сигнал, выводимый из сумматора 1921, на частичную матрицу Т-1 и выводит результат перемножения на переключатель 1929. Здесь выход перемножителя 1923 матрицы Т-1 становится вторым проверочным вектором р2. Переключатели 1925, 1927 и 1929 включаются только в свое время передачи соответствующего сигнала. То есть, во время передачи вектора s информационного слова включается переключатель 1925; во время передачи первого проверочного вектора р1 включается переключатель 1927; а во время передачи второго проверочного вектора р2 включается переключатель 1929.
За счет соответствующего выбора частичных матриц полной матрицы проверки на четность, как описано выше, матричное перемножение для ЕТ-1 относительно упрощено, посредством чего облегчается вычисление для ЕТ-1АsТ. Помимо этого, матрица φ становится единичной матрицей I, так что процесс вычисления для φ-1 для вычисления Р1Т опускается.
Как описано выше, блоковый код НППЧ гарантирует высокую эффективность памяти для хранения информации, связанной с матрицей проверки на четность согласно ее структурных характеристик, и обеспечивает эффективное кодирование за счет соответствующего выбора частичной матрицы в матрице проверки на четность. Однако из-за того, что матрица проверки на четность генерируется на поблочной основе, снижается хаотичность. Снижение хаотичности может вызвать ухудшение в рабочих характеристиках блокового кода НППЧ. То есть, поскольку нерегулярный блоковый код НППЧ превосходит по характеристикам регулярный блоковый код НППЧ, как описано выше, выбор частичной матрицы в полной матрице проверки на четность действует как очень важный фактор при разработке блокового кода НППЧ.
Теперь, со ссылкой на фиг.16, будет дано описание подробного способа генерирования блокового кода НППЧ, который проявляет великолепные рабочие характеристики, обеспечивая при этом эффективное кодирование при учете цикловых характеристик блокового кода НППЧ.
Фиг.16 является схемой, иллюстрирующей матрицу проверки на четность блокового кода НППЧ согласно варианту осуществления настоящего изобретения. На фиг.16 для структурной простоты матрица проверки на четность блокового кода НППЧ устанавливается так, что
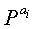
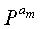
В результате блоковый код НППЧ, показанный на фиг.16, становится нерегулярным блоковым кодом НППЧ, состоящим из 15 блоков с весовыми значениями 2, 12 блоков с весовыми значениями 3 и 5 блоков с весовыми значениями 11 на основе каждого столбца матрицы проверки на четность. Поэтому распределение рангов блокового кода НППЧ, показанного на фиг.16, можно выразить уравнением (18):
В уравнении (18) fi обозначает отношение узлов переменных с рангом i ко всем узлам переменных на графе коэффициентов блокового кода НППЧ, а fpi обозначает отношение проверочных узлов с рангом i ко всем проверочным узлам на графе коэффициентов блокового кода НППЧ. Например, в случае блокового кода НППЧ с длиной блока NS=32 столбцы матрицы проверки на четность, соответствующие 15 узлам переменных среди всех 32 узлов переменных на графе коэффициентов блокового кода НППЧ, имеют весовые значения 2, столбцы матрицы проверки на четность, соответствующие 12 узлам переменных, имеют весовые значения 3, а столбцы матрицы проверки на четность, соответствующие 5 узлам переменных, имеют весовые значения 11. Даже для матрицы проверки на четность, соответствующей проверочным узлам, вес можно учитывать таким же образом, как это сделано для узлов переменных. Распределение рангов, показанное в уравнении (18), вплотную приближает распределение рангов кода НППЧ к идеальному пороговому значению n. Далее, в случае блокового кода НППЧ, показанного на фиг.16, минимальная длина цикла, существующего между узлом с рангом 2 и узлом с рангом 3, равна 12, а минимальная длина цикла между всеми узлами равна 16.
Далее, со ссылкой на фиг.20, будет дано описание процесса декодирования блокового кода НППЧ с помощью кода проверки на четность согласно варианту осуществления настоящего изобретения.
Фиг.20 является блок-схемой, иллюстрирующей внутреннее строение декодирующего устройства для блокового кода НППЧ согласно варианту осуществления настоящего изобретения. На фиг.20 декодирующее устройство для блокового кода НППЧ состоит из части 2000 узлов переменных, первого сумматора 2015, деперемежителя 2017, перемежителя 2019, контроллера 2021, памяти 2023, второго сумматора 2025, части 2050 проверочных узлов и блока 2029 жесткого решения. Часть 2000 узлов переменных состоит из декодера 2011 узлов переменных и переключателя 2013, а часть 2050 проверочных узлов состоит из декодера 2027 проверочных узлов.
Принятый сигнал, принимаемый по радиоканалу, вводится в декодер 2011 узлов переменных в части 2000 узлов переменных, и декодер 2011 вычисляет значения вероятности принятого сигнала, обновляет вычисленные значения вероятности и выводит обновленные значения вероятности на переключатель 2013 и первый сумматор 2015. Декодер 2011 узлов переменных соединяет узлы переменных согласно матрице проверки на четность, установленной ранее в декодирующем устройстве для блокового кода НППЧ, и выполняет вычисление обновлений, имеющее столько входных и выходных значений, сколько «1» соединено с узлами переменных. Число «1», соединенных с каждым узлом переменных, идентично весу каждого из столбцов, составляющих матрицу проверки на четность. Поэтому внутреннее вычисление декодера 2011 узлов переменных различно согласно весу каждого из столбцов, составляющих матрицу проверки на четность.
Первый сумматор 2015 принимает сигнал, выводимый из декодера 2011 узлов переменных, и выходной сигнал перемежителя 2019 в процессе предыдущего итеративного декодирования, вычитает выходной сигнал перемежителя 2019 в предыдущем итеративном декодировании из сигнала, выводимого из декодера 2011 узлов переменных в процессе текущего декодирования, и выводит результат вычитания на деперемежитель 2017. Если процесс декодирования является начальным процессом декодирования, выходной сигнал перемежителя 2019 должен рассматриваться как «0».
Деперемежитель 2017 деперемежает сигнал, выводимый из первого сумматора 2015, согласно заранее заданному методу и выводит деперемеженный сигнал на второй сумматор 2025 и декодер 2027 проверочных узлов. Деперемежитель 2017 имеет внутреннюю структуру, соответствующую матрице проверки на четность, потому что выходное значение для входного значения перемежителя 2019, соответствующего деперемежителю 2017, становится различным согласно позициям элементов со значением 1 в матрице проверки на четность.
Второй сумматор 2025 принимает выходной сигнал декодера 2025 проверочных узлов в процессе предыдущего итеративного декодирования и выходной сигнал деперемежителя 2017, вычитает выходной сигнал деперемежителя 2017 из выходного сигнала декодера 2027 проверочных узлов в процессе предыдущего декодирования и выводит результат вычитания на перемежитель 2019. Декодер 2027 проверочных узлов соединяет проверочные узлы согласно матрице проверки на четность, установленной ранее в декодирующем устройстве для блокового кода НППЧ, и выполняет вычисление обновлений, имеющее столько входных и выходных значений, сколько «1» соединено с проверочными узлами. Число «1», соединенных с каждым из проверочных узлов, идентично весу каждой из строк, составляющих матрицу проверки на четность. Поэтому внутреннее вычисление декодера 2027 проверочных узлов различно согласно весу каждой из строк, составляющих матрицу проверки на четность.
Перемежитель 2019 под управлением контроллера 2021 перемежает сигнал, выводимый из второго сумматора 2025, согласно заранее заданному методу и выводит перемеженный сигнал на сумматор 2015 и декодер 2011 узлов переменных. Контроллер 2021 считывает связанную с методом перемежения информацию в памяти 2023 и управляет методом перемежения перемежителя 2019 согласно считанной связанной с методом перемежения информации. Кроме того, если процесс декодирования является начальным процессом декодирования, выходной сигнал деперемежителя 2017 должен считаться как «0».
Путем неоднократного выполнения вышеприведенного процесса декодирующее устройство обеспечивает свободное от ошибок высокопроизводительное декодирование, и после того, как декодирующее устройство выполняет итеративное декодирование столько раз, сколько итераций задано заранее, переключатель 2013 отключает декодер 2011 узлов переменных от второго сумматора 2015 и в то же самое время подключает декодер 2011 узлов переменных к блоку 2029 жесткого решения, так что сигнал, выводимый из декодера 2011 узлов переменных, является входным для блока 2029 жесткого решения. Блок 2029 жесткого решения принимает жесткое решения по сигналу, выводимому из декодера 2011 узлов переменных, и выводит результат жесткого решения, и выходное значение блока 2029 жесткого решения становится конечным декодированным значением.
Как можно понять из предшествующего описания, настоящее изобретение предлагает блоковый код НППЧ с максимизированной минимальной длиной цикла в системе мобильной связи, посредством чего максимизируется исправляющая способность и улучшаются рабочие характеристики. Помимо этого, настоящее изобретение генерирует эффективную матрицу проверки на четность, посредством чего минимизируется сложность кодирования блокового кода НППЧ.
Хотя изобретение показано и описано со ссылкой на его определенное предпочтительное выполнение, специалистам будет понятно, что в нем можно делать различные изменения в форме и деталях без отхода от сущности и объема изобретения, как оно определено приложенной формулой изобретения.
Реферат
Изобретение относится к системам мобильной связи, в частности к устройству и способу кодирования-декодирования блоковых кодов низкой плотности с проверкой на четность (НППЧ). Техническим результатом является повышение надежности передачи данных и улучшение исправляющей способности кода НППЧ, достигаемый за счет того, что способ включает в себя шаги, при которых определяют размер матрицы проверки на четность на основании скорости кодирования при кодировании информации блоковым кодом НППЧ и длины кодового слова; разделяют матрицу проверки на четность определенного размера на заранее заданное число блоков; классифицируют блоки на блоки, соответствующие информационной части; размещают матрицы перестановок в заранее заданных блоках среди блоков, классифицированных как первая проверочная часть, и размещают единичные матрицы в полной нижней треугольной форме в заранее заданных блоках среди блоков, классифицированных как вторая проверочная часть; и размещают матрицы перестановок в блоках, классифицированных как информационная часть, так что минимальная длина цикла максимизируется и весовые значения являются нерегулярными на графе коэффициентов блокового кода НППЧ. 7 н. и 32 з.п. ф-лы, 20 ил.

Формула
Документы, цитированные в отчёте о поиске
Устройство для декодирования информации с исправлением ошибок
Патенты аналоги
Устройство для декодирования информации с исправлением ошибок
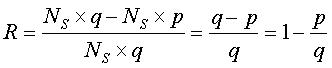
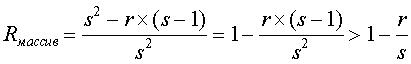
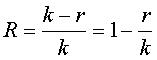
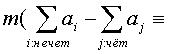
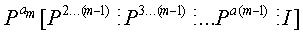
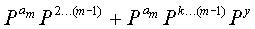
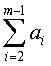
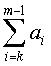
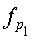
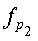

Комментарии