Кодирование и декодирование ldpc пакетов переменных размеров - RU2443053C2

Чертежи

Показать все 14 чертежа(ей)

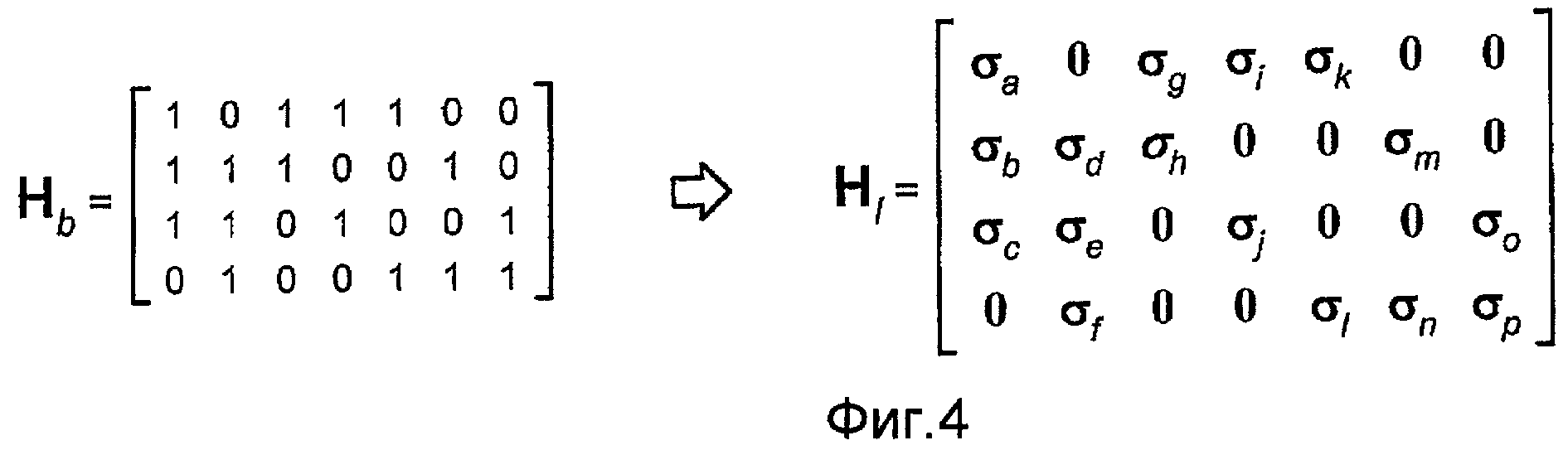
Описание

Для настоящей заявки испрашивается приоритет на основании предварительной патентной заявки США № 60/886496 под названием “LDPC HARMONIZATION”, поданной 24 января 2007 г., принадлежащей правообладателю настоящей заявки и включенной в настоящий документ путем ссылки.

Область техники, к которой относится изобретение

Изобретение относится в общем к области связи и, в частности, к методам кодирования и декодирования данных.

Уровень техники

В системе связи передатчик может кодировать пакет данных для получения битов кода, перемежения битов кода и отображения перемеженных битов в символы модуляции. Затем передатчик может обрабатывать и передавать символы модуляции по каналу связи. Канал связи может искажать передачу данных при конкретном отклике канала и дополнительно ухудшать передачу данных шумом и помехой. Приемник может получать принятые символы, которые могут быть искаженными и ухудшенными версиями переданных символов модуляции. Приемник может обрабатывать принятые символы для восстановления переданного пакета.

Кодирование, выполняемое передатчиком, может позволять приемнику надежно восстанавливать переданный пакет с ухудшенными принятыми символами. Передатчик может осуществлять кодирование на основании кода прямой коррекции ошибок (FEC), который генерирует избыточность в битах кода. Приемник может использовать избыточность для повышения вероятности восстановления переданного пакета.

Для кодирования можно использовать различные типы кода FEC. Некоторые общие типы кода FEC включают в себя сверточный код, турбокод и код контроля четности низкой плотности (LDPC). Сверточный код или турбокод может кодировать пакет из k информационных битов и генерировать кодированный пакет из приблизительно r умноженное на k битов кода, где 1/r - кодовая скорость сверточного или турбокода. Сверточный код может легко кодировать пакет любого размера, пропуская каждый информационный бит через кодер, который может каждый раз оперировать на одном информационном бите. Турбокод также может поддерживать разные размеры пакета с использованием двух составных кодеров, которые могут каждый раз оперировать на одном информационном бите, и перемежителя кода, который может поддерживать разные размеры пакета. Код LDPC может в определенных условиях работы иметь более высокую производительность, чем сверточный и турбокоды. Однако код LDPC обычно предназначен для конкретного размера пакета и может не иметь возможности быстро реагировать на пакеты изменяющихся размеров.

Поэтому в технике существует необходимость в методах поддержки эффективного кодирования и декодирования LDPC пакетов изменяющихся размеров.

Раскрытие изобретения

В настоящем документе описаны методы поддержки кодирования и декодирования LDPC. Согласно одному аспекту кодирование и декодирование LDPC пакетов изменяющихся размеров можно эффективно поддерживать с помощью множества базовых матриц контроля четности разных размеров и множества значений поднятия, равных разным степеням 2. Базовую матрицу G контроля четности размером m_B×n_B можно использовать для кодирования пакета до k_B = n_B - m_B информационных битов для получения кодированного пакета или кодового слова из n_B битов кода. Эту базовую матрицу G контроля четности можно «поднимать» на значение поднятия L для получения поднятой матрицы H контроля четности размером L·m_B×L·n_B. Поднятую матрицу H контроля четности можно использовать для кодирования пакета до L·k_B информационных битов для получения кодового слова из L·n_B битов кода. Широкий диапазон размеров пакета может поддерживаться с помощью сравнительно малого множества базовых матриц контроля четности и сравнительно малого множества значений поднятия. Поднятие также может обеспечивать эффективное параллельное кодирование и декодирование, что может повышать производительность. Кроме того, поднятие может снижать сложность описания для больших кодов LDPC.

В другом аспекте одно множество значений циклического сдвига для ненулевых элементов базовой матрицы контроля четности для одного значения поднятия (например, максимального значения поднятия) можно использовать для генерации значений циклического сдвига для всех остальных значений поднятия, равных разным степеням двойки. Согласно еще одному аспекту значения циклического сдвига s и s + L/m можно выбирать для двух ненулевых элементов в столбце базовой матрицы контроля четности, имеющем по меньшей мере три ненулевых элемента, где s - произвольное значение, и m равно степени 2. В одном варианте осуществления m равно 4, и значения циклического сдвига для двух ненулевых элементов равны s и s + L/4. Эти значения циклического сдвига могут упрощать кодирование и декодирование.

Различные аспекты и признаки раскрытия более подробно описаны ниже.

Краткое описание чертежей

Фиг.1 - система беспроводной связи.

Фиг.2 - блок-схема базовой станции и терминала.

Фиг.3 - граф Таннера для иллюстративного кода LDPC.

Фиг.4 - поднятие базовой матрицы контроля четности.

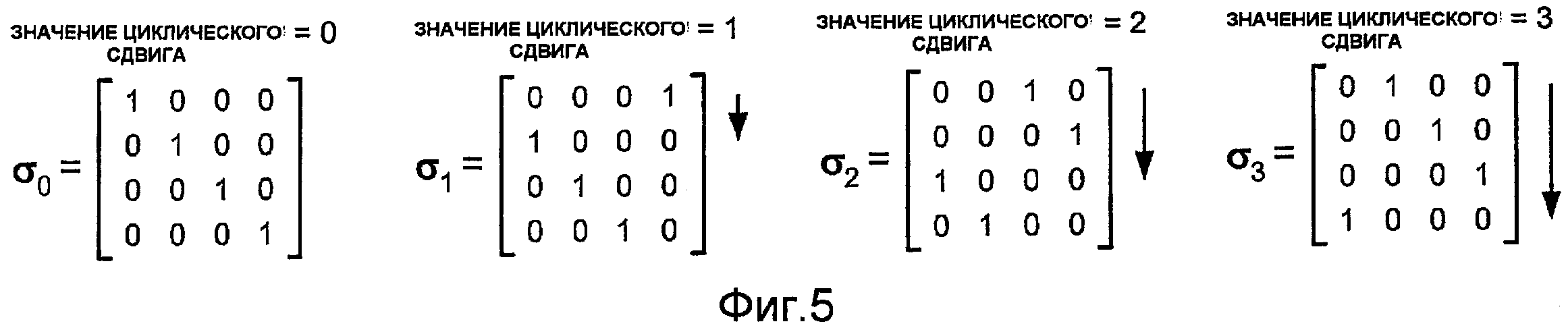
Фиг.5 - множество из четырех матриц циклической перестановки.

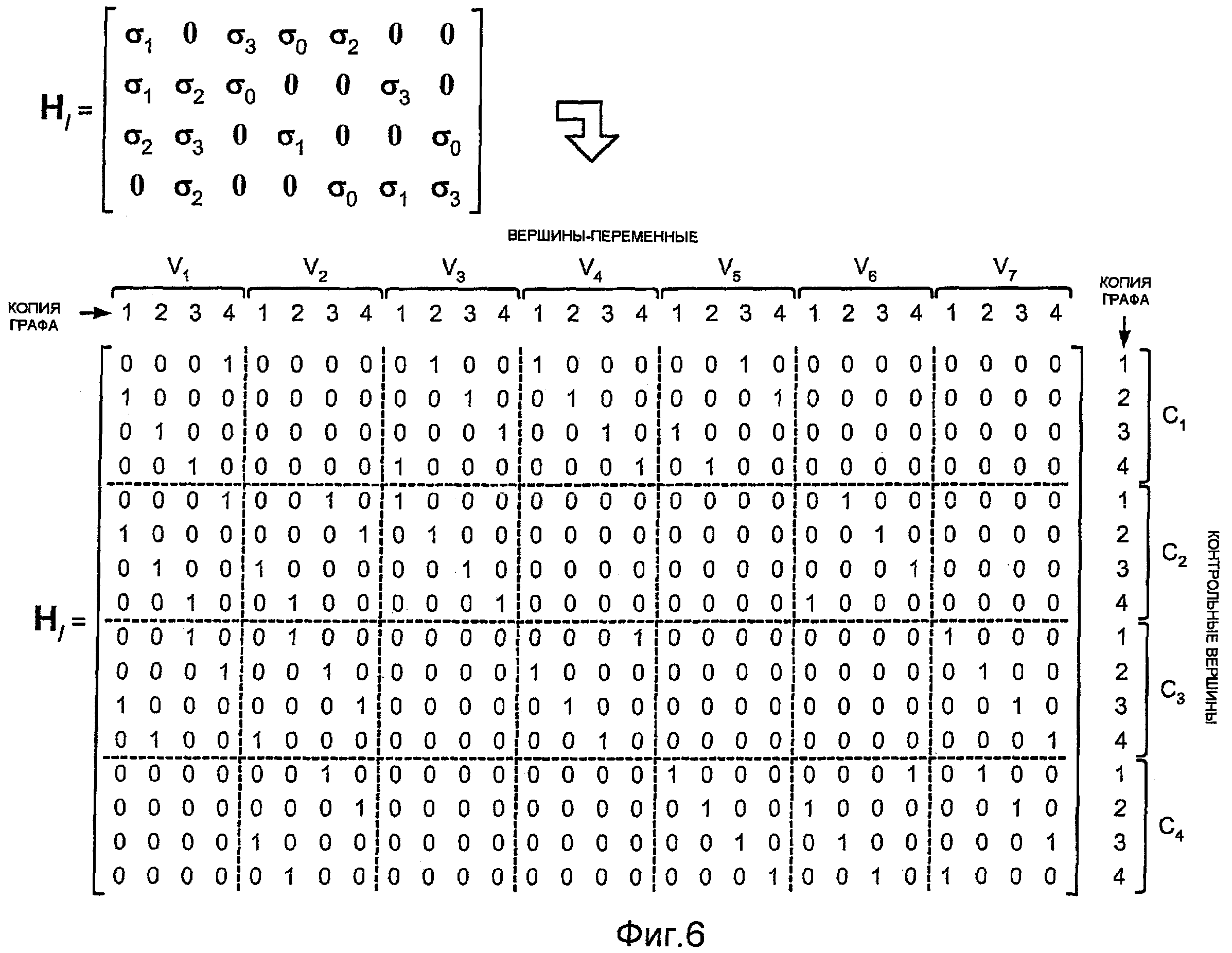
Фиг.6 - поднятая матрица контроля четности.

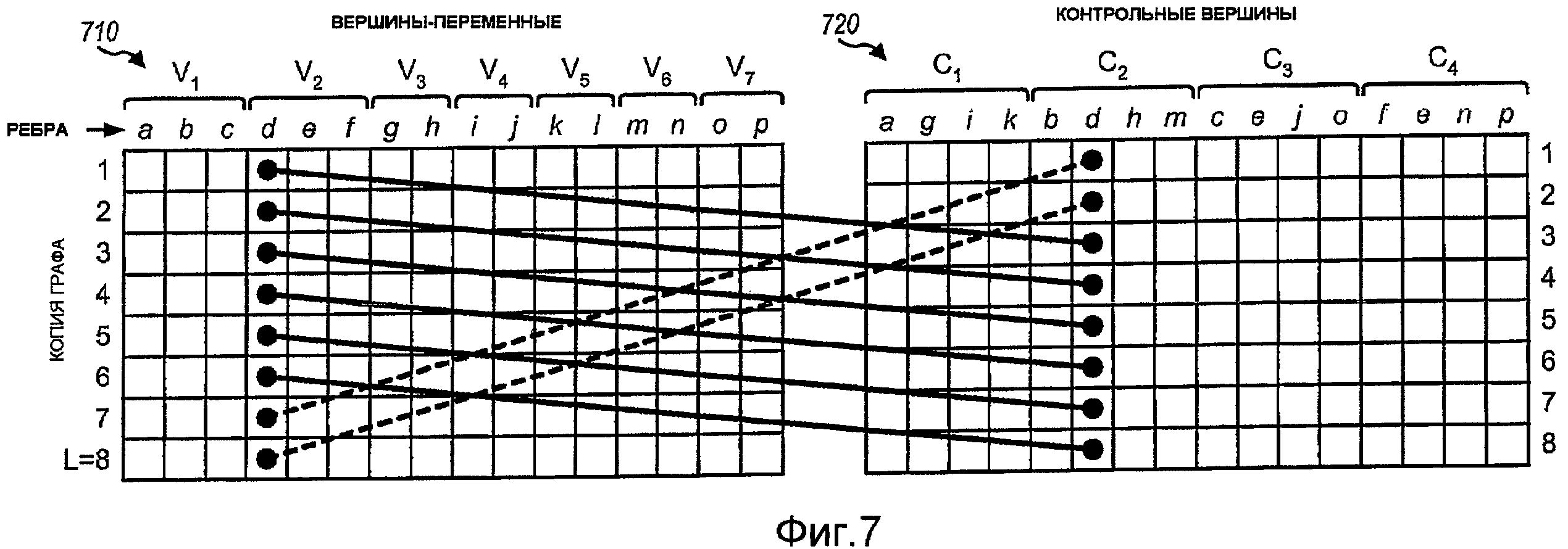
Фиг.7 - другое представление поднятой матрицы контроля четности.

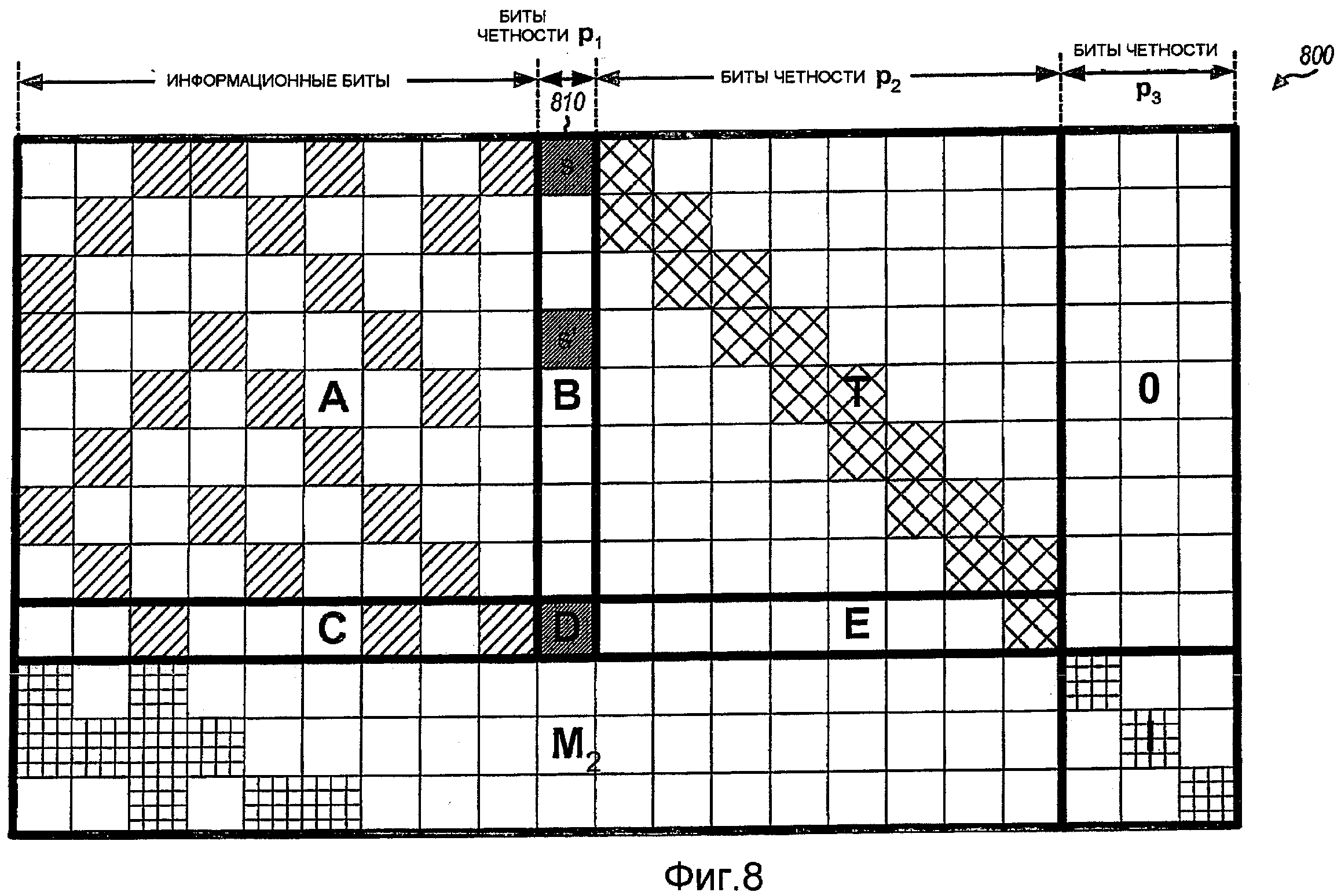
Фиг.8 - граф для поднятой матрицы контроля четности.

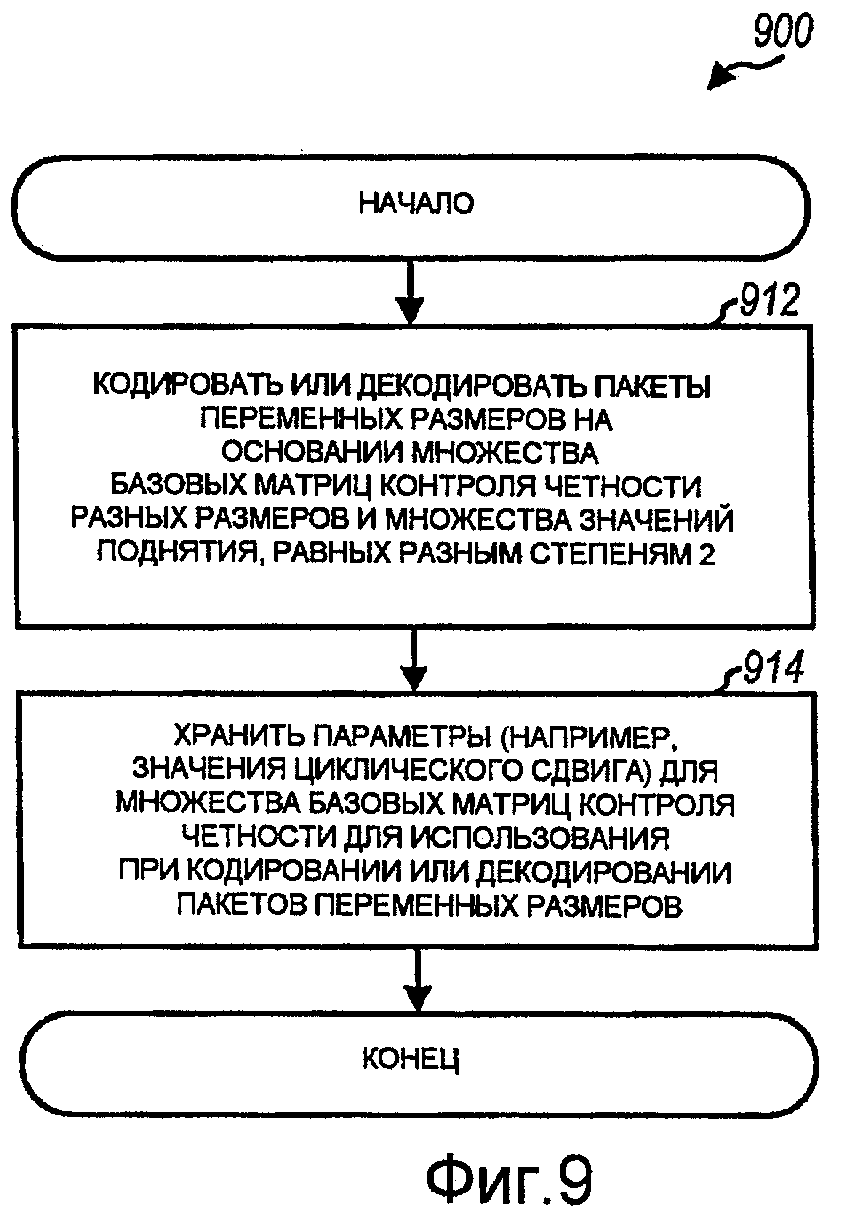
Фиг.9 - процесс для обработки данных.

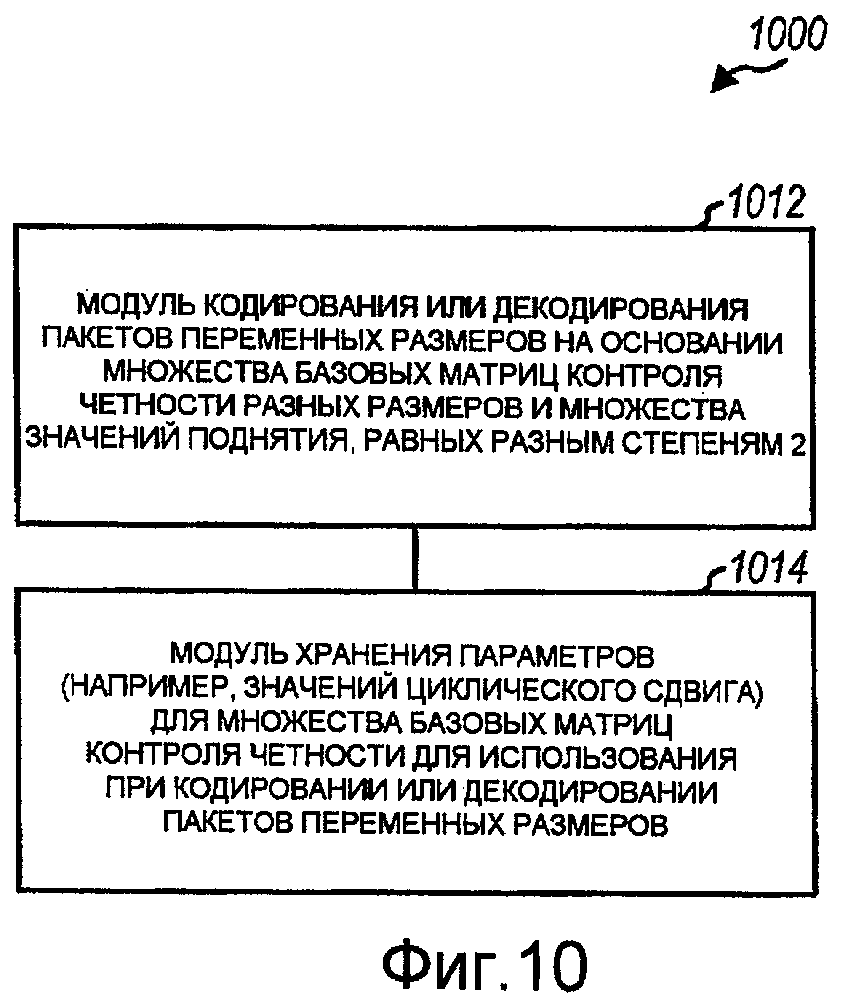
Фиг.10 - устройство для обработки данных.

Фиг.11 - процесс обработки пакета.

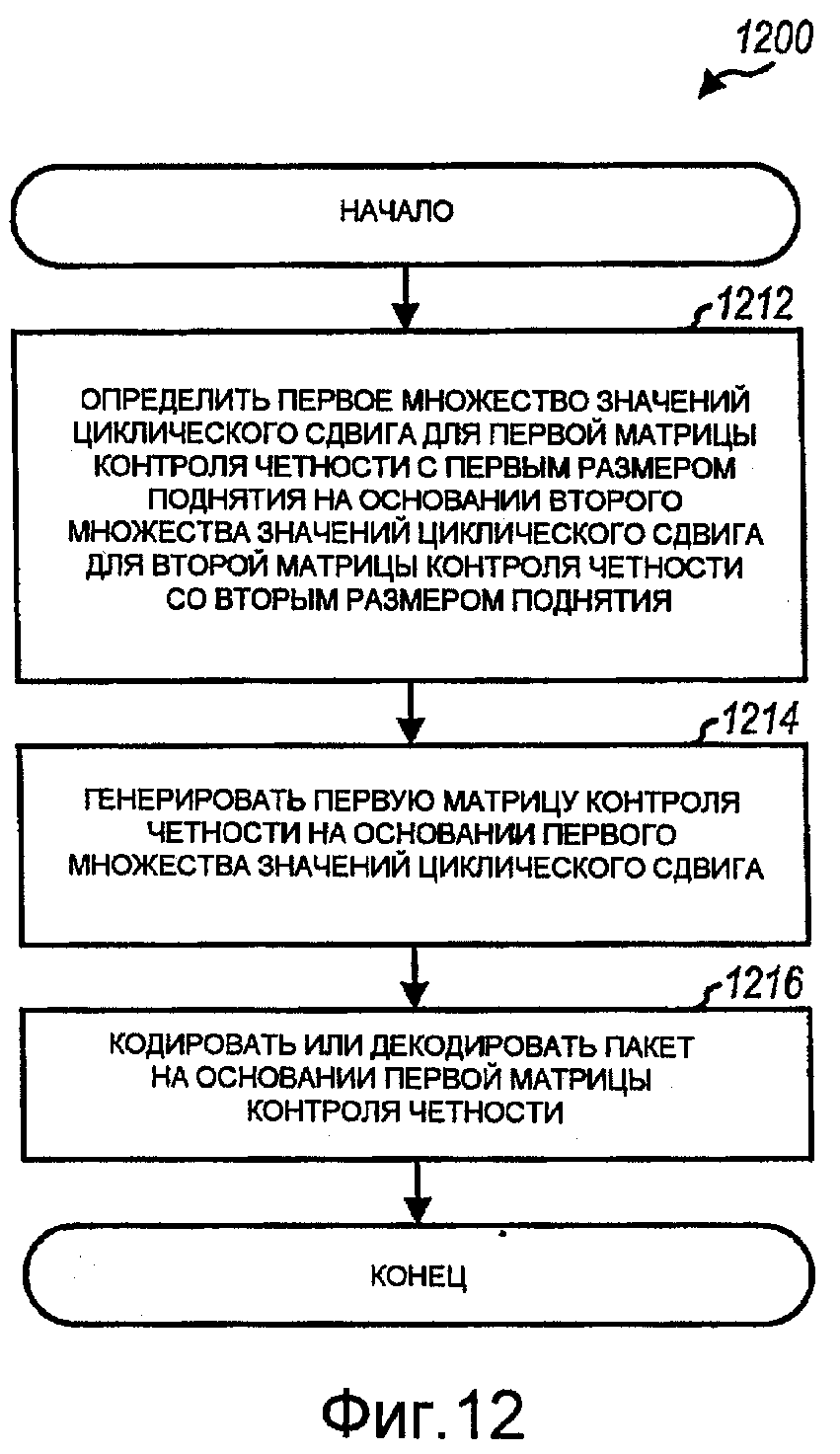
Фиг.12 - другой процесс обработки пакета.

Фиг.13 - устройство для обработки пакета.

Фиг.14 - еще один процесс обработки пакета.

Фиг.15 - еще одно устройство для обработки пакета.

Осуществление изобретения

Описанные в настоящем документе методы можно использовать для различных областей применения, например связь, вычисления, построение сетей и т.д. Методы также можно использовать для различных систем связи, в том числе беспроводных систем, проводных систем и т.д. Для ясности некоторые аспекты методов описаны ниже для системы беспроводной связи.

На фиг.1 показана система беспроводной связи 100, которую также можно именовать сетью доступа (AN). Для простоты на фиг.1 показаны только одна базовая станция 110 и два терминала 120 и 130. Базовая станция - это станция, которая осуществляет связь с терминалами, а также может именоваться точкой доступа, Узлом B, усовершенствованным Узлом B и т.д. Терминал может быть стационарным или мобильным, а также может именоваться терминалом доступа (AT), мобильной станцией, пользовательским оборудованием, абонентским блоком, станцией и т.д. Терминал может представлять собой сотовый телефон, карманный персональный компьютер (КПК), беспроводное устройство связи, беспроводной модем, карманное устройство, портативный компьютер, беспроводной телефон и т.д. Терминал может осуществлять связь с базовой станцией по прямой и/или обратной линиям связи в любой данный момент времени. Прямая линия связи (или нисходящая линия связи)- это линия связи от базовых станций к терминалам, и обратная линия связи (или восходящая линия связи) - это линия связи от терминалов к базовым станциям. Согласно фиг.1 терминал 120 может принимать данные от базовой станции 110 по прямой линии связи 122 и может передавать данные по обратной линии связи 124. Терминал 130 может принимать данные от базовой станции 110 по прямой линии связи 132 и может передавать данные по обратной линии связи 134. Описанные в настоящем документе методы можно использовать для передачи по прямой линии связи, а также по обратной линии связи.

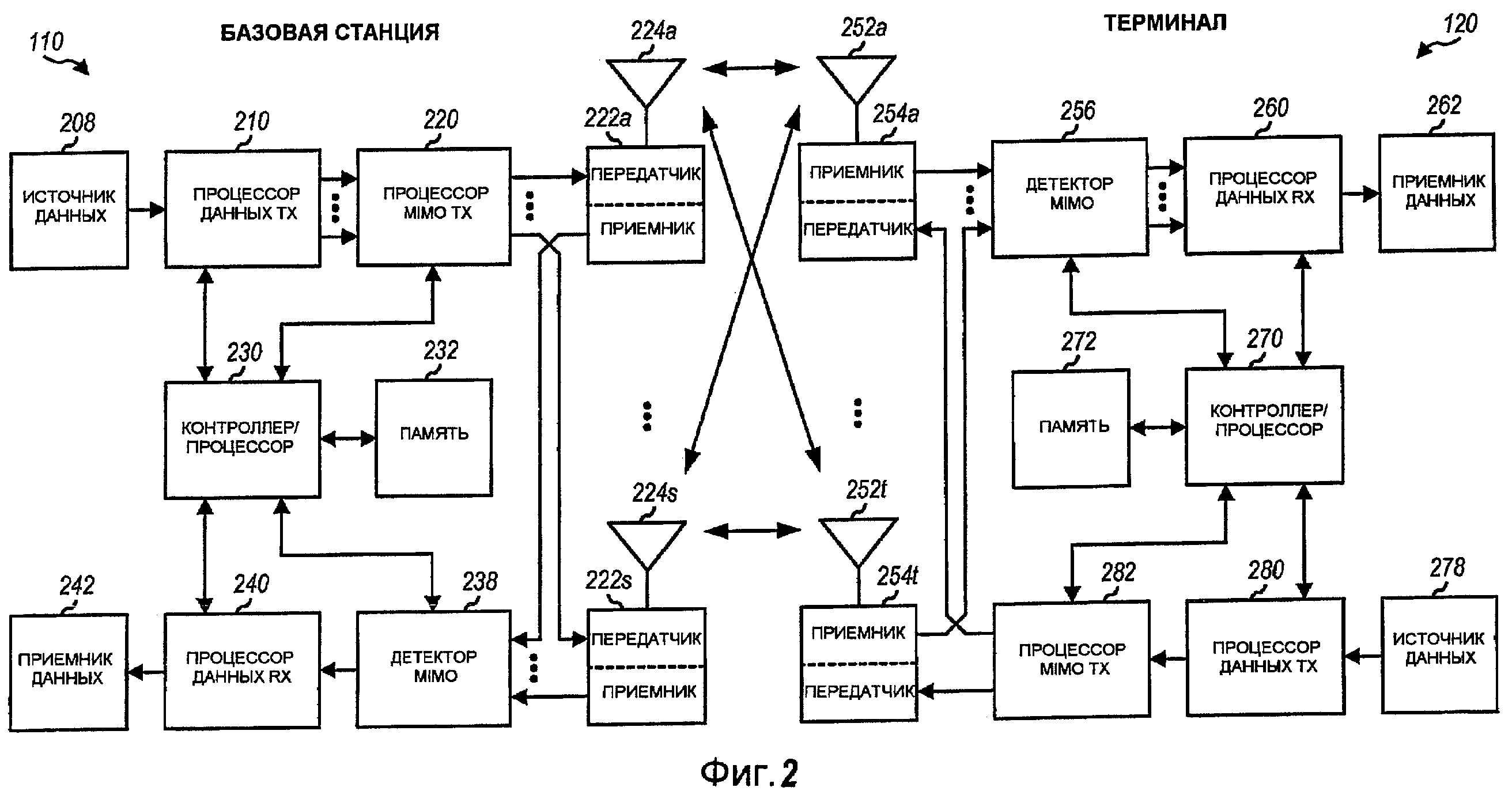
На фиг.2 показана блок-схема варианта осуществления базовой станции 110 и терминала 120, показанных на фиг.1. В этом варианте осуществления базовая станция 110 снабжена S антеннами 224a - 224s, и терминал 120 снабжен T антеннами 252a - 252t, где в общем случае S ≥ 1 и T ≥ 1.

На прямой линии связи, на базовой станции 110, процессор 210 данных передачи (TX) может принимать пакет данных из источника данных 208, обрабатывать пакет (например, кодировать, перемежать и отображать в символы), на основании формата пакета выдавать символы данных, которые являются символами модуляции для данных. Процессор MIMO TX 220 может мультиплексировать символы данных с контрольными символами, осуществлять пространственную обработку (например, предварительное кодирование), если применимо, и выдавать S выходных символьных потоков на S передатчиков (перед.) 222a - 222s. Каждый передатчик 222 может обрабатывать свой выходной символьный поток (например, для OFDM) для получения выходного чипового потока. Каждый передатчик 222 может дополнительно преобразовывать (например, преобразовывать в аналоговый вид, фильтровать, усиливать и повышать частоту) свой выходной чиповый поток и генерировать сигнал прямой линии связи. S сигналов прямой линии связи от передатчиков 222a - 222s могут передаваться через S антенн 224a - 224s, соответственно.

На терминале 120 T антенн 252a - 252t могут принимать сигналы прямой линии связи от базовой станции 110, и каждая антенна 252 может выдавать принятый сигнал на соответствующий приемник (прием.) 254. Каждый приемник 254 может обрабатывать (например, фильтровать, усиливать, понижать частоту и цифровать) свой принятый сигнал для получения выборок, дополнительно обрабатывать выборки (например, для OFDM) для получения принятых символов и выдавать принятые символы на детектор MIMO 256. Детектор MIMO 256 может осуществлять детектирование MIMO на принятых символах, если применимо, и выдавать детектированные символы. Процессор 260 данных приема (RX) может обрабатывать (например, снимать отображение в символы, отменять перемежение и декодировать) детектированные символы и выдавать декодированные данные на приемник данных 262. В общем случае обработка посредством детектора MIMO 256 и процессора 260 данных RX комплементарна обработке посредством процессора 220 MIMO TX и процессора 210 данных TX на базовой станции 110.

На обратной линии связи, на терминале 120, пакет данных может обеспечиваться источником данных 278 и обрабатываться (например, кодироваться, перемежаться и отображаться в символы) процессором 280 данных TX. Символы данных от процессора 280 данных TX могут мультиплексироваться с контрольными символами и подвергаться пространственной обработке процессором 282 MIMO TX и дополнительно обрабатываться передатчиками 254a - 254t, которые генерируют T сигналов обратной линии связи, которые могут передаваться через антенны 252a - 252t. На базовой станции 110 сигналы обратной линии связи от терминала 120 могут приниматься антеннами 224a - 224s, обрабатываться приемниками 222a - 222s, детектироваться детектором MIMO 238 и дополнительно обрабатываться процессором 240 данных RX для восстановления пакета, переданного терминалом 120.

Контроллеры/процессоры 230 и 270 могут управлять работой базовой станции 110 и терминала 120, соответственно. Контроллеры/процессоры 230 и 270 могут определять размеры пакетов, подлежащих передаче и/или приему. Контроллеры/процессоры 230 и 270 могут затем управлять кодированием посредством процессоров 210 и 280 данных TX, соответственно, и/или управлять декодированием посредством процессоров 240 и 260 данных RX, соответственно. В блоках памяти 232 и 272 могут храниться данные и программные коды для базовой станции 110 и терминала 120, соответственно.

Согласно одному аспекту кодирование и декодирование LDPC пакетов изменяющихся размеров можно эффективно поддерживать с помощью множества базовых матриц контроля четности разных размеров и множества значений поднятия, равных разным степеням 2. Базовые матрицы контроля четности могут предназначаться для базовых кодов LDPC разных скоростей (k_B, n_B), где k_B - количество информационных битов и n_B - количество битов кода. Каждый базовый код LDPC можно поднимать, как описано ниже, для получения множества поднятых кодов LDPC, которые можно использовать для кодирования или декодирования пакетов разных размеров. Диапазон размеров пакета может поддерживаться путем удлинения или сокращения кодов LDPC за счет добавления или удаления битов четности в базовом графе.

Код LDPC можно задать разреженной матрицей контроля четности, имеющей сравнительно немного ненулевых/непустых элементов и много нулевых/пустых элементов. Матрица контроля четности задает множество линейных ограничений на битах кода и может быть представлена в виде графа Таннера.

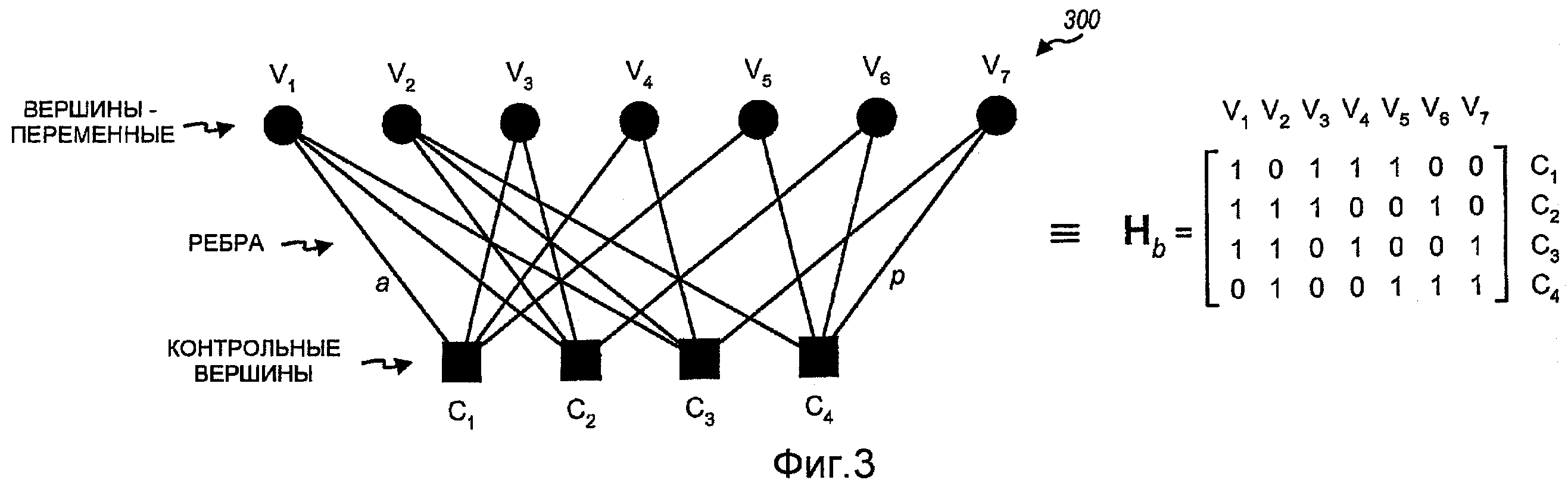
На фиг.3 показан граф Таннера 300 для иллюстративного базового кода LDPC. В этом примере граф Таннера 300 включает в себя семь вершин-переменных V₁ - V₇, представленные семью кружками, и четыре контрольные вершины C₁ - C₄, представленные четырьмя квадратиками. Каждая вершина-переменная представляет собой бит кода, который может либо передаваться, либо перфорироваться (т.е. не передаваться). Семь битов кода для вершин-переменных V₁ - V₇ образуют кодовое слово. Каждая контрольная вершина представляет ограничение, и четыре контрольные вершины C₁ - C₄ представляют четыре ограничения, которые задают базовый код LDPC. Вершины-переменные соединены с контрольными вершинами ребрами. В этом примере 16 ребер a - p соединяют семь вершин-переменных с четырьмя контрольными вершинами. Степень вершины равна количеству ребер, соединенных с этой вершиной. В этом примере вершины-переменные V₁ и V₂ являются вершинами 3 степени, и вершины-переменные V₃ - V₇ являются вершинами 2 степени. Для каждой контрольной вершины все биты кода в вершинах-переменных, соединенных с этой контрольной вершиной, подчиняются ограничению, состоящему в том, что их сумма должна быть равна 0 (по модулю 2).

На фиг.3 также показана базовая матрица H_b контроля четности, соответствующая графу Таннера 300. H_b включают в себя семь столбцов для семи вершин-переменных V₁ - V₇ и четыре строки для четырех контрольных вершин C₁ - C₄. Каждый столбец H_b включает в себя 1 элемент для каждого ребра, соединенного с вершиной-переменной, соответствующей этому столбцу. Например, столбец 1 включает в себя три 1 в строках 1, 2 и 3 для трех ребер a, b и c, соединяющих соответствующую вершину-переменную V₁ с контрольными вершинами C₁, C₂ и C₃ в графе Таннера 300. Каждый из остальных столбцов H_b включает в себя две или три 1 для двух или трех ребер, соединяющих соответствующую вершину-переменную с двумя или тремя контрольными вершинами.

Ограничения для кода LDPC можно выразить в матричной форме как:

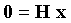
где H - матрица контроля четности m_B×n_B для кода LDPC,

x - вектор-столбец n_B×1 из n_B битов кода для кодового слова, и

0 - вектор-столбец из одних нулей.

Для простоты 0 может обозначать вектор или матрицу из одних нулей в нижеследующем описании. Матричное умножение в уравнении (1) осуществляется согласно арифметике по модулю 2. Кодовое слово считается верным, если ограничения в уравнении (1) выполняются. Кодирование пакета на основании матрицы H контроля четности для получения кодового слова x описано ниже.

Малый базовый код LDPC можно поднять для получения более крупного поднятого кода LDPC. Поднятия можно добиться путем замены каждого ненулевого элемента в базовой матрице контроля четности для базового кода LDPC матрицей перестановки L×L для получения поднятой матрицы контроля четности для поднятого кода LDPC. Это дает L копий базового графа для генерируемого базового кода LDPC. Матрицы перестановки определяют, как вершины-переменные в каждой копии графа соединяются с контрольными вершинами в L копиях графа.

На фиг.4 показан пример поднятия для базовой матрицы H_b контроля четности, показанной на фиг.3. Каждый ненулевой элемент H_b (который соответствует ребру в графе Таннера) заменяется матрицей перестановки σ L×L для получения поднятой матрицы H_l контроля четности 16 матриц перестановки для 16 ненулевых элементов H_b обозначаются σ_a - σ_p, где σ_a - матрица перестановки для ребра a на фиг.3.

Матрицы перестановки можно задавать по-разному. В одном варианте осуществления множество матриц перестановки может быть заранее задано, и матрицу перестановки для каждого ненулевого элемента базовой матрицы контроля четности можно выбирать из этого заранее заданного множества матриц перестановки. В другом варианте осуществления для ненулевых элементов базовой матрицы контроля четности используются матрицы циклической перестановки.

На фиг.5 показано множество из четырех матриц циклической перестановки для L = 4. В этом примере каждая матрица перестановки имеет размер 4×4. Матрица перестановки σ₀ для значения циклического сдвига, равного нулю, равна единичной матрице I, имеющей единицы вдоль диагонали и нули во всех остальных местах. Матрица перестановки σ₁ для значения циклического сдвига, равного единице, получается из единичной матрицы путем перемещения или сдвига самой нижней строки в верхнюю позицию. Матрица перестановки σ₂ для значения циклического сдвига, равного 2, получается из единичной матрицы путем перемещения двух самых нижних строк в верхнюю позицию. Матрица перестановки σ₃ для значения циклического сдвига, равного трем, получается из единичной матрицы путем перемещения трех самых нижних строк в верхнюю позицию. В общем случае матрица перестановки σ_s L×L для значения циклического сдвига, равного s, получается из единичной матрицы путем перемещения s самых нижних строк в верхнюю позицию, где 0 ≤ s ≤ L-1.

На фиг.6 показан пример поднятой матрицы H_l контроля четности, показанной на фиг.4, в которой каждая из 16 матриц перестановки σ_a - σ_p заменена одной из четырех матриц циклической перестановки σ₀ - σ₃, показанных на фиг.5. В нижней части фиг.6 показана поднятая матрица H_l контроля четности, в которой каждая матрица циклической перестановки заменена соответствующей матрицей 4×4 из единиц и нулей.

Замена каждого ненулевого элемента базовой матрицы H_b контроля четности матрицей перестановки 4×4 дает четыре копии базового графа для генерируемого базового кода LDPC. Для матрицы перестановки 4×4, соответствующей данной вершине-переменной V_u и данной контрольной вершине C_v, четыре столбца этой матрицы перестановки соответствуют вершине-переменной V_u в четырех копиях графа, и четыре строки этой матрицы перестановки соответствуют контрольной вершине C_v в четырех копиях графа. Единицы в матрице перестановки соответствуют ребрам, соединяющим вершину-переменную V_u в четырех копиях графа с контрольной вершиной C_v в четырех копиях графа. В частности, 1 в столбце x строки y означает, что вершина-переменная V_u в копии графа x соединена с контрольной вершиной C_u в копии графа y. Например, матрица циклической перестановки σ₁ используется для ненулевого элемента для вершины-переменной V₁ и контрольной вершины C₁ в H_l. Матрица σ₁ включает в себя 1 в столбце 1 строки 2, что означает, что вершина-переменная V₁ в копии графа 1 соединена с контрольной вершиной C₁ в копии графа 2.

На фиг.7 показано представление поднятой матрицы H_l контроля четности, сгенерированной на основании базовой матрицы H_b контроля четности, показанной на фиг.3, при L = 8. В этом представлении сетка 710 8×16 хранит ребра для семи вершин-переменных во всех восьми копиях графа. Каждая строка сетки 710 соответствует одной копии графа. 16 блоков в каждой строке соответствуют 16 ребрам a - p для семи вершин-переменных в одной копии графа. Сетка 720 8×16 хранит ребра для четырех контрольных вершин во всех восьми копиях графа. Каждая строка сетки 720 соответствует одной копии графа. 16 блоков в каждой строке соответствуют 16 ребрам a - p для четырех контрольных вершин в одной копии графа.

На фиг.7 также показаны соединения между восемью копиями вершины-переменной V₂ и восемью копиями контрольной вершины C₂ для ребра d, которое имеет матрицу циклической перестановки σ₃ в этом примере. Таким образом, восемь копий ребра d подвергаются циклическому сдвигу вниз на три позиции согласно матрице σ₃, каждое из оставшихся ребер может циклически сдвигаться на значение в пределах от 0 до 7 для L = 8.

В общем случае сетка может включать в себя по одному столбцу для каждого ребра в базовой матрице контроля четности и по одной строке для каждой из L копий графа. L копий каждого ребра могут циклически сдвигаться на величину, определяемую матрицей циклической перестановки для этого ребра.

На фиг.3-6 показан иллюстративный базовый код LDPC с базовой матрицей H_b контроля четности, показанной на фиг.3, и поднятие этого базового кода LDPC для получения более крупного кода LDPC с поднятой матрицей H_l контроля четности, показанной на фиг.6. Поднятия разных размеров можно добиться, используя матрицы циклической перестановки разных размеров. Ребра базовой матрицы H_b контроля четности могут циклически сдвигаться на значение в пределах от 0 до L-1. Значения циклического сдвига для ребер базовой матрицы контроля четности можно выбирать на основании производительности кодирования.

В одном варианте осуществления можно задать множество из шести базовых кодов LDPC для разных значений k_B в пределах от 6 до 11. В Таблице 1 приведены различные параметры шести базовых кодов LDPC согласно одному варианту осуществления. В одном варианте осуществления шесть базовых кодов LDPC можно реализовать, как описано в опубликованном документе 3GPP2 C.S0084-001 под названием “Physical Layer for Ultra Mobile Broadband (UMB) Air Interface Specification”, август 2007. Базовые коды LDPC также можно реализовать согласно другим вариантам осуществления.

В одном варианте осуществления может поддерживаться множество из девяти значений поднятия 4, 8, 16, 32, 64, 128, 256, 512 и 1024. В этом варианте осуществления наименьшее значение поднятия L_min = 4 и наибольшее значение поднятия L_max = 1024. Эти значения поднятия являются разными степенями 2, что может обеспечивать определенные преимущества. Всего 54 разных размеров пакета в пределах от 24 до 11,264 битов может поддерживаться с помощью шести базовых кодов LDPC с k_B в пределах от 6 до 11 и девяти значений поднятия в пределах от 4 до 1024. В общем случае может поддерживаться любой диапазон значений поднятия, и L_min и L_max могут принимать любые подходящие значения.

В Таблице 2 приведены параметры базовой матрицы G₀контроля четности согласно одному варианту осуществления. Согласно Таблице 1 G₀ имеет размер 27×33 и включает в себя 27 строк с индексами от 0 до 26 и 33 столбца с индексами от 0 до 32. Для каждой строки во втором столбце Таблицы 2 указана степень строки, которая соответствует количеству ненулевых элементов в строке. В третьем столбце Таблицы 2 указаны позиции столбцов для ненулевых элементов в каждой строке. В четвертом столбце указано значение циклического сдвига для каждого ненулевого элемента в каждой строке. Для L_max = 1024 значения циклического сдвига составляют в пределах от 0 до 1023. Иллюстративные варианты осуществления базовых матриц G₁ - G₅ контроля четности описаны в вышеупомянутом 3GPP2 C.S0084-001.

В одном варианте осуществления базовую матрицу контроля четности и значение поднятия можно выбирать для пакета размером k следующим образом. Прежде всего значение поднятия L можно выбирать на основании размера пакета k следующим образом:

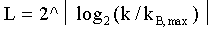
где k_B,max - максимальное количество информационных битов для всех базовых кодов LDPC, и

“   ” обозначает оператор верхнего целочисленного приближения.

k_B,max = 11 для множества базовых кодов LDPC, показанного в Таблице 1, может быть равно другим значениям для других множеств базовых кодов LDPC.

Затем базовую матрицу контроля четности можно выбрать на основании размера пакета k и выбранного значения поднятия L следующим образом:

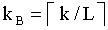
Индекс выбранной базовой матрицы контроля четности можно задать как i = k_B - 6. Выбранная базовая матрица контроля четности обозначается G в нижеследующем описании.

Выбранная базовая матрица G контроля четности и выбранное значение поднятия L могут кодировать до k_B·L информационных битов и обеспечивать n_B·L битов кода. Пакет можно заполнить нулями до длины k_B·L путем присоединения z_P = k_B·L - k нулей к концу пакета. Заполненный нулями пакет можно кодировать с поднятой матрицей контроля четности для получения n_B·L битов кода. Для кода (n, k), z_p нулей заполнения, а также n_B·L - n - z_P битов четности можно перфорировать для получения кодового слова из n битов кода.

Чтобы кодировать пакет, можно сначала генерировать поднятую матрицу H контроля четности на основании выбранной базовой матрицы G контроля четности и выбранного значения поднятия L. Затем можно кодировать пакет на основании поднятой матрицы H контроля четности.

Чтобы генерировать поднятую матрицу H контроля четности, значение циклического сдвига для каждого ненулевого элемента выбранной базовой матрицы G контроля четности можно определить следующим образом:

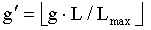
где g - значение циклического сдвига для ненулевого элемента G при условии поднятия на L_max, и

g′ - значение циклического сдвига для ненулевого элемента G при условии поднятия на L.

В четвертом столбце 2 указаны значения циклического сдвига для ненулевых элементов G₀ для L_max = 1024. Значения циклического сдвига для ненулевых элементов других базовых матриц контроля четности можно генерировать и сохранять в аналогичных таблицах. В общем случае значения циклического сдвига для ненулевых элементов G можно генерировать для L_max и можно использовать для всех значений поднятия от L_min до L_max. Это может упростить вариант осуществления, поскольку только одно множество значений циклического сдвига можно сохранять для G и использовать для всех значений поднятия. Уравнение (4), в сущности, удаляет нуль или более младших битов (LSB) из g для получения g′ для выбранного значения поднятия L. Для варианта осуществления с L_max = 1024 можно удалить один LSB, если L = 512, можно удалить два LSB, если L = 256, и т.д. Удаление LSB может сохранять соотношение между разными параметрами сдвига, например, s′ = s + L/4, описанное ниже, что может упрощать кодирование. В другом варианте осуществления нуль или более старших битов (MSB) из g можно удалить путем осуществления операции по модулю L для получения g′. g′ также можно получить другими средствами.

В одном варианте осуществления каждый ненулевой элемент G можно заменить матрицей циклической перестановки σ_g′ для получения поднятой матрицы H контроля четности. σ_g′ можно получить путем циклического сдвига единичной матрицы I на g′. В другом варианте осуществления каждый ненулевой элемент G можно заменить матрицей 2×2 для получения матрицы G′. Эта матрица 2×2 может иметь вид

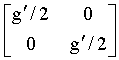
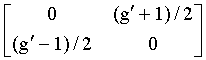
Столбцы и строки поднятой матрицы H контроля четности можно менять местами или переставлять так, чтобы результирующая матрица имела вид:

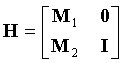
где M₁ - матрица M×N, где N = M + k_B·L,

M₂ - матрица (m_B·L-M)×N, и

0 - матрица M×(n_B·L-N) из одних нулей.

Единичную матрицу в нижнем правом углу H можно заменить нижней треугольной матрицей, которая может иметь ненулевые элементы под диагональю.

Размер M₁ может зависеть от выбранной базовой матрицы контроля четности и может быть функцией индекса кода i. M₁ может иметь следующий вид:

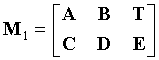
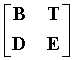
где A - матрица (M-L/2)×(k_B·L),

B - матрица (M-L/2)×(L/2),

C - матрица (L/2)×(k_B·L),

D - матрица (L/2)×(L/2),

E - матрица (L/2)×(N-k_B·L), и

T - нижняя треугольная матрица (M-L/2)×(M-L/2), имеющая единицы вдоль диагонали и нули над диагональю.

Ограничения для поднятого кода LDPC можно выразить в виде:

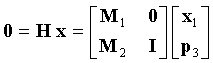
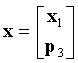
где x₁ - вектор-столбец N×1 информационных битов и битов четности, и

p₃ - (n_B·L-N)×1 вектор-столбец битов четности.

Ввиду наличия нулевой матрицы 0 в верхнем правом углу H в уравнении (5) часть уравнения (7) можно выразить как:

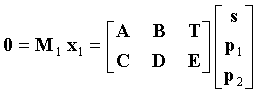
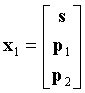
где s - вектор-столбец (k_B·L)×1 информационных битов в пакете,

p₁ - (L/2)×1 вектор-столбец битов четности, и

p₂ - (M-L/2)×1 вектор-столбец битов четности.

Для решения уравнения (8) M₁ можно предварительно перемножить с

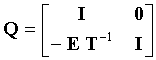
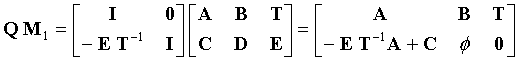
где ϕ = - ET^-1B + D.

Уравнения (8) и (9) можно объединить для получения:

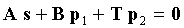
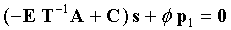
Тогда биты четности p₁, p₂ и p₃ можно вычислить следующим образом:

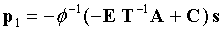
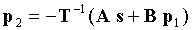
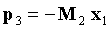
где x₁ включают в себя s, p₁ и p₂, как показано в уравнении (8). Если единичную матрицу в нижнем правом углу H заменить нижней треугольной матрицей, то уравнение (14) можно решить с использованием обратной подстановки (сверху вниз).

Вычисление p₁, p₂ и p₃ можно упростить, выполняя матричное умножение в уравнениях (12) и (13) поэтапно, сохраняя промежуточные результаты и используя промежуточные результаты на дальнейших этапах.

Поднятая матрица H контроля четности предназначена для самой низкой кодовой скорости, которую можно задать как r = k_B/n_B. H можно перфорировать для получения более высоких скоростей. Коды LDPC структурированы как внутренний “сердцевинный” код LDPC высокой скорости с внешними битами четности. Кодирование можно осуществлять последовательно для получения нужного количества битов кода. Например, сначала можно вычислять биты четности p₁, как показано в уравнении (12), затем (при необходимости) можно вычислять биты четности p₂, как показано в уравнении (13), и, наконец, (при необходимости) можно вычислять биты четности p₃, как показано в уравнении (14).

Система может поддерживать режим смешанного автоматического запроса повторной передачи (HARQ). Для HARQ передатчик может посылать первую передачу пакета на приемник и затем может, при необходимости, посылать одну или несколько дополнительных передач (или повторных передач), пока пакет не будет правильно декодирован приемником, или не будет отправлено максимальное количество передач, или не будет выполнено какое-либо другое условие окончания передачи. HARQ может повысить надежность передачи данных. Для каждого базового кода LDPC можно генерировать последовательность расширений HARQ для охвата всех кодовых скоростей, поддерживаемых системой. Расширения HARQ можно задать путем перфорации битов четности. Перфорации можно, в основном, подвергать третьи биты четности P₃, но и вторые биты четности P₂ также можно подвергать некоторой перфорации.

На фиг.8 показан базовый граф 800 базовой матрицы G контроля четности, которая может иметь вид, показанный в уравнениях (5) и (6). Граф 800 используется только в целях иллюстрации и не соответствует никаким базовым матрицам контроля четности, описанным выше. Базовый граф 800 включают в себя несколько квадратных блоков, причем каждый квадратный блок представляет элемент в базовой матрице контроля четности. Каждый ненулевой элемент базовой матрицы контроля четности представлен помеченным блоком. Каждый помеченный блок связан со значением циклического сдвига, которое определяет величину циклического сдвига для L копий ребра, полученных за счет поднятия базовой матрицы контроля четности на значение поднятия L.

Кодовое слово состоит из информационных битов и битов четности вдоль верхней части графа 800. Биты в кодовом слове могут передаваться слева направо, за исключением некоторого переупорядочивания столбцов четности.

Базовый граф 800 содержит информационные биты s, первые биты четности p₁, вторые биты четности p₂ и третьи биты четности p₃ вдоль верхней части базового графа. Первые биты четности связаны с первым множеством ограничений, вторые биты четности связаны со вторым множеством ограничений, и третьи биты четности связаны с третьим множеством ограничений. Сердцевинная часть базового графа 800 состоит из вершин-переменных, представляющих информационные биты и первые, и вторые биты четности, и вершин-ограничений, представляющих первое и второе множества ограничений. Сердцевинная часть обычно не содержит вершины-переменные 1 степени. Третьи биты четности и ограничения третьего множества ограничений (или третьи ограничения по четности) находятся друг с другом во взаимно однозначном соответствии, что демонстрирует единичная матрица в нижнем правом углу базового графа 800. Третьи биты четности и третьи ограничения по четности можно линейно упорядочить так, чтобы каждый из третьих битов четности можно было определить как четность информационных битов, первых битов четности, вторых битов четности и предыдущих третьих битов четности. Вершина третьего ограничения по четности, связанная с третьим битом четности взаимно однозначным соответствием, соединена ребрами с вершиной-переменной третьего бита четности, а также с вершинами-переменными, представляющими биты, из которых третий бит четности является битом четности.

Вариант осуществления, показанный на фиг.8, включают в себя несколько признаков, которые могут упрощать кодирование. Вершины-переменные первых и вторых битов четности имеют 2 степень или 3 степень. Для упрощения кодирования один первый бит четности может быть связан с одной вершиной-переменной 3 степени, и вторые биты четности могут быть связаны с вершинами-переменными 2 степени. Вершина-переменная 3 степени представлена столбцом 810 для матриц B и D, которые включают в себя три заштрихованных квадратных блока для трех ненулевых элементов. Вершины-переменные 2 степени могут иметь конфигурацию структуры накопительной цепи, которая также известна под названием двухдиагональной структуры. Эта двухдиагональная структура представлена треугольной матрицей T, в каждом столбце которой имеются два находящихся один на другом помеченных блока. Двухдиагональная структура может благотворно влиять на производительность кода и кодирование. Большое количество вершин-переменных 2 степени может повышать производительность, и наличие вершин-переменных 2 степени в двухдиагональной форме доводит эту возможность почти до максимума. Двухдиагональная структура также облегчает рекурсивное кодирование вершин-переменных 2 степени, наподобие сверточного кода. Будучи правильно упорядочена, структура матрицы H может включать в себя подматрицу T, в которой только диагональ (1,1), (2,2) и т.д., а также поддиагональ (2,1), (3,2) и т.д. содержат ненулевые элементы. Часто ребра, соответствующие двухдиагональной структуре, имеют значение поднятия 0, означающее отсутствие перестановки, образуя L отдельных цепей в поднятом графе.

Два из трех ребер вершины-переменной 3 степени могут соединяться в базовом графе, образуя замкнутый контур в графе, связанном с двухдиагональной структурой. Для упрощения кодирования в этом случае значения поднятия для трех ребер вершины-переменной 3 степени могут иметь вид x, s, s′ = (s+L/m) mod L, где m равно степени 2, и x и s могут иметь произвольные значения. После обращения всех циклических сдвигов код остается неизменным, поскольку это эквивалентно обращению порядка вершин-ограничений в поднятии. Таким образом, значения поднятия в виде x, s, s′ = (s+L/m) mod L также можно использовать. Кодирование можно упростить, поскольку матрицу ϕ = -ET^-1B + D можно разложить на множители низкой степени, и она сама имеет низкий вес.

Значения циклического сдвига для двух ненулевых элементов вершины-переменной 3 степени могут быть s и s′, где s может иметь произвольно выбранное значение, и s′ можно выбирать несколькими способами. В первом варианте осуществления s′ = s и ϕ^-1 является матрицей перестановки. Для этого варианта осуществления поднятый код LDPC имеет контур, проходящий вдоль накопительной цепи базового графа (через вершины 2 степени) и одну вершину 3 степени. Контур имеет кратность L, что может обеспечивать близкую к оптимальной характеристику минимального уровня ошибки (error floor), в особенности, из-за того, что базовый граф имеет короткую накопительную цепь. В другом варианте осуществления s′ = s + L/2 и ϕ^-1 равна сумме трех матриц перестановки. Для этого варианта осуществления соответствующий контур в поднятом коде LDPC проходит вдоль накопительной цепи базового графа (через вершины 2 степени) и две вершины 3 степени. Сложность умножения на ϕ^-1 все же может быть низкой. Однако этот вариант осуществления все же может быть подвержен некоторым минимальным уровням ошибки. В третьем варианте осуществления s′ = s + L/4 и ϕ^-1 равна сумме девяти матриц перестановки. Соответствующий контур в поднятом коде LDPC проходит вдоль накопительной цепи базового графа (через вершины 2 степени) и четыре вершины 3 степени. Сложность умножения на ϕ^-1 все же может быть низкой, поскольку ϕ^-1 по-прежнему может быть разреженной матрицей. Этот вариант осуществления может упрощать кодирование, одновременно избегая проблем, связанных с минимальными уровнями ошибки. Значение циклического сдвига для третьего ненулевого элемента может быть x, которое может быть другим, произвольно выбранным значением.

Описанные в настоящем документе методы можно использовать для поддержки широкого диапазона размеров пакета. Подходящий размер пакета можно выбирать на основании различных факторов, например канальных условий (которые могут определяться спектральной эффективностью или форматом пакета), объемом выделяемых ресурсов, служебной нагрузкой пилот-канала, рангом MIMO и т.д. Методы позволяют генерировать хорошие совместимые по скорости коды для любых значений k и n с использованием малого количества базовых кодов LDPC.

Описанные в настоящем документе поднятые коды LDPC могут обеспечивать реализацию параллельного кодера и декодера в различных формах. Для реализации реберно-параллельного декодера ребра в базовом графе можно обрабатывать в последовательном режиме, и параллелизма можно добиться за счет одновременной обработки L копий одного и того же ребра. Для реализации вершинно-параллельного декодера разные копии базового графа можно обрабатывать в последовательном режиме, и параллелизма можно добиться за счет одновременной обработки разных вершин в базовом графе. Благодаря использованию матриц циклической перестановки, размеры которых ограничены степенями 2, поднятие можно легко реализовать с использованием операции отсчета, в особенности, для вершинно-параллельной реализации. Операция отсчета означает обход L-контура путем отсчета от x до x+1 mod L. Это ограничение по размеру поднятия позволяет гарантировать, что все различные размеры поднятия имеют большой общий множитель, что может быть важным свойством для реализации реберно-параллельного декодера. Описанная в настоящем документе структура кода LDPC может поддерживать эффективные реализации вершинно-параллельного и реберно-параллельного декодера. Кроме того, описания графа компактны и обеспечивают значительное снижение сложности.

На фиг.9 показан вариант осуществления процесса 900 для обработки данных. Процесс 900 можно осуществлять на базовой станции, терминале или какой-нибудь другой сущности. Пакеты переменных размеров можно кодировать или декодировать на основании множества базовых матриц контроля четности разных размеров и множества значений поднятия, равных разным степеням 2 (блок 912). Множество базовых матриц контроля четности может содержать базовые матрицы контроля четности для 6, 7, 8, 9, 10 и 11 информационных битов, как описано выше, для от k_B до 2k_B-1 информационных битов, для от k_B+1 до 2k_B информационных битов, или для некоторого другого диапазона информационных битов. Множество базовых матриц контроля четности также может включать в себя некоторую другую комбинацию базовых матриц контроля четности. Множество значений поднятия может содержать значения поднятия для 4, 8, 16, 32, 64, 128, 256, 512 и 1024, как описано выше, или некоторый другой диапазон или комбинацию значений поднятия. Параметры (например, значения циклического сдвига) для множества базовых матриц контроля четности можно хранить для использования при кодировании или декодировании пакетов переменных размеров (блок 914). Каждая базовая матрица контроля четности может содержать совокупность ненулевых элементов в совокупности положений. Каждый ненулевой элемент может быть связан со значением циклического сдвига в пределах от 0 до L_max-1, где L_max - максимальное значение поднятия. Совокупность значений циклического сдвига можно хранить для совокупности ненулевых элементов каждой базовой матрицы контроля четности. Значения циклического сдвига для всех значений поднятия для каждой базовой матрицы контроля четности можно определить на основании значений циклического сдвига, сохраненных для базовой матрицы контроля четности.

На фиг.10 показан вариант осуществления устройства 1000 для обработки данных. Устройство 1000 включает в себя средство для кодирования или декодирования пакетов переменных размеров на основании множества базовых матриц контроля четности разных размеров и множества значений поднятия, равных разным степеням 2 (модуль 1012), и средство для хранения параметров (например, значений циклического сдвига) для множества базовых матриц контроля четности (блок 1014).

На фиг.11 показан вариант осуществления процесса 1100 для обработки пакета, который можно использовать для блока 912 на фиг.9. Можно определить размер пакета для пакета, подлежащего кодированию или декодированию (блок 1112). Значение поднятия можно выбирать из множества значений поднятия на основании размера пакета, например, как показано в уравнении (2) (блок 1114). Базовую матрицу контроля четности можно выбирать из множества базовых матриц контроля четности на основании размера пакета и выбранного значения поднятия, например, как показано в уравнении (3) (блок 1116). Поднятую матрицу контроля четности можно генерировать на основании выбранной базовой матрицы контроля четности и выбранного значения поднятия (блок 1118). Пакет можно кодировать или декодировать на основании поднятой матрицы контроля четности (блок 1120).

Для блока 1118 поднятую матрицу контроля четности можно генерировать на основании дополнительно значений циклического сдвига для ненулевых элементов выбранной базовой матрицы контроля четности. Значения циклического сдвига для поднятой матрицы контроля четности можно вычислять на основании значений циклического сдвига для ненулевых элементов выбранной базовой матрицы контроля четности и выбранного значения поднятия, например, как показано в уравнении (4). Затем поднятую матрицу контроля четности можно генерировать путем замены каждого ненулевого элемента выбранной базовой матрицы контроля четности матрицей циклической перестановки со значением циклического сдвига, вычисленным для ненулевого элемента.

Для кодирования на блоке 1120 информационные биты в пакете можно кодировать на основании поднятой матрицы контроля четности для получения первых битов четности, например, как показано в уравнении (12). Информационные биты и первые биты четности можно кодировать на основании поднятой матрицы контроля четности для получения вторых битов четности, например, как показано в уравнении (13). Информационные биты, первые биты четности и вторые биты четности можно кодировать на основании поднятой матрицы контроля четности для получения третьих битов четности, например, как показано в уравнении (14).

Для декодирования на блоке 1120 большой граф для поднятой матрицы контроля четности можно генерировать на основании L копий базового графа для выбранной базовой матрицы контроля четности, где L - выбранное значение поднятия. Вершины L копий базового графа можно соединять между собой на основании матриц перестановки для ненулевых элементов выбранной базовой матрицы контроля четности. Базовый граф может содержать совокупность ребер для ненулевых элементов выбранной базовой матрицы контроля четности. Для реберно-параллельного декодирования декодирование можно осуществлять параллельно для L копий одного и того же ребра в L копиях базового графа и можно осуществлять последовательно для разных ребер в L копиях базового графа. Для вершинно-параллельного декодирования декодирование можно осуществлять параллельно для вершин каждой копии базового графа и можно осуществлять последовательно для L копий базового графа.

На фиг.12 показан вариант осуществления процесса 1200 для обработки пакета. Первое множество значений циклического сдвига для первой матрицы контроля четности с первым размером поднятия можно определить на основании второго множества значений циклического сдвига для второй матрицы контроля четности со вторым размером поднятия (блок 1212). Первый и второй размеры поднятия могут быть разными степенями 2. В одном варианте осуществления блока 1212 коэффициент K можно определить на основании отношения второго размера поднятия к первому размеру поднятия, и K LSB каждого значения циклического сдвига во втором множестве можно удалить для получения соответствующего значения циклического сдвига в первом множестве. Этого можно добиться делением каждого значения циклического сдвига во втором множестве на отношение и округления в меньшую сторону до целочисленного значения для получения соответствующего значения циклического сдвига в первом множестве, как показано в уравнении (4). В другом варианте осуществления блока 1212 K MSB каждого значения циклического сдвига во втором множестве можно удалить для получения соответствующего значения циклического сдвига в первом множестве.

Первую матрицу контроля четности можно генерировать на основании первого множества значений циклического сдвига (блок 1214). Этого можно добиться путем замены каждого ненулевого элемента базовой матрицы контроля четности матрицей циклической перестановки со значением циклического сдвига в первом множестве, соответствующего ненулевому элементу. Пакет можно кодировать или декодировать на основании первой матрицы контроля четности (блок 1216).

На фиг.13 показан вариант осуществления устройства 1300 для обработки пакета. Устройство 1300 включает в себя средство для определения первого множества значений циклического сдвига для первой матрицы контроля четности с первым размером поднятия на основании второго множества значений циклического сдвига для второй матрицы контроля четности со вторым размером поднятия (модуль 1312), средство для генерации первой матрицы контроля четности на основании первого множества значений циклического сдвига (модуль 1314) и средство для кодирования или декодирования пакета на основании первой матрицы контроля четности (модуль 1316).

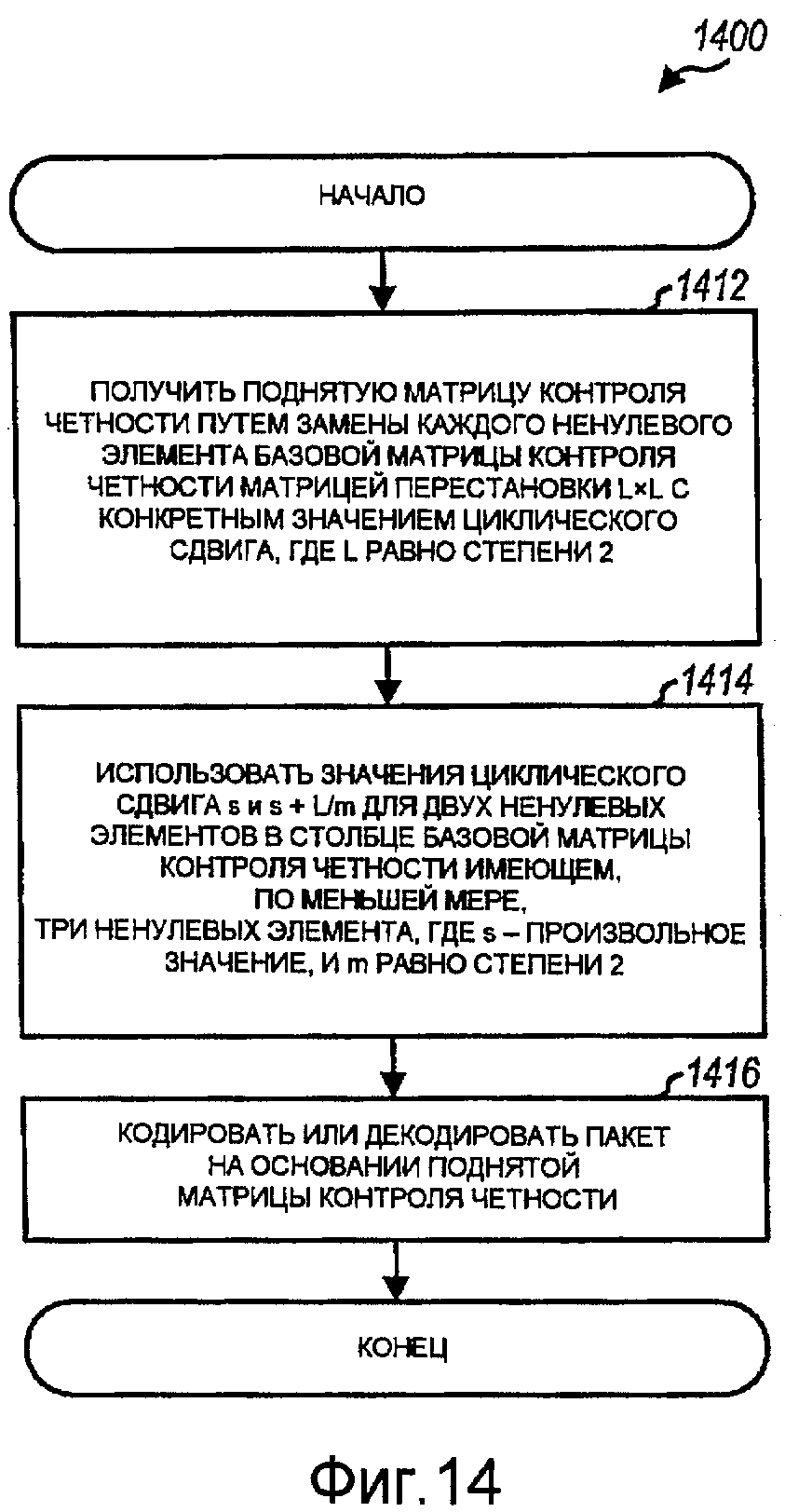
На фиг.14 показан вариант осуществления процесса 1400 для обработки пакета. Поднятую матрицу контроля четности можно получить путем замены каждого ненулевого элемента базовой матрицы контроля четности матрицей перестановки L×L с конкретным значением циклического сдвига, где L равно степени 2 (блок 1412). Значения циклического сдвига s и s + L/m можно использовать для двух ненулевых элементов в столбце базовой матрицы контроля четности, имеющем по меньшей мере три ненулевых элемента, где s - произвольное значение, и m равно степени 2 (блок 1414). В одном варианте осуществления m равно 2, и значения циклического сдвига для двух ненулевых элементов равны s и s+ L/2. В другом варианте осуществления m равно 4, и значения циклического сдвига для двух ненулевых элементов равны s и s + L/4. В еще одном варианте осуществления m равно восьми, и значения циклического сдвига для двух ненулевых элементов равны s и s + L/8. m также может быть равно другим значениям. Значение циклического сдвига x можно выбирать для третьего ненулевого элемента в столбце, имеющем по меньшей мере три ненулевых элемента. Базовая матрица контроля четности может содержать подматрицу

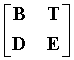
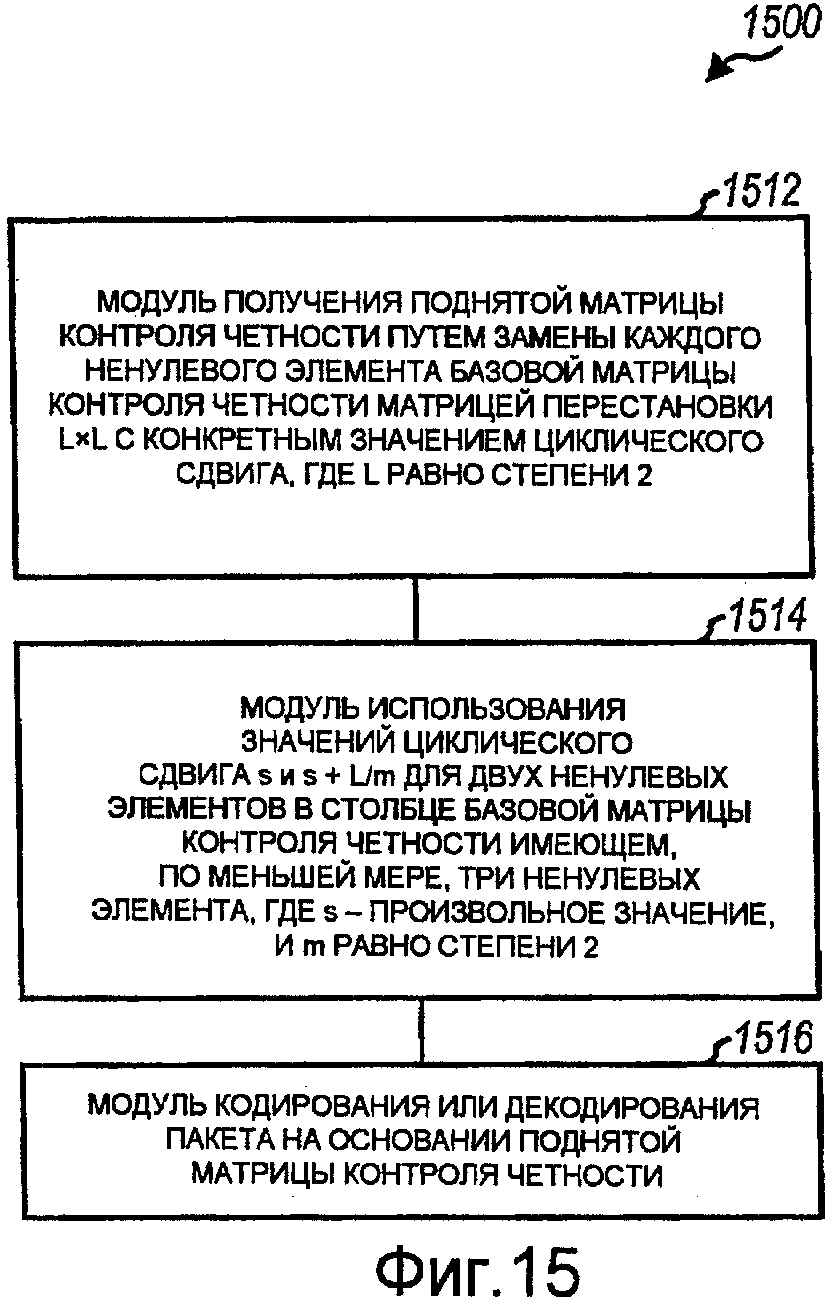
На фиг.15 показан вариант осуществления устройства 1500 для обработки пакета. Устройство 1500 включает в себя средство для получения поднятой матрицы контроля четности путем замены каждого ненулевого элемента базовой матрицы контроля четности матрицей перестановки L×L с конкретным значением циклического сдвига, где L равно степени 2 (модуль 1512), средство для использования значений циклического сдвига s и s + L/m - для двух ненулевых элементов в столбце базовой матрицы контроля четности, имеющем по меньшей мере три ненулевых элемента, где s - произвольное значение, и m равно степени 2 (модуль 1514), и средство для кодирования или декодирования пакета на основании поднятой матрицы контроля четности (модуль 1516).

Модули, показанные на фиг.10, 13 и 15, могут содержать процессоры, электронные устройства, аппаратные устройства, электронные компоненты, логические схемы, блоки памяти и т.д. или любую их комбинацию.

Описанные в настоящем документе методы можно реализовать различными средствами. Например, эти методы можно реализовать в виде оборудования, программно-аппаратного обеспечения, программного обеспечения или их комбинации. Для аппаратной реализации блоки обработки, используемые для осуществления методов на сущности (например, Узле B или терминале), можно реализовать в одной или нескольких специализированных интегральных схемах (ASIC), цифровых сигнальных процессорах (ЦСП), устройствах обработки цифровых сигналов (DSPD), программируемых логических устройствах (ПЛУ), вентильных матрицах, программируемых пользователем (FPGA), процессорах, контроллерах, микроконтроллерах, микропроцессорах, электронных устройствах, других электронных блоках, предназначенных для осуществления описанных в настоящем документе функций, или их комбинациях.

Для программно-аппаратной и/или программной реализации методы можно реализовать посредством кода (например, процедур, функций, модулей, инструкций и т.д.), которые осуществляют описанные в настоящем документе функции. В общем случае любой машиночитаемый / доступный для обращения процессора носитель, материально воплощающий программно-аппаратный и/или программный код можно использовать в реализации описанных в настоящем документе методов. Например, программно-аппаратный и/или программный код может храниться в памяти (например, памяти 232 или 272 на фиг.2) и выполняться процессором (например, процессором 230 или 270). Память можно реализовать внутри процессора или вне процессора. Программно-аппаратный и/или программный код также может храниться на машиночитаемом / доступном для обращения процессора носителе, например в оперативной памяти (ОЗУ), постоянной памяти (ПЗУ), энергонезависимой оперативной памяти (NVRAM), программируемой постоянной памяти (ППЗУ), электрически стираемой ППЗУ (ЭСППЗУ), флэш-памяти, на флоппи-диске, компакт-диске (CD), цифровом универсальном диске (DVD), магнитном или оптическом устройстве хранения данных и т.д. Код может выполняться одним или несколькими компьютерами/процессорами и может побуждать компьютер(ы)/процессор(ы) осуществлять определенные аспекты описанных в настоящем документе функций.

Вышеприведенное описание обеспечено, чтобы специалист в данной области техники мог использовать и применять настоящее описание. Специалист в данной области техники может предложить различные модификации описанного изобретения, но очевидно, что установленные в настоящем документе общие принципы можно применять к другим вариациям, не выходящим за рамки сущности или объема описания. Таким образом, описание не ограничено описанными в настоящем документе примерами и вариантами осуществления, но должно быть истолковано в наиболее широком объеме в соответствии с раскрытыми в настоящем документе принципами и новыми признаками.

Реферат

Изобретение относится к области связи и, в частности, к методам кодирования и декодирования данных. Описаны методы поддержки кодирования и декодирования контроля четности низкой плотности (LDPC). Согласно одному аспекту кодирование и декодирование LDPC пакетов изменяющихся размеров может поддерживаться с помощью наборов базовых матриц контроля четности разных размеров и наборов значений поднятия, равных разным степеням 2. Базовую матрицу G контроля четности размером mB×nB можно использовать для кодирования пакета из kB=nB-mB информационных битов для получения кодового слова из nB битов кода. Эту базовую матрицу контроля четности можно «поднимать» на значение поднятия L для получения поднятой матрицы Н контроля четности размером L·mB×L·nB. Поднятую матрицу контроля четности можно использовать для кодирования пакета до L·kB информационных битов для получения кодового слова из L·nB битов кода. Широкий диапазон размеров пакета может поддерживаться с помощью наборов базовых матриц контроля четности и наборов значений поднятия. Технический результат - обеспечение эффективности кодирования и декодирования LDPC пакетов изменяющихся размеров. 8 н. и 7 з.п. ф-лы, 15 ил., 2 табл.

Формула

3. Устройство по п.2, в котором, по меньшей мере, один процессор выполнен с возможностью выбора значения поднятия путем вычисления

где k - размер пакета, k_B,max - максимальное количество информационных битов для набора базовых матриц контроля четности, L - выбранное значение поднятия, и

обозначает оператор верхнего целочисленного приближения.

6. Способ по п.5, в котором на этапе выбора значения поднятия вычисляют

где k - размер пакета, k_B,max - максимальное количество информационных битов для набора базовых матриц контроля четности, L - выбранное значение поднятия, и

обозначает оператор верхнего целочисленного приближения.

7. Способ по п.5, в котором на этапе выбора базовой матрицы контроля четности вычисляют

,
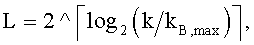
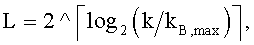
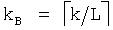
где k - размер пакета, L - выбранное значение поднятия, k_B - количество информационных битов для выбранной базовой матрицы контроля четности, и

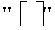
обозначает оператор верхнего целочисленного приближения.