Способ инициализации и актуализации модели сети - RU2171494C2

Чертежи

Показать все 20 чертежа(ей)

Описание

Изобретение относится к способу инициализации и актуализации модели сети, причем топологию сети создают в виде графа сети.

Модель сети может относиться к сетям самого разного рода, например электрическим, газовым или коммуникационным сетям. Для простоты, однако, ниже описана сеть энергоснабжения.

Для контроля за электрическими сетями и управления ими основополагающее значение имеет знание и изображение топологического состояния сети, а также слежение за напряжением сети. В управляющих вычислительных машинах систем управления сетями топологические модели сети инициализируют и поддерживают при этом в виде изображений процесса управляемой передающей или распределительной сети на основе статической информации, топологических данных сети и непрерывно актуализируют на основе переданных по телесвязи сообщений о состоянии выключателей и результатов измерений (динамическая информация).

Топологические модели сети используют для различных целей, например для графического изображения актуального (действительного) состояния сети, предпочтительно путем окрашивания частей изображенной сети, как это, например, описано В. Грейном и др. в статье "Dynamic Network Colouring", Proceedings of the Eighth Power Systems Computation Conference (PSCC), Хельсинки, 19-24 августа 1984 г. , стр. 489-496, а также в качестве справочной функции для глобальных блокировок, например для переключения на землю, или в качестве основы расчетов. Такие типичные расчеты могут относиться к существующему состоянию сети (State Estimation) или к моделированному состоянию сети (расчет потока нагрузки). Кроме того, имеются отдельные функции расчетов для определения локальных топологий сети.

Известные методы инициализации и актуализации основаны на алгоритмах для графов или на разреженных матрицах смежности. Для определения связанности сети (инициализация) эти методы делают необходимым исследование графа сети и определение корневого дерева для каждого компонента. Для больших сетей это означает значительные затраты. Поэтому при изменении коммутационного состояния выключателей делаются попытки выполнения действительно необходимых изменений (модификация) в структурах данных, описывающих граф сети или разреженную матрицу смежности. Определение этих необходимых изменений может быть очень сложным в зависимости от изменения в сети. Соотношение модификации и инициализации для заметных изменений составляет поэтому порядка 1:10. В случае дефекта в систему управления поступает большое число сообщений о состоянии выключателей, которые последовательно должны обрабатываться топологической функцией. Для того, чтобы в критических ситуациях не перегружать управляющую вычислительную машину непрерывной последовательной обработкой топологических модификаций, применяют методы перегрузки, которые в зависимости от ситуации вызывают топологическую модификацию или топологическую инициализацию. Все известные до сих пор методы модификации являются сложными, комплексными и незаконченными в математическом смысле, а потому подверженными ошибкам. Из-за комплексности разработанные пакеты программ очень обширны, а связанные с этим отладка программ и обучение новых сотрудников для применения этих программ очень сложны.

В области методов разреженных векторов и разреженных матриц разработаны алгоритмы, используемые также для больших электрических сетей в рамках расчетов сетей. Такие методы описаны, например, В. Брандвайном и др. в статье "Sparse Vector Methods", IEEE Transactions on Power Apparatus and Systems, Vol. PAS-104, N 4, февраль 1985 г., стр. 295-301. В этой публикации поясняются также понятия, такие как граф сети или таблица путей, которые употребляются в этом описании. Описанные Брандвайном и др. методы расчета предполагают топологию сети как уже существующую. Об исследовании возможностей применения таких методов для определения топологии неизвестно.

В основе изобретения лежит задача создания способа определения топологии сети, который обеспечивает сравнительно несложные и быстро производимые инициализацию и актуализацию модели сети.

Объектом настоящего изобретения является способ инициализации и актуализации модели сети, отличающийся тем, что топологию сети создают в виде графа сети с применением и расширением методов разреженных векторов и методов разреженных матриц, согласно которому (способу)
подготавливают зарегистрированные топологические данные сети в виде матрицы смежности терминалов,
преобразуют матрицу смежности терминалов в верхнюю треугольную матрицу, при этом возникают дополнительные фиктивные соединительные ветви,
инициализируют верхнюю треугольную матрицу, причем каждый элемент верхней треугольной матрицы инициализируют на основе соответствующего состояния сети,
каждый относящийся к включенной ветви элемент инициализируют малой отрицательной целочисленной константой K, выбранной так, что при последующих шагах обработки она не может стать больше нуля, и
каждый относящийся к выключенной или фиктивной ветви элемент инициализируют нулем,
образуют матричные произведения для всех строк i (i= от 1 до максимального числа строк), начиная с верхней треугольной матрицы и исключительно по диагонали, согласно следующему правилу: если элементы i, j и i, K≠0, элементы всех точек пересечения отрезков строк и столбцов верхней треугольной матрицы приращивают на 1, причем j и k являются текущими индексами соответствующей строки,
образуют таблицу путей из верхней треугольной матрицы, причем, таблица путей для каждой строки или каждого терминала верхней треугольной матрицы указывает инцидентный индекс терминала первого отличного от нуля элемента этой строки,
актуализируют верхнюю треугольную матрицу в случае изменения зарегистрированных топологических данных сети, т.е. изменения состояния ветви сети, посредством следующих операций:
в случае выключения ветви сети: из соответствующего актуального (= прежнего) значения элемента матрицы вычитают константу K,
если в результате этого элемент становится нулем, то элементы всех точек пересечения верхней треугольной матрицы этого элементов строки и столбца со всеми другими, не равными нулю элементами соответствующей строки или столбца убавляют на 1 соответственно справа от диагонали или под ней, если в результате этого остальные элементы становятся нулем, то для них повторяют упомянутую операцию убавления,
в случае включения ветви сети: к актуальному значению элемента матрицы прибавляют константу K,
если в результате этого элемент становится K или при дальнейших повторениях становится 1, то элементы всех точек пересечения верхней треугольной матрицы этого элемента строки и столбца со всеми другими, не равными нулю элементами соответствующей строки или столбца приращивают на 1 соответственно справа от диагонали или под ней, если в результате этого элементы становятся 1, то для них повторяют упомянутую операцию приращения,
актуализируют таблицу путей в соответствии с упомянутым образованием таблицы путей из верхней треугольной матрицы,
обозначают компоненты графа сети с помощью таблицы путей, причем исходя из первого индекса терминала таблицы всем терминалам соответствующего частичного пути присваивают одинаковое обозначение, компонентов, если при прохождении других частичных путей повторяется уже присвоенное обозначение (за счет попадания на компонент, которому уже присвоено обозначение), то это обозначение присваивают только что пройденному частичному пути, граф сети разлагают на подграфы в соответствии с числом присвоенных обозначений.

Предпочтительные варианты реализации изобретения раскрыты в нижеследующем пояснении его сущности с помощью примеров.

Способ согласно изобретению обеспечивает на порядок более быструю инициализацию или актуализацию топологической модели, чем известные способы. Кроме того, время актуализации (модификации) в значительной степени не зависит от величины сети.

Согласно предпочтительному варианту, работают с топологическим адресом, который упрощает ввод данных и позволяет интегрировать локальные топологические функции, например, топологии полей, в расчет топологии сети. Результаты измерений моделируют при этом также в виде топологических объектов, благодаря чему упрощается ввод данных и становится возможным точное описание также таких конфигураций сети, у которых прежде приходилось предусматривать дополнительные псевдоэлементы сети.

Расчеты сети, основанные на моделировании топологии сети, могут быть значительно ускорены за счет применения способа согласно изобретению, поскольку необходимые структуры данных и этапы обработки уже содержатся в предложенном способе. Новые импульсы и аспекты вытекают также для программ, таких как расчет (n-1) отказов и топологический анализ возможности наблюдения. Всем этим программам присуща оценка топологических вариантов сети. Они используют быстрый способ актуализации. Поэтому для всех постановок задач, при которых необходимо быстро установить последствия изменений в сети, ожидаются существенные улучшения. Это могут быть, например, топологические методы для сетей связи или методы оптимизации с помощью алгоритмов потока данных в сети.

Ниже перечислены сопроводительные чертежи, которые использованы для пояснения сущности изобретения.

На фиг. 1 представлены станции и распределительные подстанции;
на фиг. 2 - структура поля на распределительной подстанции;
на фиг. 3 - преобразование адресов;
на фиг. 4 - соответствие результатов измерений;
на фиг. 5 - граф-пример;
на фиг. 6 - матрица смежности терминалов и ее LDU-разложение;
на фиг. 7 - инициализация верхней треугольной матрицы;
на фиг. 8 - целочисленно инициализированная верхняя треугольная матрица;
на фиг. 9 - таблица путей и граф путей (пример);
на фиг. 10 - математическая формулировка инициализации и актуализации;
на фиг. 11 - целочисленно актуализированная верхняя треугольная матрица;
на фиг. 12 - таблица путей и граф путей для модифицированного графа-примера;
на фиг. 13 - сеть из узлов и ветвей;
на фиг. 14 - производная матрицы полных проводимостей узла;
на фиг. 15 - тест-графы для измерения мощности;
на фиг. 16 - фиктивные ветви в зависимости от величины сети и степени объединения;
на фиг. 17 - время работы центрального процессора для построения статической топологии (тест-пример);
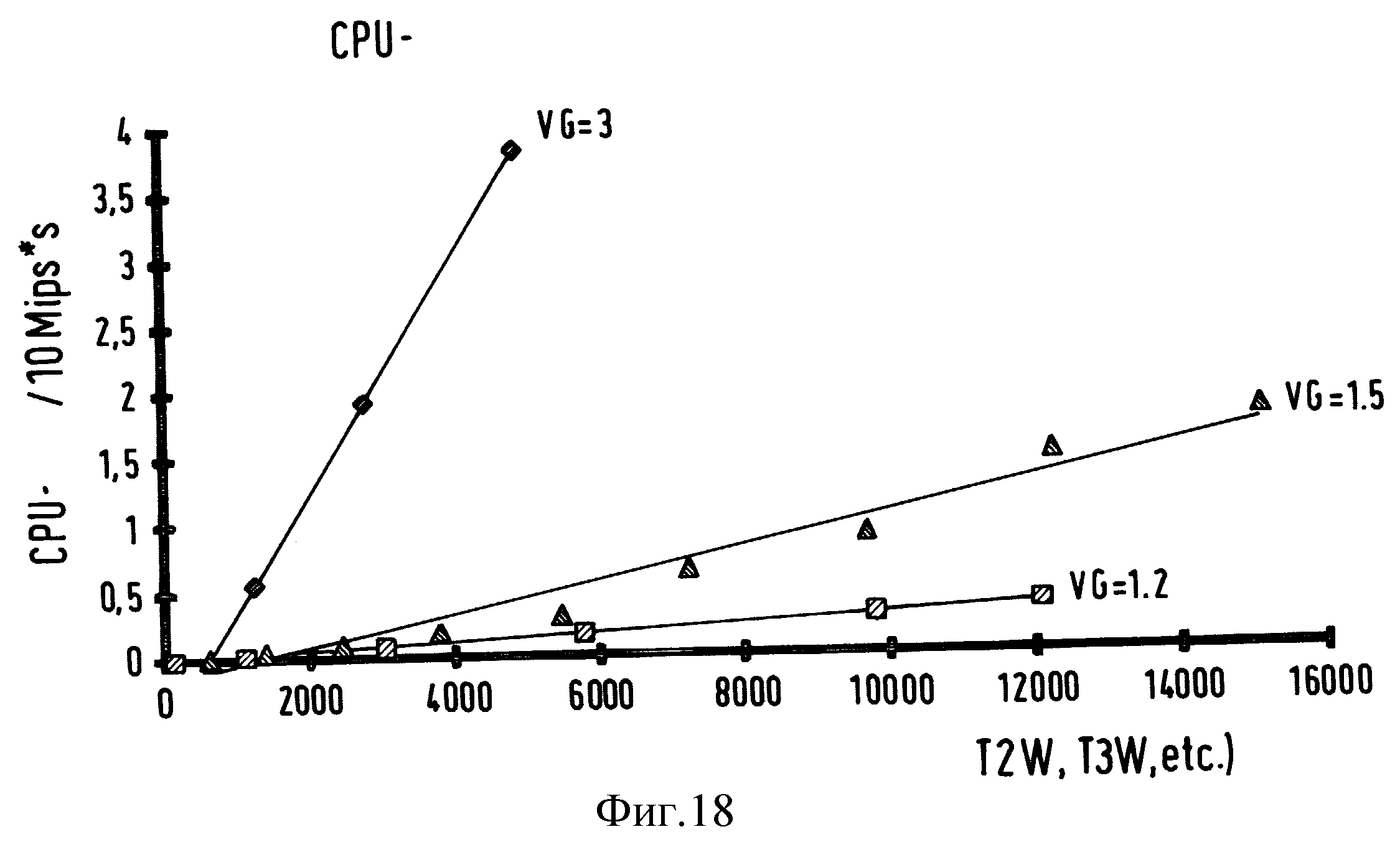
на фиг. 18 - время работы центрального процессора для инициализации статической топологии (тест-пример);
на фиг. 19 - время работы центрального процессора для актуализации (тест-пример).

Приведенные ниже примеры для пояснения способа основаны на нижеследующем установлении внешнего и внутреннего топологических адресов для электрических передающих и распределительных сетей. Это установление упрощает ввод данных и позволяет интегрировать локальные топологические функции (расчет топологии поля) в расчет топологии сети.

Электрические сети любого уровня напряжения могут быть описаны конечными точками (терминалы) и их соединениями (ветви). Соединениями при этом являются элементы сети с полным сопротивлением, такие как линия, трансформатор или элемент продольной реактивной мощности и т.д., или элементы сети без полного сопротивления, такие как силовые выключатели, разъединители или объект измерений. Конечные точки являются внешними топологическими адресами в сети и могут быть отнесены к элементам сети, таким как секции сборных шин, или частям элементов сети, например обоим концам (терминалы) линии. Для электрических передающих и распределительных сетей установлена следующая топологическая иерархия:
1. Станция (или географическая станция).

2. Распределительная подстанция (или уровень напряжения).

3. Поле.

4. Терминал.

На фиг. 1 в качестве примера изображена сеть, состоящая из трех станций с двумя распределительными подстанциями каждая. На фиг. 2 изображена структура поля на распределительной подстанции, которая (структура) сама поясняет себя за счет используемых символов и надписей.

Внешний топологический адрес является тогда структурой данных, которая для каждой из этих иерархических ступеней содержит идентификатор. Например, топологический адрес одного конца линии 1 на станции 1 (фиг. 1 и 2) можно специфицировать следующим образом.

1. Станция: 1
2. Распределительная подстанция: 1.

3. Поле: 10
4. Терминал: 10
и прочесть следующим образом: описанный топологический адрес находится на станции 1, внутри станции 1 на распределительной подстанции 1, внутри распределительной подстанции в поле 10 и внутри поля 10 на терминале 10. Фиг. 1 и 2 поясняют эти действия.

Для границы каждой иерархической ступени считается, что они не должны совпадать. Это значит, что каждый терминал может относиться только к одному полю, каждое поле - только к одной распределительной подстанции, а каждая распределительная подстанция - только к одной станции.

По технологическому описанию топологии сети можно очень просто и быстро определить абстрактные конечные точки (внутренние топологические адреса) графа сети посредством описанной ниже структуры данных, подготовляемой устройством подготовки данных.

Преобразование внутреннего топологического адреса во внешний изображено на фиг. 3 и описано ниже на примере.

Между EvuStaInStation [i] и EvuStaInStation [i + I] (распределительная подстанция на станции) находятся все распределительные подстанции станции i. В структуре данных EvuStaInStation [] содержится идентификаторы, так что соответствующие частичные адреса не должны лежать близко друг к другу, а их определяют путем непосредственного сравнения. Исключение составляет идентификатор станции, служащий индексом для EvuStaInStation []. Соответственно проходят и другие иерархические ступени. Определяемый в заключение индекс структуры данных Terminal [] является внутренним топологическим адресом точки терминала, специфицированной внешним топологическим адресом. Внутренний топологический адрес используют в качестве индекса для конечных точек (внутренний индекс терминала) графа сети.

Если учитывать поля в качестве частичного адреса, то возможно определение топологии полей в качестве неявной части топологии сети. Благодаря этому отпадают функции расчета для определения локальных топологий полей.

Также результаты измерений и защитные сообщения можно моделировать в виде топологических объектов. Это упрощает ввод данных и позволяет точно описать все конфигурации сети, у которых прежде приходилось дополнительно предусматривать псевдоэлементы сети
Результаты измерений являются переданными по телесвязи аналоговыми значениями важных величин процесса, таких как напряжение, ток, мощность и т.д., указываемых в управляющей вычислительной машине и проверяемых на превышение предельного значения. У систем управления, которые также хранят топологическую модель в управляющей вычислительной машине, результаты измерений используют в сочетании с топологией сети и электрическими параметрами элементов сети для расчета существующего и полного состояния сети (State Estimation). Для этого результаты измерений мощности должны быть отнесены соответственно к смежным элементам сети с полным сопротивлением, а результаты измерений напряжения - к узлам модели сети. Узлами называют при этом все включенные между собой без полного сопротивления элементы сети. Узлы соединяют посредством ветвей с полным сопротивлением, таких как линии и трансформаторы. До сих пор при вводе данных результаты измерений и элементы сети связывают между собой статически. Это имеет тот недостаток, что для определенных конфигураций сети результаты измерений приходится располагать иначе, чем это соответствует их фактическому расположению в сети. Этот важный недостаток устраняют за счет того, что результаты измерений мощности моделируют в виде направленных ветвей без полного сопротивления, а результаты измерений напряжения - в виде объектов с внешним топологическим адресом. Зависимое от схемы соответствие результата измерения и элемента сети осуществляется тогда топологией сети. Далее направление стрелки подсчета результатов измерений устанавливается непосредственно ориентированием ветви результатов измерений. На фиг. 4 изображено описанное топологическое соответствие. Буквой P обозначены значения активной мощности, а буквой Q - значения реактивной мощности. В зависимости от коммутационного состояния выключателей S1-S4 возникают перечисленные в таблице соответствия результатов измерений и их свойства, где L1, L2 - линии (см. в конце описания).

В то время как при статическом соответствии результат измерения может быть отнесен только к одному элементу сети, благодаря топологическому соответствию во всех случаях возможно правильное соответствие при одновременно упрощенном вводе данных. Логически те же самые действия относятся к направленным защитным сообщениям, таким как сообщения о кратковременном замыкании на землю и индикаторам короткого замыкания, которые для локализации замыканий на землю или коротких замыканий оцениваются топологической функцией.

С использованием приведенного выше установления адресов ниже в качестве примера подробно описан способ согласно изобретению. Все этапы способа можно реализовать в виде программы для вычислительной машины и автоматизировать с помощью устройства обработки данных.

1. Построение статической топологии
Граф рассматриваемой сети состоит из конечных точек, так называемых терминалов, а также ветвей без полного сопротивления и с полным сопротивлением (четырехполюсники), таких как выключатели, результаты измерений, соединители, а также линий, трансформаторов и элементов продольной реактивной мощности. Кроме того, имеются дополнительно двухполюсники, такие как генераторы и нагрузки, результаты измерений напряжения, заземляющие выключатели и т.д., имеющие только один топологический адрес, а также различные признаки и свойства, которые они передают на соответствующий подграф, например заземлено, без напряжения или под напряжением.

Структура данных способов основана на матрице смежности терминалов, которую откладывают в виде списка с прямой цепочкой и у которой каждому терминалу соответствуют смежные ветви (обозначаемые ниже Cst []). Для этой симметричной матрицы, содержащей чисто структурную информацию, определяют оптимальную последовательность исключения и дополняют Cst [] дополнительно возникающими при этом Fill In (фиктивные соединительные ветви). На основе подобия числовому LDU-разложению матрицы ниже этот этап называют структурным треугольным или LDU-разложением. Под LDU-разложением понимают разложение матрицы на произведение нижней (Lower), диагональной (Diagonal) и верхней (Upper) матриц, причем нижняя и верхняя матрицы являются соответственно треугольными матрицами. Для пояснения топологического свойства Fill In их называют в дальнейшем фиктивные ветви. Как показано ниже, структурная верхняя матрица (обозначаемая ниже Parkett []) содержит информацию о связности графа, которая при изменениях в сети может быть очень просто и быстро актуализирована в Parkett [].

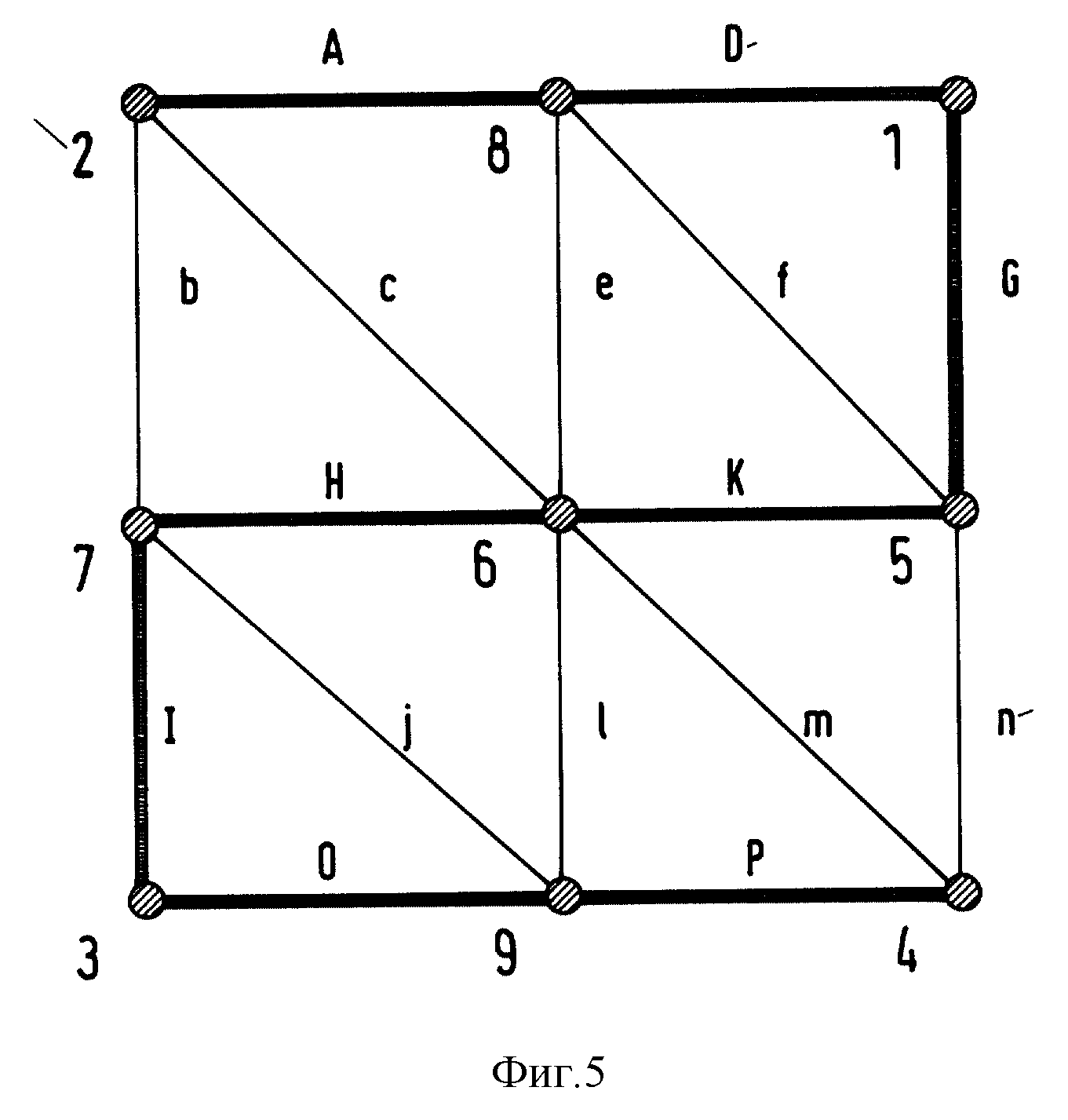
Показанный на фиг. 5 небольшой граф-пример поясняет структуры данных. Все отображенные в графе ветви являются составной частью статической топологии. Обозначенные большими буквами ветви имеют состояние EIN (ВКЛ), а маленькими - состояние AUS (ВЫКЛ). В этом примере приведены только внутренние индексы терминалов и идентификаторы ветвей. Отображение внешнего топологического адреса на внутренний происходит с помощью поясненной иерархии адресов и для наглядности может быть здесь опущено. Также тип ветвей в этом примере имеет второстепенное значение. Подробное описание поэтому опущено, не ограничивая общезначимости примера. Сеть-пример с 9 внутренними топологическими адресами и 16 четырехполюсниками или ветвями отображается на последующих ступенях на показанные выше структуры данных.

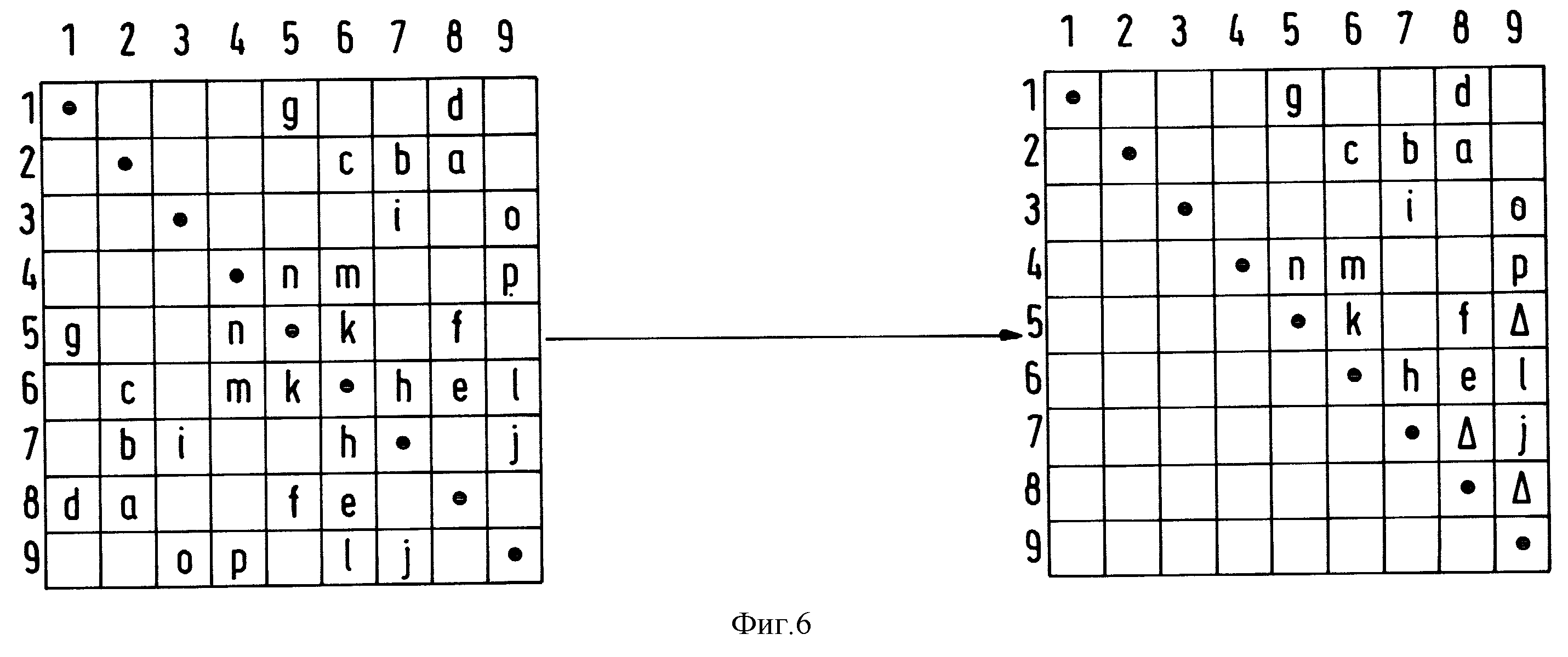
Матрица смежности терминалов для этого графа и ее LDU-разложение изображены на фиг. 6. Элементы матрицы содержат для более подробного пояснения алгоритма идентификаторы соответствующих ветвей. Отмеченные знаком Δ элементы матрицы соответствуют Fill In, т.е. фиктивным ветвям в сети. Последовательность терминалов в этом примере для простоты выбрана уже оптимальной. Внутренняя отладка программы матрицы связности терминалов происходит в виде накопленного списка с прямой цепочкой (Cst []), а LDU-матрицы - в виде одномерного массива (Parkett []) C-структур. Из-за симметрии структур откладывают только верхнюю матрицу. Ниже предполагается, что все строки верхней матрицы и все элементы этих строк сортированы в оптимальной последовательности. Каждый объект списка или массива содержит для каждого недиагонального элемента индекс противоположного терминала, индекс в списке ветвей, состояние ветви и тип ветви.

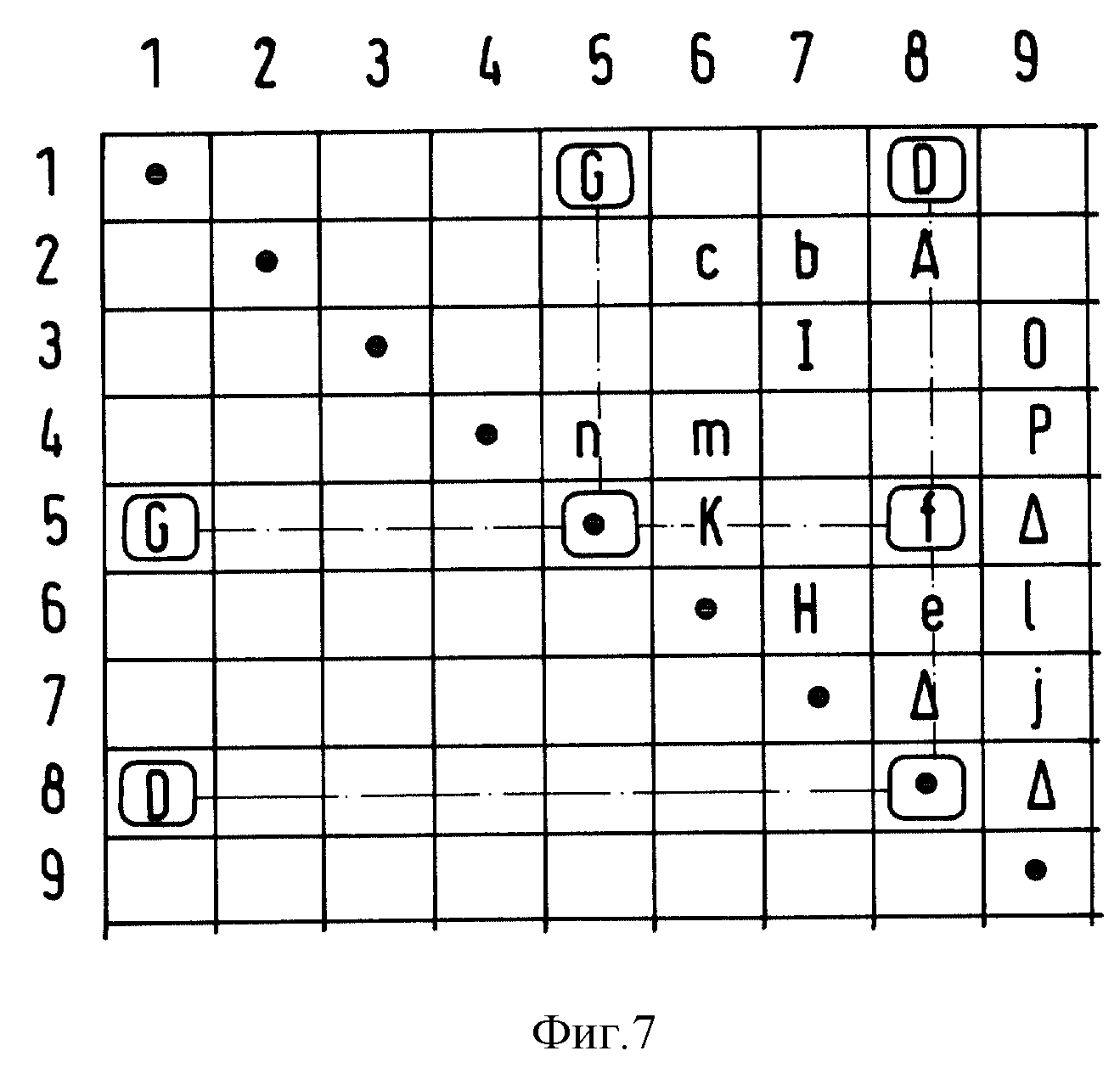
2. Инициализация верхней матрицы (фиг. 7, 8 и 10)
Каждый элемент верхней матрицы инициализируют на основе соответствующего состояния ветви.

Состояние EIN ⇒, например, K = SCHAR_MIN (-128, минимальное значение байта со знаком); состояние AUS : ⇒ 0. Для инициализированной таким образом матрицы осуществляют следующую процедуру, которую по образцу целочисленных операций называют целочисленная инициализация. Это происходит аналогично матричному произведению всех строк, начиная с первого недиагонального элемента, справа от диагонали на самих себя:
Для всех строк i
Для всех элементов j, k строки i справа от диагонали, где i = I...n, j = i + I...n, k = j...n, n = число терминалов:
В случае, если соответствующие элементы (i, j) и (k, i) матрицы ≠ 0:
Приращение элементов всех соответствующих точек пересечения отрезков строки и столбца соответственно справа от диагонали и под ней в верхней матрице на 1. За счет симметрии структуры отрезки строки и столбца идентичны.

Для первой строки на фиг. 7 первая недиагональная точка пересечения является элементом (5, 8) матрицы и этому элементу соответствует ветвь f. Этот элемент инициализирован 0 и получает актуальное значение 1.

На фиг. 7 это поясняется для первой строки. После этой целочисленной инициализации верхняя матрица имеет вид, изображенный на фиг.8. Маленькие буквы соответствуют выключенным ветвям и имеют показание счетчика состояния 0, большие буквы - включенным ветвям и имеют показание счетчика состояния SCHAR_MIN + i, причем i определяется количеством выполненных с этим элементом операций приращения. Отмеченные знаком Δ элементы матрицы соответствуют Fill In, т.е. фиктивным ветвям в сети, которые на основе целочисленных операций в соответствии с актуальной топологией получают состояние EIN или AUS. Это соответствует показанию счетчика состояния 0 или i, причем i определяется количеством выполненных с этим элементом операций приращения. Обозначенные жирными маленькими буквами ветви имеют, правда, актуальное состояние AUS, получают, однако, на основе целочисленных операций состояние соединяющей ветви и имеют также показание счетчика состояния i, где i - количество операций приращения. Кроме того, состояние ветви может зависеть также от ее типа, например, чтобы определить специальные топологии, такие как, например, топологию местной сети. Для определения топологии местной сети все трансформаторы следует задать как разъединяющие ветви.

Связанность графа можно очень просто вывести из таблицы путей (Path Table []) верхней матрицы Parkett [] (фиг. 9).

Эта таблица путей содержит для каждого индекса терминала в структуре Parkett [] противоположный индекс терминала первой смежной ветви. Эта таблица является наряду с верхней матрицей второй важной структурой данных этого топологического метода. По ней можно легко определить связанность графа сети. Эта таблица содержит столько записей со значением 0, на сколько подграфов распадается граф сети. Изображенная на фиг. 9 таблица путей может быть выведена из структуры Parkett []. Эта таблица содержит только один 0, и граф сети является поэтому связанным, что хорошо видно по графу путей на фиг.9.

За счет соответствия, например, исходной точки цвета для окрашивания графа сети или за счет соответствия признака для обозначения определенных состояний элементу этой таблицы (т.е. внутренний топологический адрес или индекс терминала) к соответствующему подграфу может быть отнесен нужный цвет или свойство путем прохождения графа путей.

3. Актуализация топологии сети (фиг. 10-12)
Предположим, что в графе-примере состояние ветви G изменяется с EIN на AUS. Целочисленный алгоритм актуализации определяет изменения для отмеченных знаком ⇒ элементов матрицы (фиг. 11).

Алгоритм для выключения или включения ветви может быть сформулирован следующим образом.

Выключение ветви.

Из соответствующего элемента верхней матрицы вычесть константу К. Если этот элемент становится 0¹:
Актуализация AUS:
Для этого элемента:
Убавление соответствующих элементов верхней матрицы на 1 для всех точек пересечения этого элемента со всеми другими, не равными нулю элементами соответствующей строки справа от диагонали или соответствующего столбца под ней. Для каждого элемента, который в результате этого становится 0, повторить актуализацию AUS.

Включение ветви:
К соответствующему элементу верхней матрицы прибавить константу К. Если этот элемент становится К¹:
Актуализация EIN:
Для этого элемента:
Убавление соответствующих элементов в верхней матрице на 1 для всех точек пересечения этого элемента со всеми другими, неравными нулю элементами соответствующей строки справа от диагонали или соответствующего столбца под ней. Для каждого элемента, который в результате этого становится К, повторить актуализацию EIN.

¹Только в этом случае изменение состояния оказывает топологическое влияние и может состояться актуализация верхней матрицы.

Для этого примера отрицательное приращение элемента 8, 9 матрицы приводит к тому, что этот элемент получает значение 0. Из этого следует, что актуализированная таблица путей получает дополнительную нулевую запись, т.е. граф сети распадается на два подграфа. Изображенная на фиг. 12 таблица путей может быть получена из актуализированной структуры Parkett []. На примере таблицы путей и графа путей очевидно, что граф распался на два подграфа. Окрашивание или передача признака возможна очень просто и очень быстро за счет обработки таблицы путей.

4. Интерфейс потока нагрузки
Структуру LDU-матрицы для расчетов потока нагрузки или короткого замыкания получают в два этапа. На первом этапе все ветви без полного сопротивления, кроме результатов измерений, объединяют в узлы. Затем результаты измерений относят к элементам сети с полным сопротивлением и на втором этапе результаты измерений также сливают с узлами. На фиг. 13 изображена сеть из узлов и ветвей. Если предположить, что ветви d, e, f, G, K не имеют полного сопротивления, то из структуры Parkett [] можно непосредственно получить (LD) U-форму матрицы полных проводимостей узлов. Соответственно результатов измерений в этом примере опущено.

Терминалы 1, 5, 6, 8 слиты в узел, тогда как все другие терминалы соединены ветвями с полным сопротивлением и поэтому сохраняются. Возникает, следовательно, изображенная на фиг. 14 верхняя форма структурной матрицы Якоби или матрицы полных проводимостей узла.

Функция фильтра устраняет все ветви без полного сопротивления и преобразует соответствующие концы ветвей (терминалы) из ветвей с полным сопротивлением в терминалы с более высоким индексом, как здесь, например, 1, 5, 6 ---> 8. Это, следовательно, уже матрица Якоби (поток нагрузки) или матрица полных проводимостей узла (короткое замыкание). Дальнейшие этапы расчета потока нагрузки осуществляются очень просто. За счет того, что LDV-разложение производят уже на уровне базовой топологии (терминал-выключатель), может отпасть множество шагов программ. Это упрощение программ в значительной мере сокращает время вычислений и уменьшает подверженность ошибкам программ расчетов, таких как State Estimation, поток нагрузки и короткое замыкание.

5. Испытательные сети
На фиг. 15 показана форма генерируемой сети, с помощью которой проводились тесты производительности алгоритма. Путем задавания параметров можно задавать степень объединения VG сети между 0 и 3, а величину сети - произвольно. Степень объединения определяется по формуле (I):

6. Производительность
6.1. Число фиктивных ветвей в зависимости от величины сети и от степени объединения
Как описано выше, матрицу полных проводимостей терминалов преобразуют в верхнюю треугольную матрицу. При этом образуются фиктивные соединительные ветви (Fill In). Число дополнительных соединительных ветвей зависит от последовательности отдельных шагов преобразования и от степени объединения VG. При построении верхней треугольной матрицы оптимизируют последовательность шагов преобразования. Поэтому зависимость ограничивается степенью объединения и числом ветвей, как это изображено на фиг. 16. Число фиктивных ветвей влияет на производительность способа. Это хорошо видно на других диаграммах для отдельных шагов программы.

6.2. Производительность отдельных шагов программы в зависимости от величины сети и от степени объединения
Время работы центрального процессора 80486 с тактовой частотой 40 МГц измерялось для следующих шагов программы в зависимости от числа ветвей и степени объединения:
1. Построение статической топологической структуры Parkett [].

2. Инициализация динамической топологии на основе актуального состояния всех ветвей сети.

3. Модификация динамической топологии на основе изменения состояния одной ветви.

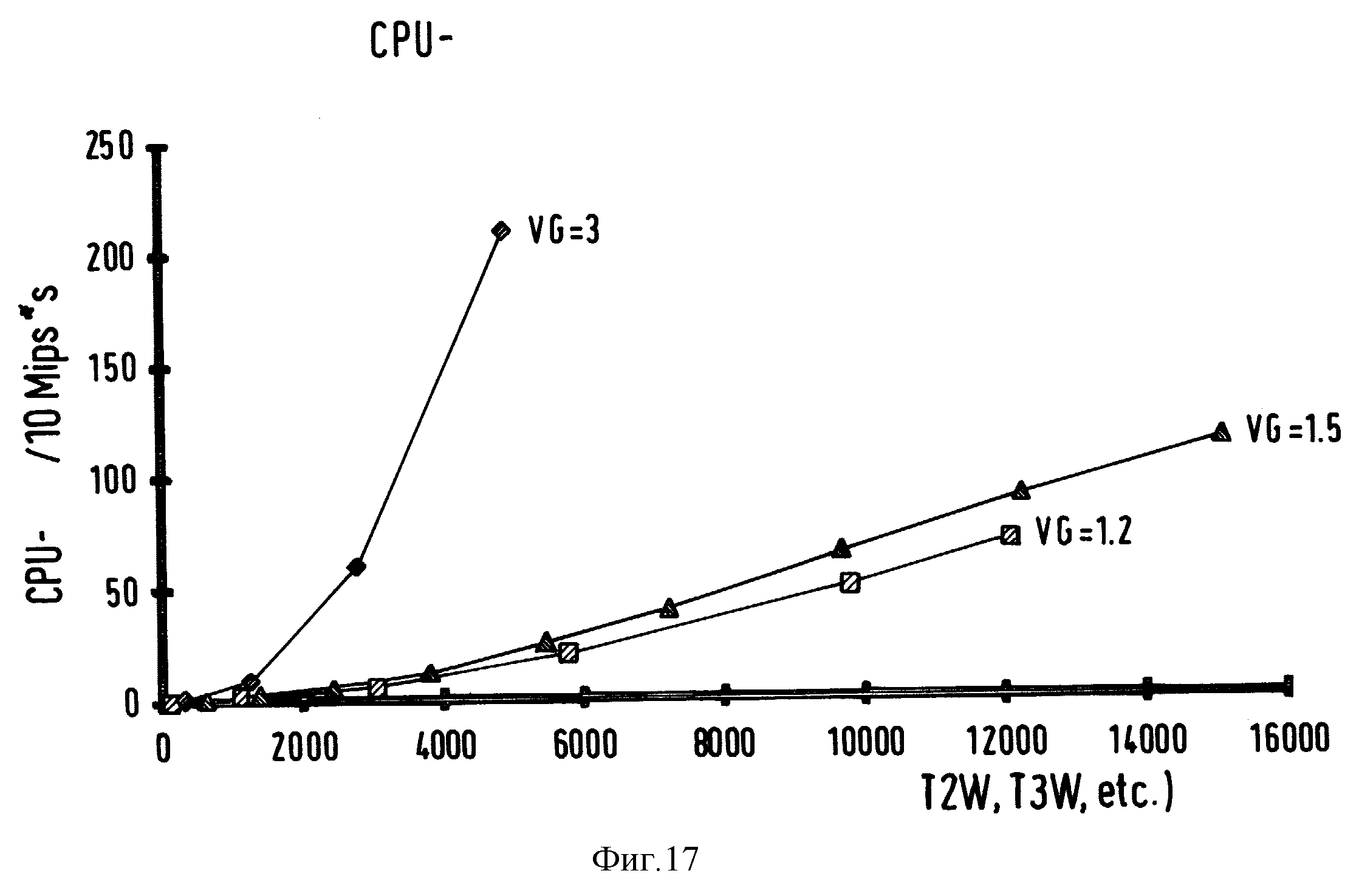
На фиг. 17 показано требуемое время работы ЦП в 10 mips•c для построения статической топологии Parkett []. Время работы ЦП производительностью 100 mips получается тогда путем деления на 100 mips.

Построение этой структуры Parkett [] самое сложное из трех шагов и является необходимым только при расширении сети. Если положить в основу ЦП производительностью 200 mips (например, DEC AXP 600), то для сети такой величины, как описано в п. 5 испытательная сеть, требуется время работы ЦП около 3 с.

Величину структуры Parkett [] вычисляют следующим образом:
(2• число ветвей + число терминалов)•16 байт
Для сети порядка испытательной сети величина структуры Parkett [] составляет около 0,6 Мбайт.

На фиг. 18 показано требуемое время работы ЦП в 10 mips•с для инициализации статической топологии Parkett [] с актуальными состояниями всех ветвей сети.

Инициализация топологии обычно необходима при запуске системы после изменений данных и в зависимости от концепции сдвоенной ЭВМ при смене ЭВМ. Для сети порядка испытательной сети инициализация на ЦП производительностью 200 mips была бы закончена примерно через 25 мс.

На фиг. 19 показано требуемое время работы ЦП в 10 mips•мс для модификации топологии Parkett [] с актуальным состоянием одной ветви сети.

Среднее время модификации топологической структуры при изменении состояния, например, выключается составляет для сети порядка испытательной сети для ЦП 80486 с тактовой частотой 40 МГц около 8,0•10^-5 с. Для ЦП производительностью 200 mips оно составляет порядка 4.0 • 10^-6 с. Это время на несколько порядков быстрее, чем время известных способов. Благодаря этому возможны совершенно новые концепции при топологической обработке и при последующих методах расчета. Например, все ветви сети после каждой модификации можно проверить на то, является ли данная ветвь единственным соединением (критическая ветвь) между двумя испытательными сетями. Для сети порядка испытательной сети и для ЦП производительностью 200 mips общее время его работы, включая модификацию, составило бы примерно
2• число ветвей •Т_{модификации} ≈ 100 мс.

Кроме того, этот пример показывает, что общее время работы ЦП для выполнения модификаций для всех выключателей в этом примере составляет около 50 мс. Это лишь приблизительно вдвое большее время, которое требуется для инициализации и которое является еще одним указанием на то, что модификация при этом способе включает в себя только действительно необходимые изменения структуры данных.

Реферат

Изобретение относится к области обработки информации и может быть использовано для создания модели сети. Техническим результатом является упрощение модели сети. Изобретение основано на воспроизведении топологии сети с применением методов разреженных векторов и методов разреженных матриц путем образования матричных произведений элементов строк матриц. 2 з.п. ф-лы, 19 ил., 1 табл.

Формула