Преобразования с общими множителями - RU2429531C2

Чертежи

Показать все 8 чертежа(ей)

Описание

Притязание на приоритет

Настоящая заявка притязает на приоритет предварительной заявки США № 60/758464, поданной 11 января 2006 г., озаглавленной “Эффективные осуществления без умножений масштабированного дискретного косинусного преобразования (DCT) и обратного дискретного косинусного преобразования (IDCT)”, правообладателем которой является заявитель настоящего изобретения, и включенной в настоящее описание в качестве ссылки.

Уровень техники

Область техники, к которой относится изобретение

Настоящее раскрытие в целом относится к обработке и, более конкретно, к способам, предназначенным для выполнения преобразований данных.

Уровень техники

Преобразования обычно используют, чтобы конвертировать данные из одной области определения в другую область определения. Например, дискретное косинусное преобразование (DCT) обычно используют, чтобы преобразовывать данные из пространственной области определения в частотную область определения, а обратное дискретное косинусное преобразование (IDCT) обычно используют, чтобы преобразовывать данные из частотной области определения в пространственную область определения. DCT широко используют для сжатия изображения/видео, чтобы выполнить отмену пространственной корреляции блоков элементов изображения (пикселей) в изображениях или кадрах видео. Результирующие коэффициенты преобразования обычно в значительно меньшей степени зависят друг от друга, что делает эти множители более подходящими для квантования и кодирования. DCT также проявляет свойство уплотнения энергии, которое является возможностью преобразовывать большую часть энергии блока пикселей только в небольшое число (обычно малого порядка) коэффициентов преобразования. Это свойство уплотнения энергии может упрощать схему алгоритмов кодирования.

Преобразования, такие как DCT и IDCT, могут быть выполнены относительно большого количества данных. Следовательно, желательно выполнять преобразования как можно эффективнее. Кроме того, желательно выполнять вычисления для преобразований с использованием простого аппаратного обеспечения для того, чтобы уменьшить стоимость и сложность.

Вследствие этого в данной области техники имеется потребность в способах, чтобы эффективно выполнять преобразования относительно данных.

Сущность изобретения

В настоящей заявке описаны способы, предназначенные для эффективного выполнения преобразований относительно данных. В соответствии с одним аспектом устройство выполняет умножение первой группы, по меньшей мере, из одной величины данных на первую группу, по меньшей мере, из одной рациональной двоичной константы, которая аппроксимирует первую группу, по меньшей мере, из одной иррациональной константы, масштабированной с помощью первого общего множителя. Устройство дополнительно выполняет умножение второй группы, по меньшей мере, из одной величины данных на вторую группу, по меньшей мере, из одной рациональной двоичной константы, которая аппроксимирует вторую группу, по меньшей мере, из одной иррациональной константы, масштабированной с помощью второго общего множителя. Каждая рациональная двоичная константа является рациональным числом с двоичным знаменателем. Первая и вторая группы, по меньшей мере, из одной величины данных имеют разные размеры. Например, первая группа может включать в себя две величины данных, а вторая группа может включать в себя четыре величины данных.

В соответствии с другим аспектом устройство выполняет умножение, по меньшей мере, одной величины данных на, по меньшей мере, одну рациональную двоичную константу, которая аппроксимирует, по меньшей мере, одну иррациональную константу, масштабированную с помощью общего множителя. Общий множитель выбирают на основании числа логических и арифметических операций, предназначенных для умножения, по меньшей мере, одной величины данных на, по меньшей мере, одну рациональную двоичную константу. Логические и арифметические операции могут содержать операции сдвига, вычитания и сложения. Общие множители дополнительно могут быть выбраны на основании точности результатов.

Различные аспекты и признаки раскрытия описаны более подробно ниже.

Краткое описание чертежей

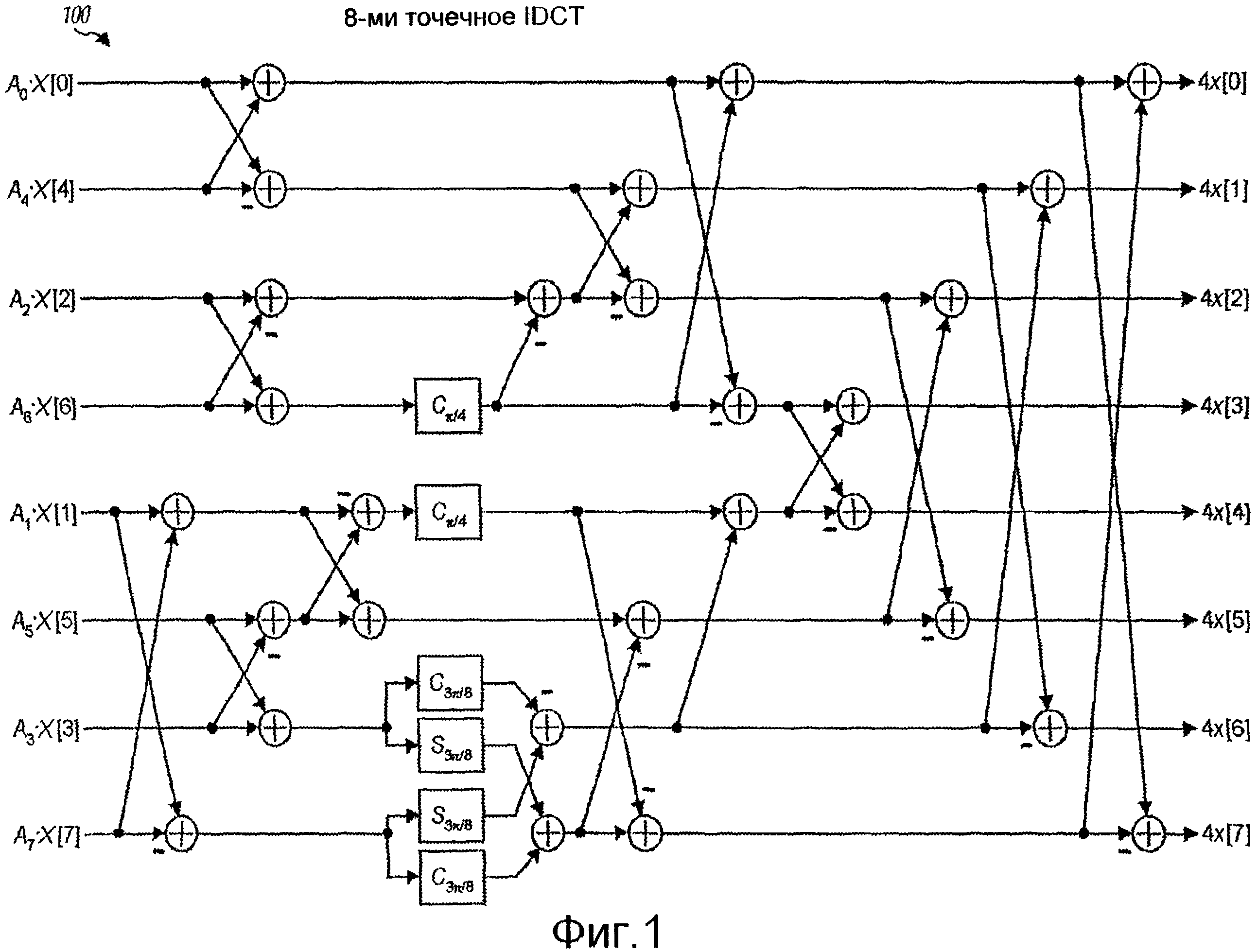
Фиг. 1 изображает граф-схему 8-точечного IDCT.

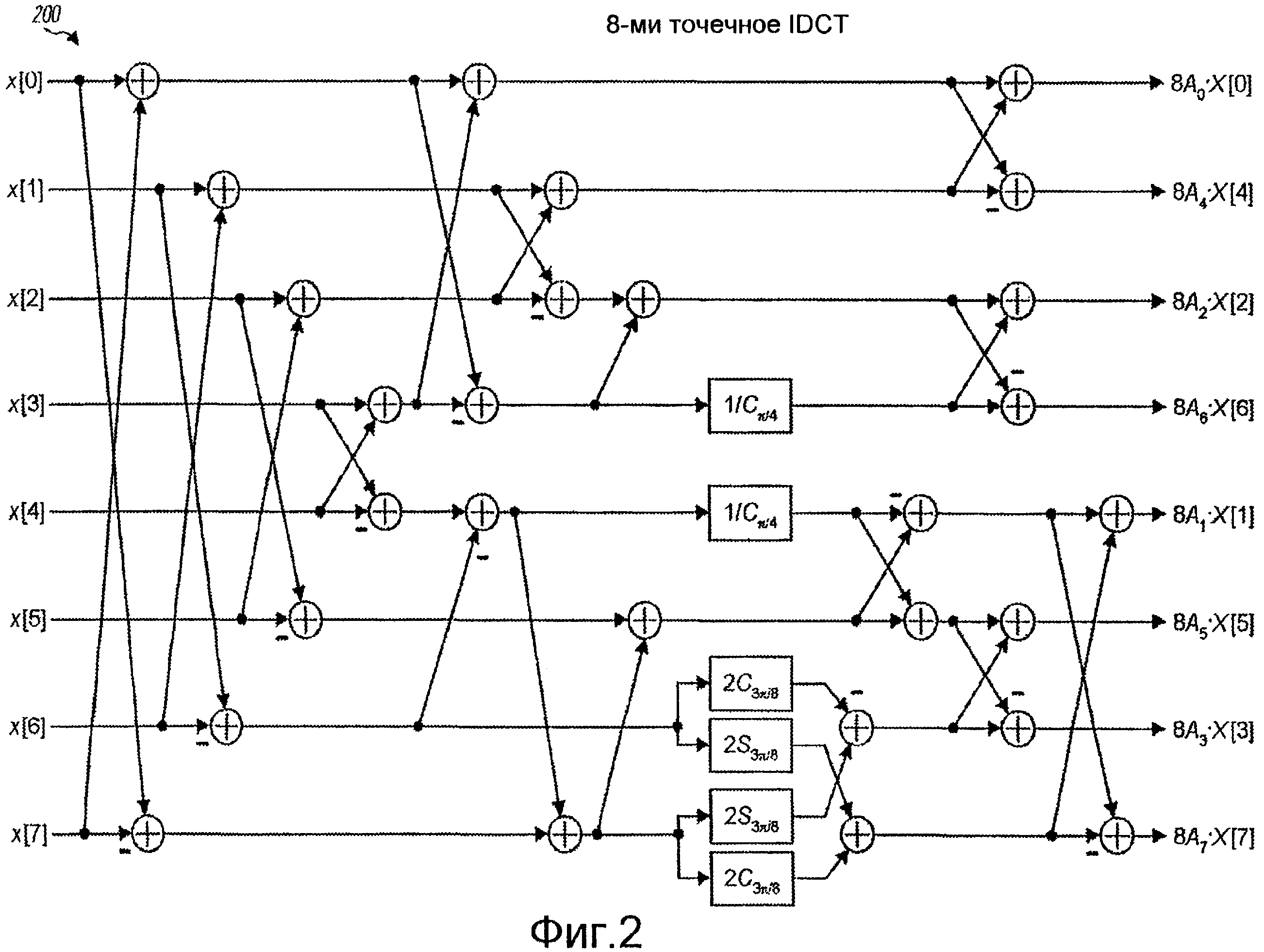
Фиг. 2 изображает граф-схему 8-точечного DCT.

Фиг. 3 изображает граф-схему 8-точечного IDCT с общими множителями.

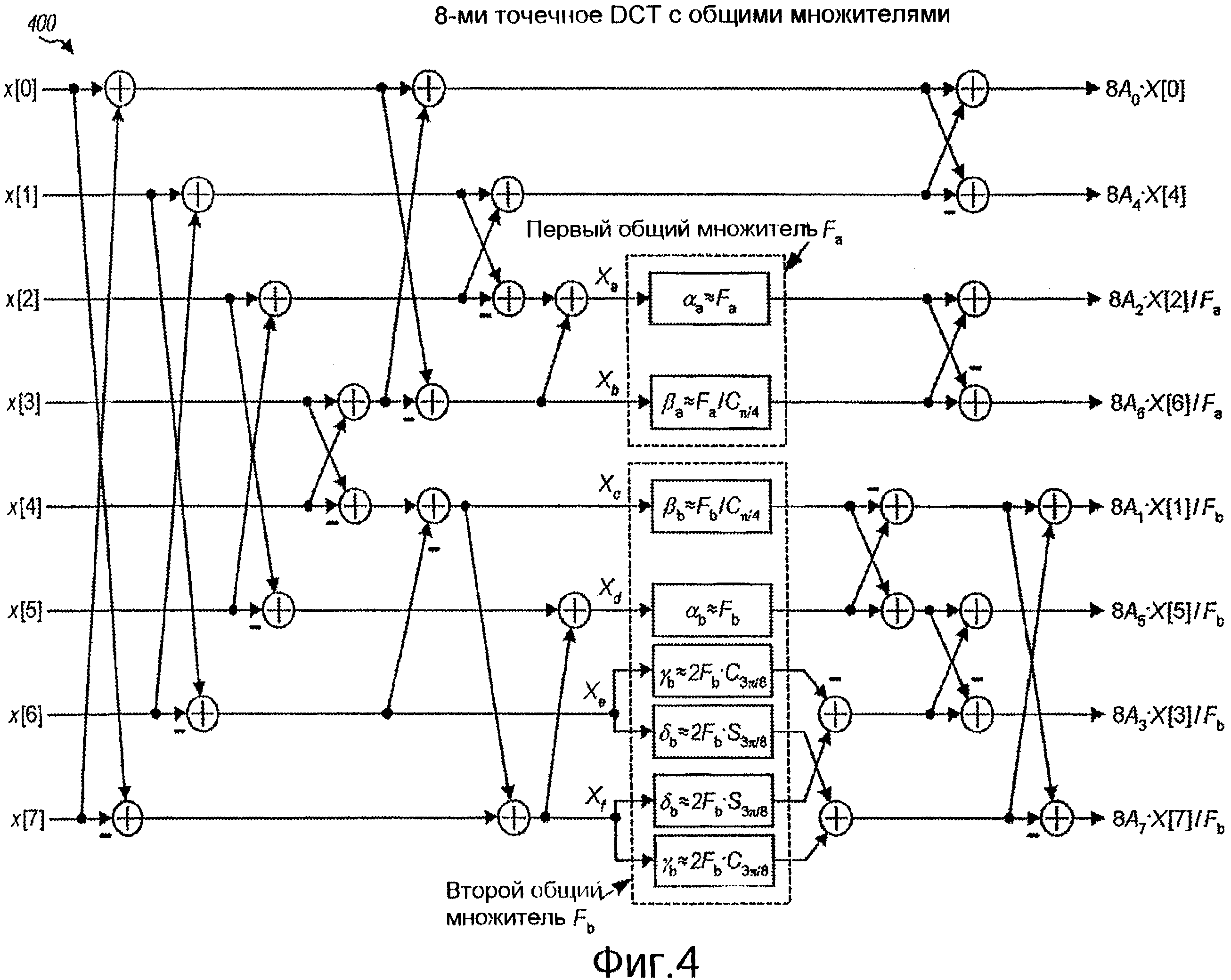
Фиг. 4 изображает граф-схему 8-точечного DCT с общими множителями.

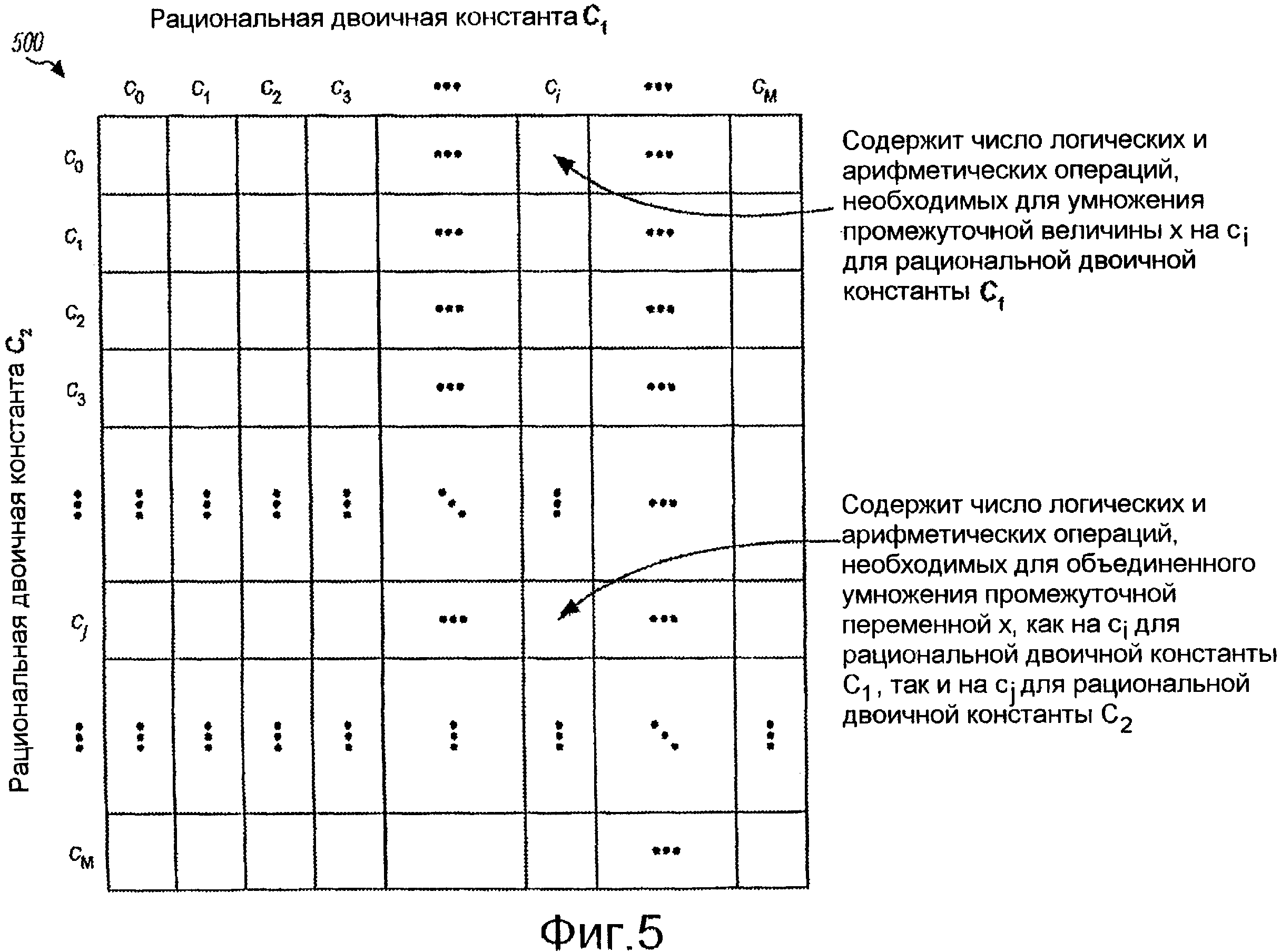
Фиг. 5 изображает справочную таблицу, хранящую номера операций для умножения на разные величины рациональной двоичной константы.

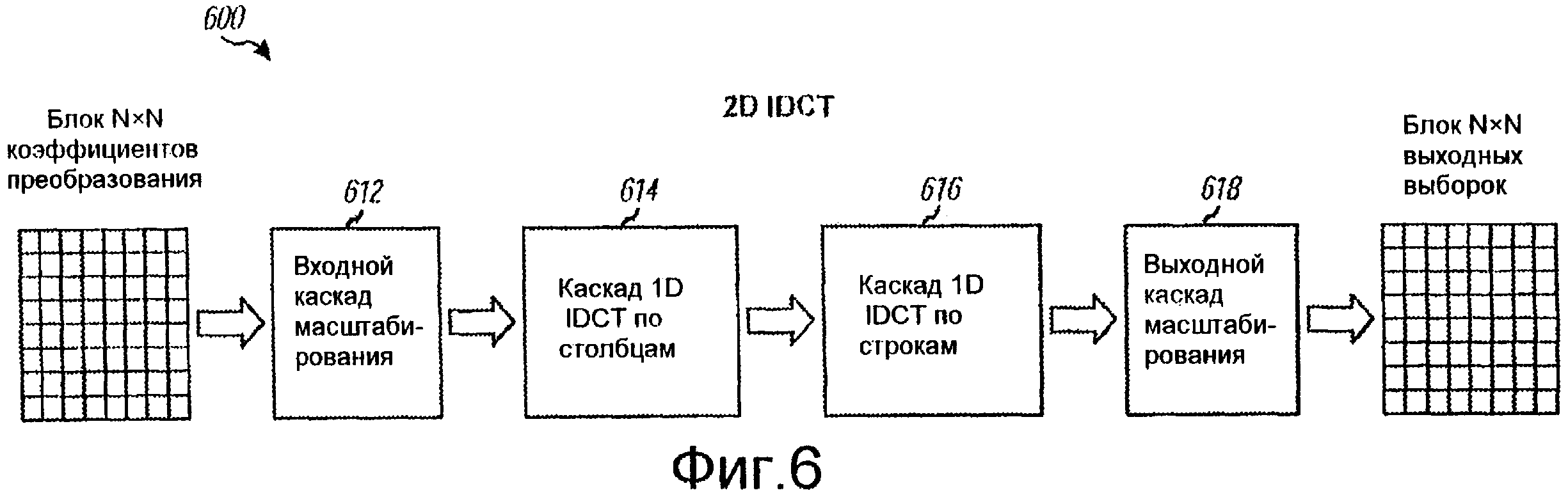
Фиг. 6 изображает блок-схему двумерного (2D) IDCT.

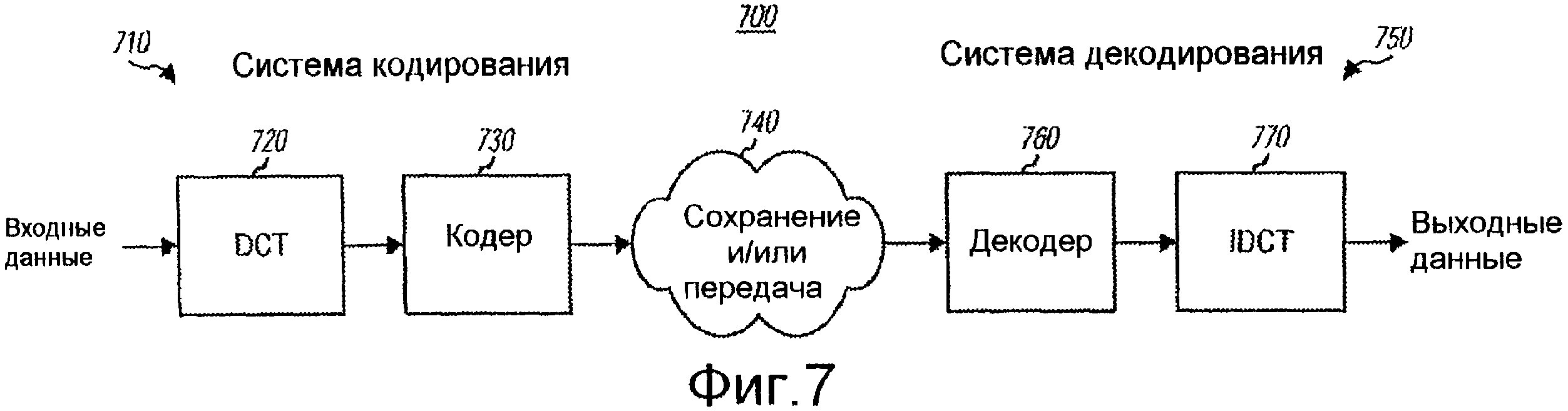
Фиг. 7 изображает блок-схему системы кодирования и декодирования изображения/видео.

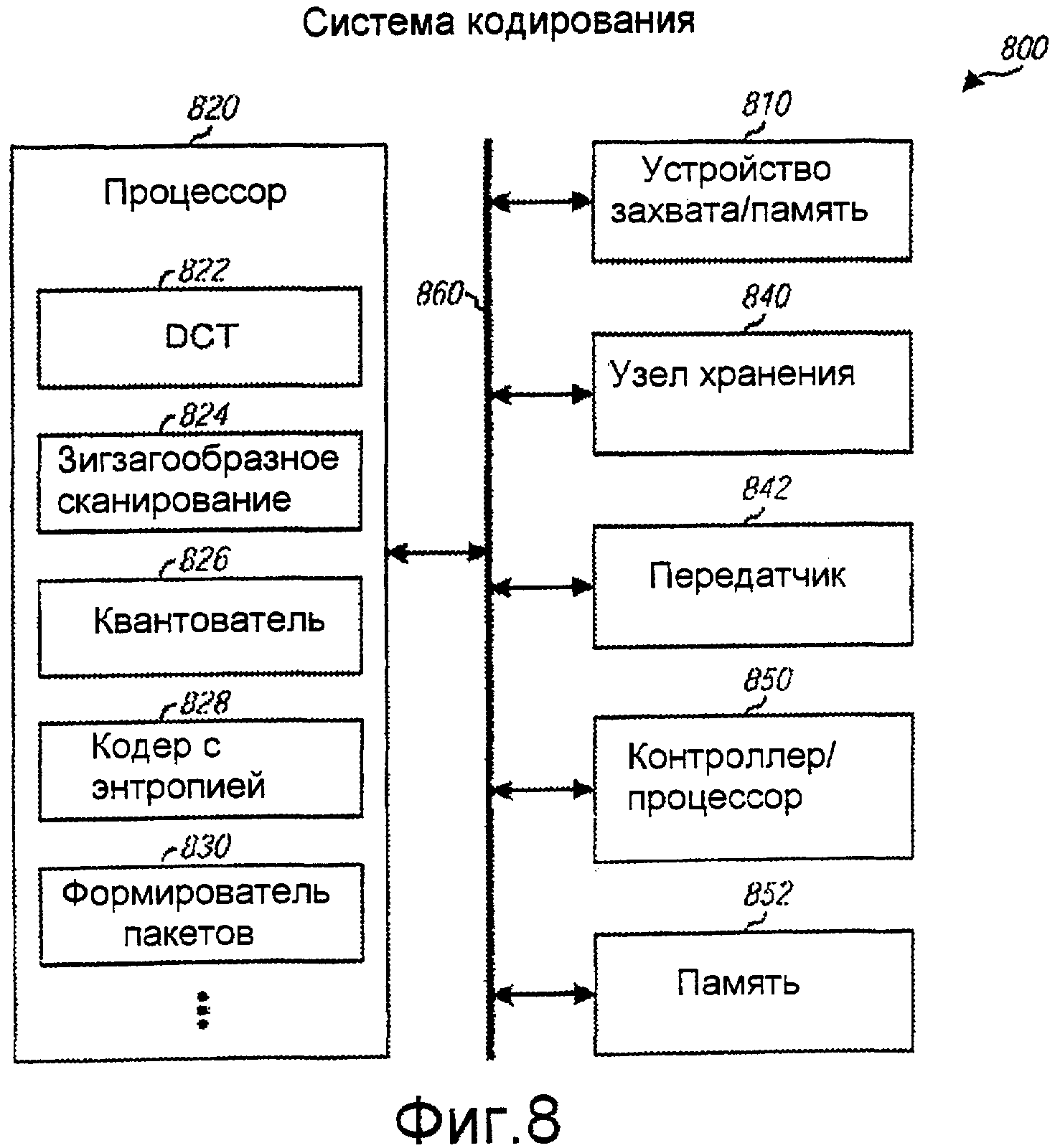
Фиг. 8 изображает блок-схему системы кодирования.

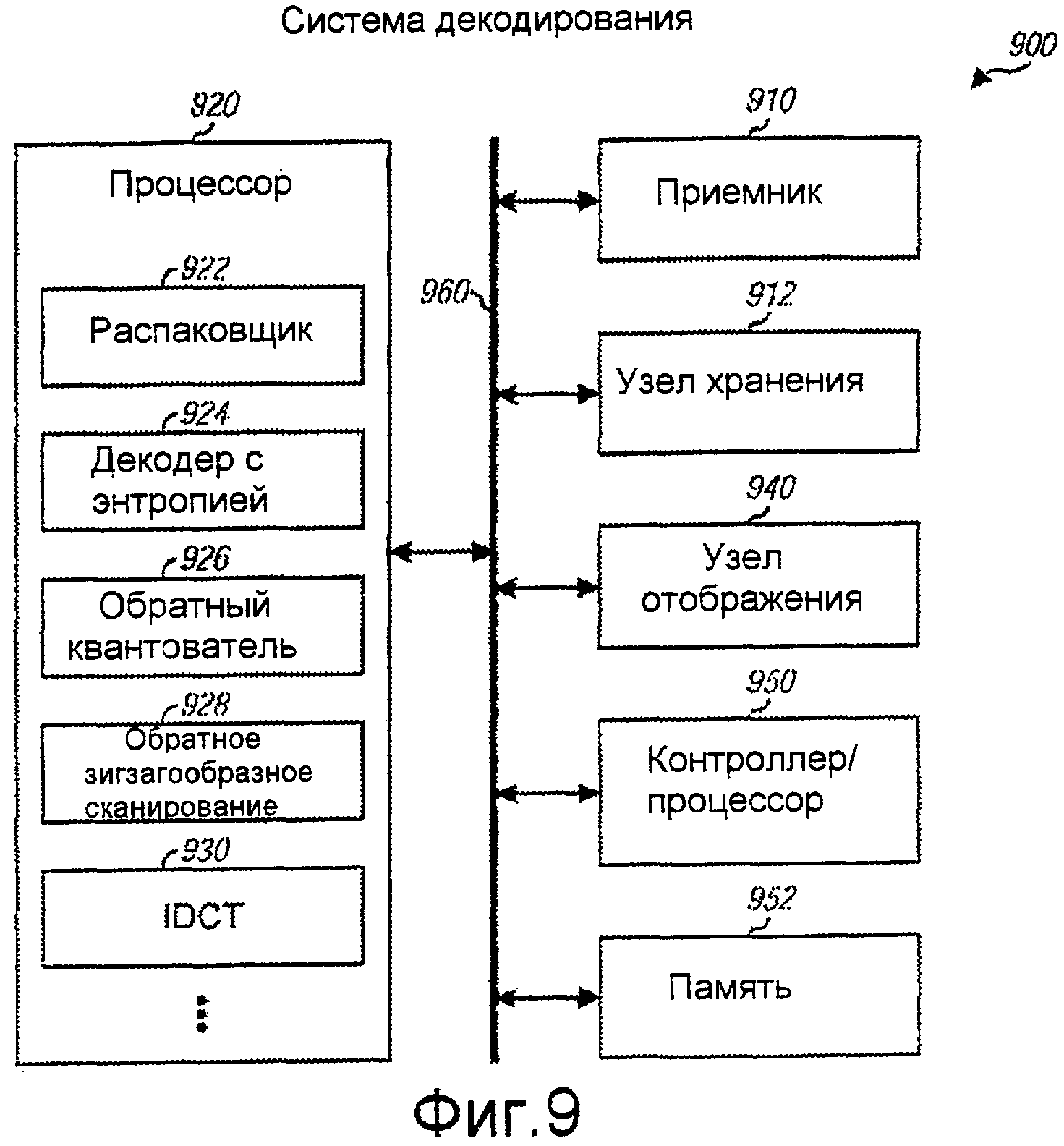
Фиг. 9 изображает блок-схему системы декодирования.

Подробное описание

Способы, описанные в настоящей заявке, могут быть использованы для различных типов преобразований, таких как DCT, IDCT, дискретное преобразование Фурье (DFT), обратное DFT (IDFT), модулированное преобразование с перекрытием (MLT), обратное MLT, модулированное комплексное преобразование с перекрытием (MCLT), обратное MCLT и т.д. Способы также могут быть использованы для различных применений, таких как обработка изображения, видео и аудио, связь, вычисление, передача данных по сети, хранение данных, графика и т.д. Обычно способы могут быть использованы для любых применений, которые используют преобразование. Для пояснения способы описаны ниже для DCT и IDCT, которые обычно используют при обработке изображения и видео.

Одномерное (1D) N-точечное DCT и 1D N-точечное IDCT типа II могут быть определены следующим образом:

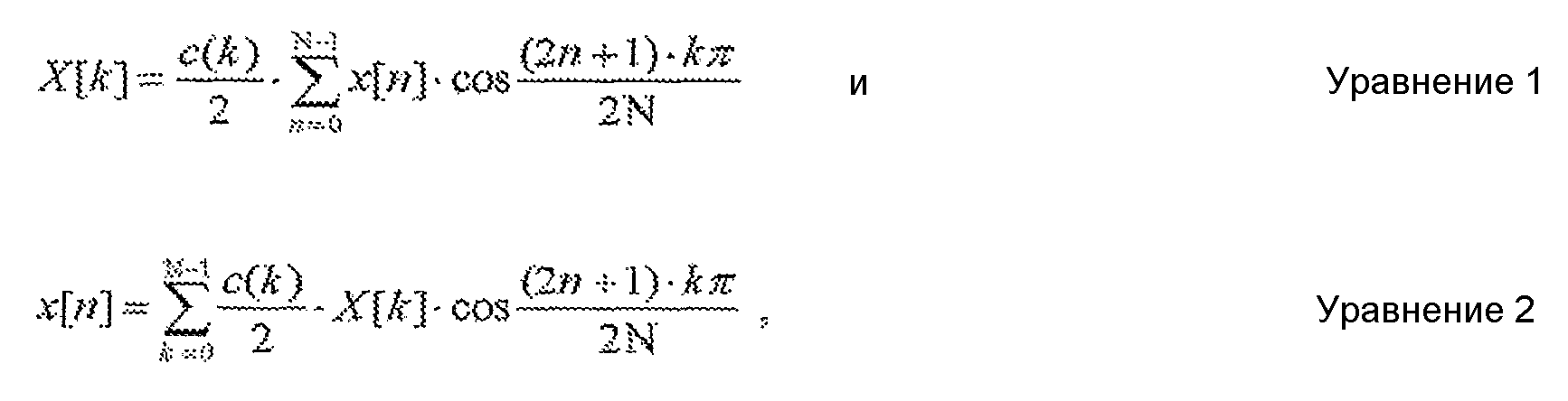
где

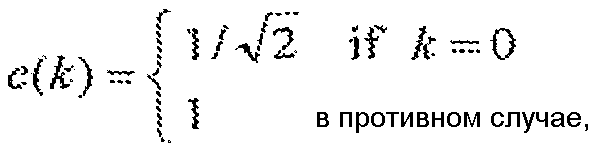
x[n] - 1D функция пространственной области определения, а

X[k] - 1D функция частотной области определения.

1D DCT в уравнении (1) оперирует N величинами пространственной области с x[0] по x[N-1] и генерирует N коэффициентов преобразования с X[0] по X[N-1]. 1D IDCT в уравнении (2) оперирует N коэффициентами преобразования и генерирует N величин пространственной области определения. DCT типа II является одним типом преобразования, и его обычно считают одним из наиболее эффективных преобразований среди нескольких преобразований уплотнения энергии, предложенных для сжатия изображения/видео.

1D DCT может быть использовано для 2D DCT, как описано ниже. Подобным образом, 1D IDCT может быть использовано для 2D IDCT. При декомпозиции 2D DCT/IDCT в каскад 1D DCT/IDCT эффективность 2D DCT/IDCT зависит от эффективности 1D DCT/IDCT. Обычно 1D DCT и 1D IDCT могут быть выполнены относительно любого размера вектора, а 2D DCT и 2D IDCT могут быть выполнены относительно любого размера блока. Однако DCT 8×8 и IDCT 8×8 обычно используют для обработки изображения и видео, когда N равно 8. Например, DCT 8×8 и IDCT 8×8 используют как стандартные компоновочные блоки в различных стандартах кодирования изображения и видео, таких как JPEG, MPEG-1, MPEG-2, MPEG-4 (P.2), H.261, H.263 и т.д.

1D DCT и 1D IDCT могут быть осуществлены в их исходных формах в уравнениях (1) и (2) соответственно. Однако существенное уменьшение вычислительной сложности может быть реализовано с помощью нахождения факторизаций, что дает в результате как можно меньшее число умножений и сложений. Факторизация для преобразования может быть представлена с помощью граф-схемы, которая указывает конкретные операции, выполняемые для этого преобразования.

Фиг. 1 изображает граф-схему 100 типичной факторизации 8-точечного IDCT. В граф-схеме 100 каждое сложение представлено с помощью символа

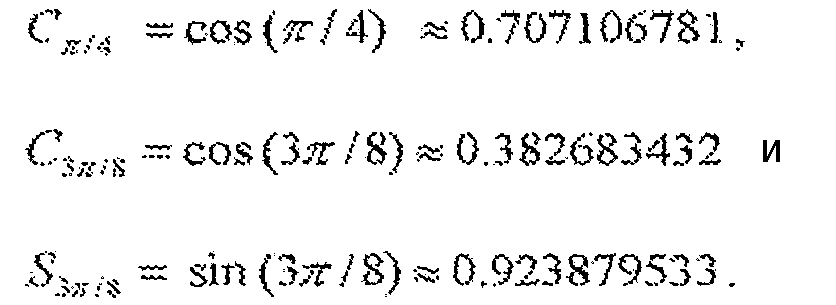
Граф-схема 100 принимает восемь масштабированных коэффициентов преобразования c A₀·X[0] и A₇·X[7], выполняет 8-точечное IDCT относительно этих множителей и генерирует восемь выходных выборок с x[0] по x[7]. A₀ по A₇ являются масштабными множителями, и их задают следующим образом:

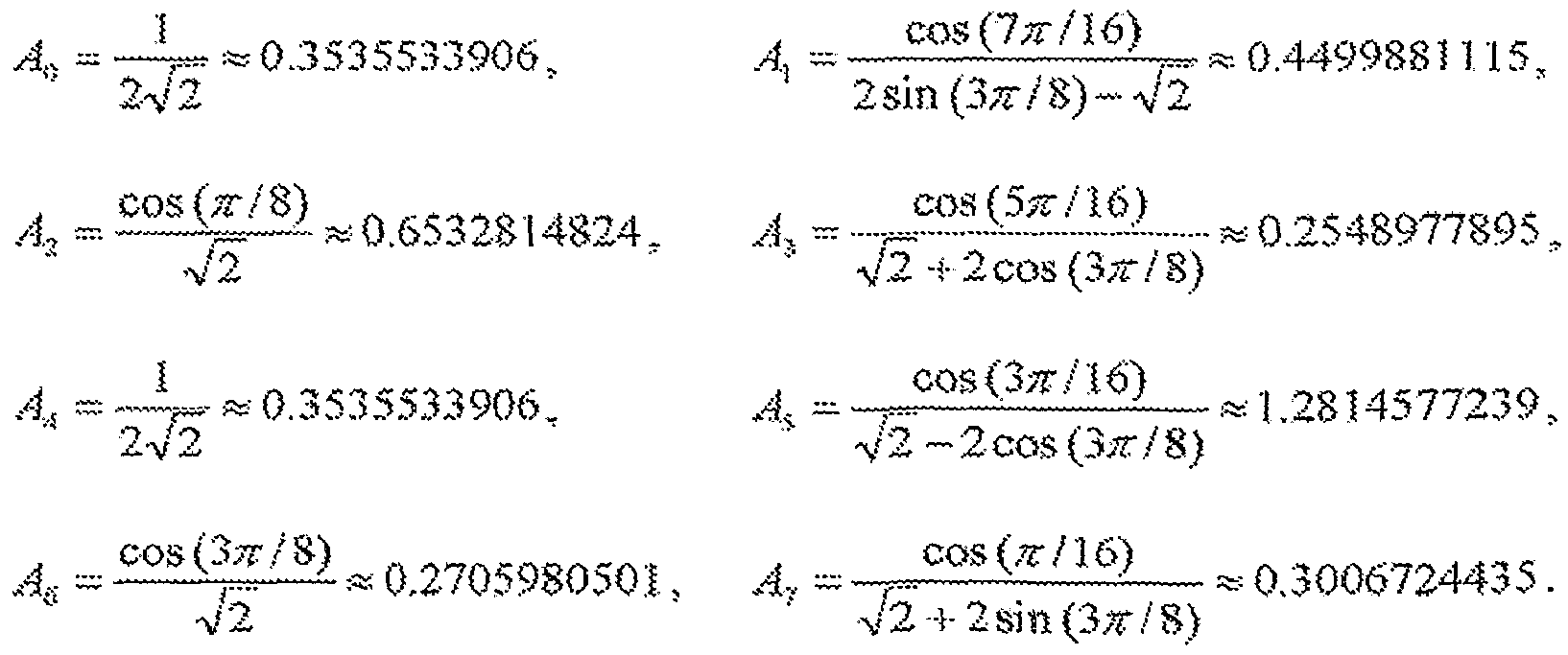
Граф-схема 100 включает в себя некоторое число операций бабочки. Операция бабочки принимает две входные величины и генерирует две выходные величины, где одна выходная величина является суммой двух входных величин, а другая выходная величина является разностью двух входных величин. Например, операция бабочки относительно входных величин A₀·X[0] и A₄·X[4] генерирует выходную величину A₀·X[0]+A₄·X[4] для верхней ветви и выходную величину A₀·X[0] - A₄·X[4] для нижней ветви.

Фиг. 2 изображает граф-схему 200 типичной факторизации 8-точечного DCT. Граф-схема 200 принимает восемь входных выборок с x[0] по x[7], выполняет 8-точечное DCT относительно этих входных выборок и генерирует восемь масштабированных коэффициентов преобразования с 8A₀·X[0] по 8A₇·X[7]. Масштабные множители с A₀ по A₇ заданы выше. Факторизация на фиг. 2 имеет шесть умножений на постоянные множители 1/C_¶/4, 2C_3¶/8 и 2S_3¶/8.

Граф-схемы для IDCT и DCT на фиг. 1 и 2 являются подобными и включают в себя умножения, по существу, на одинаковые постоянные множители (с разницей на 1/2). Такое подобие может быть выгодным для осуществления DCT и IDCT в интегральной схеме. В частности, подобие может дать возможность экономии площади кремния или кристалла, чтобы осуществить операции бабочки и умножения с константами преобразования, которые используются как в прямом, так и в обратном преобразовании.

Факторизация, изображенная на фиг. 1, дает в результате в общей сложности 6 умножений и 28 сложений, которых существенно меньше, чем число умножений и сложений, необходимых для прямого вычисления уравнения (2). Факторизация, изображенная на фиг. 2, также дает в результате в общей сложности 6 умножений и 28 сложений, которых существенно меньше, чем число умножений и сложений, необходимых для прямого вычисления уравнения (1). Факторизация на фиг. 1 выполняет поворот плоскости относительно двух промежуточных переменных с C_3¶/8 и S_3¶/8. Факторизация на фиг. 2 выполняет поворот плоскости относительно двух промежуточных переменных с 2C_3¶/8 и 2S_3¶/8. Поворот плоскости достигается с помощью умножения промежуточной переменной как на синус, так и на косинус, например cos(3¶/8) sin(3¶/8) на фиг. 1. Умножения для поворота плоскости могут быть эффективно выполнены с использованием способов вычислений, описанных ниже.

Фиг. 1 и фиг. 2 изображают типичные факторизации 8-точечного IDCT и 8-точечного DCT соответственно. Эти факторизации предназначены для масштабированного IDCT и масштабированного DCT, где “масштабированный” относится к масштабированию коэффициентов преобразования с X[0] по X[7] с помощью известных масштабных множителей c A₀ по A₇ соответственно. Другие факторизации также получены с помощью использования преобразований в другие известные быстрые алгоритмы, такие как алгоритм DFT Кули-Туки, или с помощью применения систематических процедур факторизации, таких как децимация по времени или децимация по частоте. Обычно факторизация уменьшает число умножений, но не исключает их.

Умножения на фиг. 1 и фиг. 2 выполняют на иррациональные константы, представляющие синус и косинус разных углов, которые являются кратными ¶/8 для 8-точечных DCT и IDCT. Иррациональная константа является константой, которая не является отношением двух целых. Умножения на иррациональные константы могут быть более эффективно выполнены в целочисленной арифметике с фиксированной точкой, когда каждую иррациональную константу аппроксимируют с помощью рациональной двоичной константы. Рациональная двоичная константа является рациональной константой с двоичным знаменателем и имеет вид c/2^b, где b и c - целые и b>0. Умножение целой переменной на рациональную двоичную константу может быть выполнено с помощью логических и арифметических операций, как описано ниже. Число логических и арифметических операций зависит от способа, с помощью которого выполняют вычисление, а также от величины рациональной двоичной константы.

В одном аспекте общие множители используют для того, чтобы уменьшить общее число операций для преобразования и/или чтобы увеличить точность результатов преобразований. Общий множитель является константой, которую применяют к одной или более промежуточным переменным в преобразовании. Промежуточная переменная также может быть упомянута как величина данных и т.д. Общий множитель может быть поглощен одной или более константой преобразования, а также может быть вычислен с помощью изменения одного или более масштабных множителей. Общий множитель может улучшить аппроксимацию одной или более (иррациональных) констант преобразования с помощью одной или более рациональных двоичных констант, что может затем дать в результате меньшее общее число операций и/или повышенную точность.

Обычно любое число общих множителей может быть использовано для преобразования и каждый общий множитель может быть применен к любому числу промежуточных переменных в преобразовании. В одной конструкции множество общих множителей используют для преобразования и применяют к множеству групп промежуточных переменных разных размеров. В другой конструкции множество общих множителей применяют к множеству групп промежуточных переменных одного и того же размера.

Фиг. 3 изображает граф-схему 300 8-точечного IDCT с общими множителями. Граф-схема 300 использует ту же самую факторизацию, что и граф-схема 100 на фиг. 1. Однако граф-схема 300 использует два общих множителя для двух групп промежуточных переменных.

Первый общий множитель F₁ применяют к первой группе из двух промежуточных переменных X₁ и X₂, которую генерируют на основании коэффициентов преобразования X[2] и X[6]. Первый общий множитель F₁ умножают на X₁, поглощают с помощью константы преобразования C_¶/4 и рассчитывают с помощью изменения масштабных множителей А₂ и А₆. Второй общий множитель F₂ применяют ко второй группе из четырех промежуточных переменных с X₃ по X₆, которую генерируют на основании коэффициентов преобразования X[1], X[3], X[5] и X[7]. Второй общий множитель F₂ умножают на X₄, поглощают с помощью констант преобразования С_¶/4, C_3¶/8 и S_3¶/8 и рассчитывают с помощью изменения масштабных множителей A₁, A₃, А₅ и А₇.

Первый общий множитель F₁ может быть аппроксимирован с помощью рациональной двоичной константы α₁, которая может быть умножена на X₁, чтобы получить аппроксимацию произведения X₁·F₁. Масштабированный множитель преобразования F₁·С_¶/4 может быть аппроксимирован с помощью рациональной двоичной константы β₁, которая может быть умножена на X₂, чтобы получить аппроксимацию произведения X₂·F₁·С_¶/4. Измененный масштабный множитель A₂/F₁ может быть применен к коэффициенту преобразования X[2]. Измененный масштабный множитель A₆/F₁ может быть применен к коэффициенту преобразования X[6].

Второй общий множитель F₂ может быть аппроксимирован с помощью рациональной двоичной константы α₂, которая может быть умножена на X₄, чтобы получить аппроксимацию произведения X₄·F₂. Масштабированный множитель преобразования F₂·С_¶/4 может быть аппроксимирован с помощью рациональной двоичной константы β₂, которая может быть умножена на X₃, чтобы получить аппроксимацию произведения X₃·F₂·С_¶/4. Масштабированный множитель преобразования F₂·С_3¶/8 может быть аппроксимирован с помощью рациональной двоичной константы γ₂, а масштабированный множитель преобразования F₂·S_3¶/8 может быть аппроксимирован с помощью рациональной двоичной константы δ₂. Рациональная двоичная константа γ₂, может быть умножена на X₅, чтобы получить аппроксимацию произведения X₅·F₂·С_3¶/8, а также на X₆, чтобы получить аппроксимацию произведения X₆·F₂·С_3¶/8. Рациональная двоичная константа δ₂ может быть умножена на X₅, чтобы получить аппроксимацию произведения X₅·F₂·S_3¶/8, а также на X₆, чтобы получить аппроксимацию произведения X₆·F₂·S_3¶/8. Измененные масштабные множители A₁/F₂, A₃/F₂, A₅/F₂ и A₇/F₂ могут быть применены к коэффициентам преобразования X[1], X[3], X[5] и X[6] соответственно.

Шесть рациональных двоичных констант α₁, β₁, α₂, β₂, γ₂ и δ₂ могут быть определены для шести констант следующим образом:

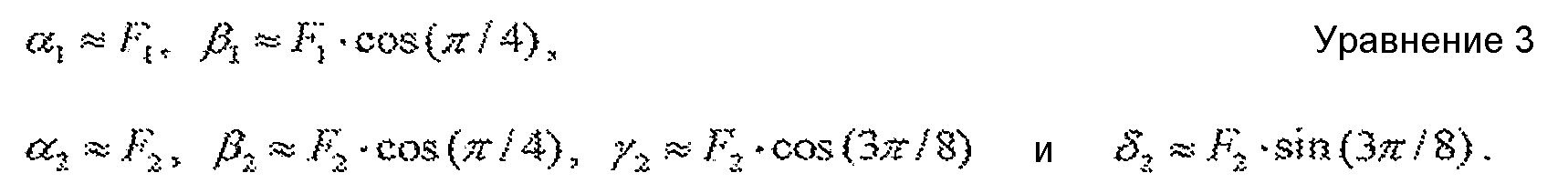
Фиг. 4 изображает граф-схему 400 8-точечного DCT с общими множителями. Граф-схема 400 использует ту же самую факторизацию, что и граф-схема 200 на фиг. 2. Однако граф-схема 400 использует два общих множителя для двух групп промежуточных переменных.

Первый общий множитель F_a применяют к первой группе из двух промежуточных переменных X_a и X_b, которую используют, чтобы генерировать коэффициенты преобразования X[2] и X[6]. Первый общий множитель F_a умножают на X_a, поглощают с помощью константы преобразования 1/C_¶/4 и вычисляют с помощью изменения масштабных множителей А₂ и А₆. Второй общий множитель F_b применяют ко второй группе из четырех промежуточных переменных с X₀ по X_f, которую используют, чтобы генерировать коэффициенты преобразования X[1], X[3], X[5] и X[7]. Второй общий множитель F_b умножают на X_d, поглощают с помощью констант преобразования 1/C_¶/4, 2C_3¶/8 и 2S_3¶/8 и рассчитывают с помощью изменения масштабных множителей A₁, A₃, А₅ и А₇.

Первый общий множитель F_а может быть аппроксимирован с помощью рациональной двоичной константы α_а, которая может быть умножена на X_а, чтобы получить аппроксимацию произведения X_a·F_a. Масштабированный множитель преобразования F_a/С_¶/4 может быть аппроксимирован с помощью рациональной двоичной константы β_а, которая может быть умножена на X_b, чтобы получить аппроксимацию произведения X_b·F_a/С_¶/4. Измененные масштабные множители A₂/F_a и A₆/F_a могут быть применены к коэффициентам преобразования X[2] и X[6] соответственно.

Второй общий множитель F_b может быть аппроксимирован с помощью рациональной двоичной константы α_b, которая может быть умножена на X_d, чтобы получить аппроксимацию произведения X_d·F_b. Масштабированный множитель преобразования F_b/С_¶/4 может быть аппроксимирован с помощью рациональной двоичной константы β_b, которая может быть умножена на X_c, чтобы получить аппроксимацию произведения X_c·F_b/С_¶/4. Масштабированный множитель преобразования 2F_b·С_3¶/8 может быть аппроксимирован с помощью рациональной двоичной константы γ_b, а масштабированный множитель преобразования 2F_b·S_3¶/8 может быть аппроксимирован с помощью рациональной двоичной константы δ_b. Рациональная двоичная константа γ_b может быть умножена на X_e, чтобы получить аппроксимацию произведения 2X_e·Fb·С_3¶/8, а также на X_f, чтобы получить аппроксимацию произведения 2X_f·F_b·С_3¶/8. Рациональная двоичная константа δ_b может быть умножена на X_c, чтобы получить аппроксимацию произведения 2X_c·F_b·S_3¶/8, а также на X_f, чтобы получить аппроксимацию произведения 2X_f·F_b·S_3¶/8. Измененные масштабные множители A₁/F_b, A₃/F_b, A₅/F_b и A₇/F_b могут быть применены к коэффициентам преобразования X[1], X[3], X[5] и X[7] соответственно.

Шесть рациональных двоичных констант α_а, β_а, α_b, β_b, γ_b и δ_b могут быть определены для шести констант следующим образом:

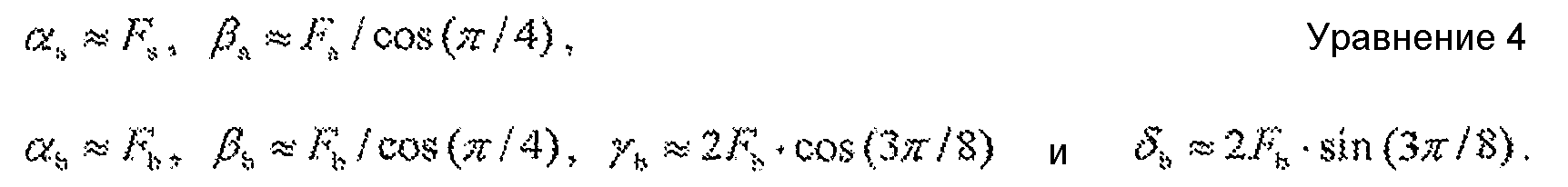
Фиг. 3 и фиг. 4 изображают типичное использование общих множителей для конкретных факторизаций 8-точечного IDCT и 8-точечного DCT, соответственно. Общие множители могут быть использованы для других факторизаций DCT и IDCT, а также для других типов преобразований. Обычно общий множитель может быть применен к группе, по меньшей мере, из одной промежуточной переменной в преобразовании. Эта группа промежуточной переменной (переменных) может быть сгенерирована из группы входных величин (например, как изображено на фиг. 3) или использована, чтобы сгенерировать группу выходных величин (например, как изображено на фиг. 4). Общий множитель может быть вычислен с помощью масштабных множителей, примененных к входным величинам или выходным величинам.

Множество общих множителей может быть применено к множеству групп промежуточных переменных, и каждая группа может включать в себя любое число промежуточных переменных. Выбор групп может зависеть от различных факторов, таких как факторизация преобразования, где константы преобразования находятся в преобразовании и т.д. Множество общих множителей может быть применено к множеству групп промежуточных переменных одного и того же размера (не изображено на фиг. 3 и фиг. 4) или разных размеров (как изображено на фиг. 3 и фиг. 4). Например, три общих множителя могут быть использованы для факторизации, изображенной на фиг. 3, причем первый общий множитель применен к промежуточным переменным X₁ и X₂, второй общий множитель применен к промежуточным переменным X₃, X₄, X₅ и X₆, а третий промежуточный множитель применен к двум промежуточным переменным, сгенерированным из X[0] и X[4].

Умножение промежуточной переменной x на рациональную двоичную константу u может быть выполнено различными способами в целочисленной арифметике с фиксированной точкой. Умножение может быть выполнено с использованием логических операций (например, сдвиг влево, сдвиг вправо, инверсия бит и т.д.), арифметических операций (например, сложение, вычитание, инверсия знака и т.д.) и/или других операций. Число логических и арифметических операций, необходимых для умножения x на u, зависит от способа, которым выполняют вычисление, и величины рациональной двоичной константы u. Разные способы вычисления могут потребовать разное число логических и арифметических операций для одного и того же умножения x на u. Данный способ вычисления может потребовать разное число логических и арифметических операций для умножения x на разные величины u.

Общий множитель может быть выбран для группы промежуточных переменных на основании критериев, таких как:

число логических и арифметических операций, чтобы выполнить умножение, и

точность результатов.

Обычно желательно минимизировать число логических и арифметических операций, необходимых для умножения промежуточной переменной на рациональную двоичную константу. В некоторых платформах аппаратного обеспечения арифметические операции (например, сложения) могут быть более сложными, чем логические операции, таким образом, уменьшение числа арифметических операций может быть более важным. В предельном случае вычислительная сложность может быть количественно оценена на основании только числа арифметических операций, без учета логических операций. В некоторых других платформах аппаратного обеспечения логические операции (например, сдвиги) могут быть более дорогими и уменьшение числа логических операций (например, уменьшение числа операций сдвига и/или полного числа сдвинутых бит) может быть более важным. Обычно может быть использовано взвешенное среднее число логических и арифметических операций, где веса могут представлять относительные сложности логических и арифметических операций.

Точность результатов количественно может быть оценена на основании различных показателей, таких как показатели, приведенные в таблице 6 ниже. Обычно желательно уменьшить число логических и арифметических операций (или вычислительной сложности) для данной точности. Также может быть желательным принимать компромиссное решение в пользу сложности ради точности, например, чтобы достичь более высокой точности за счет некоторых дополнительных операций.

Как изображено на фиг. 3 и фиг. 4, для каждого общего множителя умножение может быть выполнено относительно группы промежуточных переменных на группу рациональных двоичных констант, который аппроксимирует группу, по меньшей мере, из одной иррациональной константы (по меньшей мере, для одного коэффициента преобразования), масштабированной с помощью этого общего множителя. Умножение в целочисленной арифметике с фиксированной точкой может быть выполнено различными способами. Для пояснения способы вычисления, которые выполняют умножение с помощью операций сдвига и сложения и с использованием промежуточных результатов, описаны ниже. Эти способы вычисления могут уменьшить общее число операций сдвига и сложения для DCT и IDCT.

Умножение целой переменной x на иррациональную константу μ в целочисленной арифметике с фиксированной точкой может быть выполнено с помощью аппроксимации иррациональной константы с помощью рациональной двоичной константы следующим образом:

где μ - аппроксимируемая иррациональная константа, c/2^b - рациональная двоичная константа, b и с - целые и b>0.

Если дана целая переменная x и рациональная двоичная константа u = c/2^b, целочисленное произведение

может быть аппроксимировано с использованием последовательности промежуточных величин

где y₀=0, y₁=x, и для всех величин 2≤i≤t величины y_t получают следующим образом:

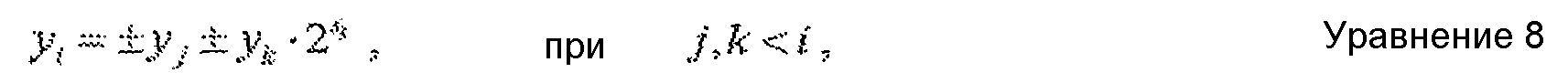
где y_k·2^Si предполагает либо сдвиг влево, либо сдвиг вправо (в зависимости от знака константы s_i) промежуточной величины y_k на |s_i| бит.

В уравнении (8) y_i может быть равно y_j+y_k2^xt, y_j-y_k2^Si или -y_j+y_k2^xt. Каждая промежуточная величина y_j в последовательности может быть получена на основании двух предыдущих промежуточных величин y_j и y_k в последовательности, где либо y_j, либо y_k может быть равна нулю. Каждая промежуточная величина y_i может быть получена с помощью одного сдвига и/или одного сложения. Сдвиг не требуется, если s_i равно нулю. Сложение не требуется, если y_j=y₀=0. Полное число сложений и сдвигов для умножения определяют с помощью числа промежуточных величин в последовательности, которое равно t, а также выражения, используемого для каждой промежуточной величины. Умножение на рациональную двоичную константу u, по существу, развертывают в последовательность операций сдвига и сложения. Последовательность определяют таким образом, что конечная величина в последовательности становится желаемым целочисленным произведением, или

Как изображено в уравнениях с (5) по (9), умножение целой переменной x на иррациональную константу μ может быть аппроксимировано с помощью последовательности промежуточных величин, сгенерированных с помощью операций сдвига и сложения, и использования промежуточных результатов (или предварительно сгенерированных промежуточных величин), чтобы уменьшить полное число операций.

Умножение целой переменной x на две иррациональные константы μ и η в целочисленной арифметике с фиксированной точкой может быть выполнено с помощью аппроксимации иррациональных констант с помощью рациональных двоичных констант следующим образом:

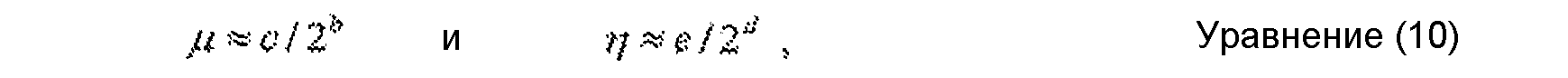
где C/2^b и e/2^d - две рациональные двоичные константы, b, c, d и e - целые, b>0 и d>0.

Если заданы целая переменная x и рациональные двоичные константы u = c/2^b и e/2^d, два целочисленных произведения

могут быть аппроксимированы с использованием последовательности промежуточных величин

где w₀=0, w₁=x и для всех величин 2≤i≤t w_i получают следующим образом:

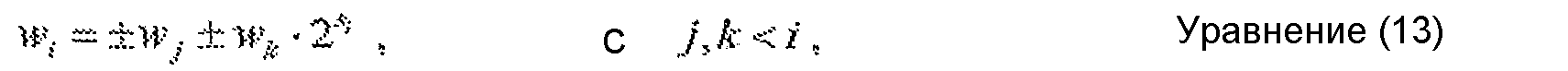
где w_k·2^Si означает сдвиг либо влево, либо вправо w_k на |s_i| бит. Последовательность определяют таким образом, что желаемые целочисленные произведения получают на шагах m и n следующим образом:

где m, n≤t и либо m, либо n равно t.

Как изображено в уравнениях с (10) по (14), умножение целой переменной x на иррациональные константы μ и η может быть аппроксимировано с помощью общей последовательности промежуточных величин, сгенерированных с помощью операций сдвига и сложения, и с использованием промежуточных результатов, чтобы уменьшить полное число операций.

В вычислении, описанном выше, тривиальные операции, такие как сложения и вычитания нулей и сдвиги на ноль бит, могут быть пропущены. Могут быть сделаны следующие упрощения:

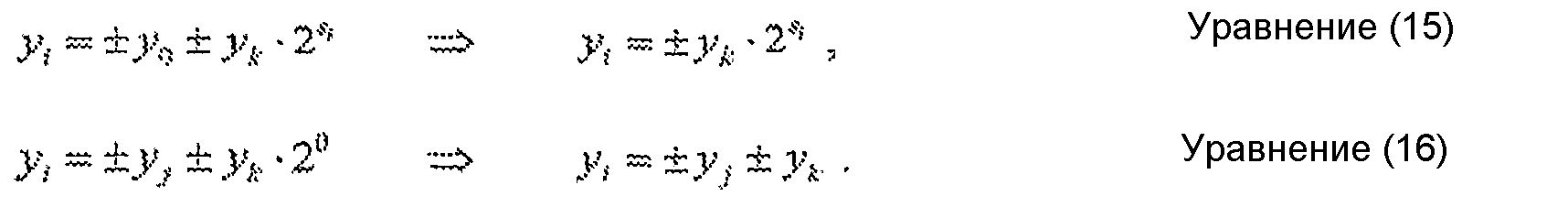
В уравнении (15) выражение слева от “

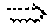
Умножения на фиг. 1 по фиг. 4 могут быть эффективно выполнены с использованием способов вычислений, описанных выше. На фиг. 1 умножение целой переменной x на константу преобразования C_¶/4 в целочисленной арифметике с фиксированной точкой может быть выполнено с помощью аппроксимации константы C_¶/4 с помощью рациональной двоичной константы следующим образом:

где

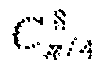
Умножение целой переменной x на константу

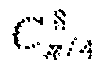
Умножение в уравнении (18) может быть выполнено с помощью следующей последовательности операций:

Двоичная величина справа от “//” является промежуточной константой, которую умножают на переменную x.

Желаемое произведение равно y₄ или y₄=y. Умножение в уравнении (18) может быть выполнено с помощью трех сложений и трех сдвигов, чтобы сгенерировать три промежуточные величины y₂, y₃ и y₄.

На фиг. 1 умножение целой переменной x на константы преобразования C_3¶/8 и S_3¶/8 в целочисленной арифметике с фиксированной точкой может быть выполнено с помощью аппроксимации констант C_3¶/8 и S_3¶/8 рациональными двоичными константами следующим образом:

где

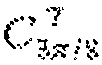
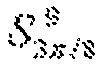
Умножение целой переменной x на константы

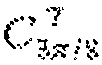
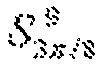
Умножения в уравнении (22) могут быть выполнены с помощью следующей последовательности операций:

Желаемые произведения равны w₆ и w₈ или w₆=y и w₈=z. Два умножения в уравнении (22) могут быть совместно выполнены с помощью пяти сложений и пяти сдвигов, чтобы сгенерировать семь промежуточных величин с w₂ по w₈. Сложения нулей пропущены при генерации w₃ и w₆. Сдвиги на ноль пропущены при генерации w₄ и w₅.

Для 8-точечного IDCT, изображенного на фиг. 1, с использованием способов вычисления, описанных выше для умножений на константы

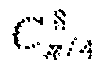
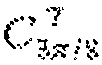
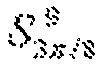
Для 8-точечного DCT, изображенного на фиг. 2, иррациональные константы 1/C_¶/4, C_3¶/8 и S_3¶/8 могут быть аппроксимированы рациональными двоичными константами. Умножения на рациональные двоичные константы могут быть выполнены с использованием способов вычислений, описанных выше.

Для IDCT, изображенного на фиг. 3, разные величины общих множителей F₁ и F₂ могут давать в результате разные полные числа логических и арифметических операций для IDCT и разные уровни точности для выходных выборок с x[0] по x[7]. Могут быть оценены разные комбинации величин F₁ и F₂. Для каждой комбинации величин может быть определено полное число логических и арифметических операций для IDCT и точность выходных выборок.

Для данной величины F₁ рациональные двоичные константы α₁ и β₁ могут быть получены для F₁ и F₁·C_¶/4 соответственно. Числа логических и арифметических операций тогда могут быть определены для умножения X₁ на α₁ и умножения X₂ на β₁. Для данной величины F₂ рациональные двоичные константы α₂, β₂, γ₂ и δ₂ могут быть получены для F₂, F₂·C_¶/4, F₂·C_3¶/8 и F₂·S_3¶/8 соответственно. Числа логических и арифметических операций тогда могут быть определены для умножения X₄ на α₂, умножения X₃ на β₂ и умножения X₅ как на γ₂, так и на δ₂. Число операций, необходимых для умножения X₆ на γ₂ и δ₂, равно числу операций, необходимых для умножения X₅ на γ₂ и δ₂.

Чтобы облегчить оценку и выбор общих множителей, число логических и арифметических операций может быть предварительно вычислено для умножения на разные возможные величины рациональных двоичных констант. Предварительно вычисленное число логических и арифметических операций может быть сохранено в справочной таблице или в некоторой другой структуре данных.

Фиг. 5 изображает справочную таблицу 500, которая хранит числа логических и арифметических операций, необходимых для умножения на разные величины рациональных двоичных констант. Справочная таблица 500 является двумерной таблицей с разными возможными величинами первой рациональной двоичной константы C₁ по горизонтальной оси и разными возможными величинами второй рациональной двоичной константы C₂ по вертикальной оси. Число возможных величин для каждой рациональной двоичной константы зависит от числа бит, использованных для константы. Например, если C₁ представлена с помощью 13 бит, тогда имеется 8192 возможные величины для C₁. Возможные величины для каждой рациональной двоичной константы обозначены как c₀, c₁, c₂, ..., c_M, где - c₀=0, c₁ - наименьшая ненулевая величина, а c_M - максимальная величина (например, c_M=8191 для 13 бит).

Элемент в i-м столбце и j-й строке справочной таблицы 500 содержит число логических и арифметических операций, необходимых для объединенного умножения промежуточной переменной x, как на c_i для первой рациональной двоичной константы C₁, так и на c_j для второй рациональной двоичной константы C₂. Величина для каждого элемента в справочной таблице 500 может быть определена с помощью оценки разных возможных последовательностей промежуточных величин для объединенного умножения на c_i и c_j для этого элемента и выбора наилучшей последовательности, например последовательности с наименьшим числом операций. Элементы в первой строке справочной таблицы 500 (с c₀=0 для второй рациональной двоичной константы C₂) содержат числа операций, необходимых для умножения промежуточной переменной x только на c₁ для первой рациональной двоичной константы C₁. Так как справочная таблица является симметричной, могут быть заполнены элементы только в половине таблицы (например, выше или ниже главной диагонали). Кроме того, число элементов для заполнения может быть уменьшено, если приняты во внимание иррациональные константы, аппроксимируемые с помощью рациональных двоичных констант C₁ и C₂.

Для данной величины F₁ могут быть определены рациональные двоичные константы α₁ и β₁. Число логических и арифметических операций, необходимых для умножения X₁ на α₁ и умножения X₂ на β₁, может быть легко определено из элементов в первой строке справочной таблицы 500, где α₁и β₁соответствуют С₁. Подобным образом для данной величины F₂ могут быть определены рациональные двоичные константы α₂, β₂, γ₂и δ₂. Число логических и арифметических операций, необходимых для умножения X₄ на α₂ и умножения X₃ на β₂, может быть определено из элементов в первой строке справочной таблицы 500, где α₂ и β₂ соответствуют С₁. Число логических и арифметических операций, необходимых для объединенного умножения X₅ на γ₂ и δ₂, может быть определено из соответствующего элемента в справочной таблице 500, где γ₂ может соответствовать С₁, а δ₂ может соответствовать С₂ или наоборот.

Для каждой возможной комбинации величин F₁ и F₂ показатели качества в таблице 6 могут быть определены для достаточного числа итераций с разными случайными входными данными. Величины F₁ и F₂, которые дают в результате низкую точность (например, невыполнение показателей), могут быть отброшены, а величины F₁ и F₂, которые дают в результате хорошую точность (например, проход показателей), могут быть сохранены.

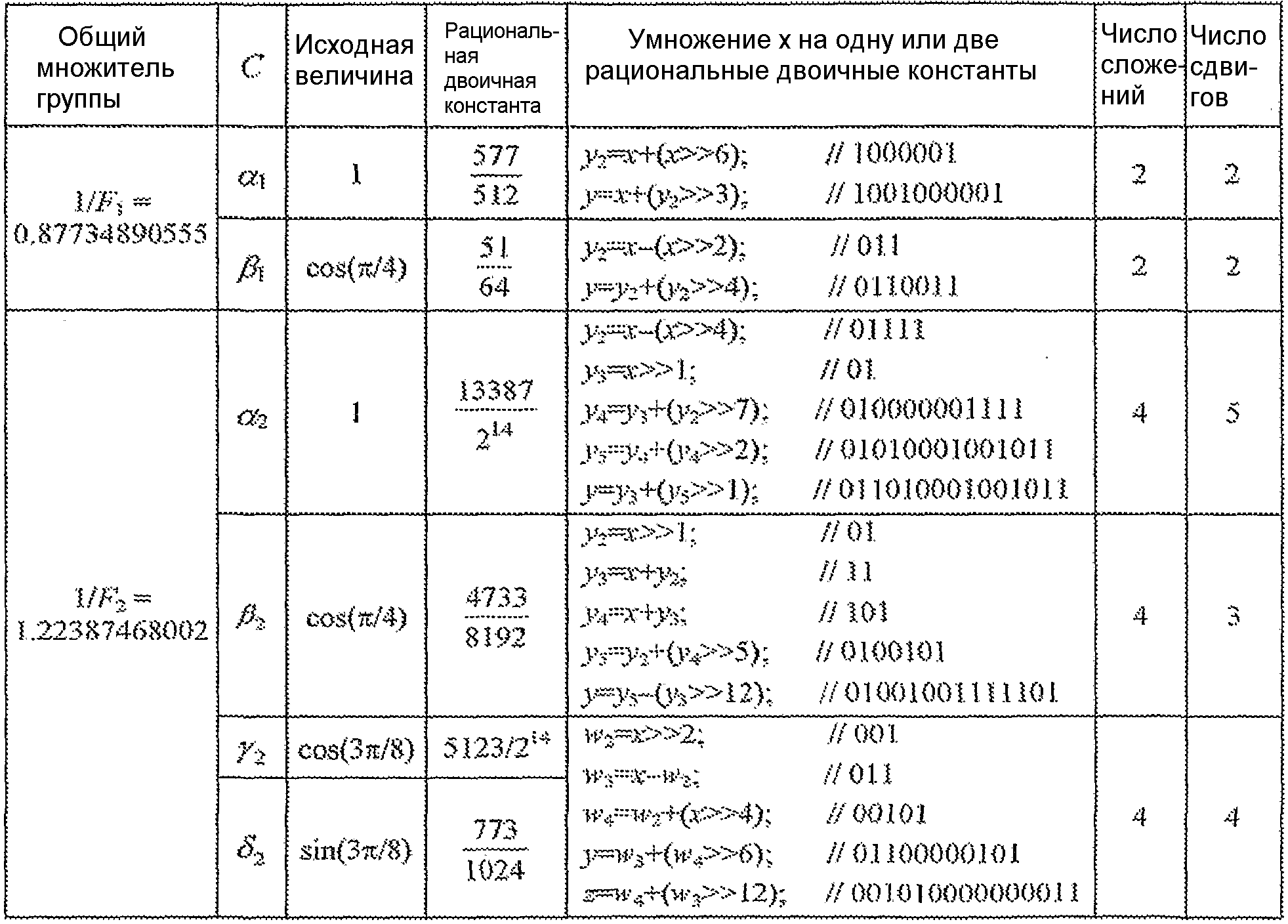
Таблицы с 1 по 5 изображают пять аппроксимаций с фиксированной точкой для IDCT на фиг. 3, которые обозначены как алгоритмы A, B, C, D и E. Эти аппроксимации представлены для двух групп множителей, причем одна группа включает в себя α₁ и β₁, а другая группа включает в себя α₂, β₂, γ₂ и δ₂. Для каждой из таблиц с 1 по 5 общий множитель для каждой группы приведен в первом столбце. Общие множители повышают точность аппроксимаций рациональной двоичной константой и могут быть объединены с соответствующими масштабными множителями в граф-схеме для IDCT. Исходные величины (которые могут быть 1 или иррациональными константами) приведены в третьем столбце. Рациональная двоичная константа для каждой исходной величины, масштабированной с помощью ее общего множителя, приведена в четвертом столбце. Последовательность промежуточных величин для умножения промежуточной переменной x на одну или две рациональные двоичные константы приведена в пятом столбце. Числа операций сложения и сдвига для каждого умножения приведены в шестом и седьмом столбцах соответственно. Полное число операций сложения для IDCT равно сумме всех операций сложения в шестом столбце плюс последний элемент снова (чтобы вычислить умножение для каждого из X₅ и X₆ как на γ₂, так и на δ₂) плюс 28 операций сложения для всех операций, бабочки в граф-схеме. Полное число операций сдвига для IDCT равно сумме всех операций сдвига в последнем столбце плюс снова последний элемент.

Таблица 1 дает детали алгоритма А, который использует общий множитель, равный 1/1,0000442471, для каждой из двух групп.

Таблица 1

Аппроксимация А (42 сложения, 16 сдвигов)

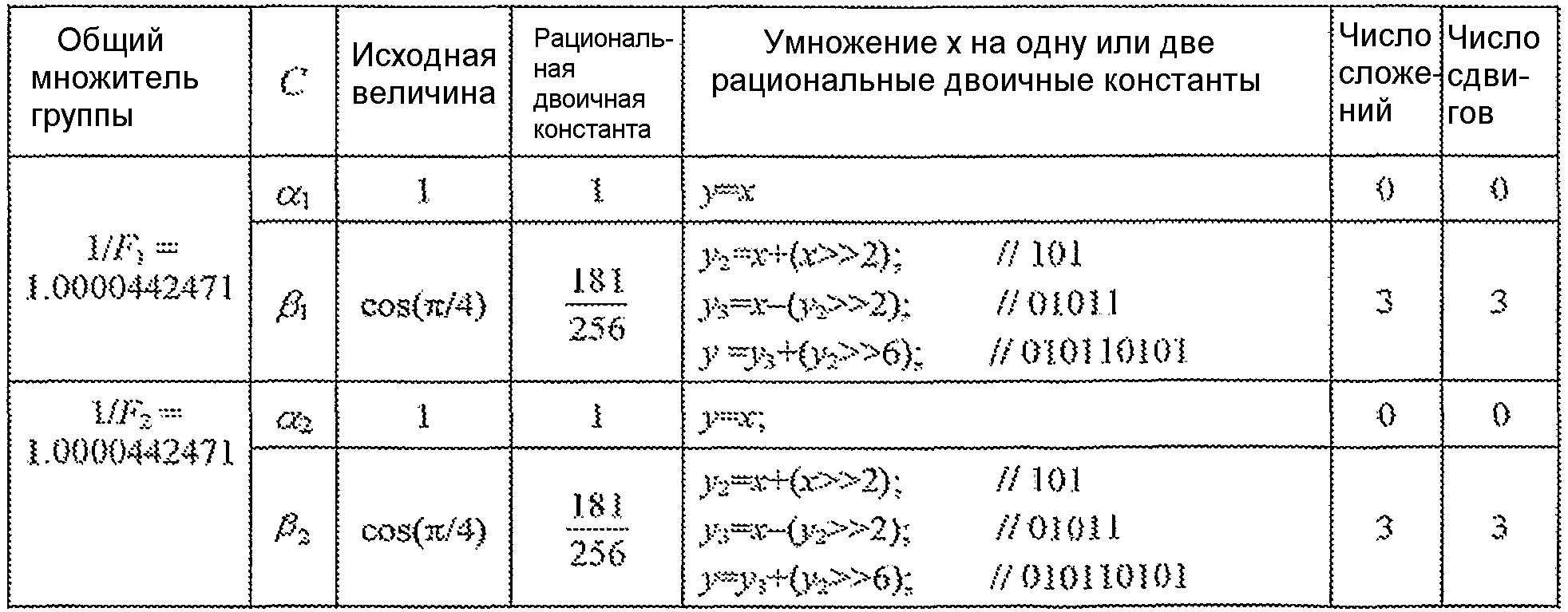
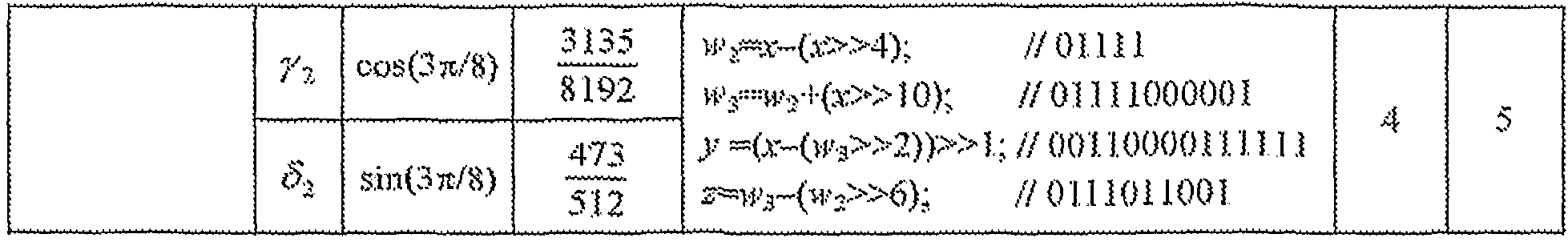
Таблица 2 дает детали алгоритма В, который использует общий множитель, равный 1/1,0000442471, для первой группы и общий множитель, равный 1/1,02053722659, для второй группы.

Таблица 2

Аппроксимация В (43 сложения, 17 сдвигов)

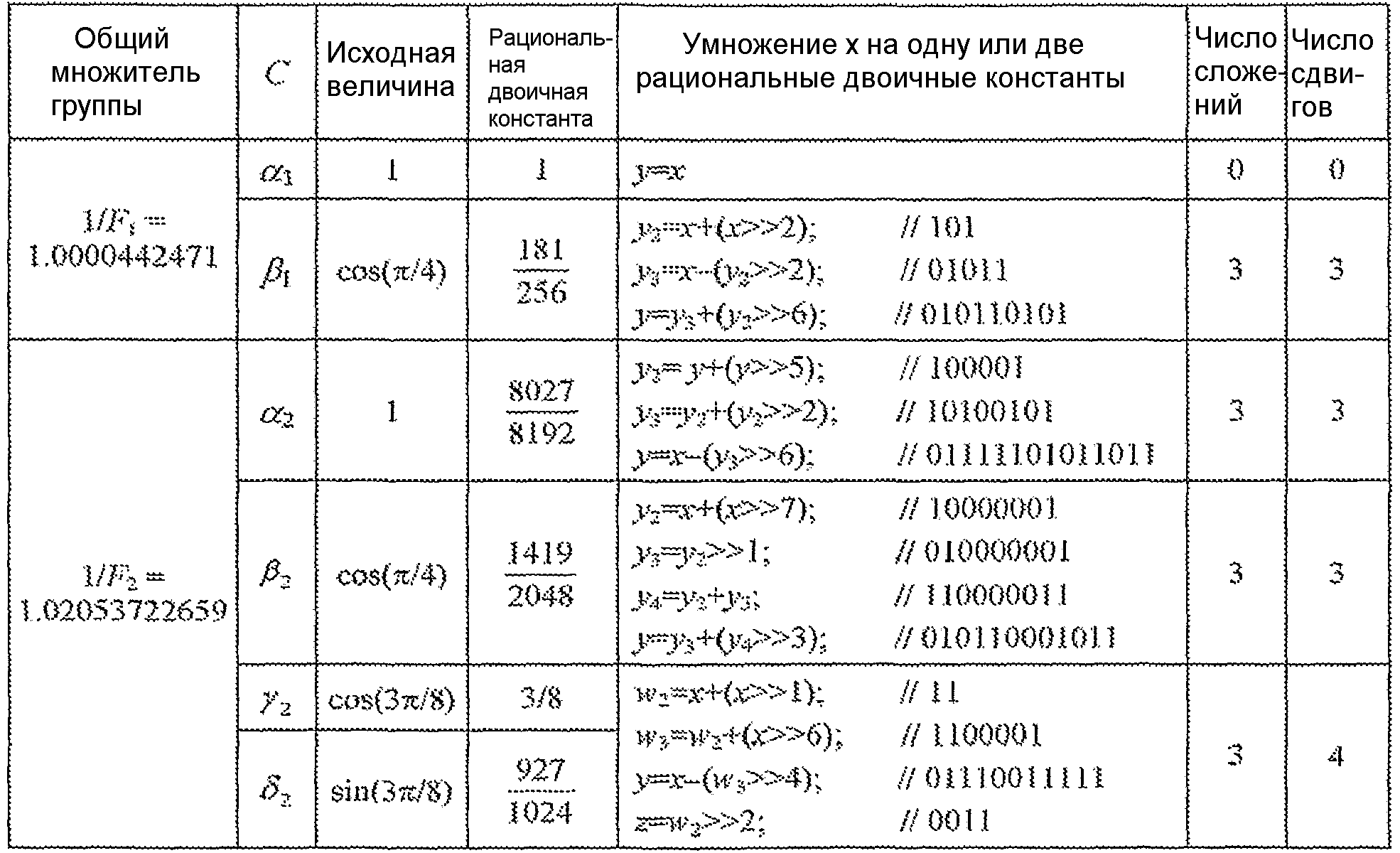
Таблица 3 дает детали алгоритма С, который использует общий множитель, равный 1/0,87734890555, для первой группы и общий множитель, равный 1/1,02053722659, для второй группы.

Таблица 3

Аппроксимация С (44 сложения, 18 сдвигов)

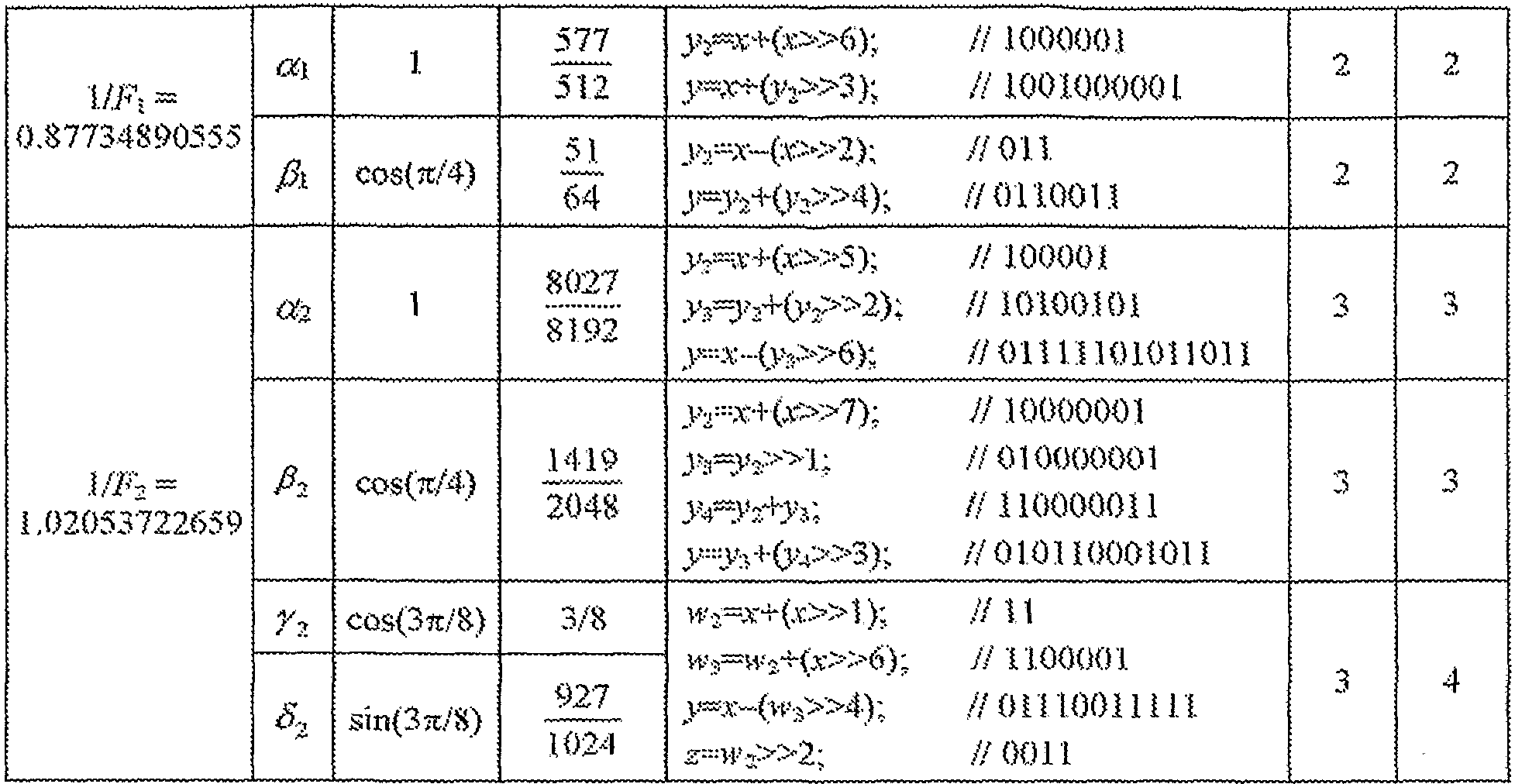
Таблица 4 дает детали алгоритма D, который использует общий множитель, равный 1/0,87734890555, для первой группы и общий множитель, равный 1/0,89062054308, для второй группы.

Таблица 4

Аппроксимация D (45 сложений, 17 сдвигов)

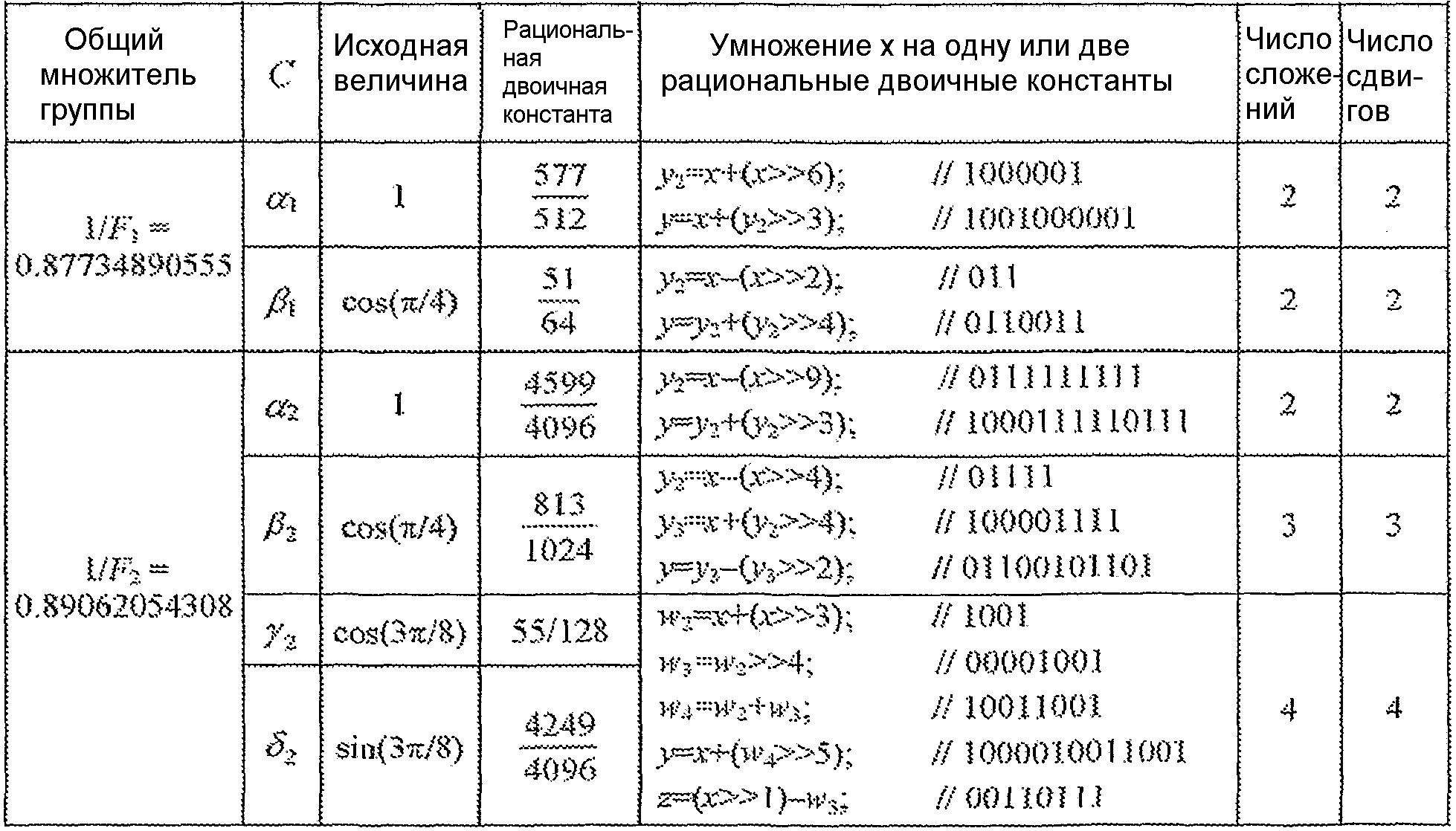
Таблица 5 дает детали алгоритма Е, который использует общий множитель, равный 1/0,87734890555, для первой группы и общий множитель, равный 1/1,22387468002, для второй группы.

Таблица 5

Аппроксимация Е (48 сложений, 20 сдвигов)

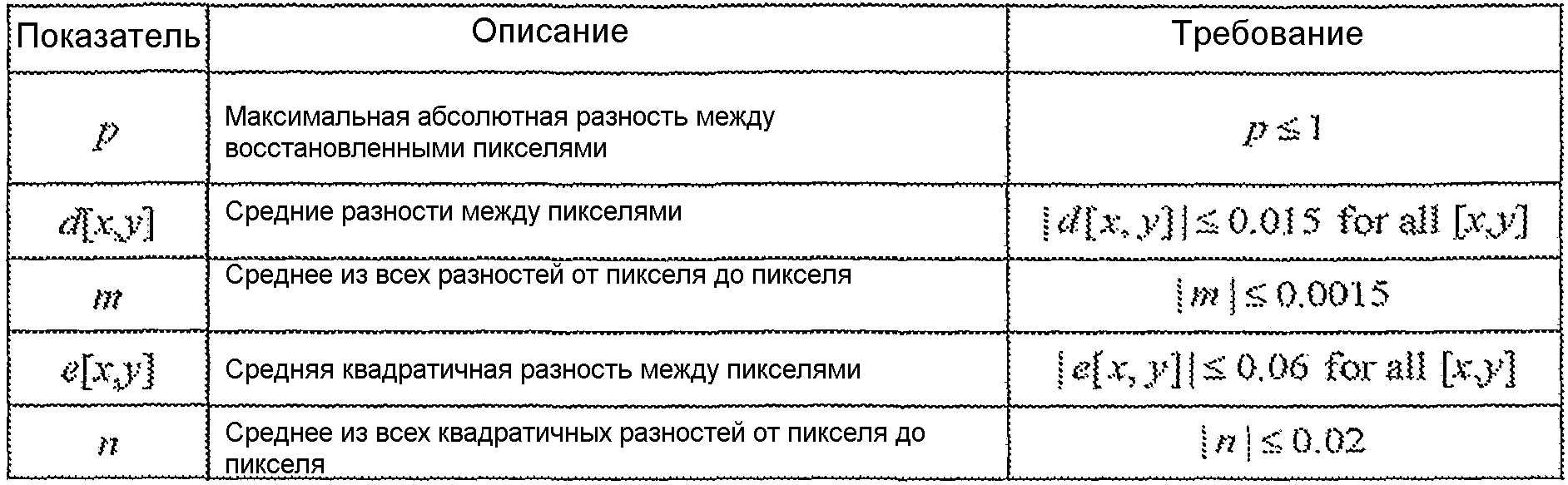
Точность выходных выборок из аппроксимирующего IDCT может быть количественно оценена на основании показателей, определенных в стандарте 1180-1190 IEEE, и в его рассматриваемых заменах. Этот стандарт определяет тестирование эталонного 64-битового DCT с плавающей точкой, за которым следует аппроксимирующее IDCT с использованием данных из генератора случайных чисел. Эталонное DCT принимает случайные данные для блока входных пикселей и генерирует коэффициенты преобразования. Аппроксимирующее IDCT принимает коэффициенты преобразования (округленные соответствующим образом) и генерирует блок восстановленных пикселей. Восстановленные пиксели сравнивают со входными пикселями с использованием пяти показателей, которые приведены в таблице 6. Кроме того, требуется, чтобы аппроксимирующее IDCT выдавало все нули при подаче нулевых коэффициентов преобразования и демонстрировало поведение почти постоянного обратного преобразования. Все пять алгоритмов с А по Е, приведенные выше, проходят все показатели в таблице 6.

Таблица 6

1D IDCT, изображенное на фиг. 3, может быть использовано для 2D IDCT. Подобным образом 1D IDCT, изображенное на фиг. 4, может быть использовано для 2D IDCT.

Фиг. 6 изображает конструкцию 2D IDCT 600, осуществленную масштабированным и разделяемым способом. 2D IDCT 600 содержит входной каскад 612 масштабирования, за которым следует первый каскад 614 масштабированного 1D IDCT для столбцов (или строк), за которым дополнительно следует второй каскад 616 масштабированного 1D IDCT для строк (или столбцов) и заканчивая выходным каскадом 618 масштабирования. Входной каскад 612 масштабирования принимает блок 8×8 коэффициентов преобразования и может предварительно умножить каждый коэффициент преобразования на константу С=2^Р или сдвинуть каждый коэффициент преобразования на Р бит влево, где Р обозначает число зарезервированных бит “мантиссы”. После масштабирования величина 2^Р-1 может быть прибавлена к постоянному коэффициенту преобразования, чтобы получить соответствующее округление в выходных выборках. Чтобы увеличить точность масштабирования, S=P+R бит могут быть использованы в преобразовании масштабных множителей в целые и сдвиги вправо на R бит могут быть выполнены после умножений. S может быть любой подходящей величиной, которая может облегчить осуществление на платформах аппаратного обеспечения, например S может быть 15 или 16 для платформ с 16-битовыми умножителями со знаком/без знака.

Первый каскад 614 1D IDCT выполняет 8-точечное IDCT относительно каждого столбца блока масштабированных коэффициентов преобразования. Второй каскад 616 1D IDCT выполняет 8-точечное IDCT относительно каждой строки промежуточного блока, сгенерированного с помощью первого каскада 614 1D IDCT. 1D IDCT для первого и второго каскадов могут оперировать непосредственно относительно их входных данных без выполнения какого-либо внутреннего предварительного или последующего масштабирования. После того как строки и столбцы обработаны, выходной каскад 618 масштабирования может сдвинуть результирующие величины из второго каскада 616 1D IDCT на Р бит вправо, чтобы сгенерировать выходные выборки для 2D IDCT. Масштабные множители и константа Р точности могут быть выбраны таким образом, что все 2D IDCT может быть осуществлено с использованием регистров желаемой длины.

2D DCT может быть выполнено подобным образом, что и 2D IDCT, 2D IDCT может быть выполнено с помощью (а) предварительного умножения блока выборок пространственной области определения, (b) выполнения 1D IDCT относительно каждого столбца (или строки) блока масштабированных выборок, чтобы сгенерировать промежуточный блок, (с) выполнения 1D IDCT относительно каждой строки (или столбца) промежуточного блока и (d) масштабирования выходных данных второго каскада 1D IDCT, чтобы сгенерировать блок коэффициентов преобразования для 2D IDCT.

Для пояснения большая часть описания выше предназначена для 8-точечного масштабированного IDCT и 8-точечного масштабированного DCT. Способы, описанные в настоящей заявке, могут быть использованы для любого типа преобразования, такого как DCT, IDCT, DFT, IDFT, MLT, обратное MLT, MCLT, обратное MCLT и т.д. Способы также могут быть использованы для любой факторизации преобразования, причем несколько типичных факторизаций приведены на фиг. 1 по фиг. 4. Группы для общих множителей могут быть выбраны на основании факторизации, как описано выше. Способы также могут быть использованы для преобразований любого размера, причем типичные 8-точечные преобразования приведены на фиг. 1 по фиг. 4. Способы также могут быть использованы в сочетании с любым критерием выбора общего множителя, таким как полное число логических и арифметических операций, полное число арифметических операций, точность результатов и т.д.

Число операций для преобразования может зависеть от способа, которым выполняют умножения. Способы вычисления, описанные выше, развертывают умножения в последовательность операций сдвига и сложения, используют промежуточные результаты, чтобы уменьшить число операций, и выполняют объединенное умножение на множество констант с использованием общей последовательности. Умножения также могут быть выполнены с помощью других способов вычисления, которые могут влиять на выбор общих множителей.

Преобразования с общими множителями, описанные в настоящей заявке, могут обеспечивать определенные преимущества, такие как:

меньшая сложность умножения вследствие объединенных умножений на масштабированном этапе,

возможное уменьшение сложности вследствие возможности объединять масштабирование с квантованием в осуществлениях JPEG, H.263, MPEG-1, MPEG-2, MPEG-4 (P.2) и других стандартов, и

увеличенная точность вследствие возможности минимизировать/распределять погрешности аппроксимаций с фиксированной точкой для иррациональных констант, используемых в умножениях, с помощью введения общих множителей, которые могут быть вычислены с помощью масштабных множителей.

Преобразования с общими множителями могут быть использованы для различных применений, таких как обработка изображения и видео, обмен данными, вычисление, передача данных по сети, хранение данных, графика и т.д. Типичное использование преобразований для обработки видео описано ниже.

Фиг. 7 изображает блок-схему системы 700 кодирования и декодирования изображения/видео. В системе 710 кодирования устройство 720 DCT принимает блок входных данных и генерирует блок коэффициентов преобразования. Блок входных данных может быть блоком N×N пикселей, блоком N×N величин разности пикселей (или остатка) или некоторого другого типа данных, сгенерированных из исходного сигнала, например видеосигнала. Величины разности пикселей могут быть разностями между двумя блоками пикселей, разностями между блоком пикселей и блоком предсказанных пикселей и т.д. N может быть равно 8 или некоторой другой величине. Кодер 730 принимает блок коэффициентов преобразования из узла 720 DCT, кодирует коэффициенты преобразования и генерирует сжатые данные. Сжатые данные могут быть сохранены в узле памяти и/или посланы через канал связи (облака 740).

В системе 750 декодирования декодер 760 принимает сжатые данные из узла памяти или канала 740 связи и восстанавливает коэффициенты преобразования. Устройство 770 IDCT принимает восстановленные коэффициенты преобразования и генерирует блок выходных данных. Блок выходных данных может быть блоком N×N восстановленных пикселей, блоком N×N величин разности восстановленных пикселей и т.д. Блок выходных данных может быть оценкой блока входных данных, предоставленных в узле 720 DCT, и может быть использован, чтобы восстанавливать исходный сигнал.

Фиг. 8 изображает блок-схему системы 800 кодирования, которая может быть использована для системы 710 кодирования на фиг. 7. Устройство захвата/память 810 может принимать исходный сигнал, выполнять конвертацию в цифровой формат и предоставляет входные/необработанные данные. Устройство 810 захвата может быть видеокамерой, цифратором или некоторым другим устройством. Процессор 820 обрабатывает необработанные данные и генерирует сжатые данные. В процессоре 820 необработанные данные могут быть преобразованы с помощью узла 822 DCT, сканированы с помощью узла 824 зигзагообразного сканирования, квантованы с помощью квантователя 826, закодированы с помощью кодера 824 с энтропией и пакетированы с помощью формирователя 830 пакетов. Узел 822 DCT может выполнять 2D DCT относительно необработанных данных в соответствии со способами, описанными выше. Каждый из узлов с 822 по 830 может быть осуществлен как аппаратное обеспечение, программно-аппаратное обеспечение и/или программное обеспечение. Например, устройство 822 DCT может быть осуществлено с помощью специализированного аппаратного обеспечения, множества инструкций для арифметического логического устройства (ALU) и т.д.

Узел 840 хранения может сохранять сжатые данные из процессора 820. передатчик 842 может передавать сжатые данные. Контроллер/процессор 850 управляет работой различных узлов в системе 800 кодирования. Память 852 сохраняет данные и программные коды для системы 800 кодирования. Одна или более шин 860 взаимно соединяет различные узлы в системе 800 кодирования.

Фиг. 9 изображает блок-схему системы 900 декодирования, которая может быть использована для системы 750 декодирования на фиг. 7. Приемник 910 может принимать сжатые данные из системы кодирования, а узел 912 хранения может сохранять принятые сжатые данные. Процессор 920 обрабатывает сжатые данные и генерирует выходные данные. В процессоре 920 сжатые данные могут быть распакованы с помощью распаковщика 922, декодированы с помощью декодера 924 с энтропией, обратно квантованы с помощью обратного квантователя 926, расположены в соответствующем порядке с помощью узла 928 обратного зигзагообразного сканирования и преобразованы с помощью узла 930 IDCT. Узел 930 IDCT может выполнять 2D IDCT относительно восстановленных коэффициентов преобразования в соответствии со способами, описанными выше. Каждый из узлов с 922 по 930 может быть осуществлен как аппаратное обеспечение, программно-аппаратное обеспечение и/или программное обеспечение. Например, узел 930 IDCT может быть осуществлен с помощью специализированного аппаратного обеспечения, набора инструкций для арифметического логического устройства (ALU) и т.д.

Узел 940 отображения отображает восстановленные изображения и видео из процессора 920. Контроллер/процессор 950 управляет работой различных узлов в системе 900 декодирования. Память 952 сохраняет данные и программные коды для системы 900 декодирования. Одна или более шин 960 взаимно соединяет различные узлы в системе 900 декодирования.

Каждый из процессоров 820 и 920 может быть осуществлен с помощью одной или более интегральных схем прикладной ориентации (ASIC), процессоров цифровых сигналов (DSP) и/или некоторого другого типа процессоров. В качестве альтернативы каждый из процессоров 820 и 920 может быть заменен одним или более оперативным запоминающим устройством (RAM), постоянным запоминающим устройством (ROM), электрически программируемыми ROM (EPROM), электрически стираемыми перепрограммируемыми ROM (EEPROM), магнитными дисками, оптическими дисками и/или другими типами энергозависимых и энергонезависимых памятей, известными в данной области техники.

Способы, описанные в настоящей заявке, могут быть осуществлены в аппаратном обеспечении, программно-аппаратном обеспечении, программном обеспечении или их комбинации. Например, логические (например, сдвиг) и арифметические (например, сложение) операции, необходимые для умножения величины данных на постоянную величину, могут быть осуществлены с помощью одной или более логик, которые также могут быть упомянуты как узлы, модули и т.д. Логика может быть аппаратной логикой, содержащей логические вентили, транзисторы и/или другие схемы, известные в данной области техники. Логика также может быть программно-аппаратной и/или программной логикой, содержащей машиночитаемые коды.

В одной конструкции устройство содержит первую логику, чтобы выполнять умножение первой группы, по меньшей мере, из одной величины данных на первую группу, по меньшей мере, из одной рациональной двоичной константы, которая аппроксимирует первую группу, по меньшей мере, из одной иррациональной константы, масштабированной с помощью первого общего множителя. Устройство дополнительно содержит вторую логику, чтобы выполнять умножение второй группы, по меньшей мере, из одной величины данных на вторую группу, по меньшей мере, из одной рациональной двоичной константы, которая аппроксимирует вторую группу, по меньшей мере, из одной иррациональной константы, масштабированной с помощью второго общего множителя. Первая и вторая группы, по меньшей мере, из одной величины данных имеют разные размеры. Первая и вторая логики могут быть отдельными логиками, одной и той же общей логикой или совместной логикой.

Для варианта осуществления с помощью программно-аппаратного и/или программного обеспечения умножение величины данных на постоянную величину может быть выполнено с помощью машиночитаемых кодов, которые выполняют желаемые логические и арифметические операции. Коды могут быть аппаратно-реализованными или сохранены в памяти (например, памяти 852 на фиг. 8 или 952 на фиг. 9) и выполнены с помощью процессора (например, процессора 850 или 950) или некоторого другого узла аппаратного обеспечения.

Способы, описанные в настоящей заявке, могут быть осуществлены в различных типах устройств. Например, способы могут быть осуществлены в различных типах процессоров, различных типах интегральных схем, различных типах электронных устройств, различных типах электронных схем и т.д.

Специалистам в данной области техники будет понятно, что информация и сигналы могут быть представлены с использованием любой из множества различных технологий и способов. Например, данные, инструкции, команды, информация, сигналы, биты, символы и элементарные посылки, которые могут упоминаться во всем вышеприведенном описании, могут быть представлены напряжениями, токами, электромагнитными волнами, магнитными полями или частицами, оптическими полями или частицами или любой их комбинацией.

Специалистам в данной области техники дополнительно понятно, что различные иллюстративные логические блоки, модули, схемы и этапы алгоритмов, описанные в связи с раскрытием, могут быть осуществлены в виде электронного аппаратного обеспечения, компьютерного программного обеспечения или комбинации того и другого. Для того чтобы понятно проиллюстрировать эту взаимозаменяемость аппаратного обеспечения и программного обеспечения, различные иллюстративные компоненты, блоки, модули, схемы и этапы описаны выше в целом в понятиях их функционального назначения. Осуществляется ли такое функциональное назначение аппаратно или программно, зависит от конкретного применения и конструктивных ограничений, наложенных на всю систему. Опытные практики могут осуществить описанное функциональное назначение различными способами для каждого конкретного приложения, но решения такого осуществления не должны интерпретироваться как вызывающие выход за рамки настоящего раскрытия.

Различные иллюстративные логические блоки, модули и схемы, описанные в связи с раскрытием, могут быть осуществлены или выполнены с помощью процессора общего назначения, DSP, ASIC, вентильной матрицы, программируемой в условиях эксплуатации (FPGA), или другого программируемого логического устройства, дискретного вентиля или транзисторной логики, дискретных компонентов аппаратного обеспечения или любой их комбинации, предназначенной для выполнения функций, описанных в настоящей заявке. Процессор общего назначения может быть микропроцессором, но в альтернативе процессор может быть любым традиционным процессором, контроллером, микроконтроллером или конечным автоматом. Процессор также может быть осуществлен как комбинация вычислительных устройств, например комбинация DSP и микропроцессора, множество микропроцессоров, один или более микропроцессор совместно с ядром DSP или любая другая такая конфигурация.

В одном или более типовых вариантах осуществления описанные функции могут быть осуществлены в аппаратном обеспечении, программном обеспечении, программно-аппаратном обеспечении или в их комбинации. Если осуществлены в программном обеспечении, функции могут быть сохранены или переданы как одна или более инструкций или код на машиночитаемом носителе. Машиночитаемая среда включает в себя как среду хранения, так и среду обмена информацией, включая любой носитель, который облегчает передачу компьютерной программы из одного места в другое. Среда хранения может быть любой имеющейся средой, доступ к которой может быть осуществлен с помощью компьютера. В качестве примера, а не ограничения такая машиночитаемая среда может содержать RAM, ROM, EEPROM, CD-ROM или другое хранилище на оптическом диске, хранилище на магнитном диске, или другие устройства магнитного хранения, или любой другой носитель, который может быть использован для переноса или хранения желаемого программного кода в виде инструкций или структур данных и доступ к которому может быть осуществлен с помощью компьютера. Также любое соединение по существу называют машиночитаемым носителем. Например, если программное обеспечение передают из web-сайта, сервера или другого удаленного источника с использованием коаксиального кабеля, волоконно-оптического кабеля, витой пары, цифровой абонентской линии (DSL) или беспроводных технологий, таких как инфракрасное излучение, радиоволны и микроволны, тогда коаксиальный кабель, волоконно-оптический кабель, витую пару, DSL или беспроводные технологии, такие как инфракрасное излучение, радиоволны и микроволны, включают в определение носителя. Понятия disk или disc, как используется в настоящем описании, включают в себя компакт-диск (CD), лазерный диск, оптический диск, цифровой универсальный диск (DVD), гибкий диск, диск blu-ray, где disks обычно воспроизводят данные магнитным способом, в то время как discs воспроизводят данные оптическим способом с помощью лазеров. Комбинации вышеперечисленного также следует включить в рамки машиночитаемой среды.

Предыдущее описание раскрытия предоставлено для того, чтобы дать возможность любому специалисту в данной области техники изготовить или использовать настоящее раскрытие. Различные модификации раскрытия могут быть без труда поняты специалистами в данной области техники, а основные принципы, определенные в настоящей заявке, могут быть применены к другим конструкциям, не выходя за рамки сущности и объема изобретения. Следовательно, не предполагается, что настоящее раскрытие ограничено примерами, изображенными в настоящей заявке, но должно соответствовать самым широким рамкам, согласующимся с принципами и новыми признаками, раскрытыми в настоящей заявке.

Реферат

Изобретения относятся к устройствам для выполнения преобразований данных. Техническим результатом является уменьшение сложности и увеличение точности преобразований. В одном варианте устройство для выполнения преобразований данных содержит первую логику выполнения умножения первой группы, по меньшей мере, из одной величины данных на первую группу, по меньшей мере, из одной рациональной двоичной константы, которая аппроксимирует первую группу, по меньшей мере, из одной иррациональной константы, масштабированной первым общим множителем, причем каждая рациональная двоичная константа является рациональным числом с двоичным знаменателем; и вторую логику для выполнения умножения второй группы, по меньшей мере, из одной величины данных на вторую группу, по меньшей мере, из одной рациональной двоичной константы, которая аппроксимирует вторую группу, по меньшей мере, из одной иррациональной константы, масштабированной вторым общим множителем, причем первая и вторая группы, по меньшей мере, из одной величины данных имеют разные размеры. 9 н. и 34 з.п. ф-лы, 9 ил., 6 табл.

Формула