Многовходовой сумматор по модулю два - RU2614370C1

Описание

Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также устройствах для формирования элементов конечных полей GF(2^ν).

В работе [1, с. 48] (Каллан Роберт. Основные концепции нейронных сетей: пер. с англ. - М: Издательский дом «Вильямс», 2001) показана структура трехслойной нейронной сети, предназначенной для выполнения сложения по модулю два (операция XOR) двух одноразрядных операндов. Данный сумматор представляет собой трехслойную нейронную сеть. Каждый нейрон реализует классическую модель формального нейрона и содержит n умножителей значений синаптических весов ω_ij на значения входного сигнала x_i, сумматор и блок, реализующий вычисления функции активации от полученной суммы

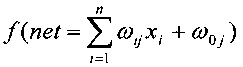
Первый слой из двух нейронов в вычислениях не участвует, а предназначен для перераспределения входных сигналов x₁ и х₂. При этом входной вектор, который включает в себя и значение смещения, равное «1», т.е. [1, х₁, х₂], умножается на матрицу синаптических весов

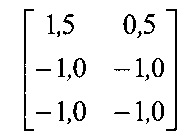
А затем производится вычисление свертки

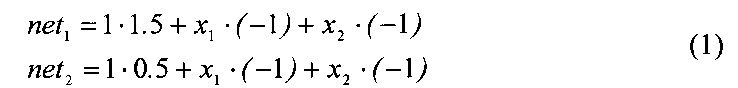
на выходе сумматоров каждого из нейрона скрытого слоя. После этого к полученному результату свертки net₁ и net₂ применяется функция активации порогового типа

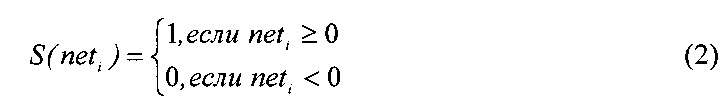
где i=1, 2.

Затем сигналы с выходов нейронов скрытого слоя, совместно со смещением, равным 1, умножаются на матрицу синаптических весов

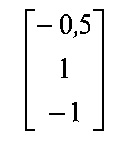
и поступают на входы сумматора, вычисляющего свертку

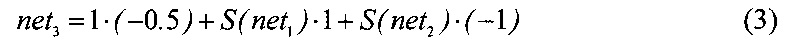
После этого к значению net₃ применяется пороговая функция активации (2). Полученный результат является суммой по модулю два.

При реализации алгоритмов цифровой обработки сигналов с использованием полиномиальной системы классов вычетов (ПСКВ), функционирующей в конечных полях GF(2^ν), необходимо использовать многовходовые сумматоры по модулю два.

Приведенную в [1] нейронную сеть можно использовать для построения многовходового сумматора по модулю, но это приведет к увеличению числа слоев и, следовательно, к повышению схемных затрат. Так при реализации n-разрядного сумматора по модулю два потребуется ⎡log₂ n⎤ подсетей, каждая из которых будет реализовать модель нейросетевого сумматора по модулю два, представленную в [1].

Таким образом, недостатком многовходового сумматора по модулю два, использующего каскадную реализацию на базе двухвходового нейросетевого сумматора, приведенного в [1], являются значительные схемные затраты.

Основной задачей предлагаемого изобретения является снижение схемных затрат на реализацию многовходового сумматора по модулю два.

Техническим результатом, достигнутым при осуществлении заявленного изобретения, является снижение схемных затрат, необходимых на реализацию многовходового сумматора по модулю два.

Указанный технический результат достигается за счет использования новой функции активации в скрытом слое, применения синаптических весов ω_ij, равных единице, что позволяют исключить из структуры формального нейрона умножители синаптических весов, а также исключения из структуры нейрона выходного слоя блока, реализующего вычисления функции активации.

Многовходовый сумматор по модулю два представляет собой трехслойную нейронную сеть, являющуюся многослойным персептроном. Входной слой содержит n нейронов, где n - количество входов, которые в вычислениях не участвуют, а предназначены для распределения входного вектора на нейроны скрытого слоя. Скрытый слой содержит

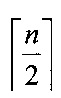
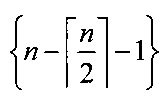
На фиг.1 приведена структура нейросетевого 8-входового сумматора по модулю два. Данный сумматор содержит восемь нейронов входного слоя 1-8, по которым поступает входной вектор, представленный в двоичном коде. Скрытый слой содержит четыре нейрона 9.1-9.4, каждый из которых содержит сумматор 10.i и блок вычисления функции активации 11.i, где i=1, 2, 3, 4. Выход блока вычисления функции активации является выходом нейрона скрытого слоя. Выходы нейронов 9.1-9.4 скрытого слоя подключены ко входу сумматора 12 нейрона выходного слоя. Выход сумматора 12 является выходом восьмивходового сумматора по модулю два.

Каждый сумматор 10.i нейрона 9.i, где i=1, 2, 3, 4, скрытого слоя имеет n+1 входов, где n=8. Первые n входов используются для принятия двоичного кода входного вектора X=[x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈]. На n+1 вход подается сигнал, который является смещением.

Входы сумматоров 10.i, входящих в состав нейрона 9.i скрытого слоя, где i=1, 2, 3, 4, подключены к выходам нейронов 1-8 входного слоя. Выход сумматора 10.i подсоединен к входу блока вычисления функции активации 11.i, выход которого является выходом нейрона 9.i скрытого слоя. Выходы нейронов 9.1-9.4 скрытого слоя подсоединены к входам сумматора 12 нейрона выходного слоя, выход которого является выходом многовходового сумматора по модулю два.

При этом выходы нейронов 1-8 входного слоя подключены к входам сумматоров 10.1-10.14 нейронов 9.1-9.4 скрытого слоя, которые реализуют операцию

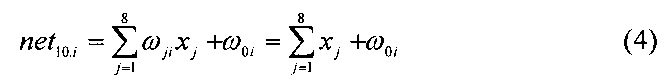
где ω_ji=1 - синаптические веса i-го нейрона скрытого слоя; х_j - значение, поступающее на вход j-го нейрона входного слоя; ω_0i - смещение i-го нейрона скрытого слоя.

Для первого нейрона 9.1 скрытого слоя, значение ω₀₁=-1. Для второго нейрона 9.2 скрытого слоя ω₀₂=-3. Для третьего нейрона 9.3 скрытого слоя ω₀₃=-5. Для четвертого нейрона 9.4 скрытого слоя ω₀₄=-7.

Результат свертки net_10.i, реализованный согласно (4), поступает на вход блока вычисления функции активации 11.i, где i=1, 2, 3, 4.

В прототипе [1] была использована пороговая функция активации, определяемая выражением (2). Чтобы сократить схемные затраты предлагается в качестве функции активации использовать функцию «стрелка Пирса», которая имеет на выходе единичное значение, если на вход подаются нулевые значения, а на остальных входных наборах ее значение равно нулю. С выхода сумматоров 10.i, i=1÷4, трехразрядный параллельный код, представляющий собой сумму (4), поступает на вход блока вычисления функции активации 11.i.

На выходе первого блока вычисления функции активации 11.1 нейрона 9.1 скрытого слоя появится единичный сигнал, если во входном векторе X=[х₁, х₂, х₃, х₄, х₅, х₆, х₇, х₈] содержится одна единица.

На выходе второго блока вычислений функции активации 11.2 нейрона 9.2 скрытого слоя появится единичный сигнал, если во входном векторе X=[x₁, х₂, х₃, х₄, х₅, х₆, х₇, х₈] содержится 3 единицы.

На выходе третьего блока вычисления функции активации 11.3 нейрона 9.3 скрытого слоя появится единичный сигнал, если во входном векторе X=[ х₁, х₂, х₃, х₄, х₅, х₆, х₇, х₈] содержится 5 единиц.

На выходе четвертого блока вычисления функции активации 11.4 нейрона 9.4 скрытого слоя появится единичный сигнал, если во входном векторе X=[ х₁, х₂, х₃, х₄, х₅, х₆, х₇, х₈] содержится 7 единиц.

Выходные сигналы 0 или 1 с выходов нейронов 9.1-9.4 скрытого слоя подаются на входы сумматора 12 нейрона выходного слоя. Результат суммы поступает на выход многовходового сумматора по модулю 2.

Рассмотрим работу многовходового сумматора по модулю два. Пусть на вход поступает вектор X=[1,1,0,0,0,0,0,0], который содержит четное число единиц. Данный вектор подается с выхода нейронов 1-8 входного слоя на входы нейронов 9.1-9.4 скрытого слоя. Сумматоры этих нейронов производят вычисления

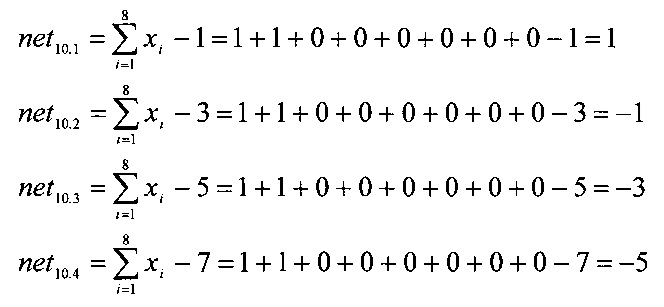
Вычисляемые ненулевые результаты net_10.i, где i=1, 2, 3, 4, поступают на входы блоков вычисления функции активации 9.i. Следовательно, с выходов последних будет сниматься нулевой результат, который поступает на входы сумматора 12. На выходе заданного сумматора будет получен сигнал

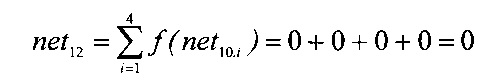
Следовательно, результат сложения двух единичных сигналов по модулю два равен нулю, т.е. 1⊕1=0.

Пусть на вход многовходового сумматора поступает вектор X=[1,1,0,0,0,0,0,1], который содержит нечетное количество единиц. Данный вектор подается с выходов нейронов 1-8 входного слоя на входы нейронов 9.1-9.4 скрытого слоя. Сумматоры этих нейронов производят вычисления

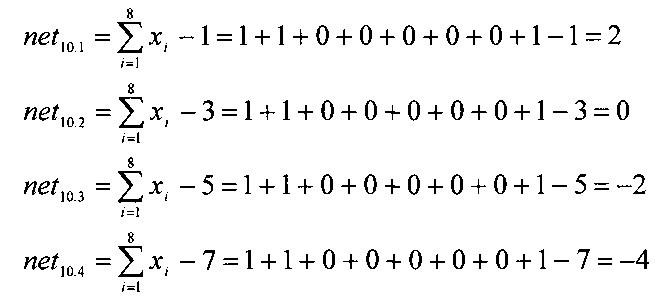
Нулевая кодовая комбинация с выхода сумматора 10.2 поступает на вход блока вычисления функции активации 9.2, который реализует функцию «стрелка Пирса». В результате этого на выходе нейрона 9.2 будет единичный сигнал. При этом на выходах всех оставшихся нейронов 9.1, 9.3, 9.4 скрытого слоя будет нулевой сигнал. Тогда на выходе сумматора 12 будет получен сигнал

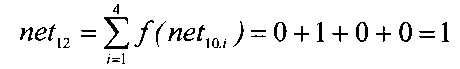
Следовательно, 1⊕1⊕1=1.

Реферат

Изобретение относится к вычислительной технике и может быть использовано в цифровых вычислительных устройствах, а также устройствах для формирования элементов конечных полей GF(2). Технический результат заключается в снижении схемных затрат, необходимых на реализацию многовходового сумматора по модулю два. Технический результат достигается за счет использования новой функции активации в скрытом слое, применения синаптических весов ω, равных единице, что позволяет исключить из структуры формального нейрона умножители синатических весов, а также исключения из структуры нейрона выходного слоя блока, реализующего вычисления функции активации. 1 ил.

Формула