Способ, система и считываемый компьютером носитель записи, содержащий компьютерную программу, имитации поведения тканого материала на уровне нити - RU2698920C2

Чертежи

Показать все 14 чертежа(ей)

Описание

Область техники, к которой относится изобретение

Настоящее изобретение относится к области имитации поведения ткани на уровне нити.

Предпосылки создания изобретения

Ткань формируется в результате переплетения нитей, представляющих собой, как правило, два набора ортогональных нитей, называемых основой и утком. На участках контакта между нитями переплетенные нити подвергаются действию сил трения, и это трение удерживает тканый материал от смещения, в отличие от трикотажных полотен, которые удерживаются от смещения с помощью сшивающих нитей. Ткани встречаются повсюду, и характеризуются разнообразием рисунков переплетения и материалов нити, как жестких, так и упругих. Обычные тканые материалы включают в себя шифон, вельвет, деним, фланель, габардин, полотно и бархат.

Крупномасштабная механика ткани определяется мелкомасштабным поведением нитей, их механическими свойствами, расположением и контактным взаимодействием. Однако популярные модели тканей, за исключением заметной работы Kaldor et al. [2008; 2010], моделируют механику не на уровне нити. Они используют или дискретные элементы, как в случае масс-пружинных систем [Breen et al. 1994; Provot 1995], или дискретизации непрерывных формул, как в случае конечно-элементных моделей [Etzmuss et al. 2003].

Такие дискретизированные модели являются зачастую достаточными для описания соответствующего поведения ткани, в частности, драпировки при умеренных силах. Но модели на уровне нити внедряют в практику захватывающие возможности для компьютерной анимации. Визуально интересные эффекты, такие как детализированный разрыв, затяжки или свободные концы нити требуют моделирования отдельных нитей. Кроме того, модели на основе нити могут стать краеугольным камнем разработки точных решений для крупномасштабной имитации тканей, нелинейностей и сложных взаимодействий, измеренных на реальных материалах [Wang et al. 2011; Miguel et al. 2012; Miguel et al. 2013].

Вычислительные затраты были ключевой задачей для решения проблемы имитации ткани на уровне нити. Описание механики отдельных нитей требует использования стержневых моделей [Pai 2002; Spillmann и Teschner 2009; Bergou et al. 2008; Casati и Bertails-Descoubes 2013], а рисунки переплетений создают ряд контактов, квадратичных по числу нитей. Моделирование тканей даже с низкой плотностью нитей вскоре приводит к скачкообразному увеличению числа степеней свободы (DoF) и контактов, а число нитей в обычных тканях может составлять порядка 100 нитей/дюйм.

Большинство моделей при имитации ткани в компьютерной графике рассматривают ткань как тонкую оболочку и составляют модель упругой деформации для описания ее механики [Terzopoulos et al. 1987]. Кроме того, при моделировании ткани возникает проблема определения энергий деформации и дискретизаций, которые являются численно надежными и соответствуют поведению реальной ткани. Некоторые ключевые стадии моделирования ткани в компьютерной графике включают в себя: масс-пружинные модели, которые аппроксимируют поведение реальных тканых материалов [Breen et al. 1994], добавление предельных напряжений для моделирования нерастяжимости [Provot 1995], эффективное решение проблемы самостолкновений [Volino et al. 1995], определение энергий деформации из ограничений с эффективным интегрированием по времени [Baraff и Witkin 1998], надежные модели для решения проблемы выпучивания [Choi and Со 2002], непротиворечивые модели изгиба [Bridson et al. 2003; Grinspun et al. 2003], эффективную нерастяжимость [Goldenthal et al. 2007] и эффективное динамическое ремеширование [Narain et al. 2012].

Последние работы в компьютерной анимации также нацелены на приведение в соответствие с нелинейным поведением в реальной ткани. Соответствующие работы включают в себя проектирование нелинейных параметрических моделей [Volino et al. 2009], оценку коэффициентов материалов по примерам силы и деформации [Wang et al. 2011; Miguel et al. 2012], а также проектирование моделей с внутренним трением для описания гистерезиса ткани [Miguel et al. 2013].

В отличие от популярных моделей тонкой оболочки, Kaldor et al. [2008] смоделировали динамику трикотажной ткани на уровне нити, что позволило им предсказать крупномасштабное поведение всех швейных изделий по фундаментальной механики нити. Они описали механику отдельных нитей с использованием модели нерастяжимых стержней и контакта между нитями в комбинации с силами жесткой пенализации и трением в скоростном фильтре. Позже в [2010], они распространили свою работу на ускорение решения проблемы контакта между нитями в результате использования линеаризации поворотных локальных сил пенализации. Однако, настоящее изобретение предлагает более эффективное решение в случае ткани, которая в целом не позволяет решить проблему контакта между нитями при пересечениях нити. Metaaphanon с соавт. [2009] предложил модель на уровне нити для ткани. Они смоделировали взаимодействие между нитями в результате задания ограничений между конечными точками пружин утка и основы. Кроме того, они спроектировали автоматический переход от масс-пружинной модели к модели на уровне нити.

Модели на уровне нити были полностью изучены в области научно-исследовательских работ по текстилю. Для предсказания механического поведения ткани при определенных режимах деформации, как правило, на основе геометрических моделей нити были использованы аналитические модели на основе нити [Hearle et al. 1969]. Эти аналитические модели, такие как нити Пирса с параметрическим круговым поперечным сечением [Peirce 1937] или намного более простые пряди Кавабата, соединенные штифтом [Kawabata et al. 1973], моделируют нити в точках перехода при условии постоянного контакта и с учетом отделения извитости. Однако, для большинства аналитических моделей эти подходы ограничиваются определенными случаями, для которых они были спроектированы, и разработка аналитического каркаса для случаев общей нагрузки была бы чрезвычайно сложной [King et al. 2005], не говоря уже о швейных изделиях в целом.

Непрерывные модели на основе мезоструктуры появились для имитации больших образцов ткани [Boisse et al. 1997; Parsons et al. 2010]. Эти модели аппроксимируют тканый материал как непрерывный, в котором каждая материальная точка представляет группу нитей. Затем каждая группа имитируется с использованием значительно упрощенной аналитической элементарной ячейки, использующей, например, модель прядей Кавабата, соединенных штифтом.

В другом семействе моделей имитировать всю ткань на уровне нити можно с использованием конечно-элементных дискретизаций объемных нитей и учетом всех взаимодействий нитей [Ng et al. 1998; Page and Wang 2000; Duan et al. 2006]. Однако большие вычислительные требования делают использование таких моделей затруднительным для умеренно больших образцов. Более высокая производительность вычислений была достигнута в результате замены сложных объемных нитей на более простые элементы, такие как балки, пряди и мембраны [Reese 2003; McGlockton et al. 2003]. Другой интересный подход заключается в обращении к дорогостоящей механике на уровне нити только при необходимости и использовании разномасштабных моделей, соединяющих непрерывность и описания на уровне нити [Nadler et al. 2006].

В некотором смысле гибридные методы базируются на подходах с точки зрения непрерывности на основе мезоструктуры, но с использованием дискретной модели для элементарных ячеек. Эти ячейки обеспечивают осевое соответствие и могут быть увеличены с помощью изгибающих пружин и пружин перехода для имитации деформации поперечного сечения и смещения в точках перехода [King et al. 2005; Xia and Nadler 2011]. Подавление смещения достигается за счет внедрения элементов прядей, перпендикулярных к нитям, для имитации контактных сил между нитями [King et al. 2005]. Однако, так как нити закрепляются в точках перехода без смещения, то эти подходы на основе элементарных ячеек предотвращают скольжение нити. Parsons и сотрудники [2013] разобрались с проблемой скольжения нитей в результате внедрения поля скорости скольжения на уровне непрерывности с силами, вычисленными на мезоуровне с использованием элементарной ячейки. Силы трения скольжения пропорциональны нормальным силам в точках перехода. Однако эти подходы, как правило, не обеспечивают возможности имитировать каждую нить в ткани, что позволяет избежать влияния интересных одиночных нитей, таких как затяжки, потертые края, разрушение нитей и вытягивание нитей. Кроме того, типичные модели на уровне нити в научно-исследовательских работах по текстилю предполагают постоянный контакт между сплетенными нитями, но не решают проблемы положений нитей при свободном движении швейных изделий, только контролируемые эксперименты. В отличие от этого подход согласно настоящему изобретению позволяет моделировать каждую нить в ткани в качестве стержня, что значительно уменьшает дорогостоящие контактные взаимодействия за счет обеспечения постоянства контакта и внедрения дополнительных степеней свободы скольжения.

Важным аспектом имитации на уровне нити является выбор стержневой модели для описания механики отдельных нитей. Pai [2002] разработал эффективный алгоритм для имитации стержней, смоделированных по теории Коссерата. Spillmann и Teschner [2007] усовершенствовали модели Коссерата для эффективного решения проблемы контактов, а затем в [2009] распространили эти модели на решение проблем разветвленных и петлеобразных структур. Bergou с соавт. [2008] представил подход для стержневой имитации, которая отделяет динамику центральной линии от квазистатического решения проблемы скручивания на основе параллельного переноса. Casati и Bertais-Descoubes [2013] недавно разработали модели на основе клотоид, предназначенные для эффективного решения проблемы динамики обогащенных гладких стержней с очень небольшим числом контрольных точек.

Как описано выше, основной проблемой имитации ткани на уровне нити является эффективное решение проблемы контакта между нитями. Sueda с соавт. [2011] представляет модель, подходящую для эффективной имитации чрезвычайно ограниченных стержней. Ключевой момент этой модели заключается в описании кинематики ограниченных стержней с использованием оптимального набора обобщенных координат, образованных так называемыми координатами Лагранжа, которые описывают абсолютное движение, и так называемыми координатами Эйлера, которые описывают скольжение на многообразиях с ограничениями. Этот подход соответствует представлению ограниченных нитей в ткани, позволяющему спроектировать дискретизацию для случая проблемы, не решенной Sueda с соавт., состоящего из двух стержней в скользящем контакте.

Ссылки

BARAFF, D., AND WITKIN, А. 1998. Large steps in cloth simulation (Большие шаги в имитации ткани). Proceedings of SIGGRAPH ACM 98, 4354.

BELL, N. AND GARLAND M., 2012. Cusp: Generic parallel algorithms for sparse matrix and graph computations (Cusp: Универсальные параллельные алгоритмы для разреженной матрицы и вычислений на графах). Version 0.3.0.

BERGOU, М., WARDETZKY, М., ROBINSON, S., AUDOLY, В., AND GRINSPUN, Е., 2008. Discrete elastic rods (Дискретные упругие стержни). ACM Trans. Graph. 27, 3, 63:163:12.

BERTHOUZOZ, F., GARG, A., KAUFMAN, D.M., GRINSPUN, E., AND AGRAWALA, M. 2013. Parsing sewing patterns into 3D garments (Парсинг выкроек в 3-D швейных изделиях). ACM Trans. Graph. 32, 4, 85:1-85:12.

BOISSE, P., BORR, M., BUET, K., AND CHEROUAT, A. 1997. Finite element simulations of textile composite forming including the biaxial fabric behavior (Конечно-элементные имитации текстильного композитного формирования, включающего в себя поведение двухосного материала). Composites Part В: Engineering 28, 4, 453-464.

BREEN, D.E., HOUSE, D.H., AND WOZNY, M.J. 1994. Predicting the drape of woven cloth using interacting particles (Предсказание драпировки тканью с использованием интерактивных частиц). Proceedings of SIGGRAPH ACM 94, 365-372.

BRIDSON, R., MARINO, S., AND FEDKIW, R. 2003. Simulation of clothing with folds and wrinkles (Имитация ткани со сгибами и морщинами). Proceedings of ACM SIGGRAPH / Eurographics Symposium on Computer animation 2003, 2836.

CASATi, R., AND BERTAILS-DESCOUBES, F. 2013. Super space clothoids (Суперпространственные клотоиды). ACM Trans. Graph. 32, 4, 48.

CHEN, Y., LIN, S., ZHONG, H., XU, Y.-Q., GUO, В., AND SHUM, H.-Y. 2003. Realistic rendering and animation of knitwear (Реалистическая визуализация и анимация трикотажа). IEEE Transactions on Visualization and Computer Graphics 9, 1 (Jan.), 43-55.

CHOI, K.-J., AND КО, H.-S. 2002. Stable but responsive cloth (Прочная, но чувствительная ткань). ACM Trans. Graph. 21, 3, 604-611.

DAVIET, G., BERTAILS-DESCOUBES, F., AND BOISSIEUX, L. 2011. A hybrid iterative solver for robustly capturing coulomb friction in hair dynamics (Гибридный итерационный решатель для полноценного описания кулонова трения в динамике волос). ACM Trans. Graph. 30, 6, 139:1-139:12.

DE JOYA, J.M., NARAIN, R., O'BRIEN, J., SAMII, A., AND ZORDAN, V. Berkeley garment library (Библиотека швейных изделий Berkeley. .

DUAN, Y., KEEFE, M., BOGETTI, T.A., AND POWERS, B. 2006. Finite element modeling of transverse impact on a ballistic fabric (Конечно-элементное моделирование поперечного воздействия на баллистическую ткань). International Journal of Mechanical Sciences 48, 1, 33-43.

ETZMUSS, O., KECKEISEN, M., AND STRASSER, W. 2003. A fast finite element solution for cloth modelling (Быстрое конечно-элементное решение для моделирования ткани). Proceedings of Pacific Graphics 2003, 244-251.

GOLDENTHAL, R., HARTMON, D., FATTAL, R., BERCOVIER, M., AND GRINSPUN, край 2007. Efficient simulation of inextensible cloth (Эффективная имитация нерастяжимой ткани). ACM Trans. Graph. 26, 3, 49.

GOLDSTEIN, H., POOLE, C.P., AND SAFKO, J.L. 2001. Classical Mechanics (Классическая механика) (3rd Edition), 3 ed. Addison-Wesley.

GRINSPUN, E., HIRANI, A.N., DESBRUN, M., AND SCHR'O DER, P. 2003. Discrete shells (Дискретные оболочки). Proceedings of ACM SiGGRAPH / Eurographics Symposium on Computer animation 2003, 6267.

HARMON, D., VOUGA, E., SMITH, В., TAMSTORF, R., AND GRINSPUN, E. 2009. Asynchronous contact mechanics (Асинхронная контактная механика). ACM Trans. Graph. 28, 3, 97.

HEARLE, J.W.S., GROSBERG, P., AND BACKER, S. 1969. Structural Mechanics of Fibers, Yarns, and Fabrics (Структурная механика волокон, нитей и тканей), vol. 1. JohnWiiey & Sons Inc, New York.

JAKOB, W., 2010. Mitsuba renderer (Рендерер Mitsuba). .

KALDOR, J.M., JAMES, D.L., AND MARSCHNER, S. 2008. Simulating knitted cloth at the yarn level (Имитация трикотажного полотна на уровне нити). ACM Trans. Graph. 27, 3, 65:165:9.

KALDOR, J.M., JAMES, D.L., AND MARSCHNER, S. 2010.. Efficient yarn-based cloth with adaptive contact linearization (Эффективная ткань на основе нити с адаптивной контактной линеаризацией). ACM Trans. Graph. 29, 4, 105:1-105:10.

KAWABATA, S., NIWA, M., AND KAWAI, H. 1973. The finitedeformation theory of plain-weave fabrics part i: The biaxialdeformation theory (Теория конечных деформаций полотняных тканых материалов, часть i: теория двухосных деформаций). Journal of the Textile Institute 64, 1, 21-46.

KAWABATA, S. 1980. The Standardization and Analysis of Hand Evaluation' ('Стандартизация и анализ ручной оценки'). Textile Machinery Society of Japan, 1980.

KING, M.J., JEARANAISILAWONG, P., AND SOCRATE, S. 2005. A continuum constitutive model for the mechanical behavior of woven fabrics (Непрерывная составная модель для механического поведения тканых материалов). Journal of Solids and Structures 42, 13, 3867-3896.

LOPEZ-MORENO, J., CIRIO, G., MIRAUT, D., AND OTADUY, M.A. 2014. GPU Visualization and Voxelization of Yarn-Level Cloth (Визуализация и вокселизация ткани на уровне нити с помощью GPU). Proceedings of the Spanish Computer Graphics Conference.

MCGLOCKTON, M.A., COX, B.N., AND MCMEEKING, R.M. 2003. A.binary model of textile composites: III. High failure strain and work of fracture in 3D weaves (Бинарная модель текстильных композитов: III. Большое напряжение до разрыва и работа разрушения в 3D-тканях). Journal of the Mechanics and Physics of Solids 51, 8, 1573-1600.

METAAPHANON, N., BANDO, Y., ЧЕН, B.-Y., AND NISHITA, T. 2009. Simulation of tearing cloth with frayed edges (Имитация разрыва ткани с потертыми краями). Comput. Graph. Forum 7, 1837-1844.

MIGUEL, E., BRADLEY, D., THOMASZEWSKI, В., BICKEL, В., MATUSIK, W., OTADUY, M.A., AND MARSCHNER, S. 2012. Data-driven estimation of cloth simulation models (Управляемые данными имитационные модели тканей). Comp. Graph. Forum 31, 519-528.

MIGUEL, Е., TAMSTORF, R., BRADLEY, D., SCHVARTZMAN, С.К., THOMASZEWSKI, В., BICKEL, В., MATUSIK, W., MARSCHNER, S., AND OTADUY, M.A. 2013. Modeling and estimation of internal friction in cloth (Моделирование и оценка внутреннего трения в ткани). ACM Trans. Graph. 32, 6, 212:1-212:10.

NADLER, В., PAPADOPOULOS, P., AND STEIGMANN, D.J. 2006. Muitiscale constitutive modeling and numerical simulation of fabric material (Разномасштабное составное моделирование и численное моделирование тканевого материала). International Journal of Solids and Structures 43, 2, 206-221.

NARAIN, R., SAMII, A., AND O'BRIEN, J.F. 2012.

NARAIN, R., SAMII, A., AND O'BRIEN, J.F. 2012. Adaptive anisotropic remeshing for cloth simulation (Адаптивное анизотропное ремеширование для имитации ткани). АСМ Trans. Graph. 31, 6, 152:1-152:10.

NG, S.-P., TSE, P.-C, AND LAU, K.-J. 1998. Numerical and experimental determination of in-plane elastic properties of 2/2 twill weave fabric composites (Численное и экспериментальное определение упругих свойств тканых композитов с саржевым переплетением 2/2 в плоскости). Composites Part В: Engineering 29, 6, 735-744.

O'BRIEN, J.F., AND HODGINS, J.K. 1999. Graphical modeling and animation of brittle fracture (Графическое моделирование и анимация хрупкого разрушения). Proceedings of ACM SIGGRAPH 99, 137146.

PAGE, J., AND WANG, J. 2000. Prediction of shear force and an analysis of yarn page for a plain-weave carbon fabric in a bias extension state (Прогнозирование силы смещения и анализ проскальзывания нити для полотняных тканых углеродных материалов в состоянии растяжения со смещением). Composites Science and Technology 60, 7, 977-986.

PAI, D.K 2002. Strands: Interactive simulation of thin solids using cosserat models (Пряди: Интерактивная имитация тонких твердых тел с использованием моделей Коссерата). Comput. Graph. Forum 21, 3, 347-352.

PARSONS, E.M., WEERASOORIYA, Т., SARVA, S., AND SOCRATE, S. 2010. Impact of woven fabric: Experiments and mesostructure-based continuum-level simulations (Воздействие тканого материала: Эксперименты и имитации на уровне непрерывности на основе мезоструктуры). Journal of the Mechanics and Physics of Solids 58, 11, 1995-2021.

PARSONS, E.M., KING, M.J., AND SOCRATE, S. 2013. Modeling yarn slip in woven fabric at the continuum level: Simulations of ballistic impact (Моделирование скольжения нити в тканом материале на уровне непрерывности: Имитации баллистического воздействия). Journal of the Mechanics and Physics of Solids 61, 1, 265-292.

PEIRCE, F.T. 1937. The geometry of cloth structure (Геометрия структуры ткани). Journal of the Textile Institute Transactions 28, 3, T45-T96.

PFAFF, Т., NARAIN, R., DE JOYA, J.M., AND O'BRIEN, J.F. 2014. Adaptive tearing and cracking of thin sheets (Адаптивный разрыв и растрескивание тонких кусков). АСМ Trans. Graph. 33, 4, 110:1-9.

PROVOT, X. 1995. Deformation constraints in a mass-spring model to describe rigid cloth behavior (Деформационные ограничения в масс-пружинной модели для описания поведения жесткой ткани). Graphics Interface, 147-154.

REESE, S. 2003. Anisotropic elastoplastic material behavior in fabric structures (Поведение упруго-пластичных материалов в тканевых структурах). IUTAM Symposium on Computational Mechanics of Solid Materials at Large Strains, 201-210.

SPILLMANN, J., AND TESCHNER, M. 2007. CoRdE: cosserat rod elements for the dynamic simulation of one-dimensional elastic objects. (CoRdE: стержневые элементы Коссерата для динамической имитации одномерных упругих объектов). Proceedings of АСМ SIGGRAPH / Eurographics Symposium on Computer Animation 2007, 6372.

SPILLMANN, J., AND TESCHNER, M. 2009. Cosserat nets (Сетки Коссерата). IEEE Transactions on Visualization and Computer Graphics 15, 2, 325-338.

SUEDA, S., JONES, G.L., LEVIN, D.I. W., AND PAI, D.K. 2011. Large-scale dynamic simulation of highly constrained strands (Крупномасштабное динамическое моделирование чрезвычайно ограниченных прядей). АСМ. АСМ Trans. Graph. 30, 4, 39:1-10.

SULLIVAN, J.M. 2008. Curves of finite total curvature (Кривые с конечной полной кривизной). Discrete Differential Geometry, A.I. Bobenko, J.M. Sullivan, P. Schroder, and G.M. Ziegler, Eds., vol. 38 of Oberwolfach Seminars. Birkh'auser, Basel, 137-161.

TANG, M., TONG, R., NARAIN, R._t MENG, C, AND MANOCHA, D. 2013. A GPU-based streaming algorithm for high-resolution cloth simulation (Поточный алгоритм на основе GPU для имитации ткани с высокой разрешающей способностью). Computer Graphics Forum 32, 7, 21-30.

TERZOPOULOS, D., PLATT, J., BARR, A., AND FLEISCHER, K. 1987. Elastically deformable models ((Упруго деформируемые модели). Proceedings of ACM SIGGRAPH 87, 205-214.

TESCHNER, M., HEIDELBERGER, В., MUELLER, M., POMERANETS, D., AND GROSS, M. 2003. Optimized spatial hashing for collision detection of deformable objects (Оптимизированное пространственное хеширование для обнаружения столкновений деформируемых объектов). Proceedings of Vision, Modeling, Visualization VMV'03, 47-54.

VOLINO, P., COURCHESNE, M., AND MAGNENAT THALMANN, N. 1995. Versatile and efficient techniques for simulating cloth and other deformable objects (Универсальные и эффективные технические решения для имитации ткани и других деформируемых объектов). Proceedings of АСМ SIGGRAPH 95, 137-144.

VOLINO, P., MAGNENAT-THALMANN, N., AND FAURE, F. 2009. A simple approach to nonlinear tensile stiffness for accurate cloth simulation (Простой подход к нелинейной жесткости на растяжение для точной имитации ткани).). АСМ Trans. Graph. 28, 4, 105:1-105:16.

WANG, H., O'BRIEN, J.F., AND RAMAMOORTHI, R. 2011. Data-driven elastic models for cloth: modeling and measurement (Управляемые данными упругие модели ткани: моделирование и измерение). АСМ Trans. Graph. 30, 4, 71:1-71:12.

XIA, W., AND NADLER, B. 2011. Three-scale modeling and numerical simulations of fabric materials (Трехмасштабное моделирование и численная имитация тканевых материалов). International Journal of Engineering Science 49, 3, 229-239.

YAMANE, K., AND NAKAMURA, Y. 2006. Stable penalty-based model of frictional contacts (Стабильная модель контактного трения на основе пенализации). Proceedings of IEEE International Conference on Robotics and Automation 2006, 1904-1909.

Описание изобретения

Крупномасштабное механическое поведение тканого материала определяется механическими свойствами нитей, рисунком переплетения и контактным трением между нитями. Использование традиционных методов имитации для решения проблем моделей упругих стержней и контакта между нитями в случае имитации тканых изделий при реальных плотностях нитей считается затруднительным. Настоящее изобретение обеспечивает эффективное решение для имитации ткани на уровне нити в результате использования новой дискретизации переплетенных нитей на основе пересечений нитей и скольжения нитей, которое позволяют моделировать контакт между нитями в неявном виде и, в общей сложности, полностью избежать проблемы контакта на пересечениях нитей. В сочетании с моделями для внутренних сил в нитях и межнитевого контактного трения, а также с решателем с массовым параллелизмом. Настоящее изобретение позволяет имитировать швейные изделия с сотнями тысяч пересечений нитей при реальных частотах кадров на настольном компьютере, демонстрирующем комбинации крупномасштабных и мелкомасштабных эффектов, вызванных механикой на уровне нити.

Первый аспект настоящего изобретения относится к реализуемому компьютером способу имитации поведения тканого материала на уровне нити. Способ содержит:

- получение структурной информации по тканому материалу, где указанная структурная информация включает в себя, по меньшей мере, расположение нитей основы, нитей утка и узлов пересечения нитей тканого материала;

- применение граничных условий на множестве временных шагов;

- описание каждого узла пересечения нитей тканого материала с помощью координаты 3D-положения и двух координат скольжения - координаты (u) скольжения и координаты (v) скольжения соответственно нити основы и нити утка;

- измерение сил в каждом узле пересечения нитей на основе силовой модели, где эти силы измеряют как в координате 3D-положения, так и в координатах (u, v) скольжения узлов пересечения нитей;

- вычисление движения каждого узла пересечения нитей на множестве временных шагов с помощью уравнений движения, полученных с использованием уравнений Лагранжа-Эйлера и подвергнутых численному интегрированию по времени, причем эти уравнения движения учитывают массовую плотность (ρ), распределенную равномерно вдоль нитей, а также измеренные силы и граничные условия.

Граничные условия задаются как внешние силы в точках пересечения нитей или как движение объекта или человека, который взаимодействует с тканым материалом, где силы между объектом/человеком и тканью измеряются в узлах пересечения нитей в контакте.

Расположение нитей основы, нитей утка и узлов пересечения нитей тканого материала включает в себя направления нитей и их плотности. Межнитевое расстояние может быть непосредственно получено из расположения нитей.

Структурная информация по тканому материалу может дополнительно включать в себя любую приводимую ниже информацию:

- 2D-рисунок тканого материала, включающего в себя вставки другого материала и места швов;

- расположение нитей основы, нитей утка и узлов пересечения нитей для каждой вставки другого материала;

- рисунок переплетения тканого материала для каждой вставки другого материала;

- плотность и ширину нитей для всех других типов нитей, используемых в тканом материале;

- механические параметры для всех других типов нитей, используемых в тканом материале, где указанных механические параметры включают в себя, по меньшей мере, любой из приводимых ниже параметров:

- модуль упругости,

- модуль изгиба,

- модуль контактного смещения,

- коэффициент трения скольжения,

- отношение демпфирования к массе,

- отношение демпфирования к упругости.

Полученная структурная информация по тканому материалу в предпочтительном варианте осуществления включает в себя коэффициент трения скольжения нитей, а силовая модель включает в себя силы трения скольжения и использует коэффициент трения скольжения и координаты скольжения.

В предпочтительном варианте осуществления полученная структурная информация по тканому материалу включает в себя жесткость нитей, а силовая модель включает в себя контакт между соседними параллельными нитями и использует координаты скольжения, жесткость нитей и межнитевое расстояние, полученное из расположения нитей.

В еще одном предпочтительном варианте осуществления полученная структурная информация по тканому материалу включает в себя модуль упругости нитей, а силовая модель включает в себя силы растяжения. Полученная структурная информация по тканому материалу может также включать в себя модуль изгиба нитей, а силовая модель может включать в себя изгибающие силы. Силовая модель может также использовать межнитевое нормальное сжатие на пересечениях нитей, использующее нормальные составляющие сил растяжения и изгиба.

Полученная структурная информация по тканому материалу в предпочтительном варианте включает в себя модуль контактного смещения нитей, а силовая модель включает в себя силы смещения.

Дополнительный аспект настоящего изобретения относится к системе имитации поведения тканого материала на уровне нити, содержащий:

- средство хранения данных для хранения структурной информация по тканому материалу, где указанная структурная информация включает в себя, по меньшей мере, расположение нитей основы, нитей утка и узлов пересечения нитей тканого материала; и

- средство обработки данных, выполненное с возможностью получения указанной структурной информации и применения граничных условий на множестве временных шагов;

описания каждого узла пересечения нитей с помощью координаты 3D-положения и двух координат скольжения - координаты скольжения и координаты скольжения соответственно нити основы и нити утка;

измерения сил в каждом узле пересечения нитей на основе силовой модели, где эти силы измеряют как в координате 3D-положения, так и в координатах скольжения узлов пересечения нитей;

вычисления движения каждого узла пересечения нитей на множестве временных шагов с помощью уравнений движения, полученных с использованием уравнений Лагранжа-Эйлера и подвергнутых численному интегрированию по времени, причем эти уравнения движения учитывают массовую плотность, распределенную равномерно вдоль нитей, а также измеренные силы и граничные условия.

Дополнительный аспект настоящего изобретения относится к носителю записи, содержащему компьютерную программу, для моделирования поведения тканого материала на уровне нити, обеспечивающую функционирование компьютера, который может использовать программный код для выполнения этапов описанного выше способа. Компьютерная программа в предпочтительном варианте осуществления хранится на средстве поддержки программ, таком как CD, DVD, карта памяти или жесткий диск.

Ключевым аспектом способа имитации ткани на уровне нити является дискретизация, сфокусированная на пересечениях нитей, состоящих из 3D-положения точки пересечения плюс две дополнительные степени свободы для описания скольжения нитей, с последующей дискретизацией стержня Эйлера. [Sueda и др. 2011]. Проблему межнитевого контакта решают в неявном виде, что позволяет полностью избежать вычисления обнаружения столкновений и реакции на столкновения между пересекающимися нитями.

На основе предложенной дискретизации составляются силовые модели для низкоуровневой механики нити. Они включают в себя силы растяжения и изгиба отдельных нитей. Но, что наиболее важно, новая дискретизация обеспечивает возможность простых формул межнитевых контактных сил, в частности, трения скольжения при пересечениях нитей и контакте между соседними параллельными нитями. Механика на уровне нити позволяет естественным путем получить интересные эффекты, такие как пластичность на уровне нити или влияние рисунка переплетения на крупномасштабное поведение.

Для надежной имитации ткани на уровне нити в динамических уравнениях применяется неявное интегрирование. Был разработан решатель с массовым параллелизмом, который использует рисунок переплетения, а также новую дискретизацию. GPU-реализация позволяет имитировать полотно с более чем 300 K узлами и 2 K нитями на настольном компьютере со скоростью чуть выше 2 мин/кадр (где один кадр составляет 1/24-ую часть секунды).

Предсказание драпировки швейных изделий принимает в качестве входных данных следующие параметры:

- 2-D расположение рисунков швейных изделий, указывающее на то, какие участки границ рисунка составляют швы. 2D-рисунок тканого материала включает в себя расположение вставок другого материала и как эти вставки другого материала сшиваются (положения швов).

- Направления нитей основы и утка на 2D-рисунках.

- Плотности нитей как в направлении основы, так и в направлении утка.

- Рисунок переплетения, то есть полотняное переплетение, саржа, сатин и т.д. Рисунок переплетения указывает на каждом пересечении нитей, какая нить - основа или уток находится сверху.

- Ширину нитей для всех различных типов нитей, используемых в швейном изделии.

- Механические параметры для всех различных типов нитей, используемых в швейном изделии.

Эти параметры включают в себя:

- Модуль упругости.

- Модуль изгиба.

- Модуль контактного смещения.

- Коэффициент трения скольжения.

- Отношение демпфирования к массе и отношение демпфирования к упругости.

Механические параметры, могут быть получены в результате выполнения испытаний Кавабата на растяжение, сдвиг и изгиб [Kawabata 1980] с последующей подгонкой параметров к кривым измерений силы-деформации.

В результате предсказания механического и визуального поведения любого вида ткани настоящее изобретение обеспечивает возможность эффективных имитаций ткани на уровне нити с высоким разрешением и коротким временем вычислений. Изобретение заменяет непрерывные модели на модели на основе конечно-элементных дискретизаций объемных нитей и модели на уровне нити, которые представляют нити основы и утка по отдельности и в результате решают проблему контакта между ними. Настоящее изобретение обеспечивает надежное, реалистическое и эффективное предсказание поведение всей ткани, начиная от поведения отдельных нитей.

Изобретение обеспечивает следующие преимущества в текстильном секторе:

- Снижение затрат, повышение производительности и увеличение гибкости в дизайне и инновации текстильных материалов. Характеристики новых материалов могут быть оценены на имитируемых прототипах.

- Выполнение текстильного анализа для оценки неправильного дизайна продуктов.

- Проведение высококачественных анимаций новых швейных изделий для целей маркетинга.

Изобретение может быть использовано в различных отраслях:

- Проектирование текстильных тканей.

- Проектирование одежды и тканей.

- Коммерциализация тканей.

- Автомобильная отрасль: текстильные элементы обивки.

- Медицина: тканые материалы для изготовления стентов и т.д.

Краткое описание чертежей

Ряд чертежей, которые помогают лучшему пониманию изобретения и которые в явной форме связаны с вариантом осуществления указанного изобретения, представленным в качестве неограничивающего примера этого изобретения, описываемого в краткой форме ниже.

Фигуры 1А, 1В и 1С - различные рисунки переплетения с увеличением поплавков: полотно, саржа и сатин.

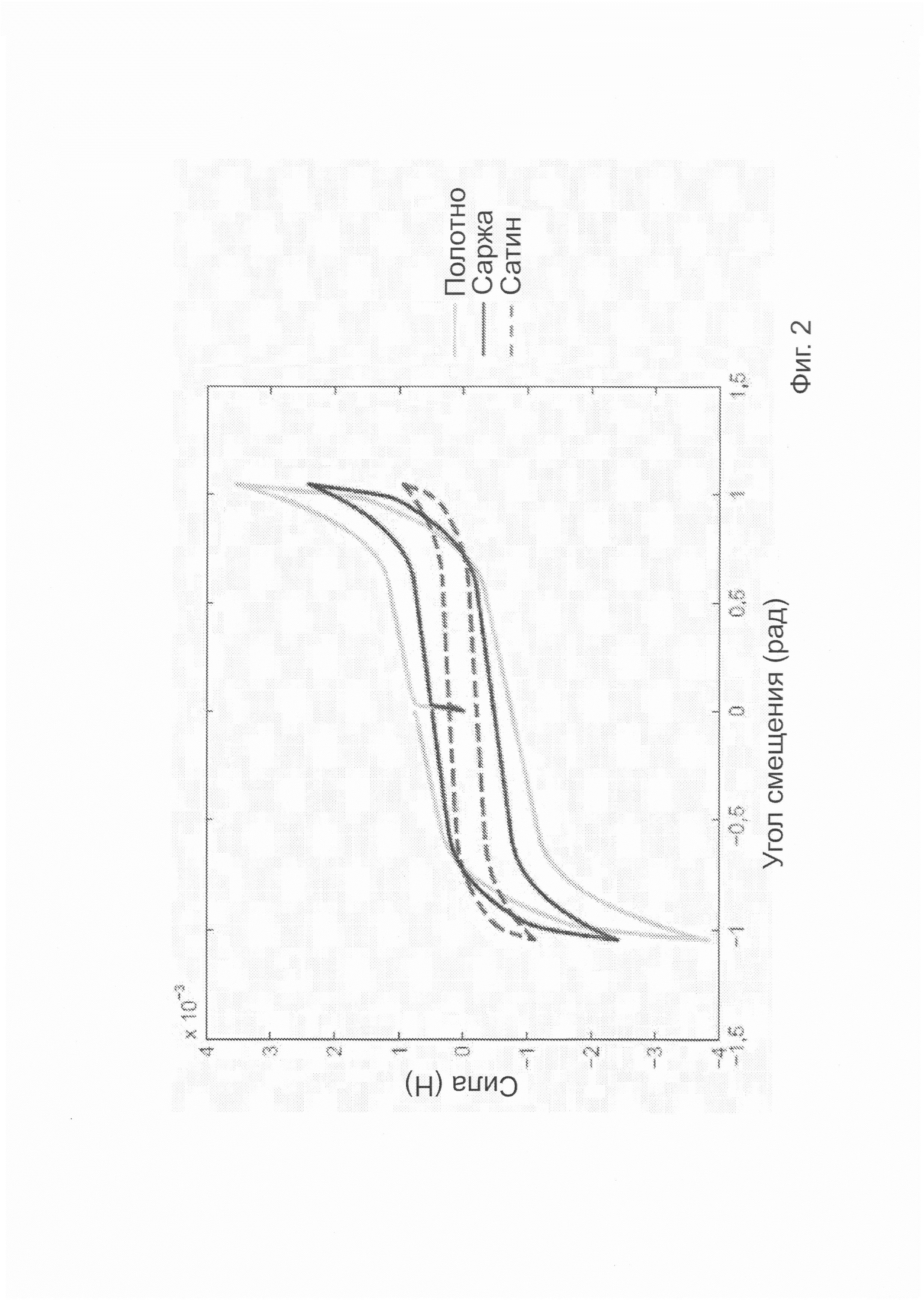
Фигура 2 - график зависимости силы от угла смещения для трех примеров драпировочных полотен на фигуре 1.

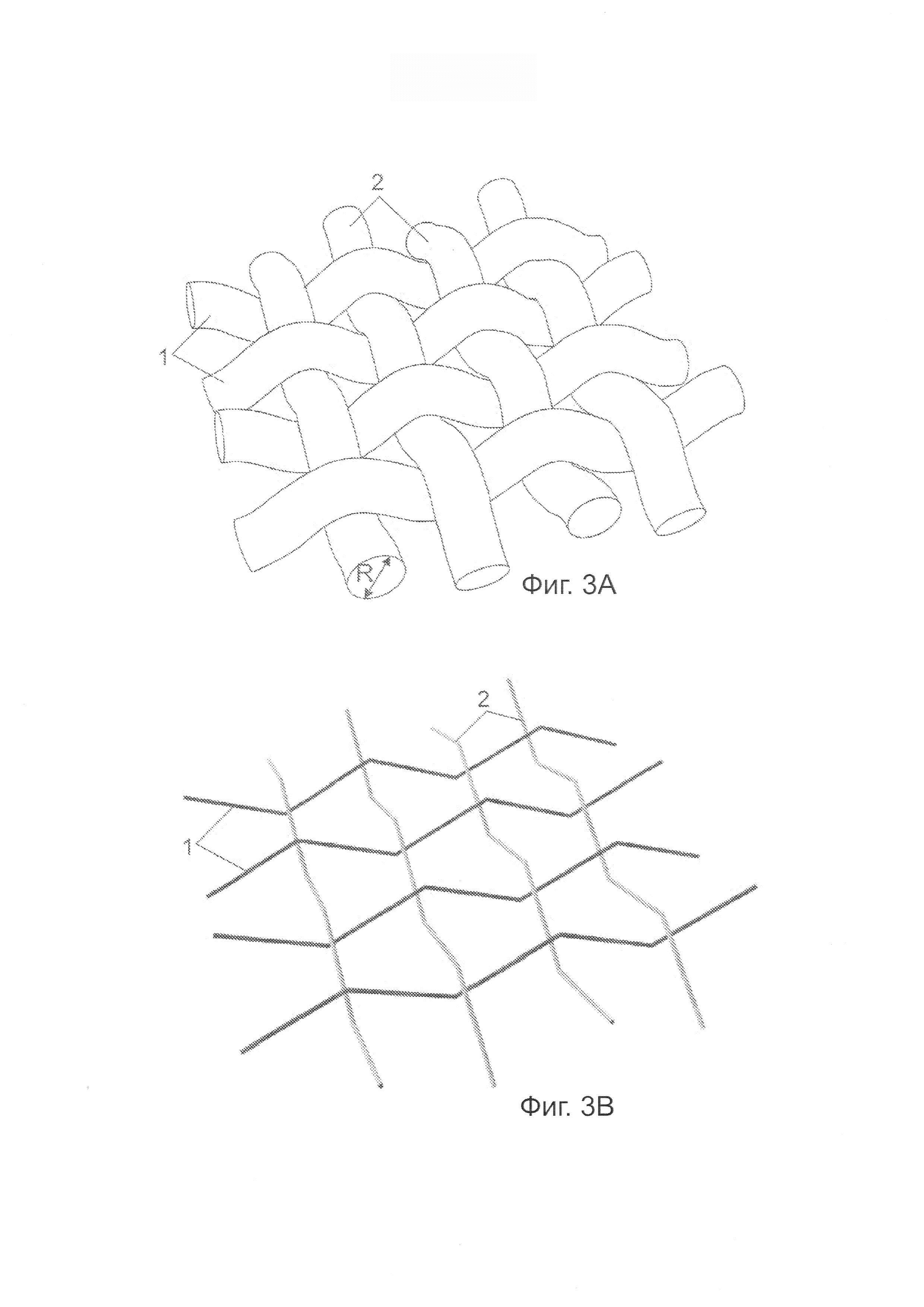
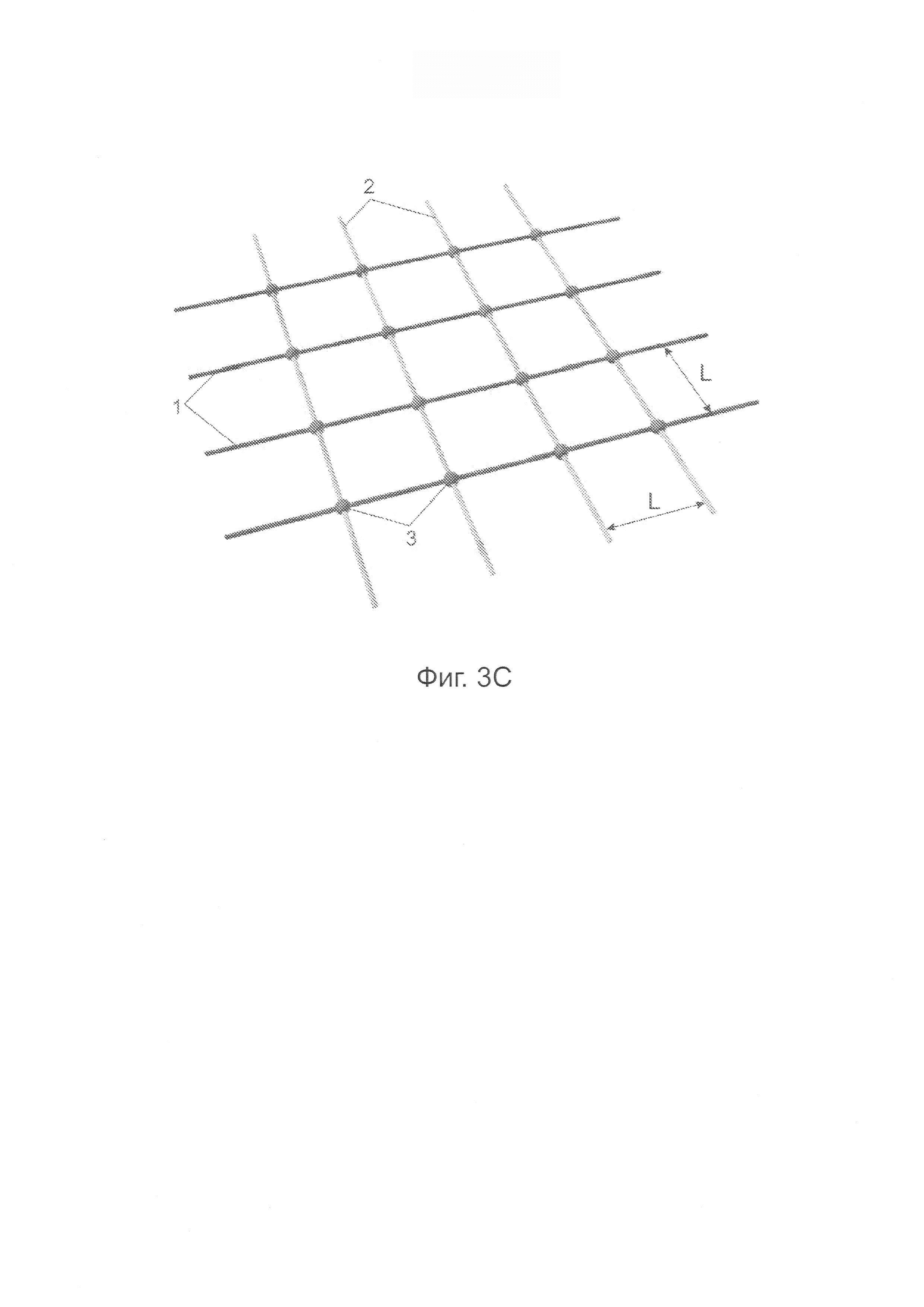
Фигуры 3А-3С - модели сплетенных нитей, используемых в настоящем изобретении: 3D-объемные нити (фиг. 3А), переплетенные стержневые сегменты с извитостью (фиг. 3В), стержневые сегменты, пересекающиеся в 5-DoF-узлах пересечения (фиг. 3С).

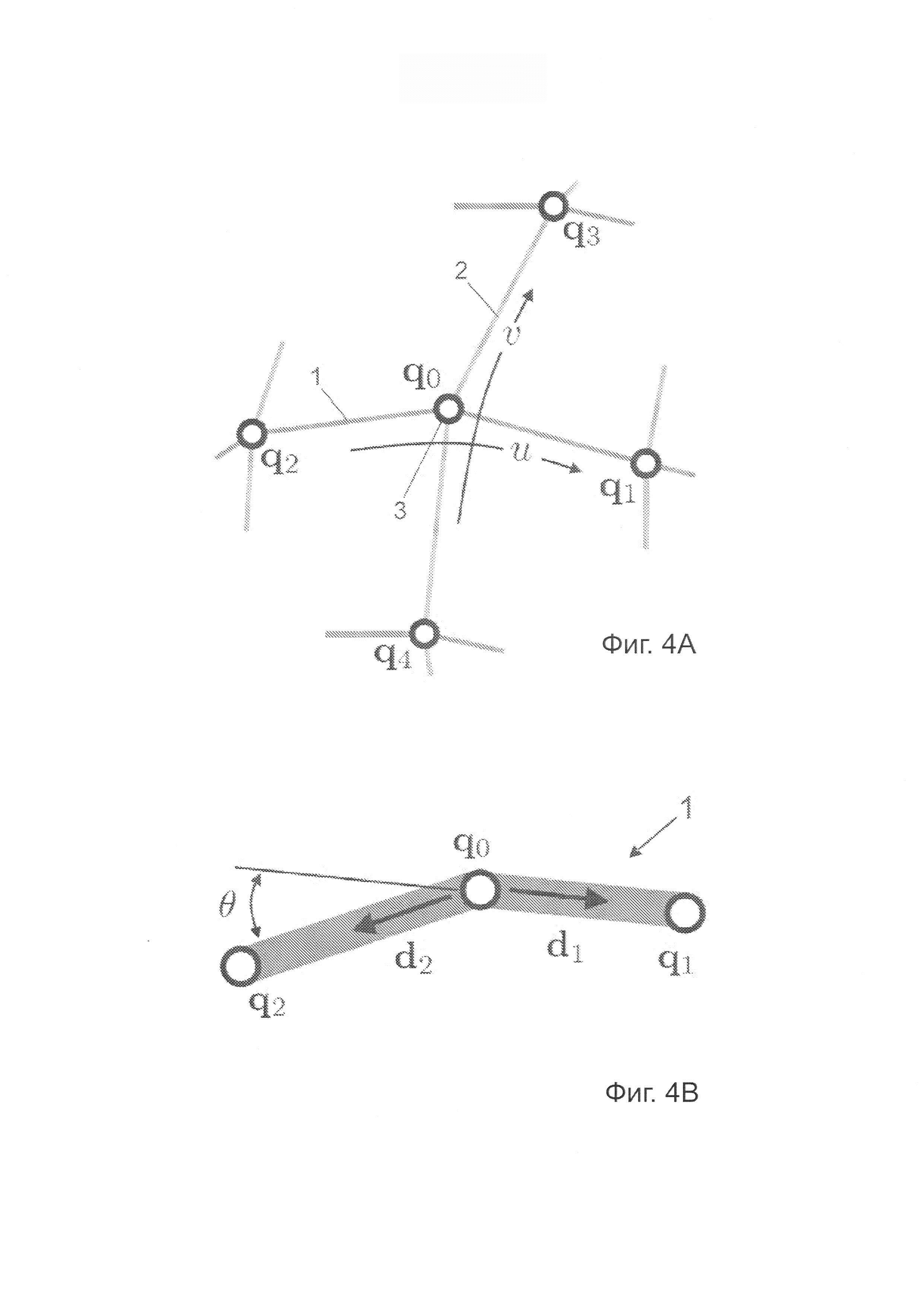
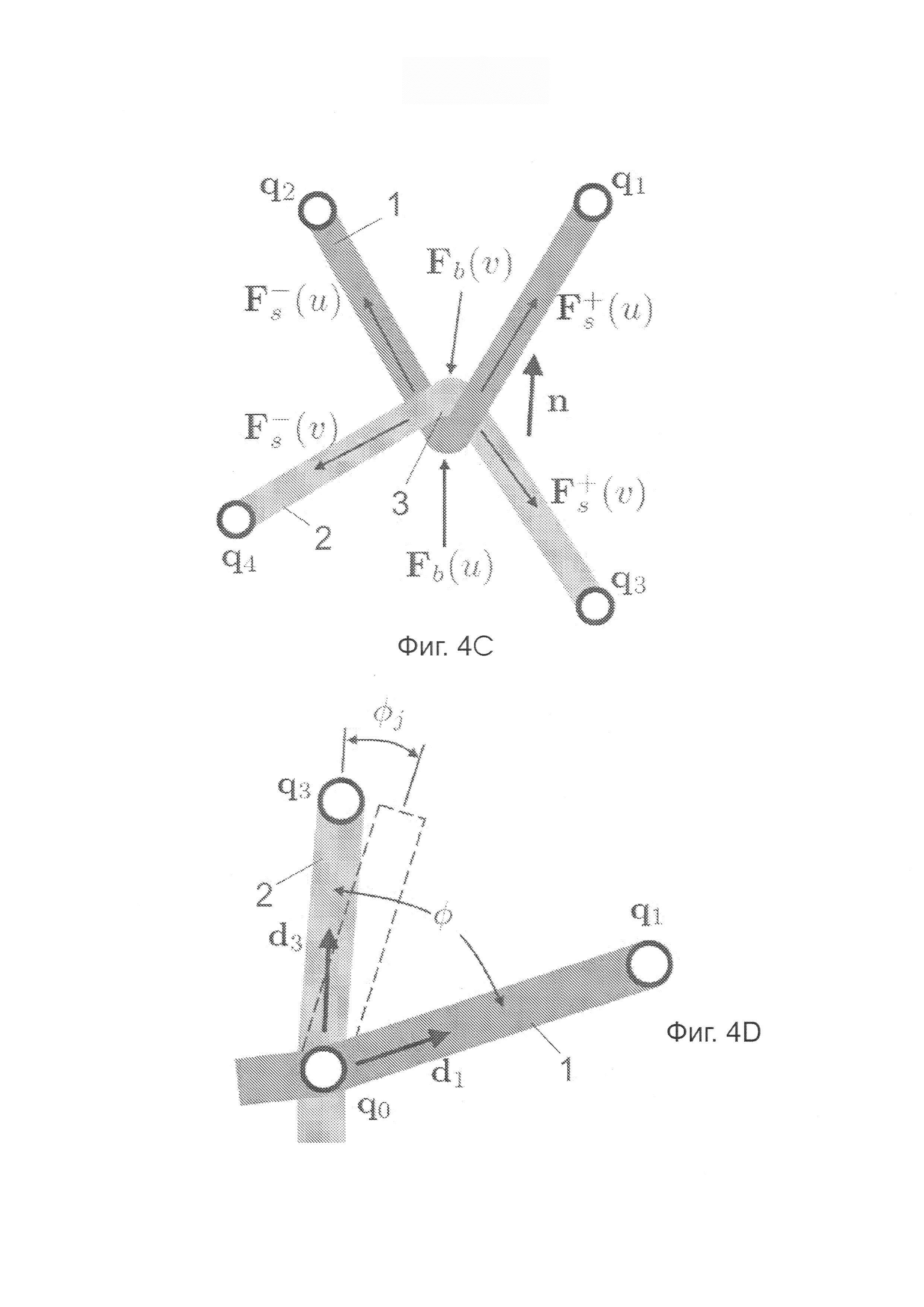
Фигура 4А - нити основы и утка, пересекающиеся в узле q0, и четыре соседние пересечения нитей. Фигура 4В - угол θ изгиба между двумя соседними сегментами основы. Фигура 4С - силы, создающие нормальное сжатие в узле пересечения. Фигура 4D - угол смещения

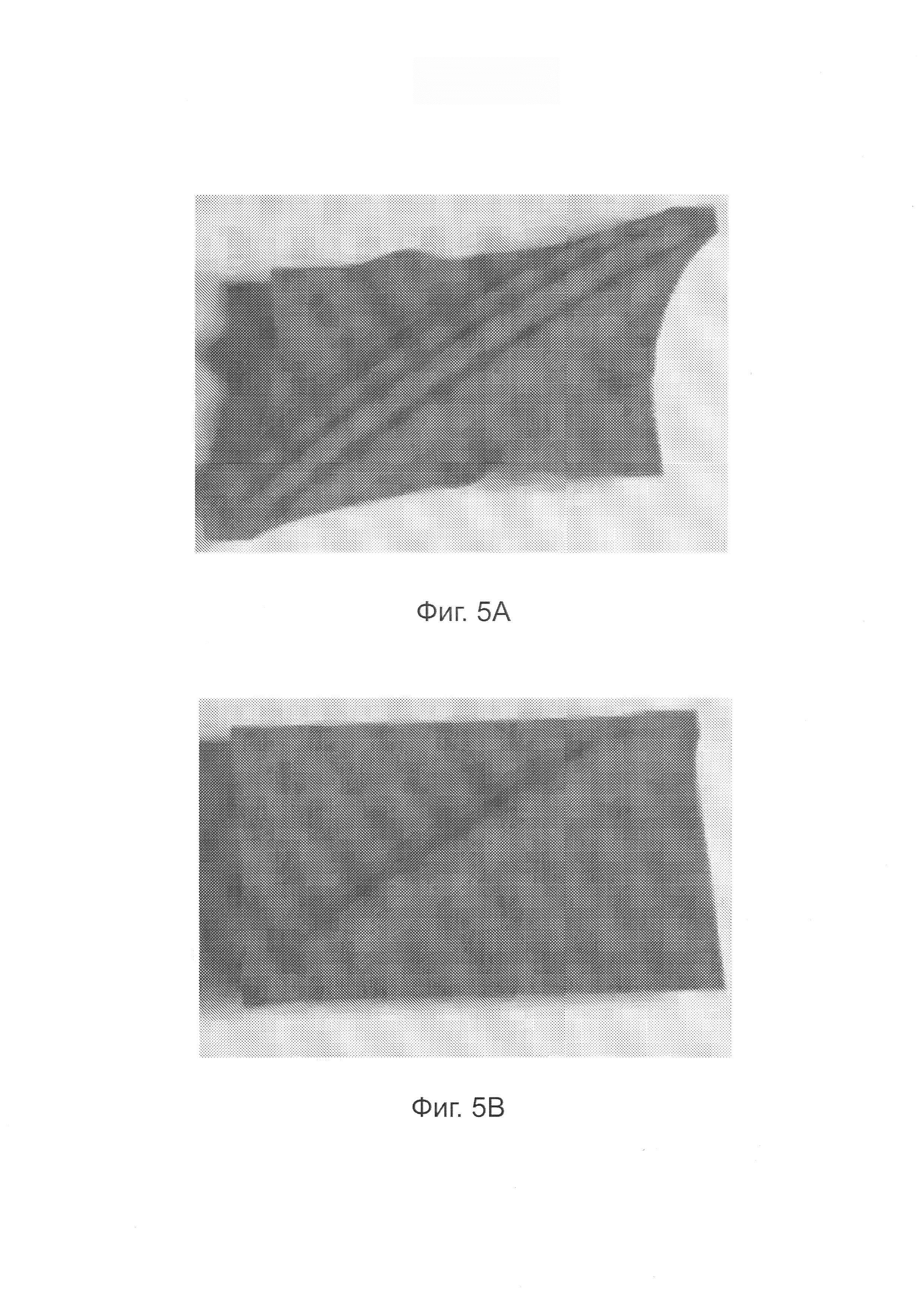
Фигуры 5А и 5В - эффекты касательного трения на образце, подвергнутом растяжению (фигура 5А) с последующим отпусканием (фигура 5В), оставляющие стойкую морщину.

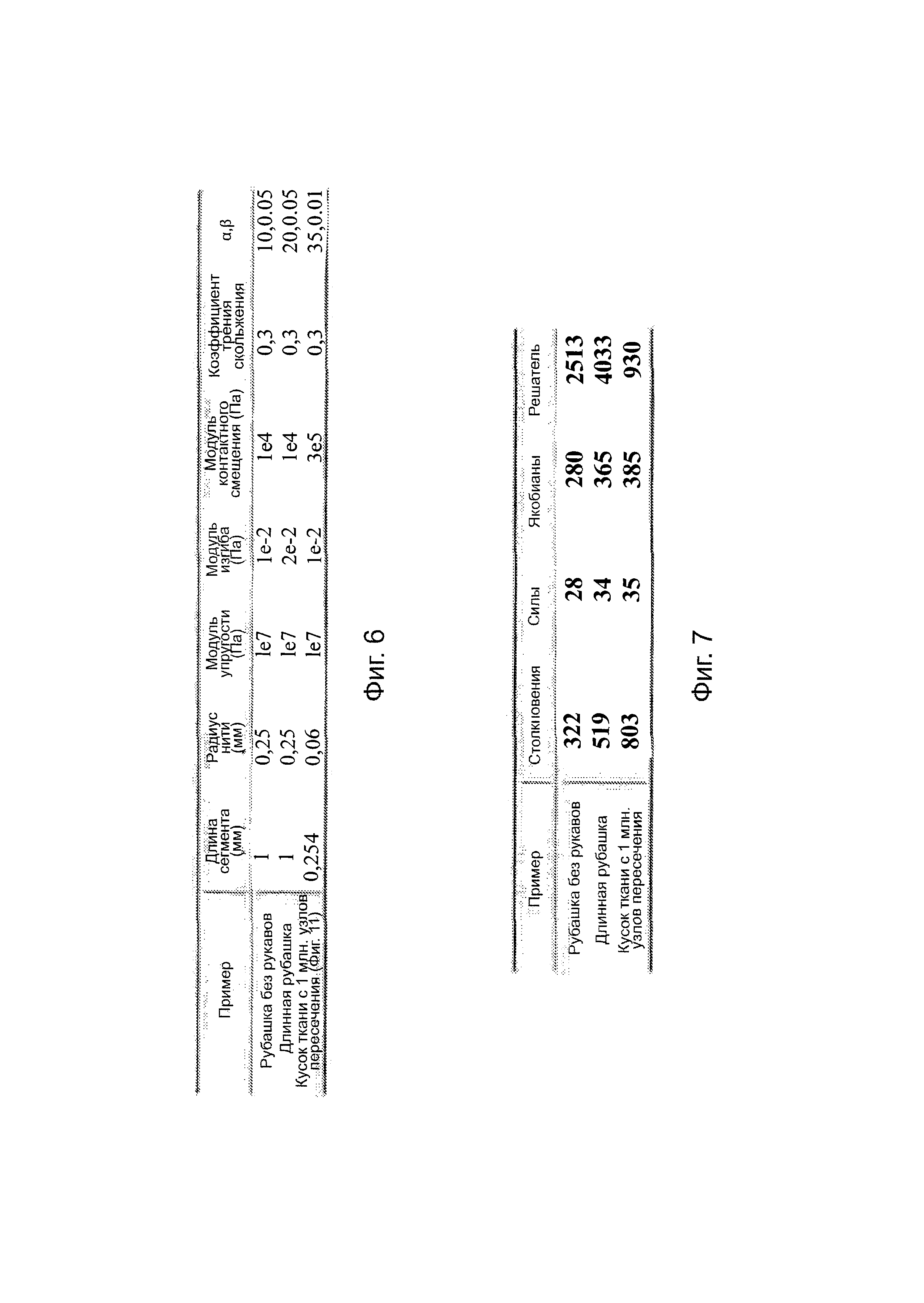
Фигура 6 - таблица значений параметров, используемых в примерах.

Фигура 7 - таблица средней стоимости каждого временного шага (в миллисекундах) для примеров с разбивкой по шагам.

Фигура 8 - пример свободной рубашки без рукавов с 2023 нитями и 350530 узлами пересечения, иллюстрирующий большие движения, а также мелкомасштабные складки и морщины.

Фигура 9 - пример длинной рубашки с 3199 нитями и 559241 узлом пересечения.

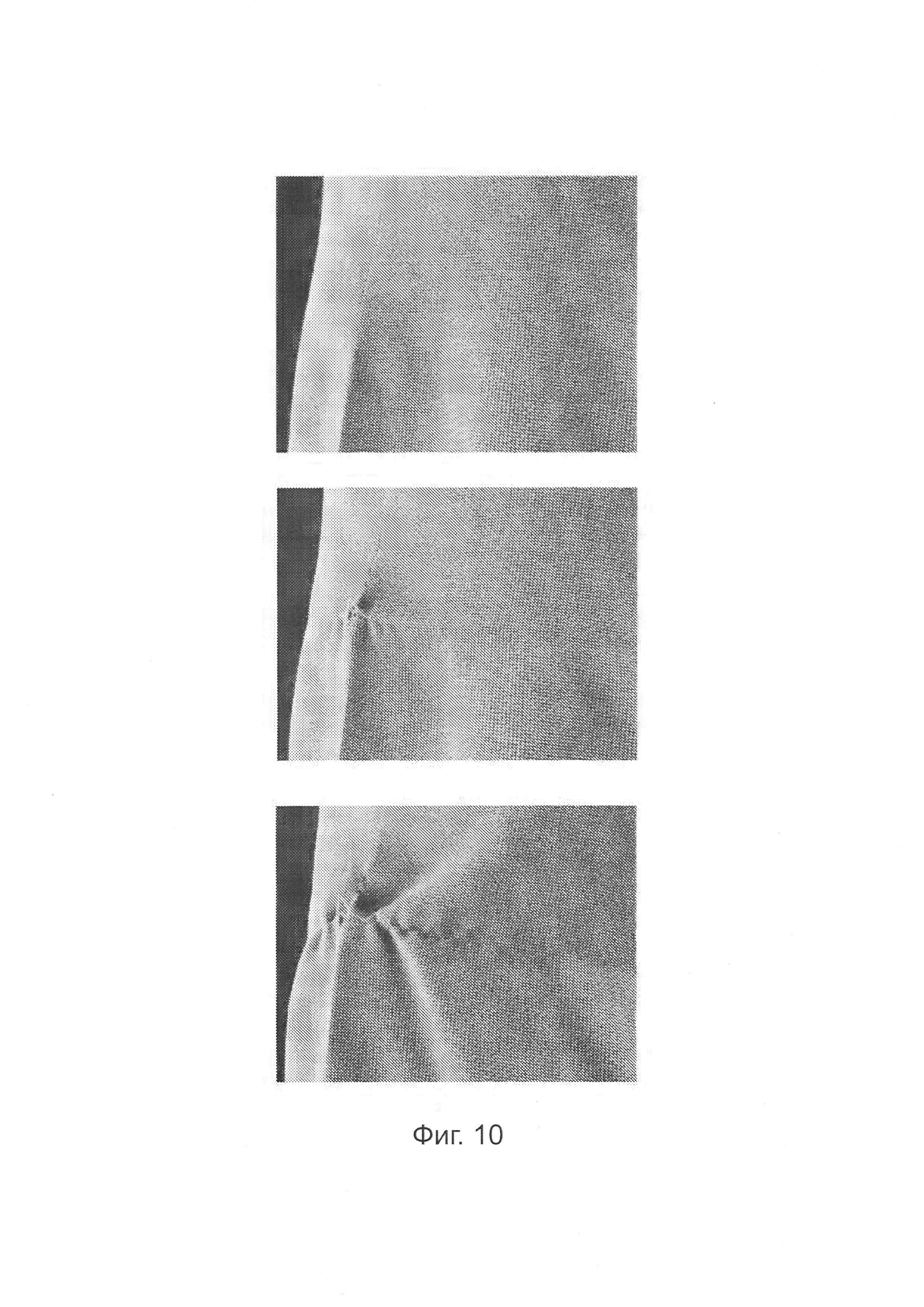
Фигура 10 - пример имитации затяжки, созданной на рубашке с 2023 нитями и 350530 узлами пересечения в результате вытягивания узла шва, на уровне нити.

Фигуры 11А-11С - примеры затяжки на свободной рубашке без рукавов на фиг. 8, созданной в области живота. Фигура 11А - затяжка, сформированная в результате вытягивания двух нитей при задерживании движения полотна в сторону. Фигура 11В - реальная затяжка при подобных условиях. Фигура 11С - затяжка на фиг. 11А в увеличенном масштабе.

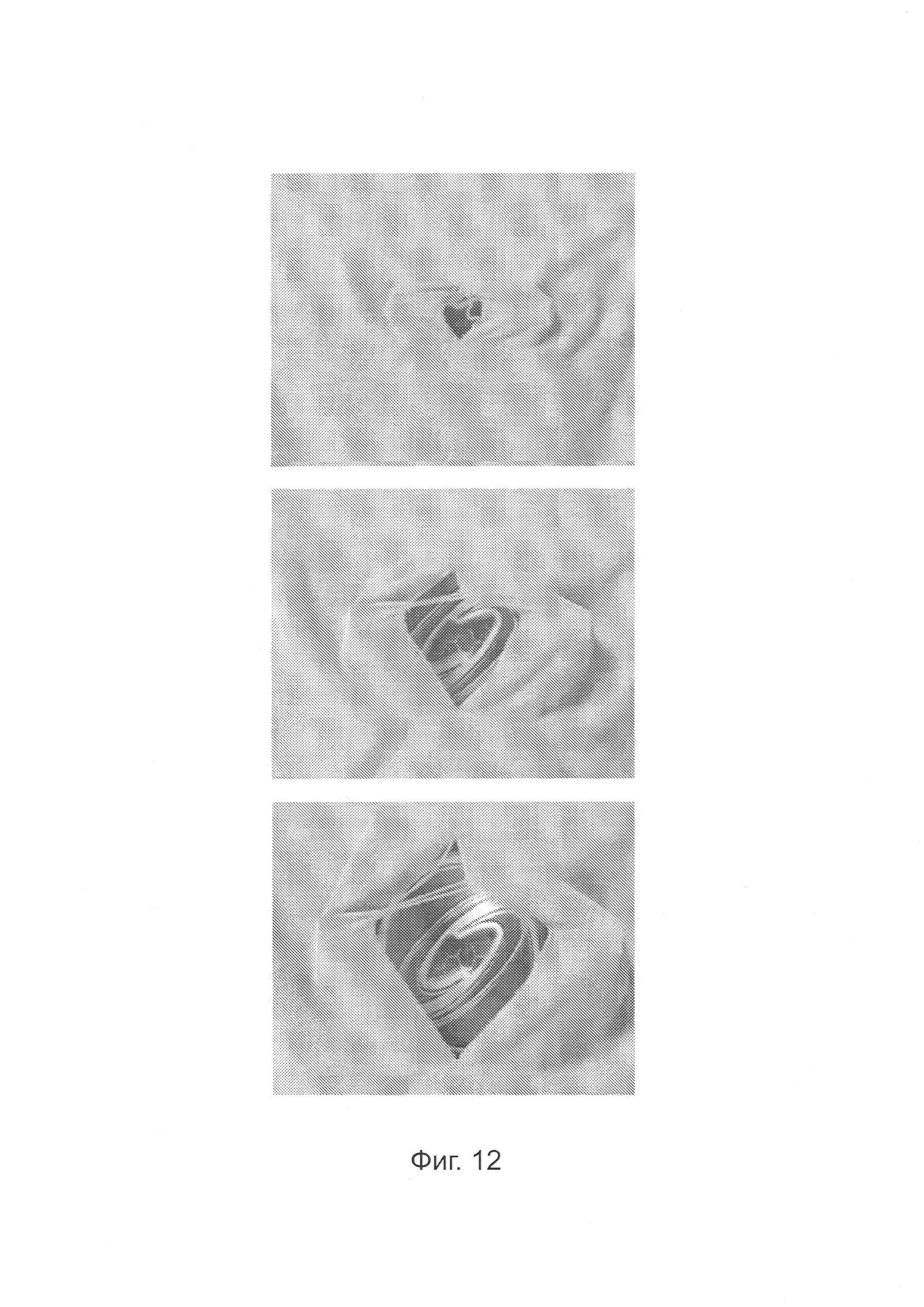
Фигура 12 - свободная рубашка без рукавов на фиг. 8, порванная в результате захвата некоторых узлов и их разделения. Нити разъединены и края обтрепываются.

Фигуры 13А и 13В - кусок полотняной ткани с числом нитей на дюйм, составляющим 100 (1 миллион узлов пересечения). Во время движения появляются мелкие морщины (фигура 13А), а при прекращении движения этого куска остаются большие драпировочные морщины (фигура 13В).

Описание предпочтительного варианта осуществления изобретения

Прежде всего рассмотрим конструирование моделей ткани на основе нити. Затем будет представлен ключевой признак модели ткани на основе нити: дискретизация кинематики нити на основе положений точек пересечения нитей и скольжения нитей. В заключение будут представлены формулы уравнений движения на основе этой дискретизации.

Для конструирования швейного изделия на уровне нити применяется подход индивидуальной адаптации. В качестве входных данных используется 2D-рисунок, который формирует швейное изделие, на каждой 2D-вставке другого материала независимо друг от друга на межнитевом расстоянии L в виде ортогональных прямых линий располагаются нити основы и утка. На каждом шве размещают дополнительную нить и соединяют нити утка и основы с нитями швов с помощью совместно используемых узлов. На границах ткани возможен выбор между добавлением шовных нитей или возможностью свободного вытягивания концов нитей. По коммерческим рисункам модели 3D-ткани могут быть получены автоматически [Berthouzoz et al. 2013], поэтому современный процесс моделирования можно также легко автоматизировать.

Зазор между двумя нитями одного и того же типа без переплетения с другой нитью образует поплавок. Различные рисунки переплетения, такие как полотняное переплетение (без поплавков), саржа, сатин и т.д. получают путем изменения распределения поплавков и, таким образом, воздействия на механику полученной ткани. Фигуры 1А, 1В и 1С показывают различные рисунки переплетения с увеличением поплавков: рисунок полотняного переплетения (фиг. 1А), рисунок саржи (фиг. 1В) и рисунок сатина (фиг. 1С). Увеличение поплавков приводит к снижению сопротивления смещению и, следовательно, к осыпанию ткани при закреплении за два угла.

Для моделирования рисунка переплетения для каждой вставки другого материала выбирается произвольная ориентация и на каждом пересечении нитей сохраняется флаг, указывающий, какая нить - основа или уток находится сверху. Эта простая стратегия позволяет осуществлять моделирование полотняного переплетения, саржи, сатина и всех других обычных переплетений. На фигуре 2 представлен график зависимости силы (в Н) от угла смещения (в радианах) для трех примеров драпировочных полотен на фигурах 1А, 1В и 1С. График ясно показывает силу смещения, трение и застревание, а также различное поведение в зависимости от рисунка переплетения.

В кинематическом представлении объем нитей не учитывается, и все нити рассматриваются как плоские, лежащие в одной и той же плоскости. Тем не менее, вычисление сил и визуализация осуществляются с учетом объема нитей. На фигурах 3А, 3В и 3С показаны модели сплетенных нитей (нитей 1 основы и нитей 2 утка), использованные в настоящем изобретении. Извитость является изгибом, внедренным в нить 1 основы и/или в нить 2 утка для обеспечения переплетения, показанного на фигуре 3А. Извитость также создает силы сжатия между переплетенными нитями, и это сжатие обеспечивает существование сил трения, которые удерживают ткань от смещения. В настоящем примере реализации извитость, приложенная к нитям как утка 2, так и основы 1, смещает эти нити на радиус нити R в противоположных направлениях, как показано на фигуре 3В. Настоящая реализация может быть распространена на допуск анизотропной извитости. Для вычисления нормальной силы 3-D объемные нити куска ткани, показанные на фигуре 3А, заменяют на переплетенные стержневые сегменты с извитостью (фигура 3В), а для всего остального - на стержневые сегменты, пересекающие узлы 3 пересечения с 5-ю степенями свободы (5-DoF) (фигура 3С). Объемный вид восстанавливается при визуализации.

Для простоты представления предполагают, что межнитевое расстояние L и радиус нити R являются одинаковыми для основы 1 и для утка 2, но, как правило, это предположение делают менее строгим, и на самом деле настоящая реализация поддерживает анизотропную ткань.

В ткани подавляющее большинство нитей находятся в контакте на пересечениях нитей, так что, как правило, можно предположить, что такие контакты поддерживаются в процессе имитации. Движение ткани может быть описано как проблема ограниченной динамики с дискретизацией нитей на основе узла плюс большое число контактных ограничений, которые поддерживают нулевое расстояние между нитями на пересечениях нитей. Но было замечено, что, вместо обнаружения и разрешения таких контактов, более эффективным является выбор подходящей дискретизации на основе пересечений нитей.

Фигура 4А показывает нити основы 1 и утка 2, пересекающиеся в узле q₀, и четыре соседних пересечений нитей (q_1f q₂, q₃, q₄). Нити основы 1 и утка 2 параметрированы на основе недеформированной длины их дуги u и v, соответственно. Следовательно, u является недеформированной длиной нити основы (1) между точкой (3) пересечения и одной конечной точкой нити; a v является недеформированной длиной нити утка (2) между точкой (3) пересечения и одной конечной точкой нити. Затем пересечение нитей описывается координатой х 3D-положения и параметрическими координатами материальных точек основы 1 и утка 2 на пересечениях нитей. Изменение координат u и v моделирует скольжение нитей соответственно основы и утка. Пересечение нитей рассматривается как 5-DoF-узел с 3-мя DoF Лагранжа и 2-мя DoF Эйлера. Обозначим координаты

При этом предлагается дискретизировать ткань при помощи комбинации 5-DoF-узлов пересечения нитей и регулярных 3-DoF-узлов. 5-DoF узел задается на каждом пересечении нитей, а регулярные 3-DoF узлы - на конечных точках нитей. Фигура 4А показывает регулярную, структуру с узлом 3 пересечения нитей и четырьмя соседними узлами.

С учетом сегмента основы [q₀, q_i] (и точно так же для сегментов утка) положения линейно интерполируются в соответствии с длиной дуги u. Затем 3D-положение точки внутри сегмента определяется по формуле:

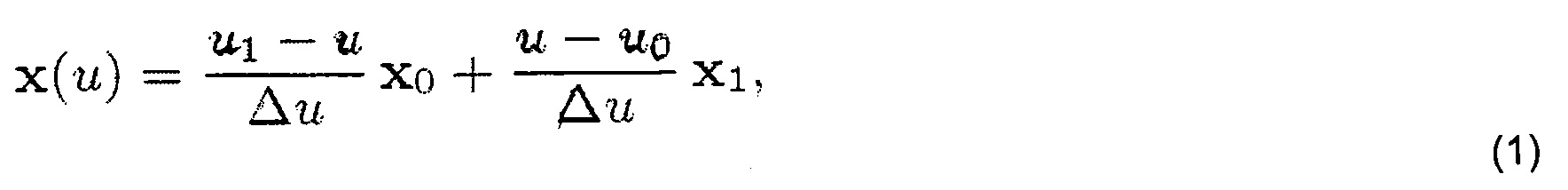
где Δu=u1-u0 - остаток длины сегмента.

Скорость точки внутри сегмента зависит от скоростей точек пересечения нитей, а также от скольжения нитей, и определяется дифференцированием уравнения (1):

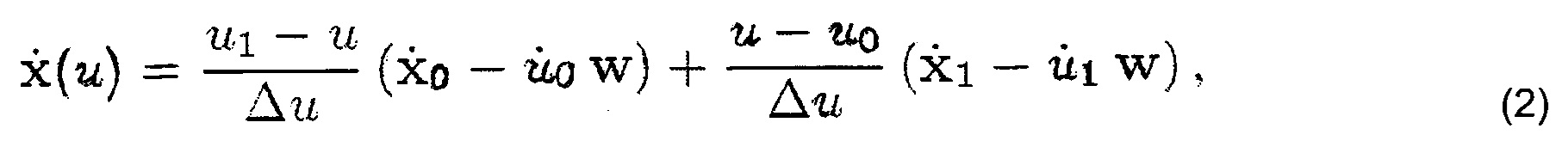
где

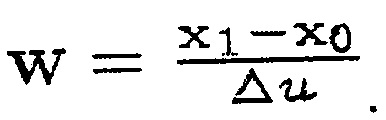
В результате объединения координат пересечения всех нитей определяется вектор обобщенных координат q. Затем с использованием уравнений Лагранжа-Эйлера [Goldstein et al. 2001] могут быть извлечены уравнения движения. Кинетическая энергия составляет

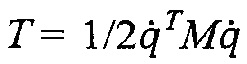
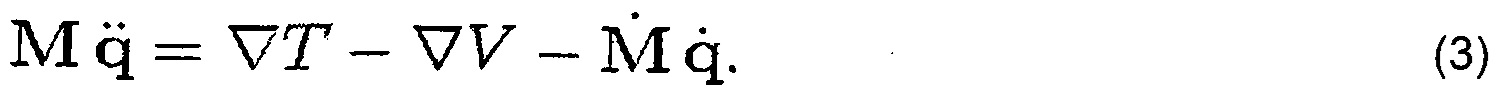
Предполагается, что масса распределена равномерно вдоль нитей, с плотностью ρ. При этом после уравнения (2) скорости для произвольной точки в сегменте основы кинетическая энергия сегмента [q₀, q₁] (и точно так же для сегмента утка) составляет:

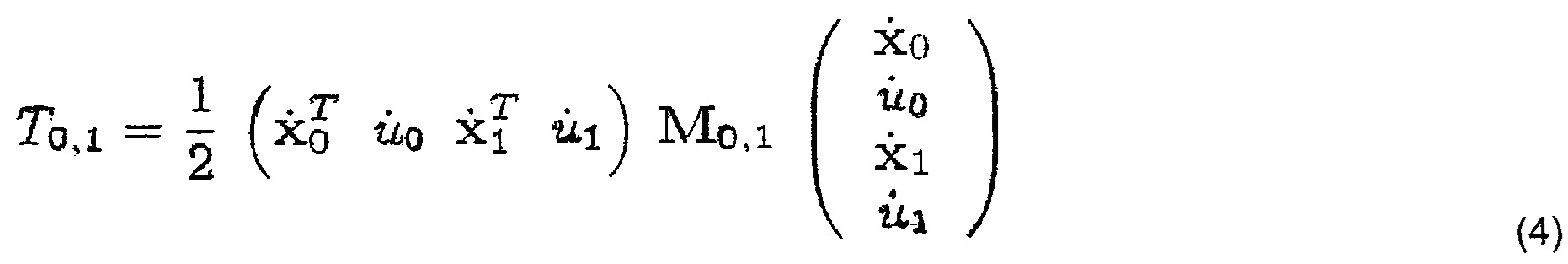
где

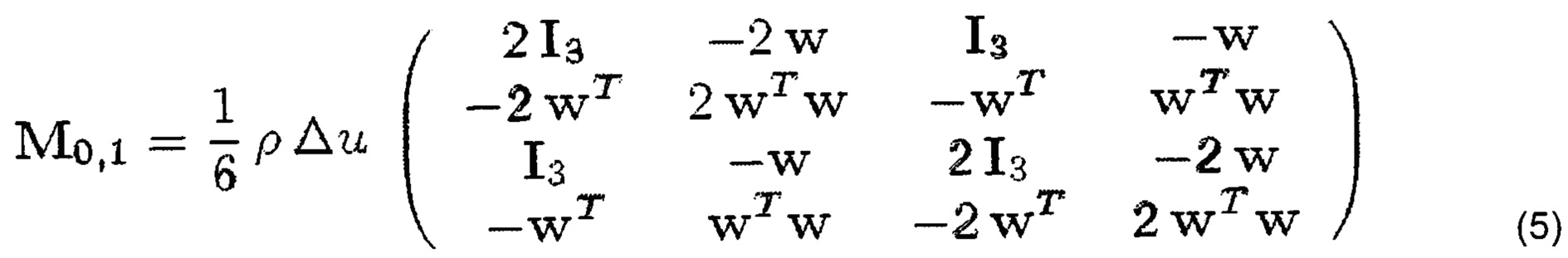
Потенциальная энергия включает в себя множество составляющих, таких как силу тяжести и консервативные внутренние силы. Сила тяжести определяется, например, для сегмента основы [q₀, q₁] как

Рассмотрим теперь формулу внутренних сил в деталях. В дополнение к консервативным силам, извлеченным из энергетических потенциалов, непосредственно в правую сторону уравнений Эйлера-Лагранжа (3) включены также другие силовые составляющие, такое как силы трения и контактные силы. Включено также демпфирование по модели демпфирования по Рэлею, использующей в качестве параметров отношение демпфирования к массе и отношение демпфирования к упругости, с массой и пропорциональными жесткости составляющими, управляемыми соответственно параметрами α и β.

Для силовой модели рассматриваются два типа внутренних сил в ткани. Силы, обусловленные деформацией отдельных нитей, включают в себя силы растяжения и изгиба. Скрученность нити не рассматривается, так как ее влияние на ткань является минимальным. Далее рассмотрим внутренние силы, обусловленные контактом между переплетенными нитями, которые включают в себя нормальное сжатие, трение скольжения, сдвиг и контакт между параллельными нитями.

Консервативные силы описываются в краткой форме с использованием энергетических потенциалов. В общем случае эти потенциалы создают силы как на точках пересечения нитей, так и на координатах скольжения. Кроме того, применение численного интегрирования требует вычисления Якобианов сил, включающих в себя смешанные составляющие, относящиеся к точкам пересечения и координатам скольжения.

Моделирование растяжения осуществляется в соответствии с подходом Шпильмана с соавт. [2007], определяющим энергию растяжения, находящуюся в квадратичной зависимости от напряжения вдоль центральной линии нити. При настоящей дискретизации деформация растяжения является постоянной на каждом сегменте нити. Для сегмента основы [q₀, q₁] это просто

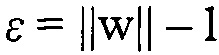
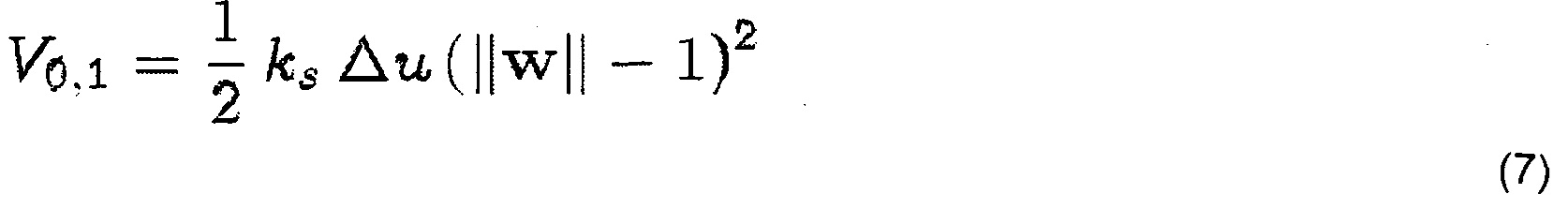
где k_s=YπR², a Y - модуль упругости. Нити ткани зачастую являются близкими к нерастяжимым, что требует использования высокого модуля упругости. В другом варианте обеспечить нерастяжимость можно с помощью ограничений и множителей Lagrange. Однако для настоящей реализации был разработан решатель для неявного интегрирования, подробное описание которого будет приведено ниже и который обеспечивает возможность эффективной имитации жестких нитей.

Для модели изгиба выполняется подход дискретной дифференциальной геометрии, определяющий энергии изгиба на основе дискретной кривизны пересечений нитей по отдельности для нитей основы и утка. Существуют несколько возможных определений дискретной кривизны на пересечениях нити [Sullivan 2008], но в данном документе кривизна определяется просто как угол между сегментами нити. В результате деления на длину дуги между центрами сегмента эта кривизна преобразуется в плотность кривизны. Для нити 1 основы на фигуре 4В с учетом угла θ между сегментами [q₂, q₀] и [q₀, q_i] плотность кривизны в узле q₀ определяется как

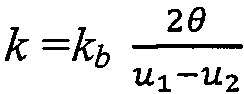
где k_b=BπR², а В - модуль изгиба. При сколь угодно близких пересечениях нитей выражение может становиться численно неустойчивым. Однако из-за модели контакта между параллельными нитями, описываемой ниже, этого практически не происходит. Bergou с соавт. [2008] выбрал другую метрику дискретной кривизны, основанную на тангенсе угла между сегментами. При полном изгибе нити полученная энергия возрастает до бесконечности, что на практике создает также чрезмерное сопротивления изгибу. Еще один вариант состоит в использовании метрики дискретной кривизны на основе синуса половинного угла между сегментами, но эта метрика приводит к созданию энергии невыпуклого изгиба.

Ткань удерживается от смещения за счет межнитевого трения, а допустимые силы трения определяются в зависимости от межнитевого нормального сжатия на пересечениях нитей. Настоящая дискретизация нити не учитывает относительное движение между нитями основы 1 и утка 2 вдоль их нормального направления, и, следовательно, нормальное сжатие не может моделироваться как упругий потенциал. Вместо этого в данном документе предлагается квазистатическая аппроксимация, которая описывает эффекты требуемого трения. По существу, сила сжатия оценивается путем усреднения нормальных составляющих сил основы и утка, показанных на фигуре 4С, и затем это сжатие может быть использовано для моделирования сил трения и смещения [Page and Wang 2000].

Ниже приводится подробное описание вычислений. На каждом пересечении 3 нитей с использованием положения узла и его соседних четырех узлов вычисляется плоскость оптимальной подгонки. В качестве нормального направления n выбирается нормаль плоскости в направлении от нити 1 основы к нити 2 утка. Извитость прикладывается путем смещения положений точек основы и утка в нормальном направлении на радиус нити (фигура 3В), после чего силы изгиба вычисляются повторно. На каждом пересечении нитей путем суммирования нормальных составляющих сил F_s и F_b соответственно растяжения и изгиба (на фигуре 4С верхние индексы + и - обозначают соответственно положительное и отрицательное направления нити) и усреднения полученных в результате сил для направлений основы и утка оценивается сила сжатия, то есть

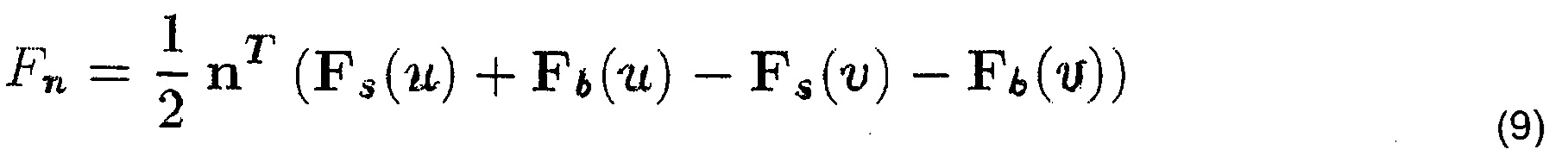
При отрицательной силе сжатия считается, что нити разделяются, а сила стремится к нулю. Существует возможность распространения этой модели на решение проблемы сцепления.

При этом мы учитываем только за силы растяжения и изгиба. При растягивании ткани растяжение преобладает над сжатием. Однако, в отсутствие растягивания преобладает изгиб. Для ткани гладкого переплетения решающее значение имеют несоосности, создаваемые извитостью, в противном случае силы трения не смогут удерживать нити от смещения, и это является причиной повторного вычисления сил изгиба после смещения точек основы и утка.

На каждом пересечении нитей также вычисляются силы трения, позволяющие предотвратить скольжение между нитями основы 1 и утка 2. Межнитевое трение моделируется с использованием аппроксимации кулоновой модели на основе пенализации, подобной одной из моделей Яманэ и Накамуры [2006]. Настоящая дискретизация на основе пересечений нитей значительно упрощает формулу трения, и простая пружина в каждой координате скольжения приводит к эффективным результатам.

С учетом пересечения нитей q₀ мы задаем якорное положение

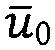
Кулонова модель задает предел μF_n упругой составляющей силы трения, где μ - коэффициент трения скольжения, a F_n - межнитевое сжатие, вычисленное в уравнении (9) выше. Если предел не достигается, то контакт находится в контактном режиме, и сила определяется пружиной. При превышении предела контакт находится в режиме скольжения, и сила задается кулоновым пределом. Таким образом, в случае контактного режима и в случае режима скольжения сила трения основы вычисляется соответственно как:

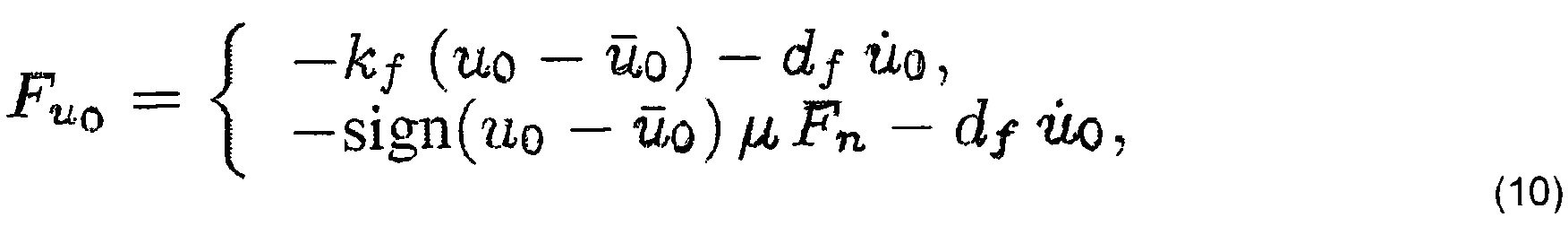
Кроме того, в режиме скольжения якорное положение поддерживается на постоянном расстоянии от координаты основы, при котором сила пружины равняется кулонову пределу.

На пересечениях 3 нитей соседние нити основы 1 и утка 2 поворачиваются поверх друг друга в зависимости от угла смещения

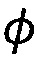
Для описания всех этих эффектов для каждой пары сегментов основы и утка на пересечениях нитей моделируют силу углового трения и упругий потенциал, которые зависят от угла смещения

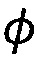
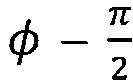
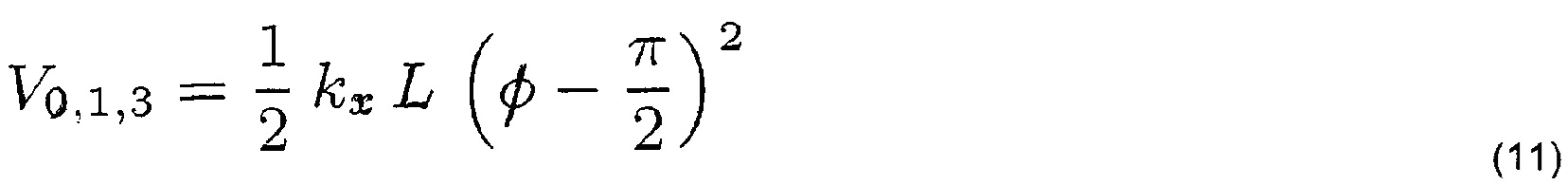
где k_x=SR², a S - контактный модуль смещения.

Нормальное сжатие увеличивает сопротивление смещению, и мы моделируем этот эффект в результате придания жесткости смещения зависимости от силы сжатия, то есть k_x(F_n). Кроме того, при переплетении сегментов нитей или основы или утка, рассматривают также подавление смещения, и моделирование осуществляют в соответствии со следующей эвристикой. Мы определяем угол подавления смещения

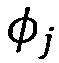
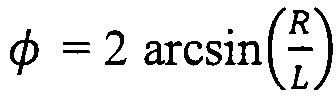
Моделирование трения смещения может быть осуществлено с использованием угловой пружины между текущим углом смещения

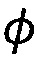
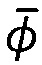
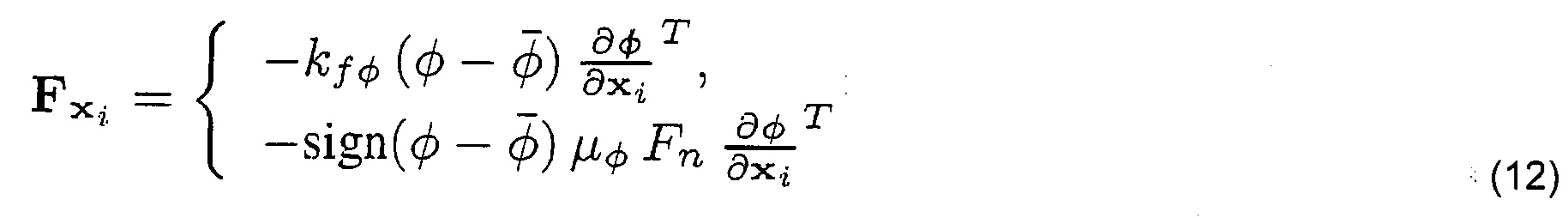
Одним из визуальных эффектов внутреннего трения является создание стойких морщин, как показано Miguel и сотрудниками [2013]. Фигура 5А показывает небольшой образец ткани, который был подвергнут сначала растяжению, а затем отпусканию (фигура 5В), на котором остается стойкая морщина вдоль направления растяжения, обусловленная трением смещения.

Контакт между соседними параллельными нитями можно легко смоделировать путем добавления энергии пенализации при чрезмерном сближении двух пересечений нитей. Мы определяем пороговое значение расстояния d равным четырехкратному радиусу нити в случае одной переплетенной нити между двумя пересечениями и двукратному радиусу в случае, когда две нити образуют поплавок. С учетом, например, того, что нити утка проходят через q₀ и q_i на фигуре 4А, мы определяем плотность энергии на основе расстояние между точками пересечения, и интегрируем эту плотность по утку полусегментам, приходящимся на оба узла. Предположение о практической нерастяжимости нитей позволяет аппроксимировать расстояние между точками пересечения как разность между координатами скольжения основы. При этом, как и в случае смещения, было установлено, что интегрирование плотности энергии достаточно осуществить с использованием заранее определенного межнитевого расстояния L, и, таким образом, избежать необходимости вычисления сил комплексного сцепления с координатами скольжения утка. Полученная энергия пенализации с жесткостью k_c в случае u₁-u₀1-u₀≥d выражается соответственно как:

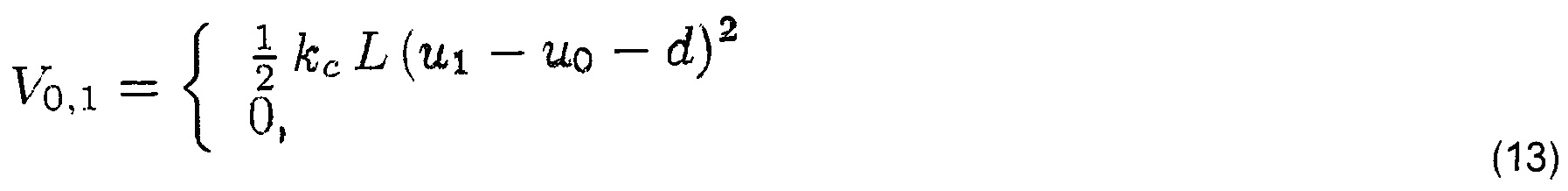
Проблему контакта между переплетенными нитями решают в неявном виде с помощью настоящей дискретизации, что позволяет, как указано выше, легко решить проблему контакта между соседними параллельными нитями. В то же время контакт с другими объектами, а также дальние самостолкновения требует решения проблемы столкновений в явном виде. Возможно использование существующих методов обнаружения и разрешения столкновений. Таким образом, определяют тонкий объем вокруг ткани, который позволяет вычислить глубину проникновения и реализовать реакцию на столкновение через энергию пенализации.

Для обнаружения контакта с объемными объектами были использованы дистанционные поля. В примерах, рассматриваемых ниже, были использованы только жесткие или расчлененные объекты, что позволяло в качестве предварительной обработки ограничиться однократным вычислением дистанционного поля. С учетом объекта О на каждом временном шаге мы опрашиваем каждый узел нитей х относительно дистанционного поля О, и в случае, когда расстояние до О меньше, чем у (в примерах, у - четырехкратный радиус нити R), определяем столкновение. Информацию о столкновениях формируют с помощью точки пересечений х, ближайшей точки р на поверхности О и контактной нормали n. В качестве контактной нормали была использована нормаль в р, однако возможны и другие варианты.

Для обнаружения самостолкновений были определены небольшие объемные элементы на поверхности ткани, и узлы нитей были опрошены относительно этих объемных элементов в соответствии с подходом Teschner et al. [2003]. Из четырех узлов, определенных каждой парой соседних нитей основы и утка, было сформировано два треугольника, а для формирования каждого объемного элемента в каждой точке пересечения эти треугольники были спроецированы на расстояние у в направлении нормали и в противоположном направлении (оценка нормали была рассмотрена ранее). Все узлы были опрошены относительно спроецированных треугольников, а для отбора было выполнено хеширование параллелепипедов ААВВ спроецированных треугольников на регулярной сетке [Teschner et al. 2003]. Если точка х находится внутри спроецированного треугольника, то определяют столкновение, находят спроектированную точку р на поверхности и путем интерполяции нормалей узлов треугольника вычисляют контактную нормаль n.

Для ответа на столкновения как с внешними объектами, так и при самостолкновениях, определяют силу пенализации на точку столкновения х при расстоянии пенализации n^T(р-х)+у и направлении n. В случае самостолкновении мы также распределяем противодействующую силу в узлы, которые определяют треугольник, используя в качестве весов барицентрические координаты р в треугольнике. В дополнение к ответной пенализации прикладывают Кулоново трение, аппроксимированное с помощью зажатых пружин [Yamane and Nakamura 2006].

Очевидным ограничением ответа на основе пенализации на тонких объектах является вероятность проблем восстановления. В примерах, приведенных ниже, восстановление было предотвращено путем добавления к ответной пенализации составляющей демпфирования. Более надежным решением будет использование барьерного метода [Harmon et al. 2009].

Для обеспечения сходимости уравнения движения (3) интегрируют с использованием обратного неявного интегрирования Эйлера [Baraff и Witkin 1998] с помощью метода Ньютона и адаптации временных шагов. На практике, большинство шагов решения требуют только одной итерации Ньютона, но мы допускаем возможность осуществления до пяти шагов, прежде, чем разделяем на два временных шага. В стоимости имитации доминирует решение линейных систем типа Av=b, где v=q является вектором обобщенных скоростей, а матрица системы определяется как:

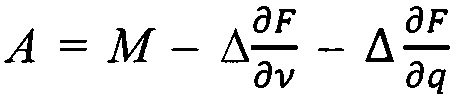
Линейную систему решают с использованием метода сопряженных остатков (CR), являющегося более надежным, чем метод сопряженных градиентов (CG) для матриц, близких к полуопределенным, так как вычисляет решение линейной задачи методом наименьших квадратов за счет несколько более высокой стоимости и потребления памяти.

Преимуществом существующей модели ткани на уровне нити является сильная регулярностью системной матрицы А, которая обеспечивает возможность высокоэффективной реализации численного интегрирования на процессорах GPU, подобных GPU-решателям ткани для регулярных треугольных сеток [Tang et al. 2013]. Вычисление внутренних сил, их Якобианов и решение линейной систем параллелизируется на GPU, а обнаружение столкновений выполняется на CPU. В общем и целом, узким местом решателя является векторное умножение разреженной матрицы, необходимое на каждой итерации PCR.

Таким образом, этот продукт был оптимизирован множественными способами с использованием регулярность ткани на уровне нити и нашей дискретизацией пересечений нитей. Вследствие регулярности рисунка переплетения внутренняя сила узла дает ненулевые Якобианы относительно 13 узлов (исключая столкновения, каждый узел взаимодействует с 12 соседями плюс с собой). Затем системную матрицу А расщепляют на сумму регулярной матрицы A_r и оставшейся хвостовой матрицы A_t, где A_r содержит 13 регулярных блоков 5×5 на узел, a A_t содержит другие блоки, возникающие в результате столкновений. В количестве, составляющем только 14% от стоимости продукта даже с простым запоминающим устройством СОО. Коэффициенты A_r хранятся в плотной матрице с развертыванием по столбцам с одной строкой и 325=13×25 столбцами на узел (2:53 Кбайт на узел с двойной точностью). Индексы A_r требуют гораздо меньшую матрицу с одной строкой и только 13 столбцами на узел. Продукты, включающие в себя A_r, параллелизируются на поузловой основе, а запоминающее устройство с развертыванием по столбцам для коэффициентов предоставляет чрезвычайно эффективный коалесцентный доступ к данным. Стратегия параллелизации имитирует один из форматов матрицы ELL и HYB в библиотеке Cusp Cuda [Bell and Garland 2012], но благодаря параллелизации на уровне узлов получает более, чем 40%-ное ускорение над Cusp в разреженных матрично-векторных продуктах.

В целом, достигается 16х-24х ускорение по многопотоковой реализации CPU в зависимости, в основном, от числа узлов (более высокое ускорение для большего числа узлов) и числа столкновений (более низкая скорость для большего числа столкновений, так как столкновения обрабатываются на CPU).

Для офлайновой визуализации результатов геометрия нити преобразовывается в объемное представление на микроволоконном уровне и используется трассировщик объемных дорожек Mitsuba [Jacob 2010]. Он учитывает анизотропное рассеивание микроволокон с использованием микрофленной модели. Для учета извитости для каждой нити генерируется полилиния со смещенными положениями узлов. Нити полилинии сглаживаются с использованием сплайнов Catmull-Rom, и затем для определения объемного представления геометрии нити, передаваемой в визуализатор Mitsuba используется усовершенствованный вариант способа Lumislice [Chen et al. 2003; Lopez-Moreno et al. 2014]. Каждая сглаженная нить состоит из тысяч скрученных микроволокон, а срезы, представляющие распределение плотности микроволокон, задаются на регулярных шагах и инкрементных поворотах перпендикулярно вдоль сегмента нити. Плотность вычисляется путем пересечения абсолютного положения каждого текселя на каждом срезе с 3-D-объемом текстуры. Это делается в программе построения теней фрагмента с асинхронными вызовами магазина 3-D-текстур. Настоящая реализация основана на программе построения теней OpenGL и приведена в качестве примера геометрии, и до 8 М срезов обрабатывается в течение менее, чем 100 мс на стандартном настольном компьютере. Касательные микроволокон, которые также хранятся в 3-D-текстуре, обеспечивают вычисление дифференциалов положений текселей на текущем и предыдущем срезах, отличающихся, главным образом, поворотом вдоль оси нити. Вследствие асинхронного характера вызовов текселей в программе построения теней предыдущий срез является недоступным и, следовательно, локальные дифференциалы предварительно вычисляются и передаются каждому срезу в виде текстура. В целом, плотность и ориентация нитей на уровне микроволокне хранятся в объемных текстурах (3 Гбайт на кадр в примерах).

Ниже приводится описание визуальных и численных крупномасштабных примеров для нескольких сценариев имитирования ткани. Все примеры были исполнены на четырехъядерном процессоре Core i7 Intel 3770 CPU с частотой 3,4 ГГц, объемом памяти 32 Гбайт и видеокартой NVIDIA Titan Black с памятью 6 Гбайт. Как было указано выше, обнаружение столкновений параллелизируется на CPU, в то время как решение динамики параллелизируется на GPU. Все имитации исполнялись с временным шагом 1 мс. Значения параметров, используемых в этих примерах, приведены на фигуре 6, типовые временные интервалы - на фигуре 7.

Примеры следующие:

- Свободная рубашка без рукавов: манекенщица была одета в свободную рубашку без рукавов из 2023 нитей и 350530 узлов пересечения, с одним швом на каждой стороне и одним швом на каждом плече (см. фигуру 8). Плотность нити составляет одну нить на миллиметр (25 нитей на дюйм). Манекенщица выполняет высоко динамические движения каратэ. Имитация показывает крупномасштабное движение и складки с разрешением на уровне нити в комбинации с мелкомасштабными эффектами. Динамика ткани и контактное разрешение являются устойчивыми даже при таких сложных движениях. Несмотря на высоко динамичное движение манекенщицы, имитация является надежной.

- Длинная рубашка: рубашка с рукавами была разработана в качестве одежды для танцующей манекенщицы (см. фигуру 9). Рубашка выполнена из 3199 нитей и 559241 узла пересечения, со швами по бокам тела, на плечах, на стыках рукавов и тела и вдоль рукавов. Плотность нити составляет одну нить на миллиметр (25 нитей на дюйм). В сравнении со свободной рубашкой без рукавов эта имитация показывает более высокую сложность вследствие большего количества узлов пересечений и дополнительной динамики и контактной механики рукавов. Как показывают мелкие морщины повсюду на рукавах, использование модели на уровне нити по существу создает динамику ткани высокого разрешения.

- Затяжки: Эти примеры показывают, как экстремальные деформации ткани создают очень сложные пластические деформации на уровне нити, а также влияние локальной динамика нити на глобальную форму ткани. Затяжка в свободной рубашке без рукавов было создана результате зажатия узла на боковом шве стороны и его очень быстрого вытягивания (см. фигуру 10). Деформация, обусловленная вытягиванием, создает небольшое отверстие: нить основы, которую вытягивают, отодвигает нити утка, что является ярким примером скольжения нити и контактной динамики нити. Кроме того, затяжка перемещается по всей рубашке, показывая мелкие морщины как сложный эффект скольжения нити и трения. Такой пластический эффект может быть достигнут только в результате имитации ткани на уровне нити при взаимодействии между нитями. Мелкомасштабные деформации, показывающие скольжение нити, и мелкие морщины сочетаются с крупномасштабным движением рубашки.

Вторая затяжка создается в области живота свободной рубашки без рукавов результате вытягивания узла пересечения и закрепления четырех соседних узлов, которые находятся не на вытягиваемых нитях (см. фигуры 11А, 11В и 11С). Эта структура может имитировать вытягивание нити при местном задерживании движения ткани в сторону рукой. Морщины ткани, формирующие крестообразную форму, показывают другой знакомый рисунок затяжки.

- Разрыв: Имитация разрыва ткани с использованием модели на уровне нити является простым делом, так как сложное и визуально богатое поведение потертых краев и рыхлых нитей происходит естественным образом с динамикой на уровне нити. Разрушение было реализовано просто путем расщепления нитей при превышении порога растягивающего напряжения с последующим шагом отпускания для обеспечения корректного снятия напряжения и предотвращения беспорядочного распространения трещин. Могут быть использованы и более сложные подходы, такие как тензоры разделения [O'Brien and Hodgins 1999] и локальные подшаги отпускания [Pfaff et al. 2014. Повторная дискретизация узла часто срабатывает при разрушении и высокопластичном поведении из-за выталкивания нити и скольжения мимо конца нити.

Свободная рубашка без рукавов была порвана в результате защемления двух наборов узлов пересечения в области туловища и их вытягивания в противоположных направлениях, что привело к образованию вертикальной трещины и ромбовидного отверстия, как показано на фигуре 12. При этом отдельные нити отделяются от краев трещины и провисают или растягиваются через края через отверстие. Эти свободные нити и полученные потертые края обычно наблюдаются при разрыве многих видов ткани. Более тонкие пластические деформации можно наблюдать вокруг трещины, в основном, вследствие скольжения нити.

- Рисунки переплетения: модель на уровне нити позволяет легко проектировать и моделировать различные рисунки переплетения. Как уже упоминалось ранее, проектирование ткани для определенного рисунка переплетения - это всего лишь вопрос установки флага для каждого узла, который указывает, какая нить находится сверху. Рисунки переплетения непосредственно влияют на глобальное и локальное поведение ткани, главным образом вследствие различного числа поплавков. Например, на смещение в значительной степени влияет число пересечений и поплавков в ткани. Визуальный аспект ткани также изменяется в соответствии с рисунком.

Три куска ткани размером 25×25 см (см. фигуры 1А, 1В и 1С) были имитированы в состоянии подвешивания за два угла. Плотность нити составляет одну нить на миллиметр (25 нитей на дюйм). Эти три куска являются совершенно одинаковыми, за исключением рисунка переплетения, причем первый кусок имеет полотняное переплетение (фигура 1А), второй является саржей (фигура 1В), а третий - сатином (фигура 1С). Фигуры 1А, 1В и 1С показывают фотоснимок каждого куска после двух секунд имитации. Куски показывают явно различное поведение, от фигуры 1А к фигуре 1С морщины движутся к нижнему краю, нижний край ткани падает ниже, а верхний край приобретает большую кривизну. Эти эффекты обусловлены снижением жесткости смещения для переплетений с большим числом поплавков, что в действительности является ожидаемым результатом. Снижение жесткости смещения приводит к улучшению качества драпировки. Визуально ткани на этих трех фотоснимках также отличаются друг от друга. Эффект "просвечиваемости" в верхней части каждого куска вследствие растяжения показывает различные ткацкие структуры ткани. Также можно наблюдать, как образец саржевой ткани показывает свой характерный диагональный рисунок.

Эти три куска были подвергнуты испытанию на раме смещения и было измерено общее смещение в зависимости от времени. Результаты измерений представлены в виде графиков на фигуре 2, показывающей графики зависимости силы от угла для каждого рисунка переплетения. Графики показывают гистерезис, обусловленный трением и нелинейностью вследствие застревания, наблюдаемого на реальных тканях [Miguel et al. 2012], так же как влияние рисунка переплетения. Как и ожидалось, рисунки переплетения с большим числом поплавков являются менее стойкими к смещению.

Была осуществлена и имитация четвертого куска ткани с использованием полотняного переплетения, но на этот раз с 4 нитями на миллиметр (100 нитей на дюйм). С учетом размера куска эта плотность нити преобразуется в 1 миллион узлов пересечения. Этот пример, представленный на фигурах 13А и 13В, показывает возможность решения проблемы модели с очень высокой плотностью нити, выявляемой в обычных тканых материалах, таких как постельное белье. Небольшие морщины появляются во время движения (фигура 13А), пока ткань не прекращает движения, после чего появляются большие драпировочные морщины (фигура 13В). Согласно текстильной номенклатуре 100 нитей на дюйм эквивалентны плотности ткани 200.

Таким образом, настоящее изобретение представляет собой эффективный способ имитации ткани на уровне нити. Ключевой новинкой является распределение пересечений нити, которое решает проблему контакта между нитями в неявном виде и обеспечивает эффективное представление скольжения между нитями. Эффекты, такие как межнитевое трение, смещение и контакт также описываются с помощью простых силовых моделей. Эта модель на уровне нити обеспечивает возможность имитации эффектов, таких разрыв с потертыми краями, пластичность вследствие затяжек или нелинейное поведение, обусловленное мелкомасштабным трением.

Одним из преимуществ моделей на уровне нити является возможность тиражирования нелинейной механики реальной ткани с высокой точностью воспроизведения. Это требует оценки параметров модели по измерениям силы-деформации реальной ткани. Результаты подгонки можно сравнить с результатами нелинейных моделей ткани.

Модель аппроксимирует сжатие между пересекающимися нитями в качестве функции сил растяжения и изгиба. Другая возможность может состоять в том, чтобы включить в себя сжатие в качестве дополнительной степени свободы и добавить потенциал сжатия к энергии системы. Моделирование сил растяжения в настоящее время осуществляют с использованием потенциала растяжения, но другой возможностью может быть предположение о нерастяжимости нитей и учет сжатия, возникающего во время растяжения, обусловленного извитостью.

Даже несмотря на то, что приведенные примеры изобретения ограничиваются ортогональными рисунками переплетения, дискретизация является общей и может быть использована применительно к произвольным конфигурациям переплетенных нитей. Одно простое расширение может обеспечить решение проблемы трехосного переплетения.

Реализация использует запросы на глубину проникновения и ответ на столкновение на основе пенализации. Чтобы обеспечить надежность при решении проблемы контактов, необходимо использовать энергии жесткой пенализации, и величина перемещения на временном шаге должна быть ограничена. Надежность может быть повышена в результате использования непрерывного обнаружения столкновений и ответа на основе ограничений, несмотря на то, что препятствием может стать решение проблемы контакта.

Реферат

Изобретение относится к области имитации поведения ткани на уровне нити. Технический результат заключается в обеспечении имитации поведения ткани на уровне нити с высоким разрешением и коротким временем вычислений. Способ включает в себя получение распределения нитей (1) основы, нитей (2) утка и узлов (3) пересечения нитей; описание каждого узла (3) пересечения нитей с помощью координаты (х) 3D-положения и двух координат скольжения - координаты (u) скольжения и координаты (v) скольжения соответственно нити (1) основы и нити (2) утка; измерение сил в каждом узле (3) пересечения нитей на основе силовой модели, где эти силы измеряют в координате (х) 3D-положения и в координатах (u, v) скольжения; и вычисление движения на каждом узле (3) пересечения нитей с помощью уравнений движения, полученных с использованием уравнений Лагранжа-Эйлера и подвергнутых численному интегрированию по времени, причем эти уравнения движения учитывают массовую плотность (ρ), распределенную равномерно вдоль нитей, а также измеренные силы и граничные условия. 3 н. и 8 з.п. ф-лы, 24 ил.

Формула