Способ вычисления физического значения, способ численного анализа, программа вычисления физического значения, программа численного анализа, устройство вычисления физического значения и устройство численного анализа - RU2519331C2
Код документа: RU2519331C2
Чертежи

Описание
ОБЛАСТЬ ТЕХНИКИ
Настоящее изобретение относится к способу вычисления физического значения, способу численного анализа, программе вычисления физического значения, программе численного анализа, устройству вычисления физического значения и устройству численного анализа.
ПРЕДШЕСТВУЮЩИЙ УРОВЕНЬ ТЕХНИКИ
В известном уровне техники в качестве способов численного анализа для распределения скоростей потока, распределения напряжений, распределения тепла и т.п. посредством численного анализа известные методики включают в себя метод конечных элементов, метод конечных объемов, метод вокселей и метод частиц.
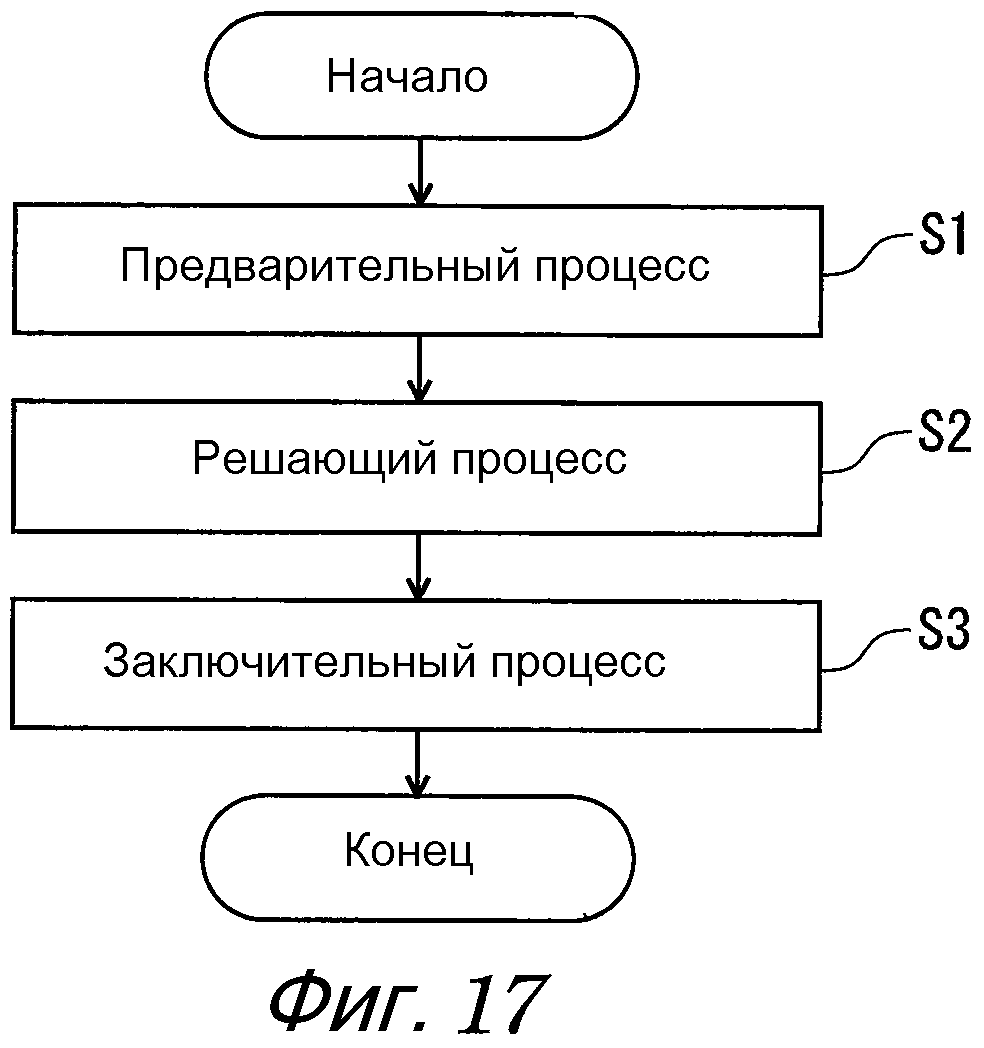
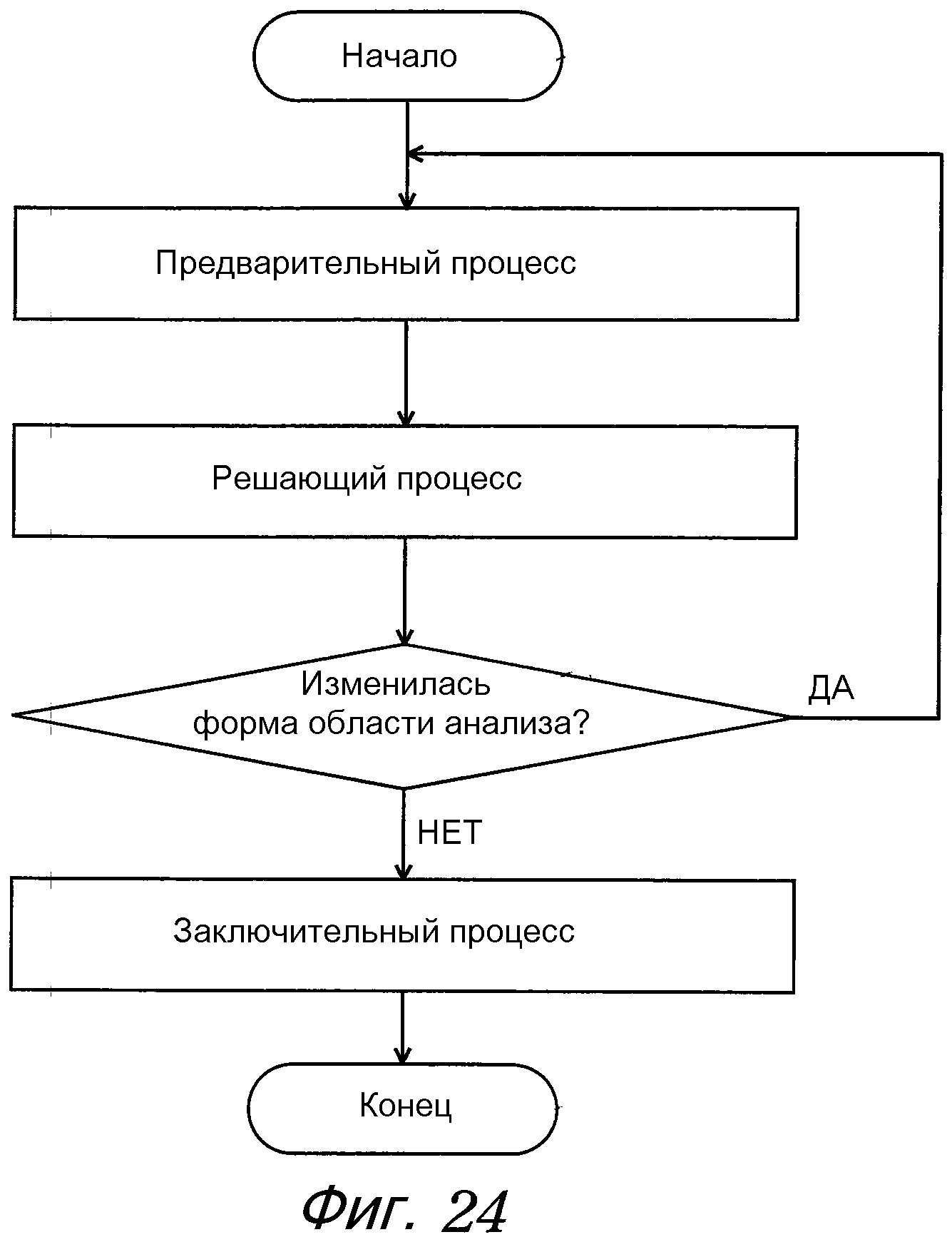
Обычно такой способ численного анализа строится из предварительного процесса, решающего процесса и заключительного процесса. Тогда предварительный процесс формирует модель расчетных данных. Затем решающий процесс вычисляет вышеупомянутые физические значения с использованием модели расчетных данных и основного уравнения, подвергнутого дискретизации (в дальнейшем называемого дискретизированным основным уравнением).
Например, в традиционном методе конечных объемов область анализа делится на множество областей. Затем физические значения в каждой разделенной области вычисляются с использованием объема каждой разделенной области, площади граничной поверхности между соседними разделенными областями и вектора нормали к граничной поверхности.
В методе конечных объемов предварительный процесс формирует модель расчетных данных (обычно называемую сеткой), содержащую координаты вершин (Вершина) каждой разделенной области. Затем решающий процесс вычисляет объем вышеупомянутой разделенной области, площадь граничной поверхности и вектор нормали к граничной поверхности, используя Вершину и т.п., содержащуюся в модели расчетных данных, а затем вычисляет физические значения с использованием этих значений. Вершина указывает значения для определения геометрической формы разделенной области. Таким образом, признается, что в методе конечных объемов решающий процесс вычисляет объем разделенной области, площадь граничной поверхности и вектор нормали к граничной поверхности с использованием геометрической формы разделенной области.
Дополнительно в методе конечных объемов может предоставляться часть, где частично не выполняется условие совместного использования вершин для соседних разделенных областей. Таким образом, в методе конечных объемов ограничение на разделенную область отчасти смягчается в некоторых случаях. Тем не менее, тип элемента для анализа, который нужно использовать, ограничивается, например, четырехгранным элементом, шестигранным элементом, призменным элементом и пирамидальным элементом.
Здесь, как показано в Патентном документе 1, также предложен метод конечных объемов без ограничения типа элемента для анализа. Тем не менее, даже в таком методе конечных объемов без ограничения на тип элемента для анализа, аналогично традиционному методу конечных объемов, описанному выше, предварительный процесс формирует модель расчетных данных, содержащую координаты вершин (Вершина) каждой разделенной области, а затем решающий процесс вычисляет физические значения с использованием Вершины, содержащейся в модели расчетных данных.
Дополнительно, как широко известно, метод конечных элементов является способом вычисления физических значений в каждой разделенной области с использованием интерполирующей функции. Однако, аналогично методу конечных объемов, решающий процесс использует геометрическую форму разделенной области, определенную Вершиной и т.п.
Метод вокселей и метод частиц являются способами численного анализа, допускающими простое формирование модели расчетных данных по сравнению с методом конечных элементов и методом конечных объемов.
Метод вокселей является способом, в котором данные вокселей для задания области анализа с использованием множества вокселей (прямоугольная сетка), имеющих форму прямоугольного параллелепипеда и в основном один и тот же размер, формируются в виде модели расчетных данных, и вычисление физических значений выполняется с использованием данных вокселей, так что выполняется численный анализ. Методы вокселей схематически делятся на тип со взвешенной невязкой, который использует основное уравнение на основе метода взвешенных невязок, и тип без интегрирования, который использует модель клеточного автомата, решеточную модель Больцмана или т.п. Тогда, в соответствии с этим методом вокселей, не нужна Вершина и т.п., которую нужно использовать в качестве данных вокселей.
В соответствии с таким методом вокселей, область анализа задается просто путем разделения области анализа на воксели. Таким образом, модель расчетных данных формируется за короткое время.
С другой стороны, метод частиц является способом, в котором данные частиц формируются в виде модели расчетных данных для задания области анализа с помощью множества частиц, и вычисление физических значений выполняется с использованием этих данных частиц, так что выполняется численный анализ. Метод частиц, относящийся к типу без интегрирования, использует модель межчастичного взаимодействия в качестве основного уравнения. Метод частиц не содержит разделенные области и поэтому не требует Вершины и т.п. Таким образом, в соответствии с таким методом частиц область анализа легко задается путем равномерного распределения частиц в области анализа, так что модель расчетных данных формируется за короткое время.
ИЗВЕСТНЫЙ УРОВЕНЬ ТЕХНИКИ
ПАТЕНТНЫЙ ДОКУМЕНТ
Патентный документ 1: Описание изобретения в опубликованной заявке на патент США № 2008/0021684
СУЩНОСТЬ ИЗОБРЕТЕНИЯ
ПРОБЛЕМЫ, КОТОРЫЕ ДОЛЖНЫ БЫТЬ РЕШЕНЫ ПОСРЕДСТВОМ ИЗОБРЕТЕНИЯ
В случае, где геометрическая форма каждой разделенной области используется в решающем процессе, как в традиционном способе численного анализа, например методе конечных элементов и методе конечных объемов, очевидно, что модель расчетных данных обязательно содержит данные, описывающие геометрическую форму разделенной области.
С целью задания геометрической формы разделенной области необходима вершинная связность (Связность Вершины; в дальнейшем называемая Связностью (Connectivity)) в дополнение к Вершине. Таким образом, в методе конечных элементов и методе конечных объемов необходимо, чтобы модель расчетных данных содержала Вершину и Связность.
Здесь, в частности, Связность определяется с помощью информации о соответствии общих номеров узлов, последовательно заданных вершинам всех разделенных областей, и локальных номеров узлов, последовательно заданных вершинам в одной разделенной области.
Как широко известно, модель расчетных данных, содержащая такую Вершину и Связность, требует весьма большой работы для формирования.
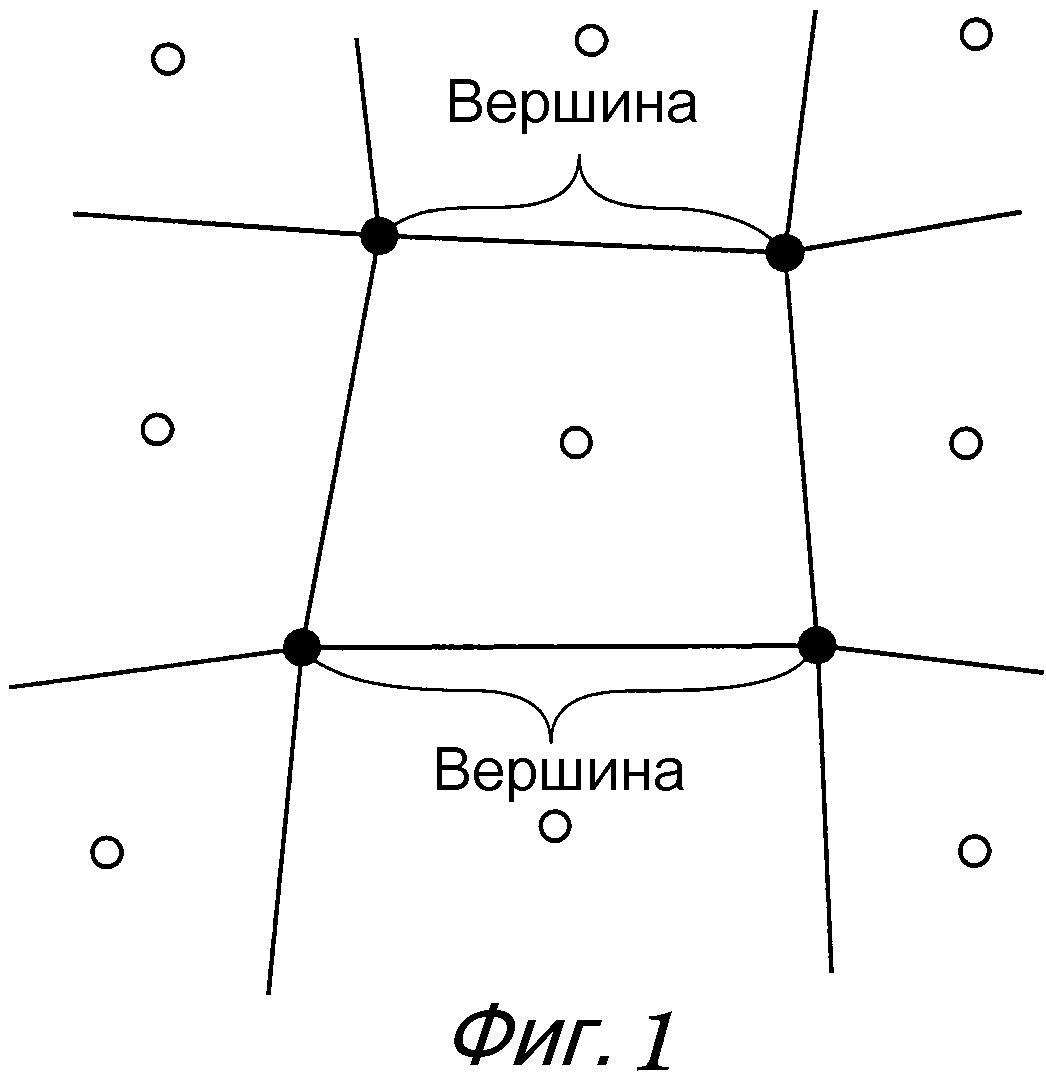
Например, в модели расчетных данных, используемой в методе конечных элементов, модель расчетных данных нужно формировать так, что должно выполняться условие, по которому соседние разделенные области всегда совместно используют Вершину, как показано на фиг. 1. Таким образом, чтобы все разделенные области выполняли это условие, необходимо довольно большое время.
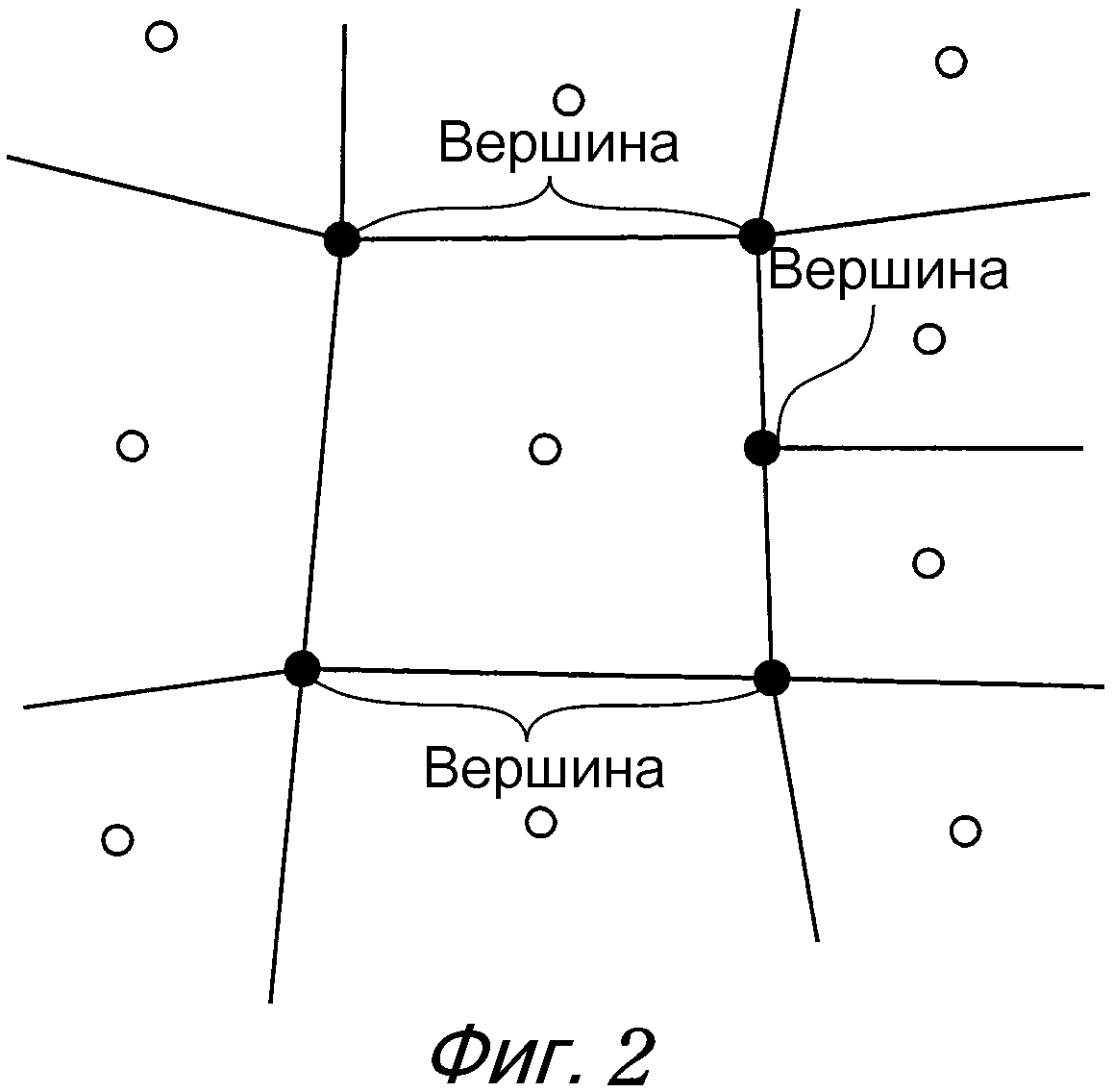
С другой стороны, в модели расчетных данных, используемой в методе конечных объемов, допускается наличие Вершины, не используемой совместно соседними разделенными областями, как показано на фиг. 2. Это увеличивает гибкость формирования сетки по сравнению с методом конечных элементов. Тем не менее, даже в методе конечных объемов модель расчетных данных нужно формировать на условиях, что не используемая совместно Вершина располагается, по меньшей мере, на границе соседних разделенных областей, и что форма разделенной области обычно совпадает с типом элемента для анализа, установленным заранее. Таким образом, сложно сказать, что гибкость формирования сетки является высокой.
Более того, в последние годы численный анализ выполняется в области анализа, извлеченной из данных о трехмерной форме, например данных трехмерной CAD (системы автоматизированного проектирования). Тем не менее, данные о трехмерной форме не являются данными, сформированными для численного анализа. Таким образом, содержатся данные, которые указывают перекрывающиеся поверхности, пересечение поверхностей, зазоры между поверхностями, небольшое отверстие и т.п. То есть включается много условий, которые не подходят для формирования модели расчетных данных, содержащей Вершину и Связность. Таким образом, чтобы разрешить формирование модели расчетных данных, содержащей Вершину и Связность, данные о трехмерной форме нужно модифицировать или изменить. Тогда, чтобы разрешить модификацию или изменение данных о трехмерной форме с целью формирования модели расчетных данных, содержащей Вершину и Связность, нужно выполнить довольно большую ручную работу, которая требует опыта и метода проб и ошибок. Это порождает большую проблему во время практического использования метода конечных элементов или метода конечных объемов.
Кроме того, как и в методе конечных объемов, в случае, когда решающий процесс вычисляет объем разделенной области, площадь граничной поверхности и вектор нормали к граничной поверхности, объем вычисления дополнительно увеличивается в решающем процессе, так что вычислительная нагрузка на решающий процесс дополнительно увеличивается.
В методе вокселей модель расчетных данных можно сформировать за короткое время. Тем не менее, возникает следующая проблема. В методе вокселей область анализа задается в основном вокселями (прямоугольная сетка), имеющими одинаковый размер. В общем, в методе конечных элементов и методе конечных объемов размер элемента (размер каждой разделенной области) устанавливается небольшим в области, где нужна более высокая точность анализа, чтобы вычисление физических значений точно выполнялось в этой области. Более того, размер элемента для другой области устанавливается большим, чтобы уменьшалась вычислительная нагрузка для этой области. Тем не менее, в методе вокселей все воксели в основном имеют один и тот же размер. Таким образом, когда воксели задаются небольшими, вычислительная нагрузка становится весьма большой. В отличие от этого, когда воксели задаются большими, точность анализа ухудшается.
Дополнительно в методе вокселей каждую область анализа нужно задавать путем размещения вокселей (прямоугольная сетка), имеющих одинаковый размер. Таким образом, область анализа не может быть гладкой возле границы с внешней областью, и поэтому в некоторых случаях образует ступенчатую форму. То есть, даже когда фактическая область, которую нужно проанализировать, содержит наклонную плоскость, искривленную поверхность или т.п., область представляется в ступенчатой форме в данных вокселей. Таким образом, форма области анализа в методе вокселей становится отличной от фактической формы области, которую нужно проанализировать. Это ухудшает точность анализа.
Соответственно, предложен усовершенствованный способ, называемый методом скошенных ячеек, в котором ступенчатая область в данных вокселей обрезается по наклонной плоскости или искривленной поверхности (коррекция границы), присутствующей в фактической области, которую нужно проанализировать. Тем не менее, в этом усовершенствованном способе коррекция границы легко формирует весьма небольшие разделенные области. В таком случае, когда формируются такие небольшие разделенные области, точность анализа ухудшается.
Дополнительно в этом усовершенствованном способе формирование скошенных ячеек и решающий процесс используют Вершину.
Как описано выше, метод вокселей без коррекции границы не требует Вершины и т.п. Тем не менее, существует ограничение в формировании вокселей, то есть в так называемом формировании сетки. А именно, когда необходима достаточная точность анализа, количество вокселей увеличивается, и также увеличивается вычислительная нагрузка в решающем процессе. Это порождает проблему. Более того, в результате в усовершенствованном способе по методу вокселей с коррекцией границы становится необходимой Вершина. Таким образом возникает влияние геометрической формы разделенных областей. В результате весьма большая ручная работа, требующая опыта и метода проб и ошибок, становится необходимой для обработки по формированию разделенных областей возле границы с внешней областью. Таким образом, модель данных формы не может быть сформирована за короткое время.
С другой стороны, метод частиц требует вычисления отношения связи конкретной частицы с другими частицами. Таким образом, нужно искать частицы, присутствующие в окрестности конкретной частицы. Затем эти алгоритмы ближнего соседа частицы выполняются над всеми частицами в принципе. Тем не менее, в методе частиц каждая частица движется в зависимости от времени и поэтому отношение связи между частицами всегда меняется. Таким образом, алгоритмы ближнего соседа нужно выполнять в каждый момент изменения времени при анализе. Это вызывает увеличение вычислительной нагрузки. Таким образом, предпринята попытка, чтобы аккуратно выбирать частицы, над которыми должен выполняться поиск соседства, чтобы уменьшалась вычислительная нагрузка в алгоритмах ближнего соседа. Тем не менее, например, когда количество частиц увеличивается с целью повышения точности анализа, вычислительная нагрузка увеличивается пропорционально квадрату количества частиц.
В таком методе частиц, чтобы численный анализ был осуществлен в рамках практического времени, необходимо использовать большое количество CPU (центральных процессорных модулей) в большой машине параллельной обработки данных. Например, в реальном случае вычисление, завершенное за половину дня обычным решающим устройством по методу конечных объемов, использующим Вершину и Связность на одном CPU, заняло больше одной недели у метода частиц, применяющего параллельное вычисление с использованием 32 CPU.
Кроме того, даже в методе частиц, когда частицы плотно размещаются, вычислительная нагрузка увеличивается значительно. Когда частицы размещаются небрежно, точность анализа ухудшается.
Дополнительно, как подробно описано позже, в методе частиц, когда анализируется физическое явление, например текучая среда, структура, тепло и диффузия на основе закона сохранения физического значения, сохранение выполняется не полностью.
Например, отсутствует информация касательно площади, занимаемой на граничной поверхности частицей, размещенной так, чтобы быть обращенной к граничной поверхности между областью анализа и внешней областью. Таким образом, даже когда нужно ввести условие, что тепло поступает через граничную поверхность, количество тепла, введенное в каждую частицу, не распознается точно. Таким образом, не получается точное количественное значение.
Настоящее изобретение разработано в связи с проблемами в традиционных способах численного анализа, описанных выше, таких как метод конечных элементов, метод конечных объемов, метод вокселей, усовершенствованная методика в методе вокселей и метод частиц. Цель настоящего изобретения - снизить рабочую загрузку при формировании модели расчетных данных и снизить вычислительную нагрузку в решающем процессе, не вызывая ухудшения точности анализа.
РЕШЕНИЕ ПРОБЛЕМ
Чтобы решить вышеупомянутую проблему, настоящее изобретение применяет конфигурацию способа вычисления физического значения для вычисления физических значений в способе численного анализа для численного анализа физического явления, содержащем этап вычисления физических значений, состоящего в вычислении физических значений в области анализа, разделенной на множество разделенных областей, не ограниченных формой прямоугольной сетки, где на этапе вычисления физических значений физические значения вычисляются с использованием дискретизированного основного уравнения, которое использует значения, не требующие координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность) и которое выводится на основе метода взвешенных невязок; и модели расчетных данных, в которой объемы разделенных областей и характеристические значения граничной поверхности, указывающие характеристики граничных поверхностей соседних разделенных областей, предоставляются в виде значений, не требующих координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность).
Дискретизированное основное уравнение, используемое в настоящем изобретении, не является традиционным уравнением, выраженным в виде, содержащем значения (Вершина и Связность), которые определяют геометрическую форму каждой разделенной области, а является уравнением, не требующим значений, которые определяют геометрическую форму каждой разделенной области. Дискретизированное основное уравнение, используемое в настоящем изобретении, получается путем намеренной остановки посередине процесса выведения, на основе метода взвешенных невязок, традиционного уравнения, использующего значения, которые определяют геометрическую форму. Такое дискретизированное основное уравнение, используемое в настоящем изобретении, выражается в значениях, не требующих геометрической формы разделенной области (то есть значениях, не требующих Вершины и Связности), и тогда может выражаться в виде, например, зависящем исключительно от двух вещей: объема разделенной области и характеристического значения граничной поверхности.
То есть в традиционном методе конечных элементов или методе конечных объемов объект, который нужно проанализировать, делится на малые области в качестве исходного условия. Таким образом, дискретизированное основное уравнение выводится на предположении, что используются значения, определяющие геометрическую форму каждой малой области, то есть Вершина и Связность. В отличие от этого дискретизированное основное уравнение, используемое в настоящем изобретении, выводится из отличного и полностью нового образа мышления по сравнению с известным уровнем техники.
Тогда настоящее изобретение отличается применением дискретизированного основного уравнения, выведенного из такого нового образа мышления. Таким образом, в отличие от традиционного способа численного анализа способ в соответствии с настоящим изобретением решает традиционные проблемы вне зависимости от геометрической формы и предоставляет различные виды примечательных результатов.
Здесь ниже объясняется тот факт, что объем разделенной области и характеристическое значение граничной поверхности являются значениями, не требующими Вершины и Связности, которые определяют конкретную геометрическую форму разделенной области. Здесь значения, не требующие Вершины и Связности, указывают значения, которые можно задать без использования Вершины и Связности.
Например, когда рассматривается объем разделенной области, множественные вероятности присутствуют для геометрической формы разделенной области, чей объем принимает заранее установленное значение. То есть геометрическая форма разделенной области, чей объем принимает заранее установленное значение, может быть кубом или сферой. Затем, например, при ограничении, что полная сумма всех разделенных областей совпадает с объемом всей области анализа, объемы разделенных областей могут быть заданы путем вычисления с оптимизацией, выполненного, например, так, что объем каждой разделенной области должен быть как можно пропорциональнее кубу среднего расстояния от каждой соседней разделенной области. Таким образом, объем разделенной области можно признать в качестве величины, не требующей конкретной геометрической формы разделенной области (величины, не требующей Вершины и Связности).
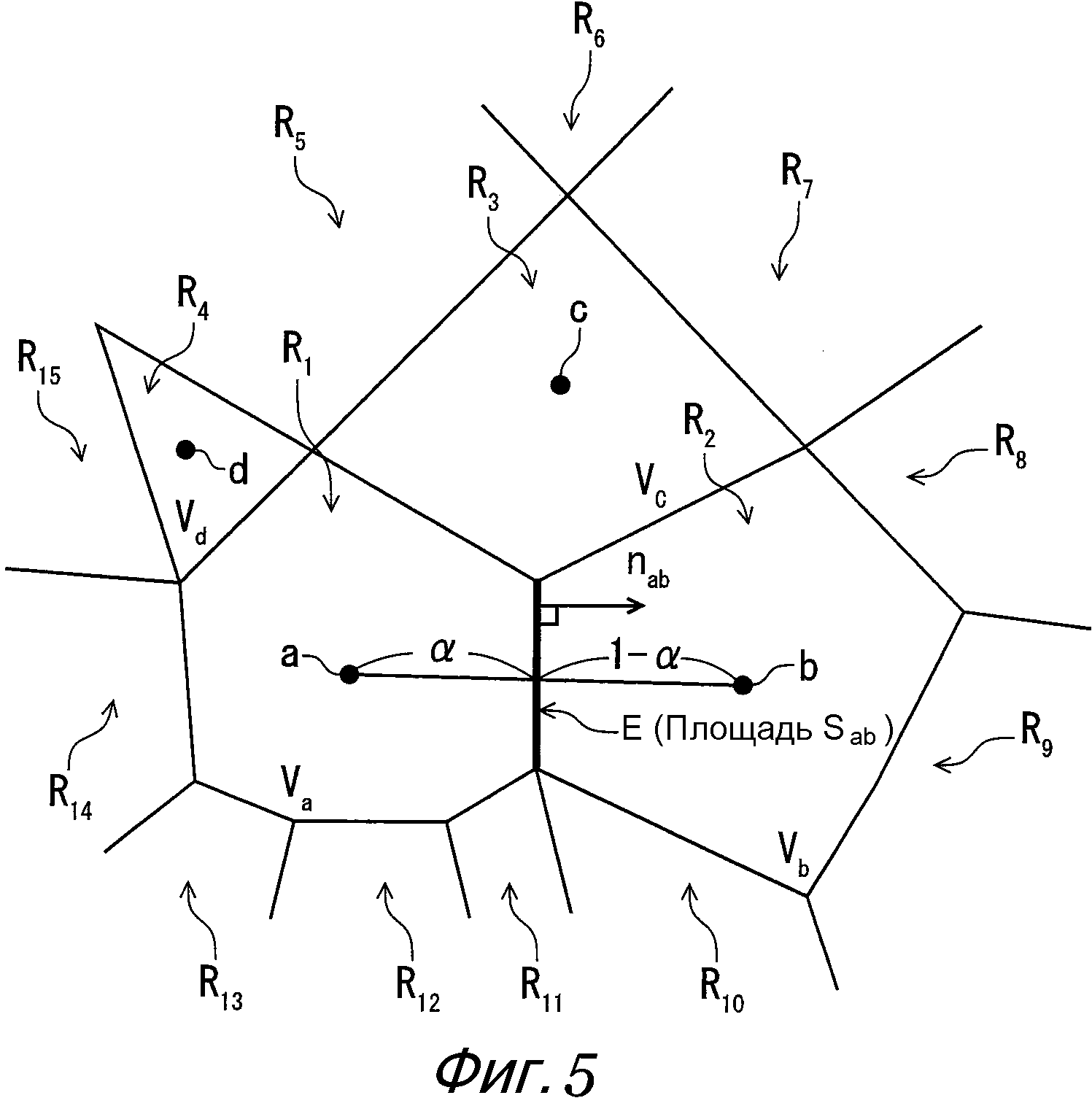
Дополнительно характеристическое значение граничной поверхности может быть, например, площадью граничной поверхности, вектором нормали к граничной поверхности или контурной длиной граничной поверхности. Однако для геометрической формы разделенной области (то есть геометрической формы граничной поверхности) существуют многочисленные возможности, где характеристическое значение граничной поверхности имеет заранее установленное значение. Тогда, например, при ограничении, что длина среднего взвешенного вектора площади вектора нормали становится нулем для всех граничных поверхностей, окружающих разделенные области, характеристическое значение граничной поверхности может быть задано путем вычисления с оптимизацией, выполненного так, что направление вектора нормали к граничной поверхности становится ближе к отрезку прямой, который соединяет контрольные точки двух соседних разделенных областей (см. фиг. 5), и что полная сумма общих площадей граничных поверхностей разделенной области должна быть как можно пропорциональнее третьей-второй степени объема разделенной области. Таким образом, характеристическое значение граничной поверхности можно признать в качестве величины, не требующей конкретной геометрической формы разделенной области (величины, не требующей Вершины и Связности).
Дополнительно в настоящем изобретении описание, что "область анализа, разделенная на множество разделенных областей, не ограниченных формой прямоугольной сетки" указывает, что, по меньшей мере, одна из множества разделенных областей, составляющих область анализа, не имеет форму прямоугольной сетки. То есть обозначение указывает, что область анализа содержит разделенную область, имеющую форму, отличную от формы прямоугольной сетки.
Дополнительно в настоящем изобретении обозначение, что "используются только значения, не требующие Вершины и Связности", указывает, что значения, которые нужно подставить в дискретизированное основное уравнение, являются только значениями, не требующими Вершины и Связности.
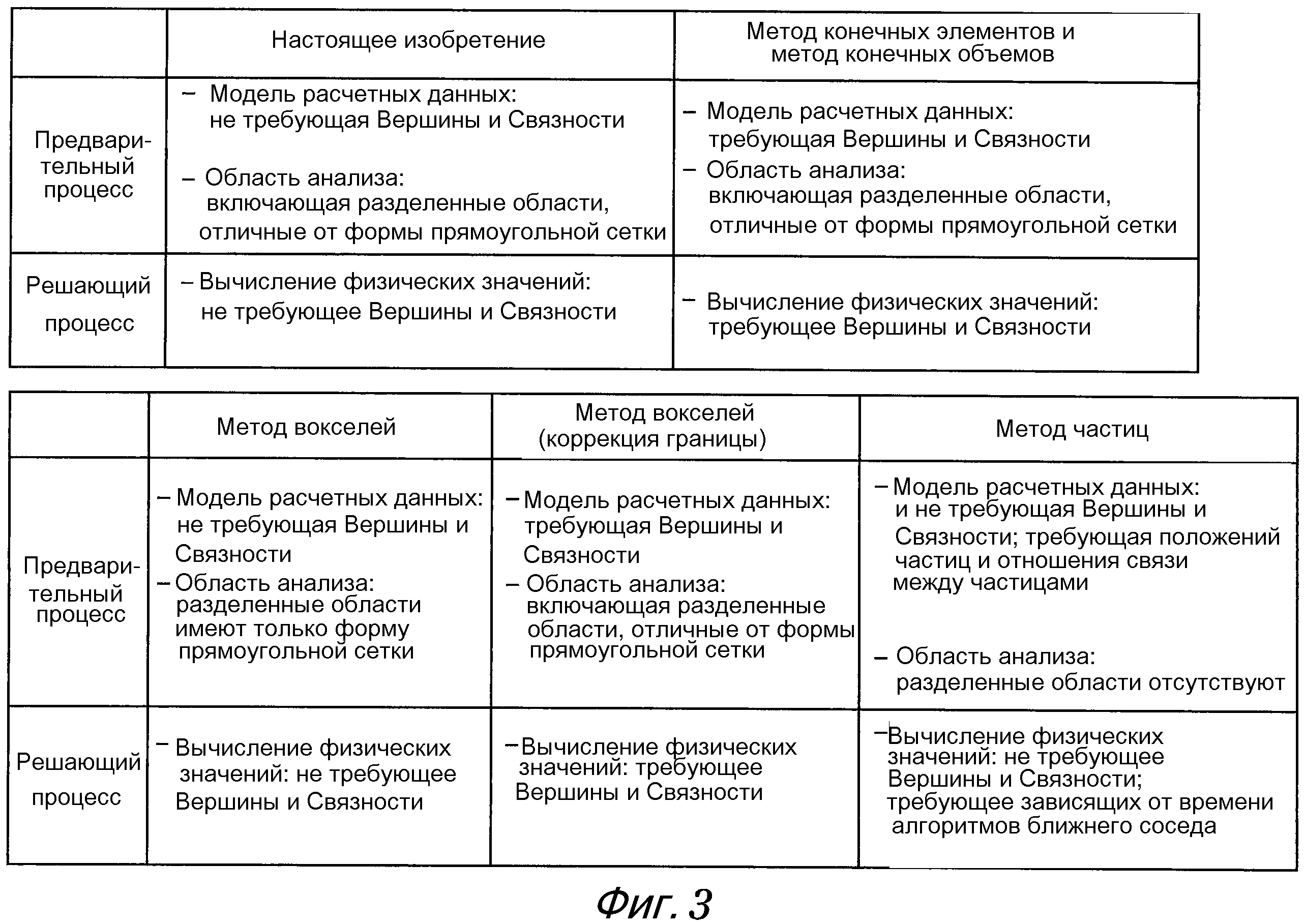
Далее, со ссылкой на концептуальную схему фиг. 3, ниже приводится более подробное описание для примечательных результатов настоящего изобретения с помощью подхода сравнения предварительного процесса и решающего процесса в способе численного анализа, использующем настоящее изобретение, и в традиционном способе численного анализа.
В случае способа численного анализа, использующего настоящее изобретение, как показано на фиг. 3, в решающем процессе (этап вычисления физических значений в настоящем изобретении) физические значения в разделенных областях вычисляются с использованием дискретизированного основного уравнения, которое использует только значения, не требующие Вершины и Связности. Таким образом, в момент решения дискретизированного основного уравнения модель расчетных данных, сформированная в предварительном процессе, не должна содержать Вершину и Связность.
Затем, когда используется настоящее изобретение, объем разделенной области и характеристическое значение граничной поверхности используются в качестве значений, не требующих Вершины и Связности. Таким образом, модель расчетных данных, сформированная в предварительном процессе, не содержит Вершину и Связность, а содержит объем разделенной области, характеристическое значение граничной поверхности и другие вспомогательные данные (например, информацию о связи разделенных областей и координаты контрольных точек, которые описываются позже).
По существу, когда используется настоящее изобретение, как описано выше, физические значения в каждой разделенной области могут вычисляться на основе объема разделенной области и вышеупомянутого характеристического значения граничной поверхности, то есть на основе значений, не требующих геометрической формы разделенной области. Таким образом, физические значения могут вычисляться в состоянии, когда модель расчетных данных не содержит геометрическую форму разделенной области, то есть Вершину и Связность. Таким образом, когда используется настоящее изобретение, в предварительном процессе достаточно, чтобы формировалась модель расчетных данных, которая содержит, по меньшей мере, объем разделенной области и характеристическое значение граничной поверхности (площадь граничной поверхности и вектор нормали к граничной поверхности). Таким образом, физические значения могут вычисляться без формирования модели расчетных данных, содержащей Вершину и Связность.
Модель расчетных данных, не содержащая Вершину и Связность, не требует геометрической формы разделенной области и поэтому может формироваться без ограничения, вызванного геометрической формой разделенной области.
Таким образом, также значительно смягчается ограничение на коррекционную работу для данных о трехмерной форме. Таким образом, модель расчетных данных, не содержащая Вершину и Связность, можно сформировать гораздо проще модели расчетных данных, содержащей Вершину и Связность. Таким образом, в соответствии с настоящим изобретением снижается рабочая загрузка при формировании модели расчетных данных.
Дополнительно, даже когда используется настоящее изобретение, в предварительном процессе могут использоваться Вершина и Связность. То есть в предварительном процессе объем разделенной области, характеристики граничной поверхности и т.п. могут вычисляться с использованием Вершины и Связности. Даже в таком случае в решающем процессе физические значения могут вычисляться при условии, что доступен объем разделенной области и характеристики граничной поверхности. Таким образом, даже в случае, когда Вершина и Связность используются в предварительном процессе, можно избежать ограничения на геометрическую форму разделенной области, например ограничения, вызванного деформацией, кручением или т.п. разделенной области. Это снижает рабочую загрузку при формировании модели расчетных данных.
Дополнительно, когда используется настоящее изобретение, в предварительном процессе отменяется ограничение на геометрическую форму разделенной области. Таким образом, разделенная область может переходить в произвольную форму. Таким образом, область анализа можно легко подогнать под фактическую область, которую нужно проанализировать, без увеличения количества разделенных областей. Таким образом, точность анализа можно повысить без увеличения вычислительной нагрузки.
Дополнительно, когда используется настоящее изобретение, плотность распределения разделенных областей также может произвольно меняться. Таким образом, точность анализа также можно дополнительно повысить, позволяя при этом увеличение вычислительной нагрузки до необходимой степени.
Дополнительно, когда используется настоящее изобретение, в отличие от традиционного способа численного анализа, в решающем процессе вычисление объема разделенной области и характеристического значения граничной поверхности не должно использовать Вершину и Связность. Таким образом, вычислительную нагрузку в решающем процессе также можно снизить.
Дополнительно в настоящем изобретении, когда форма области анализа не меняется, перемещение разделенных областей не нужно. Таким образом, не нужны алгоритмы ближнего соседа, которые должны выполняться в каждый момент изменения времени в методе частиц. Соответственно, вычислительная нагрузка является небольшой. Дополнительно, как подробно описано позже, когда используется настоящее изобретение, в отличие от метода частиц физические значения могут вычисляться в состоянии, когда выполняются законы сохранения физических значений.
С другой стороны, в методе конечных объемов, который является традиционным способом численного анализа, предварительный процесс формирует модель расчетных данных, содержащую Вершину и Связность, выражающие геометрическую форму разделенной области. Тогда решающий процесс вычисляет объем разделенной области и характеристическое значение граничной поверхности (площадь граничной поверхности и вектор нормали к граничной поверхности) с использованием Вершины и Связности, содержащихся в модели расчетных данных, а затем вычисляет физические значения в каждой разделенной области. В этом случае необходимо, чтобы ограничение на геометрическую форму, то есть на отношение между Вершиной и Связностью, не вызывало проблему. Таким образом, модель расчетных данных (то есть сетку) нужно формировать в рамках ограничения, например деформации и кручения разделенной области. Это порождает проблему огромной ручной работы при формировании модели расчетных данных, как описано выше.
Дополнительно, также в методе конечных элементов решающий процесс вычисляет физические значения с использованием Вершины и Связности, содержащихся в модели расчетных данных. Таким образом, предварительный процесс должен формировать модель расчетных данных, содержащую Вершину и Связность, выражающие геометрическую форму разделенной области. Таким образом, появляется огромная ручная работа при формировании модели расчетных данных.
Дополнительно в методе вокселей, который является традиционным способом численного анализа, как показано на фиг. 3, в момент вычисления физических значений в решающем процессе Вершина и Связность не нужны. Однако форма разделенной области ограничивается вокселем. Таким образом, как описано выше, возникает проблема, что граница с внешней областью имеет ступенчатую форму. Соответственно, как описано выше, когда необходима достаточная точность анализа, количество вокселей увеличивается, и также увеличивается вычислительная нагрузка в решающем процессе. Это порождает проблему. Кроме того, в методе вокселей с коррекцией границы Вершина в конечном счете используется в момент вычисления объема и т.п. разделенной области. Таким образом, на формирование модели расчетных данных влияет геометрическая форма разделенной области.
Дополнительно в методе частиц, который является традиционным способом численного анализа, отсутствует понятие разделенной области. Таким образом, как показано на фиг. 3, в момент вычисления физических значений в решающем процессе Вершина и Связность не нужны. Однако перемещение частиц, которые задают модель расчетных данных, вместо разделенных областей вызывает увеличение вычислительной нагрузки, как описано выше. Дополнительно в методе частиц вычисление физических значений в состоянии, когда выполняется закон сохранения, является сложным.
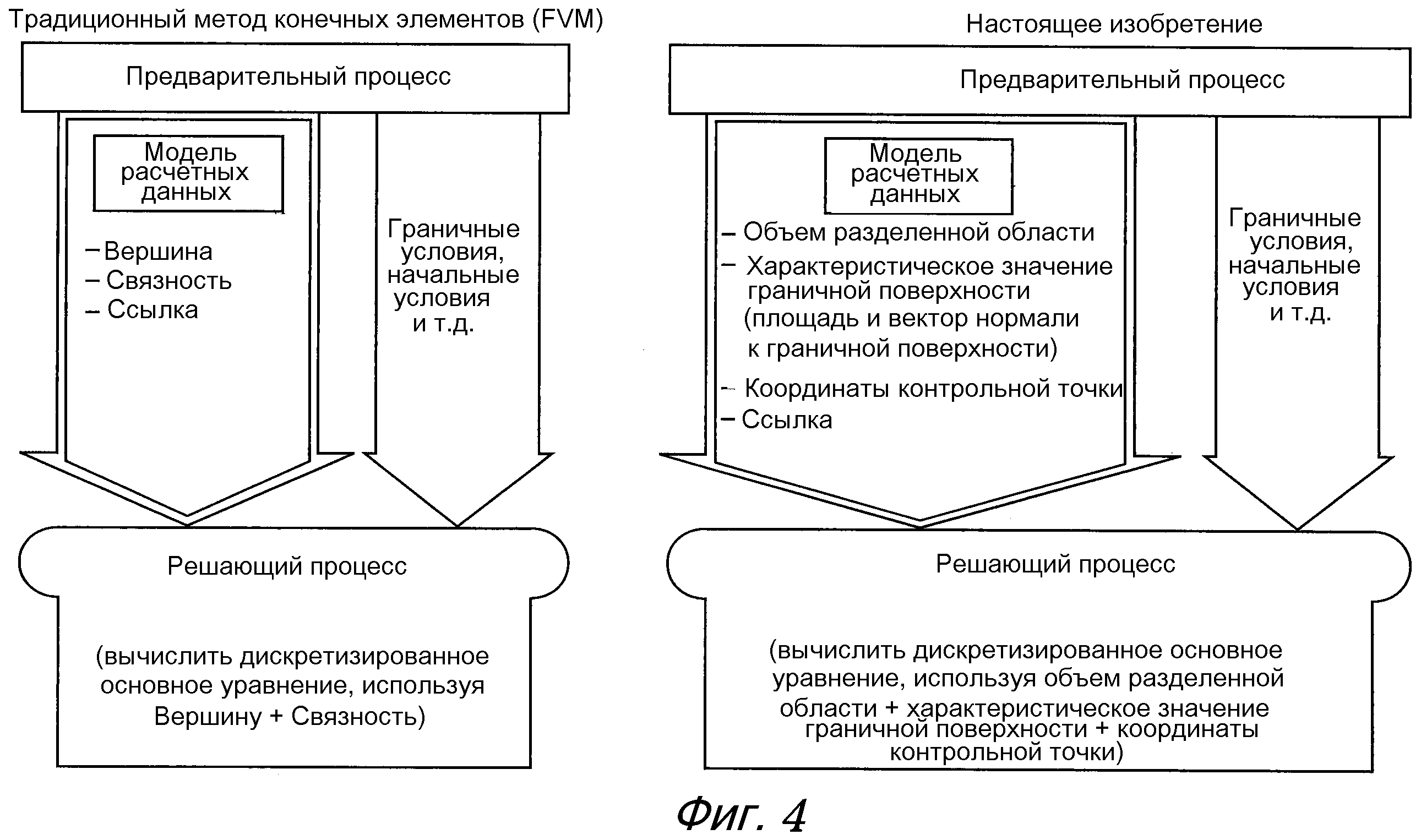
Далее со ссылкой на фиг. 4 приводится сравнение между настоящим изобретением и традиционным методом конечных объемов с дополнительными подробностями.
В традиционном методе конечных объемов, который описан выше, предварительный процесс формирует модель расчетных данных, содержащую Вершину и Связность, которые определяют геометрическую форму разделенной области, полученную путем разделения сетки. Дополнительно, обычно решающий процесс требует информации о связи (в дальнейшем называемой ссылкой) для разделенной области. Таким образом, предварительный процесс формирует модель расчетных данных, содержащую Вершину, Связность и ссылку.
Тогда в традиционном методе конечных объемов, как показано на фиг. 4, модель расчетных данных, содержащая Вершину, Связность, ссылку и граничное условие, начальное условие и т.п., необходимые в решающем процессе, передаются из предварительного процесса в решающий процесс. Затем решающий процесс решает дискретизированное основное уравнение с использованием Вершины, Связности и т.п., содержащихся в переданной модели расчетных данных, и посредством этого вычисляет физические значения.
С другой стороны, в настоящем изобретении предварительный процесс формирует модель расчетных данных, содержащую объем каждой разделенной области, размещенной произвольно, характеристическое значение граничной поверхности (площадь граничной поверхности и вектор нормали к граничной поверхности) и ссылку. Дополнительно, как подробно описано позже, в настоящем изобретении в некоторых случаях, при необходимости, модель расчетных данных снабжается координатами контрольной точки, размещенной внутри каждой разделенной области.
Затем в настоящем изобретении, как показано на фиг. 4, модель расчетных данных, содержащая объем разделенной области, характеристическое значение граничной поверхности и ссылку (координаты контрольной точки, при необходимости), граничное условие, начальное условие и т.п. передаются из предварительного процесса в решающий процесс. Решающий процесс решает дискретизированное основное уравнение, используя объем разделенной области, характеристическое значение граничной поверхности и т.п., содержащиеся в переданной модели расчетных данных, и посредством этого вычисляет физические значения.
Затем, как видно из фиг. 4, существенное отличие настоящего изобретения от традиционного метода конечных объемов состоит в том, что решающий процесс вычисляет физические значения без использования Вершины и Связности. Этот момент является исключительным признаком настоящего изобретения. Этот признак следует из того, что решающий процесс использует дискретизированное основное уравнение, которое использует только значения, не требующие Вершины и Связности.
В результате, как показано на фиг. 4, в настоящем изобретении Вершину и Связность не нужно передавать в решающий процесс. Таким образом, достаточно, чтобы предварительный процесс формировал модель расчетных данных, не содержащую Вершину и Связность. Таким образом, по сравнению с традиционным методом конечных объемов, в настоящем изобретении можно гораздо проще сформировать модель расчетных данных. Соответственно, снижается рабочая загрузка при формировании модели расчетных данных.
Дополнительно, в некоторых случаях форма области анализа, на которой нужно выполнить численный анализ, меняется последовательно во времени, то есть область анализа включает в себя подвижную границу. В таком случае разделенные области нужно двигать и деформировать в соответствии с подвижной границей.
В традиционном методе конечных объемов вычисление физических значений в случае, в котором включается подвижная граница, достигается с помощью способа, в котором Вершина при каждом перемещении подвижной границы сохраняется заранее, или, в качестве альтернативы, с помощью способа, в котором разделение областей повторно выполняется, когда исчислимость утрачена из-за чрезмерной деформации разделенной области. В отличие от этого в настоящем изобретении вычисление физических значений в случае, в котором включается подвижная граница, достигается с помощью способа, в котором объем разделенной области, характеристики граничной поверхности и т.п. вместо Вершины вычисляются и сохраняются заранее, или, в качестве альтернативы, с помощью способа, в котором повторно выполняется разделение областей.
В традиционном методе конечных объемов или, в качестве альтернативы, в настоящем изобретении в случае, когда выбирается какой угодно из вышеупомянутых способов, нужно формировать множество моделей расчетных данных. Тем не менее, в традиционном методе конечных объемов в ситуации, когда формирование всего лишь одной модели расчетных данных требует огромного объема работ, формирование множества моделей во многих случаях становится недостижимым в диапазоне практически доступного объема работ.
С другой стороны, в настоящем изобретении модель расчетных данных не должна содержать Вершину и Связность, и согласованность Вершины и Связности не нужно учитываться при обработке с разделением областей. Таким образом, модель расчетных данных можно вычислять с весьма высокой скоростью. Соответственно, физические значения легко вычисляются в случае, где включается подвижная граница.
Здесь ниже приводится дополнительное описание для вышеупомянутой ссылки. Ссылка является информацией, описывающей отношение между разделенными областями, в которых физические значения меняются друг с другом. Тогда разделенные области, чье отношение описывается в этой ссылке, не должны пространственно прилегать друг к другу. То есть они могут пространственно отстоять друг от друга. Такая ссылка не имеет отношение к Вершине или Связности. Таким образом, по сравнению с Вершиной и Связностью ссылка может формироваться за весьма короткое время.
Далее подробно описывается принцип способа численного анализа (в дальнейшем называемый настоящим способом численного анализа), использующего настоящее изобретение, то есть принцип, когда физические значения могут вычисляться с использованием дискретизированного основного уравнения, выведенного на основе метода взвешенных невязок, и с использованием объема разделенной области и характеристического значения граничной поверхности. Здесь в нижеследующем описании символ, окруженный [], указывает вектор, представленный на чертежах полужирным шрифтом.
Сначала модель расчетных данных в настоящем способе численного анализа определяется использованием объема каждой разделенной области, полученной путем разделения области анализа, и характеристического значения граничной поверхности, указывающего характеристики граничной поверхности между соседними разделенными областями.
Фиг. 5 - концептуальная схема, показывающая пример модели расчетных данных в настоящем способе численного анализа, как описано выше.
На фигуре ячейки R1, R2, R3… являются разделенными областями, полученными путем разделения области анализа, и имеют объемы Va, Vb, Vc… соответственно. Дополнительно граничная поверхность E является поверхностью, через которую физические значения меняются между ячейкой R1 и ячейкой R2, и соответствует граничной поверхности в настоящем изобретении. Дополнительно площадь Sabобозначает площадь граничной поверхности E и является одним из характеристических значений граничной поверхности в настоящем изобретении. Кроме того, [n]abобозначает вектор нормали к граничной поверхности E и является одним из характеристических значений граничной поверхности в настоящем изобретении. Дополнительно каждая из контрольных точек a, b, c… размещается внутри каждой из ячеек R1, R2 и R3. На фиг. 5 каждая контрольная точка размещается в положении центра тяжести каждой из ячеек R1, R2, R3…. Однако каждую из контрольных точек a, b, c… не нужно размещать в положении центра тяжести каждой из ячеек R1, R2, R3…. Кроме того, α обозначает расстояние от контрольной точки a до граничной поверхности E в случае, где расстояние от контрольной точки a до контрольной точки b задается равным 1. Таким образом, α является соотношением, указывающим точку внутреннего разделения, где граничная поверхность E располагается на отрезке прямой, соединяющем контрольную точку a и контрольную точку b.
Здесь граничная поверхность находится между каждыми соседними ячейками, а не только между ячейкой R1 и ячейкой R2. Тогда вектор нормали к граничной поверхности и площадь граничной поверхности также предоставляются для каждой граничной поверхности.
Затем строится фактическая модель расчетных данных в виде группы данных, содержащей данные размещения для контрольных точек a, b, c…; данные объема, указывающие объемы Va, Vb, Vc… ячеек R1, R2, R3…, где располагаются контрольные точки a, b, c…; данные о площади, указывающие площадь каждой граничной поверхности; и данные вектора нормали, указывающие вектор нормали к каждой граничной поверхности.
То есть модель расчетных данных в настоящем способе численного анализа определяется посредством объемов Va, Vb, Vc… ячеек R1, R2, R3…; площадей граничных поверхностей, которые являются характеристическими значениями граничной поверхности, указывающими характеристики граничных поверхностей между соседними ячейками R1, R2, R3…; и векторов нормали к граничным поверхностям, которые являются характеристическими значениями граничной поверхности, указывающими характеристики граничных поверхностей между соседними ячейками R1, R2, R3….
Здесь ячейки R1, R2, R3… имеют контрольные точки a, b, c… соответственно. Таким образом, объемы Va, Vb, Vc… ячеек R1, R2, R3… можно признать в качестве объемов пространств (контрольных объемов), виртуально занятых контрольными точками a, b, c… соответственно.
Дополнительно, при необходимости модель расчетных данных в настоящем способе численного анализа содержит данные соотношения, содержащие каждое соотношение α, указывающее точку внутреннего разделения, где каждая граничная поверхность располагается на отрезке прямой, соединяющем контрольные точки, расположенные по обеим сторонам граничной поверхности.
Следующее описание приводится для примера вычисления физических значений, когда скорость потока в каждой ячейке (разделенной области) области анализа вычисляется с использованием вышеупомянутой модели расчетных данных. Здесь скорость потока в каждой контрольной точке признается в качестве скорости потока в каждой ячейке.
Сначала в настоящем вычислении физических значений в настоящем способе численного анализа в случае анализа текучей среды используются уравнения Навье-Стокса, выраженные следующим уравнением (1), и уравнение непрерывности, выраженное следующим уравнением (2).
[Выражение 1]
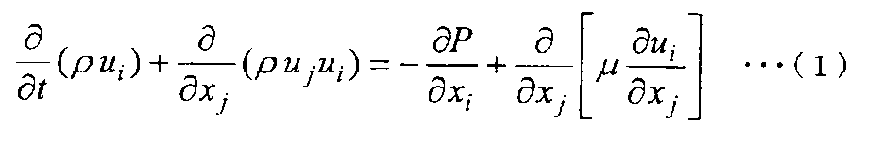
[Выражение 2]
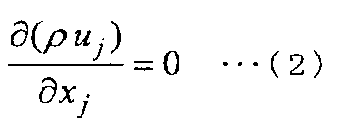
Здесь в уравнениях (1) и (2) t обозначает время, xi(i=1, 2, 3) обозначает координаты в декартовой системе координат, ρ обозначает плотность текучей среды, ui (i=1, 2, 3) обозначает составляющие скорости потока текучей среды, P обозначает давление, μ обозначает коэффициент вязкости текучей среды, а нижние индексы i (i=1, 2, 3) и j (j=1, 2, 3) обозначают составляющие направления в декартовой системе координат. Дополнительно обозначение суммирования применяется для нижних индексов j.
Затем, когда уравнения (1) и (2) интегрируются по объему контрольного объема на основе метода взвешенных невязок, уравнение (1) переписывается в следующее уравнение (3), а уравнение (2) переписывается в следующее уравнение (4).
[Выражение 3]
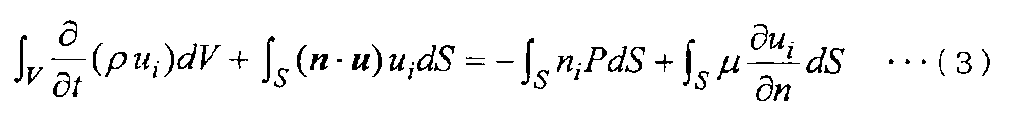
[Выражение 4]
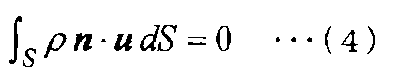
Здесь, в уравнениях (3) и (4) V обозначает объем контрольного объема, ∫VdV обозначает интегрирование по объему V, S обозначает площадь контрольного объема, ∫SdS обозначает интегрирование по площади S, [n] обозначает вектор нормали к S, ni (i=1, 2, 3) обозначает составляющие вектора нормали [n], и ∂/∂n обозначает производную по нормали.
Здесь для простоты описания плотность ρ и коэффициент вязкости μ текучей среды устанавливаются постоянными. Однако подход, применяющий эти постоянные, здесь можно распространить даже для случая, когда значения свойств материалов текучей среды меняются в зависимости от времени, пространства, температуры и т.п.
Затем в контрольной точке a на фиг. 5 площадь Sab граничной поверхности E дискретизируется, так что каждое уравнение преобразуется в приближенное уравнение в виде алгебраического уравнения. В результате уравнение (3) переписывается в следующее уравнение (5), а уравнение (4) переписывается в следующее уравнение (6).
[Выражение 5]
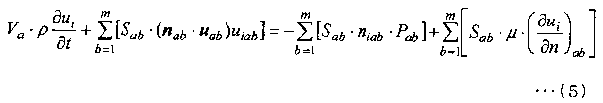
[Выражение 6]
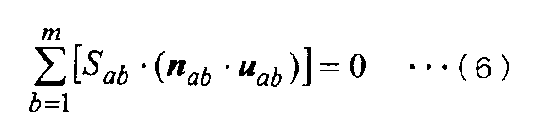
Здесь [n]ab, [u]ab, uiab, niab, Pab и (∂ui/∂n)ab, которые имеют нижние индексы a и b, являются физическими значениями на граничной поверхности E между контрольной точкой a и контрольной точкой b. Дополнительно niab является составляющей [n]ab. Кроме того, m является количеством всех контрольных точек в отношении связи с контрольной точкой a (отношение наличия граничной поверхности между ними).
Затем, когда уравнения (5) и (6) делятся на Va (объем контрольного объема контрольной точки a), уравнение (5) переписывается в следующее уравнение (7), а уравнение (6) переписывается в следующее уравнение (8).
[Выражение 7]
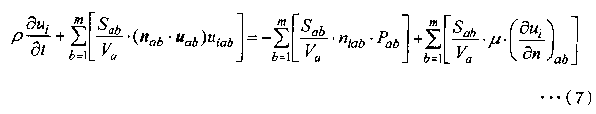
[Выражение 8]
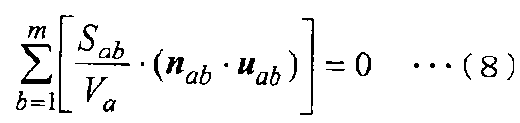
Здесь принимается следующее уравнение (9).
[Выражение 9]
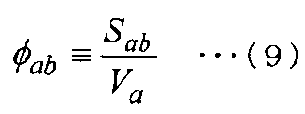
Затем уравнение (7) переписывается в следующее уравнение (10), а уравнение (8) переписывается в следующее уравнение (11).
[Выражение 10]
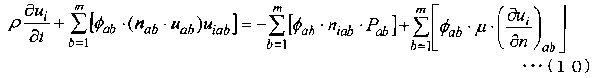
[Выражение 11]
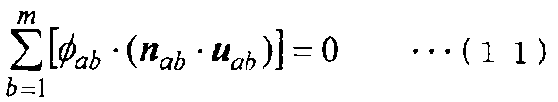
В уравнениях (10) и (11) каждое из [u]ab, uiab, Pab и (∂ui/∂n)ab получается приблизительно как среднее взвешенное (среднее взвешенное, где принимается во внимание противопотоковая схема в случае адвективного члена) физического значения в контрольной точке a и контрольной точке b, и определяется в зависимости от расстояния и направления между контрольными точками a и b, позиционного отношения (вышеупомянутое соотношение α) с граничной поверхностью E, расположенной между ними, и направления вектора нормали к граничной поверхности E. Здесь [u]ab, uiab, Pab и (∂ui/∂n)ab являются значениями, независимыми от геометрической формы граничной поверхности E (то есть значениями, не требующими Вершины и Связности, которые определяют форму ячейки).
Кроме того, ψab, заданная уравнением (9), является величиной (площадь/объем) и поэтому является величиной, независимой от геометрической формы контрольного объема (то есть значениями, не требующими Вершины и Связности, которые определяют форму ячейки).
То есть эти уравнения (10) и (11) являются рабочими формулами на основе метода взвешенных невязок, в котором физическое значение может вычисляться с использованием только значений, не требующих Вершины и Связности, которые определяют форму ячейки.
Таким образом, когда вышеупомянутая модель расчетных данных формируется перед вычислением физических значений (решающий процесс), а затем модель расчетных данных и дискретизированные основные уравнения (10) и (11) используются при вычислении физических значений, скорость потока можно вычислить при вычислении физических значений полностью без использования геометрической формы контрольного объема (то есть Вершины и Связности, которые определяют форму ячейки).
По существу, скорость потока может вычисляться при вычислении физических значений полностью без использования Вершины и Связности. Таким образом, модель расчетных данных не должна содержать Вершину и Связность. Соответственно, в момент формирования модели расчетных данных не накладывается ограничение геометрической формой ячейки и поэтому форма ячейки может устанавливаться произвольно. Таким образом, в соответствии с настоящим способом численного анализа можно значительно смягчить ограничение на коррекционную работу для данных о трехмерной форме, как описано выше.
Здесь в момент фактического решения уравнений (10) и (11) физические значения, такие как [u]ab и Pab на граничной поверхности E, интерполируются обычно с помощью линейной интерполяции. Например, когда физическое значение в контрольной точке a обозначается с помощью ψa, а физическое значение в контрольной точке b обозначается с помощью ψb, физическое значение ψab на граничной поверхности E получается с помощью следующего уравнения (12).
[Выражение 12]
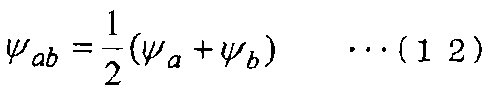
Кроме того, используя соотношение α, указывающее точку внутреннего разделения, где граничная поверхность располагается на отрезке прямой, который соединяет контрольные точки, расположенные по обеим сторонам граничной поверхности, физическое значение ψab также можно получить с помощью следующего уравнения (13).
[Выражение 13]
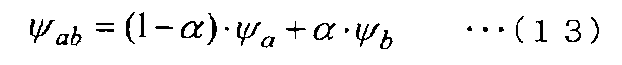
Таким образом, когда модель расчетных данных содержит данные соотношения, описывающие соотношение α, физическое значение на граничной поверхности E может вычисляться в соответствии с уравнением (13), используя среднее взвешенное, соответствующее расстояниям от контрольной точки a и от контрольной точки b.
Кроме того, уравнения (уравнения Навье-Стокса или т.п.) для модели сплошной среды содержат частную производную 1-го порядка (частные дифференциалы), как показано в уравнении (1).
Здесь в отношении производных в уравнениях для модели сплошной среды порядок дифференциала понижается путем преобразования интегрирования по объему в интеграл по поверхности, используя интегрирование по частям, теорему Гаусса о дивергенции или обобщенную теорему Грина. Таким образом, дифференциал 1-го порядка превращается в дифференциал нулевого порядка (скалярную величину или векторную величину).
Например, в соответствии с обобщенной теоремой Грина, когда физическое значение обозначается ψ, выполняется следующее уравнение (14).
[Выражение 14]
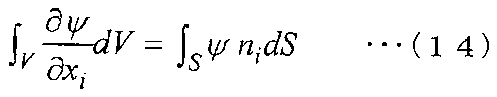
Здесь в уравнении (14) ni (i=1, 2, 3) обозначают составляющие i-направления единичного вектора нормали [n] к поверхности S.
В результате преобразования интегрирования по объему в интеграл по поверхности дифференциалы членов 1-го порядка в уравнении для модели сплошной среды обрабатываются как скалярные величины или векторные величины на граничной поверхности. Тогда эти значения можно интерполировать от физических значений в отдельных контрольных точках с помощью вышеупомянутой линейной интерполяции или т.п.
Дополнительно, как описано позже, некоторое уравнение для модели сплошной среды содержит частную производную второго порядка.
Когда подынтегральное выражение в уравнении (14) дифференцируется еще на один порядок, получается следующее уравнение (15). Затем член дифференциала второго порядка в уравнении для модели сплошной среды переписывается в следующее уравнение (16) на граничной поверхности E с использованием преобразования интегрирования по объему в интеграл по поверхности.
[Выражение 15]
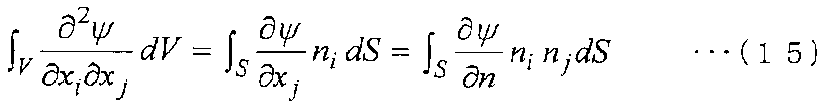
[Выражение 16]
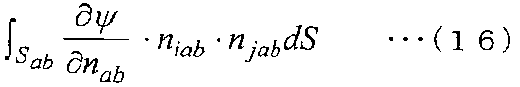
Здесь в уравнении (15) ∂/∂n обозначает дифференциал по направлению нормали. В уравнении (16) ∂/∂nab обозначает дифференциал [n]ab-го направления.
То есть на основании преобразования интегрирования по объему в интеграл по поверхности член дифференциала второго порядка в уравнении для модели сплошной среды принимает вид произведения между дифференциалом нормального направления физического значения ψ (дифференциал в направлении нормали [n]ab к Sab) и составляющими niab и njab в [n].
Здесь ∂ψ/∂nab в уравнении (16) приблизительно выражается в следующем уравнении (17).
[Выражение 17]
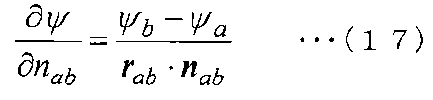
Здесь вектор [r]ab между контрольными точками между контрольной точкой a и контрольной точкой b задается в виде следующего уравнения (18) на основе вектора
[r]a положения контрольной точки a и вектора [r]b положения контрольной точки b.
[Выражение 18]
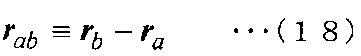
Таким образом, поскольку площадь граничной поверхности E равна Sab, уравнение (16) переписывается в следующее уравнение (19). Соответственно уравнение (16) может вычисляться с использованием этого выражения.
[Выражение 19]
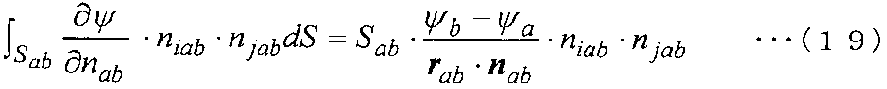
При выведении уравнения (16) признаются следующие факты.
Все линейные частные дифференциальные уравнения могут выражаться линейной суммой членов, образованной из константы или из частной производной первого, второго или другого порядка, умноженной на коэффициент. В уравнениях (15) - (18), когда физическое значение ψ заменяется частной производной ψ первого порядка, интегрирование по объему частной производной высшего порядка может вычисляться как интеграл по поверхности частной производной низшего порядка, как показано в уравнении (14). Таким образом, когда эта процедура повторяется последовательно от частного дифференциала низшего порядка, частные производные во всех членах, содержащихся в линейном частном дифференциальном уравнении, могут вычисляться из физического значения ψ в контрольной точке; ψab, которое является ψ на граничной поверхности, вычисленным в соответствии с уравнением (12) или уравнением (13); расстояния между контрольными точками, полученного из вектора между контрольными точками, заданного уравнением (18); площади Sab граничной поверхности E, показанной в уравнении (5); и составляющих niab и njab вектора нормали, показанных в уравнении (16). Далее в нелинейном частном дифференциальном уравнении член, состоящий, например, из произведения между ψ и частной производной ψ первого порядка, или член, состоящий из квадрата частной производной первого порядка, каждый из которых является нелинейным членом, показанным в уравнении (20), можно получить путем численного вычисления с помощью итерационного вычисления. То есть итерационное вычисление может выполняться таким образом, что ψ и частная производная первого порядка в каждом члене приблизительно выражаются вычисленными значениями, полученными в предшествующем на один шаг итерационном вычислении. В соответствии с таким способом, все нелинейные члены в частном дифференциальном уравнении можно получить с помощью численного вычисления.
Приведенное выше описание выполнено для конкретного случая уравнений для модели сплошной среды. Однако, как видно из приведенного выше описания, дискретизация, не требующая Вершины и Связности, применима к любым другим видам частных дифференциальных уравнений. Тем не менее закон сохранения требует другого условия выполнения. Этот момент описывается позже.
[Выражение 20]
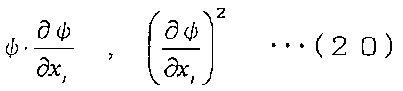
Здесь в настоящем способе численного анализа вычисление физических значений не требует Вершины и Связности, как описано выше. Таким образом, в момент формирования модели расчетных данных (предварительный процесс) в случае, где объем контрольного объема и площадь и вектор нормали к граничной поверхности вычисляются без использования Вершины и Связности, скорость потока может вычисляться с использованием дискретизированных основных уравнений, показанных в уравнениях (10) и (11), и полностью без использования геометрической формы контрольного объема (то есть геометрической формы ячейки).
Однако в настоящем способе численного анализа объем контрольного объема, и площадь, и вектор нормали к граничной поверхности не нужно вычислять без использования конкретной геометрической формы контрольного объема. То есть решающий процесс не использует Вершину и Связность. Таким образом, даже если использовалась конкретная геометрическая форма контрольного объема, в частности, Вершина и Связность, то отсутствует ограничение касательно разделенной области, то есть ограничение на деформацию или кручение разделенной области, как в традиционном методе конечных элементов или методе конечных объемов. Соответственно, модель расчетных данных можно легко вычислить, как описано выше.
Далее в настоящем способе численного анализа, в зависимости от условий, вышеупомянутый вектор нормали можно заменить вектором расстояния, который соединяет контрольные объемы. Причина для этого описывается ниже.
В случае, где вектор нормали [n]ab к граничной поверхности E, показанной на фиг. 5, находится в таком же направлении, что и вектор расстояния [r]ab, который соединяет контрольную точку a и контрольную точку b, вектор нормали [n] выражается в виде следующего уравнения (21).
[Выражение 21]
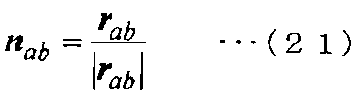
Таким образом, в случае, где вектор нормали [n]ab к граничной поверхности E находится в таком же направлении, что и вектор расстояния [r]ab, когда уравнение (21) подставляется в дискретизированные основные уравнения, показанные в уравнениях (10) и (11), получаются дискретизированные основные уравнения в случае, где вектор нормали [n]ab находится в направлении, соединяющем контрольные точки a и b. То есть в случае, где граничная поверхность и вектор, который соединяет контрольные точки, расположенные по обеим сторонам граничной поверхности, ортогональны друг другу, вектор нормали в дискретизированных основных уравнениях можно заменить вектором расстояния.
В соответствии с такими дискретизированными основными уравнениями, вектор нормали [n]ab к граничной поверхности E может определяться только из координат положения контрольной точки.
Дополнительно, когда граничная поверхность E и вектор расстояния становятся как можно ортогональнее, повышается точность при вычислении физических значений. Таким образом, когда вектор нормали заменяется вектором расстояния, повышается точность вычисления.
Кроме того, произвольность в векторе нормали можно зафиксировать в направлении, соединяющем контрольные точки.
Однако в случае, где утрачена произвольность в векторе нормали, в некоторых случаях нельзя придать гибкость ориентации граничной поверхности. В таком случае по сравнению со случаем, где имеется произвольность в векторе нормали, возникает ограничение на задание объема контрольного объема и граничной поверхности в момент формирования модели расчетных данных. Дополнительно в случае, где вектор нормали заменяется вектором, соединяющим контрольные точки, необходим вектор расстояния, и поэтому координаты контрольной точки необходимы с целью вычисления вектора расстояния. Таким образом, модель расчетных данных должна содержать координатные данные контрольной точки или, в качестве альтернативы, данные вектора расстояния. Однако даже в этом случае в настоящем способе численного анализа вычисление физических значений не требует Вершины и Связности.
Далее, с целью разъяснения разницы между настоящим изобретением и методом частиц ниже описывается условие, по которому закон сохранения физического значения должен выполняться при вычислении физических значений.
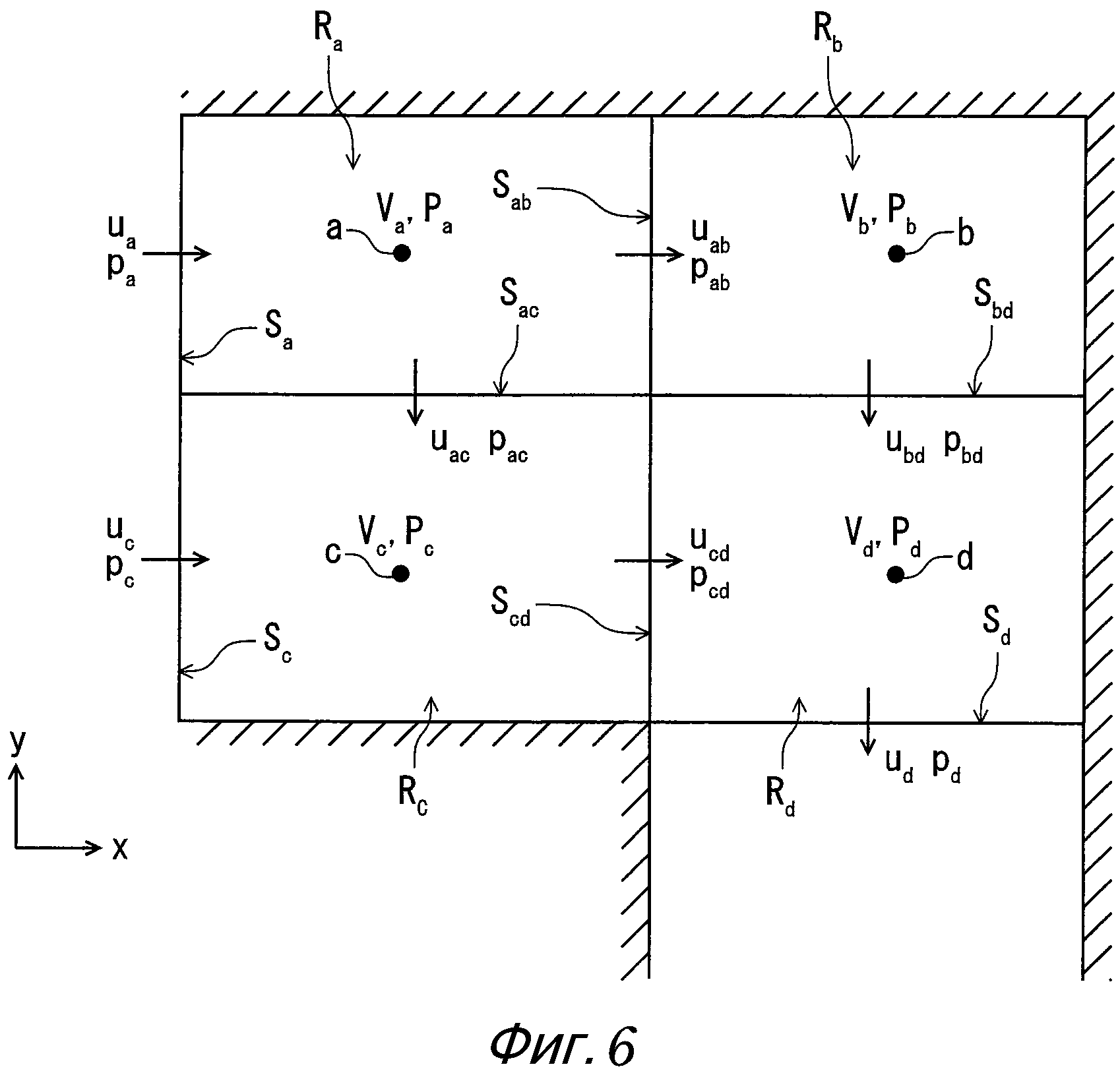
Например, как показано на фиг. 6, рассматриваются ячейки Ra, Rb, Rc и Rd, которые делят L-образный проход на четыре секции. Здесь контрольные точки a, b, c и d, размещенные внутри ячеек Ra, Rb, Rc и Rd соответственно, располагаются в центрах ячеек Ra, Rb, Rc и Rd. Дополнительно вектор скорости потока на каждой граничной поверхности предполагается перпендикулярным граничной поверхности.
Здесь на фиг. 6 Va является объемом ячейки Ra (объем контрольного объема контрольной точки a), Vb является объемом ячейки Rb (объем контрольного объема контрольной точки b), Vc является объемом ячейки Rc (объем контрольного объема контрольной точки c), Vd является объемом ячейки Rd (объем контрольного объема контрольной точки d), ρa является плотностью в ячейке Ra, ρb является плотностью в ячейке Rb, ρc является плотностью в ячейке Rc, ρd является плотностью в ячейке Rd, Sa является площадью граничной поверхности между ячейкой Ra и внешней областью, Sc является площадью граничной поверхности между ячейкой Rc и внешней областью, Sd является площадью граничной поверхности между ячейкой Rd и внешней областью, Sab является площадью граничной поверхности между ячейкой Ra и ячейкой Rb, Sac является площадью граничной поверхности между ячейкой Ra и ячейкой Rc, Sbd является площадью граничной поверхности между ячейкой Rb и ячейкой Rd, Scd является площадью граничной поверхности между ячейкой Rc и ячейкой Rd, ua является скоростью потока на граничной поверхности между ячейкой Ra и внешней областью, uc является скоростью потока на граничной поверхности между ячейкой Rc и внешней областью, ud является скоростью потока на граничной поверхности между ячейкой Rd и внешней областью, uab является скоростью потока на граничной поверхности между ячейкой Ra и ячейкой Rb, uac является скоростью потока на граничной поверхности между ячейкой Ra и ячейкой Rc, ubd является скоростью потока на граничной поверхности между ячейкой Rb и ячейкой Rd, ucd является скоростью потока на граничной поверхности между ячейкой Rc и ячейкой Rd, ρa является плотностью в ячейке Ra, ρab является плотностью на граничной поверхности между ячейкой Ra и ячейкой Rb, ρac является плотностью на граничной поверхности между ячейкой Ra и ячейкой Rc, и ρbd является плотностью на граничной поверхности между ячейкой Rb и ячейкой Rd.
Дискретизация уравнения сохранения массы рассматривается в четырех контрольных точках a, b, c и d (в четырех ячейках Ra, Rb, Rc, Rd), показанных на фиг. 6. Здесь дискретизированное основное уравнение, полученное путем дискретизации уравнения сохранения массы, приводится в позже описанном уравнении (43).
Дискретизированное основное уравнение в контрольной точке a показано в следующем уравнении (22).
[Выражение 22]
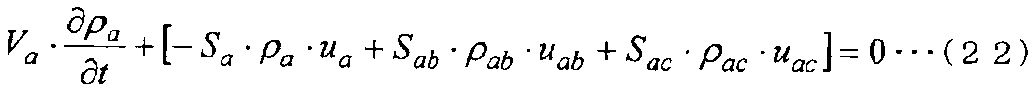
Дискретизированное основное уравнение в контрольной точке b показано в следующем уравнении (23).
[Выражение 23]
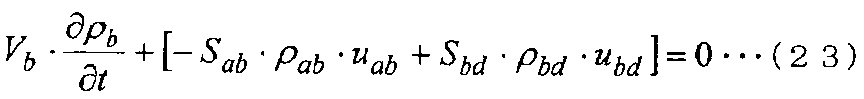
Дискретизированное основное уравнение в контрольной точке c показано в следующем уравнении (24).
[Выражение 24]
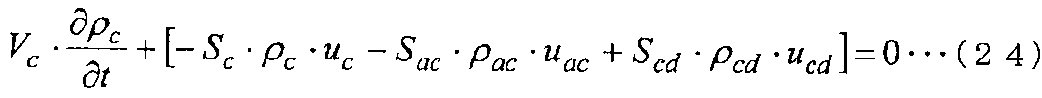
Дискретизированное основное уравнение в контрольной точке d показано в следующем уравнении (25).
[Выражение 25]
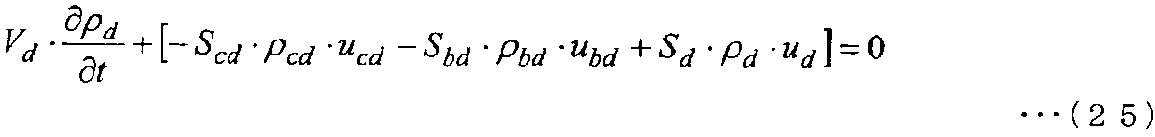
Затем, когда уравнения (22) - (25) складываются вместе, получается следующее уравнение (26).
[Выражение 26]
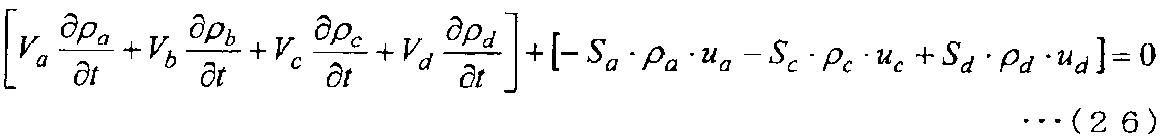
На основе того, что объемы Va, Vb, Vc и Vd контрольных объемов контрольных точек a, b, c и d являются постоянными относительно времени, объемы перемещаются в дифференцируемые по времени члены. Тогда уравнение (26) переписывается в следующее уравнение (27).
[Выражение 27]
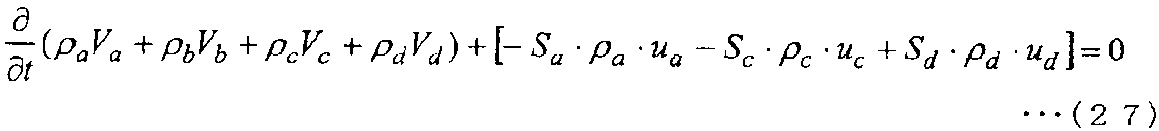
Здесь, когда общий объем, занимаемый контрольными объемами контрольных точек a, b, c и d, обозначается Vabcd, а средняя плотность обозначается ρ(черта сверху)abcd, общий объем Vabcd выражается следующим уравнением (28), а средняя плотность ρ(черта сверху)abcd выражается следующим уравнением (29).
[Выражение 28]
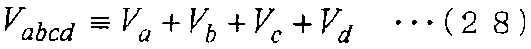
[Выражение 29]
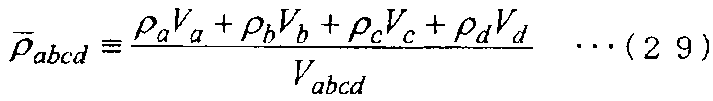
Таким образом, уравнение (27) переписывается в следующее уравнение (30).
[Выражение 30]
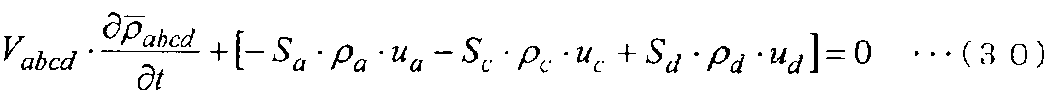
Уравнение (30) указывает, что разность между поступающим потоком массы во всей области, занимаемой контрольными объемами контрольных точек a, b, c и d, и вытекающим потоком массы равна изменению за единицу времени в средней плотности (изменению массы относительно времени) во всей области, занимаемой контрольными объемами контрольных точек a, b, c и d. То есть уравнение сохранения массы, дискретизированное в каждой из контрольных точек a, b, c и d, также справедливо в области, занимаемой контрольными объемами всех контрольных точек.
А именно, когда каждое дискретизированное основное уравнение в области контрольного объема, указанной контрольной точкой, складывается для всех контрольных точек, должно быть получено уравнение, которое удовлетворяет закону сохранения для всей области анализа, служащей в качестве объекта вычисления.
Затем, когда общее количество контрольных точек обозначается N и складываются уравнения сохранения массы, показанные в уравнении (43), получается следующее уравнение (31).
[Выражение 31]
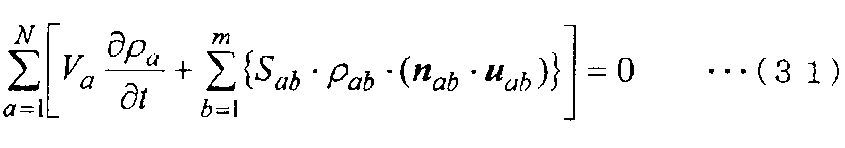
В уравнении (31) площадь граничной поверхности между контрольными точками предполагается одинаковой, если смотреть со стороны контрольной точки a и если смотреть со стороны контрольной точки b. Таким образом, поток массы (ρ[n]·[u])·S между контрольными точками имеет противоположный знак, положительный или отрицательный, и имеет одинаковое абсолютное значение на стороне контрольной точки a и на стороне контрольной точки b. Соответственно, сумма потока массы сводится к нулю. То есть уравнение (31) указывает, что разность между поступающей массой и вытекающей массой во всей области, которую нужно вычислить, равна изменению массы за единицу времени во всей области. Соответственно, уравнение (31) служит в качестве уравнения сохранения массы во всей области анализа.
Таким образом, чтобы уравнение (31) удовлетворяло закону сохранения массы во всей области, которую нужно вычислить, необходимыми являются условие, что площадь граничной поверхности одинакова между двумя контрольными точками; и условие, что вектор нормали имеет одно и то же абсолютное значение, если смотреть со стороны одной контрольной точки и если смотреть со стороны другой контрольной точки.
Кроме того, чтобы выполнялся закон сохранения массы, необходимо условие, что объем, занимаемый контрольными объемами всех контрольных точек, совпадает с общим объемом области анализа, как показано в следующем уравнении (32).
[Выражение 32]
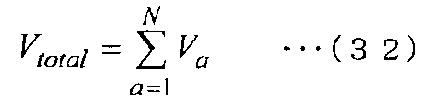
Этот факт легко признать, поскольку плотность ρ сплошной среды выражается одной переменной ρ1=ρ2=…=ρ.
По существу, чтобы выполнялся закон сохранения массы, необходимо условие, что полная сумма объемов контрольных объемов всех контрольных точек совпадает с объемом области анализа.
Здесь приведено описание для уравнения сохранения массы. Однако закон сохранения должен выполняться также для импульса и энергии сплошной среды. Таким образом, также для этих физических значений, чтобы выполнялся закон сохранения, когда каждое из позже описанных уравнений (50) и (55) складывается для всех контрольных точек, необходимыми являются условие, что объем, занимаемый контрольными объемами всех контрольных точек, совпадает с общим объемом области анализа; условие, что площадь граничной поверхности одинакова между двумя контрольными точками; и вектор нормали имеет одно и то же абсолютное значение (с противоположным, положительным или отрицательным, знаком), если смотреть со стороны одной контрольной точки и если смотреть со стороны другой контрольной точки.
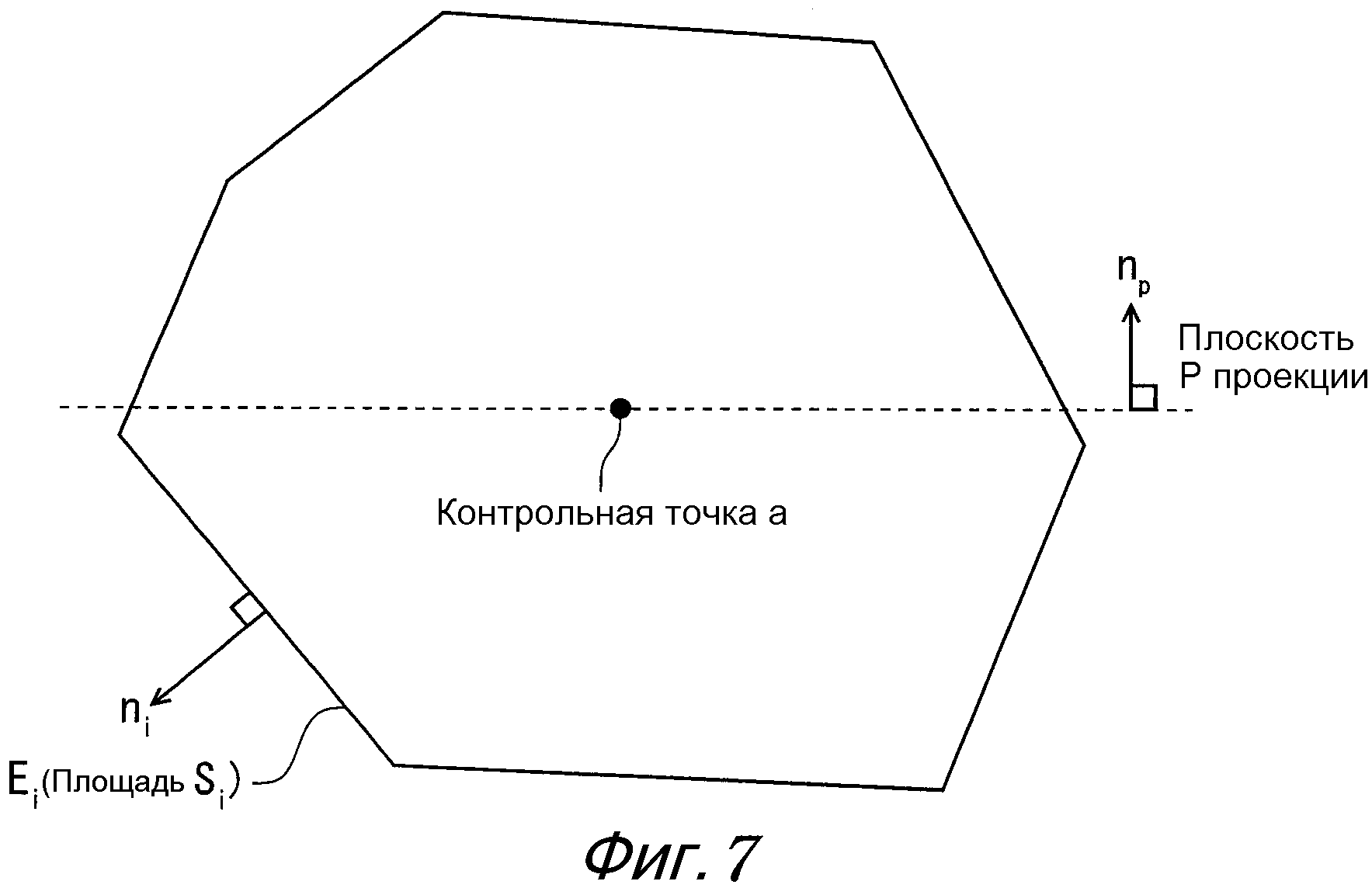
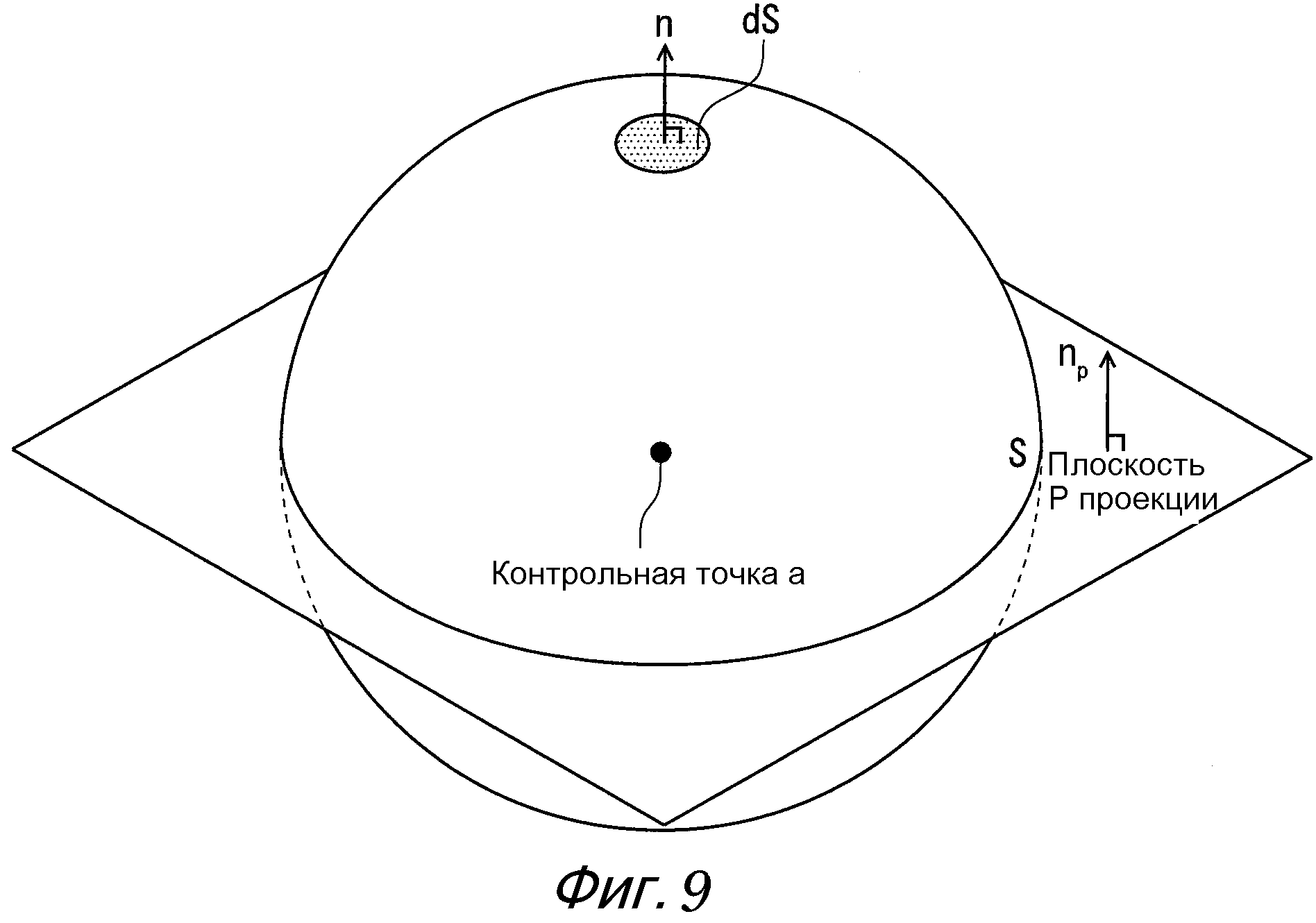
Дополнительно, чтобы выполнялся закон сохранения, в случае, где рассматривается контрольный объем, занимаемый контрольной точкой a, как показано на фиг. 7, необходимо условие, что выполняется следующее уравнение (33), когда рассматривается бесконечно большая плоскость P проекции, которая проходит через контрольную точку a и имеет единичный вектор нормали [n]P с произвольным направлением.
[Выражение 33]
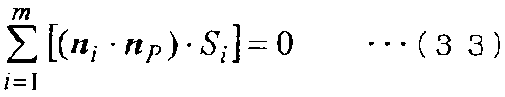
Здесь на фиг. 7 и в уравнении (33) Si является площадью граничной поверхности Ei, [n]i является единичным вектором нормали к граничной поверхности Ei, и m является общим количеством поверхностей контрольного объема.
Уравнение (33) указывает, что многогранник, составляющий контрольный объем, образует замкнутое пространство. Это уравнение (33) выполняется, даже когда часть многогранника, составляющего контрольный объем, является вогнутой поверхностью.
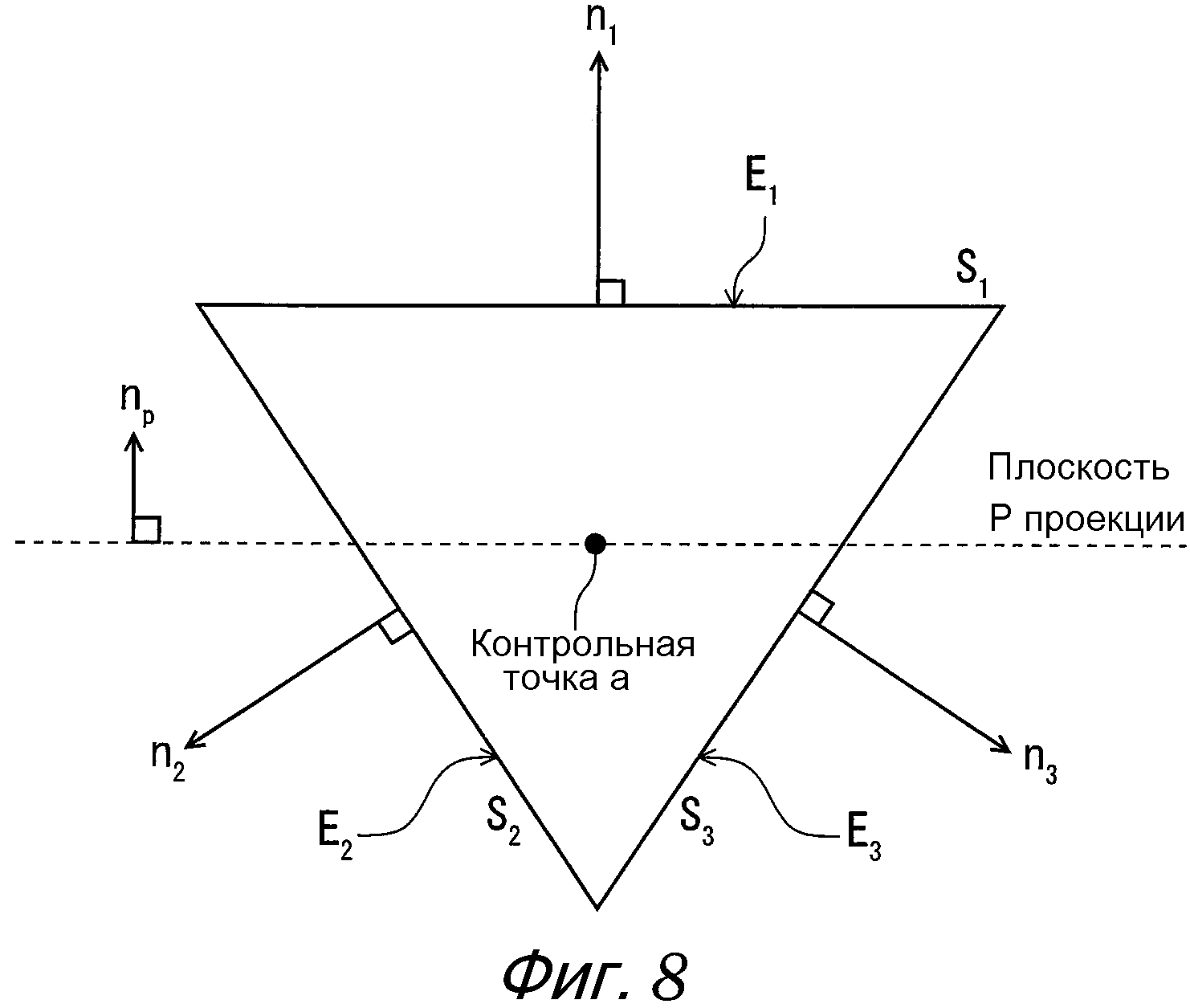
Здесь, как показано на фиг. 8, уравнение (33) также выполняется для треугольника в двух измерениях. Дополнительно, когда находится предел, так что одна поверхность многогранника превращается в бесконечно малую поверхность dS, и m делается ∞, получается следующее уравнение (34). Это выполняется даже для объекта с замкнутой искривленной поверхностью, который показан на фиг. 9.
[Выражение 34]
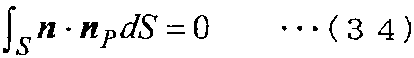
Условие, при котором выполняется уравнение (33), является необходимым для условия, что выполняется теорема Гаусса или обобщенная теорема Грина, показанные в уравнении (14).
Тогда обобщенная теорема Грина является теоремой, предоставляющей основу для дискретизации сплошной среды. Таким образом, в случае, где интегрирование по объему меняется на интеграл по поверхности в соответствии с теоремой Грина, а затем выполняется дискретизация, обязательным является условие, что выполняется уравнение (33), чтобы выполнялся закон сохранения.
По существу, в момент выполнения численного анализа с использованием модели расчетных данных и вычисления физических значений, описанных выше, необходимы три следующих условия, чтобы выполнялся закон сохранения для физического значения.
(а) Сумма объемов контрольных объемов всех контрольных точек (объем всех разделенных областей) совпадает с объемом области анализа.
(b) Площадь граничной поверхности одинакова между двумя контрольными точками, и вектор нормали имеет одно и то же абсолютное значение, если смотреть со стороны одной контрольной точки (одна из разделенных областей, расположенных по обеим сторонам граничной поверхности) и если смотреть со стороны другой контрольной точки (другая из разделенных областей, расположенных по обеим сторонам граничной поверхности).
(c) Уравнение (33) выполняется, когда рассматривается бесконечно большая плоскость P проекции, которая проходит через контрольную точку (проходит через разделенную область) и которая имеет единичный вектор нормали [n]P в произвольном направлении.
То есть, когда нужно, чтобы выполнялся закон сохранения, нужно сформировать такую модель расчетных данных, чтобы эти условия выполнялись. Однако, как описано выше, в настоящем способе численного анализа в момент формирования модели расчетных данных форма ячейки может деформироваться произвольно. Таким образом, модель расчетных данных может быть легко сформирована так, чтобы выполнялись три вышеупомянутых условия.
Ниже подробно описываются причина, по которой метод MPS (Полунеявный метод движущихся частиц), который является традиционным методом частиц, не может удовлетворять закону сохранения; причина увеличения вычислительной нагрузки; и преимущество настоящего способа численного анализа перед методом частиц.
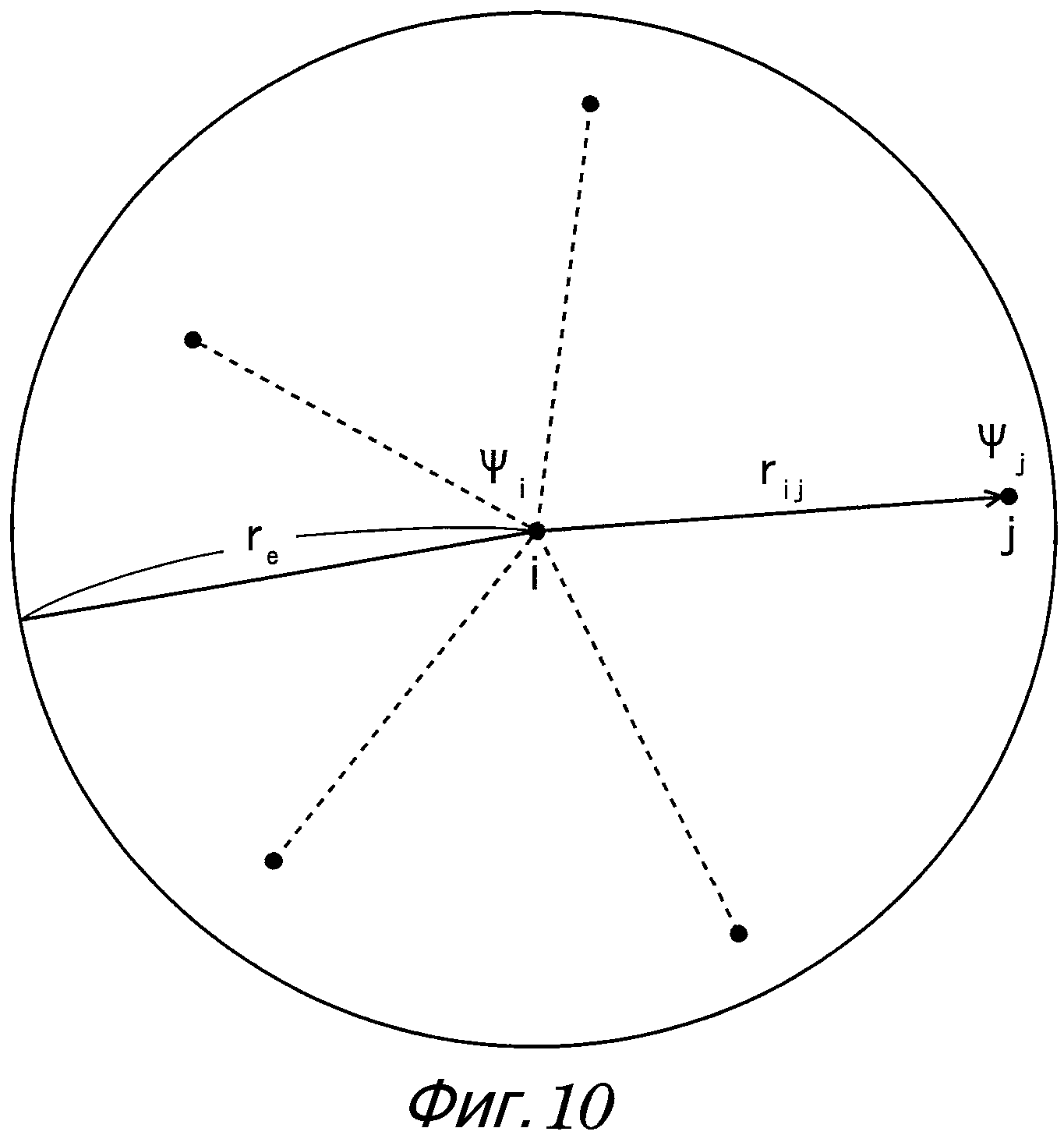
Метод MPS является методикой, в которой обнаруживаются частицы, присутствующие в сфере радиуса re, заданной подходящим образом, затем устанавливается отношение связи с каждой частицей, а затем выполняется вычисление. Например, как показано на фиг. 10, когда множество частиц j присутствует вокруг частицы i, лапласиан (∇2ψ)i для частицы i приблизительно выражается в виде следующего уравнения (35).
[Выражение 35]
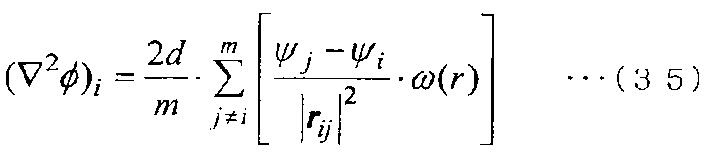
Здесь на фиг. 10 ψi обозначает физическое значение на частице i, ψj обозначает физическое значение на частице j, а [r]ij обозначает вектор расстояния от частицы i до частицы j.
Кроме того, d в уравнении (35) обозначает постоянную, указывающую размерность, и поэтому равно трем в случае трех измерений. Кроме того, ω(r) в уравнении (35) является весовой функцией, выраженной следующим уравнением (36). Дополнительно m в уравнении (35) является количеством частиц в отношении связи.
[Выражение 36]
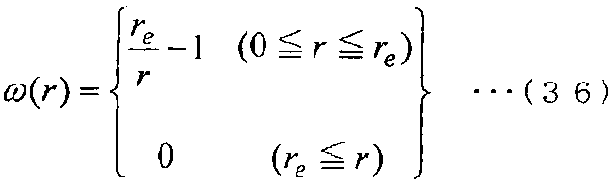
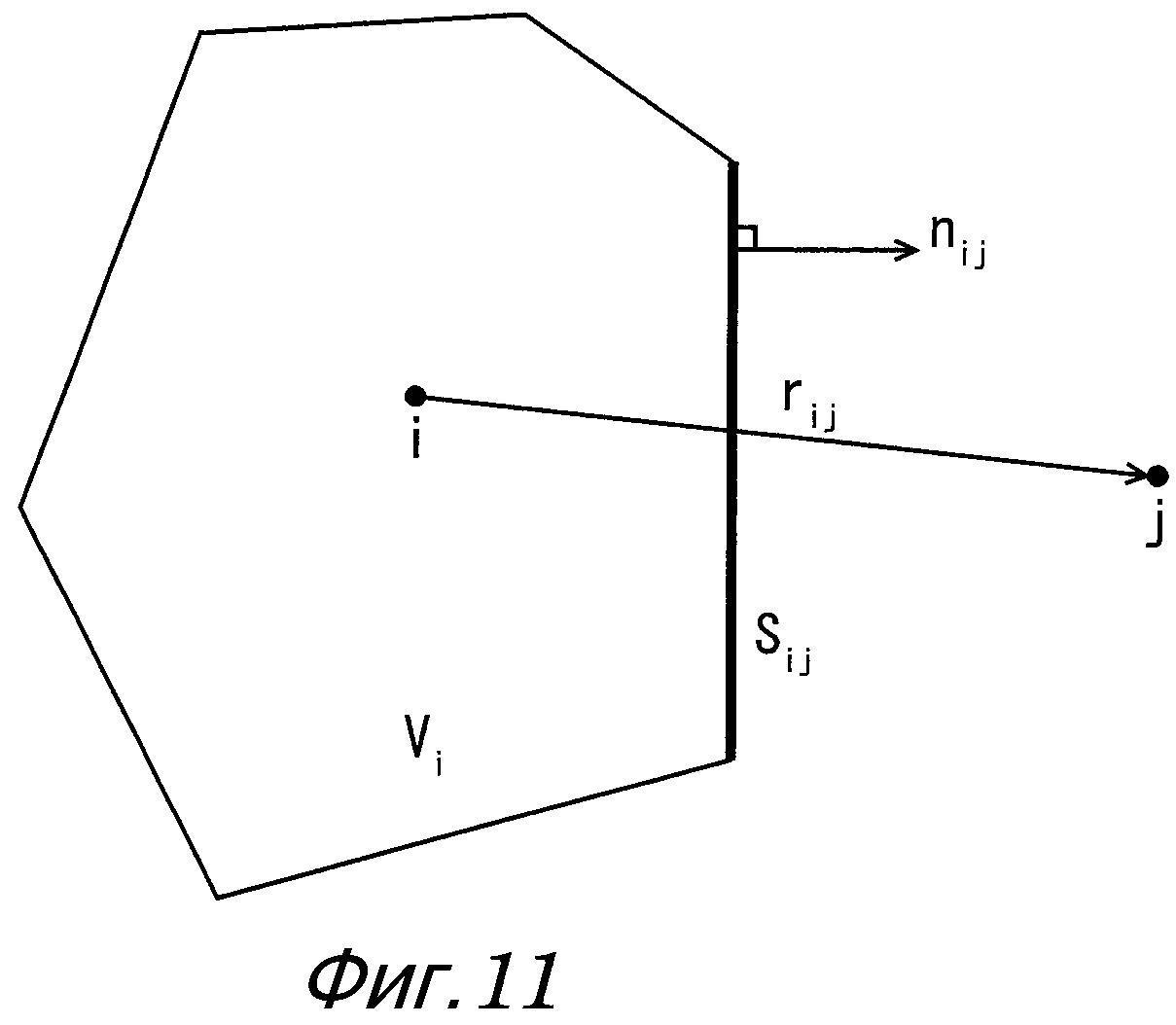
С другой стороны, как показано на фиг. 11, в случае, где частицы i и j признаются в качестве контрольных точек, где контрольный объем частицы i равен Vi, где площадь граничной поверхности между частицей i и частицей j равна Sij, где вектором нормали к граничной поверхности между частицей i и частицей j является [n]ij и где вектором расстояния от частицы i до частицы j является [r]ij, лапласиан (∇2ψ)i для частицы i приблизительно выражается в виде следующего уравнения (37).
[Выражение 37]

Затем, когда уравнение (36) и уравнение (37) сравниваются друг с другом, в случае, где [r]ij и [n]ij предположительно направлены в одном и том же направлении, получаются следующие уравнения (38) и (39).
[Выражение 38]
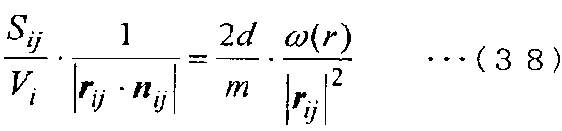
[Выражение 39]
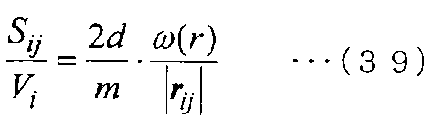
Размерность одинакова (1/расстояние) в левой стороне и правой стороне уравнения (39). Таким образом, формулировку метода MPS можно интерпретировать как методику, по которой величина (площадь/объем) (то есть соотношение, заданное уравнением (9)) в правой стороне, показанной в следующем уравнении (40), вычисляется только из расстояния между двумя частицами i и j.
[Выражение 40]
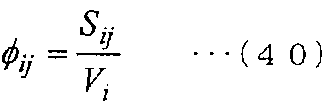
Тем не менее, даже когда площадь Sij граничной поверхности и объем Vi нужно вычислить из отношения связи m частиц, уравнения отношения недостаточно. Таким образом, нельзя определить конкретное численное значение и поэтому определяется только соотношение в уравнении (40).
Соответственно, если площадь Sij граничной поверхности и объем Vi вычислялись из дискретизированного основного уравнения в методе MPS, то это не гарантирует, что выполняются вышеупомянутые условия (а)-(c), необходимые для выполнения закона сохранения. Это указывает, что метод MPS обладает большой проблемой при выполнении закона сохранения.
В случае, где численный анализ применяется к некоторой проблеме в технике, в особенности к задаче проектирования изделий или к задаче проектирования предприятия, весьма важна оценка количественных значений (давление, температура, количество тепла и т.п.). Тем не менее, когда численный анализ не удовлетворяет закону сохранения, определенность не гарантируется.
То есть в методе MPS выполнение законов сохранения, например сохранение массы, сохранение момента и сохранение энергии, не гарантируется и поэтому не гарантируется количественное определение.
В отличие от этого, в соответствии с настоящим способом численного анализа, законы сохранения выполняются и поэтому гарантируется определенность.
Здесь в методе MPS, как описано выше, частицы перемещаются совместно с изменением времени. Таким образом, например, необходимо выполнять алгоритмы ближнего соседа, по которым обнаруживаются частицы, присутствующие в вышеупомянутой сфере радиуса re. Это вызывает большую вычислительную нагрузку при вычислении физических значений.
В отличие от этого, в настоящем способе численного анализа контрольный объем и контрольная точка не перемещаются, даже когда меняется время. Таким образом, в случае, где заранее известно отношение размещения контрольных объемов и контрольных точек, вычисление физических значений достигается без алгоритмов ближнего соседа. Это снижает вычислительную нагрузку при вычислении физических значений по сравнению с методом MPS. Здесь даже в случае, где отношение расположения контрольных объемов и контрольных точек не известно заранее, достаточно, чтобы обработка по заданию отношения размещения контрольных объемов и контрольных точек выполнялась только один раз вначале.
Приведенное выше описание выполнено для примера вычисления физических значений с использованием дискретизированного основного уравнения, выведенного из уравнений Навье-Стокса и уравнения непрерывности на основе метода взвешенных невязок. Однако дискретизированное основное уравнение, которое нужно использовать в настоящем способе численного анализа, этим не ограничивается.
То есть любое дискретизированное основное уравнение, которое выводится из различных видов уравнений (например, уравнения сохранения массы, уравнения сохранения импульса, уравнения сохранения энергии, уравнения адвекции-диффузии и волнового уравнения) на основе метода взвешенных невязок и которое может вычислять физические значения с использованием только значений, не требующих Вершины и Связности, может использоваться в настоящем способе численного анализа.
Тогда на основании таких характеристик дискретизированного основного уравнения вычисление достигается с помощью бессеточного подхода, который не требует так называемой сетки, которая необходима в традиционном методе конечных элементов или методе конечных объемов. Дополнительно, даже если Вершина и Связность, которые определяют геометрическую форму ячейки, использовались в предварительном процессе, отсутствует ограничение на сетку, в отличие от метода конечных элементов, метода конечных объемов и метода вокселей в соответствии с известным уровнем техники. Это снижает рабочую загрузку, связанную с формированием модели расчетных данных.
Описанное ниже является фактом, что дискретизированное основное уравнение, которое использует только значения, не требующие Вершины и Связности, можно вывести из уравнения сохранения массы, уравнения сохранения импульса, уравнения сохранения энергии, уравнения адвекции-диффузии и волнового уравнения на основе метода взвешенных невязок, то есть фактом, что настоящий способ численного анализа может применять другие основные уравнения.
(1) Уравнение сохранения массы
Уравнение сохранения массы в системе координат Эйлера выражается в дифференциальной форме в виде следующего уравнения (41).
[Выражение 41]
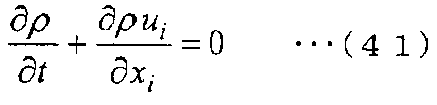
Здесь в уравнении (41) t - время, xi (i=1, 2, 3) - координаты в декартовой системе координат, ρ - плотность, ui (i=1, 2, 3) - составляющие скорости деформации, и нижний индекс i (i=1, 2, 3) - составляющие направления в декартовой системе координат. Дополнительно обозначение со знаком суммы применяется для нижнего индекса i.
Затем, когда уравнение (41) интегрируется по объему V контрольных объемов контрольных точек на основе метода взвешенных невязок, получается следующее уравнение (42).
[Выражение 42]
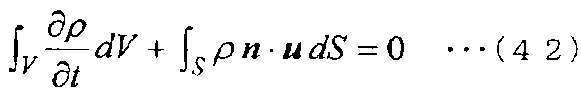
Далее, дискретизируя уравнение для контрольной точки a, показанной на фиг. 5, чтобы преобразовать его в алгебраическое уравнение, получается следующее уравнение (43).
[Выражение 43]
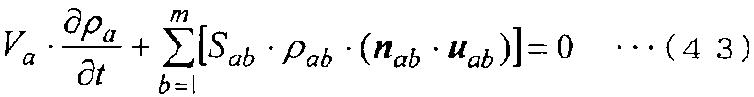
Здесь ρab и [n]ab, которые имеют нижние индексы a и b, являются физическими значениями на граничной поверхности E между контрольной точкой a и контрольной точкой b. Кроме того, m является количеством всех контрольных точек в отношении связи с контрольной точкой a (отношение наличия граничной поверхности между ними).
Затем, когда уравнение (43) делится на Va, которое является объемом контрольного объема контрольной точки a, получается следующее уравнение (44). Затем, когда применяется следующее уравнение (45), получается следующее уравнение (46), в котором дискретизируется уравнение сохранения массы.
[Выражение 44]
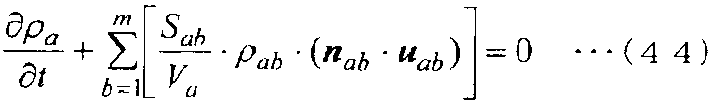
[Выражение 45]
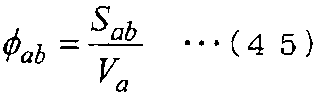
[Выражение 46]
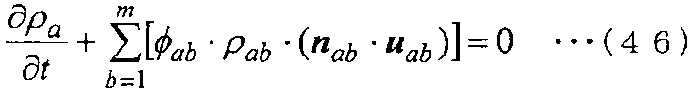
Такое уравнение (46) является уравнением, которое выводится на основе метода взвешенных невязок и использует только значения, не требующие Вершины и Связности. Таким образом, такое уравнение может использоваться в качестве дискретизированного основного уравнения в настоящем способе численного анализа.
Здесь, как описано выше, дискретизированное основное уравнение, используемое в настоящем изобретении, получается путем намеренной остановки посередине процесса выведения, на основе метода взвешенных невязок, традиционного уравнения, использующего значения, которые определяют геометрическую форму.
То есть уравнение (46) получается в процессе, в котором уравнение сохранения массы выводится в качестве уравнения, которое использует Вершину и т.п., на основе метода взвешенных невязок.
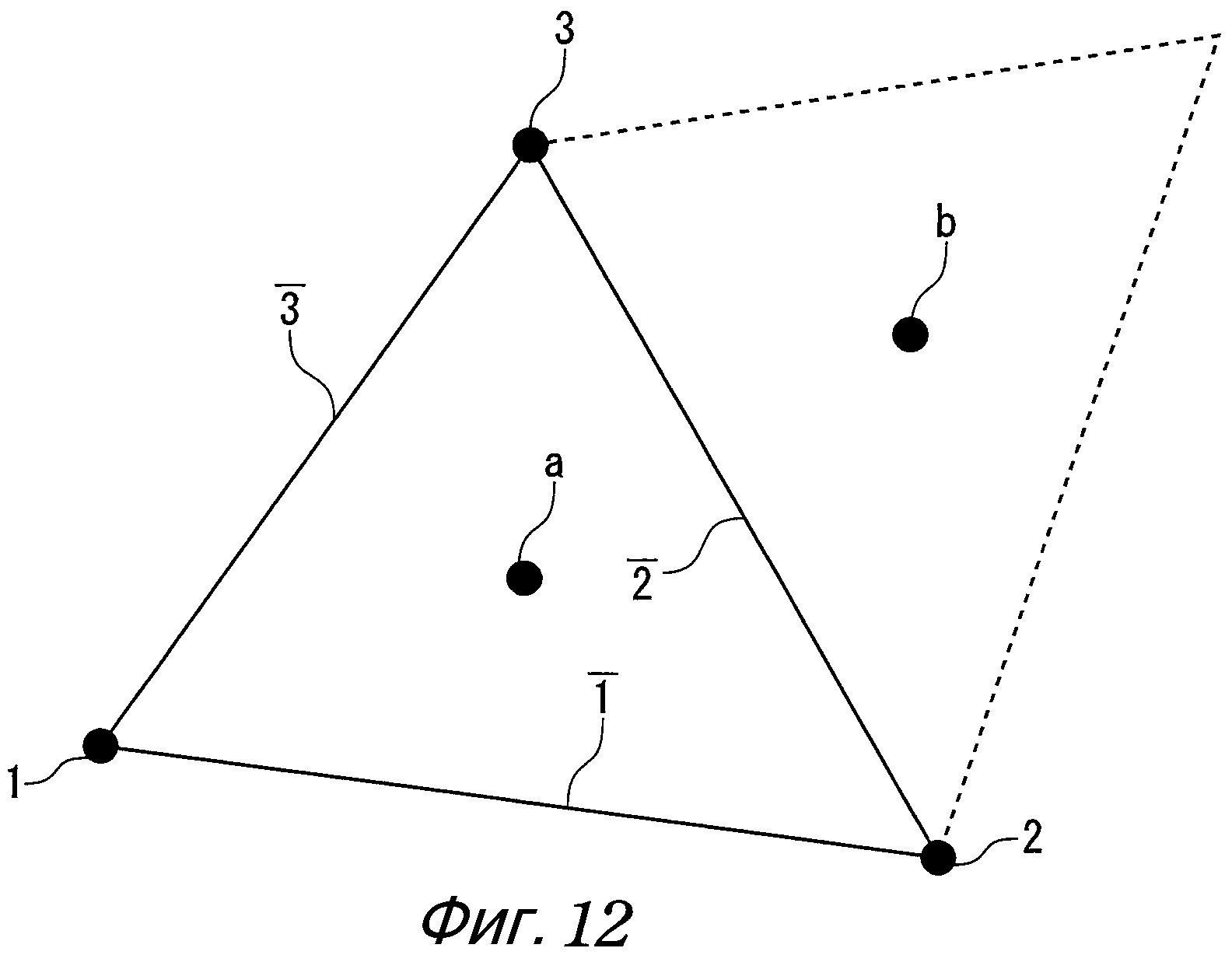
Здесь фиг. 12 является схематическим представлением, показывающим ячейку, имеющую двумерную треугольную форму. Площадь, длина стороны и вектор нормали треугольника a на фиг. 12 показаны в следующей таблице. Здесь символ × в следующей таблице обозначает векторное произведение.
Как показано на фиг. 12, когда ячейка имеет двумерную треугольную форму, уравнение сохранения массы преобразуется в дискретизированное основное уравнение, которое использует Вершину и т.п., на основе метода взвешенных невязок, и получается следующее уравнение (47).
[Выражение 47]
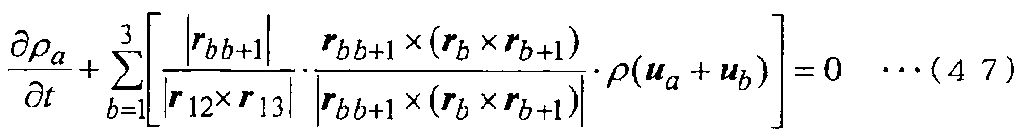
Здесь в уравнении (47) [r]i - вектор положения (координаты) вершины (Вершина)i, а символ × обозначает векторное произведение векторов. Кроме того, ρab и ρ являются неизменными, [r]ij равен [r]j-[r]i, и [r]4 идентичен [r]1.
(2) Уравнение сохранения импульса
Уравнение сохранения импульса в системе координат Эйлера выражается в дифференциальной форме в виде следующего уравнения (48).
[Выражение 48]
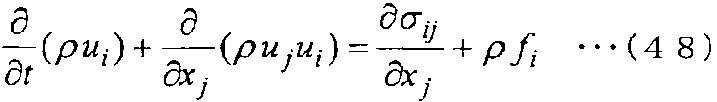
Здесь в уравнении (48) σij (i, j=1, 2, 3) указывает внутреннее напряжение в сплошной среде, а fi (i=1, 2, 3) указывает внешнюю силу (например, силу тяжести), действующую на сплошную среду. Остальные значения аналогичны таковым в уравнении (41). Дополнительно обозначение со знаком суммы применяется для нижних индексов j.
Это уравнение (47) является основным уравнением для поля напряжения в структуре, материале, текучей среде или т.п.
Затем, когда уравнение (47) интегрируется по объему V контрольных объемов контрольных точек на основе метода взвешенных невязок, получается следующее уравнение (49).
[Выражение 49]
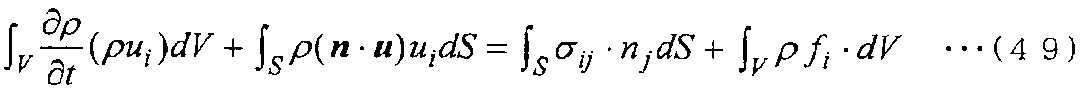
Далее, дискретизируя уравнение для контрольной точки a, показанной на фиг. 5, чтобы преобразовать его в алгебраическое уравнение, получается следующее уравнение (50).
[Выражение 50]
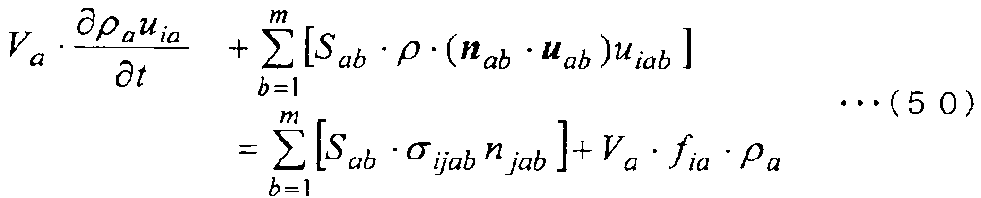
Когда уравнение (50) делится на Va, которое является объемом контрольного объема контрольной точки a, а затем применяется уравнение (45), получается следующее уравнение (51), в котором дискретизируется уравнение сохранения импульса.
[Выражение 51]
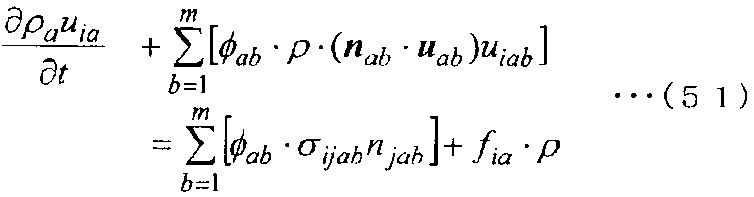
Здесь, когда симметрия в тензоре напряжений учитывается в уравнении сохранения импульса, уравнение сохранения момента импульса также может дискретизироваться аналогично уравнению сохранения импульса.
(3) Уравнение адвекции-диффузии
Явление адвекции/диффузии конкретного вещества C в сплошной среде выражается уравнением адвекции-диффузии, показанным в следующем уравнении (52).
[Выражение 52]
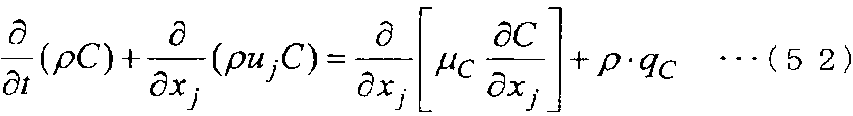
Здесь в уравнении (52) C - концентрация вещества C, μC - коэффициент диффузии вещества C, qC - член, соответствующий источнику (поглотителю) вещества C, ρ - плотность сплошной среды, а ui обозначает скорость деформации сплошной среды.
Затем, когда уравнение (52) интегрируется на основе метода взвешенных невязок, а затем дискретизируется и преобразуется в дискретизированное основное уравнение, получается следующее уравнение (53).
[Выражение 53]
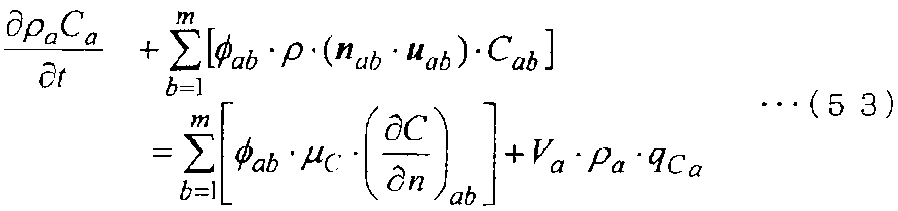
Здесь значения, например Ca, имеющие нижний индекс a, являются физическими значениями в контрольной точке a. Значения, такие как Cab, имеющие нижние индексы ab, являются физическими значениями на граничной поверхности между контрольной точкой a и контрольной точкой b.
(4) Уравнение сохранения энергии
Закон сохранения энергии делится на сохранение тепловой энергии и сохранение кинетической энергии. Однако сохранение кинетической энергии включается в вышеупомянутое сохранение импульса. Таким образом, здесь общий вид уравнения сохранения тепловой энергии показан в следующем уравнении (54).
[Выражение 54]
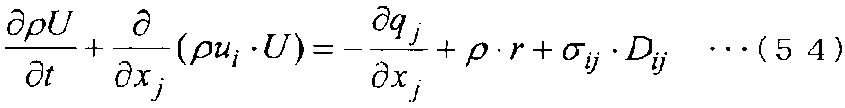
Здесь в уравнении (54) U - внутренняя энергия сплошной среды, qi - вектор теплового потока, r - источник тепла и член, соответствующий источнику (поглотителю) тепловой энергии, σij - тензор напряжений, а Dij - тензор скорости деформации. Здесь член двойного тензорного произведения σij·Dij называется мощностью напряжений. Дополнительно обозначение со знаком суммы применяется для нижних индексов i и j.
Затем, когда уравнение (54) интегрируется на основе метода взвешенных невязок, а затем дискретизируется и преобразуется в дискретизированное основное уравнение, получается следующее уравнение (55).
[Выражение 55]
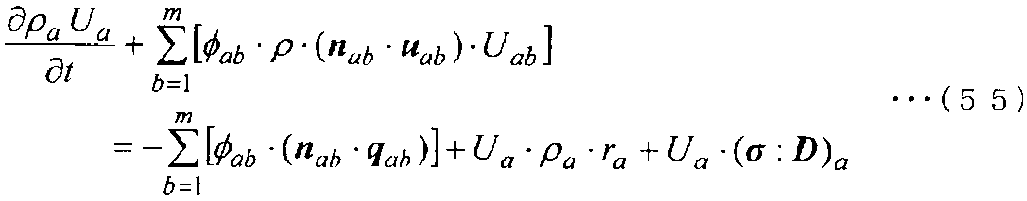
Затем, в дополнение к тепловому потоку, потоки всех немеханических энергий, например электрических и химических энергий, складываются в вектор теплового потока [q], при этом уравнение сохранения энергии служит в качестве уравнения, выражающего сохранение энергии в весьма широком диапазоне.
(5) Волновое уравнение
Вышеупомянутые уравнения для физических законов, выраженных в форме сохранения, такие как уравнение сохранения массы, уравнение сохранения импульса, уравнение сохранения энергии и уравнение адвекции-диффузии, являются уравнениями, обладающими свойствами частных дифференциальных уравнений, называемых "параболическим типом" и "эллиптическим типом". В отличие от этого волновое уравнение, выражающее распространение волны или распространение колебания, называется "гиперболическим типом", и его общий вид показан в следующем уравнении (56).
[Выражение 56]
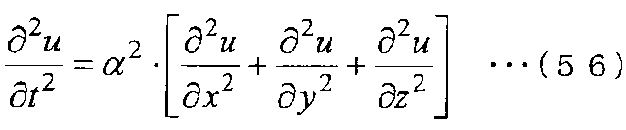
Здесь в уравнении (56) u - амплитуда или смещение, а α - скорость распространения волны.
Затем, когда уравнение (56) интегрируется на основе метода взвешенных невязок, а затем дискретизируется и преобразуется в дискретизированное основное уравнение, получается следующее уравнение (57).
[Выражение 57]
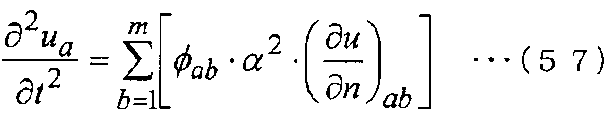
Как видно из уравнения (56), в направлении пространства напрямую применима методика дискретизации, не требующая геометрической формы контрольного объема. Тем не менее, в направлении времени включается частная производная второго порядка, и поэтому используется способ интегрирования по точному времени.
Эти уравнения (46), (51), (53), (55) и (57) являются уравнениями, которые выводятся на основе метода взвешенных невязок и могут вычислять физические значения с использованием только значений, не требующих Вершины и Связности. Таким образом, такие уравнения могут использоваться в качестве дискретизированного основного уравнения в настоящем способе численного анализа.
Тогда, используя вышеупомянутое дискретизированное основное уравнение, настоящий способ численного анализа может применяться для численного анализа установившегося или неустановившегося явления в гидроаэродинамике, теплопроводности, адвекции-диффузии, строительной механике, волне или их сочетании.
Потом, когда используется настоящий способ численного анализа, численный анализ может выполняться в состоянии, в котором легко создаются составляющие, рассчитанные в разных системах координат. Причина в том, что в настоящем способе численного анализа, в отличие от элемента, используемого в методе конечных элементов, не нужна конкретная геометрическая форма контрольного объема, и потому что "расстояние" между двумя соседними контрольными точками не обязательно должно быть расстоянием в системе абсолютных координат, а может быть "расчетным расстоянием".
Таким образом, в соответствии с настоящим способом численного анализа, как показано на фиг. 13, в случае, где численный анализ нужно выполнять в состоянии, в котором создаются составляющие A, B и C, выполненные в разных системах координат, численный анализ может выполняться без согласования систем координат этих составляющих.
Здесь способ численного анализа, называемый общим методом конечных элементов, является методикой, которая полностью препятствует пересечению между элементами, как показано на фиг. 14 или 15. Таким образом, в прикладном программном обеспечении, используемом в методе конечных элементов, когда обнаруживается пересечение между элементами, выводится ошибка. Тогда, как описано выше, такая ситуация в методе конечных элементов вызывает весьма большую рабочую загрузку при формировании модели расчетных данных.
С другой стороны, в соответствии с настоящим способом численного анализа, как показано на фиг. 14 или 15, разрешается пересечение в связи между контрольными точками. Причина в том, что информационные значения, такие как объем контрольного объема, занимаемого каждой контрольной точкой (объем разделенной области), площадь граничной поверхности и вектор нормали к граничной поверхности, не должны обладать конкретной геометрической формой. Таким образом, даже когда связь между контрольными точками пересекается, можно выполнить вычисление физических значений.
Таким образом, снижается ограничение в момент формирования модели расчетных данных. Кроме того, гибкость при формировании модели расчетных данных значительно увеличивается. Тем не менее, в случае, где нужно рассмотреть физическое явление в текучей среде или т.п., имеется свойство, что информация от контрольных точек, близких к конкретной контрольной точке, обновляет физическое значение конкретной контрольной точки. Это создает вероятность того, что когда отдаленные контрольные точки связываются, точность вычисления ухудшается. Таким образом, даже в настоящем способе численного анализа предпочтительно, чтобы связь между контрольными точками образовывалась в подходящем диапазоне.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
Фиг. 1 - концептуальная схема, показывающая пример модели расчетных данных в соответствии с традиционным методом конечных элементов.
Фиг. 2 - концептуальная схема, показывающая пример модели расчетных данных в соответствии с традиционным методом конечных объемов.
Фиг. 3 - таблица для сравнения настоящего изобретения с традиционным способом численного анализа.
Фиг. 4 - схема для подробного сравнения настоящего изобретения с традиционным методом конечных объемов.
Фиг. 5 - концептуальная схема, показывающая пример модели расчетных данных в настоящем способе численного анализа.
Фиг. 6 - схематическое представление, показывающее множество разделенных областей для описания условия, необходимого для выполнения закона сохранения физического значения в настоящем способе численного анализа.
Фиг. 7 - схематическое представление, показывающее бесконечно большую плоскость проекции, которая проходит через контрольную точку и имеет единичный вектор нормали в произвольном направлении.
Фиг. 8 - схематическое представление, описывающее условие, необходимое для выполнения закона сохранения физического значения в случае, где рассматривается двумерный треугольный контрольный объем.
Фиг. 9 - схематическое представление, описывающее условие, необходимое для выполнения закона сохранения физического значения в случае, где рассматривается сферический контрольный объем.
Фиг. 10 - схематическое представление, показывающее поиск соседства в методе частиц.
Фиг. 11 - схематическое представление, показывающее контрольный объем в настоящем способе численного анализа.
Фиг. 12 - схематическое представление, показывающее ячейку, имеющую двумерную треугольную форму.
Фиг. 13 - схематическое представление, показывающее состояние, в котором создаются составляющие, выполненные в разных системах координат.
Фиг. 14 - схематическое представление, показывающее ситуацию, когда элементы пересекаются друг с другом.
Фиг. 15 - схематическое представление, показывающее ситуацию, когда связи между контрольными точками пересекаются друг с другом.
Фиг. 16 - структурная схема, схематически показывающая аппаратную конфигурацию устройства численного анализа в соответствии с вариантом осуществления настоящего изобретения.
Фиг. 17 - блок-схема алгоритма, показывающая способ численного анализа в соответствии с вариантом осуществления настоящего изобретения.
Фиг. 18 - блок-схема алгоритма, показывающая предварительный процесс, выполняемый в способе численного анализа в соответствии с вариантом осуществления настоящего изобретения.
Фиг. 19 - блок-схема алгоритма, показывающая решающий процесс, выполняемый в способе численного анализа в соответствии с вариантом осуществления настоящего изобретения.
Фиг. 20 - схематическое представление, показывающее ситуацию, когда внутреннее пространство кабины транспортного средства, содержащееся в данных о трехмерной форме, доводится малыми замкнутыми поверхностями.
Фиг. 21 - схематическое представление, показывающее ситуацию, когда область анализа, включающая внутреннее пространство кабины транспортного средства, содержащееся в данных о трехмерной форме, образуется с помощью разделенных областей, имеющих одинаковую форму прямоугольной сетки.
Фиг. 22 - схематическое представление, показывающее ситуацию, где удалены разделенные области, выходящие за пределы внутреннего пространства кабины.
Фиг. 23 - схематическое представление, показывающее ситуацию, где промежуток, образованный между граничной поверхностью области анализа и граничной поверхностью внутреннего пространства кабины, заполняется новыми разделенными областями.
Фиг. 24 - блок-схема алгоритма, показывающая способ численного анализа в случае, где область анализа включает в себя подвижную границу, в соответствии с вариантом осуществления настоящего изобретения.
ВАРИАНТ ОСУЩЕСТВЛЕНИЯ ИЗОБРЕТЕНИЯ
Со ссылкой на чертежи описанное ниже является способом вычисления физического значения, способом численного анализа, программой вычисления физического значения, программой численного анализа, устройством вычисления физического значения и устройством численного анализа в соответствии с настоящим изобретением.
Здесь нижеследующее описание приводится для варианта осуществления способа численного анализа, включающего способ вычисления физического значения в соответствии с настоящим изобретением, программы численного анализа, включающей программу вычисления физического значения в соответствии с настоящим изобретением, и устройства численного анализа, включающего устройство вычисления физического значения в соответствии с настоящим изобретением.
Кроме того, нижеследующий вариант осуществления приводится для случая, когда скорость потока воздуха во внутреннем пространстве кабины транспортного средства вычисляется посредством численного анализа.
Фиг. 16 - структурная схема, схематически показывающая аппаратную конфигурацию устройства A численного анализа в соответствии с настоящим вариантом осуществления.
Как показано на фигуре, устройство A численного анализа в соответствии с настоящим вариантом осуществления создается из компьютера, такого как персональный компьютер и рабочая станция, и содержит CPU 1, запоминающее устройство 2, привод 3 DVD (Цифровой многофункциональный диск), устройство 4 ввода, устройство 5 вывода и устройство 6 связи.
CPU 1 электрически подключен к запоминающему устройству 2, приводу 3 DVD, устройству 4 ввода, устройству 5 вывода и устройству 6 связи и обрабатывает сигналы, введенные от этих различных видов устройств, а затем выводит результаты обработки.
Запоминающее устройство 2 создается из внешнего запоминающего устройства, такого как память, и внутреннего запоминающего устройства, такого как накопитель на жестком диске, и хранит информацию, введенную от CPU 1, и выводит сохраненную информацию в ответ на команду, введенную от CPU 1.
Тогда запоминающее устройство 2 в соответствии с настоящим вариантом осуществления содержит запоминающее устройство для программ 2a и участок 2b хранения данных.
Запоминающее устройство для программ 2a хранит программу P численного анализа. Эта программа P численного анализа является прикладной программой, выполняемой в заранее установленной операционной системе (OS), и побуждает устройство A численного анализа, созданное из компьютера в соответствии с настоящим вариантом осуществления, выполнять численный анализ. Тогда программа P численного анализа побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве, например, средства формирования модели расчетных данных и средства вычисления физических значений.
Тогда, как показано на фиг. 16, программа P численного анализа содержит программу P1 предварительного процесса, программу P2 решающего процесса и программу P3 заключительного процесса.
Программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять предварительный процесс, необходимый для исполнения решающего процесса, и побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства формирования модели расчетных данных, чтобы формировать модель расчетных данных. Дополнительно программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять установку условий, необходимых для исполнения решающего процесса, и, дополнительно, выполнять формирование файла F входных данных решателя, накапливающего модель расчетных данных и установленные условия, описанные выше.
Затем, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства формирования модели расчетных данных, программа P1 предварительного процесса сначала побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления получать данные о трехмерной форме, включающие внутреннее пространство кабины транспортного средства, а затем выполнять формирование области анализа, выражающей внутреннее пространство кабины транспортного средства, включенное в полученные данные о трехмерной форме.
Здесь, как подробно описано позже, в настоящем варианте осуществления решающий процесс использует дискретизированное основное уравнение, описанное в вышеупомянутом способе численного анализа, использующем настоящее изобретение (дискретизированное основное уравнение, которое использует только значения, не требующие Вершины и Связности, и которое выводится на основе метода взвешенных невязок). Таким образом, в момент формирования модели расчетных данных форма разделенной области и форма области анализа могут меняться произвольно при условии, что выполняется закон сохранения. Таким образом, работа по коррекции или изменению внутреннего пространства кабины транспортного средства, включенного в данные о трехмерной форме, достигается путем простой доводки или т.п. Таким образом, программа P1 предварительного процесса в соответствии с настоящим вариантом осуществления побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления доводить с помощью малых замкнутых поверхностей внутреннее пространство кабины транспортного средства, включенное в полученные данные о трехмерной форме, чтобы выполнить доводку для ремонта отверстия или промежутка, присутствующего во внутреннем пространстве кабины транспортного средства.
После этого программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления формировать разделенные области, имеющие одинаковый размер, и выполнять формирование области анализа, включающей всю область внутреннего пространства кабины, подвергнутого доводке. Затем программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления отсечь области, выходящие за пределы внутреннего пространства кабины, в числе разделенных областей, сформированных в одинаковом размере, чтобы выполнить формирование области анализа, представляющей внутреннее пространство кабины. В то же время, поскольку решающий процесс использует вышеупомянутое дискретизированное основное уравнение, можно легко отсечь области, выходящие за пределы внутреннего пространства кабины в области анализа. Это устраняет ситуацию, в которой граница с внешним пространством имеет ступенчатую форму, как в методе вокселей. Дополнительно, в отличие от метода скошенных ячеек метода вокселей, формирование области анализа около границы с внешним пространством не требует специальной корректировки или обработки, которая вызывает довольно большую ручную работу, требующую опыта и метода проб и ошибок. То есть в отличие от метода вокселей настоящий вариант осуществления не содержит проблемы, связанной с обработкой для границы с внешним пространством.
Здесь в настоящем варианте осуществления, как описано позже, промежуток между внутренним пространством кабины и отсеченной областью заполняется разделенными областями, имеющими новую произвольную форму, так что область анализа создается из разделенных областей, чьи формы не ограничиваются формой прямоугольной сетки. Дополнительно область анализа заполняется разделенными областями без наложения.
Более того, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства формирования модели расчетных данных, программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять обработку по виртуальному размещению одной контрольной точки внутри каждой разделенной области, заключенной в сформированной области анализа, представляющей внутреннее пространство кабины, а затем сохранять информацию о размещении касательно контрольных точек и данные объема касательно контрольного объема, занимаемого каждой контрольной точкой.
Дополнительно, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства формирования модели расчетных данных, программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять вычисление площади и вектора нормали к каждой граничной поверхности, которая является граничной поверхностью между разделенными областями, описанными выше, а затем сохранять площадь и вектор нормали граничных поверхностей.
Дополнительно, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства формирования модели расчетных данных, программа P1 предварительного процесса побуждает устройство формировать информацию о связи (Ссылку) касательно контрольных объемов (контрольных точек), а затем сохранять Ссылку.
Затем программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления собирать объем контрольного объема, занимаемого вышеупомянутой отдельной контрольной точкой, площадь и вектор нормали к граничной поверхности, информацию о размещении (координаты) касательно контрольных точек (то есть разделенные области) и Ссылку и затем формировать модель расчетных данных.
Дополнительно, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять установку условий, необходимых для исполнения вышеупомянутого решающего процесса, программа P1 предварительного процесса побуждает устройство выполнять установку свойства, установку граничных условий, установку начальных условий и установку условий вычисления.
Здесь значения свойств материалов указывают плотность, коэффициент вязкости и т.п. воздуха во внутреннем пространстве кабины.
Граничные условия определяют правила, используемые в момент обмена физическим значением между контрольными точками, и в настоящем варианте осуществления являются приведенным выше дискретизированным основным уравнением на основе уравнений Навье-Стокса, показанных в уравнении (10), и дискретизированным основным уравнением на основе уравнения непрерывности, показанного в уравнении (11).
Дополнительно граничные условия включают в себя информацию, задающую разделенные области, обращенные к граничной поверхности между внутренним пространством кабины и внешним пространством.
Начальные условия задают физические значения в начале исполнения решающего процесса и являются начальными значениями для скорости потока каждой разделенной области.
Условия вычисления являются условиями касательно вычисления в решающем процессе и являются, например, количеством итераций и критерием сходимости.
Дополнительно программа P1 предварительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления сформировать GUI (Графический интерфейс пользователя). Точнее говоря, программа P1 предварительного процесса побуждает дисплей 5a, предоставленный в устройстве 5 вывода, отобразить графику и формирует состояние, в котором разрешено действие посредством клавиатуры 4a и мыши 4b, предоставленных в устройстве 4 ввода.
Программа P2 решающего процесса (программа вычисления физического значения) побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять решающий процесс и побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве устройства вычисления физического значения.
Тогда, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства вычисления физических значений, программа P2 решающего процесса побуждает устройство выполнять вычисление физических значений над физическими значениями в области анализа, используя файл F входных данных решателя, содержащий объем контрольного объема, площадь граничной поверхности и вектор нормали, предоставленные в модели расчетных данных.
Затем, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства вычисления физических значений, программа P2 решающего процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять формирование матрицы коэффициентов дискретизации для уравнений Навье-Стокса и уравнения непрерывности, содержащихся в файле F входных данных решателя, а затем выполнять формирование таблицы данных для формирования матрицы.
Дополнительно, побуждая устройство A численного анализа в соответствии с настоящим вариантом осуществления работать в качестве средства вычисления физических значений, программа P2 решающего процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять создание уравнения большой разреженной матрицы для вычисления матрицы, показанного в следующем уравнении (58), используя дискретизированное основное уравнение на основе уравнений Навье-Стокса, показанных в описанном выше уравнении (10), и дискретизированное основное уравнение на основе уравнения непрерывности, показанного в уравнении (11), описанном выше.
[Выражение 58]
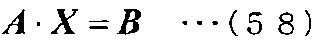
Здесь, в уравнении (58) [A] обозначает большую разреженную матрицу, [B] обозначает вектор граничного условия, и [X] обозначает решение.
Кроме того, когда в вышеупомянутом дискретизированном основном уравнении присутствует дополнительное условие, например несжимаемость, программа P2 решающего процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять встраивание дополнительного условия в матричное уравнение.
Затем программа P2 решающего процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять вычисление решения матричного уравнения по методу CG (методу сопряженных градиентов) или т.п., обновление решения с использованием следующего уравнения (59) и оценку условия сходимости и посредством этого получать конечный результат вычисления.
[Выражение 59]
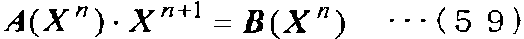
Программа P3 заключительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять заключительный процесс и побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять обработку на основе результата вычисления, полученного в решающем процессе.
Точнее говоря, программа P3 заключительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять процесс визуализации и обработку по извлечению для результата вычисления.
Здесь процессом визуализации является, например, обработка по побуждению устройства 5 вывода вывести отображение очертания поперечного сечения, векторное отображение, отображение эквиконтурной поверхности и анимированное отображение. Дополнительно обработкой по извлечению является обработка по побуждению устройства 5 вывода извлечь количественные значения в области, заданной оператором, а затем вывести их в виде численных значений или графика или, в качестве альтернативы, извлечь количественные значения в области, заданной оператором, а затем вывести их в виде файла.
Кроме того, программа P3 заключительного процесса побуждает устройство A численного анализа в соответствии с настоящим вариантом осуществления выполнять автоматическое формирование отчета, отображение невязки вычисления и анализ.
Как показано на фиг. 16, участок 2b хранения данных хранит: файл F входных данных решателя, содержащий модель M расчетных данных, данные граничных условий D1, описывающие граничные условия, данные D2 условий вычисления, описывающие условия вычисления, данные D3 свойств материалов, описывающие значения свойства материалов, и данные D4 начальных условий, описывающие начальные условия; данные D5 о трехмерной форме; данные D6 результата вычисления и т.п. Дополнительно участок 2b хранения данных временно хранит промежуточные данные, сформированные в ходе обработки посредством CPU 1.
Привод 3 DVD выполнен так, что в него можно вставлять DVD-носитель X. Затем, в ответ на команду, введенную от CPU 1, привод DVD выводит данные, сохраненные на DVD-носителе X. В настоящем варианте осуществления программа P численного анализа хранится на DVD-носителе X. Затем, в ответ на команду, введенную от CPU 1, привод 3 DVD выводит программу P численного анализа, сохраненную на DVD-носителе X.
Устройство 4 ввода является человекомашинным интерфейсом между устройством A численного анализа в соответствии с настоящим вариантом осуществления и оператором и содержит клавиатуру 4a и мышь 4b, служащие в качестве указательных устройств.
Устройство 5 вывода выводит визуально сигнал, введенный от CPU 1, и содержит дисплей 5a и принтер 5b.
Устройство 6 связи выполняет передачу данных между устройством A численного анализа в соответствии с настоящим вариантом осуществления и внешним устройством, например CAD-устройством C, и электрически подключается к сети B, например внутренней LAN (локальной сети) предприятия.
Далее способ численного анализа, использующий устройство A численного анализа, имеющее вышеупомянутую конфигурацию в соответствии с настоящим вариантом осуществления (способ численного анализа в соответствии с настоящим вариантом осуществления), описывается ниже со ссылкой на блок-схему алгоритма из фиг. 17-19.
Как показано на блок-схеме алгоритма фиг. 17, способ численного анализа в соответствии с настоящим вариантом осуществления состоит из предварительного процесса (этап S1), решающего процесса (этап S2) и заключительного процесса (этап S3).
Здесь, перед выполнением способа численного анализа в соответствии с настоящим вариантом осуществления CPU 1 извлекает из DVD-носителя X программу P численного анализа, сохраненную на DVD-носителе X, вставленном в привод 3 DVD, а затем сохраняет программу в запоминающем устройстве 2a для программ в запоминающем устройстве 2.
Затем, когда сигнал, инструктирующий начало численного анализа, вводится посредством устройства 4 ввода, CPU 1 выполняет численный анализ на основе программы P численного анализа, сохраненной в запоминающем устройстве 2. Точнее говоря, CPU 1 выполняет предварительный процесс (этап S1) на основе программы P1 предварительного процесса, сохраненной в запоминающем устройстве 2a для программ, затем выполняет решающий процесс (этап S2) на основе программы P2 решающего процесса, сохраненной в запоминающем устройстве 2a для программ, а затем выполняет заключительный процесс (этап S3) на основе программы P3 заключительного процесса, сохраненной в запоминающем устройстве 2a для программ. По существу, когда CPU 1 выполняет предварительный процесс (этап S1) на основе программы P1 предварительного процесса, устройство A численного анализа в соответствии с настоящим вариантом осуществления работает в качестве средства формирования модели расчетных данных. Дополнительно, когда CPU 1 выполняет решающий процесс (этап S2) на основе программы P2 решающего процесса, устройство A численного анализа в соответствии с настоящим вариантом осуществления работает в качестве средства вычисления физических значений.
Фиг. 18 - блок-схема алгоритма, показывающая предварительный процесс (этап S1). Как показано на фигуре, когда запускается предварительный процесс (этап S1), CPU 1 побуждает устройство 6 связи получать данные D5 о трехмерной форме, включающие в себя внутреннее пространство кабины транспортного средства, от CAD-устройства C по сети B (этап S1a). CPU 1 сохраняет полученные данные D5 о трехмерной форме в участке 2b хранения данных в запоминающем устройстве 2.
Затем CPU 1 выполняет анализ данных D5 о трехмерной форме, полученных на этапе S1a (этап S1b), чтобы обнаружить взаимно перекрывающиеся искривленные поверхности, взаимно пересекающиеся искривленные поверхности, промежуток между искривленными поверхностями, небольшое отверстие и т.п., содержащиеся в данных о трехмерной форме D5, сохраненных в участке 2b хранения данных.
Затем CPU 1 выполняет обработку по коррекции или изменению для данных о трехмерной форме D5, полученных на этапе S1a (этап S1c).
Более конкретно, как показано на фиг. 20, CPU 1 выполняет доводку с использованием малых замкнутых поверхностей на внутреннем пространстве K кабины, включенном в данные D5 о трехмерной форме, чтобы скорректировать данные D5 о трехмерной форме для внутреннего пространства кабины так, чтобы устранялись взаимно перекрывающиеся искривленные поверхности, взаимно пересекающиеся искривленные поверхности, промежуток между искривленными поверхностями, небольшое отверстие и т.п.
Здесь CPU 1 формирует GUI при обработке по коррекции или изменению (этап S1c). Затем, когда команда (например, команда, задающая область доводки) вводится посредством GUI, CPU выполняет обработку по коррекции или изменению, где отражается эта команда.
Затем CPU 1 выполняет формирование модели расчетных данных (этап S1d).
Более конкретно, как показано на фиг. 21, на основе данных D5 о трехмерной форме, скорректированных или измененных на этапе S1c, CPU 1 сначала выполняет формирование области K1 анализа, которая включает в себя всю область внутреннего пространства кабины и которая равномерно делится на разделенные области, имеющие одинаковую форму (прямоугольная сетка). Здесь предполагается, что область K1 анализа делится на разделенные области, имеющие одинаковую форму, с целью сокращения времени. Однако разделенные области, составляющие область анализа K1, не обязаны иметь одинаковые формы и могут иметь произвольные формы.
Затем, как показано на фиг. 22, CPU 1 удаляет разделенные области, выходящие за пределы внутреннего пространства кабины K, чтобы область анализа K размещалась во внутреннем пространстве K кабины без выхода за пределы. В результате, как показано на увеличенном изображении фиг. 22, промежуток Y образуется между граничной поверхностью K1F области K1 анализа и граничной поверхностью KF внутреннего пространства K кабины.
Затем, как показано на фиг. 23, CPU 1 заполняет промежуток Y новыми разделенными областями RA, которые составляют часть области анализа.
Как подробно описано выше при объяснении принципа, в способе численного анализа в соответствии с настоящим вариантом осуществления формируется модель расчетных данных, не содержащая Вершину и Связность. Тогда формирование модели расчетных данных может выполняться без ограничения на геометрическую форму каждой разделенной области. То есть в момент формирования модели расчетных данных разделенные области, составляющие область K1 анализа, могут иметь произвольные формы. Таким образом, в момент заполнения промежутка Y новыми разделенными областями RA CPU 1 может произвольно задавать формы разделенных областей RA, как показано в увеличенном изображении на фиг. 23. Таким образом, заполнение промежутка Y с помощью разделенных областей RA выполняется довольно просто. Например, вместо конфигурации, в которой оператор выполняет работу посредством GUI, в достаточной мере достижимо автоматическое формирование разделенных областей RA. Если промежуток Y предварительно заполнялся разделенными областями в традиционном методе конечных объемов, как описано выше, то разделенные области нужно размещать так, что не должна возникнуть деформация или кручение в соответствии с ограничением на геометрическую форму разделенной области. Эта работа является ручной работой оператора и поэтому вызывает огромную нагрузку на оператора и увеличение времени анализа.
Далее CPU 1 виртуально помещает одну контрольную точку внутри каждой разделенной области, включенной в область анализа, представляющую внутреннее пространство кабины. Здесь CPU 1 вычисляет центр тяжести разделенной области, а затем виртуально размещает одну контрольную точку в каждом центре тяжести. Затем CPU 1 вычисляет информацию о расположении касательно контрольных точек и объем контрольного объема, занимаемого каждой контрольной точкой (объем разделенной области, где размещается контрольная точка), а затем временно сохраняет их в участке 2b хранения данных в запоминающем устройстве 2.
Дополнительно CPU 1 вычисляет площадь и вектор нормали к каждой граничной поверхности, которая является граничной поверхностью между разделенными областями, а затем временно сохраняет площади и векторы нормали к этим граничным поверхностям в участке 2b хранения данных в запоминающем устройстве 2.
Дополнительно CPU 1 формирует Ссылку, а затем временно сохраняет Ссылку в участке 2b хранения данных в запоминающем устройстве 2.
Затем CPU 1 приводит в форму базы данных информацию о размещении касательно контрольных точек, объем контрольного объема, занимаемого каждой контрольной точкой, площадь и вектор нормали каждой граничной поверхности и Ссылку, которые сохранены в участке 2b хранения данных, чтобы сформировать модель M расчетных данных, а затем сохранить сформированную модель расчетных данных в участке 2b хранения данных в запоминающем устройстве 2.
Здесь на таком этапе S1d область анализа, включающая в себя внутреннее пространство кабины, равномерно делится на разделенные области, имеющие одинаковую форму, затем удаляются разделенные области, выходящие за пределы внутреннего пространства кабины, а затем промежуток, возникший между областью анализа и внутренним пространством кабины, заполняется новыми разделенными областями, так что формируется итоговая область анализа K2. Таким образом, реализуется состояние, что вся область внутреннего пространства кабины заполняется разделенными областями без наложения.
Таким образом, модель расчетных данных удовлетворяет вышеупомянутым трем условиям с (а)-(c), необходимым для удовлетворения закона сохранения.
Более того, в настоящем варианте осуществления на этапе S1d применяется конфигурация, в которой сначала формируются разделенные области, затем размещаются контрольные точки, а затем объем разделенной области назначается каждой контрольной точке.
Однако в настоящем изобретении сначала контрольные точки могут размещаться на области анализа, а затем каждой контрольной точке может назначаться объем.
В частности, например, сообщается вес каждой контрольной точке на основе радиуса, вызывающего столкновение с другой контрольной точкой, или, в качестве альтернативы, на основе расстояния до контрольной точки в отношении связи (связанной посредством Ссылки).
Здесь весом контрольной точки i является wi, опорным объемом является V+, и объем Vi, назначенный контрольной точке i, равен показанному в следующем уравнении (60).
[Выражение 60]
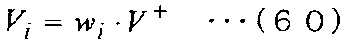
Более того, полная сумма объемов Vi отдельных контрольных точек равна объему Vtotal области анализа. Таким образом, выполняется следующее уравнение (61).
[Выражение 61]
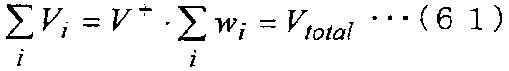
В результате эталонный объем V+ получается из следующего уравнения (62).
[Выражение 62]
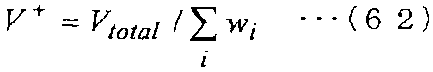
Таким образом, объем, который нужно назначить каждой контрольной точке, получается из уравнений (61) и (62).
В соответствии с этим способом в предварительном процессе объемы разделенных областей, которые нужно предоставить в модели расчетных данных, получаются без использования Вершины и Связности.
Дополнительно при формировании модели расчетных данных (этап S1d) CPU 1 формирует GUI. Затем, когда посредством GUI вводится команда (то есть команда, задающая плотность разделенной области, или команда, задающая форму разделенной области), CPU выполняет обработку, в которой отражается эта команда. Таким образом, оперируя с GUI, оператор может произвольно регулировать размещение контрольных точек и формы разделенных областей.
Однако CPU 1 проверяет выполнение трех условий, необходимых для выполнения закона сохранения, который хранится в программе численного анализа. Затем, когда команда, введенная посредством GUI, нарушает эти условия, CPU отображает ситуацию на дисплее 5a.
Затем CPU 1 выполняет задание данных свойств материалов (этап S1e). В частности, CPU 1 показывает экран ввода для значений свойств материалов на дисплее 5a посредством GUI. Затем сигналы, указывающие значения свойств материалов, введенные посредством клавиатуры 4a или мыши 4b, временно сохраняются в качестве данных свойств материалов D3 в участке 2b хранения данных, так что устанавливаются значения свойств материалов. Здесь упомянутые значения свойств материалов указывают характерные значения текучей среды (то есть воздуха) во внутреннем пространстве кабины, такие как плотность, коэффициент вязкости и т.п. воздуха.
Затем CPU 1 выполняет установку данных граничных условий (этап S1f). В частности, CPU 1 показывает экран ввода для граничных условий на дисплее 5a посредством GUI. Затем сигналы, указывающие граничные условия, введенные посредством клавиатуры 4a или мыши 4b, временно сохраняются в качестве данных граничных условий D1 в участке 2b хранения данных, так что устанавливаются данные граничных условий. Здесь упомянутые граничные условия указывают: дискретизированное основное уравнение, которое определяет физическое явление во внутреннем пространстве кабины; информацию, которая задает контрольные точки, обращенные к граничной поверхности между внутренним пространством кабины и внешним пространством; условия для теплопроводности между внутренним пространством кабины и внешним пространством и т.п.
Здесь в способе численного анализа в соответствии с настоящим вариантом осуществления целью является получение скорости потока во внутреннем пространстве кабины с помощью численного анализа. Таким образом, вышеупомянутые дискретизированные основные уравнения являются дискретизированным основным уравнением (10) на основе вышеупомянутых уравнений Навье-Стокса и дискретизированным основным уравнением (11) на основе уравнения непрерывности.
Здесь эти дискретизированные основные уравнения выбираются, например, с помощью способа, в котором множество дискретизированных основных уравнений, заранее сохраненных в программе P численного анализа, отображаются на дисплее 5a, а затем оператор выбирает любое уравнение или уравнения из отображенного множества дискретизированных основных уравнений, используя клавиатуру 4a и мышь 4b.
Затем CPU 1 выполняет установку данных начальных условий (этап S1g). В частности, CPU 1 показывает экран ввода для начальных условий на дисплее 5a посредством GUI. Затем сигналы, указывающие начальные условия, введенные посредством клавиатуры 4a или мыши 4b, временно сохраняются в качестве данных начальных условий D4 в участке 2b хранения данных, так что устанавливаются данные начальных условий. Здесь упомянутое начальное условие указывает начальную скорость потока в каждой контрольной точке (каждой разделенной области).
Затем CPU 1 выполняет установку данных условий вычисления (этап S1h). В частности, CPU 1 показывает экран ввода для условий вычисления на дисплее 5a посредством GUI. Затем сигналы, указывающие условия вычисления, введенные посредством клавиатуры 4a или мыши 4b, временно сохраняются в качестве данных D2 условий вычисления в участке 2b хранения данных, так что устанавливаются данные условий вычисления. Здесь упомянутые условия вычисления указывают условия для вычисления в решающем процессе (этап S2), такие как количество итераций и критерий сходимости.
Затем CPU 1 выполняет формирование файла F входных данных решателя (этап S1i).
В частности, CPU 1 сохраняет в файле F входных данных решателя модель M расчетных данных, сформированную на этапе S1d, данные D3 свойств материалов, установленные на этапе S1e, данные граничных условий D1, установленные на этапе S1f, данные D4 начальных условий, установленные на этапе S1g, и данные D2 условий вычисления, установленные на этапе S1h, и посредством этого формирует файл F входных данных решателя. Здесь файл F входных данных решателя сохраняется в участке 2b хранения данных.
Когда завершается предварительный процесс (этап S1), который описан здесь, CPU 1 выполняет решающий процесс (этап S2), показанный на блок-схеме алгоритма на фиг. 19, на основе программы P2 решающего процесса.
Как показано на фиг. 19, когда запускается решающий процесс (этап S2), CPU 1 получает файл F входных данных решателя, сформированный в предварительном процессе (этап S1) (этап S2a). Здесь в случае, где предварительный процесс и решающий процесс выполняются одним устройством (устройством A численного анализа в соответствии с настоящим вариантом осуществления), как в способе численного анализа в соответствии с настоящим вариантом осуществления, файл F входных данных решателя уже хранится в участке 2b хранения данных. Таким образом этот этап S2a можно пропустить. Тем не менее, в случае, где предварительный процесс (этап S1) и решающий процесс (этапы S2) выполняются совместно разными устройствами, нужно получить файл F входных данных решателя, переданный посредством сети или съемного диска, и поэтому нужно выполнить настоящий этап S2a.
Затем CPU 1 оценивает соответствие входных данных решателя (этап S2b). Здесь входные данные решателя являются данными, сохраненными в файле F входных данных решателя, и включают в себя модель M расчетных данных, данные граничных условий D1, данные D2 условий вычисления, данные D3 свойств материалов и данные D4 начальных условий.
В частности, CPU 1 анализирует, все ли виды входных данных решателя, необходимые для выполнения вычисления физических значений в решающем процессе, хранятся в файле F входных данных решателя, и посредством этого оценивает согласованность входных данных решателя.
Затем, когда оценивается, что входные данные решателя имеют несогласованность, CPU 1 отображает ошибку на дисплее 5a (этап S2b), а затем отображает экран, посредством которого вводятся данные несогласованной части. После этого на основе сигнала, введенного посредством GUI, CPU 1 выполняет регулировку входных данных решателя (этап S2c), а затем снова выполняет этап S2a.
С другой стороны, когда на этапе S2b оценивается, что входные данные решателя обладают согласованностью, CPU 1 выполняет начальное вычисление (этап S2e).
В частности, CPU 1 формирует матрицу коэффициентов дискретизации из дискретизированных основных уравнений (то есть дискретизированного основного уравнения (10) на основе уравнений Навье-Стокса и дискретизированного основного уравнения (11) на основе уравнения непрерывности), сохраненных в данных граничных условий D1, а затем формирует таблицу данных для вычисления матрицы, чтобы выполнить начальное вычисление.
Затем CPU 1 выполняет создание уравнения большой разреженной матрицы (этап S2f). В частности, используя дискретизированное основное уравнение (10) на основе уравнений Навье-Стокса и дискретизированное основное уравнение (11) на основе уравнения непрерывности, CPU 1 выполняет создание уравнения большой разреженной матрицы для вычисления матрицы, показанного в вышеупомянутом уравнении (58).
Затем CPU 1 оценивает, накладывается ли дополнительное условие, например несжимаемость и контакт, на дискретизированное основное уравнение. Такое дополнительное условие хранится, например, в качестве данных граничных условий в файле F входных данных решателя.
Затем, когда оценивается, что дополнительное условие накладывается на дискретизированное основное уравнение, CPU 1 выполняет встраивание дополнительного условия в большое матричное уравнение (этап S2h), а затем выполняет вычисление большого матричного уравнения (этап S2i). В отличие от этого, когда оценивается, что никакое дополнительное условие не накладывается на дискретизированное основное уравнение, CPU 1 не выполняет встраивание дополнительного условия в большое матричное уравнение (этап S2h), а затем выполняет вычисление большого матричного уравнения (этап S2i).
Затем CPU 1 решает большое матричное уравнение с помощью, например, метода CG (метода сопряженных градиентов) и затем выполняет обновление решения с использованием вышеупомянутого уравнения (59) (этап S2j).
Затем CPU 1 оценивает, достигла ли невязка уравнения (59) условия сходимости (этап S2g). В частности, CPU 1 вычисляет невязку уравнения (59), затем сравнивает результат с условием сходимости, содержащимся в данных D2 условий вычисления, а затем оценивает, достигла ли невязка уравнения (59) условия сходимости.
Затем, когда оценивается, что невязка еще не достигла условия сходимости, CPU 1 выполняет обновление значений свойств материалов, а затем снова выполняет этап S2g. То есть CPU 1 повторяет этапы с S2f по S2g вместе с выполнением обновления значений свойств материалов, пока невязка уравнения (59) не достигнет условия сходимости.
С другой стороны, когда оценивается, что невязка достигла условия сходимости, CPU 1 получает результат вычисления (этап S2l). В частности, CPU 1 сохраняет решение физического значения, вычисленного на непосредственно предшествующем этапе S2i, в виде данных результата вычисления в участок 2b хранения данных, чтобы добиться получения результата вычисления.
В результате такого решающего процесса (этап S2) вычисляется скорость потока воздуха во внутреннем пространстве кабины. Здесь такой решающий процесс (этап S2) соответствует способу вычисления физического значения в настоящем изобретении.
Когда завершается вышеупомянутый решающий процесс (этап S2), CPU 1 выполняет заключительный процесс (этап S3) на основе программы P3 заключительного процесса.
В частности, например, в ответ на команду, введенную посредством GUI, CPU 1 формирует, например, данные очертания поперечного сечения, векторные данные, данные эквиконтурной поверхности и анимационные данные из данных результата вычисления и затем визуализирует данные на устройстве 5 вывода.
Дополнительно, в ответ на команду, введенную посредством GUI, CPU 1 извлекает количественные значения (результат вычисления) в части внутреннего пространства кабины и преобразует их в вид численных значений или графика, затем визуализирует численные значения и график на устройстве 5 вывода и дополнительно выводит численные значения и график вместе в виде файла. Дополнительно в ответ на команду, введенную посредством GUI, на основе данных результата вычисления CPU 1 выполняет, например, автоматическое формирование отчета, отображение невязки вычисления и анализ, а затем выводит результат.
В соответствии с устройством A численного анализа, способом численного анализа и программой численного анализа из настоящего варианта осуществления предварительный процесс формирует модель M расчетных данных, содержащую объем контрольного объема, площадь и вектор нормали к граничной поверхности, а затем решающий процесс вычисляет физическое значение в каждом контрольном объеме, используя объем контрольных объемов, площадь и вектор нормали к граничной поверхности, содержащиеся в модели M расчетных данных.
То есть, как описано в вышеупомянутом способе численного анализа, в соответствии с устройством A численного анализа, способом численного анализа и программой численного анализа из настоящего варианта осуществления, численный анализ выполняется без формирования модели расчетных данных, содержащей Вершину и Связность. Это также значительно смягчает ограничение на работу по коррекции или изменению для данных о трехмерной форме. Таким образом, модель M расчетных данных можно сформировать гораздо проще модели расчетных данных, содержащей Вершину и Связность. Таким образом, снижается рабочая загрузка при формировании модели расчетных данных.
Дополнительно в устройстве A численного анализа, способе численного анализа и программе численного анализа в соответствии с настоящим вариантом осуществления, в отличие от традиционного способа численного анализа, решающему процессу не нужно вычислять объем контрольного объема, площадь и вектор нормали к граничной поверхности с использованием Вершины и Связности. Это снижает вычислительную нагрузку в решающем процессе.
Таким образом, в соответствии с устройством A численного анализа, способом численного анализа и программой численного анализа из настоящего варианта осуществления, рабочая загрузка снижается при формировании модели расчетных данных, и снижается вычислительная нагрузка в решающем процессе.
Более того, в устройстве A численного анализа, способе численного анализа и программе численного анализа в соответствии с настоящим вариантом осуществления область анализа заполняется разделенными областями без наложения. Таким образом, выполняются три вышеупомянутых условия (а)-(c), необходимые для выполнения закона сохранения, и поэтому вычисление скорости потока выполняется с соблюдением закона сохранения.
Здесь модель M расчетных данных в соответствии с настоящим вариантом осуществления может быть легко сформирована из данных о сетке, используемых в традиционном методе конечных объемов или методе конечных элементов, данных частиц, используемых в традиционном методе частиц, или простых данных точечной группы. Даже в этом случае не нужна коррекция разделенных областей в области границы с внешним пространством, в отличие от метода вокселей.
Например, в случае, где модель расчетных данных нужно сформировать из данных о сетке, каждый элемент можно признать в качестве разделенной области в соответствии с настоящим вариантом осуществления (контрольный объем, занимаемый контрольной точкой), так что формирование выполняется легко. Более того, в случае, где модель расчетных данных нужно сформировать из данных частиц, замкнутое пространство, полученное путем заполнения области анализа замкнутыми пространствами, окружающими контрольную точку, размещенную в области анализа, можно признать в качестве разделенной области (контрольный объем, занимаемый контрольной точкой) в соответствии с настоящим вариантом осуществления, так что формирование выполняется легко.
Дополнительно, в соответствии с устройством A численного анализа, способом численного анализа и программой численного анализа из настоящего варианта осуществления, которые описаны выше, рабочая загрузка для модели расчетных данных в предварительном процессе снижается значительно, а также снижается вычислительная нагрузка в решающем процессе.
Таким образом, даже в случае, где формы областей анализа меняются последовательно во времени, то есть даже в случае, где область анализа включает в себя подвижную границу, настоящее изобретение дает возможность вычисления физических значений за практическое время посредством повторения предварительного процесса и решающего процесса каждый раз, когда происходит изменение формы в области анализа, как показано на блок-схеме алгоритма из фиг. 24.
Дополнительно, в настоящем варианте осуществления при вычислении физических значений в случае, где нужно вычислить скорость потока на граничной поверхности, среднее взвешенное скоростей потока в контрольных точках, расположенных по обеим сторонам граничной поверхности, вычисленное с использованием веса, соответствующего соотношению расстояний от контрольных точек до граничной поверхности, может применяться в качестве скорости потока на граничной поверхности.
В таком случае, по сравнению со случаем, где среднее скоростей потока в контрольных точках, расположенных по обеим сторонам граничной поверхности, просто принимается в качестве скорости потока на граничной поверхности, можно более точно вычислить скорость потока во внутреннем пространстве кабины. Тем не менее, в таком случае модель расчетных данных должна содержать данные о соотношении α, которое указывает точку внутреннего разделения, где граничная поверхность располагается на отрезке прямой, который соединяет контрольные точки, расположенные по обеим сторонам граничной поверхности. С этой целью предварительный процесс формирует модель M расчетных данных, дополнительно содержащую соотношение расстояний от контрольных точек, размещенных внутри соседних контрольных объемов, до граничной поверхности, расположенной между контрольными объемами. После этого решающий процесс вычисляет скорость потока на граничной поверхности на основе этого соотношения.
Здесь при вычислении физических значений в случае, где вектор, который соединяет контрольные точки, ортогонален граничной поверхности, расположенной между контрольными точками, вычисление физических значений может выполняться с помощью замены вектора нормали единичным вектором вектора расстояния, который соединяет контрольные точки.
Тем не менее, в таком случае модель расчетных данных должна содержать данные, указывающие вышеупомянутый вектор расстояния, или, в качестве альтернативы, координаты положения контрольных точек, необходимые для вычисления вектора расстояния. Таким образом, предварительный процесс формирует модель M расчетных данных, которая дополнительно включает в себя вектор расстояния, соединяющий отдельные контрольные точки, размещенные внутри соседних контрольных объемов, или, в качестве альтернативы, координаты контрольных точек, необходимые для вычисления вектора расстояния. Затем, когда вектор расстояния ортогонален граничной поверхности между контрольными точками, скорость потока вычисляется с помощью замены вектора расстояния вектором нормали к граничной поверхности.
Предпочтительный вариант осуществления настоящего изобретения описан выше со ссылкой на прилагаемые чертежи. Однако очевидно, что настоящее изобретение не ограничивается вышеупомянутым вариантом осуществления. Формы, сочетания и т.п. частей компонентов, показанных в варианте осуществления, являются примерами и могут изменяться по-разному в соответствии с конструктивным требованием или т.п. в диапазоне, не отклоняющемся от сущности настоящего изобретения.
Вышеупомянутый вариант осуществления описан для конфигурации, в которой скорость потока воздуха вычисляется посредством численного анализа с использованием дискретизированных основных уравнений, выведенных из уравнений Навье-Стокса, которые являются модификацией уравнения сохранения импульса, и из уравнения непрерывности.
Однако настоящее изобретение этим не ограничивается. А именно, физические значения могут вычисляться посредством численного анализа с использованием дискретизированного основного уравнения, выведенного, по меньшей мере, из любого из уравнения сохранения массы, уравнения сохранения импульса, уравнения сохранения вращательного момента, уравнения сохранения энергии, уравнения адвекции-диффузии и волнового уравнения.
Дополнительно вышеупомянутый вариант осуществления описан для конфигурации, в которой вектор нормали к граничной поверхности и площадь граничной поверхности применяются в качестве характеристического значения граничной поверхности в соответствии с настоящим изобретением.
Однако настоящее изобретение этим не ограничивается. А именно, другая величина (то есть длина контура граничной поверхности) может применяться в качестве характеристического значения граничной поверхности.
Более того, вышеупомянутый вариант осуществления описан для конфигурации, в которой модель расчетных данных формируется так, что удовлетворяются три вышеупомянутых условия, необходимые для соблюдения закона сохранения.
Однако настоящее изобретение этим не ограничивается. А именно, в случае, где не нужно соблюдать закон сохранения, модель расчетных данных не нужно формировать так, что удовлетворяются три вышеупомянутых условия.
Более того, вышеупомянутый вариант осуществления описан для конфигурации, в которой объем разделенной области признается в качестве объема контрольного объема, занимаемого контрольной точкой, размещенной внутри разделенной области.
Однако настоящее изобретение этим не ограничивается. А именно, контрольную точку нет необходимости размещать внутри разделенной области. В таком случае численный анализ достигается с помощью замены объема контрольного объема, занимаемого контрольной точкой, объемом разделенной области.
Кроме того, вышеупомянутый вариант осуществления описан для конфигурации, в которой программа P численного анализа является мобильной, будучи сохраненной на DVD-носителе X.
Однако настоящее изобретение этим не ограничивается. А именно, может применяться конфигурация, в которой программа P численного анализа является мобильной, будучи сохраненной на другом съемном носителе.
Кроме того, программа P1 предварительного процесса и программа P2 решающего процесса могут храниться на взаимно обособленных съемных носителях в мобильном виде. Дополнительно программа P численного анализа может передаваться по сети.
Кроме того, вышеупомянутый вариант осуществления описан для конфигурации, в которой каждая граничная поверхность является плоскостью. Однако настоящее изобретение этим не ограничивается. А именно, любая граничная поверхность может быть искривленной поверхностью.
Настоящая заявка описана подробно со ссылкой на конкретный вариант осуществления. Однако специалисту в данной области техники очевидно, что различные виды изменений и исправлений могут выполняться без отклонения от сущности и объема настоящего изобретения.
Настоящая заявка основывается на заявке на патенте Японии (Выложенная заявка на патент Японии № 2009-150945), зарегистрированной 25 июня 2009 г. Содержимое включается в этот документ путем отсылки.
ОПИСАНИЕ НОМЕРОВ ССЫЛОК
A … устройство численного анализа (устройство вычисления физического значения)
P … программа численного анализа
P1 … программа предварительного процесса
P2 … программа решающего процесса (программа вычисления физического значения)
P3 … программа заключительного процесса
M … модель расчетных данных
Vi … объем, виртуально занимаемый частицей i
Sij … площадь граничной поверхности между частицей i и частицей j
rij … вектор расстояния от i до j
nij … вектор нормали к Sij
1 … CPU
2 … запоминающее устройство
2a … запоминающее устройство для программ
2b … участок хранения данных
3 … привод DVD
4 … устройство ввода
4a … клавиатура
4b … мышь
5 … устройство вывода
5a … дисплей
5b … принтер
Реферат
Изобретение относится к способам, устройствам и машиночитаемым носителям для вычисления физического значения и численного анализа. Технический результат заключается в снижении рабочей нагрузки при формировании модели расчетных данных и снижении вычислительной нагрузки в решающем процессе без ухудшения точности анализа. Способ вычисления физического значения, выполняемый компьютером, содержит этап вычисления физических значений, на котором посредством центрального процессорного модуля вычисляют физические значения в области анализа, разделенной на множество разделенных областей, с использованием дискретизированного основного уравнения, которое использует значения, не требующие координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность), и которое выводят на основе метода взвешенных невязок и модели расчетных данных, в которой объемы разделенных областей и характеристические значения граничной поверхности, указывающие характеристики граничных поверхностей соседних из разделенных областей, предоставляют в виде значений, не требующих координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность), и дискретизированное основное уравнение и модель расчетных данных сохраняют в запоминающем устройстве. 6 н. и 7 з.п. ф-лы, 24 ил.
Формула
этап вычисления физических значений, на котором вычисляют физические значения в области анализа, разделенной на множество разделенных областей, где
на этапе вычисления физических значений физические значения вычисляют посредством CPU с использованием дискретизированного основного уравнения, которое использует значения, не требующие координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность), и которое выводят на основе метода взвешенных невязок; и модели расчетных данных, в которой объемы разделенных областей и характеристические значения граничной поверхности, указывающие характеристики граничных поверхностей соседних из разделенных областей, предоставляют в виде значений, не требующих координат вершин (Вершина) разделенных областей и информации о связности вершин (Связность); и
дискретизированное основное уравнение и модель расчетных данных сохраняют в запоминающем устройстве.
предварительный процесс, выполняемый центральным процессорным модулем, для формирования модели расчетных данных; и
решающий процесс, выполняемый центральным процессорным модулем, для вычисления физических значений в области анализа посредством способа вычисления физического значения на основе модели расчетных данных и основного уравнения, где
в решающем процессе используют способ вычисления физического значения по любому из пп.1-3.
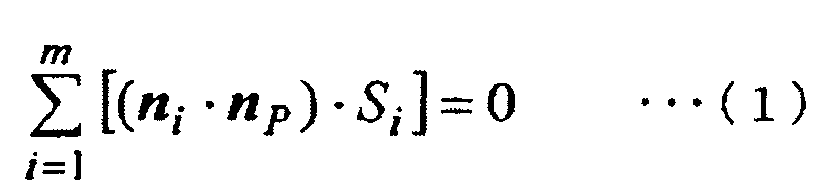
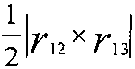
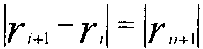
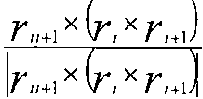

Комментарии