Автоматизированное построение маршрута логического вывода в миварной базе знаний - RU2607995C2
Код документа: RU2607995C2
Чертежи






Описание
Область техники, к которой относится изобретение
Настоящее изобретение относится, в целом, к области контрольно-вычислительной техники и может быть использовано при разработке экспертных систем, систем автоматизированного управления и при создании баз знаний. Более конкретно, настоящее изобретение относится к способам и к системам для автоматизированного построения маршрута логического вывода в базе знаний.
Предшествующий уровень техники
Развитие информационных систем и технологий обуславливает необходимость создания и применения различных программных систем поддержки принятия решения (СППР). СППР состоят из двух основных компонент: хранилище данных и аналитические средства.
В качестве хранилища данных могут выступать модели предметных областей, различные документы и базы знаний. База знаний (БЗ) в информатике и исследованиях искусственного интеллекта - это особого рода база данных, разработанная для оперирования знаниями (метаданными). База знаний содержит структурированную информацию, покрывающую некоторую область знаний, для использования кибернетическим устройством (или человеком) с конкретной целью. Современные базы знаний работают совместно с системами поиска информации, имеют классификационную структуру и формат представления знаний. Полноценные базы знаний содержат в себе не только фактическую информацию, но и правила логического вывода, допускающие автоматические умозаключения о вновь вводимых фактах и, как следствие, осмысленную обработку информации. Иерархический способ представления в базе знаний набора понятий и их отношений в классических реализациях называется онтологией.
Аналитические средства СППР предназначены для оказания помощи в принятии решений на основе использования данных, в зависимости от типа которых СППР можно разделить на оперативные и стратегические. Оперативные СППР предназначены для немедленного реагирования на текущую ситуацию, а стратегические основаны на анализе информации из разных источников с привлечением сведений, содержащихся в системах, аккумулирующих опыт решения проблем.
СППР могут опираться на различные методы принятия решений. Выделяют три основных этапа их разработки:
- извлечение и представление знаний;
- принятие решений;
- построение "человеко-машинных" (диалоговых) систем.
Прежде всего описывается предметная область, так как, чем больше информации о рассматриваемой ситуации вовлечено в процесс принятия решения, тем более обоснованный вывод будет получен. Как известно, существуют различные подходы, методы и языки представления данных. В настоящее время наиболее широкое применение находят технологии, основывающиеся на онтологиях, и технологии, основывающиеся на когнитивных картах. Следует отметить, что и для технологий, основывающихся на онтологиях, и для технологий, основывающихся на когнитивных картах, характерно использование достаточно медленных алгоритмов поиска решения, зачастую - поиск в глубину. Так, когнитивные карты представляют собой взвешенный граф взаимовлияний объектов/факторов друг на друга и имеют как положительный, так и отрицательный веса. При поиске решения осуществляют поиск пути по графу с минимальным или максимальным весом, вследствие чего происходит перебор всех вершин, что порождает большую вычислительную сложность, в худшем случае стремящуюся к полному перебору.
В US 2014/0114949 A1 описана система управления знаниями, содержащая онтологическую базу знаний и средство поиска по базе знаний. Однако принципы построения и работы с онтологиями подразумевают субъективность, что приводит к существенному различию описания предметных областей разными экспертами. При этом предложенные методы поиска решения обладают либо NP-полной сложностью, либо требуют накопления большого опыта. В дополнение к этому, в случае применения онтологий и стандартных методов их обработки невозможно произвести вычисления и придать значения объектам внутри онтологий.
Также из RU 2485581 C1 известна поисковая экспертная система, содержащая базу знаний в формате информационного графа и машину логического вывода. Однако для данного известного технического решения также характерно то, что "для наполнения БЗ 1 информацией требуется поиск и привлечение профессиональных экспертов высокого уровня".
Сущность изобретения
Задачей настоящего изобретения является создание способов и систем для автоматизированного построения маршрута логического вывода в миварной базе знаний, которые бы обеспечили, по меньшей мере, более быстрый поиск решения.
Для решения указанной задачи согласно одному аспекту предложен машинореализуемый способ автоматизированного построения маршрута логического вывода в базе знаний, содержащей представление модели предметной области в виде объектов и связей, организованных в ориентированный двудольный граф. Объекты содержат параметры, а связи содержат правила, и каждое правило имеет по меньшей мере одну входную переменную и по меньшей мере одну выходную переменную, а каждый связанный с правилом параметр является либо его входной переменной, либо выходной переменной. Согласно предложенному способу, формируют совокупность известных параметров и задают один или более искомых параметров. Выполняют обработку для каждого известного параметра, ранее не проходившего данную обработку, в целях нахождения искомых параметров. Данная обработка содержит этапы, на которых: определяют запускаемые правила, в которых известный параметр является входной переменной, для которых известны все остальные входные переменные и которые не запускались раньше, затем запускают эти определенные запускаемые правила и дополняют совокупность известных параметров выходными переменными запущенных правил. Если найдены все искомые параметры, упомянутую обработку прекращают. Естественным альтернативным критерием прекращения выполнения рассматриваемой обработки является установление невозможности получения решения, исходя из имеющихся известных параметров, т.е. если будет выяснено, что от текущих известных параметров нельзя дойти до искомых параметров. После этого, в соответствии с предложенным способом, строят последовательность из запущенных правил в порядке их запуска. Построенная таким образом последовательность правил представляет маршрут логического вывода. В соответствии с предпочтительным вариантом осуществления, предложенный способ дополнительно содержит этап, на котором фильтруют построенную последовательность правил так, чтобы в ней присутствовали только те правила, запуск которых непосредственно задействовался для нахождения искомых параметров.
Совокупность известных параметров может представлять собой очередь или стек, при этом известные параметры поочередно извлекаются из очереди или стека, соответственно, для выполнения упомянутой обработки. Так, если для известного параметра запускаемые правила не определены, извлекают из очереди или стека следующий известный параметр и выполняют в отношении него упомянутую обработку.
Способ может дополнительно содержать этап, на котором выводят на дисплейное устройство найденные искомые параметры и построенный маршрут логического вывода. Способ также может дополнительно содержать этап, на котором вводят известные параметры через пользовательский интерфейс.
Способ может дополнительно содержать этап, на котором, если по результатам упомянутой обработки, по меньшей мере, часть искомых параметров не найдена, выводят сообщение об ошибке и/или ненайденные искомые параметры.
Предпочтительно, для каждого параметра хранится, в виде по меньшей мере одного списка, информация о всех правилах, для которых он является входной или выходной переменной, и для каждого правила хранится, в виде по меньшей мере одного списка, информация о всех его входных и выходных переменных, включая информацию о количестве входных и выходных переменных.
Предпочтительно, для каждого параметра, найденного при упомянутой обработке, дополнительно сохраняют информацию о том, посредством какого запущенного правила, в котором он является выходной переменной, данный параметр был найден, и для каждого запускаемого правила дополнительно сохраняют информацию о том, какой из параметров, являющихся входной переменной этого правила, привел при упомянутой обработке к определению того, что данное правило является запускаемым.
Предпочтительно, для каждого правила дополнительно сохраняют индикатор, показывающий, было ли правило запущено или нет, при этом после запуска правила индикатор модифицируют так, чтобы он показывал, что правило было запущено.
Предпочтительно, объекты дополнительно содержат классы, при этом каждый класс может включать в себя другие классы и/или параметры, причем каждый параметр относится только к одному классу; связи дополнительно содержат отношения, причем каждое отношение описывает взаимосвязь между абстрактными переменными, при этом каждое правило включает в себя ссылку на отношение.
Представление модели предметной области предпочтительно также содержит одно или более ограничений, при этом входными переменными каждого ограничения являются значения параметров. Каждое ограничение содержит ссылку на отношение, выражающее условие, которому должны удовлетворять входные переменные, и выходной переменной каждого ограничения является булевская переменная.
Способ может дополнительно содержать этапы, на которых: выполняют запуск по меньшей мере одного ограничения посредством задания соответствующих известных параметров в качестве его входных переменных; и выводят сообщение об ошибке и останавливают выполнение способа, если условие, выражаемое данным ограничением, не удовлетворяется этими соответствующими известными параметрами.
Фильтрация построенной последовательности правил согласно предложенному способу предпочтительно содержит этапы, на которых: формируют список искомых параметров из упомянутых искомых параметров; пока список искомых параметров не пустой, извлекают из списка искомых параметров искомый параметр и выявляют правило, посредством которого выбранный искомый параметр был непосредственно определен; если выявленное правило ранее не было добавлено в формируемую глобальную последовательность правил, формируют локальную последовательность правил, задействованных для определения выбранного искомого параметра, начиная с добавления выявленного правила в локальную последовательность правил, при этом при упомянутом формировании локальной последовательности правил, для каждого правила, начиная с упомянутого выявленного правила: определяют параметр-инициатор, который является входной переменной правила и которым при упомянутой обработке был инициирован запуск правила; если у правила есть одна или более других входных переменных, то для каждой из этих одной или более других входных переменных добавляют параметр, являющийся этой входной переменной, в начало списка искомых параметров и определяют место вставки локальной последовательности правил, которая должна быть создана для добавленного параметра, в глобальную последовательность правил, при этом место вставки указывает правило, перед которым в глобальной последовательности правил должна вставляться локальная последовательность правил, которая должна быть создана для добавленного параметра; пока формирование локальной последовательности правил не завершено: выбирают правило из запущенных правил, выходной переменной которого является упомянутый параметр-инициатор, и проверяют, присутствует ли выбранное правило в глобальной последовательности правил и является ли оно местом вставки, если выбранное правило присутствует в глобальной последовательности правил или является местом вставки, то завершают формирование локальной последовательности правил, если выбранное правило не присутствует в глобальной последовательности правил и не является местом вставки, то добавляют выбранное правило в конец формируемой локальной последовательности правил и проверяют, является ли данное правило правилом, входными переменными которого являлись только известные параметры, и если входными переменными выбранного правила являлись только известные параметры, то завершают формирование локальной последовательности правил; и если для искомого параметра определено место вставки, вставляют сформированную локальную последовательность правил в место вставки в глобальной последовательности правил, в противном случае, добавляют локальную последовательность правил в конец глобальной последовательности правил. Сформированная таким образом глобальная последовательность правил представляет собой оптимизированный маршрут логического вывода.
Способ может дополнительно содержать этап, на котором при добавлении правила в локальную последовательность правил заносят выходные переменные этого правила в формируемый список найденных параметров, если эти выходные переменные не присутствуют в списке найденных параметров. Искомые параметры, присутствующие в списке найденных параметров, удаляют из списка искомых параметров.
Предпочтительно, каждая из локальной последовательности правил и глобальной последовательности правил представляет собой список, а список искомых параметров представляет собой связанный список.
Согласно другому аспекту предложена компьютерно-реализованная система для автоматизированного построения маршрута логического вывода в вышеописанной базе знаний. Система содержит: средство для формирования совокупности известных параметров и для задания одного или более искомых параметров; средство для выполнения обработки для каждого известного параметра, ранее не проходившего данную обработку, в целях нахождения искомых параметров. Упомянутая обработка содержит: определение запускаемых правил, в которых известный параметр является входной переменной, для которых известны все остальные входные переменные и которые не запускались раньше, а также запуск этих определенных запускаемых правил и дополнение совокупности известных параметров выходными переменными запущенных правил. Если найдены все искомые параметры, упомянутая обработка прекращается. Предложенная система дополнительно содержит средство для построения последовательности из запущенных правил в порядке их запуска, которая представляет маршрут логического вывода. Согласно предпочтительному варианту осуществления настоящего изобретения, предлагаемая система может также содержать средство для фильтрации построенной последовательности правил так, чтобы в ней присутствовали только те правила, запуск которых непосредственно задействовался для нахождения искомых параметров. Данная фильтрация предпочтительно выполняется способом, указанным выше.
Согласно еще одному аспекту предложено компьютерное устройство, приспособленное для автоматизированного построения маршрута логического вывода в вышеописанной базе знаний. Компьютерное устройство содержит один или более процессоров и один или более блоков хранения данных, в которых хранятся машиноисполняемые инструкции, которые при их исполнении одним или более процессорами предписывают одному или более процессорам: формировать совокупность известных параметров и задавать один или более искомых параметров; выполнять обработку для каждого известного параметра, ранее не проходившего данную обработку, в целях нахождения искомых параметров, при этом упомянутая обработка содержит: определение запускаемых правил, в которых известный параметр является входной переменной, для которых известны все остальные входные переменные и которые не запускались раньше, а также запуск этих определенных запускаемых правил и дополнение совокупности известных параметров выходными переменными запущенных правил, при этом, если найдены все искомые параметры, упомянутая обработка прекращается; и строить последовательность из запущенных правил в порядке их запуска, которая представляет маршрут логического вывода. Согласно предпочтительному варианту осуществления настоящего изобретения, машиноисполняемые инструкции при исполнении также предписывают одному или более процессорам фильтровать построенную последовательность правил так, чтобы в ней присутствовали только те правила, запуск которых непосредственно задействовался для нахождения искомых параметров. Данная фильтрация предпочтительно выполняется способом, указанным выше.
Согласно еще одному аспекту предложен считываемый компьютером носитель, на котором сохранены исполняемые компьютером инструкции, которые при их исполнении предписывают компьютеру выполнять вышеописанный способ автоматизированного построения маршрута логического вывода в базе знаний.
Технический результат, на достижение которого направлено настоящее изобретение, заключается, по меньшей мере, в повышении скорости и качества обработки знаний (в частности, в более быстром построении маршрута логического вывода с последующей его оптимизацией), чем дополнительно обеспечивается расширение функционала методов логического вывода.
Перечень фигур чертежей
Вышеуказанные и иные аспекты и преимущества настоящего изобретения раскрыты в нижеследующем подробном его описании, приводимом со ссылками на фигуры чертежей, на которых:
Фиг. 1 - иллюстративная схема трехмерного представления данных согласно предлагаемому подходу;
Фиг. 2 - двудольный ориентированный граф представления миварной сети;
Фиг. 3 - иллюстративная логическая блок-схема способа построения маршрута логического вывода согласно настоящему изобретению;
Фиг. 4 - пример треугольника и биграфа по нему в соответствии с предлагаемым подходом;
Фиг. 5 - иллюстративная логическая блок-схема способа оптимизации построенного маршрута логического вывода согласно предпочтительному варианту осуществления настоящего изобретения;
Фиг. 6а, б, в - примеры ветвлений для иллюстрации способа по Фиг. 5;
Фиг. 7 - иллюстрация тестового интерфейса для предметной области «Геометрия. Решение задач по теме "Треугольник"» согласно варианту осуществления настоящего изобретения;
Фиг.8 - иллюстрация тестового интерфейса по Фиг. 7 с введенными входными данными и полученными результатами;
Фиг.9 - иллюстрация примера результата расчета в тестовом интерфейсе для предметной области "Диагноз по симптомам" согласно варианту осуществления настоящего изобретения.
Подробное описание изобретения
Предлагаемый здесь миварный подход, в общем, базируется на эволюционных базах данных и знаний. Важными достоинствами миварного подхода являются линейный матричный метод поиска логического вывода на адаптивной сети правил и эволюционное миварное пространство с возможностью параллельной обработки данных.
Миварное пространство представляет собой множество осей, множество элементов осей, множество точек пространства и множество значений точек. Введем A = {an}, n=1..N, где А - множество названий осей миварного пространства, N - количество осей миварного пространства. Тогда
где Fn - множество элементов оси an, in - идентификатор элемента множества Fn, In=|Fn|. Множества Fn образуют многомерное пространство: М=F1×F2×…×Fn. m=(i1, i2, …, iN), m∈M, m - точка многомерного пространства, (i1, i2, …, iN) - координаты точки m.
Существует множество значений точек многомерного пространства M:
CМ = {ci1,i2,…,iN|i1=1…I1, i2=1…I2, … ,in=1…IN},
где ci1,i2,…,iN - значение точки многомерного пространства М с координатами (i1, i2, …, iN). Для каждой точки пространства М не существует или существует единственное значение из множества СМ. Таким образом, СМ - множество изменений состояний модели данных, представляемой в многомерном пространстве. Для перехода между многомерным пространством и множеством значений точек введено отношение μ: Cx=μ(Mx), где Mx⊆M, Mx=F1x×F2x×…×FNx.
Для описания модели данных в миварном информационном пространстве необходимо выделить три оси: ось отношений О, ось признаков (свойств) S и ось элементов (объектов) предметной области V (см. Фиг. 1). Эти множества являются независимыми. Миварное пространство можно выразить кортежем вида
В многомерном пространстве каждому значению атрибута отношения соответствует точка с определенными координатами. Отношения связывают элементы пространства. Множество всех точек многомерного пространства соответствует модели данных. При миварном подходе ее структура определяется точками пространства, которые хранят соответствующие значения атрибутов отношения. Миварная сеть может быть представлена в виде двудольного графа.
Одним из базовых понятий предлагаемого миварного подхода является понятие миварной сети (МС). Обобщенно говоря, миварная сеть обеспечивает формализацию и представление человеческих знаний в виде связанного многомерного пространства. Более конкретно, МС - это способ представления в виде двудольного ориентированного графа части информации миварного пространства, образуемой объектами и связями между ними, которые в совокупности представляют модель данных предметной области, при этом связи включают в себя правила для обработки объектов. Иными словами, МС предметной области является частью знаний миварного пространства по этой области. Двудольный ориентированный граф состоит из объектов (Р) и правил (R) (см. Фиг. 2), где P - это V из миварного пространства, а R - это O. Биграф миварной сети может быть представлен в виде двумерной матрицы P×R следующим образом:
1. сеть состоит из элементов двух видов (двух долей графа): вершин графа - объектов (Р) и ребер графа - правил (R) (см. Фиг. 2);
2. для каждой переменной Р в явном виде хранится информация о всех правилах R, для которых она является входной (X) или выходной (Y) переменной с явным указанием этого;
3. для каждого правила R в явном виде хранится информация о всех его входных и выходных переменных Р, включая и информацию о количестве входных (X) и выходных (Y) переменных;
4. хранение всей необходимой информации такой сети организуется на основе технологий баз данных, адаптированных под работу с миварным информационным пространством;
5. в каждом элементе миварной сети, будь то вершина или ребро, однозначно и полностью определены все смежные ребра и вершины. Находясь в любом месте миварной сети, всегда известно, откуда в него можно прийти и куда из него можно перейти, что исключает использование переборов при поиске логического вывода на миварной сети. Это является прямым следствием того, что МС представляется в виде двудольного ориентированного графа.
Иными словами, МС - это особый способ формализации и представления информации в виде множеств двух и более типов, которые потом связываются между собой. Множество первого типа называется "Объекты". Множество второго типа называется "Правилами". В примитивном плане, "Объект" - это то, что отвечает на вопрос "кто?", "что?". "Объект" может быть реальным (например, человек, предмет, географический пункт) и абстрактным (например, событие, счет покупателя, изучаемый учебный курс). Детализированность зависит от требований рассматриваемой предметной области. "Правила" - формализованный преобразователь или индикатор знаний. "Правила" в общем виде состоят из набора входов, набора выходов и внутреннего алгоритма обработки входных данных в выходные. "Правилами", например, могут быть математические формулы, продукционные правила "ЕСЛИ-ТО", индикаторы типа связи двух объектов, целые сервисы.
Уже два этих множества позволяют построить двудольный ориентированный граф за счет связывания множеств разных типов: "объект-правило" и "правило-объект". Взаимосвязи типа "объект-объект" и "правило-правило" запрещены. В общем виде взаимосвязь имеет вид: "объект(ы)-правило-объект(ы)". Первым указывается элемент, из которого исходит взаимосвязь. Вторым указывают тот элемент, куда приходит взаимосвязь. За счет этого устанавливается ориентированность графа и исключаются возможности неверного толкования или преобразования объектов за счет обратного прохода по взаимосвязи.
При таком построении МС обладает свойством масштабируемости, так как в любой момент времени можно добавить элементы множеств любых имеющихся типов, без необходимости изменения методов их обработки.
Одна из ключевых особенностей МС заключается в том, что для ее описания необязательно нужен эксперт. В большинстве случаев достаточно просто перенести объективно существующие объекты и связи (правила) в миварный вид.
Еще одним ключевым понятием предлагаемого миварного подхода является понятие миварной машины логического вывода (ММЛВ). ММЛВ, вообще говоря, представляет собой модуль обработки данных, выполненный с возможностью, по меньшей мере, получать поисковый запрос, определять имеющиеся входные и требующиеся выходные объекты, строить маршрут логического вывода на основе линейного матричного метода, преобразовывать его в алгоритм и производить вычисления.
Ниже в качестве иллюстрации будет рассмотрен пример работы метода миварного поиска маршрута логического вывода.
В области информационных технологий классический поиск маршрута логического вывода на сети правил относят к классу NP-полных задач. В данной заявке применяется другой подход, и, как было сказано ранее, его суть состоит в том, что для некоторой МС строится матрица или граф. Так как он подразумевает одинаковый метод поиска в матрице и графе, дальнейшее описание будет вестись на примере матрицы.
Пусть известны m правил и n параметров (входящих в правила либо в качестве входных переменных, либо в качестве получаемых, то есть выходных переменных). Тогда в матрице V (m×n), каждая строка которой соответствует одному из правил и содержит информацию об используемых в правиле переменных, могут быть представлены все взаимосвязи между правилами и параметрами. При этом в каждой строке все входные переменные этого правила на соответствующих позициях матрицы помечаются символом x, все выходные - y, все параметры, которые уже получили в процессе вывода или задания исходных данных некоторое конкретное значение, - z, а все искомые (выходные) параметры, то есть те, которые необходимо "вывести" из исходных (входных) данных, - w. Кроме того, добавим в матрицу V одну строку и один столбец для хранения в них служебной информации. Напомним, что количество служебной информации может видоизменяться для различных конкретных реализаций. Получаем матрицу V размерности (m+1) × (n+1), в которой отражена вся структура исходной сети правил. Сразу отметим, что структура этой логической сети может изменяться в любое время, то есть это сеть правил с изменяемой (эволюционной) структурой. Пример такой матрицы показан выше в Таблице 1.
Для поиска маршрута логического вывода в отношении матрицы МС производят действия по следующим этапам.
a) В строке (m+1) известные параметры помечают z, а искомые - w. Например, в Таблице 2 в строке (m+1) символом z отмечены позиции: 1, 2, 3, а символом w - позиция (n-2).
b) Осуществляют последовательно, например, сверху вниз, поиск таких правил, которые могут быть активированы, то есть у которых известны все входные переменные. Если таких правил нет, то маршрута логического вывода нет и необходимо запросить уточнение (добавление) входных данных. Если такие правила, которые могут быть активированы, есть, то у каждого из них в соответствующем месте служебной строки делается пометка, что правило может быть запущено. Например, можно задавать '1' в этих позициях матрицы V, что и показано в Таблице 3 в ячейке (1, n+1).
c) Если таких правил несколько, то осуществляется выбор по заранее определенным критериям такого или таких правил, которые должны быть активированы в первую очередь. При наличии достаточных ресурсов одновременно могут запускаться сразу несколько правил.
d) Имитация запуска правила осуществляется путем присваивания выводимым в этом правиле переменным значением "известно", то есть в нашем примере z. Запущенное правило, для удобства дальнейшей работы, помечается дополнительно, например, цифрой '2', что, естественно, не является обязательным.
e) После имитации запуска правил проводят анализ достижения цели, то есть анализируют получение требуемых значений путем сравнения служебных символов в служебной строке. Если в служебной строке (m+1) осталось хоть одно значение "искомая" (то есть w), то осуществляют дальнейший поиск маршрута логического вывода. В противном случае, задача считается успешно решенной, а все задействованные правила в соответствующем порядке их запуска и образуют искомый маршрут логического вывода.
f) Прежде всего определяют наличие таких правил, которые могут быть запущены после определения новых значений на предыдущем этапе. Если таких правил нет, то маршрута вывода нет и поступают аналогично этапу b рассматриваемого метода. Если такие правила есть, то продолжают поиск маршрута вывода. В клетке (2, n+1) появилась '1', как признак возможности запуска этого правила (см. Таблицу 4).
g) На следующем этапе опять аналогично этапу d имитируют запуск правил, далее аналогично этапам e и f выполняют необходимые действия столько раз, сколько требуется для получения результата. При необходимости повторяют этапы b - g до достижения результата. При этом результат может быть как положительный - маршрут вывода существует, так и отрицательный - логического вывода нет из-за неопределенности входных данных. Для наглядности продолжим пошаговое выполнение нашего примера. Итак, в нашем примере необходимо провести имитацию запуска правила 2.
i) Как видно из Таблицы 5, в ячейках (m+1, 4) и (m+1, 5) получаем признак выводимости параметров 4 и 5, а в клетке (2, n+1) формируем признак того, что правило уже было запущено, то есть ставим цифру '2'. После этого проводим анализ служебной строки и видим, что не все искомые параметры известны. Значит, необходимо продолжить обработку матрицы V размерности (m+1)×(n+1). Анализ этой матрицы показывает возможность запуска правила m (см. Таблицу 6).
j) Итак, в служебной строке больше не осталось искомых правил, а в клетках таблицы появились новые значения: в ячейке (m, n+1)-'2', а в ячейке (m+1, n-2) вместо значения w появилось значение z. Таким образом, получен положительный результат, следовательно, маршрут логического вывода при заданных исходных значениях существует.
Далее со ссылкой на Фиг. 3 дается описание предпочтительного варианта осуществления способа 300 построения маршрута логического вывода в базе знаний с использованием предложенного здесь миварного подхода.
На этапах 301 и 302 происходит ввод известных параметров и задается (например, передается или вводится через пользовательский интерфейс) список искомых параметров. На этапе 303 из известных параметров формируется очередь или стек. Допускается использование очередей разных типов (LIFO, FIFO и т.п.), в зависимости от выбранного вида будет меняться лишь этап 313.
На этапе 304 происходит проверка на то, известны ли уже все искомые параметры. Данная проверка не только позволяет завершить поиск, когда все искомые параметры станут известными, но также позволяет избежать запуск поиска алгоритма в том случае, если искомые переменные были также переданы в списке известных параметров.
Если результатом этапа 304 является ИСТИНА, то на этапе 305 происходит выдача найденных значений и алгоритма, составляющего маршрут логического вывода. Если же результатом блока 304 является ЛОЖЬ, то запускается проверка на этапе 306.
На этапе 306 проверяют, пуста ли очередь известных параметров, т.е. есть ли в ней еще необработанные параметры. Если результатом этапа 306 является ИСТИНА, то вызывается этап 307. В зависимости от конкретной реализации и цели на этапе 307 может выводиться (например, на экран дисплея) как простое "нет решения", так и список тех искомых параметров, которые удалось найти, вместе с соответствующим им алгоритмом, а также список не найденных параметров.
Если результатом этапа 306 является ЛОЖЬ, то на этапе 308 забирается один известный параметр из их очереди. На этапе 309 получают связанные с ним правила, а именно выявляются те правила, в которых известный параметр является входной переменной. Выявленные правила могут при этом быть организованы в список. На этапе 310 проверяют, можно ли запустить какие-либо правила из списка выявленных правил. Запустить можно лишь те правила, в которых известны все входные переменные и которые не запускались раньше. Если нет таких правил, то возвращаются к этапу 306 и повторяют этапы 308, 309, 310.
Если результатом блока 310 является ИСТИНА, то на этапе 311 происходит запуск правил, и, исходя из их выходных переменных, на этапе 312 обновляется список известных параметров и их значений, а на этапе 313 параметры, найденные на этапе 311, заносятся в очередь известных параметров. Затем происходит возврат к этапу 304 и выполняется соответствующая ему проверка.
В результате, получается последовательность из запущенных правил в порядке их запуска (например, список), каковая последовательность правил, в соответствии с вышесказанным, представляет построенный маршрут логического вывода.
Данная методика поиска маршрута логического вывода позволяет уйти от полного перебора всех возможных правил на каждом шаге и тем самым уйти от NP-полной задачи в сторону линейного уровня сложности.
Как говорилось выше, МС может быть представлена в виде двудольного ориентированного графа. На Фиг.4 схематично приведены треугольник и возможный биграф по нему. В эллипсах указаны параметры, а в прямоугольниках - правила. На этом графе наглядно показано, что у объектов хранится информация о том, с какими правилами они связаны (на графе это представлено в виде стрелок) и их роль в этих правилах (направление стрелок), а в правилах хранится информация о том, с какими объектами они связаны (на графе это показано с помощью стрелок). В конкретных реализациях подобные взаимосвязи могут быть реализованы за счет различного рода списков. Например, внутри описания параметра "Сторона a" может лежать:
- список правил, в которых "Сторона a" участвует в качестве входной переменной. Такими правилами в рассматриваемом примере являются "теорема косинусов для b", "теорема косинусов для с";
- список правил, в которых "Сторона a" является выходной переменной ("теорема косинусов для а");
- объединение предыдущих списков.
Аналогичная информация содержится в правилах в списках их входных и выходных переменных.
Такая архитектура позволяет уменьшить количество переборов правил на каждой итерации логического поиска по миварной матрице (блоки 309 и 310 на Фиг. 3), так как перебираются не все правила, а правила, связанные лишь с выбранным объектом (параметром).
Однако могут возникнуть ситуации, когда в ходе поиска алгоритма, составляющего маршрут логического вывода, в него добавляются лишние шаги. Пример рассматривается со ссылкой на Таблицы 7а-7в.
В Таблице 7а показано изначальное состояние системы. Известен параметр P1, а P4 нужно найти. На первом шаге можно запустить правила R1 и R2 и узнать P2 и P3, соответственно, что и происходит в Таблице 7б. После этого остается только запустить правило R3 и узнать P4 (см. Таблицу 7в).
В итоге, мы запустили правила R1, R2 и R3. Но, если присмотреться к нашей сети, станет очевидно, что запуск правила R2 нам был не нужен для вычисления P4.
Такие лишние шаги могут привести к увеличению времени расчета. В целях дополнительного ускорения вычисления и создания более точных прецедентов раскрытый выше подход может быть расширен удалением всех необязательных шагов вычисления в целях оптимизации получаемого маршрута логического вывода.
Для этого при выполнении способа построения маршрута логического вывода, описанного выше со ссылкой на Фиг. 3, в каждый найденный параметр записывается то, какое правило было для этого запущено, а в каждое правило добавляется информация, какой параметр инициировал запуск данного правила, выступая в роли его входной переменной (т.е. параметр-инициатор). При этом параметры, найденные в процессе выполнения, организуются в список.
В соответствии с вышесказанным, для каждого параметра хранится, предпочтительно в виде по меньшей мере одного списка, информация о всех правилах, для которых он является входной или выходной переменной, а для каждого правила хранится, опять же предпочтительно в виде по меньшей мере одного списка, информация о всех его входных и выходных переменных. Соответственно, реализация такого добавления/записи информации будет очевидной для специалиста, для чего могут быть использованы, например, широко известные технологии и инфраструктуры программирования.
Операции по фильтрации маршрута логического вывода представлены в виде блок-схемы способа 500 по Фиг. 5.
Итак, на этапе 501 формируется список из искомых параметров. В конкретных реализациях допускается использование связанных списков, так как скорость вставки в них выше, чем скорость вставки в другие структуры хранения данных. Затем на этапе 502 список найденных параметров очищается, так как во время выполнения вышеописанного базового способа 300 в него могли попасть параметры, расчет которых был необязателен для итогового маршрута (алгоритма) (см. Фиг. 3).
На этапе 503 осуществляют проверку на предмет того, пустой ли связанный список искомых параметров. Если результатом этапа 503 является ИСТИНА, то происходит завершение выполнения способа 500. Если же результатом этапа 503 является ЛОЖЬ, то вызывается этап 504.
На этапе 504 из списка искомых параметров забирается параметр и выявляется правило, по которому непосредственно высчитали взятый параметр. На этапе 505 проверяют, добавлено ли выявленное правило в формируемую глобальную последовательность (например, список) правил.
Если результатом этапа 505 является ЛОЖЬ, то происходит переход к этапу 506, где формируется локальная последовательность правил, также именуемая здесь "локальный алгоритм", из правил, задействованных для определения выбранного искомого параметра. При этом данное формирование начинается с добавления правила, выявленного для рассматриваемого искомого параметра на этапе 504, в локальный алгоритм и определения его параметра-инициатора.
Локальный алгоритм - это, по сути, список переходов от искомого параметра к известным. Формат записи локального алгоритма может варьироваться в зависимости от реализации. Например, в случае с P5 по Фиг. 6а локальный алгоритм может быть представлен как: P5<-R3, R3<-P3, P3<-R1, R1<-P1, где '<-' обозначает направление перехода. Как уже говорилось неоднократно выше, вершины биграфа (параметры) "знают" о своих исходящих и входящих связях (правилах), а правила, в свою очередь, "знают" свои входные и выходные параметры, поэтому допускается более сокращенная запись локального алгоритма в виде цепочки правил, например, R3, R1.
Как видно из приведенной записи локального алгоритма и Фиг.6б, существуют ситуации, когда в правиле имеется более одного входа (т.е. входной переменной), и, следовательно, есть параметры, информация о которых не будет сохранена в формируемом таким образом списке переходов. Такие параметры заносятся в начало списка искомых параметров, чтобы в дальнейшем для каждого из них построить его собственный локальный алгоритм.
Дабы не нарушить глобальную последовательность правил, при упомянутом добавлении параметра в список искомых параметров в системе также сохраняется место вставки его локального алгоритма в глобальную последовательность правил. В общем случае, место вставки есть указание того, непосредственно перед каким правилом в формируемой глобальной последовательности правил должен быть вставлен локальный алгоритм.
Во время построения алгоритма могут возникнуть два класса ситуаций, они изображены на Фиг. 6а, б. Первый из них здесь называется "веткой" ("ветка вниз" - Фиг. 6а, "ветка вверх" - Фиг. 6б). Как видно из рисунка Фиг. 6а, производя поиск P7 и P5, мы получаем две разные ветки алгоритма. В данном случае, R5 не запустится и не попадет в алгоритм, если не будет известен P6. Дойдя до R5, P4 будет добавлен в список искомых с указанием места вставки 'перед R5'. Здесь стоит отметить, что в локальном алгоритме расчета P6 встречается P4, и он будет удален из списка искомых.
В ситуации "ветка вверх", чтобы посчитать P7, нужно сначала посчитать от P1 до P4, от P4 до P6 и от P3 до P5. Здесь место вставки - это R5, алгоритмы расчета P5, P6 и P4 нужно вставить перед этим правилом.
На Фиг.6в представлена "цикличная" ситуация. Наш алгоритм на время разделяется и затем сходится опять, так как, чтобы найти P7, нам нужны и P6, и P5. Место вставки - опять же 'перед R5'.
Пошаговый пример применения места вставки будет более подробно разобран ниже, после описания всего способа 500 по Фиг. 5.
На этапе 507 проверяют, достигнут ли конец локального алгоритма (т.е. известный параметр). Если результатом этапа 507 является ИСТИНА, то происходит переход к этапу 503. Если же результатом этапа 507 является ЛОЖЬ, то происходит переход к этапу 508.
На этапе 508 выбирают правило из их последовательности, построенной по итогам выполнения способа 300 по Фиг.3, выходной переменной которого является параметр-инициатор правила, добавленного последним в формируемый локальный алгоритм. Далее по описанию этапов способа 500 выбранное правило именуется текущим. Затем на этапе 509 проверяют, есть ли уже текущее правило в формируемой глобальной последовательности правил, как в случае с R1 из примера, приведенного выше, или является ли оно местом вставки. Если результатом блока 509 является ИСТИНА, то происходит переход на этап 512. Если же результатом этапа 509 является ЛОЖЬ, то происходит переход на этап 510.
На этапе 510 все выходные параметры текущего правила добавляются в список найденных параметров, при этом они, естественно, проверяются на дублирование. Заодно проверяется список искомых параметров на наличие этих параметров, и при совпадении они удаляются из списка искомых. Схожий пример мы видели при рассмотрении Фиг.6а, где в локальном алгоритме P6 встречалось P4, которое было удалено из списка искомых.
На этапе 511 текущее правило добавляется в конец формируемого локального алгоритма, и происходит переход к этапу 507.
На этапе 512, если для рассматриваемого искомого параметра определено место вставки в глобальную последовательность правил, то сформированный локальный алгоритм вставляется в это место вставки; в противном случае, локальный алгоритм добавляется в конец формируемой глобальной последовательности правил. С этапа 512 осуществляется переход на этап 503.
Сформированная таким путем глобальная последовательность правил представляет собой оптимизированный маршрут логического вывода.
Описанный выше способ позволяет очистить общий алгоритм вычисления задачи от лишних шагов и осуществить запуск только необходимых для решения задачи правил, что позволяет ускорить работу всего предлагаемого логического вывода, особенно на больших задачах.
Теперь рассмотрим ситуацию по Фиг. 6б более внимательно. Изначально, в списке искомых параметров у нас значится только P7. В данном параметре хранится информация, что его рассчитали в правиле R5. В R5 известно, что у него три входа P4, P5 и P6, причем допустим, что параметром-инициатором правила R5 в алгоритме является P4. Поэтому остальные входы P6 и P5 добавляются в начало списка известных параметров. Местом вставки их локальных алгоритмов указывается R5. Дальнейший локальный алгоритм содержит P4<-R2, R2<-P2, P2<-R1, R1<-P1. Полный список локальных переходов для P7 выглядит следующим образом: P7<-R5, R5<-P4, P4<-R2, R2<-P2, P2<-R1, R1<-P1. В глобальную последовательность мы заносим только цепочку правил и получаем: R5<-R2<-R1.
Теперь давайте построим локальный алгоритм P6. В общем виде его можно записать следующим образом: P6<-R4, R4<-P4, P4<-R2, R2<-P2, P2<-R1, R1<-P1. Берем правило R4. У него только один вход, поэтому мы не добавляем ничего в список искомых параметров. Для P6 местом вставки является R5, поэтому R4 ставим над ним. Глобальная последовательность на этом шаге выглядит следующим образом: R5<-R4<-R2<-R1. Теперь берем правило R2. Оно уже есть в глобальной последовательности, значит вся оставшаяся часть локального алгоритма уже содержится в ней и нет смысла тратить время на лишние проверки.
Мы извлекаем P5 из списка искомых. Его локальный алгоритм довольно короток: P5<-R3, R3<-P3. Берем R3. Его нет в глобальной последовательности правил, место вставки выше R5. Получаем в результате: R5<-R3<-R4<-R2<-R1.
Далее дается описание структурного развития миварного подхода.
В ходе дальнейшего развития предложенного подхода к представлению данных объекты были разделены на параметры и классы, связи - на отношения и правила, а также введена новая сущность - ограничение.
Базовый миварный матричный подход, описанный выше, подразумевает работу с плоскими моделями предметных областей, где все параметры являются одноранговыми. Однако очень многое вокруг нас обладает иерархическими связями. Например, дивизия состоит из рот, институт из факультетов, те, в свою очередь, из кафедр и так далее. Зачастую, такие иерархические связи содержат в себе дополнительную информацию, которой нельзя пренебречь. Например, они позволяют отличить один объект от другого, сказать, что в этой семье отца зовут Геннадием, а в другой - Вячеславом. Для реализации подобных взаимоотношений в миварном пространстве и миварной сети было принято решение разбить существовавший ранее элемент "объект" на параметры и классы.
Параметр - единичный конечный на данном уровне абстракции объект, обладающий значением. Примером может служить длина стороны AB треугольника ABC. Параметр является листом в дереве иерархии элементов в модели. Параметр может быть связан лишь с одним внутренним узлом (классом).
Класс - внутренний узел дерева иерархии. Класс не обладает значением и может содержать в себе другие внутренние узлы (другие классы) и/или листья (параметры). Например, классом может быть "треугольник", который внутри себя будет хранить параметры сторон и углов. Также классом может быть "дивизия", внутри которой могут быть не только собственные параметры (название, списочная численность, месторасположения и т.д.), но и другие классы, например роты. Введение классов позволяет упростить описание модели, содержащей несколько однотипных объектов. Не надо вводить все заново или искать параметры, разбросанные по всей модели. Достаточно просто скопировать и вставить новый экземпляр. Еще одним отличием класса от параметра является то, что он может содержать в себе список внутренних правил класса.
Внутреннее правило класса - правило, задействующее только параметры, являющиеся дочерними для данного класса. Например, для треугольника будет являться внутренним правилом "угол С=180 - угол А - угол B", так как все эти углы являются дочерними параметрами класса 'треугольник'. Введение внутренних правил класса позволяет упростить создание схожих объектов по образцу, так как внутренние правила будут автоматически генерироваться для нового экземпляра класса. За исключением этого, они ничем не отличаются от простых правил.
Отношение - обновленный элемент миварного пространства. Отношение описывает взаимосвязь между абстрактными переменными. Например, "a=b-c" - абстрактная формула вычитания. В отношении хранится его тип, список входных и список выходных переменных, типы использованных переменных и описание. Отношения бывают:
1. математическими. Примером может быть простая формула "a=b-c";
2. условными. Например, "Если y равен 10, то х равен 14, иначе х равен 7";
3. программируемыми. Примером может служить программный код со своими входами и выходами;
4. строковыми. Например, "любит", "связан";
5. системными. Например, "часть-целое";
6. местоположения. Например, "над", "справа" и т.д.
Правило содержит в себе ссылку на отношение и связывает конкретные объекты из модели. Это сделано для упрощения описания предметных областей и многократного повторного использования одних и тех же, даже сложных программируемых свойств. Например, у нас есть математическое отношение с формулой "a=b-c". Она может означать, как остаток средств на счету после оплаты чего-либо, так и сколько у нас осталось яблок, если было 10 и мы одно отдали. Правила содержат, по меньшей мере:
1. перечень входных переменных;
2. перечень выходных переменных;
3. идентификатор отношения.
Ограничение - новый элемент миварного пространства. Как следует из названия, этот элемент накладывает ограничения на значения параметров. Например, в прямоугольном треугольнике один из углов всегда 90° или какой-то параметр при расчетах всегда должен быть больше 0. Ограничения похожи по свой структуре на правила. Они также имеют ссылку на отношение, которое обязательно является условным и имеет вид "Если (условие), ТО правда, ИНАЧЕ ложь", и привязаны к параметрам конкретной модели. Разница в том, что они:
1. имеют только входы, а выход является булевской переменной;
2. при срабатывании останавливают вычисление модели и выводят сообщение об ошибке.
Механизм ограничений позволяет более точно передавать информацию о реальном мире и отслеживать его изменение. Благодаря ограничениям можно сигнализировать о каких-то нештатных ситуациях в АСУТП, либо указывать на неверно подготовленные исходные данные.
Прецедент - случай или событие, имевшее место в прошлом и служащее примером или основанием для аналогичных действий в настоящем. В миварном подходе можно не только сохранять ранее рассчитанные алгоритмы, но и строить по ним прецеденты в виде отдельного правила, объединяющего все уникальные входы в правила внутри этого локального алгоритма и часть, последние или все выходы из них (зависит от конкретной реализации). Прецедент в миварном подходе - особая запись некогда рассчитанного алгоритма, длиною более одного шага, позволяющая рассматривать прецедент, как новое правило миварного подхода. Каждый шаг алгоритма обладает:
1. списком входных параметров;
2. информацией о запущенном правиле;
3. списком выходных правил.
При этом на вход последующего шага могут передаваться, и нередко передаются, параметры, являющиеся выходами одного из предыдущих шагов. Такие входные параметры называются "рассчитанными". Если же на вход передается параметр, который не является выходом одного из предыдущих шагов, то такой параметр называется "уникальным".
Прецедент, как и правило, содержит:
1. список входных параметров;
2. список выходных параметров;
3. идентификатор отношения.
Для правильной работы прецедента необходимо гарантировать, что все "уникальные" входные параметры будут переданы на вход прецедента, так как без них не сможет быть выполнен вложенный в прецедент алгоритм расчета.
Что касается перечня выходных параметров прецедента, то он может образовываться одним из следующих способов:
1. только выходные параметры последнего шага алгоритма. Применим для алгоритмов, где в качестве искомых параметров указывались параметры, рассчитываемые на последнем шаге;
2. только параметры, отмеченные, как 'искомые', при расчете алгоритма, по которому создается прецедент;
3. все параметры, являющиеся выходными параметрами шагов алгоритма внутри прецедента.
В качестве идентификатора отношения может выступать:
1. отдельно сохраненный алгоритм;
2. отношение, в котором объединены все шаги алгоритма, по которому создан прецедент.
Под уникальными входами в правила понимаются входы, которые не являются выходом правила внутри локального алгоритма. Например, на Фиг.6а уникальный вход только один - P1. В качестве отношения данного правила будет записано последовательное и суммарное отношение всех входящих в локальный алгоритм отношений. Формирование правила-прецедента, не отличающегося от обычного правила по структуре, и позволяет использовать их наряду с другими правилами при логическом выводе. Иными словами, прецеденты могут обрабатываться в том же месте и алгоритме, что и простые правила. Для некоторых задач допускается их отдельное использование.
Вышеописанные способы реализуются на практике на основе широко известных компьютерных и сетевых технологий и технологий программирования. Так, могут быть использованы один или несколько компьютеров, содержащих стандартные аппаратные компоненты, такие как процессор, различные виды запоминающих устройств (память, кэши различного уровня, жесткие диски и т.п.), сетевые адаптеры, дисплейные устройства, устройства ввода/вывода и т.п., программно-аппаратные компоненты, такие как BIOS, и программные компоненты, такие как операционная система, драйверы, различные базовые API и библиотеки, каковой компьютер(ы) конфигурируется на основе известных технологий программирования (например, какой-либо из известных реализаций объектно-ориентированного программирования) для осуществления способов, отвечающих настоящему изобретению. Например, может быть разработан пакет программного обеспечения из средств программного кода, который инсталлируется на компьютер(ы), в том числе путем его копирования на машиночитаемые носители данных из состава компьютера(ов). Средства программного кода пакета, при их считывании и исполнении процессором или процессорами из состава компьютера(ов), предписывают компьютеру(ам) выполнять этапы вышеописанных способов согласно настоящему изобретению. По сути, компьютерное устройство, сконфигурированное таким образом, может рассматриваться как материальная реализация миварной машины логического вывода (ММЛВ) согласно настоящему изобретению. Также допускается программно-аппаратная реализация ММЛВ в виде соответствующим образом сконфигурированного блейд-сервера (например, путем "прошивки", выполняемой по одной из известных технологий).
Ниже в целях иллюстрации приводится пример использования миварного подхода в предметной области «Геометрия. Решение задач по теме "Треугольник"».
При описании предметной области «Геометрия. Решение задач по теме "Треугольник"» перечнем переменных выступали всевозможные стороны, отрезки, углы и т.д. В качестве отношений и правил выступали всевозможные взаимосвязи между этими переменными: различные теоремы, аксиомы и т.д. На момент проведения теста данная предметная область насчитывала 69 параметров, 51 отношение и 223 правила.
Пользователю предоставлена возможность задания переменным требуемых известных значений и отмечания искомых параметров, например, через графический пользовательский интерфейс (GUI), отображаемый на дисплее, иллюстративный пример которого дан на Фиг.7.
Приведем простой пример решения задачи. Для начала рассматривается, как все это проходит в тестовом интерфейсе по Фиг. 8, затем в краткой форме проходят этапы логического вывода по матрице.
Для демонстрации в интерфейс были введены следующие параметры (см. Фиг. 8):
- угол А = 30°,
- угол В = 70°,
- сторона а=5 см.
Выделены следующие параметры для поиска:
- радиус r вписанной окружности,
- высота На, опущенная из угла А на сторону а.
В результате в таблицу логического вывода добавляются введенные, найденные по ходу решения, но не запрашиваемые изначально, а также найденные значения.
Далее, в текстовой форме отображаются все выполненные действия по выбору правил для вычисления, сообщения о подключении к вычислению новых необходимых параметров, сообщения о найденных значениях параметров, пример чего приведен ниже в Таблице 8.
Таблица 8
Пример алгоритма вычисления согласно рассматриваемому примеру

Теперь разберем данный пример более детально. Как упоминалось выше, данная предметная область состоит из 69 параметров и 223 правил. Отобразить такую матрицу на бумаге не представляется возможным, поэтому ограничимся лишь ее участком, интересующим нас.
Исходя из описания миварной сети матрица состоит из параметров и правил. Параметры в нашем случае представляют собой стороны, углы, высоты и т.д. Правила представляют собой взаимосвязи, алгоритмы вычисления тех или иных величин, например теорема синусов, теорема косинусов, расчет радиуса вписанной окружности и т.д. Таким образом мы получаем следующую матрицу.
Как следует из матрицы выше, на первом этапе может быть запущено сразу 3 правила: 'Сумма углов треуг.', 'Теорема Sin() для стороны b' и 'теорема Sin() для радиуса описанной окружности'. Так как в предметной области нет никаких ограничений на очередность, то все эти правила мы помечаем как запущенные и в служебном столбце ставим '2', а в служебной строке отмечаем их выходы как известные. В таком случае матрица принимает следующий вид.
После первого этапа стали известны дополнительные параметры, и теперь можно запустить правила 'Высота Ha, зная угол C' и 'Sin() углов и окружности для радиуса вписанной окр.', чтобы найти искомые параметры. "Запускаем" эти правила. Проставляем значения. Задача решена.
Ниже рассматривается пример использования миварного подхода в предметной области "Диагноз по симптомам".
На основе миварного подхода была создана медицинская модель диагноза по симптомам, приспособленная анализировать отмеченные симптомы и ставить наиболее подходящий диагноз.
Модель диагноза по симптомам функционирует по принципу интеллектуального медицинского справочника, указывая врачу возможные варианты диагноза болезней. В итоге дифференциального диагноза врач получает список диагнозов, возможных при наличии выбранного сочетания симптомов.
Модель предназначена для использования как для практикующих врачей, так и для людей, волнующихся за свое здоровье, а также она может применяться как обучающее средство диагностики болезней в подготовке студентов медицинских институтов.
Модель представляет:
1. перечень симптомов, разделенных для удобства поиска по областям и системам;
2. перечень заболеваний, также разделенных по основным группам;
3. анализы (пользователь может выбирать, учитывать ли результаты анализов или же проигнорировать их).
Входными данными для модели диагноза по симптомам являются симптомы, которые пользователь отмечает самостоятельно, а также пользователь может отметить результаты анализов и выбрать, учитывать их или нет. Выходными данными станет выданный системой диагноз(ы). Взаимодействие, опять же, осуществляется посредством специализированного GUI.
При анализе входных данных модель пользуется математической формулой, которая "подражает" аналитическому заключению специалиста при приеме пациента: она учитывает не одиночные симптомы (как существующие на сегодняшний день системы), а группу симптомов, характерных и достаточных для постановки данного диагноза.
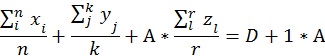
где:
QUOTE


QUOTE
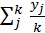
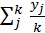
А - метка учета результатов анализов;
QUOTE


D - заложенная точность подбора диагноза.
Предположим, что пользователь отмечает большое количество симптомов:
1. повышение температуры;
2. слабость;
3. головная боль;
4. боли в мышцах и суставах;
5. быстрая утомляемость;
6. сыпь на щеках в форме бабочки;
7. проблемы со зрением;
8. изменение личности;
9. лихорадка;
10. нарушение сна;
11. артрит малых суставов;
12. изменение пигментации кожи;
13. пятнистая сыпь.
Врач-специалист, зацепившись за специфический симптом "сыпь на щеках в форме бабочки", сразу же будет подозревать системную волчанку и может не заметить ретинопатию или лекарственное расстройство зрения или другие более редкие заболевания, которые могут быть завуалированы острым течением волчанки, но разработанная модель сразу же выдаст несколько диагнозов (см. Фиг. 9):
1. системная волчанка,
2. пресбиопия,
что поможет сориентироваться специалисту и вовремя направить пациента на обследование к офтальмологу.
Модель проверяет все отмеченные диагнозы и, на данный момент, выполняет логический вывод со 184 шагами.
Ниже приведен пример вывода результатов:
Шаг № 1
Описание правила: Системная красная волчанка
Входные параметры:
Значение коэффициента = 0;
Боль в суставе = 1;
Ремиттирующая лихорадка = 1;
Нарушение сна = 1;
Артрит малых суставов = 1;
Пигментация кожи = 1;
Пятнистая сыпь = 1;
Снижение или отсутствие аппетита = 1;
Бабочкообразная сыпь = 1;
Формула на псевдоязыке:
var x, p1, p2, p3, p4, p5, p6, p7, p8, a1, a2, a3, a4;
if(x==1 && p1+p2+p3+p4+p5+p6+p7+p8>=6 && a1+a2+a3+a4==4)
{
y = "Возможна системная красная волчанка";
}
else if(x==0 && p1+p2+p3+p4+p5+p6+p7+p8 >= 6)
{
y = "Возможна системная красная волчанка";
}
else
{
y = "Признаки системной красной волчанки не выявлены";
}
Результат:
Системная красная волчанка = Возможна системная красная волчанка;
Шаг № 2
Описание правила: Пресбиопия
Входные параметры:
Снижение зрения = 1;
Утомляемость = 1;
Головная боль = 1;
Формула на псевдоязыке:
if (p1+p2+p3==3)
{
y = "Возможна пресбиопия";
}
else
{
y = "Пресбиопии не выявлено";
}
Результат:
Пресбиопия = Возможна пресбиопия;
Чтобы представить данный расчет в виде матрицы, зададим каждому симптому идентификатор, пример чего приведен ниже в Таблице 12.
Тогда получится следующая матрица, иллюстрируемая Таблицей 13:
Как видно из этой матрицы, оба тестовых примера могут быть запущены.
Теперь рассмотрим сложность переборов. Как было подробно описано выше, все известные элементы добавляются в очередь, далее проходя по каждому элементу из очереди, в конец очереди заносятся все смежные объекты (с указанием того, из какого объекта в них пришли), но объекты заносятся в очередь только в том случае, если они еще не были посещены. Благодаря этому миварный проход не может зациклиться или пройти один и тот же элемент более одного раза. Это обусловлено тем, что в процессе обхода миварной матрицы в каждый элемент была записана информация о том, из какого элемента произошел переход в текущий элемент миварной сети. Такая информация позволяет построить цепочки от искомых элементов к известным. Из блок-схем видно, что параметры на обработку вставляются при необходимости в список, поэтому при реализации была выбрана структура "связанный список", вставка элементов в структуры такого типа занимает O(1). В алгоритме происходит частая проверка на то, был ли добавлен элемент в логический вывод, для этого использовалась такая структура данных, как множество, для определения содержания элемента в множестве в среднем требуется время O(1). Отсюда следует, что сложность алгоритма зависит от количества объектов в модели и в данном случае стремится к O(n) (где n - количество элементов миварной матрицы, т.е. как правил, так и параметров). А при решении реальных локальных задач сложность, зачастую, гораздо меньше и равна O(m), где m - количество задействованных во время просчета элементов и m≤n.
Ниже дается краткий сравнительный анализ предложенного здесь подхода с подходами, основывающимися на онтологиях и когнитивных картах, в которых, как было отмечено выше, используются более медленные алгоритмы поиска.
На основе вышеизложенного приходим к выводу, что с помощью миварного подхода можно описать и выполнить все, что есть в онтологиях. В дополнение к этому, в миварном подходе есть целый ряд дополнительных преимуществ. Таким образом, СППР на основе миварных сетей могут являться как стратегическими, так и оперативными системами. Следовательно, можно сказать, что миварный подход обобщает и развивает онтологии, которые, в свою очередь, могут рассматриваться как частный случай миварных сетей.
Таким образом, видно, что в миварном подходе можно описать и выполнить все, что есть в когнитивных картах. Дополнительно к этому, в миварном подходе есть целый ряд дополнительных преимуществ. Следовательно, можно говорить, что миварный подход обобщает и развивает когнитивные карты. А когнитивные карты, в свою очередь, могут рассматриваться как частный случай миварных сетей.
Более подробно сравнительный анализ подхода, предложенного в настоящей заявке, и вышеуказанных подходов предшествующего уровня техники приведен в публикациях "Сравнительный анализ возможностей когнитивных карт и миварных сетей для построения систем поддержки принятия решений", Чибирова М.О., Автоматизация и управление в технических системах (АУТС), ISSN 2306-1561, №1.1(8), 2014, сс. 40-54 и "Анализ подходов к построению систем поддержки принятия решений: Онтологии и Мивары", Чибирова М.О., Автоматизация и управление в технических системах (АУТС), ISSN 2306-1561, №1.2(9), 2014, сс. 44-60, которые во всей своей полноте включены в настоящее описание посредством ссылки.
Изобретение было раскрыто выше со ссылкой на конкретные варианты его осуществления. Для специалистов могут быть очевидны и иные варианты осуществления изобретения, не меняющие его сущности, как она раскрыта в настоящем описании. Соответственно, изобретение следует считать ограниченным по объему только нижеследующей формулой изобретения.
Реферат
Изобретение относится к области контрольно-вычислительной техники. Технический результат заключается в сокращении времени построения маршрута логического вывода. Указанный результат достигается за счет базы знаний, содержащей представление модели предметной области в виде объектов и связей, организованных в ориентированный двудольный граф, при этом объекты содержат параметры, причем связи содержат правила и каждое правило имеет входную переменную и выходную переменную, а каждый связанный с правилом параметр является его входной либо выходной переменной. Формируют совокупность известных параметров и задают искомые параметры. Запускают одновременно несколько запускаемых правил, в которых известный параметр является входной переменной, для которых известны все остальные входные переменные, при этом имитацию запуска правила осуществляют путем присваивания выводимым в этом правиле переменным значений «известно». Если найдены все искомые параметры, упомянутую обработку прекращают и задача считается решенной, в противном случае осуществляют дальнейший поиск маршрута логического вывода. Строят последовательность из запущенных правил в порядке их запуска, при этом построенная последовательность правил представляет маршрут логического вывода. 8 н. и 28 з.п. ф-лы, 15 табл., 9 ил.

Комментарии