Способ и устройство для локального правила состязательного обучения, которое приводит к разреженной связности - RU2586864C2

Чертежи

Описание

УРОВЕНЬ ТЕХНИКИ

Область техники, к которой относится изобретение

Некоторые аспекты настоящего раскрытия в целом относятся к технике нейронных систем, а конкретнее - к способу и устройству для обучения вычислительной сети с использованием локального правила обучения, которое создает разреженную связность.

Уровень техники

Развитие мозга у людей и животных подвергается резкому увеличению темпов роста синапсов в раннем детстве, вслед за чем происходит массовое отсечение синапсов, которое удаляет приблизительно половину синапсов к периоду полового созревания. Синаптическая перезапись (структурная пластичность) продолжается в зрелом мозге, но в более медленном темпе. Выявлено, что отсечение синапсов зависит от активности и предназначено для удаления более слабых синапсов. Вследствие этого оно может объясняться синаптической пластичностью, при которой синапсы состязаются за конечные ресурсы, такие как нейротрофные факторы. Отсечение синапсов помогает повысить эффективность мозга, которая может быть в целом определена как одни и те же функциональные возможности с меньшим количеством синапсов. Поскольку передача сигналов через синапсы требует энергии, более высокая эффективность также означает более низкую энергию.

Существующие неконтролируемые правила обучения моделируют состязание синапсов за ограниченные ресурсы явным образом, посредством мультипликативной или субтрактивной нормализации, либо неявным образом. Однако явные нормализации могут быть нелокальными, то есть они требуют знания всех входных весов нейрона, чтобы обновлять каждый из них по отдельности. Однако это может быть не биологически правдоподобным. Правило Оджа, с другой стороны, использует только локальную информацию, имеющуюся в распоряжении у синапса, для вычисления обновления его веса, но оно асимптотически ограничивает сумму квадратов весов, что не имеет биологического обоснования.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

Некоторые аспекты настоящего раскрытия предусматривают способ обучения вычислительной сети. Способ в целом включает в себя вычисление выходного сигнала блока обработки в вычислительной сети по меньшей мере частично на основании по меньшей мере одного существующего веса и изменение по меньшей мере одного веса блока обработки с использованием локального правила обучения, при этом локальное правило обучения создает разреженную связность между блоками обработки вычислительной сети.

Некоторые аспекты настоящего раскрытия предусматривают устройство вычислительной сети. Устройство в целом включает в себя первую схему, выполненную с возможностью вычислять выходной сигнал устройства в вычислительной сети по меньшей мере частично на основании по меньшей мере одного существующего веса, и вторую схему, выполненную с возможностью изменять по меньшей мере один вес устройства с использованием локального правила обучения, при этом локальное правило обучения создает разреженную связность между устройствами вычислительной сети.

Некоторые аспекты настоящего раскрытия предусматривают устройство вычислительной сети. Устройство в целом включает в себя средство для вычисления выходного сигнала устройства в вычислительной сети по меньшей мере частично на основании по меньшей мере одного существующего веса и средство для изменения по меньшей мере одного веса блока обработки с использованием локального правила обучения, при этом локальное правило обучения создает разреженную связность между устройствами вычислительной сети.

Некоторые аспекты настоящего раскрытия предусматривают компьютерный программный продукт для обучения вычислительной сети. Компьютерный программный продукт в целом включает в себя компьютерно-читаемый носитель, содержащий код для вычисления выходного сигнала блока обработки в вычислительной сети по меньшей мере частично на основании по меньшей мере одного существующего веса и изменения по меньшей мере одного веса блока обработки с использованием локального правила обучения, при этом локальное правило обучения создает разреженную связность между блоками обработки вычислительной сети.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

С тем чтобы метод, которым описаны вышеперечисленные признаки настоящего раскрытия, стал понятен в деталях, более конкретное описание, кратко обобщенное выше, может быть воспринято посредством ссылки на аспекты, некоторые из которых проиллюстрированы на прилагаемых чертежах. Должно быть отмечено, однако, что прилагаемые чертежи иллюстрируют только некоторые типичные аспекты этого раскрытия, а потому не должны рассматриваться ограничивающими его объем, ввиду того, что описание может допускать другие, в равной степени действенные аспекты.

Фиг. 1 иллюстрирует примерный блок обработки нейронной системы в соответствии с некоторыми аспектами настоящего раскрытия.

Фиг. 2A-2D иллюстрируют примерный геометрический анализ асимптотических решений в соответствии с некоторыми аспектами настоящего раскрытия.

Фиг. 3 иллюстрирует операции для обновления весов синапсов нейронной системы с использованием локального правила обучения в соответствии с некоторыми аспектами настоящего раскрытия.

Фиг. 3A иллюстрирует примерные компоненты, способные к выполнению операций, проиллюстрированных на фиг. 3.

Фиг. 4A-4D иллюстрируют разные центростремительные рецепторные поля простой клетки, обучаемой посредством четырех разных правил в соответствии с некоторыми аспектами настоящего раскрытия.

Фиг. 5A-5D иллюстрируют распределения весов относящейся к сетчатке нервной клетки в простую клетку (RGC-в-S1) в соответствии с некоторыми аспектами настоящего раскрытия.

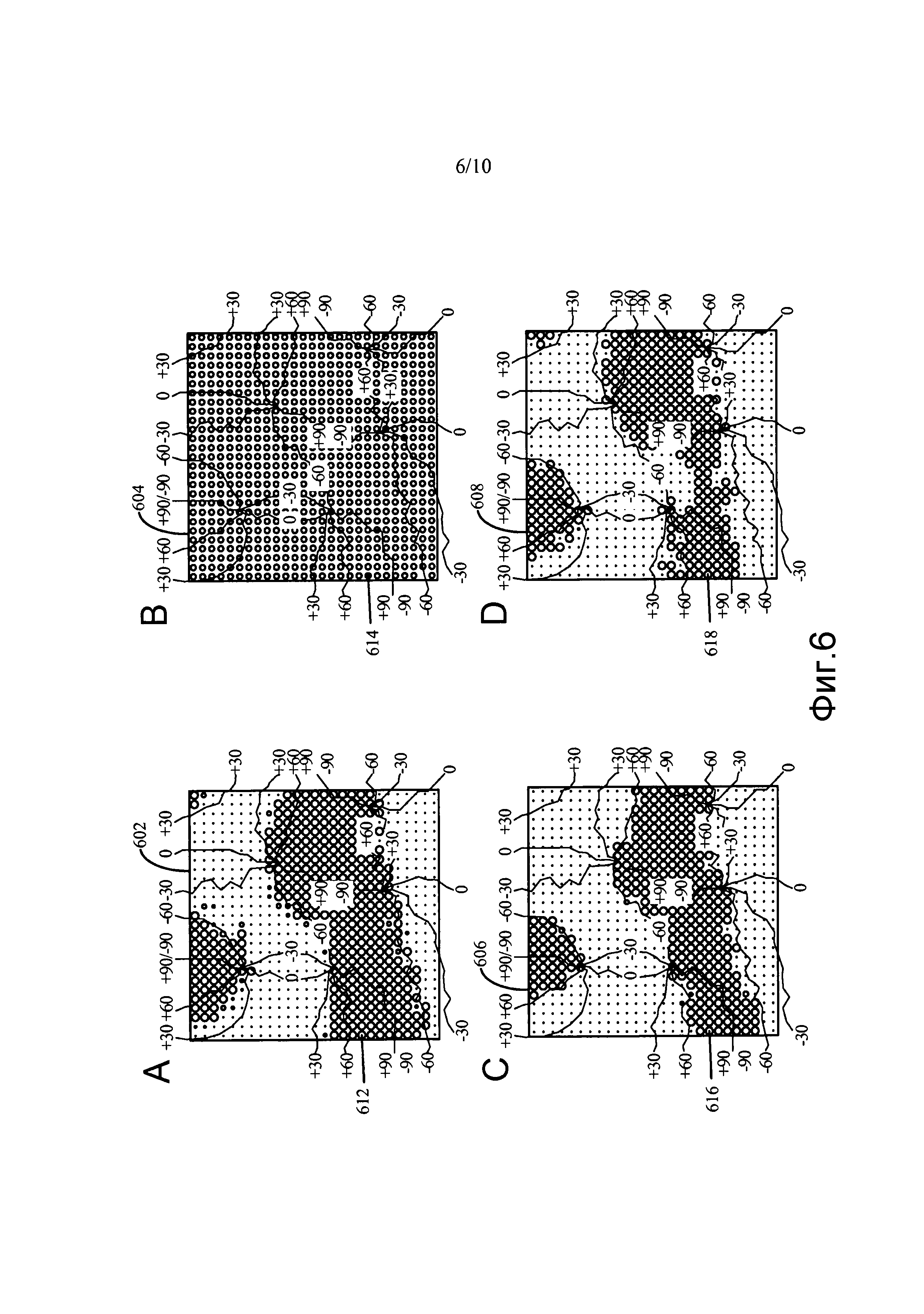
Фиг. 6A-6D иллюстрируют отображение ориентации простой клетки со связями из пула простых клеток с такой же сложной клеткой в соответствии с некоторыми аспектами настоящего раскрытия.

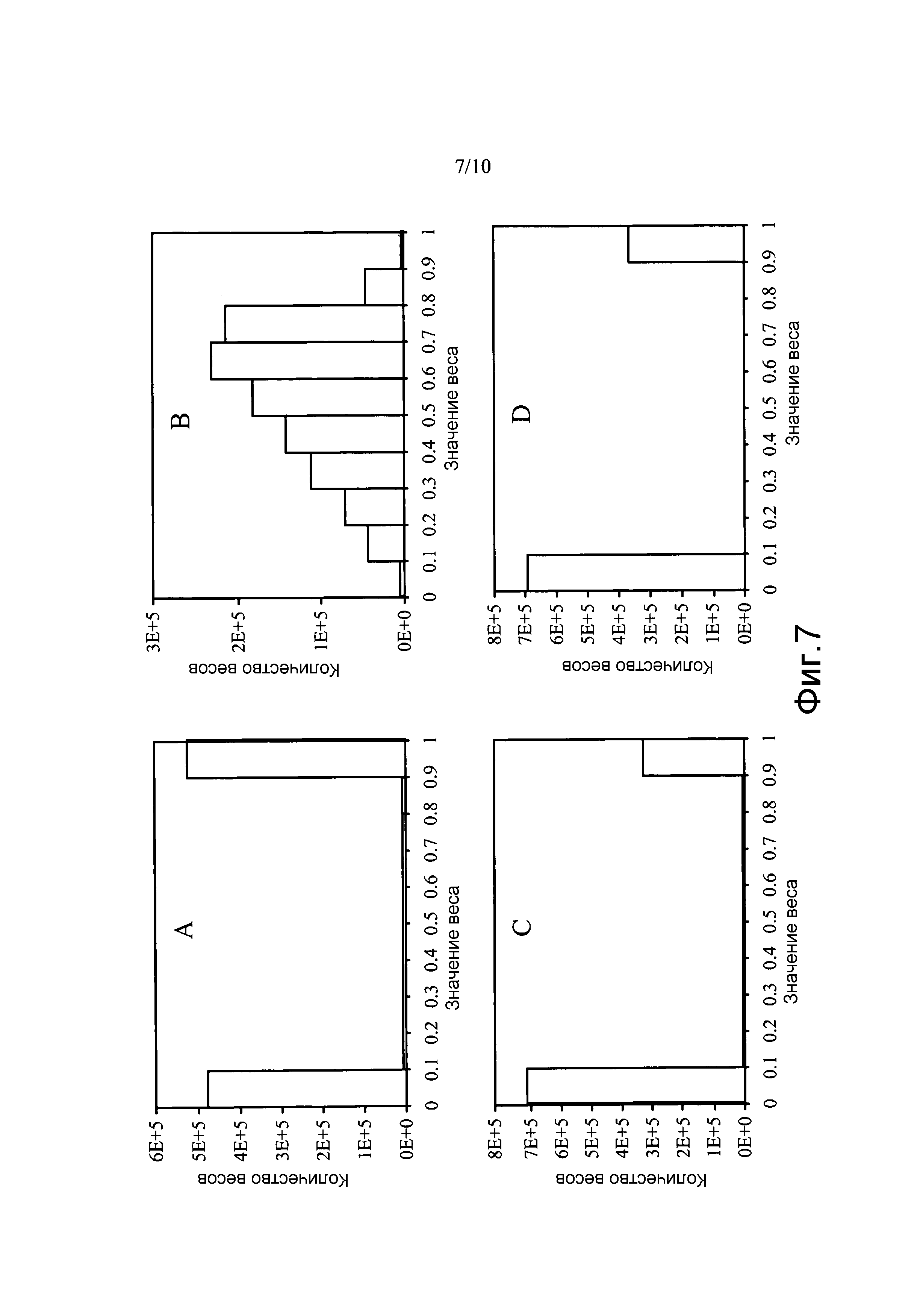
Фиг. 7A-7D иллюстрируют распределение весов простой клетки в сложную клетку (S1-в-C1), обученное посредством четырех разных правил, в соответствии с некоторыми аспектами настоящего раскрытия.

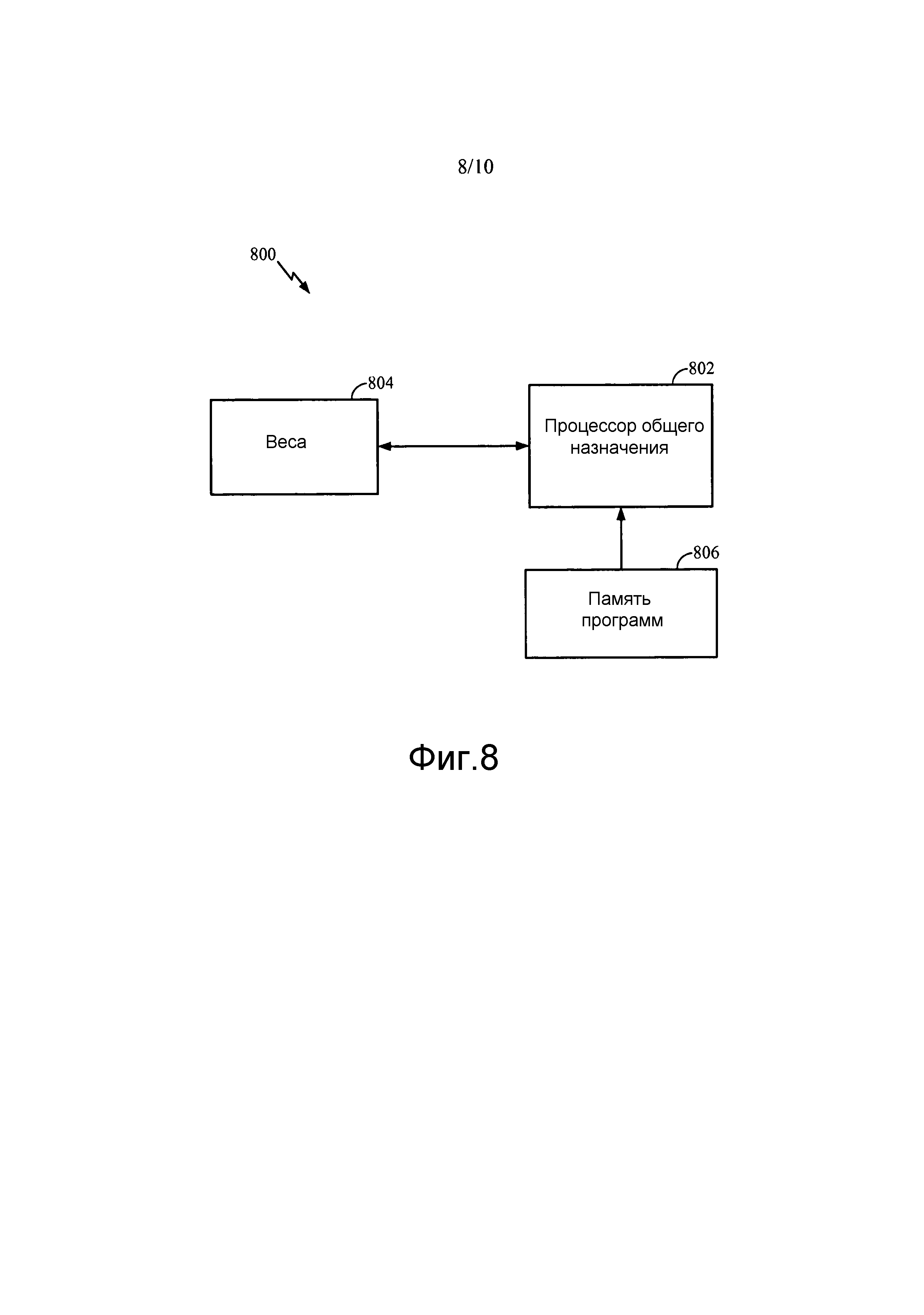
Фиг. 8 иллюстрирует примерную программную реализацию локального правила обучения с использованием процессора общего назначения в соответствии с некоторыми аспектами настоящего раскрытия.

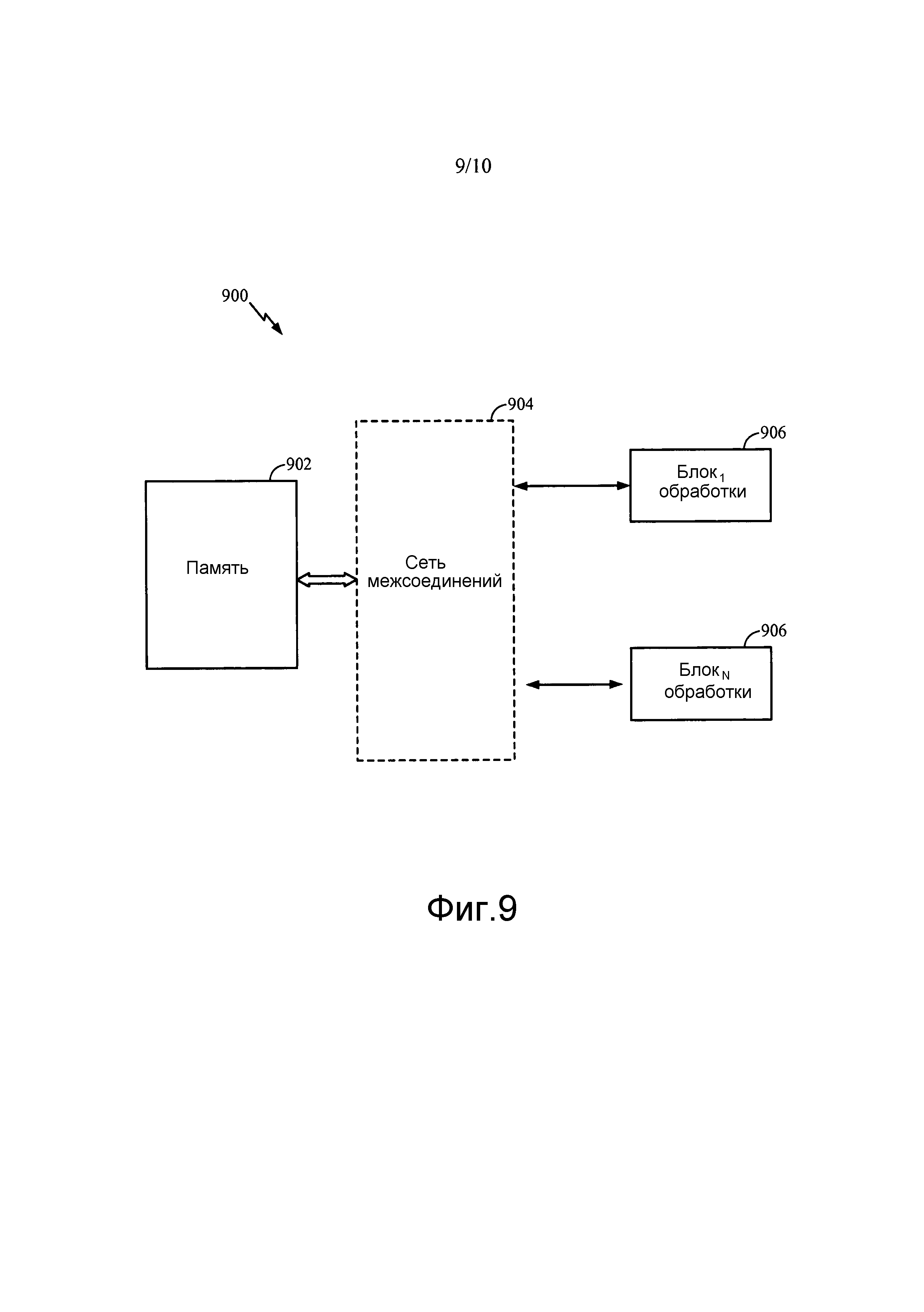
Фиг. 9 иллюстрирует примерную реализацию локального правила обучения, где память весов сопряжена с отдельными блоками распределенной обработки, в соответствии с некоторыми аспектами настоящего раскрытия.

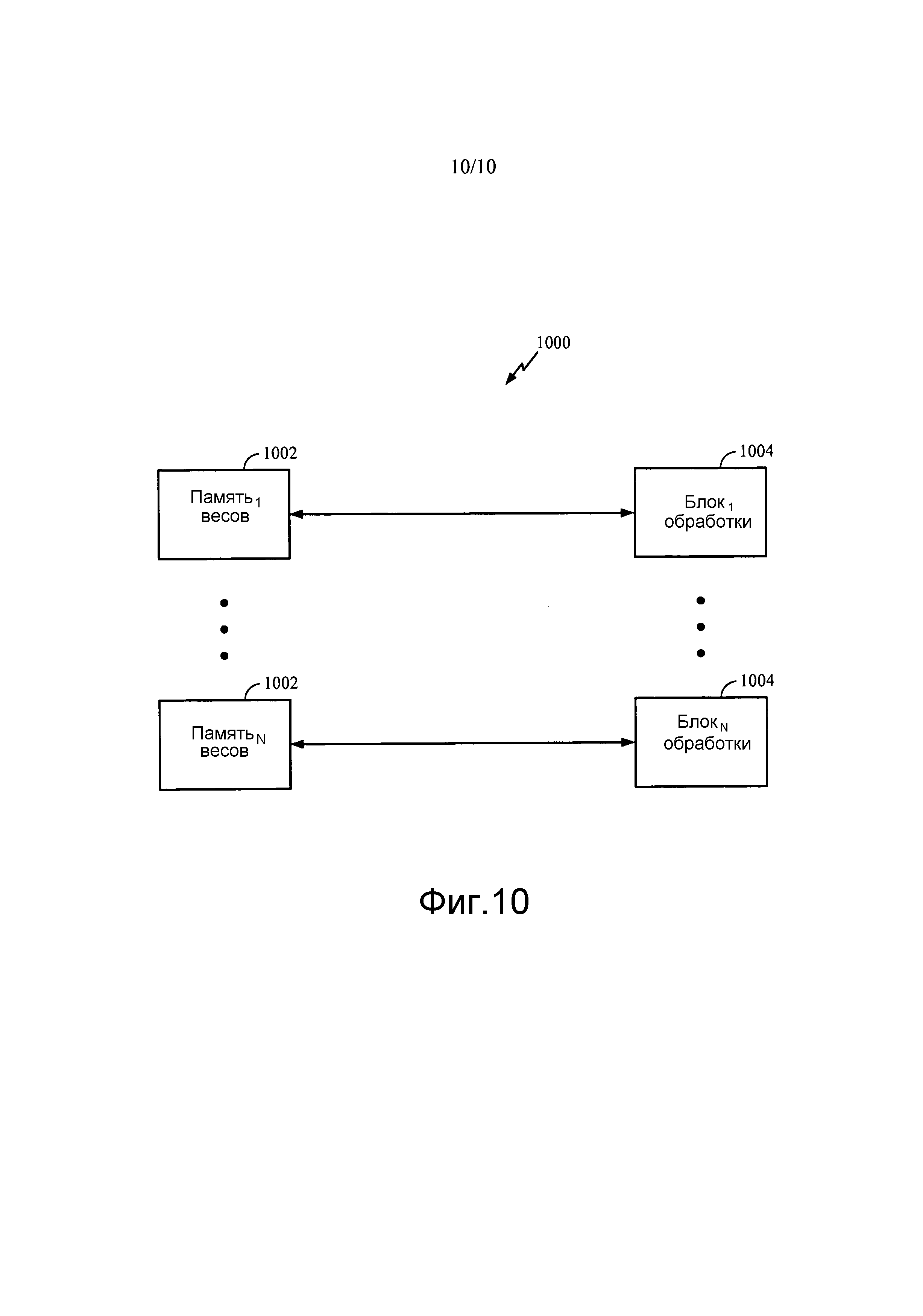
Фиг. 10 иллюстрирует примерную реализацию локального правила обучения, основанную на распределенной памяти весов и распределенных блоков обработки, в соответствии с некоторыми аспектами настоящего раскрытия.

ПОДРОБНОЕ ОПИСАНИЕ

Различные аспекты раскрытия полнее описаны в дальнейшем со ссылкой на прилагаемые чертежи. Однако это раскрытие может быть воплощено во многих иных формах и не должно толковаться в качестве ограниченного какими-нибудь конкретными конструкцией или функционированием, представленными на всем протяжении этого раскрытия. Скорее, эти аспекты приведены так, что это раскрытие будет всесторонним и полным и будет полностью передавать объем раскрытия специалистам в данной области техники. На основании сведений, приведенных в материалах настоящей заявки, специалист в данной области техники должен принимать во внимание, что объем раскрытия предназначен для охвата любого аспекта раскрытия, раскрытого в материалах настоящей заявки, реализованного независимо или комбинированного с любым другим аспектом раскрытия. Например, устройство может быть реализовано или способ может быть осуществлен на практике с использованием любого количества аспектов, изложенных в материалах настоящей заявки. В дополнение подразумевается, что объем раскрытия должен охватывать такое устройство или способ, которые осуществляются на практике с использованием других конструкций, функциональных возможностей либо конструкций и функциональных возможностей в дополнение к или иных, чем различные аспекты раскрытия, изложенные в материалах настоящей заявки. Должно быть понятно, что любой аспект раскрытия, раскрытый в материалах настоящей заявки, может быть воплощен одним или более элементов формулы изобретения.

Слово «примерный» используется в материалах настоящей заявки, чтобы означать «служащий в качестве примера, экземпляра или иллюстрации». Любой аспект, описанный в материалах настоящей заявки как «примерный», не обязательно должен толковаться в качестве предпочтительного или преимущественного над другими аспектами.

Хотя конкретные аспекты описаны в материалах настоящей заявки, многие варианты и перестановки этих аспектов подпадают под объем раскрытия. Хотя упомянуты некоторые выгоды и преимущества предпочтительных аспектов, не подразумевается, что объем раскрытия должен ограничиваться конкретными выгодами, применениями или целями. Скорее, аспекты раскрытия подразумеваются широкоприменимыми к разным технологиям, конфигурациям системы, сетям и протоколам, некоторые из которых проиллюстрированы в качестве примера на фигурах и в последующем описании предпочтительных аспектов. Подробное описание и чертежи скорее являются всего лишь иллюстрирующими раскрытие, нежели ограничивающими объем раскрытия, определенный прилагаемой формулой изобретения и ее эквивалентами.

ПРИМЕРНАЯ НЕЙРОННАЯ СИСТЕМА

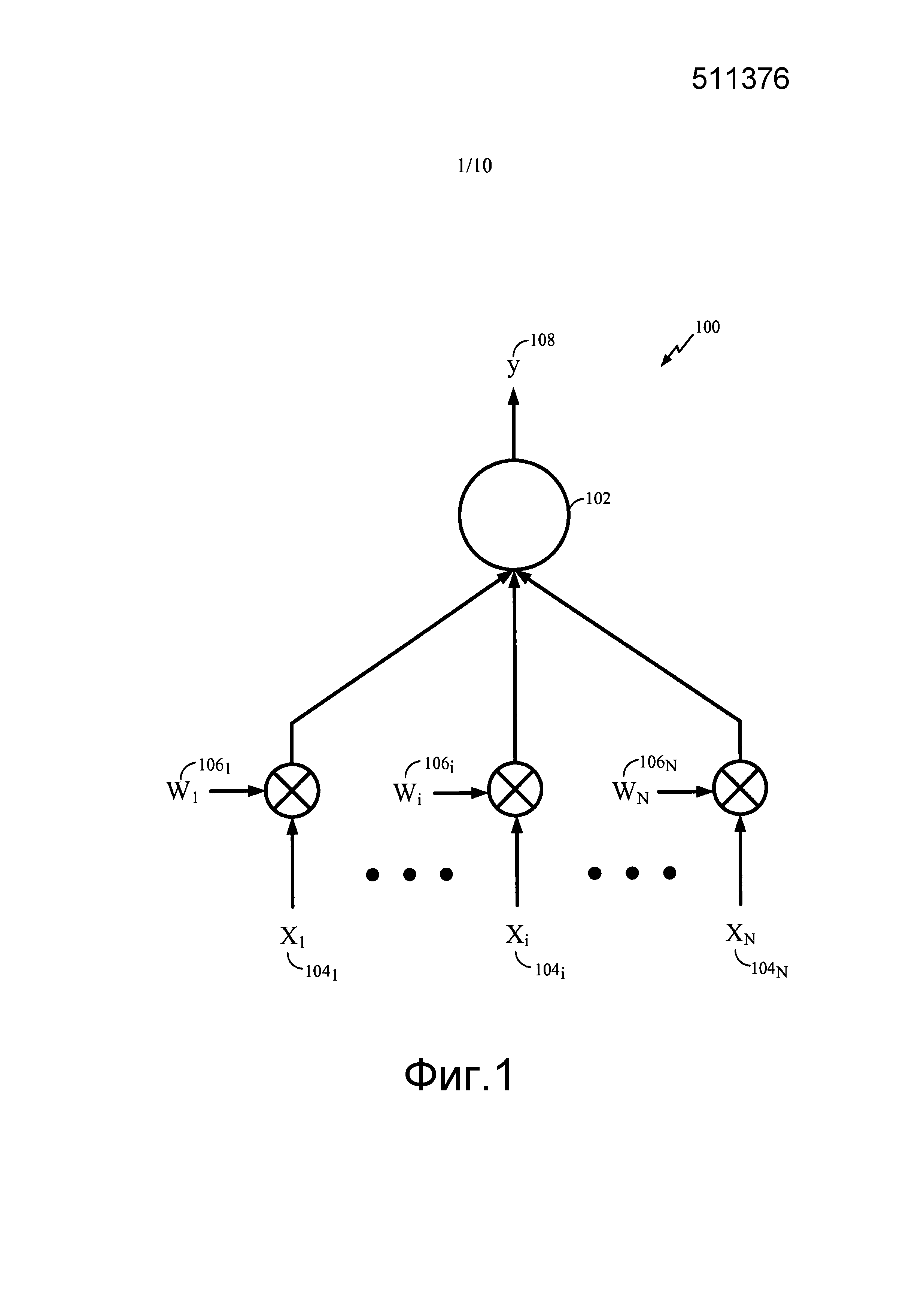
Фиг. 1 иллюстрирует пример 100 блока 102 обработки (например, нейрона) вычислительной сети (например, нейронной системы) в соответствии с некоторыми аспектами настоящего раскрытия. Нейрон 102 может принимать многочисленные входные сигналы 104₁-104_N (x₁-x_N), которые могут быть сигналами, внешними для нейронной системы, или сигналами, сформированными другими нейронами той же самой нейронной системы, или теми и другими. Входной сигнал может быть током или напряжением, вещественнозначным или комплекснозначным. Входной сигнал может содержать числовое значение с представлением с фиксированной точкой или плавающей точкой. Эти входные сигналы могут подаваться на нейрон 102 через синаптические связи, которые масштабируют сигналы согласно настраиваемым синаптическим весам 106₁-106_N (w_1-w_N), где N может быть общим количеством входных связей нейрона 102.

Нейрон 102 может комбинировать масштабированные входные сигналы и использовать комбинированные масштабированные сигналы для формирования выходного сигнала 108 (то есть сигнала y). Выходной сигнал 108 может быть током или напряжением, вещественнозначным или комплекснозначным. Выходной сигнал может содержать числовое значение с представлением с фиксированной точкой или плавающей точкой. Выходной сигнал 108 затем может передаваться в качестве входного сигнала в другие нейроны той же самой нейронной системы или в качестве входного сигнала в тот же самый нейрон 102, либо в качестве выходного сигнала нейронной системы.

Блок 102 обработки (нейрон) может имитироваться электрической схемой, а его входные и выходные связи могут имитироваться проводами с синаптическими цепями. Блок 102 обработки, его входные и выходные связи также могут имитироваться программным кодом. Блок 102 обработки также может имитироваться электрической схемой, тогда как его входные и выходные связи могут имитироваться программным кодом. В одном из аспектов настоящего раскрытия блок 102 обработки в вычислительной сети может содержать аналоговую электрическую схему. В еще одном аспекте блок 102 обработки может содержать цифровую электрическую схему. В еще одном другом аспекте блок 102 обработки может сдержать смешанную сигнальную электрическую схему как с аналоговыми, так и цифровыми компонентами. Вычислительная сеть может содержать блоки обработки в любой из вышеупомянутых форм. Вычислительная сеть (нейронная система), использующая такие блоки обработки, может использоваться в большом диапазоне применений, таких как распознавание образов и закономерностей, машинного обучения, управления электроприводом и тому подобного.

ЛОКАЛЬНОЕ ПРАВИЛО СОСТЯЗАТЕЛЬНОГО ОБУЧЕНИЯ С ОГРАНИЧЕНИЕМ L1

Некоторые аспекты настоящего раскрытия поддерживают локальное правило состязательного обучения для обновления весов, ассоциированных с одним или более блоков обработки (нейронов) вычислительной сети (нейронной системы), таких как веса 106₁-106_N, проиллюстрированные на фиг. 1). Применяемое локальное правило состязательного обучения может приводить к разреженной связности между блоками обработки, то есть некоторые из весов могут быть равными нулю или находиться ниже определенного порогового значения, как только процесс обучения закончен.

В некотором аспекте обычное правило обучения Хебба синаптических весов может быть выражено в качестве

где Δw_i - изменение i-ого синаптического веса w_i,

- скорость обучения, x_i - i-ый входной сигнал (пресинаптическая реакция), а y - выходной сигнал нейрона (постсинаптическая реакция). Правило, определенное уравнением (1), может вызывать неограниченный рост веса, таким образом, претерпевая неудачу в том, чтобы учитывать ограниченные ресурсы мозга для потенцирования синапсов и получающегося в результате состязания между синапсами за эти ресурсы.

Несколько модификаций в отношении правила Хебба могут помочь преодолеть его недостатки. Например, пассивный член затухания веса может быть добавлен в уравнение (1) для ограничения роста веса:

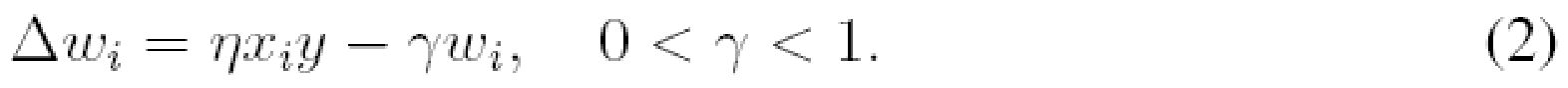
Это правило может отсекать связи с низкой активностью, и оно может отсечь все связи, если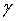

не подобрано тщательно. Кроме того, так называемое правило «входной звезды», в котором член затухания может стробироваться постсинаптической активностью y, может обойти эту проблему, как задано посредством:

Аналогичное правило, как определенно уравнением (3), может использоваться в самоорганизующихся отображениях. Должно быть отмечено, что это правило может сходиться к w_i=x_i.

Может быть предложено правило ковариантности, которое может убирать смещение правила Хебба, обусловленное ненулевыми средними значениями x_i и y, и одновременно может добавлять синаптическое подавление в качестве заданного согласно:

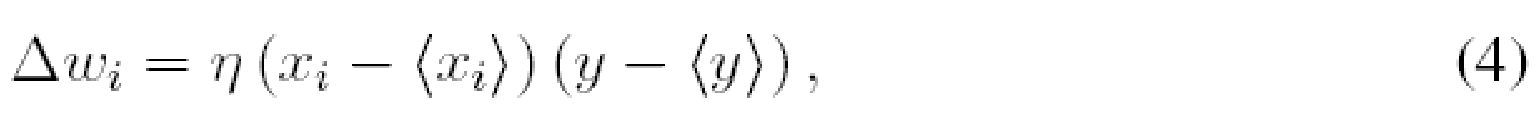
где i> и - средние пресинаптическая и постсинаптическая активности соответственно. Точно такое, как правило Хебба, правило, определенное уравнением (4), может не ограничивать рост веса и может не форсировать синаптическое состязание.

Для достижения состязания синапсов может использоваться постсинаптическое пороговое значение, которое прирастает быстрее, чем линейно, в зависимости от средней постсинаптической активности . Получающееся в результате правило обучения, называемое правилом BCM (правилом Байенстока-Купера-Мура), может быть записано в качестве:

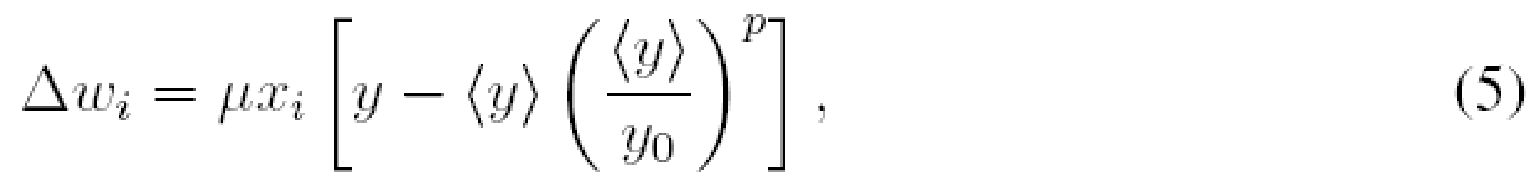
где y₀ представляет асимптотическое целевое значение для , а p>1 является константой.

Для предотвращения неограниченного роста весов веса могут делиться на их сумму, чтобы сохранять их постоянными, как задано посредством:

где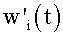

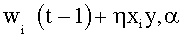
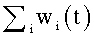
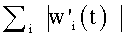
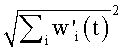
= является целевым значением для , а t - временной индекс. Этот тип ограничения весов может называться мультипликативной нормализацией. В своей исходной форме мультипликативная нормализация может применяться к однополярным весам. Однако она может быть расширена до двухполярных весов посредством замены знаменателя в уравнении (6) на норму L₁ . Она также может быть модифицирована для ограничения длины весового вектора (нормы L₂) посредством замены знаменателя на . Так как веса в уравнении (6) могут обучаться согласно правилу Хебба, а затем масштабироваться общим коэффициентом, оба правила обучения, определенные уравнениями (1) и (6), могут сходиться к весовым векторам, указывающим в одном и том же направлении, но имеющим разные длины.

Также можно вычитать равную величину из каждого веса после того, как они были модифицированы по правилу обучения, определенному уравнением (1), причем величина выбирается так, чтобы общая сумма весов могла оставаться постоянной:

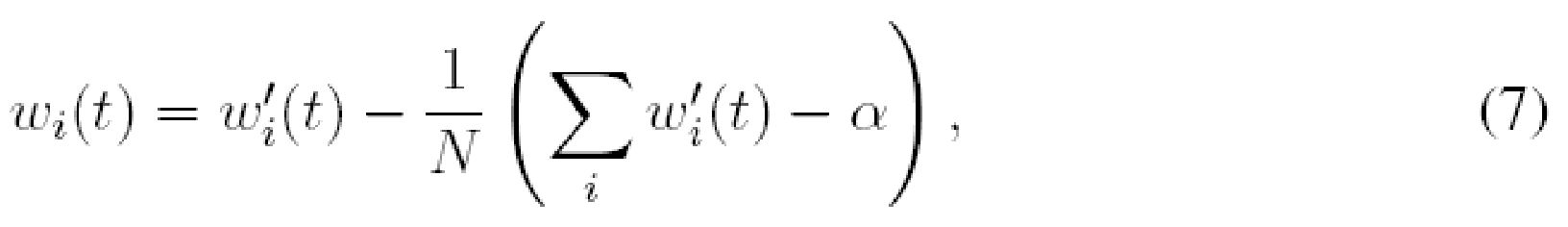
где N - количество входных сигналов. Этот тип ограничения весов может называться субтрактивной нормализацией. С подстановкой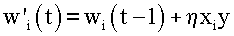

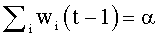
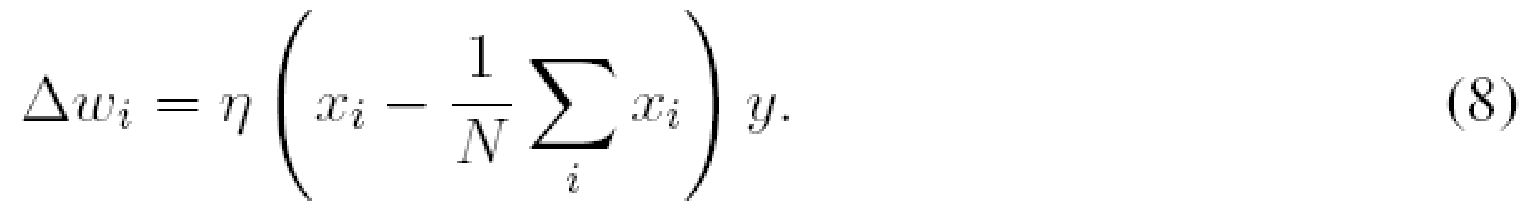
в уравнение (7) и с учетом , в таком случае правило обучения, определенное согласно (7), может сокращаться до

Субтрактивная нормализация типично может применяться к однополярным весам и, таким образом, может требовать ограничения нулем для предохранения весов от изменения их знака. При ограничении нулем все входные веса нейрона, обученные согласно уравнению (7), могут асимптотически сходиться к нулю кроме одного веса. Для предотвращения единственного ненулевого веса также может накладываться верхнее ограничение на величину веса. Основной недостаток как мультипликативной, так и субтрактивной нормализаций может состоять в том, что они нелокальны, то есть они могут требовать знания всех входных весов или входных сигналов нейрона для вычисления каждого веса по отдельности.

Локальное правило обучения, известное в качестве правила обучения Оджа, может ограничивать L₂ нормой входного весового вектора в точке равновесия. В общей форме правило Оджа может быть записано в качестве:

где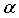

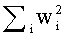
- целевое значение для в точке равновесия. Несмотря на то, что это правило может создавать состязание между синаптическими весами за ограниченные ресурсы, моделирование этих ресурсов в качестве суммы квадратов весов может не быть биологически обоснованным.

Вышеупомянутые правила обучения типично могут применяться к униполярным весам, чтобы подчиняться принципу, согласно которому, связям из возбуждающих нейронов может быть необходимо иметь положительные веса, а связям из тормозящих нейронов может быть необходимо иметь отрицательные веса. В аспекте весам может не быть позволено менять свой знак посредством использования ограничения нулем. Если правило может обособлять центростремительные, ограничение нулем часто может приводить к весовым векторам со многими нулевыми элементами (разреженным векторам). Однако если весам предоставлена возможность менять свой знак, то вышеупомянутые правила могут сходиться к весовым векторам с несколькими нулевыми элементами (неразреженным векторам).

Согласно некоторым аспектам настоящего раскрытия, модификация правила Оджа, определенная уравнением (9), предложена в качестве заданного посредством:

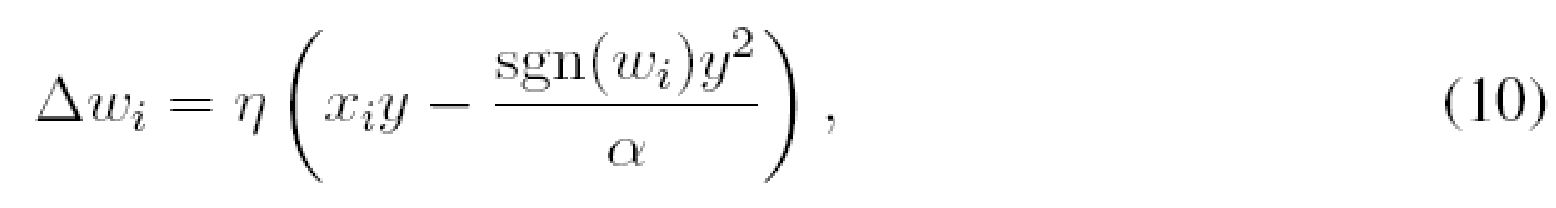
где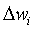

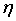
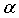
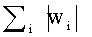
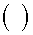
- изменение i-ого синаптического веса w_i, - скорость обучения, x_i - i-ый входной сигнал (пресинаптическая реакция), y выходной сигнал нейрона (постсинаптическая реакция), - целевое значение для , а sgn - знаковая функция.

Для того чтобы доказать, что предложенное правило, заданное уравнением (10), ограничивает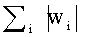

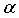
до в точке равновесия, может быть предположено, что выходной сигнал y формируется в качестве взвешенной суммы входных сигналов нейрона, то есть:

Подстановка уравнения (11) в уравнение (10) и учет среднего по времени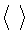

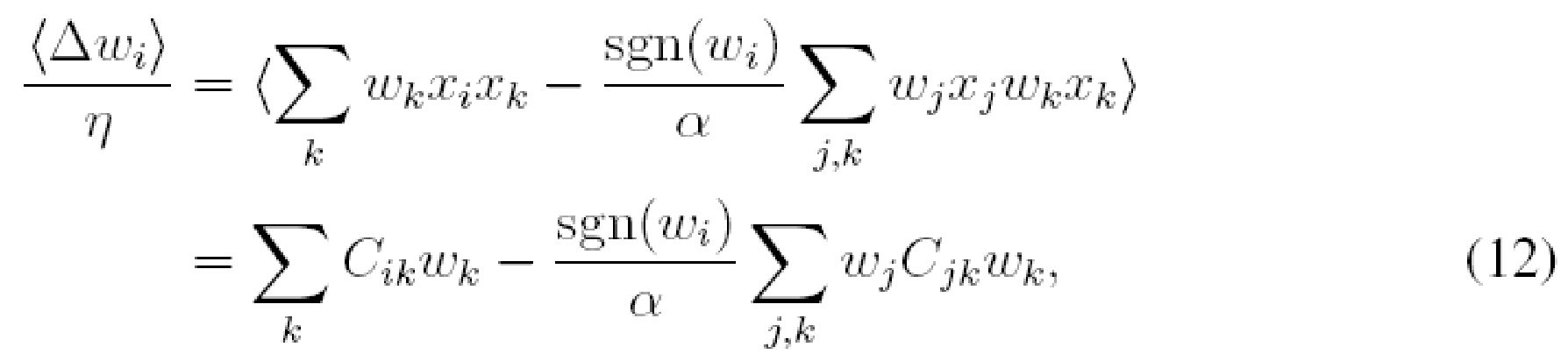
результата с допущением, что изменения весов являются медленными относительно времени, в течение которого представлены входные закономерности, могут приводить к:

или в матричной форме

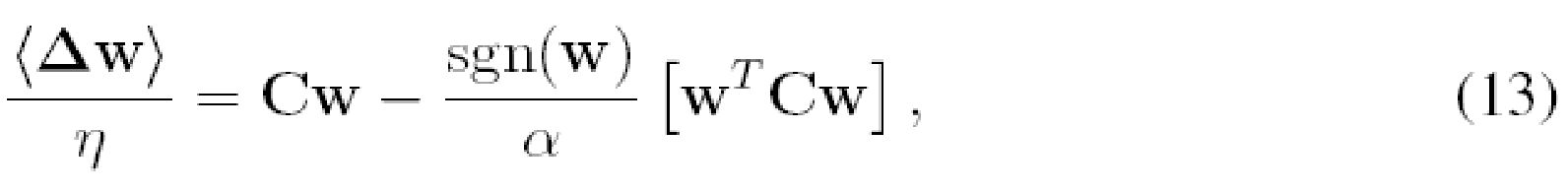
где w - входной весовой вектор, T в верхнем индексе означает транспонирование, C с элементом C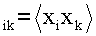

является матрицей корреляции входных сигналов.

В точке равновесия среднее изменение весов должно быть равным нулю, то есть:

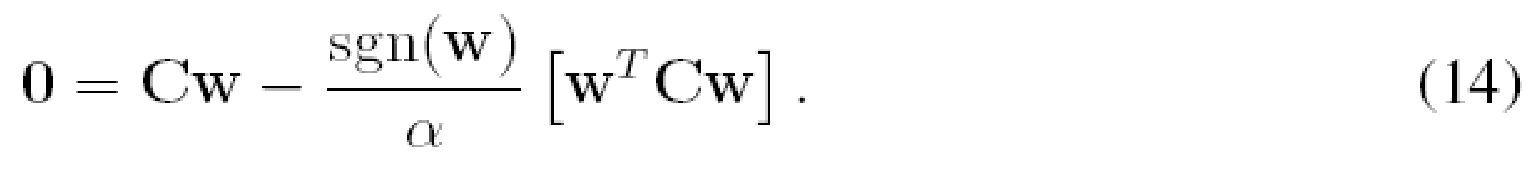
Умножение обеих сторон уравнения (14) на w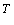

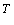
слева, деление получающегося в результате уравнения на скаляр [w Cw] и перегруппировка членов может приводить к:

то есть норма L₁ весового вектора w может быть равной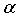

в точке равновесия.

Подобным образом может быть доказано, что следующее правило может ограничивать норму L₀ весового вектора в точке равновесия:

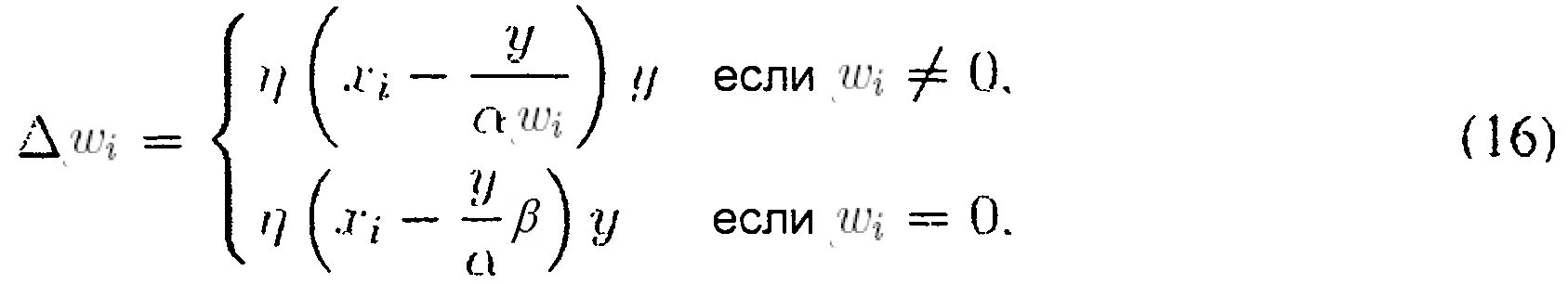
где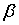

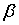
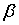
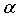
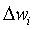
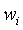
- ограничение (например, =1 или =0), и - целевое значение для счета ненулевых элементов в w. Вследствие деления на w_i, правило, определенное уравнением (16), может создавать большие обновления когда является близким к 0, заставляя его колебаться около 0 и никогда не достигая целевого значения, если не используется ограничение нулем. С другой стороны, правило обучения, определенное уравнением (10), может не показывать такое поведение и может сходиться к разреженному w с или без ограничения нулем, как будет подробнее показано ниже.

В качестве простого примера может быть рассмотрен линейный нейрон с двумя входами x₁ и x₂ и соответствующими весами w₁ и w₂. В таком случае выходной сигнал нейрона может быть задан посредством:

где все величины могут быть положительными, отрицательными или нулевыми. Если входные сигналы являются нулевым средним значением, то выходной сигнал y также может быть нулевым средним значением, и правило ковариантности, определенное уравнением (4), может сокращаться до правила Хебба, определенного уравнением (1). Правило Хебба может рассматриваться в качестве этапа оптимизации в направлении градиента стоимостной функции E:

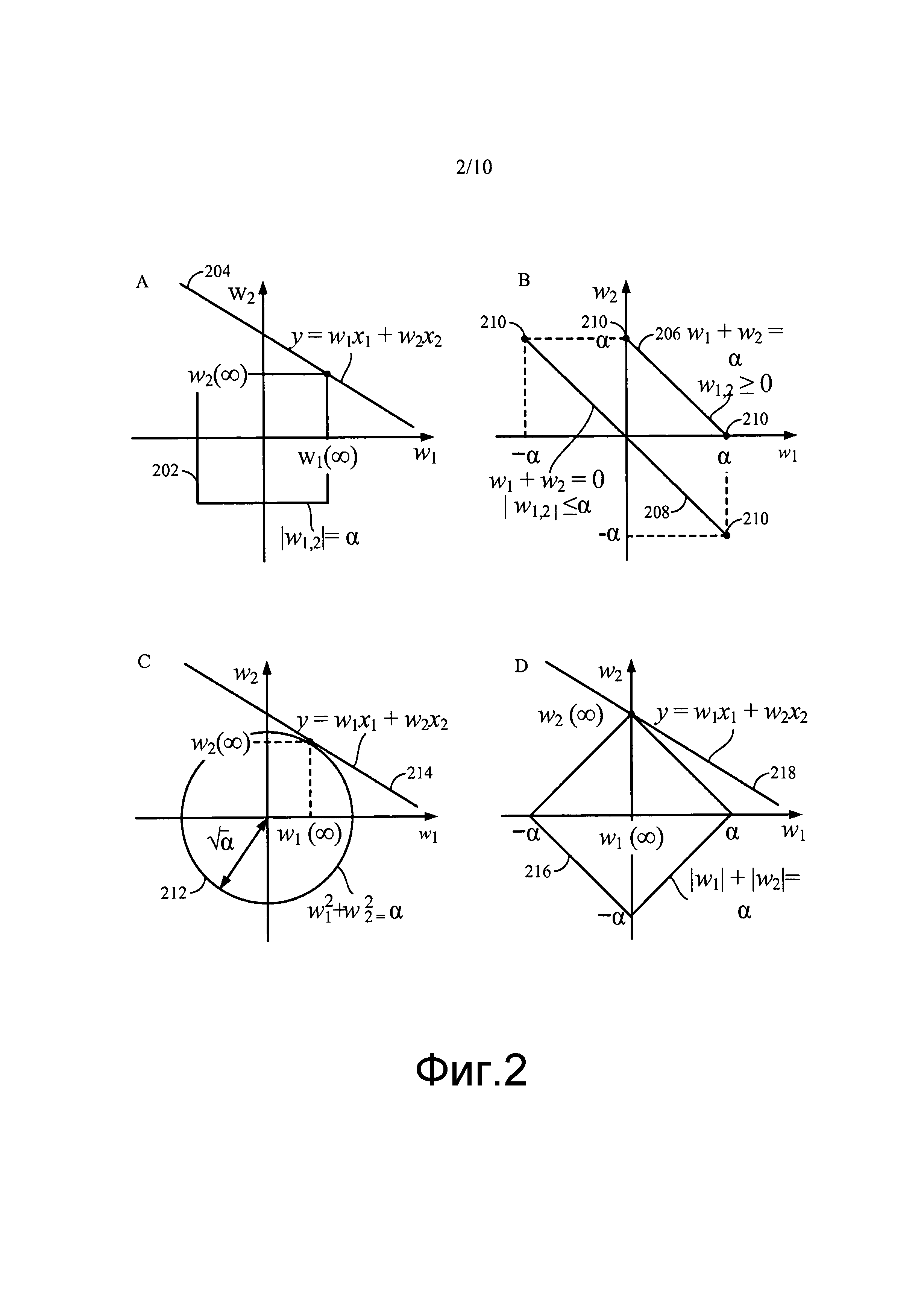
Может быть показано, что E=y²/2, то есть правило Хебба, может максимизировать энергию нейрона, таким образом, неограниченный рост величин весов. Может быть два возможных пути решения градиентного подъема: вдоль левой (y<0) и правой (y>0) сторон параболы y²/2, в зависимости от начального значения y. Для простоты это начальное значение может предполагаться положительным из условия, чтобы правило обучения, определенное уравнением (18), проходило по правой стороне параболы y²/2. В этом случае максимизация y²/2 может быть эквивалентна максимизации y. Для предотвращения неограниченного роста весов ограничение может накладываться на величины весов: |w₁|≤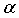

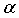
и |w₂|≤ . Это ограничение может изображать квадрат 202 на плоскости (w₁; w₂), как проиллюстрировано на фиг. 2A. Прямая линия 204 может изображать все возможные (w₁; w₂) решения для данных y, x₁, и x₂. Наклон линии 204 может определяться посредством -x₁/x₂, и его положение относительно центра может определяться посредством y/x₂. Максимизация y может перемещать линию 204 от центра (вверх, если x₂>0, или вниз, если x₂<0). Асимптотическое решение (w₁(∞); w₂(∞)) может быть найдено посредством перемещения линии 204 в направлении увеличения y до тех пор, пока она не прикасается к квадрату 202 только в одной точке, которая всегда может быть одним из углов за исключением x₁=0 или x₂=0. Как может наблюдаться на фиг. 2A, для подавляющего большинства входных сигналов правило Хебба с заданными ограничениями может приводить к решению, в котором все веса имеют максимальную величину, |w₁|=|w₂|=α.

Правило Хебба с субтрактивной нормализацией, определенное уравнением (7), может поддерживать общую сумму весов постоянной, то есть w₁+w₂=α. Это ограничение может изображать прямую линию 206, проходящую через (α, 0) и (0, α) на плоскости (w₁; w₂), как проиллюстрировано на фиг. 2B. Проиллюстрированы два ограничения: линия 206 может быть ассоциирована с отрицательными весами, а еще одна линия 208 может быть ассоциирована с двухполярными весами. Возможные асимптотические решения помечены с помощью 210. Субтрактивная нормализация типично может применяться к неотрицательным весам, в каком случае α>0, и веса ограничены в нуле, то есть w₁≥0 и w₂≥0. Асимптотическими решениями могут быть (α, 0) и (0, α), которые оба являются разреженными. Если весам предоставлена возможность менять свой знак, то асимптотические решения могут быть неограниченными до тех пор, пока ограничения не применяются принудительно. Если максимальная величина веса ограничена в α, то асимптотическими решениями могут быть (-α, α) и (α, -α), которые оба являются неразреженными.

Для приближения первого порядка правило Оджа, определенное уравнением (9), может разбиваться на Хеббов член (первый член в круглых скобках уравнения (9)) и член ограничения (второй член в круглых скобках уравнения (9)). Хеббов член может максимизировать выходной сигнал y при условии, что начальный выходной сигнал y положителен, а второй член может накладывать ограничение w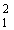

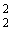
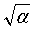
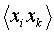
+w =α на асимптотическое решение. Это ограничение может изображать окружность 212 с радиусом в плоскости (w₁; w₂), как проиллюстрировано на фиг. 2C. Асимптотическое решение (w₁(∞); w₂(∞)) может быть найдено в качестве точки, в которой линия 214 решений, определенная уравнением (17), является касательной к окружности 212. Как может наблюдаться на фиг. 2C, может быть невозможным получать разреженное решение с помощью правила Оджа за исключением x₁=0 или x₂=0. Более скрупулезный анализ может показать, что правило Оджа может сходиться к главному собственному вектору ковариационной матрицы данных, C, с C_ik= .

Некоторые аспекты настоящего раскрытия поддерживают локальное правило обучения, определенное уравнением (10), которое может накладывать асимптотическое ограничение |w₁|+|w₂|=α. Это ограничение может изображать ромб 216 со всеми сторонами, равными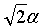

на плоскости (w₁;w₂), как проиллюстрировано на фиг. 2D. Асимптотическое решение (w₁(∞);w₂(∞)) может быть найдено перемещением линии 218 решений, определенной уравнением (17), в направлении увеличения выходного сигнала y до тех пор, пока она не прикасается к ромбу 216 только в одной точке, которая всегда бывает одной из вершин за исключением |x₁|=|x₂|. Поэтому для подавляющего большинства входных сигналов предложенное правило может давать разреженное решение (то есть один из двух весов может быть нулевым).

В общем случае N входных весов правило, определенное уравнением (10), теоретически может сходиться к решению всего лишь с одним ненулевым весом величины α. Может быть желательным предоставлять весовому вектору возможность иметь больше, чем один ненулевой элемент. Для достижения такового верхний предел на каждой величине веса, w_max, может накладываться из условия, чтобы w_max<α, где α/w_max может быть целевым значением для счета ненулевых элементов в w. В аспекте выбор α может быть произвольным. Однако если всем входным сигналам и выходным сигналам в сети требуется находиться в пределах одних и тех же границ (например, x_i∈[−1; 1] и y∈[−1; 1]), то надлежащим значением для α может быть единица. В этом случае единственными входными параметрами, требуемыми для правила обучения, могут быть скорость обучения,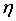

, и предел величины веса, w_max≤1.

Правило с ограничением L₀, определенное уравнением (16), также может принудительно применяться для сохранения входных сигналов и выходных сигналов сети в пределах одних и тех же границ посредством ограничения максимальной величины веса до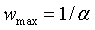

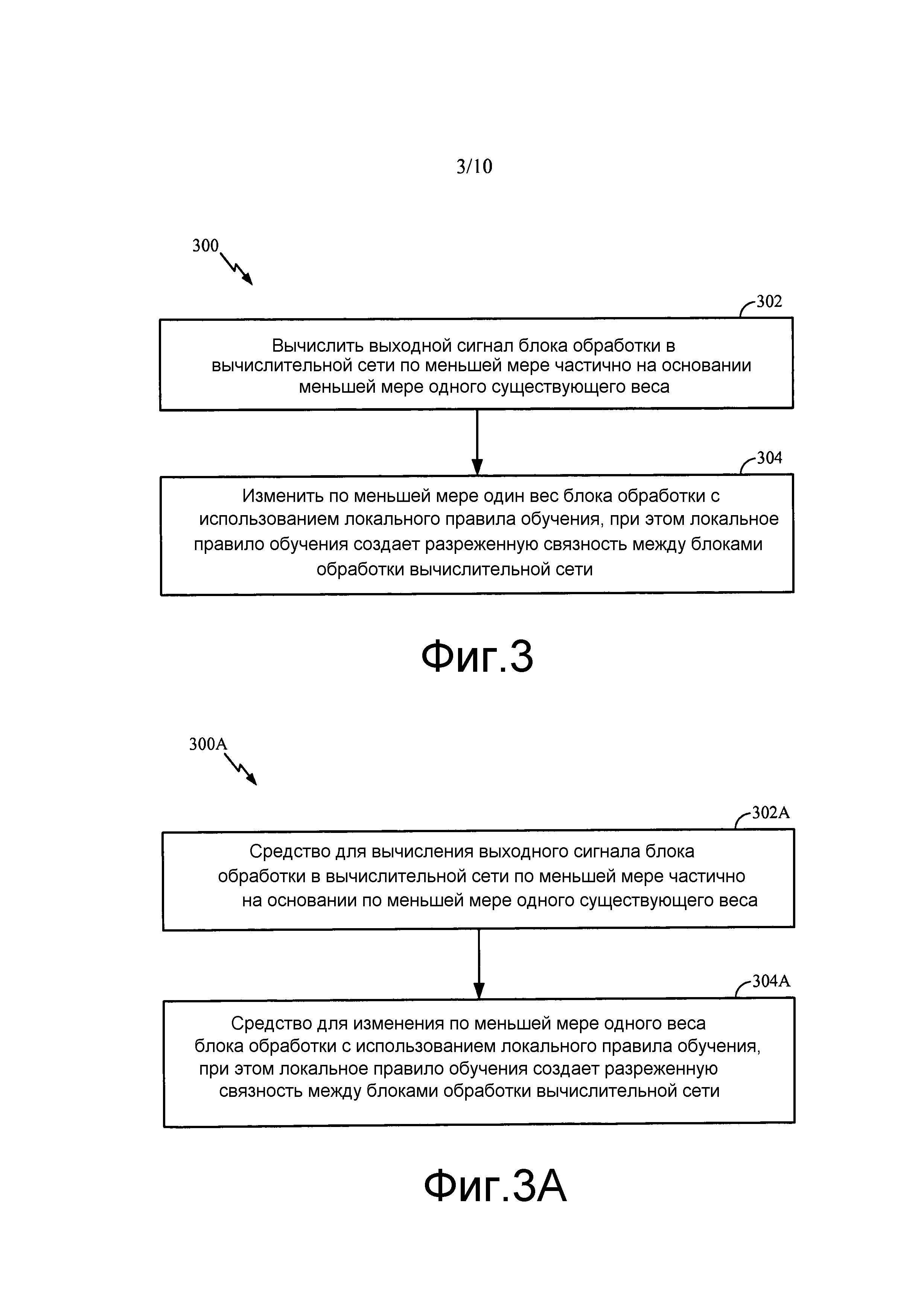
, где α - количество ненулевых элементов в каждом весовом векторе.

Фиг. 3 иллюстрирует примерные операции 300 для обучения вычислительной сети (нейронной сети) в соответствии с аспектами настоящего раскрытия. На 302 выходной сигнал блока обработки (нейрона) в вычислительной сети может вычисляться по меньшей мере частично на основании по меньшей мере одного существующего веса. На 304 по меньшей мере один вес блока обработки может изменяться с использованием локального правила обучения, при этом локальное правило обучения может создавать разреженную связность между блоками обработки вычислительной сети.

В соответствии с некоторыми аспектами настоящего раскрытия изменение по меньшей мере одного веса с использованием локального правила обучения может содержать обновление по меньшей мере одного веса на основании по меньшей мере одного из: одного или более входных сигналов в блоке обработки, выходного сигнала или по меньшей мере одного существующего веса до изменения. Согласно некоторым вариантам осуществления разреженная связность может создаваться после множественного обновления по меньшей мере одного веса.

Для демонстрации некоторых вариантов осуществления настоящего раскрытия правило обучения, определенное уравнением (10), и его отличие от других правил могут использоваться для обучения весов прямой связи в модели нейронной сети первичной зрительной коры (V1). Сеть может состоять из четырех двухмерных слоев: фоторецепторов, относящихся к сетчатке нервных клеток (RGC), простых клеток (S1) V1 и сложных клеток (C1) V1. Фоторецепторы могут отображаться 1:1 в пиксели входного изображения. Каждый фоторецептор может кодировать яркость соответствующего пикселя в диапазоне [-1, 1]. Выходные сигналы фоторецепторов могут подаваться в ретиноскопически отображенные RGC через связи постоянного веса, выполняющие пространственную фильтрацию входного изображения с помощью разности гауссианов (DoG).

Выходной сигнал каждого RGC может рассчитываться в качестве линейной суммы взвешенных входных сигналов. Он может быть положительным, отрицательным или нулевым. Такая RGC может объединять клетки ON (включения) и OFF (выключения) с одними и теми же входными весами противоположной полярности. Ее выходной сигнал может быть равен разности соответствующих выходных сигналов клетки ON и клетки OFF. Выходные сигналы RGC могут подаваться в простые клетки через адаптивные двухполярные веса, которые могут моделировать разность между весами из соответствующих клеток ON и OFF. Эти веса RGC-в-S1 могут определять рецептивные поля простых клеток. Слой S1 также может иметь поперечные связи с возбуждением ближнего действия и торможением дальнего действия. Эти поперечные связи могут помогать простым клеткам самоорганизовываться в отображение ориентации с цевочными колесами и линейными зонами. Каждая простая клетка S1 может моделироваться в качестве суммы взвешенных входных сигналов, проведенных через полупериодный выпрямитель, который может сохранять положительную часть выходного сигнала и отсекать отрицательную часть до нуля. Положительные выходные сигналы S1 могут подаваться в C1 через адаптивные положительные веса.

Прежде всего, связи RGC-в-S1 обучались с использованием четырех правил: правила Хебба с субтрактивной нормализацией, определенного уравнением (7), правила Оджа, определенного уравнением (9), предложенного локального правила обучения, определенного уравнением (10) и модифицированного локального правила обучения, определенного согласно (16). Все четыре правила могут приводить к ограничению весов, при этом обучаемые веса могут ограничиваться диапазоном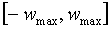

.

Фиг. 4A-4D иллюстрируют примеры выявленных весовых матриц RGC-в-S1, в которых заполненные окружности представляют собой положительные веса (область ON), а пустые окружности представляют собой отрицательные веса (область OFF). Диаметр окружности может быть пропорциональным величине веса. Веса могут обучаться посредством четырех вышеупомянутых правил с ограничением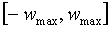

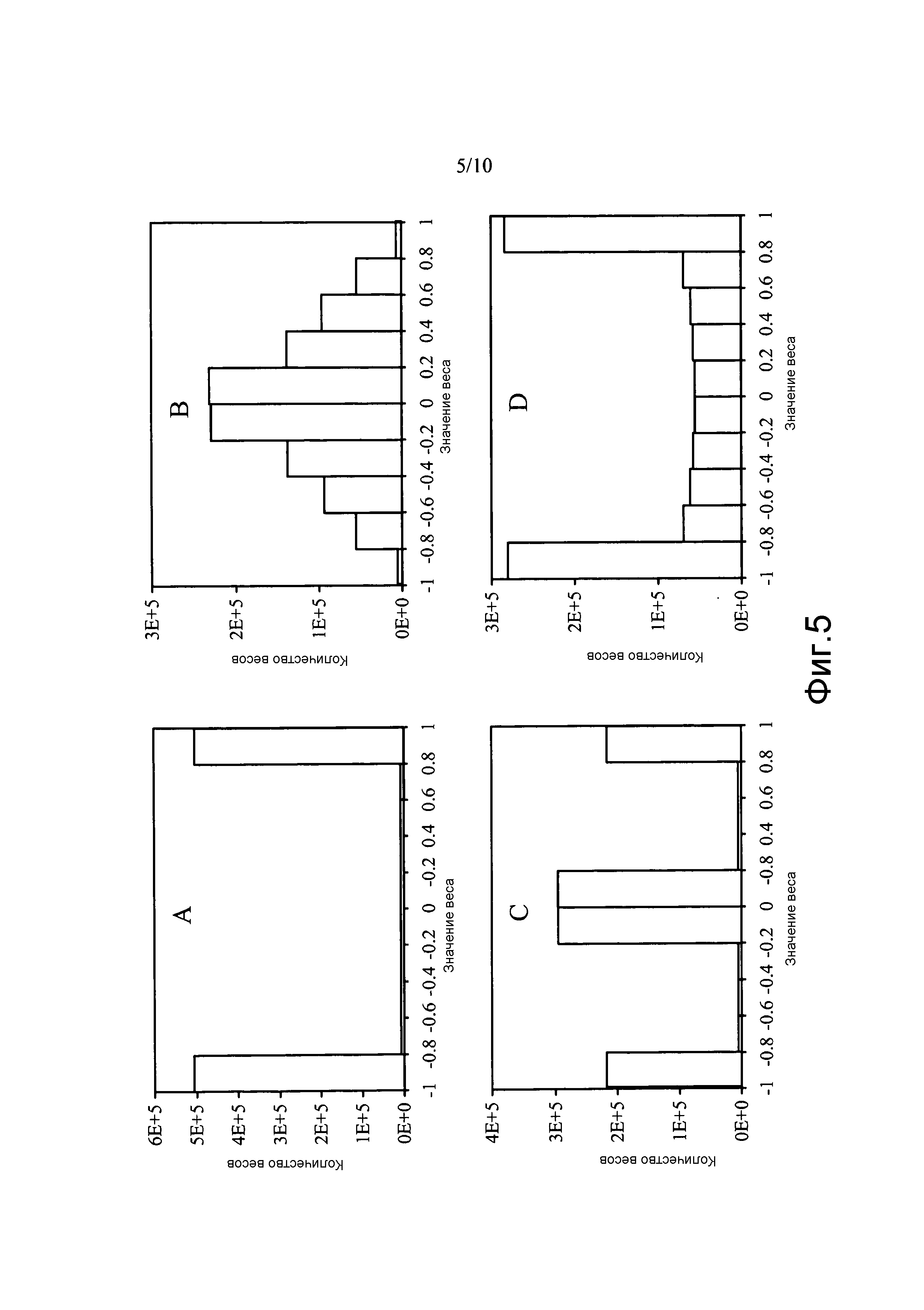
. Фиг. 4A иллюстрирует веса, обученные посредством правила Хебба с субтрактивной нормализацией. Фиг. 4B иллюстрирует веса, обученные посредством правила Оджа. Фиг. 4C иллюстрирует веса, обученные посредством правила, определенного уравнением (10) с ограничением L₁. Фиг. 4D иллюстрирует веса, обученные посредством правила с ограничением L₀, определенным уравнением (16).

Фиг. 5A-5D иллюстрируют соответствующие распределения всех весов RGC-в-S1. Как проиллюстрировано на фиг. 5A, правило Хебба с субтрактивной нормализацией может сходиться к весам максимальной величины. Правило Оджа, проиллюстрированное на фиг. 5B, может сходиться к градуированным весам, некоторые из которых могут иметь малые, но ненулевые значения. Предложенное правило, определенное уравнением (10), проиллюстрированным на фиг. 5C, может сходиться к весовой матрице с вполне определенными областями ON и OFF и многим, близким к нулю элементам. Правило, определенное уравнением (16), проиллюстрированным на фиг. 5D, может претерпевать неудачу в том, чтобы сходиться к разреженной весовой матрице вследствие деления на w_i, которое может заставлять малые веса колебаться около нуля. Может быть невозможным получать в точности нулевые веса без ограничения нулем ни в каком из правил. Поэтому для оценки разрежения весовых матриц могут подсчитываться веса, которые являются нулевыми в пределах выбранной ошибки округления. С ошибкой округления 0:01w_max, приблизительно 54% весов RGC-в-S1, обученных посредством предложенного правила, определенного уравнением (10), могут быть нулевыми, тогда как могут быть нулевыми менее чем 3% весов, обученных посредством других трех правил.

Фиг. 6A-6D иллюстрируют те же самые четыре правила, используемых для обучения связей S1-в-C1. На этот раз каждое правило может иметь добавочное ограничение весов до [0, w_max]. Фрагмент слоя S1 проиллюстрирован на фиг. 6A-6D, которые показывают двухмерную компоновку простых клеток в качестве графика изоориентированных контуров их предпочтительных ориентаций (значения над контурами представляют собой предпочтительные ориентации простых клеток, расположенных под этими контурами). Прямоугольники 602, 604, 606, 608 могут очерчивать пул клеток S1, чьи выходные сигналы могут подаваться в одну и ту же сложную клетку. Пустые окружности 612, 614, 616, 618 внутри прямоугольников могут указывать силы связи из этих простых клеток в выбранную сложную клетку: чем больше окружность, тем больше вес. Фиг. 6A иллюстрирует веса, обученные посредством правила Хебба с субтрактивной нормализацией. Фиг. 6B иллюстрирует веса, обученные посредством правила Оджа. Фиг. 6C иллюстрирует веса, обученные посредством правила, определенного уравнением (10) с ограничением L₁. Фиг. 6D иллюстрирует веса, обученные посредством правила, определенного уравнением (16) с ограничением L₀.

Фиг. 7A-7D иллюстрируют соответствующие распределения всех весов S1-в-C1. На фиг. 7A может наблюдаться, что правило Хебба с субтрактивной нормализацией может создавать разреженную связность S1-в-C1 вследствие нулевой нижней границы. Фиг. 7B иллюстрирует, что правило Оджа создает связи переменной длины со всеми простыми ячейками внутри прямоугольника, даже с теми, которые с ортогональными ориентациями. Согласно некоторым аспектам настоящего раскрытия, как проиллюстрировано на фиг. 7C, предложенное локальное правило обучения, определенное уравнением (10), может создавать сильные связи с простыми клетками сходных ориентаций и связи нулевой силы с простыми клетками других ориентаций, что может быть совместимым с биологическими данными избирательных по ориентации и инвариантных к смещению сложных клеток. Правило обучения, определенное уравнением (16), как проиллюстрировано на фиг. 7D, также может создавать разреженную связность S1-в-C1, обусловленную отсечением отрицательных весов по нулю.

Фиг. 8 иллюстрирует примерную программную реализацию 800 вышеупомянутого локального правила обучения с использованием процессора 802 общего назначения, в соответствии с некоторыми аспектами настоящего раскрытия. Существующие веса, ассоциированные с каждым блоком обработки (нейроном) вычислительной сети (нейронной сети), могут храниться в блоке 804 памяти, тогда как команды, имеющие отношение к локальному правилу обучения, приводимые в исполнение на процессоре 802 общего назначения, могут загружаться из памяти 806 программ. Согласно некоторым аспектам настоящего раскрытия загруженные команды могут содержать код для вычисления выходного сигнала каждого блока обработки в вычислительной сети по меньшей мере частично на основании по меньшей мере одного существующего веса, хранимого в блоке 804 памяти. Кроме того, загруженные команды могут содержать код для изменения по меньшей мере одного веса такого блока обработки согласно локальному правилу обучения, при этом локальное правило обучения может создавать разреженную связность между блоками обработки вычислительной сети. В аспекте настоящего раскрытия код для изменения по меньшей мере одного веса такого блока обработки может содержать код для обновления по меньшей мере одного веса на основании по меньшей мере одного из: одного или более входных сигналов в таком блоке обработки, вычисленного ранее выходного сигнала или по меньшей мере одного существующего веса до изменения. Обновленные веса могут сохраняться в блоке 804 памяти, заменяя старые веса.

Фиг. 9 иллюстрирует примерную реализацию 900 вышеупомянутого локального правила обучения, где память 902 весов сопряжена посредством сети 904 взаимосвязей с отдельными блоками 906 (распределенной) обработки (нейронами) вычислительной сети (нейронной сети) в соответствии с некоторыми аспектами настоящего раскрытия. По меньшей мере один существующий вес, ассоциированный с блоком 906 обработки, может загружаться из памяти 902 через соединение(я) сети 904 межсоединений в такой блок 906 обработки. Блок 906 обработки может быть выполнен с возможностью вычислять свой выходной сигнал по меньшей мере частично на основании по меньшей мере одного существующего веса. Кроме того, блок 906 обработки может быть выполнен с возможностью изменять по меньшей мере один вес, ассоциированный с таким блоком обработки, согласно локальному правилу обучения, при этом локальное правило обучения может создавать разреженную связность между блоками 906 обработки вычислительной сети. В аспекте настоящего раскрытия изменение по меньшей мере одного веса согласно локальному правилу обучения дополнительно может содержать обновление по меньшей мере одного веса на основании по меньшей мере одного из: одного или более входных сигналов в блоке 906 обработки, вычисленного ранее выходного сигнала блока 906 обработки или по меньшей мере одного существующего веса до изменения. Обновленные веса могут сохраняться в памяти 904, заменяя старые веса, ассоциированные с таким блоком 906 обработки.

Фиг. 10 иллюстрирует примерную реализацию 1000 вышеупомянутого локального правила обучения, основанную на распределенной памяти 1002 весов и распределенных блоков 1004 обработки, в соответствии с некоторыми аспектами настоящего раскрытия. Как проиллюстрировано на фиг. 10, один банк 1002 памяти весов может сопрягаться непосредственно с одним блоком 1004 обработки (нейроном) вычислительной сети (нейронной сети), при этом такой банк 1002 памяти может хранить по меньшей мере один существующий вес, ассоциированный с таким блоком 1004 обработки. Блок 1004 обработки может быть выполнен с возможностью вычислять свой выходной сигнал по меньшей мере частично на основании по меньшей мере одного существующего веса, загруженного из соответствующего банка 1002 памяти весов. Кроме того, блок 1004 обработки может быть выполнен с возможностью изменять по меньшей мере один вес, ассоциированный с таким блоком обработки, согласно локальному правилу обучения, при этом локальное правило обучения может создавать разреженную связность между блоками 1004 обработки вычислительной сети. В аспекте настоящего раскрытия изменение по меньшей мере одного веса блоком 1004 обработки согласно локальному правилу обучения дополнительно может содержать обновление по меньшей мере одного веса на основании по меньшей мере одного из: одного или более входных сигналов в блоке 1004 обработки, вычисленного ранее выходного сигнала блока 1004 обработки или по меньшей мере одного существующего веса до изменения. Обновленные веса могут сохраняться в соответствующем банке 1002 памяти, заменяя старые веса.

Согласно аспектам настоящего раскрытия предложенное правило обучения может ограничивать норму L1 входного весового вектора нейрона в точке равновесия. Правило обучения может быть локальным и собственным, что может делать реализации аппаратных средств и программного обеспечения более простыми. Это правило может сходиться к более разреженному весовому вектору, чем обучаемый, посредством исходного правила Оджа с или без ограничения нулем. Такая разреженная связность может приводить к более высокой избирательности нейронов к определенным признакам, которые могут обнаруживаться в многих биологических исследованиях. Еще одним преимуществом ограничения нормы L1 вместо нормы L2 может быть простота сохранения входных сигналов и выходных сигналов в сети в пределах одних и тех же границ посредством выбора α=1.

Различные операции способов, описанных выше, могут выполняться любым пригодным средством, способным к выполнению соответствующих функций. Средство может включать в себя различные компонент(ы) и/или модуль(и) аппаратных средств и/или программного обеспечения, в том числе, но не в качестве ограничения, схему, специализированную интегральную схему (ASIC) или процессор. В целом, в тех случаях, когда есть операции, проиллюстрированные на фигурах, такие операции могут иметь соответствующие аналогичные компоненты «средство плюс функция» с подобной нумерацией. Например, операции 300, проиллюстрированные на фиг. 3, соответствуют компонентам 300A, проиллюстрированным на фиг. 3A.

При использовании в материалах настоящей заявки термин «определение» охватывает широкое многообразие действий. Например, «определение» может включать в себя расчет, вычисление, обработку, выведение, изучение, отыскивание (например, отыскивание в таблице, базе данных или другой структуре данных), выявление и тому подобное. К тому же «определение» может включать в себя прием (например, прием информации), осуществление доступа (например, осуществление доступа к данным в памяти) и тому подобное. К тому же «определение» может включать в себя принятие решения, отбор, выбор, создание и тому подобное.

При использовании в материалах настоящей заявки фраза, упоминающая «по меньшей мере один из» списка элементов, указывает на любую комбинацию таких элементов, в том числе одиночные элементы системы. В качестве примера, «по меньшей мере одно из: a, b или c» подразумевается охватывающим: a, b, c, a-b, a-c, b-c и a-b-c.

Различные операции способов, описанных выше, могут выполняться любым пригодным средством, способным к выполнению операций, таким как различные компонент(ы), схема(ы) и/или модуль(и) аппаратных средств и/или программного обеспечения. Вообще, любые операции, проиллюстрированные на фигурах, могут выполняться соответствующим функциональным средством, способным к выполнению операций.

Различные иллюстративные логические блоки, модули и схемы, описанные в связи с настоящим раскрытием, могут быть реализованы или выполнены с помощью процессора общего назначения, цифрового сигнального процессора (DSP), специализированной интегральной схемы (ASIC), сигнального устройства программируемой пользователем вентильной матрицы (FPGA) или другого программируемого логического устройства (PLD), дискретной вентильной или транзисторной логики, дискретных компонентов аппаратных средств или любой их комбинации, предназначенной для выполнения функций, описанных в материалах настоящей заявки. Процессором общего назначения может быть микропроцессор, но в альтернативном варианте процессор может быть доступным для коммерческого приобретения процессором, контроллером, микроконтроллером или конечным автоматом. Процессор также может быть реализован в виде комбинации вычислительных устройств, например комбинации DSP и микропроцессора, множества микропроцессоров, одного или более микропроцессоров вместе с DSP-ядром, или любой другой такой конфигурации.

Этапы способа или алгоритма, описанные в связи с настоящим раскрытием, могут быть воплощены непосредственно в аппаратных средствах, в модуле программного обеспечения, выполняемом процессором, или в комбинации этих двух. Модуль программного обеспечения может находиться на любом виде запоминающего носителя, который известен в данной области техники. Некоторые примеры запоминающих носителей, которые могут использоваться, включают в себя оперативное запоминающее устройство (RAM), постоянное запоминающее устройство (ROM), флэш-память, память EPROM, память EEPROM, регистры, жесткий диск, съемный диск, CD-ROM и так далее. Модуль программного обеспечения может содержать одиночную команду или многочисленные команды и может быть распределен по нескольким разным кодовым сегментам, среди разных программ и по многочисленным запоминающим носителям. Запоминающий носитель может быть присоединен к процессору из условия, чтобы процессор мог считывать информацию с и записывать информацию на запоминающий носитель. В альтернативном варианте запоминающий носитель может быть составляющим одно целое с процессором.

Способы, раскрытые в материалах настоящей заявки, содержат один или более этапов или действий для выполнения описанного способа. Этапы и/или действия способа могут взаимно заменяться друг другом, не выходя из объема формулы изобретения. Другими словами, пока не предписан определенный порядок этапов или действий, порядок и/или использование отдельных этапов и/или действий могут модифицироваться, не выходя из объема формулы изобретения.

Описанные функции могут быть реализованы в аппаратных средствах, программном обеспечении, программно-аппаратных средствах или любой их комбинации. Если реализованы в программном обеспечении, функции могут храниться или передаваться в качестве одной или более команд или кода на компьютерно-читаемом носителе. Компьютерно-читаемые носители включают в себя как компьютерные запоминающие носители, так и среду связи, в том числе любой носитель, который содействует передаче компьютерной программы из одного места в другое. Запоминающий носитель может быть любым имеющимся в распоряжении носителем, к которому может осуществляться доступ компьютером. В качестве примера, а не ограничения, такие компьютерно-читаемые носители могут содержать RAM, ROM, EEPROM, CD-ROM или другое оптическое дисковое запоминающее устройство, магнитное дисковое запоминающее устройство или другие магнитные устройства хранения данных, либо любой другой носитель, который может использоваться для переноса или хранения требуемого кода в виде команд или структур данных, и к которым может осуществляться доступ компьютером. К тому же любое соединение, по сути, выражается компьютерно-читаемым носителем. Например, если программное обеспечение передается с интернет-сайта, сервера или из другого удаленного источника с использованием коаксиального кабеля, волоконно-оптического кабеля, витой пары, цифровой абонентской линии (DSL) или беспроводных технологий, таких как инфракрасная (IR), радиочастотная и микроволновая, то коаксиальный кабель, волоконно-оптический кабель, витая пара, DSL или беспроводные технологии, такие как инфракрасная, радиочастотная и микроволновая, включены в определение носителя. Термин «диск», при использовании в материалах настоящей заявки, включает в себя компакт-диск (CD), лазерный диск, оптический диск, цифровой многофункциональный диск (DVD), гибкий магнитный диск и диск Blu-ray^®, причем магнитные диски обычно воспроизводят данные магнитным образом, тогда как оптические диски воспроизводят данные оптически с помощью лазеров. Таким образом, в некоторых аспектах компьютерно-читаемые носители могут содержать постоянные компьютерно-читаемые носители (например, материальные носители). В дополнение, что касается других аспектов, компьютерно-читаемые носители могут содержать временные компьютерно-читаемые носители (например, сигнал). Комбинации приведенного выше также должны быть включены в объем компьютерно-читаемых носителей.

Таким образом, некоторые аспекты могут содержать компьютерный программный продукт для выполнения операций, представленных в материалах настоящей заявки. Например, такой компьютерный программный продукт может содержать компьютерно-читаемый носитель, содержащий команды, сохраненные (и/или закодированные) на нем, причем команды исполняются одним или более процессорами для выполнения операций, описанных в материалах настоящей заявки. В некоторых аспектах компьютерный программный продукт может включать в себя упаковочный материал.

Программное обеспечение или команды также могут передаваться через среду передачи. Например, если программное обеспечение передается с веб-сайта, сервера или другого удаленного источника с использованием коаксиального кабеля, волоконно-оптического кабеля, витой пары, цифровой абонентской линии (DSL) или беспроводных технологий, таких как инфракрасная, радиочастотная и микроволновая, то коаксиальный кабель, волоконно-оптический кабель, витая пара, DSL или беспроводные технологии, такие как инфракрасная, радиочастотная и микроволновая, включены в определение среды передачи.

Кроме того, должно быть принято во внимание, что модули и/или другие надлежащие средства для выполнения способов и технологий, описанных в материалах настоящей заявки, могут загружаться и/или иным образом получаться пользовательским терминалом и/или базовой станцией, как применимо. Например, такое устройство может быть присоединено к серверу для содействия передаче средства для выполнения способов, описанных в материалах настоящей заявки. В качестве альтернативы различные способы, описанные в материалах настоящей заявки, могут поставляться через средство хранения (например, RAM, ROM, физический запоминающий носитель, такой как компакт-диск (CD) или гибкий магнитный диск, и т.д.) из условия, чтобы пользовательский терминал и/или базовая станция могли получать различные способы при присоединении или установке средства хранения в устройство. Более того, может использоваться любая другая пригодная технология для поставки способов и технологий, описанных в материалах настоящей заявки, на устройство.

Должно быть понятно, что формула изобретения не ограничена точной конфигурацией и компонентами, проиллюстрированными выше. Различные модификации, изменения и варианты могут быть произведены в компоновке, работе и деталях способов и устройства, описанных выше, не выходя из объема формулы изобретения.

Несмотря на то что вышеизложенное направлено на аспекты настоящего раскрытия, другие и дополнительные аспекты раскрытия могут быть придуманы, не выходя из его основного объема, а его объем определен формулой изобретения, которая следует далее.

Реферат

Группа изобретений относится к нейронным системам и может быть использована для локального правила состязательного обучения, которое дает в результате разреженную связность среди блоков обработки сети. Техническим результатом является повышение эффективности обучения вычислительной сети. Способ содержит этапы, на которых: вычисляют выходной сигнал блока обработки в вычислительной сети по меньшей мере частично на основании по меньшей мере одного существующего веса и изменяют по меньшей мере один вес блока обработки с использованием локального правила обучения, при этом локальное правило обучения создает разреженную связность между блоками обработки вычислительной сети посредством ограничения нормы весового вектора, содержащего веса, ассоциированные со связями между блоком обработки, до заданного значения. 4 н. и 56 з.п. ф-лы, 11 ил.

Формула