Способ оценивания очковой линзы, способ проектирования очковой линзы и способ изготовления очковой линзы - RU2511711C2

Чертежи

Показать все 27 чертежа(ей)

Описание

Область техники, к которой относится изобретение

Настоящее изобретение относится к способу оценивания очковых линз, при этом способ используют для оценивания характеристик, когда очковые линзы проектируют или изготавливают, и к способу проектирования очковых линз, и способу изготовления очковых линз с использованием его.

Уровень техники

Для оценивания или проектирования очковых линз были предложены различные способы оценивания и способы проектирования, обеспечивающие получение оптимальной видимости, и, в частности, предложен способ, в котором основное внимание обращено на зрение в состоянии ношения очковых линз. Упомянем, например, патентный документ 1 (опубликованная рассмотренная заявка №НЕ102-39767В на патент Японии (предварительная публикация №SHO57-10113A патента Японии)), патентный документ 2 (публикация №2008-511033А нерассмотренной заявки на патент Японии (перевод заявки РСТ)) и патентный документ 3 (публикация №2000-506628А нерассмотренной заявки на патент Японии (перевод заявки РСТ)), в которых рассматривается видимость левым и правым глазами при ношении пары очковых линз. Кроме того, например, в патентном документе 4 (предварительная публикация №НЕ101-221722А патента Японии), непатентном документе 9 (Bernard et al., “Traps in displaying optical performances of a progressive-addition lens”, Applied Optic, vol.31, №19 (1992), pp.3586-3593) и непатентном документе 10 (“Handbook of Visual Information Processing”, Edited by the Vision Society of Japan, Asakura Publishing Co., Ltd. (2000), p.285, фиг.7.1) нет упоминания относительно бинокулярного зрения, однако описаны конкретные примеры оптических систем, в которых представлено относительное положение предмета, очковой линзы и глазного яблока.

Для прояснения проблем сначала рассмотрим примеры из патентных документов 1-3, которые относятся к улучшению бинокулярного зрения с помощью очков.

Изобретение, описанное в патентном документе 1, представляет собой прорывное изобретение в части подхода к бинокулярной функции. В патентном документе 1 описано необходимое условие, при выполнении которого реализуется бинокулярная функция. А именно, рассмотрены диапазон астигматизма в монотонно расширяющейся полосе, классификация астигматизма и ошибка юстировки по всей линзе, диапазоны призматических действий левой и правой очковых линз и условие относительно направлений перекосов изображения, наводимых призматическими действиями. Однако, если сделать переоценку, исходя из современного уровня изобретение, описанное в патентном документе 1, имеет несколько серьезных недостатков.

Во-первых, вычисление аберрации линии фиксации, проходящей от линзы, выполняется без учета закона Листинга для одного глаза, в соответствии с которым происходит основное движение глазного яблока. В этом случае результат вычисления остаточного астигматизма становится неопределенным и нельзя сказать, что достигается определенный результат, описанный в документе. Кроме того, движение глазного яблока одного глаза можно рассматривать как вращательное движение, выполняемое при центрировании относительно одной точки в глазном яблоке, то есть относительно центра поворота. Фронтальную плоскость, включающую в себя центр поворота на месте, от которого взгляд глазного яблока направлен вперед, называют поверхностью Листинга. В соответствии с законом основных движений глазного яблока ось поворота лежит на поверхности Листинга, и этот закон называют законом Листинга.

Во-вторых, написано, что прогрессивные участки левой и правой линз находятся в пределах диапазонов призматических действий линз и что получаются почти одинаковые астигматизмы и ошибки юстировки, и нарушения фокусировки являются одинаковыми, следовательно, стереоскопическое зрение (оно представляет собой бинокулярное зрение) является хорошим. Однако в патентном документе 1 не показано, что баланс астигматизмов и ошибок юстировки является хорошим для стереоскопического зрения, и не доказана количественно пригодность линз. В связи с этим остается неясным, каким образом конфигурированы очковые линзы, описанные в патентном документе 1.

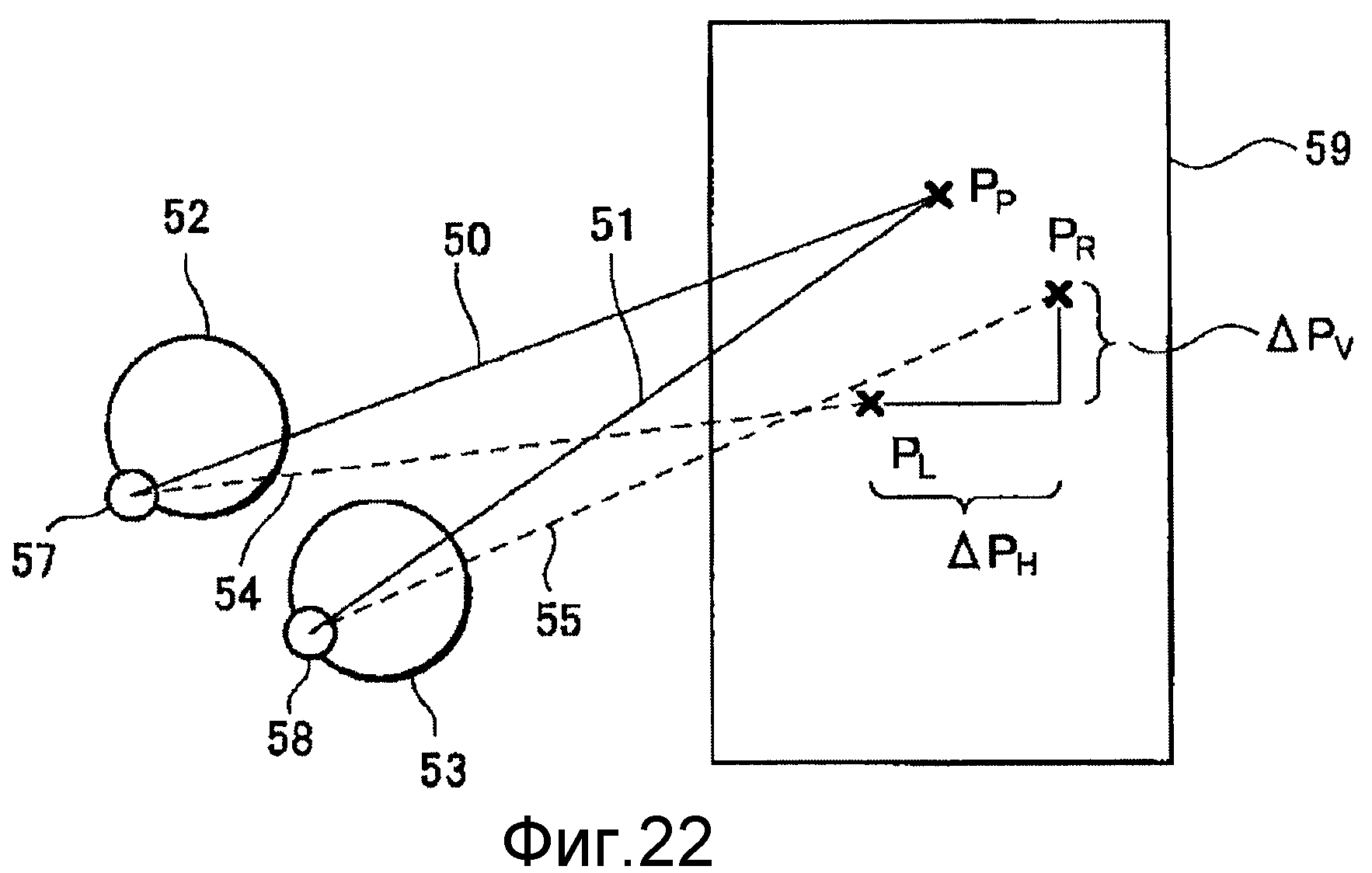
В-третьих, в строках 25-44 на странице 5 патентного документа 1 пояснение фиг.2 из документа представлено не для оптической системы, предназначенной для бинокулярного зрения. Эта фигура показана как фиг.22 настоящей заявки. Когда на фиг.22 глазные яблоки 57 и 58 обращены прямо на точку Р_Р на предметной поверхности 59, зрительные оси 50 и 51 направлены к точке Р_Р. Очковые линзы 52 и 53 расположены перед глазными яблоками 57 и 58. Вследствие призменного действия очковых линз 52 и 53 левый глаз 57 видит, что точка Р_Р помещена в точке P_L пересечения зрительной оси 54 и поверхности 59, и правый глаз 58 видит, что точка Р_Р помещена в точке P_R пересечения. В строках 41-42 на той же странице описано, что зависимость между зрительными осями, показанными на фиг.22, может быть найдена, когда одна очковая линза является симметричной относительно главного меридиана. Однако, как можно видеть из формулы Прентиса, (P=(h×D)/10), призматическое действие пропорционально преломляющему действию. Поэтому это утверждение справедливо для линз только в случае, когда левая и правая линза являются идентичными.

Кроме того, формула Прентиса является приближенной формулой, которая является достаточной при обычном использовании, и это означает, что призматическое действие Р линзы пропорционально расстоянию h (в миллиметрах) от центра и преломляющему действию D (дптр). Вкратце, поскольку оптические рефракции левой линзы и правой линзы обычно различаются, описанное выше утверждение не является очевидным и не является установленным. Кроме того, после пояснения фиг.2 в патентном документе 1 дальнейшие пояснения на протяжении всего документа основаны на одной линзе из левой линзы и правой линзы без задания системы координат и начала координат, которыми точно определяется точка Р_Р объекта. Поэтому конфигурация непригодна для оптической системы, предназначенной для выполнения бинокулярной функции.

В-четвертых, протяженность дисторсии, показанная на фиг.4 патентного документа 1, является трудной для понимания. Эта фигура показана как фигура 23 в настоящей заявке. В патентном документе 1 пояснение имеется в строке 17 в правом столбце на странице 5, где поясняется, что на фигуре представлено изображение эквидистантной и симметричной решетки. Фиг.23 представляет собой фигуру, на которой связанные с положением разности в горизонтальном направлении изображены относительно точки Р_Р, тогда как точка сетки решетки на поверхности расположена в точке Р_Р. Можно видеть, что сетка особенно искажена на нижнем периферийном участке. В строках 25-27 в том же столбце патентного документа 1 поясняется, что здесь имеется седлообразная дисторсия или бочкообразная дисторсия. То есть в патентном документе 1 указывается, что имеется зависимость между связанными с положением разностями ΔР_Н в горизонтальном направлении и дисторсией. В предположении, что имеется зависимость между связанными с положением разностями ΔР_Н в горизонтальном направлении и дисторсией, решетка искажается в случае, когда все линии 54 и 55 зрения имеют иные точки пересечения, а не точку Р_Р на поверхности 59. Однако поскольку в этом случае связанные с положением разности в горизонтальном направлении равны 0, возникает противоречие, заключающееся в том, что фиг.23 становится фигурой, на которой нет искажений. Следовательно, зависимость между связанными с положением разностями ΔР_Н в горизонтальном направлении и дисторсией отсутствует. Кроме того, описывается, что искаженная фигура обрабатывается в мозгу как изображение, образованное прямыми линиями. Однако не описано исходное положение относительно возможности обработки фигуры как образованной линиями, когда фигура искажена, хотя это является важным вопросом. Поэтому невозможно определенно понять, исключается или нет в мозгу дисторсия, показанная на фиг.23, с образованием прямых линий.

В-пятых, объект не находится на поверхности. По существу, объект произвольно определяется проектировщиком. Поэтому в общем случае очковые линзы проектируют так, чтобы характеристики очковых линз были более высокими для произвольного объекта, определяемого проектировщиком. Однако в патентном документе 1 способ оценивания ограничен объектами-кандидатами, адаптируемыми для очковых линз, при чтении букв в натянутой газете или на стене. В патентном документе 1 для точек в пределах объекта, за исключением точки фиксации, имеются большие различия в расстояниях от обоих глазных яблок. Поэтому становится трудно одновременно корректировать рефракционную ошибку на основании точки фиксации, остаточный астигматизм и призматическое действие линзы. Следовательно, призматическое действие линзы становится более значительным. Таким образом, в системе, в которой объект находится на поверхности, трудно оценивать бинокулярное зрение.

В патентном документе 2 предложен способ проектирования очковых линз. В способе проектирования рассматривается состояние, в котором направление вперед взгляда человека, носящего пару очковых линз, сдвигается в сторону ведущего глаза. Если сдвиг, описанный в патентном документе 1, является справедливым для зрения на малое расстояние, то это является представляющим интерес явлением и, конечно, должно быть изобретением, в котором используется физиологическое явление. Однако патентному документу 2 присущи проблемы, описываемые ниже.

Во-первых, измеряемым объектом является живой организм. Поэтому существует проблема точности измерения. В примере, описанном в абзаце 0030 патентного документа 2, сообщается, что сдвиг равен 2 см. Если он составляет 2 см, то его легко измерять, но если сдвиг меньше, становится трудно выполнять стабильное измерение. В абзаце 0063 патентного документа 2 описано, что он может быть измерен с «абсолютной ошибкой меньше или равной 3 мм». Однако с учетом того, что обычная величина смещения оптических центров для зрения на малое расстояние в прогрессивной линзе равна 2,5 мм, величина ошибки является очень большой.

Во-вторых, проблема заключается в том, что признак «направление взгляда вперед сдвигается в сторону ведущей линзы» противоречит закону равных иннерваций Геринга, который является единственным законом, относящимся к бинокулярным движениям глаз. Трудно улучшить бинокулярную функцию проектированием очковых линз с помощью измерения, которое основано на явлении, противоречащем закону равных иннерваций Геринга. При этом пояснение закона равных иннерваций Геринга можно найти в непатентном документе 8 (написанном Ryoji Osaka, Sachio Nakamizo, and Kazuo Koga, “Binocular Movement and Hering Theory, Experimental Psychology of eye movement”, The University of Nagoya Press (1993), Chapter 3, pp.60-61, написана Sachio Nakamizo). Теория Геринга, относящаяся к бинокулярному движению, состоит из гипотезы, заключающейся в том, что существуют иннервация содружественного поворота глазных яблок (ипсилатерального бинокулярного движения, которая создает бинокулярное движение, и иннервация вергенции (контралатерального бинокулярного движения), гипотезы равных иннерваций обоих глаз, которая означает равенство во всех случаях величин иннерваций, приданных соответствующим глазам (закон Геринга), и гипотезы аддитивности иннерваций, которая означает сохранение аддитивности между иннервациями двух типов.

Кроме того, это является особым мнением, известно, что центр поворота не фиксирован и во время движения глаза он движется, а также сдвигается. Например, в опубликованной, рассмотренной заявке №SHO42-9416B на патент Японии показано (в строках 16-21 на странице 4 в правом столбце), что центр поворота является таким, что он не перемещается при центрировании относительно единственной точки, а в зависимости от использования он перемещается при центрировании относительно различных точек. Утверждение «сдвиг направления взгляда вперед» в патентном документе 2 можно пояснить исходя из того факта, что центр поворота глазного яблока сам сдвигается. То есть при условии, что центры поворота перемещаются, средняя точка между центрами поворота левого и правого глазных яблок также перемещается и направление взгляда вперед также перемещается. Таким образом, считается, что предположение о симметричном движении левого и правого глазных яблок лучше соответствует физиологическому факту, чем предположение об асимметричном движении левого и правого глазных яблок, которое настойчиво утверждается в патентном документе 2.

В-третьих, в абзаце 0039 патентного документа 2 написано, что «достигается исключительная бинокулярная фузия». Однако степень ее не ясна. В частности, написано, что если наблюдается астигматизм (он считается остаточным астигматизмом), меньше или равный 0,5 дптр, то имеется комфортное поле зрения. Однако наблюдается рефракционная ошибка, зависящая от расстояния до объекта. Поэтому комфортное поле зрения не реализуется, за исключением случая, когда предполагается, что объект расположен на месте где рефракционная ошибка равна 0. В осуществлении патентного документа 2 показаны две фигуры, которые представляют собой график рефракционных ошибок и график имеющихся астигматизмов в зависимости от условий наблюдения. Однако об их балансе не упоминается. Поэтому без показа баланса или зависимости между рефракционной ошибкой и наблюдаемым астигматизмом трудно понять, можно ли получать комфортные поля зрения.

Кроме того, некорректно утверждать, что «бинокулярная фузия становится лучше» после показа на диаграммах только рефракционных ошибок и наблюдаемого астигматизма. Расстройства, при которых бинокулярное зрение нарушается даже в случае, если левый и правый глаза имеют хорошие зрительные способности, могут обнаруживаться у многих косоглазых пациентов. Обычное оценивание рефракционной ошибки и астигматизма, такое как оценивание в этом патентном документе 2, непригодно для характеристик, специфических для бинокулярного зрения.

В-четвертых, как и в случае патентного документа 1, предметом в этом патенте, как видно из фиг.1 или фиг.4 патентного документа 2, является поверхность. То есть можно привести положения, аналогичные изложенным в четвертом замечании, относящемся к патентному документу 1.

В патентном документе 3 раскрыт способ, касающийся очковой линзы так называемого панорамного типа, при этом линза выполнена криволинейной от передней стороны к задней стороне. Кроме того, на странице 13 или странице 15 патентного документа 3 имеются некоторые сведения относительно внеосевой призматической диспаратности. В этом документе в основном описаны недостатки, имеющие отношение к бинокулярному зрению, при этом бинокулярное зрение является основным тезисом патентного документа 3.

Во-первых, написано, что способ, раскрытый в патентном документе 3, является способом, касающимся очковой линзы панорамного типа или очковой линзы защитных очков. Однако конфигурации их неясны. В основной части изобретения, раскрытого в патентном документе 3, предполагается, что имеются предписанная область и периферийная височная область. Как описано на страницах 28-30 патентного документа 3, различие между этими двумя областями заключается в форме поверхностей. При этом способ пояснения различия не основан на оценивании результатов вычислений с прослеживанием луча, которые обычно используют в настоящее время, а представляет собой упрощенный способ, в соответствии с которым на основании формы вычисляют поверхность линзы и который использовали в прошлом для пояснения прогрессивной линзы. Поэтому сила рефракции и астигматизм являются производными величинами кривой, которая вычисляется по производным поверхности. Кроме того, отсутствует описание, касающееся движения глазного яблока в соответствии с законом Листинга, который в настоящее время обычно принимают во внимание при проектировании. Таким образом, имеется отличие от оценивания или проектирования, которое основано на физиологическом базисе, таком как закон Листинга. Кроме того, периферийная височная область является настолько произвольной, что отличие ее от предписанной области становится неясным. Таким образом, для периферийной височной области не сформулировано ограничивающее условие. Следовательно, можно считать, что описание является справедливым только для обычного проектирования линзы.

Во-вторых, что касается определения внеосевой призматической диспаратности, описанной в нижней части страницы 13 патентного документа 3, то там сказано только то, что «нарушение бинокулярного зрения возникает, когда астигматизм височной части и астигматизм носовой части не равны». Однако это описание является недостаточным и нельзя понять, каких астигматизмов это касается. Кроме того, что касается способа коррекции внеосевой призматической диспаратности, то имеется только указание на странице 14 патентного документа 3 на то, что асферическая поверхность является общепринятой. Таким образом, описание является недостаточным. Кроме того, хотя ясно, что оценивание выполняют относительно одной очковой линзы, на странице 13 патентного документа 3 имеется заключение о том, что «нарушение бинокулярного зрения отсутствует». Основание для этого заключения непонятно.

В-третьих, на странице 15 патентного документа 3 упомянуто о настройке силы рефракции, астигматизма и диспаратности призматического действия линзы и балансе элементов для оптической коррекции. Однако нельзя понять указание, что нарушение бинокулярного зрения является приемлемым, поскольку нарушение находится в пределах диапазона значений из таблицы на странице 15. В таблице можно прочитать, что степень коррекции снижается по мере повышения предписанной рефракции линзы. Можно прочитать, что «ошибка корректируется в достаточной степени при меньшей коррекции, а нарушение бинокулярного зрения является приемлемым», и это означает, что, когда предписанная рефракция линзы становится больше, толерантность пациента относительно бинокулярного зрения становится выше. Это утверждение трудно понять, поскольку указание относительно толерантности основано на оценке одного глаза. Что касается сущности патентного документа 3, в котором даже не раскрыт способ определения толерантности относительно бинокулярного зрения, то трудно прогнозировать, можно ли осуществлять проектирование так, чтобы толерантность стала меньшей или равной такой толерантности, как обычная, стандартная для очковых линз. То есть в случае описания такой толерантности в состоянии, в котором бинокулярное зрение даже не определялось, нелегко применить эту толерантность к проектированию линзы согласно другому общему предписанию.

В данном случае представляется, что оценивание бинокулярного зрения через оценивание одного глаза основано на соображении, заключающемся в том, что височная часть и носовая часть должны быть одинаковыми, поскольку при взгляде вправо правая височная часть используется в правой линзе и носовая часть используется в левой линзе. Однако это является случаем, когда оговаривается, что левая линза и правая линза являются одинаковыми, на что обращалось внимание, например, при рассмотрении третьей проблемы патентного документа 1. Такое предписание является очень редким. Кроме того, предполагается случай, когда предписания для левого глаза и правого глаза являются почти одинаковыми. В этом случае, учитывая, что предел чувствительности сенсорной фузии по углу составляют около 10 угловых секунд, трудно получить бинокулярное зрение при такой грубой концепции. Кроме того, при использовании линз общего применения проблематично использовать оценку и расчет, основанные на такой толерантности, которая не имеет физиологической основы, для организма человека, даже если предписания для левого и правого глаз известны заранее. В результате имеется опасность получения дискомфорта или может повышаться утомляемость.

Далее рассматривается возможность построения оптической системы предмет - очковые линзы - бинокулярные глазные яблоки путем расширения обычной оптической системы предмет - очковая линза - единственное глазное яблоко. На фиг.5 непатентного документа 9 показана типичная оптическая система предмет - очковая линза - единственное глазное яблоко. Как показано на фиг.24 настоящей заявки, начало системы координат оптической системы из фиг.5 находится в центре поворота глазного яблока, а азимутальный угол α и угол β возвышения в угле наблюдения показаны как соответствующие значения координат. В дополнение к этому расстояние от центра поворота глазного яблока до линзы обозначено как q'. Такую оптическую систему предмет - очковая линза - единственное глазное яблоко, как показанную на фиг.24, постоянно применяют (в данном случае угол наблюдения является одной переменной), начиная с эры Чернинга, то есть уже более 100 лет. Поскольку глазное яблоко вращается, в этой системе начало координат помещают в центр поворота глазного яблока. Конструктивную базовую точку помещают в геометрическом центре линзы, который является базовой точкой аберрации. При задании конструктивной базовой точки в качестве базовой точки аберрацию представляют разностями оптических параметров вдоль линии фиксации, которая продолжается от центра поворота глазного яблока до предмета через базовую точку линзы. Кроме того, в случае зрения на большое расстояние общепринято не показывать предмет, поскольку предмет расположен на бесконечном расстоянии. Чтобы перейти от этой оптической системы к системе бинокулярного зрения, начало координат следует сделать соответствующим двум центрам поворотов глазных яблок. Поэтому требуется некоторая изобретательность.

Вслед за этим предмет рассматривается в случае, когда оптическая система предмет - очковая линза - единственное глазное яблоко используется для зрения на малое расстояние. В этом случае технически линзу для зрения на малое расстояние можно считать очковой линзой. Однако на самом деле линза заменяется линзой для зрения на большое расстояние. Поэтому рассмотрим фиг.2 патентного документа 4, на которой показана оптическая система с прогрессивной линзой. Изображение этой фигуры показано на фиг.25 настоящей заявки. На фиг.25 показаны сфера Т дальних точек относительно зрительной оси 1 при наблюдении вдаль от центра C_R поворота глазного яблока Р через прогрессивную линзу L и состояния дальнего взгляда (∞) и ближнего взгляда (0,5 м = 2 дптр). «Предмет» на этой фигуре специально предназначен для прогрессивной линзы и является одним из нескольких примеров, в которых схематично показан предмет для ближнего взгляда. Как показано на фиг.25, предмет на бесконечности изображен на участке дальнего взгляда. Обычно в отрасли по изготовлению очковых линз предмет принято выражать в диоптриях. При выражении в диоптриях, как в этом примере, становится видимым бесконечный интервал. Однако для оценивания характеристики линзы нет необходимости квалифицировать предмет таким способом, даже если линза представляет собой прогрессивную линзу. В данном случае представляется, что это было сделано только для задания значения при оптимизации вычисления. Объектом изобретения, описанного в патентном документе 4, является только единственная очковая линза, рассматриваемая на всем протяжении документа, и нет упоминания относительно бинокулярного зрения. Поэтому неясно, каким станет предмет при переходе от оптической системы, показанной на фиг.5, к бинокулярной системе.

Заявитель считает, что на дату подачи настоящей заявки отсутствовала система предмет - очковые линзы - бинокулярные глазные яблоки, в том числе в описанных выше патентных документах и непатентных документах. Поэтому будет рассмотрена конфигурация бинокулярного зрения, которая часто встречается в психологии и т.д. Она не является конфигурацией бинокулярного зрения, когда носят пару очковых линз. Однако она представляет собой систему предмет - бинокулярные глазные яблоки. В качестве примера можно рассмотреть круг Виса-Мюллера или круг изоконвергенции, описанный на странице 39 непатентного документа 3 (Howard, I.P. and Rogers, B.J., “Binocular vision and stereopsis”, Chapter 2, New York, Oxford Press (1995), pp.1-736) или на странице 285 непатентного документа 10 и т.д.

На фиг.26 представлена диаграмма, показывающая круг C_V Виса-Мюллера и круг С_С изоконвергенции, описанные в непатентном документе 10. Круг C_V Виса-Мюллера задается окружностью, которая проходит через узловые точки n_L и n_R левого и правого глазных яблок и точку F, когда левый глаз Le и правый глаз Re фиксируют точку F. Кроме того, круг С_С изоконвергенции задается окружностью, которая проходит через центры C_L и C_R поворотов обоих глазных яблок Le и Re и точку F фиксации. На фиг.26 средняя точка и медианная плоскость центров C_L и C_R обоих глазных яблок обозначены точкой М и пунктирной линией Р_М, соответственно. Как ясно из фиг.26, круг C_V Виса-Мюллера является геометрическим гороптером (набором точек внешних предметов, которые возбуждают соответствующие точки на сетчатке обоих глаз; предметы на гороптере не создают различий в изображении на сетчатке), представленным кругом, соединяющим видимую точку F фиксации предмета и узловые точки n_L и n_R обоих глазных яблок. Однако при ношении пары очковых линз на этом круге C_V Виса-Мюллера изоконвергенция не возникает и, кроме того, отсутствует характеристика, которая является эквидистантной сама по себе. Поэтому невозможно выполнять оценивание при проектировании очковой линзы. Однако в соответствии с законами зрительного направления Уэллса-Геринга имеется преимущество, заключающееся в том, что, как общепризнано, начало координат находится на круге Виса-Мюллера и что точки на круге Виса-Мюллера расположены почти эквидистантно относительно самих себя. Круг С_С изоконвергенции, который имеет сходство с кругом C_V Виса-Мюллера, а именно, узловые точки из круга Виса-Мюллера заменяются центрами поворотов глазных яблок, а остальные участки являются такими же, как в круге Виса-Мюллера, представлен окружностью, которая проходит через центры поворотов обоих глазных яблок. В данном случае законы зрительного направления Уэллса-Геринга являются законами, имеющими отношение к вопросу «какая картина окружающего мира видна одним глазом, хотя смотрят два глаза». Законы зрительного направления Уэллса-Геринга не являются законами, которые прямо отвечают на этот вопрос, но они известны как законы, которые определяют, в каком зрительном направлении видна картина окружающего мира. Что касается этих законов, то положения (а) и (b), указанные ниже, являются известными. (а) - Начало зрительного направления находится на циклопическом глазе, который предполагается находящимся на средней точке между обоими глазами. (b) - Предмет на зрительной оси может быть виден на линии (оси направления), соединяющей точку пересечения осей обоих глаз и циклопический глаз.

Например, на странице 56 непатентного документа 3 имеется эмпирический гороптер. Изображение из документа показано на фиг.27 настоящей заявки. На фиг.27 прослеживаются эмпирический горизонтальный гороптер H_L и эмпирический вертикальный гороптер H_V, которые можно психологически воспринимать как равноудаленную форму. Эмпирический вертикальный гороптер H_V имеет такую характеристику, что он отклонен на 2-5° от вертикального направления V_t к обратной стороне (стороне, отнесенной от глазных яблок L_e и R_e). Этим подтверждается экспериментальный факт облегчения чтения при отклонении во время чтения на угол около 10°. Поскольку индивидуальная изменчивость является значительной, угол следует выбирать как индивидуальный элемент. Однако выбирать трудно, поскольку фактические измеряемые значения являются небольшими. Кроме того, диапазон, в котором можно смотреть с соблюдением равного удаления, представлен только цилиндрическим участком на фигуре, а другого участка нет. Поэтому гороптер нельзя использовать в качестве системы глазных линз.

Как описано выше, в системе предмет - очковые линзы - бинокулярные глазные яблоки, в которой предмет обнаруживается обоими глазами, пара очковых линз и оба глазных яблока обычно однозначно не определены. В области психологии существует теория, в соответствии с которой окрестность средней точки вершин роговых оболочек обоих глазных яблок принимают за начало зрительного направления. Однако, если эту точку задавать в качестве начала, то точка будет перемещаться при повороте глазного яблока в одну и другую сторону и согласованность в случае обычной системы предмет - линза - единственное глазное яблоко будет утрачена. Можно рассмотреть случай, когда точку на средней линии, такую, что расстояние между точкой фиксации и центром поворота одного глазного яблока равно расстоянию между точкой фиксации и центром поворота другого глазного яблока, берут в качестве начала зрительного направления. Однако это является проблематичным по той же причине. Обычно имеются несколько случаев, в которых можно делать попытку улучшать бинокулярное зрение обработкой призматических действий очковых линз. Однако при реализации способа оценивания характеристик бинокулярного зрения желательно, чтобы способ оценивания был в большей степени основан на знании физиологии.

На основании изложенного выше задача настоящего изобретения заключается в разрешении проблем, описанных ниже.

1. Определение начала зрительного направления и системы координат, которые являются пригодными для оценивания характеристик бинокулярного зрения при ношении пары очковых линз.

2. Подробное рассмотрение «предмета», который тесно связан с оцениванием характеристик бинокулярного зрения.

3. Выполнение количественного оценивания характеристик бинокулярного зрения, которое основано на известных физиологических данных о бинокулярной функции, при этом оценивание является справедливым на всей поверхности бинокулярного поля зрения и оценивание не зависит от формы предмета.

Краткое изложение

Ниже описывается способ оценивания очковых линз согласно настоящему изобретению, включающий в себя этапы 1-3, предназначенный для разрешения упомянутых выше проблем.

1. В качестве первого этапа способ включает в себя этап задания оптической системы с использованием системы координат, для которой начало помещают на среднюю точку центров поворотов обоих глазных яблок и в которой предмет точно определен зрительным направлением от начала координат, при этом оптическая система включает в себя предмет, левую и правую очковые линзы и оба глазных яблока. То есть в настоящем изобретении конфигурация, которая была общепринятой в течение более одного столетия и в которой центр поворота глазного яблока задавали в качестве начала зрительного направления, аннулируется и начало зрительного направления системы предмет - очковые линзы - оба глазных яблока, предназначенной для бинокулярного зрения, задают на средней точке между центрами поворотов обоих глазных яблок в соответствии с законами зрительного направления Уэллса-Геринга. Для выполнения оптических вычислений система включает в себя наблюдаемый предмет, очковые линзы и глазные яблоки. Систему координат можно выбирать произвольно, но поскольку полярные координаты обычно принимают для системы предмет - очковая линза - единственное глазное яблоко, полярные координаты являются предпочтительными. В такой системе координат можно определять характеристики бинокулярного зрения. А именно, характеристики бинокулярного зрения обозначают в этой системе координат в значениях углов, образованных относительно предмета, в частности азимутального угла и угла возвышения. В данном случае в этой системе нет необходимости, чтобы центры поворотов глазных яблок были фиксированными точками при движениях глазных яблок в системе.

2. В качестве второго этапа способ включает этап вычисления эталонного значения угла конвергенции с линиями фиксаций, для которых точку фиксации предмета задают как направление наблюдения, при этом точка фиксации является точкой пересечения, в которой линии фиксаций пересекаются друг с другом после прохождения через конструктивные базовые точки левой и правой очковых линз. Предмет в системе предмет - очковая линза - одно глазное яблоко, где система определена согласно настоящему изобретению, представляет собой произвольный предмет, а настоящее изобретение не ограничено предметом. Предмет задают так, чтобы пояснение его было конкретным. В настоящем изобретении предпочтительно, чтобы предмет удовлетворял следующим условиям. В случае однофокусной линзы расстояния являются одинаковыми при взгляде от себя, а именно, полусфера перед глазами является предпочтительной. В случае полусферы радиус можно задавать, например, расстоянием между точкой пересечения линий фиксаций и началом координат, при этом линии фиксаций исходят из центров поворотов левого и правого глазных яблок и проходят через левую и правую конструктивные базовые точки. Что касается способа обозначения, то можно использовать обозначение диоптриями, которое применяется в отрасли, и положение предмета можно точно определять диоптриями.

В случае прогрессивной рефракционной линзы предмет находится в угле обзора со стороны начала координат в направлении наблюдения точки пересечения линий фиксаций, которые исходят из центров поворотов левого и правого глазных яблок и проходят через конструктивные базовые точки. В таком случае предмет в медианной плоскости становится предметом, который является аналогичным предмету, показанному на фиг.2 патентного документа 4, то есть показанному на фиг.25 настоящей заявки. Право замены другими точками остается за проектировщиком прогрессивной рефракционной линзы. Во многих патентах на прогрессивные рефракционные линзы предмет обычно не раскрывается. Поэтому в случае однофокусной линзы предмет можно заменять полусферой, радиус которой определяется конструктивной базовой точкой, и выполнять оценивание. На более частном этапе форму линзы задают такой, чтобы предписанное значение получалось в конструктивной базовой точке очковой линзы в системе предмет для обоих глаз - очковые линзы - оба глазных яблока. Вычисляют предписанное значение и угол конвергенции от центров поворотов глазных яблок к очковым линзам на обоих глазах и задают эталонное значение угла конвергенции.

3. В качестве третьего этапа способ включает в себя этап вычисления угла конвергенции относительно линий фиксаций, при этом линии фиксаций продолжаются до предметной точки оценивания в произвольном угле наблюдения и проходят через левую и правую очковые линзы, и вычисления аберрации конвергенции по разности между углом конвергенции и эталонным значением угла конвергенции. Рассмотрены вергентные движения глазных яблок (контралатеральное бинокулярное движение) согласно закону равных иннерваций Геринга, то есть закону движения бинокулярного зрения, а именно, «аберрация конвергенции», которая является характеристикой бинокулярного зрения, получаемой по движению конвергенции. Конвергенции включают в себя конвергенцию, которая основана на линиях фиксаций на стороне изображения, то есть исходящих из центров поворотов левого и правого глазных яблок к левой и правой очковым линзам, и конвергенцию, которая основана на линиях фиксаций на стороне предмета, то есть исходящих от левой и правой очковых линз к предмету. На стороне изображения и стороне предмета можно находить угол конвергенции и аберрацию конвергенции, которую получают по углу конвергенции с помощью определения, описанного ниже, и нахождение на обеих сторонах находится в объеме настоящего изобретения. Углы конвергенции и аберрации конвергенции на стороне изображения и стороне предмета имеют соответствующие пропорциональные зависимости, так что коэффициенты пропорциональности приблизительно пропорциональны оптической силе линзы. Однако значения на стороне предмета изменяются в зависимости от формы линзы. Поэтому в настоящем изобретении более предпочтительно использовать угол конвергенции, основанный на линиях фиксации на стороне изображения.

На следующем конкретном этапе вычисляют, например, рефракционную ошибку, которая зависит от точки оценивания предмета в системе предмет - очковые линзы - оба глазных яблока, остаточный астигматизм и угол конвергенции, а именно, начиная от центра поворота глазного яблока и продолжая до очковой линзы. Разность конвергенций в точке оценивания получают, задавая угол конвергенции, полученный на втором этапе, в качестве эталонного. В дальнейшем разность конвергенций будет определяться как «аберрация конвергенции».

Как описывалось выше, в настоящем изобретении дано определение началу направления наблюдения, которое применимо для бинокулярного зрения. Поэтому, когда предписанное значение является иным или когда оправа имеет иной угол наклона или угол возвышения, становится возможным выполнять сравнение оптических параметров до и после замены очков и становится возможным выполнять состоятельное оценивание. Кроме того, в пределе, когда расстояние между глазными яблоками становится равным 0, возникает система предмет - очковая линза - единственное глазное яблоко, которую обычно использовали раньше. Поэтому не создается никакого противоречия с обычным проектированием по единственному глазу. Кроме того, даже при изменении расстояния между глазными яблоками предмет остается приблизительно эквивалентным. Иначе говоря, при фиксированном предмете становится возможным определение сравнительных достоинств, имеющих отношение к фузии, очков пациентов (людей, носящих очки), имеющих различные расстояния между центрами поворотов глазных яблок, путем оценивания описанных выше аберраций конвергенции.

Ниже изложены причины, по которым на конвергенции сосредоточено внимание при оценивании бинокулярной функции. А именно, на основании сведений о функциональном аспекте биологических систем известно, что латентный период конвергенции составляет 150-200 мс, импульсивное движение глазных яблок происходит в течение 200 мс и около 800 раз в секунду, регуляция двигательного акта составляет 350-400 мс и аккомодационный зрачковый рефлекс составляет 400-450 мс. С учетом этого и перемещений линий фиксаций предмета во время наведенного диспаратностью движения конвергенции, которое является комбинацией конвергенции и импульсивного движения глазных яблок, регуляция и аккомодационный зрачковый рефлекс почти не изменяются по сравнению с движением конвергенции и импульсивным движением. Поэтому аберрация конвергенции считается имеющей более высокий приоритет, чем другие аберрации, рефракционная ошибка и остаточный астигматизм.

Кроме того, когда предмет является плоской поверхностью, как в обычном способе, обычную рефракционную ошибку и остаточный астигматизм корректируют, деформируя очковую линзу. Однако при этом конвергенцию не рассматривают вообще. Поскольку конвергенция значительно изменяется в зависимости от точки фиксации, имеется случай, когда фузия бинокулярной функции становится затруднительной, а бинокулярная характеристика ухудшается. В противоположность этому в настоящем изобретении, когда предмет для однофокусной линзы задают на полусфере, изменение визуальной обстановки во время поворота глазного яблока является небольшим. Кроме того, по выбору можно не касаться предмета для прогрессивной рефракционной линзы, но вследствие аберрации конвергенции становится возможным количественное оценивание предмета, при котором изменение визуальной обстановки является небольшим.

[Результат изобретения]

Благодаря аберрации конвергенции, определяемой в способе оценивания очковых линз согласно настоящему изобретению, становится возможным оценивание, основанное на вергентных движениях глазных яблок (контралатеральном бинокулярном движении) в соответствии с законом равных иннерваций Геринга, который является законом движения бинокулярного зрения, то есть основанное на знании законов физиологии, то есть полученное на основании движения конвергенции. Поскольку имеется одно эталонное значение для оценивания, становится возможным равномерное оценивание по всему бинокулярному полю зрения и возможен произвольный предмет. Кроме того, вследствие аберрации конвергенции становится возможным количественное оценивание условия фузии, которая является характеристикой бинокулярного зрения.

Краткое описание чертежей

На чертежах:

фиг.1 - диаграмма, показывающая систему предмет - очковые линзы - глазные яблоки, предназначенную для пояснения предмета, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению;

фиг.2 - диаграмма, показывающая эталонное значение угла конвергенции на стороне изображения в системе предмет - очковые линзы - глазные яблоки, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению;

фиг.3 - диаграмма, показывающая эталонное значение угла конвергенции в системе предмет - очковые линзы - глазные яблоки, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению;

фиг.4 - диаграмма наблюдения в системе предмет - очковые линзы - глазные яблоки, показанной на фиг.2, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению, с направления, которое является перпендикулярным к медианной плоскости, и иллюстрирующая аберрацию конвергенции, определяемую на стороне изображения в направлении, перпендикулярном к плоскости;

фиг.5 - диаграмма наблюдения в системе предмет - очковые линзы - глазные яблоки, показанной на фиг.2, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению, с направления, которое является перпендикулярным к медианной плоскости, и иллюстрирующая аберрацию конвергенции, определяемую на стороне предмета в направлении, перпендикулярном к плоскости;

фиг.6 - диаграмма, показывающая угол конвергенции на стороне изображения в точке оценивания в системе предмет - очковые линзы - глазные яблоки, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению;

фиг.7 - диаграмма, показывающая угол конвергенции на стороне предмета в точке оценивания в системе предмет - очковые линзы - глазные яблоки, которая используется в осуществлении способа оценивания очковых линз согласно настоящему изобретению;

фиг.8 - диаграмма, показывающая систему предмет - очковые линзы - глазные яблоки для сравнительного примера;

фиг.9 - диаграмма, показывающая блок-схему последовательности действий согласно осуществлению способа проектирования очковых линз настоящего изобретения;

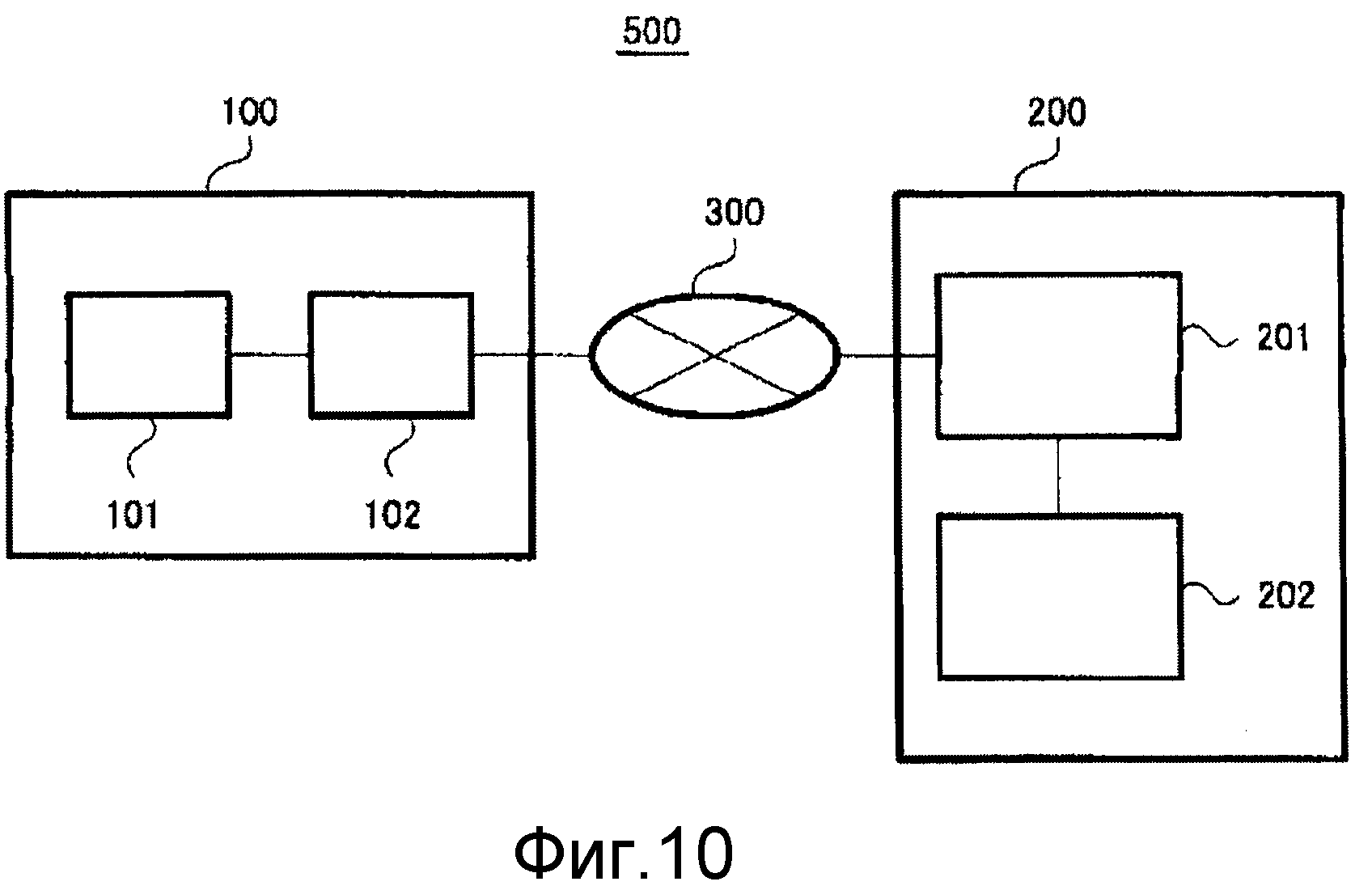
фиг.10 - схематичное представление конфигурации системы изготовления согласно осуществлению способа изготовления очковых линз настоящего изобретения;

фиг.11 - функциональная схема компьютера на стороне изготовления в системе изготовления согласно осуществлению способа изготовления очковых линз настоящего изобретения;

фиг.12 - диаграмма, показывающая параллельную поверхности составляющую аберрации конвергенции из первого осуществления способа оценивания очковых линз настоящего изобретения;

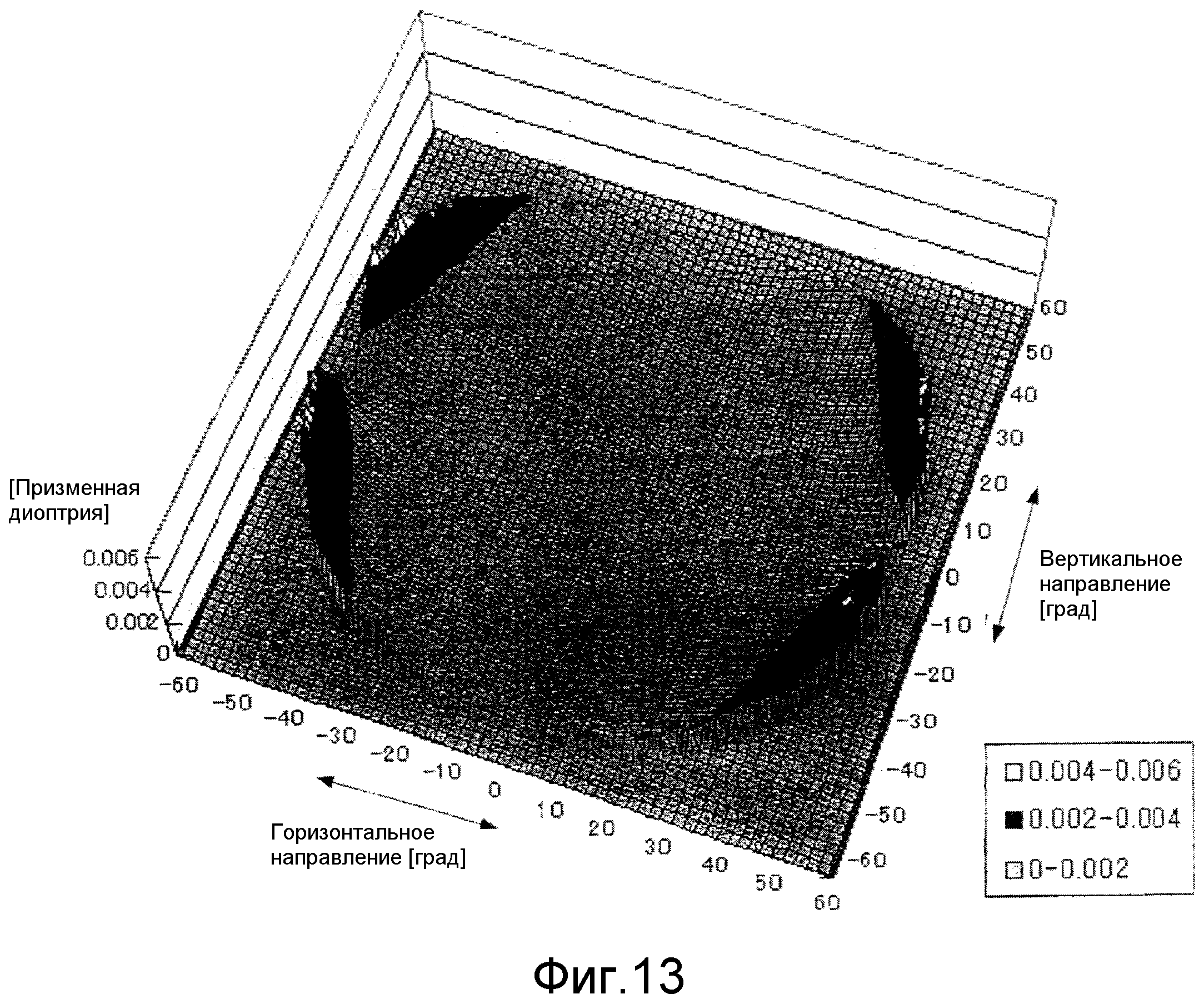
фиг.13 - диаграмма, показывающая перпендикулярную к поверхности составляющую аберрации конвергенции из первого осуществления способа оценивания очковых линз настоящего изобретения;

фиг.14 - диаграмма, показывающая параллельную поверхности составляющую аберрации конвергенции из второго осуществления способа оценивания очковых линз настоящего изобретения;

фиг.15 - диаграмма, показывающая перпендикулярную к поверхности составляющую аберрации конвергенции из второго осуществления способа оценивания очковых линз настоящего изобретения;

фиг.16 - диаграмма, показывающая параллельную поверхности составляющую аберрации конвергенции из третьего осуществления способа оценивания очковых линз настоящего изобретения;

фиг.17 - диаграмма, показывающая перпендикулярную к поверхности составляющую аберрации конвергенции из третьего осуществления способа оценивания очковых линз настоящего изобретения;

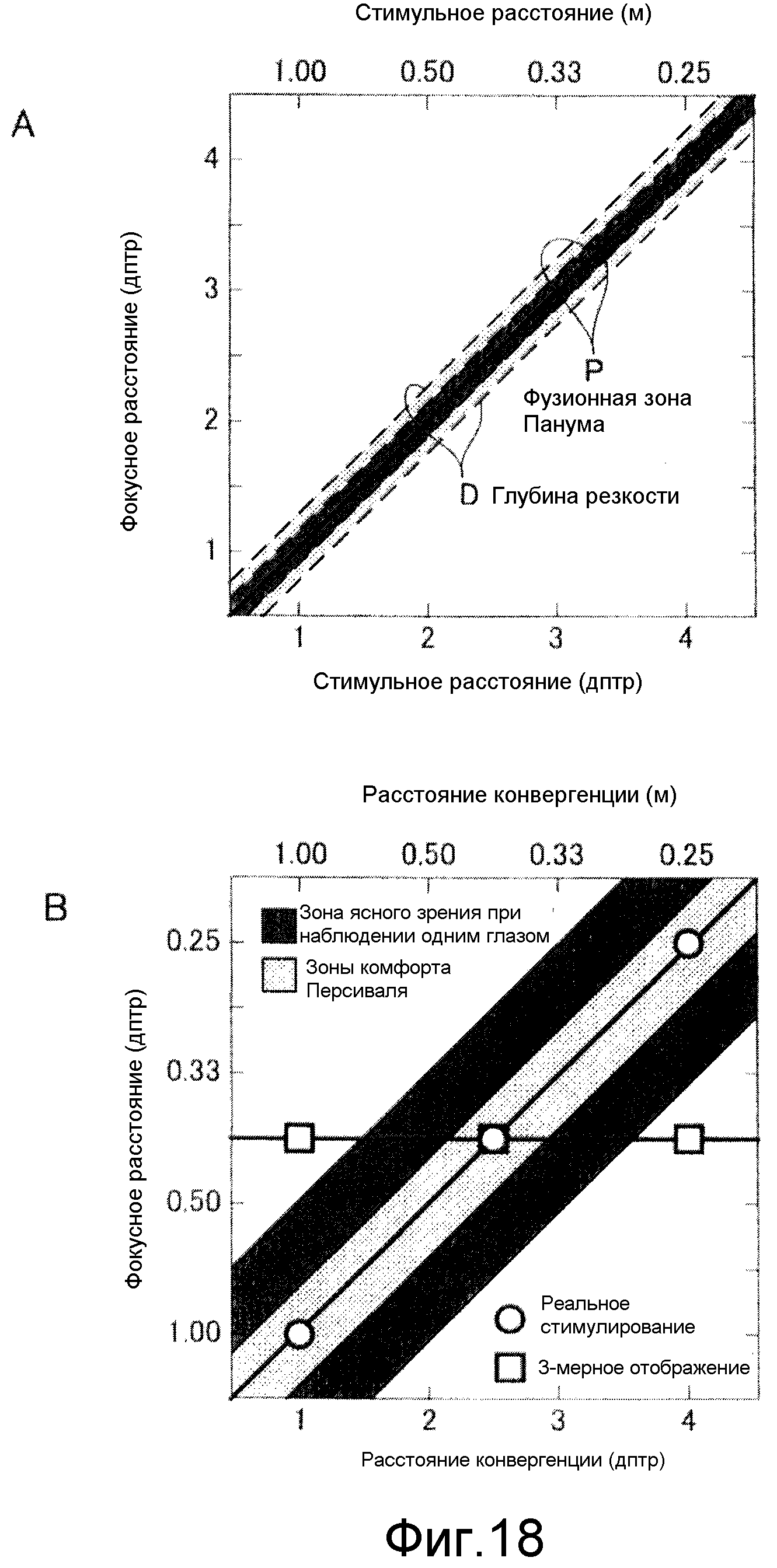
фиг.18А - схематичная диаграмма, показывающая сенсорную фузию, и фиг.18В - схематичная диаграмма, показывающая моторную фузию;

фиг.19А - пример вычисления угла конвергенции, когда межзрачковое расстояние PD составляет 60 мм, и фиг.19В - пример вычисления угла конвергенции, когда межзрачковое расстояние PD составляет 65 мм;

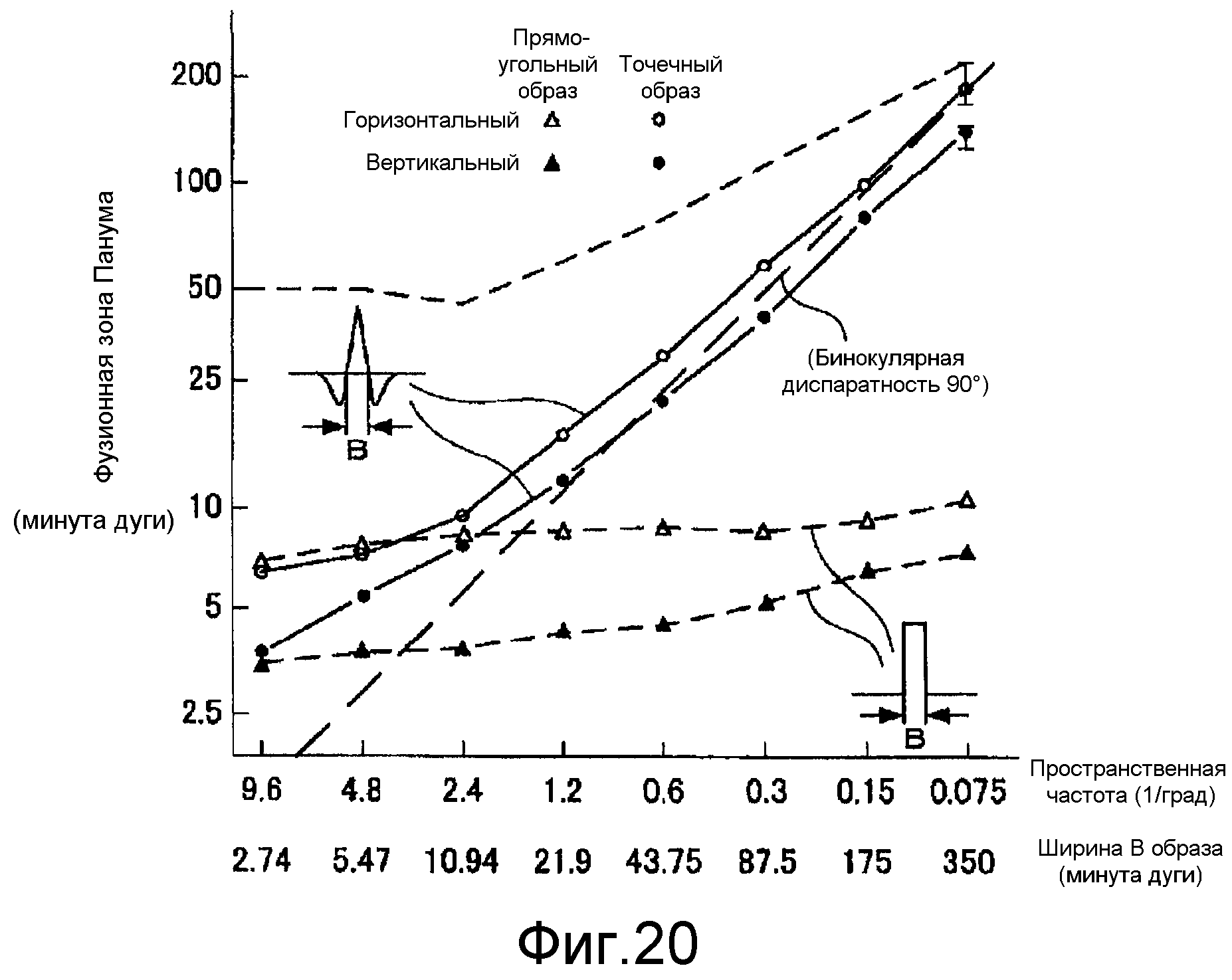
фиг.20 - график, показывающий фузионную зону Панума в зависимости от пространственной частоты предмета;

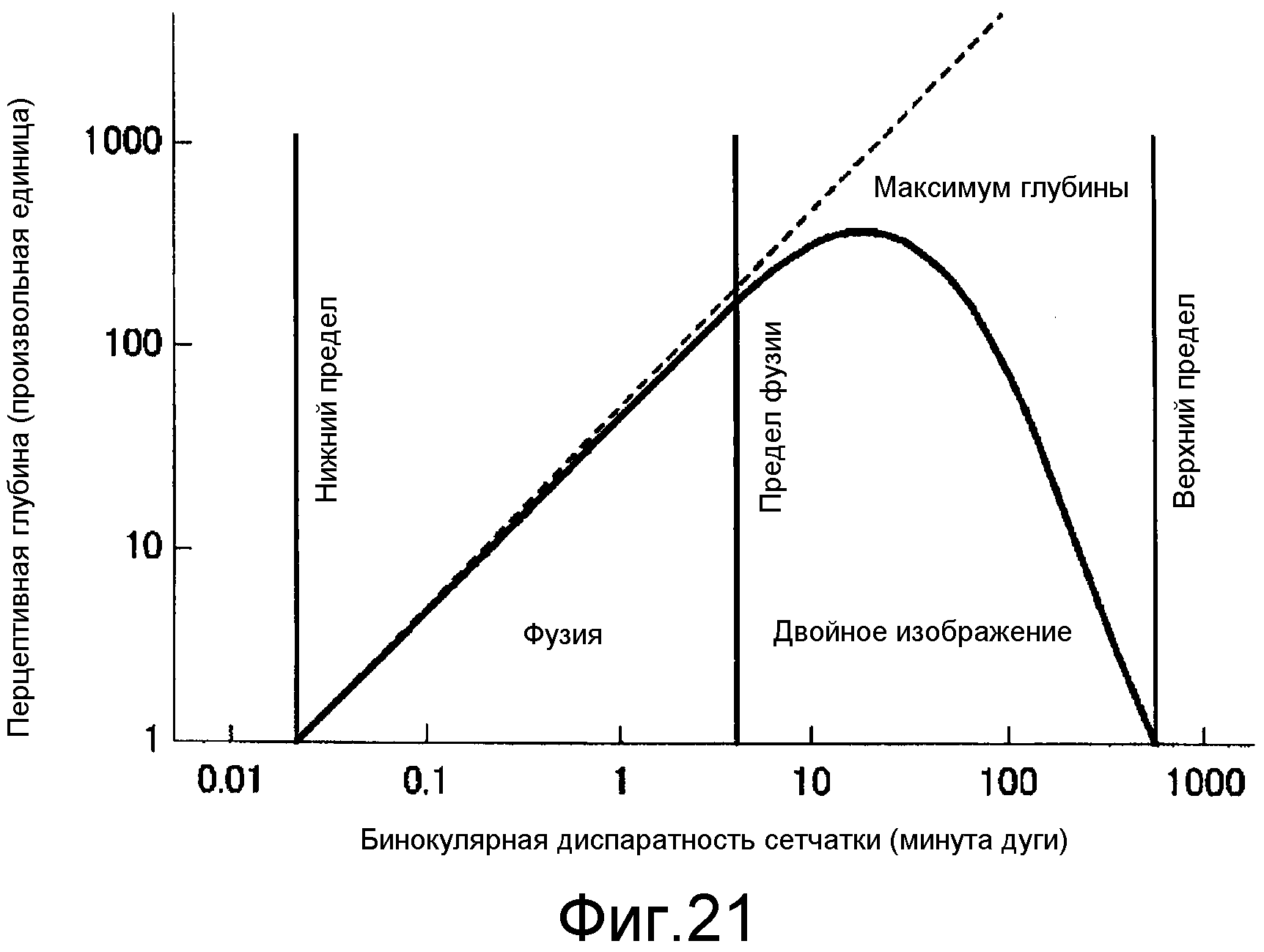
фиг.21 - график, показывающий зависимость между диспаратностью горизонтального изображения на сетчатке и перцептивной глубиной;

фиг.22 - диаграмма, показывающая диспаратность на предметной поверхности;

фиг.23 - диаграмма, показывающая дисторсию в обычном способе;

фиг.24 - диаграмма, показывающая конфигурацию обычной системы очковая линза - глазное яблоко для единственного глаза;

фиг.25 - диаграмма, показывающая конфигурацию обычной системы предмет - очковая линза - глазное яблоко для единственного глаза;

фиг.26 - диаграмма, показывающая круг Виса-Мюллера и круг изоконвергенции; и

фиг.27 - диаграмма, показывающая эмпирический гороптер.

Подробное описание осуществлений

Осуществления настоящего изобретения поясняются ниже, но настоящее изобретение не ограничено осуществлениями, описываемыми ниже. Они поясняются в следующем порядке.

[1] Способ оценивания очковых линз

-(1) Первый этап (процесс задания системы предмет - очковые линзы - бинокулярные глазные яблоки)

-(2) Второй этап (процесс вычисления эталонной аберрации)

-(3) Третий этап (процесс вычисления аберраций в произвольных точках)

-(4) Разность из обычного примера

-(5) Пояснение различия на основании фактической линии фиксации

-(6) Пояснение порога фузии

[2] Способ проектирования очковых линз

[3] Способ изготовления и система для изготовления очковых линз

[4] Осуществления способа оценивания очковых линз

-(1) Первое осуществление (пример, в котором степень астигматизма равна 0)

-(2) Второе осуществление (пример, в котором разность между сферическими преломляющими действиями левой и правой линз больше или равна -2 дптр)

-(3) Третье осуществление (пример, в котором угол возвышения составляет 20°)

До конкретного пояснения осуществления настоящего изобретения будут пояснены технические допущения и термины, используемые в осуществлении.

Чтобы выполнить оценивание или проектирование очковой линзы, необходимо найти конструктивную базовую точку. Эти конструктивные базовые точки несколько различаются для однофокусной линзы и для многофокусной линзы. Поэтому они поясняются отдельно. В случае однофокусной линзы конструктивная базовая точка представляет собой место, в котором измеряют предписанные значения (сферическое преломляющее действие, степень астигматизма, оси астигматизма, значение призматического действия линзы, ось призматического действия линзы) и в котором к тому же линия фиксации пересекает линзу. Эту точку также называют точкой наблюдения, местом нахождения глаза или точкой оптической центрировки. Когда призматическое действие линзы отсутствует, конструктивную базовую точку рассматривают в качестве оптического центра. При обычном предписании конструктивную базовую точку линзы согласовывают с межзрачковым расстоянием в горизонтальном направлении и согласовывают с местом несколько ниже зрачка (около 10° при центрировке относительно центра поворота, около 4 мм) в вертикальном направлении, затем ее помещают на оправу. В случае линзы для чтения индивидуальное проектирование специально не выполняют, а вместо него используют линзу общего применения. Поэтому в случае предписания на линзу для чтения конструктивную базовую точку предусматривают на месте, где линия фиксации, начинающаяся с некоторого расстояния до предмета (25 см - 50 см), пересекает линзу, а в горизонтальном направлении конструктивную базовую точку задают на несколько меньшем расстоянии (на 2-5 мм) (его называют межзрачковым расстоянием для близи и иногда обозначают аббревиатурой NPD), чем межзрачковое расстояние. В вертикальном направлении конструктивную базовую точку согласовывают с местом несколько ниже зрачка (около 20° при центрировке относительно центра поворота, около 9 мм) и помещают ее на оправу. В случае многофокусной линзы, такой как прогрессивная линза, базовые точки предусматривают раздельно, чтобы определять предписанные значения для зрения на большое расстояние (сферическое преломляющее действие, степень астигматизма, оси астигматизма), место нахождения глаза (место должно быть согласовано со зрачком), точку измерения призматического действия линзы, предписанные значения для зрения на малое расстояние (оптические силы, добавляемые к предписанным значениям для зрения на большое расстояние, а именно, добавляемую рефракцию). Обычно место нахождения глаза согласовывают со зрачком, а базовые точки помещают на оправу.

В осуществлении проектирование линзы выполняют, обычно используя известный способ прослеживания луча. Например, в непатентном документе 1 (написанном Tomowaki Takahashi, “Lens design”, Tokai University Press (1994)) описаны технологии, касающиеся оптимизации проектирования линзы способом прослеживания луча и аберрации волнового фронта. Аберрация волнового фронта описана в непатентном документе 2 (Takeshi Noguchi et al., “Active optics experiments I, Shack-Hartman wave-front analyzer to measure F/5 mirrors”, Publ. Natl. Astrron. Obs. Japan, vol.1 (1989), pp.49-55) и т.д. Кроме того, в области техники, относящейся к очковым линзам, при проектировании линз используют прибор для измерения линз, который вычисляет аберрацию (рефракционную ошибку, астигматизм и т.д.) по результату измерения волнового фронта после прохождения его через очковую линзу.

При рассмотрении предмета через очковую линзы аберрацию, обусловленную линзой, вдоль главного луча, поступающего от предмета в центр поворота глазного яблока, можно аппроксимировать аберрациями низших порядков, поскольку диаметр зрачка глазного яблока является небольшим. Применительно к области техники, относящейся к очковым линзам, в рамках этой заявки будет пояснены аберрации низших порядков. Аберрации низших порядков включают в себя, например, рефракционную ошибку, остаточный астигматизм и хроматическую аберрацию.

В случае линзы для дали значения обычно предписывают так, чтобы рефракционная сила глазного яблока вычиталась из рефракционной силы линзы, вследствие чего предмет на переднем удаленном месте может быть ясно виден в конструктивной базовой точке (обычно, в точке линзы при наблюдении переднего удаленного места от глазного яблока через линзу). Можно сказать, что недостаточная рефракционная сила компенсируется линзой. В то же время аберрация равна 0. Когда астигматизм существует около глазного яблока в конструктивной базовой точке, предписывают согласование астигматизма с астигматической осью линзы. Астигматическая ось пересекает перпендикулярно главный луч и, кроме того, астигматическая ось является главным меридианом рефракционной силы. Как и в случае глазного яблока, главный меридиан представляет собой путь луча, который идет от предмета и достигает центра поворота глазного яблока через очковую линзу. Когда глазное яблоко поворачивается в соответствии с законом Листинга, то в отличие от обычной коаксиальной оптической системы очковая линза является неподвижной и направление глазного яблока изменяется относительно очковой линзы. В то же время в другой точке, а не в конструктивной базовой точке, рефракционная сила линзы несколько отличается от рефракционной силы в конструктивной базовой точке вследствие свойства линзы. Как раз в этом случае рефракционную силу глазного яблока вычитают из рефракционной силы линзы. Полученное в результате вычитания значение характеризует аберрацию системы линза - глазное яблоко.

Что касается вычитания аберраций, то поскольку при повороте вдоль астигматической оси линзы в соответствии с законом Листинга (в главном меридиональном направлении имеются два направления) астигматическая ось линзы совпадает с астигматической осью глазного яблока, достаточно выполнить вычитание только по каждому осевому направлению. Прежде аберрацию в этом случае называли аберрацией линзы. Однако, если направление поворота глазного яблока иное, чем направление астигматической оси линзы, астигматическая ось линзы становится отличающейся от астигматической оси глазного яблока. Поэтому рефракционную силу линзы разлагают в направлении астигматической оси глазного яблока, и среднее величин, величин соответствующих разложенных рефракционных сил за вычетом рефракционных сил в соответствующих направлениях, становится тем, что называют рефракционной ошибкой. Поскольку эта рефракционная ошибка представляет собой среднее значение, она не связана с различием астигматических осей и она эквивалентна рефракционной ошибке в случае, когда астигматические оси совпадают друг с другом. Однако астигматизм принимает иное значение, которое отличается от значения в случае, когда оси совпадают друг с другом.

В данном случае в предположении, что описанные выше значения, полученные вычитанием рефракционных сил по двум направлениям астигматических осей глазного яблока, представляют собой аберрацию А и аберрацию В, рефракционная ошибка является средним значением аберрации А и аберрации В, а остаточный астигматизм является разностью между аберрацией А и аберрацией В. Прежде, когда закон Листинга не требовался, а именно, в случае, когда глазное яблоко поворачивалось наряду с астигматической осью очковой линзы, он не назывался остаточным астигматизмом, а он назывался астигматизмом. В этом случае рефракционная ошибка называлась средней ошибкой косых пучков (МОЕ) и ошибка астигматизма иногда называлась ошибкой астигматизма косых пучков (ОАЕ).

Кроме того, если угловую разность между главным лучом от центра поворота глазного яблока до задней поверхности линзы и главным лучом от передней поверхности линзы до предмета обозначить δ и число Аббе обозначить ν, то хроматическая аберрация будет выражаться в соответствии с 100×tanδ/ν.

[1] Способ оценивания очковых линз

Ниже подробно поясняются этапы с первого по третий реализации описанного выше способа оценивания очковых линз согласно настоящему изобретению.

(1) Первый этап (этап задания системы предмет - очковые линзы - бинокулярные глазные яблоки)

Для уточнения признаков настоящего изобретения сначала будет подробно описан предмет. Будет описана оптическая система для выполнения оптического расчета бинокулярного зрения согласно настоящему изобретению, то есть система предмет - бинокулярные очковые линзы - бинокулярные глазные яблоки. В настоящем изобретении предмет согласован с диоптрийной системой обозначений, которая используется в промышленной практике. Поэтому на фигуре можно показывать предмет на любом расстоянии. Как вариант на фигуре может быть показан предмет для зрения на малое расстояние, а предмет для зрения на большое расстояние может быть предметом на бесконечном расстоянии.

Предпочтительный предмет, используемый в качестве предмета для способа оценивания очковых линз настоящего изобретения показан на фиг.1. Пояснение, приводимое ниже, представляет собой пояснение, основанное на линии фиксации на стороне изображения, а пояснение, основанное на линии фиксации на стороне предмета, опускается, поскольку для него все самое важное является тем же самым, кроме пояснительной диаграммы. Как показано на фиг.1, сначала задают центр 1R поворота правого глазного яблока и центр 1L поворота левого глазного яблока. На фиг.1 показана компоновка на горизонтальной поверхности 20, которая включает в себя оба центра 1R и 1L поворотов глазных яблок. На фиг.1 средняя точка обоих центров 1R и 1L поворотов глазных яблок задана в начале 1 системы координат в системе предмет - очковые линзы - бинокулярные глазные яблоки. Затем предмет 4 находят на предметной сферической поверхности 5, которая является полусферой на передней стороне глаза, центрированной относительно начала 1 координат с радиусом, определяемым расстоянием от начала 1 координат до точки 3 фиксации. Центры 1R и 1L поворотов обоих глазных яблок расположены во фронтальной плоскости. Когда предмет 4 расположен на бесконечности, ее рассматривают как предел, где радиус предметной сферической поверхности 5 возрастает. Кроме того, местоположение предмета 4 определяют, используя угол от средней линии 6, при этом средняя линия 6 проходит через начало 1 координат, в качестве переменной вместо угла поля зрения на стороне изображения, продолжающейся от центров 1L и 1R поворотов обоих глазных яблок до очковых линз, или угла поля зрения на стороне предмета от линии, продолжающейся от очковых линз до предмета, как и в случае обычной оптической системы. То есть произвольное положение предмета 4 определяют как функцию угла, при этом угол основан на средней линии 6 от начала 1 координат системы. Этим углом θ определяется направление бинокулярного зрения. Кроме того, как показано, например, на фиг.24, направление θ бинокулярного зрения может быть разделено на горизонтальное направление и вертикальное направление. В дополнение к этому прямая линия, соединяющая центры поворотов обоих глазных яблок, является отрезком 2 прямой между глазными яблоками.

Далее поясняются местоположения очковых линз. Очковые линзы помещают между точкой фиксации предписанного значения для зрения на большое расстояние и соответствующими центрами 1L и 1R поворотов глазных яблок. Очковые линзы имеют предписанные значения в конструктивных базовых точках линз, и они имеют произвольные наклоны относительно горизонтальной поверхности и фронтальной плоскости (передний угол наклона, угол возвышения) и эксцентриситеты (эксцентричность в вертикальном направлении, эксцентричность в горизонтальном направлении). Расстояние от задней вершины линзы до центра поворота глазного яблока обычно составляет 27 мм или 24-36 мм, как описано в строках 4-5 снизу в правом столбце на странице 2 опубликованной рассмотренной заявки №42-9416В на патент Японии. В отдельных случаях лучше выполнять проектирование для расстояния, большего чем 27± 1 мм или равного ему.

Далее, что касается движения глазных яблок, то предполагается, что один глаз подчиняется закону Листинга, а бинокулярные глаза подчиняются закону равных иннерваций Геринга. Центры 1L и 1R поворотов глазных яблок перемещаются, когда глазные яблоки поворачиваются вверх и вниз или вправо и влево, так что расстояния от центров поворотов до вершин роговой оболочки изменяются. То есть, когда левый и правый глазные яблоки видят ближайшую точку ясного видения, они сходятся вследствие наличия зависимости аккомодация-конвергенция, однако известно, что в этом случае центры 1L и 1R поворотов перемещаются. Для удобства пояснения в настоящем изобретении поясняется система, в которой центры 1L и 1R поворотов глазных яблок являются фиксированными.

(2) Второй этап (этап вычисления эталонной аберрации)

На втором этапе, описываемом ниже, чтобы сделать конструктивные базовые точки пары очковых линз из системы предмет для обоих глаз - очковые линзы - бинокулярные глазные яблоки базовыми при вычислении аберраций, линзам придают такие формы, чтобы они обеспечивали заданные, предписанные значения в конструктивных базовых точках. В прогрессивных линзах конструктивные базовые точки обычно находятся на различных, отстоящих друг от друга местах, таких как точка измерения рефракции для зрения на большое расстояние, точка измерения рефракции для зрения на малое расстояние и точка измерения призматического действия линзы. Кроме того, в принципе, для однофокусной линзы, которая одновременно представляет собой линзу дли зрения на малое расстояние, различные величины, предназначенные для оптических расчетов, вычисляют вдоль главной оси, продолжающейся от точки фиксации на предмете до центра поворота и проходящей через точку измерения рефракции для зрения на малое расстояние. С другой стороны, имеется случай, когда предписывается определять межзрачковое расстояние для близи просто вычитанием 2 мм из межзрачкового расстояния (его называют PD) и заданием его в качестве точки наблюдения.

В любом случае линзам придают такие формы, чтобы предписанные значения обеспечивались в конструктивных базовых точках. Линзам придают формы тогда, когда предписанные значения сходятся в процессе оптимизации вычислений. В дополнение к этому в случаях оценивания пары очковых линз для ношения, которые представляют собой линзы общего применения, имеются ситуации, в которых очковые линзы и зрительные оси, проходящие через конструктивные базовые точки, не являются перпендикулярными. В этих случаях небольшие аберрации возникают в конструктивных базовых точках вследствие наклонов, но достигаются приближенные предписанные значения.

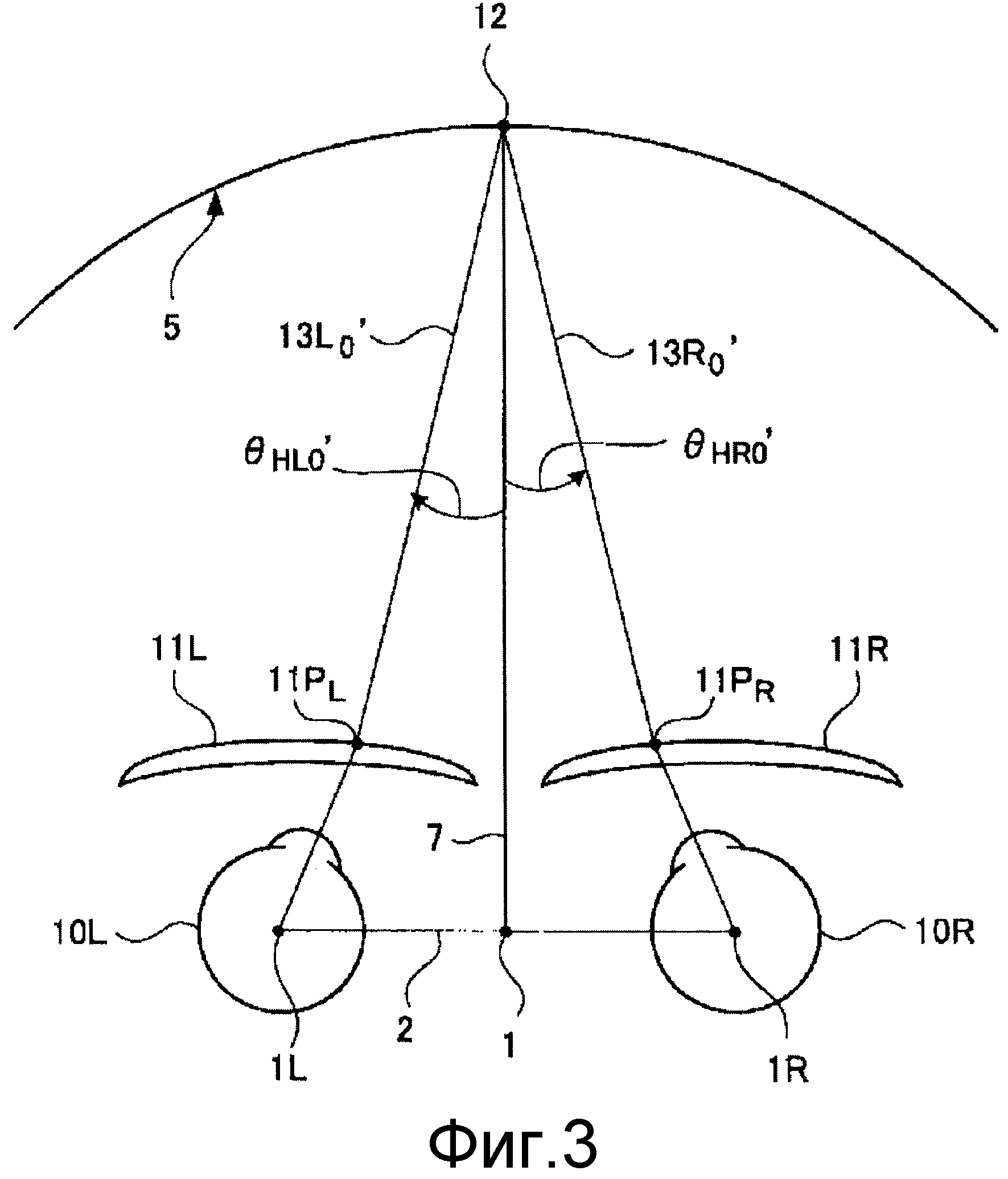
В данном случае предписанными значениями являются сферическое преломляющее действие, степень астигматизма, астигматическая ось, призматическое действие линзы, ось призматического действия линзы и дополнительная рефракция. Поскольку аберрация определяется как отличие от эталонного значения, эти предписанные значения становятся эталонными. На фиг.2 показан вид сверху обоих глазных яблок 10L и 10R. На фиг.2 частям, соответствующим фиг.1, даны те же самые позиции, а совпадающие пояснения опущены. Линии 13L0 и 13R0 фиксаций, которые проходят через соответствующие базовые точки левой очковой линзы 11L и правой очковой линзы 11R от левого глаза 10L и правого глаза 10R, соответственно, преломляются очковыми линзами 11L и 11R, становятся направлениями 13L0' и 13R0' глаз и пересекаются друг с другом на предмете 12 в медианной плоскости 7 на предметной сферической поверхности 5. То есть, используя способ прослеживания нормального луча, системе придают такую конфигурацию, что предмет 12 (предмет, расположенный на месте, где линии 13R0 и 13L0 фиксаций, исходящие из центров 1L и 1R поворотов глазных яблок левого и правого глаз 10L и 10R и проходящие через конструктивные базовые точки 11PL и 11PR, пересекаются на предметной сферической поверхности 5 после прохождения через линзы) оказывается расположенным в медианной плоскости 7. Даже если он не оказывается расположенным в медианной плоскости 7, этого достигают, обеспечивая конвергенцию во время процесса оптимизации вычислений. В данном случае причина того, что предмету 3 на фиг.1 и предмету 12 на фиг.12 приданы различные позиции, заключается в том, что в общем случае конструктивные базовые точки 11PL и 11PR очковых линз 11L и 11R не находятся в горизонтальной плоскости 20.

Чтобы определить угол конвергенции, для удобства последующего пояснения в этом случае составляющую проекции в направлении, перпендикулярном к медианной плоскости медианной линии относительно линий 13L0 и 13R0 фиксаций левого и правого глаз 10L и 10R, определяют как «параллельную поверхности составляющую», а составляющую в направлении, параллельном медианной плоскости, определяют как «перпендикулярную к поверхности составляющую». В данном случае «медианной линией» согласно настоящему изобретению считается линия, проходящая через среднюю точку (начало координат) центров поворотов левого и правого глазных яблок на стороне изображения, проходящая через конструктивную точку на стороне предмета и имеющая среднее направляющих косинусов левой и правой линий фиксаций при выражении линии в значениях направляющих косинусов. Параллельные поверхности составляющие углов между левой и правой линиями 13L0, 13R0 фиксаций и медианными линиями, относящимися к линиям 13L0, 13R0 фиксаций, обозначены как θ_HL0 и θ_HR0 соответственно. Кроме того, перпендикулярные к поверхности составляющие углов между левой и правой линиями 13L0, 13R0 фиксаций и медианными линиями, относящимися к линиям 13L0, 13R0 фиксаций, обозначены как θ_VL0 и θ_VR0 соответственно. В дополнение к этому угол конвергенции в параллельном поверхности направлении θ_СН0 определяется как сумма θ_HR0 и θ_HL0. Знаки θ_CH0, θ_HR0 и θ_HL0 являются произвольными при условии, что они обладают непротиворечивостью, но в настоящем изобретении, когда глазные яблоки находятся в состоянии конвергенции, все они являются положительными значениями. Положительные и отрицательные значения изменяются на обратные, когда глазные яблоки находятся в состоянии дивергенции. Точно так же перпендикулярная к поверхности составляющая обозначена как θ_CV0, и она определяется суммой θ_VR0 и θ_VL0. Обычно центры поворотов левого и правого глазных яблок находятся почти в одной и той же горизонтальной поверхности, но имеются несколько случаев, когда они несколько отклоняются. Поэтому, что касается параллельного поверхности направления, то θ_CV0 придают положительное значение во время состояния конвергенции и придают отрицательное значение во время состояния дивергенции. Представление формулами горизонтальной относительно поверхности составляющей θ_CH0 и перпендикулярной к поверхности составляющей θ_CV0 угла конвергенции, который должен быть эталонным (эталонным значением угла конвергенции), имеет следующий вид:

θ_CH0=θ_HR0+θ_HL0,

θ_CV0=θ_CR0+θ_VL0.

В общем случае значение θ_CV0 равно 0 и форму линзы и базовую точку задают так, чтобы оно становилось 0.

На фиг.3 представлен вид, на котором показано, что углы θ_HL0 и θ_HR0 зрения, определенные на стороне изображения на фиг.2, сопоставлены с углами θ_HL0' и θ_HR0' зрения с помощью линий 13L0' и 13R0' фиксаций на стороне предмета. На фиг.4 и фиг.5 представлены виды, показывающие сбоку изображения на фиг.2 и фиг.3 соответственно. Можно видеть, что медианная линия 13RL0 линий 13L0 и 13R0 фиксаций на стороне изображения и медианная линия 13RL0' линий 13L0' и 13R0' фиксаций на стороне предмета проходят через начало 1 координат и отклонены от медианной линии 6, которая продолжается до предмета 12. В дополнение к определению на стороне изображения нижеследующее получено для стороны предмета

θ_CH0'=θ_HR0'+θ_HL0',

θ_CV0'=θ_VR0'+θ_VL0'.

(3) Третий этап (процесс вычисления аберрации в произвольной предметной точке оценивания)

Определения оптических расчетов и т.д. для бинокулярной системы, поясненные на втором этапе, будут далее описаны подробно, и оценивание оптики будет выполнено в произвольной точке оценивания линзы. Схематичная конфигурация бинокулярной системы в произвольном бинокулярном направлении показана на фиг.6. Подробности оптических вычислений будут поясняться с обращением к фиг.6. Произвольное положение предмета в произвольном бинокулярном направлении относительно начала 1 координат бинокулярной системы задают как точку 22 оценивания. Наряду с линиями фиксаций, начинающимися из центров 1L и 1R поворотов левого и правого глаз, проходящих через токи 11NL и 11NR оценивания левой и правой очковых линз 11L и 11R, преломляющихся и проходящих через точку 22 оценивания, используя способ прослеживания луча, задают продолжающиеся линии 13L и 13R на стороне изображения, относящиеся к линиям фиксаций. В данной ситуации в примере, показанном на фигуре, изображен случай, в котором точка 22' пересечения линий 13L и 13R фиксаций расположена за пределами предметной сферы 5. Даже если при единственном испытании пересечение линий 13L' и 13R' фиксаций не будет находиться в точке 22 оценивания, оптические лучи, которые сходятся в точке 22 оценивания, можно вычислять с требуемой точностью, изменяя углы лучей, излучаемых из центров 1L и 1R поворотов глазных яблок.

Что касается горизонтальной относительно поверхности составляющей θ_СН угла конвергенции в точке 22 оценивания, то в этом случае она определяется в соответствии с приведенным ниже:

θ_CH=θ_HR+θ_HL.

Точно так же вертикальную к поверхности составляющую θ_CV угла конвергенции в точке 22 можно определить в соответствии с приведенным ниже:

θ_CV=θ_VR+θ_VL.

В данном случае параллельные поверхности составляющие углов, ограниченные медианной линией 26, относящейся к линиям 13L и 13R фиксаций, и линии 13L и 13R фиксаций, которые включают в себя медианную линию 26, относящуюся к линиям 13L и 13R фиксаций, и которые параллельны поверхности, перпендикулярной к медианной поверхности, заданы как θ_HL и θ_HR, и точно так же в вертикальном направлении перпендикулярные к поверхности составляющие, которые включают в себя медианную линию 26 и которые параллельны поверхности, параллельной медианной поверхности, заданы как θ_VL и θ_VR.

То есть, параллельная поверхности составляющая и перпендикулярная к поверхности составляющая аберрации конвергенции в точке 22 оценивания выражаются в следующем виде:

(параллельная поверхности составляющая аберрации конвергенции): θ_CH-θ_CH0,

(перпендикулярная к поверхности составляющая аберрации конвергенции): θ_CV-θ_CV0.

На фиг.7 представлена диаграмма, показывающая углы θ_HL' и θ_HR' конвергенции в случае, когда они определены совместно с линиями 13L' и 13R' фиксаций на стороне изображения. В этом случае параллельные поверхности составляющие углов, ограниченных медианной линией 27, относящейся к линиям 13L' и 13R' фиксаций, и линии 13L' и 13R' фиксаций, которые включают в себя медианную линию 27, относящуюся к линиям 13L' и 13R' фиксаций, и которые параллельны поверхности, перпендикулярной к медианной поверхности, заданы как θ_HL' и θ_HR', и точно так же в вертикальном направлении перпендикулярные к поверхности составляющие, которые включают в себя описанную выше медианную линию 27 и которые параллельны поверхности, параллельной медианной поверхности, заданы как θ_VL' и θ_VR'. В то же время, как и в случае описанных выше определений на стороне изображения, параллельная поверхности составляющая и перпендикулярная к поверхности составляющая аберрации конвергенции, определяемые на стороне предмета в точке 22 оценивания, основанные на

θ_CH'=θ_HR'+θ_HL',

θ_CV'=θ_VR'+θ_VL',

выражаются в следующем виде:

(параллельная поверхности составляющая аберрации конвергенции): θ_CH'-θ_CH0',

(перпендикулярная к поверхности составляющая аберрации конвергенции): θ_CV'-θ_CV0'.

Разности оптических значений вдоль линий 13L и 13R фиксаций, показанных на фиг.6, относительно оптических значений вдоль линий 13L0 и 13R0 фиксаций, поясненных на фиг.2, представляют собой аберрации. А именно, сферическое преломляющее действие, степень астигматизма, оси астигматизма и угол конвергенции, которые вычисляют на втором этапе, задают в качестве эталонов, а на третьем этапе рефракционную ошибку и остаточный астигматизм вычисляют на основании различий в сферических преломляющих действиях, степенях астигматизма и осях астигматизма. Что касается угла конвергенции, то аберрацию конвергенции получают на основании описанного выше определения. Если еще раз определить детально, то, как упоминалось, аберрация конвергенции является разностью углов конвергенции при задании оптической величины вдоль главного луча, при этом главный луч продолжается от предмета до центра поворота глазного яблока и проходит через конструктивную базовую точку.

Аберрация конвергенции, определенная в настоящем изобретении, отличается от обычной разности бинокулярных изображений на сетчатке. В частности, аберрация конвергенции отличается от обычной разности бинокулярных изображений на сетчатке в том смысле, что она является аберрацией в угле конвергенции в состоянии, в котором носят левую и правую корректирующие очковые линзы, в том смысле, что она является аберрацией, когда наблюдается предмет, задаваемый в бинокулярном направлении (произвольная точка 22 оценивания на предметной сферической поверхности 5, включая медианную поверхность), и в том смысле, что она определяется не узловыми точками, а линиями фиксации, проходящими через центры поворотов глазных яблок. Кроме того, она отличается от разности бинокулярных изображений на сетчатке в том смысле, что имеются движения глазных яблок. В данном случае определение разности бинокулярных изображений на сетчатке основано на страницах 283-287 непатентного документа 10.

Кроме того, аберрация конвергенции, определенная в настоящем изобретении, также отличается от угла конвергенции, который фигурирует в психологии. Что касается «угла конвергенции», определяемого в психологии, то имеется его описание, например, в “Convergence movement and binocular stereopsis” (Optical Review, vol.23, №1 (January 1994), pp.17-22). В этом описании показано, что это «угол между точкой фиксации (точкой пересечения зрительных осей) и точкой поворота каждого из глаз (центров поворотов)». Различия между аберрацией конвергенции и углом конвергенции заключаются в том, что она является аберрацией угла конвергенции в состоянии, в котором носят левую и правую корректирующие линзы, в том, что она является аберрацией, когда наблюдается предмет, который задается в направлении бинокулярного зрения, и в том, что углу между линиями фиксаций, проходящими через левую и правую базовые точки очковых линз, придают эталонное значение для получения разности аберраций. Можно видеть, что значение совершенно отличается от аберрации конвергенции согласно настоящему изобретению, которая определяется на основании углов наблюдения от линий фиксации, которые проходят через очковые линзы и достигают точки оценивания.

(4) Разности из обычного примера

Здесь будут еще раз рассмотрены разности между аберрациями конвергенции и разность в горизонтальном направлении или разность в вертикальном направлении, описанные в патентном документе 1. В нижеследующих 5 пунктах рассматриваются разности аберраций конвергенции:

-а. Определение основано на вергентных движениях глазных яблок (контралатеральном бинокулярном движении) из закона равных иннерваций Геринга, который является законом бинокулярного зрения, а именно, определение основано на знании законов физиологии, получаемых в результате изучения конвергентного движения.

-b. Можно использовать произвольный предмет, определенный в направлении бинокулярного зрения.

-с. Оценки на одной и той же основе можно делать на протяжении всего поля зрения, поскольку имеется одна основа для оценок.

-d. За счет образования параллельной поверхности составляющей и перпендикулярной к поверхности составляющей получают соответствующее физиологии определение для случая разделения на две составляющие и для случая смещения от горизонтальной поверхности.

-е. Положение предмета не определено на поверхности, а определено в стереоскопическом пространстве.

В этом месте будет выполнен подробный анализ разности в горизонтальном направлении и разности в вертикальном направлении, описанных в патентном документе 1. Горизонтальная составляющая из фиг.2 патентного документа 1 показана на фиг.8. Поскольку вертикальное направление является аналогичным, ниже поясняется только разность ΔР_Н положений в горизонтальном направлении, описанная на странице 5 в строке 35 патентного документа 1. Как показано на фиг.8, расстояние между центрами поворотов обоих глазных яблок задано равным PD и расстояние от центров поворотов обоих глазных яблок до поверхности 59, включающую точку Р, задано равным L. Кроме того, точка равного деления центров поворотов обоих глазных яблок, которая также является точкой на поверхности 59 предмета, задана как точка q, но эта точка не показана на фигурах в патентном документе 1. Точка q определена как точка пересечения, в которой пересекаются линии Lr, L1 фиксаций, исходящие от центров поворотов обоих глазных яблок в направлении вперед, и поверхность 59. Углы наблюдения линий Lr, L1 фиксаций заданы как α_R и α_L, а углы наблюдения, относящиеся к линиям 54 и 55 фиксаций, от линий Lr, L1 фиксаций, заданы как Δα_R и Δα_L соответственно.

В таком случае разность ΔР_Н положений в горизонтальном направлении выражается в следующем виде:

ΔP_H=L×tan(α_R+Δα_R)-L×tan(α_L+Δα_L)-PD.

Кроме того, при использовании (α_R), (α_L) и L для расстояния PD между центрами поворотов обоих глазных яблок имеем следующее соотношение:

PD=L×tan(α_R)-L×tan(α_L).

Разность в горизонтальном направлении описывается как результат деления разности положений в горизонтальном направлении на расстояние L до предмета. Поэтому нижеследующими формулами устанавливается:

Разность в горизонтальном направлении =

=tan(α_R+Δα_R)-tan(α_L+Δα_L)-PD/L.

Заменив PD, получаем следующее:

Разность в горизонтальном направлении =

=tan(α_R+Δα_R)-tan(α_L+Δα_L)-(tan(α_R)-tan(α_L)).

В данном случае, только когда Δα_R и Δα_L являются достаточно малыми в центральной части поля зрения, нижеследующей приближенной формулой устанавливается:

Разность в горизонтальном направлении =Δα_R-Δα_L.

Таким образом, «разность в горизонтальном направлении» в патентном документе 1 в очень ограниченной узкой области центральной части поля зрения представляет собой разность углов конвергенции, когда наблюдают точку Р на той же самой поверхности 59, при этом угол между линиями Lr и L1 фиксаций делают эталонным. Однако она становится величиной, которая не связана с углом конвергенции в другой области помимо центральной части, в которой Δα_R и Δα_L являются большими, и она становится значением, которое не имеет основы в физиологии.

Если разность в горизонтальном направлении, которая не имеет физиологической основы, использовать в качестве оценочной функции, можно понять, что будут иметься следующие проблемы при оценивании характеристик пары очковых линз.

1. Точка Р и точка q должны быть на той же самой предметной поверхности 59, как указанной при пояснении фигуры Цейса. Поэтому, за исключением поверхности, для которой предметная поверхность является параллельной фронтальной плоскости, для разности в горизонтальном направлении базовая точка изменяется для каждого из расстояний до предмета, и не может быть способа оценивания для всей линзы. То есть отсутствует такое свойство, как аберрация.

2. Когда предмет находится на такой же предметной поверхности 59, как в случае патента Цейса, он становится одноосновным и отсутствует такое свойство, как аберрация. Однако, когда (α_R), (α_L), (Δα_R) и (Δα_L) становятся большими, то поскольку функция тангенса проявляет нелинейность в зависимости от угла, отсутствует согласованность с углом конвергенции, который представлен разностью Δα_R-Δα_L углов. Поэтому на периферии поля зрения разность в горизонтальном направлении не имеет физиологической основы.

3. Аналогичным образом, когда линии 14 и 15 фиксаций сдвинуты от горизонтальной плоскости, возникает разность относительно исходного угла конвергенции.

В соответствии с поясненным выше определением из патентного документа 1 не может быть единообразного определения для всей предметной поверхности, и оценочная функция становится не имеющей физиологической основы вокруг периферии поля зрения. Неправомерно оценивать бинокулярное зрение, используя неясное определение, для которого нет никакой основы.

(5) Пояснение различия на основании фактической линии фиксации

Далее подробно поясняются различия между линией фиксации согласно способу прослеживания луча в настоящем изобретении и фактической линией фиксации. Что касается параллельного поверхности направления, то имеется произвольное отношение соответствия в пределах границ дивергенции и границ конвергенции глазных яблок. Поэтому имеется возможность, что в параллельном поверхности направлении линии 13L0' и 13R0' фиксаций из фиг.6 всегда будут проходить через точку 22 оценивания. В данном случае это поясняется в соответствии с непатентным документом 8. При задании через θ ипсилатерального бинокулярного движения, через µ контралатерального бинокулярного движения, через M_R момента правого глаза, через M_L момента левого глаза закон равных иннерваций Геринга можно выразить следующими формулами:

θ+µ/2=M_R,

θ-µ/2=M_L.

В таком случае в пределах границ дивергенции и границ конвергенции глазных яблок произвольные M_R и M_L можно выражать в зависимости от θ и µ. То есть при произвольных движениях левого и правого глазных яблок в продолжение ипсирального бинокулярного движения и контралатерального бинокулярного движения в параллельном поверхности направлении может осуществляться прохождение через точку 22 оценивания.

Однако в перпендикулярном к поверхности направлении левое и правое глазные яблоки фактически не могут поворачиваться независимо. Поэтому с первого взгляда кажется, что глазные яблоки не могут поворачиваться в соответствии со способом вычисления линий фиксаций согласно настоящему изобретению. Однако вследствие движения моторная фузия может стать ближе к вертикальной фузии, и ее можно обнаруживать в перпендикулярном к поверхности направлению в зоне Панума. Непроизвольная фузия в перпендикулярном к поверхности направлении может иметь пороговое значение. Поэтому при линиях фиксаций, найденных с помощью способа прослеживания луча, аберрация конвергенции в перпендикулярном к поверхности направлении не вступает в противоречие с фактическими линиями фиксаций. Однако, если вертикальные фузионные вергентные движения глаз, которые больше порогового значения или равны ему, становятся перпендикулярной к поверхности составляющей, то естественно, что они не могут быть реализованы. Способ вычисления линий фиксаций путем прослеживания луча в настоящем изобретении означает определение возможности или невозможности вращательного движения глазного яблока.

В этом осуществлении упомянутые выше рефракционную ошибку, остаточный астигматизм и аберрацию конвергенции вычисляют по мере приближения аберраций к точке оценивания (обычно каждый шаг составляет 1-10° в направлении бинокулярного зрения на всей поверхности линзы, и имеются случаи, когда линии фиксаций существуют только в одном из левого направления и правого направления, а точки также являются базовыми точками) предмета в направлении бинокулярного зрения в системе предмет - очковые линзы - бинокулярные глазные яблоки. По вычисленной аберрации конвергенции оценивание выполняют следующим образом. В частности, получают пороговые значения для сенсорной фузии и моторной фузии, соответственно, а оценивание выполняют на основании того, находятся они или нет в пределах определенного диапазона.

В этом месте будет добавлено пояснение относительно бинокулярных функций, включая фузию, на которых сосредоточено внимание в настоящем изобретении. Бинокулярные функции большей частью распределяют по категориям на симультанное зрение, фузию и стереоскопическое зрение. Например, подробные пояснения их имеются в непатентном документе 3. В непатентном документе 3 они распределены по категориям в структуры, так что фузия делается возможной, когда симультанное зрение делается возможным, а стереоскопическое зрение делается возможным, когда фузия делается возможной. В настоящем изобретении внимание сосредоточено на фузии, а пояснения других функций опущены. Однако однозначно установлено, что без фузии не реализуется стереоскопическое зрение, которое является высшей функцией бинокулярного зрения. Фузия является функцией зрения, которая объединяет части зрительной информации с отдельной подачей на один соответствующий глаз. Она является сенсорной фузией, которая объединяет предметы в один без движения глазных яблок. Конвергентное, дивергентное движение и вертикальные фузионные движения глазных яблок, предназначенные для получения сенсорной фузии, называют моторной фузией. Она описана, например, в непатентном документе 4 (David M. Hoffman, et al., “Vergence-accommodation conflicts hinder visual performance and cause visual fatigue”, Journal of Vision, vol.8, №3, 33 (2008)), в котором сделано подразделение на моторную фузию и сенсорную фузию.

Диаграммы связи конвергенция-аккомодация из фиг.2 на странице 4 непатентного документа 4 разделены на две группы, относящиеся к сенсорной фузии и моторной фузии. Они показаны на фиг.18А и фиг.18В. На фиг.18А показана сенсорная фузия, при этом по горизонтальной оси представлено стимульное расстояние, которое отражает величину стимула (единица: диоптрия, дптр), а по горизонтальной оси представлено фокусное расстояние (дптр). На фиг.18В показана моторная фузия, при этом по горизонтальной оси представлено расстояние (дптр) конвергенции, а по вертикальной оси представлено фокусное расстояние (м). Что касается фиг.18А, то можно понять, что при сенсорной фузии фузионная зона Р Панума и глубина резкости являются связанными. Что касается фиг.18В, то можно понять, что при моторной фузии относительная конвергенция и относительная аккомодация являются связанными. При сравнении фиг.18А и фиг.18В можно понять, что моторная фузия в несколько раз больше сенсорной фузии.

Кроме того, способ измерения и стандартное значение, имеющее отношение к моторной фузии, описаны, например, в непатентном документе 5 (написанном Yukio Izumi, Toshinari Kazami, “Examination of Binocular Function”, Revised Version, Waseda Optometry College (1985), p.5).

Будет пояснен способ выражения угла конвергенции. При задании через МА метрового угла через θ минуты дуги, через Р призменной диоптрии и через PD межзрачкового расстояния (единица: мм) удовлетворяются нижеследующие выражения (1-3). В данном случае через

Справочные примеры численных расчетов показаны на фиг.19А и фиг.19В. На фиг.19А межзрачковое расстояние равно PD=0,06 м, а на фиг.19В оно равно PD=0,065 м. В каждом из численных примеров на фиг.19А и фиг.19В приведены в качестве параметров расстояние (см), метровый угол МА, минута дуги (мин), Δ (диоптрия).

Далее будут дополнены пояснения относительно сенсорной фузии и моторной фузии. Сенсорная фузия представляет собой фузию, при которой отсутствует движение глазных яблок, а моторная фузия представляет собой фузию при наличии движения глазных яблок. Этим они отличаются друг от друга. Сенсорная фузия будет пояснена в соответствии со стр.131-132 непатентного документа 6 (Edited by Keiji Uchikawa, Satoshi Shioiri, “Vision II”, Asakura Publishing Co., Ltd. (2007), pp.131-132). В непатентном документе 6 написано следующее: «Чтобы два изображения на сетчатке, имеющие бинокулярную диспаратность, воспринимались как одно, необходимо, чтобы величина диспаратности находилась в пределах определенного диапазона. Эту зону называют фузионной зоной Панума (или фузионной зоной изображения), поскольку Панум впервые измерил эту зону в процессе систематических экспериментов. Фузионная зона зависит от стимульных условий (таких как пространственно-временная частота, положение сетчатки, наличие или отсутствие периферического стимула, способ измерений или критерий определения) и изменяется в значительной степени, от нескольких минут до нескольких градусов. Поэтому ее нельзя представлять с помощью конкретного результата эксперимента».

В данном случае бинокулярная диспаратность представляет собой разность между зрительными осями, стягивающими узловые точки левого и правого глазных яблок и точкой фиксации. В упрощенном случае невозможно провести различие между узловой точкой и центром поворота, поскольку несовпадение узловой точки и центра поворота очень небольшое по сравнению с расстоянием во внешнем мире. Что касается диапазона сенсорной фузии, то возможность измерения его в процессе отдельного эксперимента зависит от пространственной частоты, то есть зависит от формы и размера визуального предмета. Эта зависимость описана, например, в непатентном документе 7 (Schor C. Wood, I. Ogawa J., “Binocular sensory fusion is limited by spatial resolution”, Vision Research, 24 (7), (1984), pp.661-665). На фиг.20 показана фигура со стр.584 непатентного документа 7. Эта фигура широко используется, и использование ее описано на стр.316 непатентного документа 3. На фиг.20 по горизонтальной оси показана пространственная частота (то есть обратная величина ширины образа), а по вертикальной оси показана фузионная зона Панума. На фиг.20 представлены для сравнения результат для предмета в виде прямоугольного образа и результат для предмета в виде изображения случайных точек.

Как показано на фиг.20, в состоянии, в котором глазное зрение является сильным, а пространственная частота высокой, фузионная зона является относительно узкой и почти постоянной. Кроме того, фузионная зона различается в горизонтальном направлении и в вертикальном направлении, и существует пространственная анизотропия. Когда пространственная частота является высокой, а именно на центральной ямке сетчатки, фузионная зона в вертикальном направлении меньше фузионной зоны в горизонтальном направлении или равна ей. Известно, что различия фузионной зоны Панума проявляются в зависимости от условия предъявления предмета. Например, широко известно, что фузионная зона Панума является более широкой в случае прямоугольного образа, который возникает повседневно, чем в случае точечного изображения.

Что касается пояснения диапазона диспаратности в горизонтальном направлении, то зависимость между горизонтальной диспаратностью сетчатки и перцептивной глубиной показана на фиг.21 (страница 86 непатентного документа 6). На фиг.21 по горизонтальной оси показано бинокулярная диспаратность сетчатки обоих глаз в горизонтальном направлении, а по вертикальной оси показана перцептивная глубина в зависимости от бинокулярной диспаратности сетчатки. Из фиг.21 можно понять, что величина глубины возрастает пропорционально повышению бинокулярной диспаратности, но после прохождения предела фузии это возрастание больше не является пропорциональным, а после того как глубина достигает максимума, глубина уменьшается. Следовательно, поскольку максимум глубины и предел фузии имеют различные значения, можно сказать, что фузия и стереоскопическое зрение представляют собой различные физиологические явления. Имеются индивидуальные различия в значениях максимума глубины и предела фузии, и они изменяются в зависимости от условий, таких как пространственная частота или время предъявления. Поэтому бинокулярная диспаратность сетчатки, соответствующая диапазону от предела фузии до максимума глубины, можно приближенно трактовать как «фузионную зону Панума».

Имеются документы, в которых описаны измеренные значения моторной фузии и сенсорной фузии, отличающиеся от приведенных выше. Из всесторонней оценки раскрытий этих документов следует, что сенсорная фузия является частью моторной фузии. В данном случае эти результаты получены большей частью на основании психологических измерений.

(6) Пояснение порогового значения фузии

Начиная с этого места вернемся к пояснению этапов реализации способа оценивания очковых линз согласно настоящему изобретению. В осуществлении на основании значения аберрации конвергенции, полученного на описанном выше этапе, определяют, возможна ли сенсорная фузия или возможна моторная фузия. В качестве показателей порогового значения сенсорной фузии можно рассматривать фузионную зону Панума и фокусные расстояния глазных яблок. Однако, как уже описывалось, для количественного определения их требуются точные и тщательные измерения, зависящие от условий стимулирования фузии. К тому же, поскольку природа их такая, что невозможно описать их путем конкретного измерения, их задают, не полагаясь на измерение. Что касается способа задания, то они могут произвольно выбираться из известных измеренных значений, по усмотрению разработчика с учетом условий использования очковых линз. В частности, для горизонтального направления фузионной зоны Панума пригодна середина интервала от предела фузии бинокулярной диспаратности сетчатки до максимума глубины. Исходя из фиг.21 для горизонтального направления пригодна половина бинокулярной диспаратности сетчатки. Кроме того, что касается фокусного расстояния, заявитель не смог обнаружить какого-либо надежного определенного значения. Из описанных численных значений, полученных на основании горизонтальной диспаратности сетчатки 15'-60', для диоптрийной ширины является пригодным диапазон приблизительно 0,06-0,3. Кроме того, диапазон 4'-30' является пригодным для вертикальной диспаратности сетчатки. То есть в качестве порогового значения сенсорной фузии можно задавать 0,06-0,3 дптр в горизонтальном направлении и 0,016-0,15 дптр в вертикальном направлении.

Как ясно из сравнения схематичной диаграммы 18А сенсорной фузии со схематичной диаграммой 18В моторной фузии, пороговые значения моторной фузии можно задавать от двух до нескольких раз более высокими, чем пороговое значение сенсорной фузии. Кроме того, например, на основании способа измерения из непатентного документа 5 можно индивидуально измерять положительную относительную конвергенцию, отрицательную относительную конвергенцию и вертикальные фузионные вергентные движения глазных яблок, которые являются измеряемыми величинами, и вычислять и получать их в соответствии с возрастом и т.д., и полученные результаты задавать в качестве пороговых значений моторной фузии. Моторная фузия, например, при наличии аберрации конвергенции в момент времени, когда линии фиксации движутся, находится в пределах пороговых значений положительной относительной конвергенции, отрицательной относительной конвергенции и вертикальных фузионных вергентных движений глазных яблок, это означает, что условие фузии удовлетворяется относительно конвергенции. Поскольку в данном случае ее диапазоном является предел фузии, имеется опасность утомления глаз вблизи порога. Поэтому предпочтительно, чтобы пороговые значения моторной фузии, в которые она может быть встроена с комфортом, задавались в зонах комфорта Персиваля (в пределах одной трети от центра диапазона относительной конвергенции, при этом относительная конвергенция является суммой положительной конвергенции и отрицательной относительной конвергенции, и в пределах 3 призменных диоптрий для угла конвергенции). Кроме того, в упрощенном случае предпочтительно, чтобы они находились в пределах одной трети от соответствующих центров положительной относительной конвергенции и отрицательной относительной конвергенции.

То же самое можно сказать относительно средней рефракционной ошибки. То есть когда рефракционная ошибка находится в пределах диапазона положительной относительной аккомодации и отрицательной относительной аккомодации, измеряемых способом измерения, описанным, например, в непатентном документе 5, то можно определить, что фузия является возможной. Зоны комфорта Персиваля являются состоятельными при наличии рефракционной ошибки. То есть, диапазоны в пределах 1/3 являются предпочтительными. То есть когда аберрация конвергенции находится в пределах одной трети положительной относительной конвергенции и отрицательной относительной конвергенции и когда средняя рефракционная ошибка находится в пределах одной трети положительной относительной аккомодации и отрицательной относительной аккомодации, можно сказать, что возможна комфортная фузия, в случае которой менее вероятно возникновение нарушения зрения в части бинокулярного зрения.

[2] Способ расчета и способ изготовления очковых линз

Далее поясняется способ расчета и способ изготовления очковых линз в соответствии с настоящим изобретением. Способ расчета очковых линз согласно осуществлению включает в себя этап выполнения оптимизации вычислений с использованием аберрации конвергенции в качестве показателя оценочной функции.

В этом месте будет изложен расчет формы линзы при общей оптимизации вычислений, которая также используется в осуществлении. Что касается формы линзы и предмета, то в общем случае поверхность выражают моделированием поверхности в общей свободной форме, таким как NURBS (неравномерный рациональный B-сплайн), или известным числовым выражением. Кроме того, толщину и структуру выражают с учетом подходящих коэффициентов. В то же время форму линзы и предмета определяют коэффициентами, которые являются компонентами. На первом этапе известные параметры вводят в компьютер. Известные параметры включают в себя предмет, структурную взаимосвязь предмет - линза - глазное яблоко, ограничивающие условия (например, достижение определенного заданного значения в конструктивной базовой точке, толщина не должна становиться отрицательной и т.д.), оценочную функцию, для которой аберрация линзы считается показателем и т.д. На следующем этапе оптимизации вычислений комбинацию коэффициентов компонентов линзы находят таким образом, чтобы оценочные функции, получаемые по точкам оценивания на предмете становились меньше при удовлетворении ограничивающих условий. Что касается условия конвергенции, то сводящие вычисления повторяют до нахождения минимального значения оценочной функции или комбинации коэффициентов, при которых оценочные функции становятся по существу меньшими. Когда условие конвергенции удовлетворяется и итерационное вычисление завершают, определяют коэффициенты компонентов линзы. Этапы в целом называются определением формы линзы или проектированием линзы. При таком известном вычислении с оптимизацией проектирование линзы находится в эквивалентной взаимосвязи с известным предметом, в структурной взаимосвязи, с ограничивающими условиями и оценочными функциями. То есть, когда предмет, структурная взаимосвязь, ограничивающие условия и оценочные функции определены, конструкция линзы является однозначно определенной.

На фиг.9 представлена блок-схема последовательности действий для пояснения способа проектирования очковых линз согласно настоящему изобретению. Когда процесс проектирования начинают, сначала вводят (этап S0) данные относительно материалов линзы, данные о форме, которые основаны на технических требованиях, имеющих отношение к предписанию, о центральной толщине, данные, имеющие отношение к форме глаз, лица и оправы, и в зависимости от необходимости измеренные значения относительной конвергенции и т.д., заданные величины пороговых значений фузии, которые основаны на индивидуальном суждении проектировщика. Подробности относительно описанных выше данных приведены ниже.

-а. Данные, имеющие отношение к материалам линзы.

В частности, они включают в себя 3-мерную форму очковой линзы, показатель преломления и число Аббе, и т.д.

-b. Данные о форме, которые основаны на технических требованиях, имеющих отношение к предписанию

Предписанные рефракции, такие как S-рефракция, С-рефракция, астигматический угол, призматическое действие линзы, призменный угол, предписанная дальность видимости.

-с. Центральная толщина

Ее вводят только тогда, когда линза является положительной линзой.

-d. Данные, имеющие отношение к форме глаз, лица и оправы

В частности, они включают в себя фронтальный угол наклона линзы, угол возвышения, PD (расстояние между зрачками обоих глаз), VR (расстояние между центром поворота глазного яблока и задней вершиной очковой линзы) и т.д.

-е. Заданные величины пороговых значений фузии

Пороговые значения моторной фузии и пороговые значения сенсорной фузии, определяемые в соответствии с индивидуальной изменчивостью или назначением, вычисляют на основании индивидуальных измеренных значений (например, измеренных значений относительной конвергенции, положительной относительной конвергенции, отрицательной относительной конвергенции, вертикальных фузионных вергентных движений глазных яблок) и вводят. Или вводят пороговые значения, выбранные проектировщиком в соответствии с целевой установкой владельца очков.

Затем в соответствии со способом проектирования очковых линз этого осуществления систему координат конфигурируют (этап S1) в соответствии с системой предмет - очковые линзы - оба глаза. Далее в этой системе координат оптические аберрации вычисляют (этап S2) на основании описанных выше входных данных. В частности, средние ошибки рефракции и астигматизм минимизируют, используя известный способ прослеживания луча, вследствие чего получают предписанные рефракции в конструктивных базовых точках и вместе с ними углы конвергенции на линиях фиксаций, проходящих через конструктивные базовые точки, которые становятся эталонными аберрациями конвергенции. Получаемым углам конвергенции придают эталонные значения аберрации конвергенции.

Затем в соответствии со способом проектирования очковых линз согласно этому осуществлению в каждой из базовых точек очковых линз аналогичным образом, используя способ прослеживания луча, вычисляют (этап S3) средние ошибки рефракции и астигматизм, а также аберрации конвергенции, и эти значения получают вычитанием эталонных значений аберраций конвергенции, полученных на этапе S3, из углов конвергенции.

Далее в соответствии со способом проектирования очковых линз согласно осуществлению выполняют оптимизацию вычислений, например, демпфированными методами наименьших квадратов, чтобы вычисленные значения оценочных функций, в данном случае, например, значения аберраций конвергенции стали минимальными. На этом этапе дополнительно определяют, будут ли они меньше, чем описанные пороговые значения, или равны им. Кроме того, на этом этапе определение может быть сделано не для всей области оценивания, а в пределах заданного участка, включающего конструктивные базовые точки, например в пределах радиуса 3-5 мм. Когда определяют, что значения аберраций конвергенции на этом этапе S4 не меньше, чем пороговые значения и не равны им («нет» на этапе S4), данные о форме корректируют (этап S5) с тем, чтобы скорректировать оптические аберрации. В данном случае корректируют, например, переменные параметры преломляющей поверхности. Когда на этапе S4 определяют, что значения аберраций конвергенции меньше, чем пороговые значения («да» на этапе S4), впоследствии определяют (этап S6), завершилось ли оценивание на всей поверхности линзы.

Когда на этапе S6 определяют, что оценивание не завершилось («нет» на этапе S6) на всей поверхности линзы и остается возможность вычислений для других базовых точек, то в процессе возвращаются к этапу S3, и вводят значения оптических характеристик на других точках линзы. Когда определяют, что оценивание во всех заданных точках оценивания завершилось («да» на этапе S6), оценивание завершают и определяют (этап S7) конструктивные параметры на всей поверхности линзы.

В случае выполнения упомянутых выше этапов способ проектирования очковых линз согласно осуществлению завершают. В данной ситуации информация, вводимая на этапе S1, не ограничена описанной выше информацией, и можно вводить другую информацию и добавлять другую информацию для вычисления оценочных функций. Кроме того, очковые линзы изготавливают, обрабатывая линзы на основании найденных оптических конструктивных параметров. К тому же можно добавлять параметры формы, например исходные параметры формы изготовителя или корректирующие коэффициенты, определяемые на предприятии (на оборудовании изготовителя).

И после обработки задних поверхностей линз на основании найденных оптических конструктивных параметров очковые линзы могут выпускаться как продукт.

[3] Система для изготовления очковых линз

Далее поясняется осуществление системы для изготовления очковых линз, в которой реализуется способ изготовления очковых линз согласно настоящему изобретению. На фиг.10 представлена структурная схема системы для изготовления очковых линз. Как показано на фиг.10, в системе 500 имеются измерительное устройство 101 на стороне пункта 100 приема заказов на изготовление очков, которым измеряют зрение и относительную конвергенцию или положительную относительную конвергенцию и отрицательную относительную конвергенцию глаз клиента, который заказывает линзы, и компьютер 102 на стороне приема заказов, который обеспечивает возможность ввода различной информации, включая значения, измеряемые измерительным устройством, и обработки данных, необходимых для заказа очковых линз. В данном случае, когда результаты измерений, имеющие отношение к конвергенции, такой как относительная конвергенция, не являются входными данными, данные, имеющие отношение к фузии, которая зависит от выбора заказчика, могут быть входными данными. Кроме того, для выбора пороговых значений фузии на стороне изготовителя линзы входными данными могут быть такие, как возраст или назначение.

На другой стороне относительно стороны приема заказов, например на стороне изготовителя 200 линз, предусмотрен компьютер 201, который подключен к линии 300 связи, такой как Интернет, для приема информации, выводимой с компьютера 102 на стороне заказа. Компьютер 201 на стороне изготовления обладает функцией выполнения операций, необходимых для приема заказов на очковые линзы и в то же время обладает функцией реализации способа проектирования очковых линз, такого как способ, поясненный на фиг.9. То есть информация, необходимая для проектирования очковых линз, которая направляется от компьютера 102 на стороне приема заказов, включает в себя относительную конвергенцию и данные, используемые при выборе пороговых значений для конвергенции. Затем компьютер 201 на стороне изготовления выполняет оптимизацию вычисления, имеющего отношение к аберрации конвергенции, с использованием системы предмет - очковые линзы - глазные яблоки, которая задается с использованием настоящего изобретения, и определяет оптические конструктивные параметры и одновременно выводит информацию об изготовлении, предназначенную для изготовления очковых линз, получаемую на основании оптических конструктивных параметров, в устройство 202 для обработки линз.

Кроме того, информация, вводимая в компьютер 201 на стороне изготовления, не ограничена информацией, которая показана на этапе S0 из фиг.9, описанном выше, и можно вводить другую информацию и добавлять другую информацию к вычислению оценочной функции. Кроме того, очковые линзы получают обработкой линз на основании найденных оптических конструктивных параметров, и в это время могут быть добавлены параметры формы, такие как собственные параметры формы изготовителя или корректировочные коэффициенты, определяемые на предприятии (на оборудовании изготовителя).

На фиг.11 показана функциональная схема согласно осуществлению, предназначенная для пояснения функции компьютера 201 на стороне изготовления, при этом компьютер 201 на стороне изготовления является основной частью системы для изготовления очковых линз. Как показано на фиг.11, компьютер 201 на стороне изготовления включает в себя блок 203 ввода данных, предназначенный для ввода данных различных видов, передаваемых с компьютера 102 на стороне приема заказов, блок 204 вычисления угла конвергенции и аберраций конвергенции, предназначенный для вычисления эталонных значений угла конвергенции или аберраций конвергенции на основании входных данных, блок 205 оптимизации аберраций конвергенции, предназначенный для вычислительной оптимизации оценочных функций, включающих аберрации конвергенции в качестве показателя, и блок 206 оценивания аберраций конвергенции, предназначенный для сравнения значений аберраций конвергенции с заданными пороговыми значениями. Компьютер 201 на стороне изготовления также включает в себя блок 207 коррекции конструктивных данных, предназначенный для коррекции конструктивных данных, например данных о форме линзы, когда необходимо корректировать оптические характеристики в результате выполнения оценивания в блоке 206 оценивания аберрации конвергенции, блок 208 определения оптических конструктивных параметров, предназначенный для определения оптических конструктивных параметров, когда оценивание в каждой из точек оценивания завершено, и блок 209 вывода конструктивных данных, предназначенный для вывода конструктивных данных, основанных на оптических конструктивных параметрах, в устройство 202 для обработки линз.

С измерительного устройства 101 в пункте 100 приема заказов на изготовление очков, показанном на фиг.10, вводится зрение клиента, который заказывает очковые линзы, и измеренные значения относительной конвергенции и т.д., а также информация о клиенте, заказывающем очки, которую можно использовать для задания пороговых значений конвергенции, а на компьютере 102 на стороне приема заказов добавляется заданный технологический процесс, и передается к изготовителю 200 линз по линии 300 связи. В компьютер 201 (компьютер на стороне изготовления) у изготовителя 200 линз вводятся данные о форме, которые основаны на данных, имеющих отношение к материалам линзы или техническим требованиям, и данные, имеющие отношение к глазам, лицу и форме оправы, которые принимаются на блоке 203 ввода данных, и в то же время вводятся данные, такие как данные, необходимые для задания пороговых значений конвергенции.

Далее блок 204 вычисления угла конвергенции и аберраций конвергенции вычисляет аберрации конвергенции по эталонным значениям аберраций конвергенции и углов конвергенции в точках оценивания, основанных на входных данных (предписанных значениях). Блок 205 оптимизации аберраций конвергенции получает необходимые значения оптических характеристик, таких как астигматизмы в соответствующих точках оценивания очковых линз, при этом вычисленные аберрации конвергенции полагаются оценочными функциями, и вычисляет по оценочным функциям оптимизированные значения оптических характеристик в соответствующих точках оценивания. Оптимизация вычисления выполняется демпфированным методом наименьших квадратов и т.д.

После этого блок 206 оценивания аберраций конвергенции сравнивает значения аберраций конвергенции, вычисленные блоком 204 вычисления угла конвергенции и аберраций конвергенции, с заданными пороговыми значениями. На основании результата сравнения от блока 206 оценивания аберраций конвергенции, а именно в случае, когда значения аберраций конвергенции не достигают заданных значений, блок 207 коррекции конструктивных данных корректирует конструктивные данные очковых линз так, чтобы аберрации конвергенции находились в пределах заданного диапазона фузии. Блок 208 определения оптических конструктивных параметров определяет оптические конструктивные параметры в соответствующих точках оценивания. И когда оценивание во всех заданных оценочных точках завершается, найденные оптические конструктивные параметры для всех поверхностей линз передаются с блока 209 вывода конструктивных данных в устройство 202 для обработки линз, которое показано на фиг.10.

В качестве устройства 202 для обработки линз используется обычное устройство для изготовления очковых линз, в котором используется, например, процесс резания и полировки линзы на основании входных данных о кривизне передней поверхности или задней поверхности линзы, или кривизне обеих поверхностей. Поскольку устройство 202 для обработки линз является известным устройством, используемым в качестве устройства для изготовления очковых линз, конкретное пояснение устройства опускается.

[4] Осуществление способа оценивания очковых линз

Далее поясняются результаты выполнения оценивания аберраций конвергенции бинокулярного зрения различных очковых линз, для которого используется способ оценивания очковых линз согласно осуществлению настоящего изобретения.

(1) Первое осуществление (пример степени 0 дптр астигматизма)

В качестве первого осуществления рассматривается пример вычислений аберраций конвергенции для случая, когда левая и правая очковые линзы имеют сферическую диоптрийную силу 4 дптр и степень астигматизма 0 дптр. Результаты показаны на фиг.12 и фиг.13. Этот пример является примером оценивания однофокусных очковых линз, а итерационное вычисление для оптимизации не выполнялось. Предмет задавался на полусферической поверхности бесконечного радиуса, которая центрировалась относительно начала 1 координат в направлении наблюдения в системе координат, поясненной в описанном выше осуществлении. А именно, оценивание выполняли для дальнего вида. Очковая линза представляла собой двухстороннюю асферическую линзу общего применения, и она была успешно скорректирована в соответствии с функцией остроты зрения, описанной в WO2002/088828, WO2004/018988 или в описании PCT/JP2008/069791, имеющих отношение к заявке настоящего изобретения. Чтобы прояснить результат способа оценивания настоящего изобретения, в этом примере передний угол наклона, угол возвышения и эксцентричность линзы полагали равными 0. Расстояние от вершины роговой оболочки до центра поворота глазного яблока было 27,7 мм, число Аббе задавали равным 32, радиус линзы задавали равным 75 мм и межзрачковое расстояние задавали равным 62 мм. Две части, состоящие из фиг.12 и фиг.13, представляют собой один набор, и на них в виде диаграмм показаны оценки в соответствующих точках оценивания очковой линзы. А именно, горизонтальная ось и вертикальная ось представляют бинокулярные направления, горизонтальная ось представляет горизонтальное направление, вертикальная ось представляет вертикальное направление и единицей является величина угла. На фиг.12 показаны аберрации конвергенции в параллельном поверхности направлении, на фиг.13 показаны аберрации конвергенции в перпендикулярном к поверхности направлении, а единицей на обеих фигурах является призменная диоптрия. Как показано на фиг.12 и фиг.13, параллельные поверхности составляющие и перпендикулярные к поверхности составляющие аберраций конвергенции являются очень малыми, и они меньше 0,005 призменной диоптрии или равны этой величине почти во всех зонах. То есть фузия успешно выполняется, а характеристика бинокулярного зрения является хорошей. Кроме того, можно считать, что аберрации конвергенции выражаются не только в скалярной форме, но также и в векторной форме. Это также находится в объеме настоящего изобретения.

(2) Второе осуществление (пример, в котором разность между левой и правой сферическими диоптрийными силами больше -2 дптр или равны им)

Далее во втором осуществлении выполнялось оценивание очковых линз, которое в общем случае касалось определения анизометропии (большей чем -2 дптр или равной ей, слева и справа). В этом примере сферическую диоптрийную силу правой очковой линзы задавали равной -4 дптр, степень астигматизма задавали равной 0 дптр, то есть такой же, как для линзы, использовавшейся в описанном выше первом осуществлении. С другой стороны для левой очковой линзы сферическую диоптрийную силу задавали равной -6 дптр, степень астигматизма задавали равным 0 дптр, а другие условия задавали такими же, как и в описанном выше первом осуществлении. Этот пример также является примером оценивания очковых линз, а итерационное вычисление для оптимизации не выполнялось. Результаты вычислений аберраций конвергенции показаны на фиг.14 и фиг.15. На фиг.14 показана параллельная поверхности составляющая аберраций конвергенции, а на фиг.15 показана перпендикулярная к поверхности составляющая аберраций конвергенции. Параллельная поверхности составляющая и перпендикулярная поверхности составляющая являются очень большими, и в общем случае в очковых линзах для коррекции анизометропии аберрации конвергенции являются большими от центра линзы по радиальному направлению. Как показано на фиг.14 и фиг.15, аберрации конвергенции больше 5 призменных диоптрий, а зона сенсорной фузии является узкой. А именно, при ношении этих очковых линз фузия осуществляется за счет моторной фузии. Поэтому считается, что отсутствует перерыв в поворотном движении глазных яблок. Когда возникает зрительное утомление, можно считать, что оно является одной из причин.

(3) Третье осуществление (пример, в котором угол возвышения равен 20°)

Далее в третьем осуществлении вычисляли аберрации конвергенции для случая, когда в оправе имелся угол возвышения. Результаты показаны на фиг.16 и фиг.17. В третьем осуществлении сферическую диоптрийную силу и степень астигматизма задавали такими, как для линзы, использованной в приведенном выше первом осуществлении, и для оценивания степени действия угла возвышения в этом примере угол возвышения задавали равным 20°. Остальные условия были такими же, как в описанном выше первом осуществлении. На фиг.16 показана параллельная поверхности составляющая аберраций конвергенции, а на фиг.17 показана вертикальная к поверхности составляющая аберраций конвергенции. Третье осуществление также является примером оценивания очковых линз, а итерационное вычисление для оптимизации не выполнялось. В третьем осуществлении отличие заключается в том, что среди аберраций конвергенции параллельная поверхности составляющая, показанная на фиг.16, является очень большой по сравнению с перпендикулярной к поверхности составляющей, показанной на фиг.17. Кроме того, по сравнению со вторым осуществлением деградация параллельной поверхности составляющей является значительной, и становится ясно, что очковая линза при угле возвышения 20° оказывает большее воздействие на бинокулярное зрение, чем очковая линза для анизометропии (степень различия 2 дптр).

Из приведенного выше можно видеть, что становится возможным количественно оценивать бинокулярное зрение очковых линз, используя аберрации конвергенции, способом оценивания очковых линз согласно осуществлению настоящего изобретения. В дополнение к этому, хотя пример вычисления опущен, можно расширять обеспечиваемую фузией зону бинокулярного зрения благодаря оптимизации с использованием аберрации конвергенции в качестве показателя оценочных функций. А именно, можно улучшать характеристику бинокулярного зрения. Кроме того, настоящее изобретение не ограничено конфигурациями, поясненными в описанных выше осуществлениях, и различные модификации и изменения возможны без отступления от конфигурации изобретения, например, при задании предмета на другом месте, а не на полусфере.

Реферат

Изобретение относится к области офтальмологии и направлено на обеспечение равномерного оценивания очковых линз по всему бинокулярному полю зрения, количественное оценивание условия фузии, которая является характеристикой бинокулярного зрения, что обеспечивается за счет того, что оптическую систему определяют, используя систему координат, в которой начало находится на средней точке центров поворотов обоих глазных яблок, а предмет точно определяется зрительным направлением от начала координат. При этом эталонное значение угла конвергенции вычисляют, используя линии фиксаций зрительных направлений к предмету, который находится на пересечении линий фиксации после прохождения через конструктивные базовые точки очковых линз. Угол конвергенции вычисляют между линиями фиксации, проходящими через очковые линзы и продолжающимися к предметной точке оценивания в заданном зрительном направлении, и вычисляют аберрации конвергенции по разности между углом конвергенции и эталонным значением θугла конвергенции. 4 н. и 3 з.п. ф-лы, 27 ил.

Формула