Схема для компенсации дисперсии в оптических системах передачи с помощью оптического фильтра - RU2115145C1

Чертежи

Описание

Изобретение относится к схеме для компенсации дисперсии в оптических системах передачи с помощью оптического фильтра.

При передаче информации по волоконно-оптическим линиям связи с лежащими в области гигабит/с скоростями передачи данных по световоду дисперсия в волокне является определяющей для преодолеваемой длины участка. Это, в частности, справедливо также в окне длин волн в окрестности 1,55 мкм, так как здесь затухание может быть уменьшено с помощью оптических усилителей, в то время как дисперсия стандартного волокна с примерно 17 пс/нм/км имеет довольно большие положительные значения. Поэтому существует интерес к компонентам, которые имеют отрицательную дисперсию и могут образовывать вместе со стандартным волокном свободную от дисперсии среду передачи. Для очень широкополосных применений, таких как частотное уплотнение (WDM), было бы, кроме того, желательным также иметь возможность компенсировать (составляющие при 1,55 мкм примерно 0,6 пс/нм²/км) нарастание дисперсии стандартного волокна. Кроме того, могут представлять интерес компоненты, которые имеют переменную ( также по знаку) дисперсию, чтобы, например, иметь возможность компенсировать остаточную дисперсию дисперсионно-сдвинутого волокна на длине волны передатчика.

Для компенсации дисперсии является интересным использование пассивных, линейных принципов, так как они, коль скоро не появляются никакие нелинейные эффекты в передаче, позволяют применение компенсационных компонентов в любом месте оптического участка передачи. Кроме того, в частности, в случае пассивных принципов существуют шансы на благоприятные с точки зрения расходов и компактные компоненты.

В связи с компенсацией дисперсии наряду с (сегодня уже коммерчески предлагаемыми) компенсирующими дисперсию волокнами уже были представлены различные компоненты: интерферометры Фабри-Перо, кольцевые резонаторы, каскадированные интерферометры Маха-Цендера, каскадированные кристаллы с двойным преломлением, свободная оптика с решетками, решетки Брэгга с переменным в зависимости от места периодом решетки (Chirped Grating).

Изобретение показывает по сравнению с этим другой путь для компенсации дисперсии в оптических системах передачи.

Изобретение относится к схеме для компенсации дисперсии в оптических системах передачи с помощью оптического фильтра; эта схема отличается тем, что в качестве фильтра отрицательной дисперсии предусмотрен оптический трансверсальный фильтр, причем в дальнейшем развитии изобретения оптический трансверсальный фильтр может содержать ряд следующих друг за другом на расстоянии τ 2 эксплуатируемых в качестве разветвителей направленных ответвителей и ряд также следующих друг за другом на расстоянии τ 2 эксплуатируемых в качестве объединителей направленных ответвителей, причем соответственно второй выход каждого направленного ответвителя эксплуатируемых в качестве разветвителя направленных ответвителей ведет к второму входу соответствующего эксплуатируемого в качестве объединителя направленного ответвителя.

Изобретение несет с собой преимущество в значительной степени свободно выбираемых процессов дисперсии и пропускания, причем установленное фильтром произведение из дисперсии и квадрата ширины полосы может увеличиваться примерно линейно с количеством ветвей фильтрата.

На фиг. 1 показана принципиальная схема трансверсального фильтра; на фиг. 2 - пример выполнения оптического трансверсального фильтра; на фиг. 3 - ход передаточной функции фильтра для компенсации дисперсии; на фиг. 4 - импульсный ответ к этой передаточной функции; на фиг. 5 - пропускание и дисперсия фильтра для компенсации дисперсии; на фиг. 6 - пропускание и дисперсия оптимированного фильтра для компенсации дисперсии.

Фиг. 1 показывает схематически трансверсальный фильтр с линией задержки из N звеньев временной задержки (τ) с временем задержки τ и из N+1 снабженных устанавливаемыми коэффициентными звеньями a₀,...,A_N на соответствующие коэффициенты фильтрования (значения отсчета) ответвлениями, ведущими к сумматору Σ . Трансверсальные фильтры являются общеизвестными (например, Боккер. Передача данных. Берлин-Гейдельберг-Нью Йорк, 1976, т. 1, глава 5.3.2) и не нуждаются здесь в более подробном пояснении, реализация оптических трансверсальных фильтров в планарной форме на кремниевой подложке также известна сама по себе (из J. Lightwave Technol.,т 12 1994, с. 664-669), так что это также не нуждается здесь в более подробном пояснении. Простую структуру оптического трансверсального фильтра показывает фиг. 2.

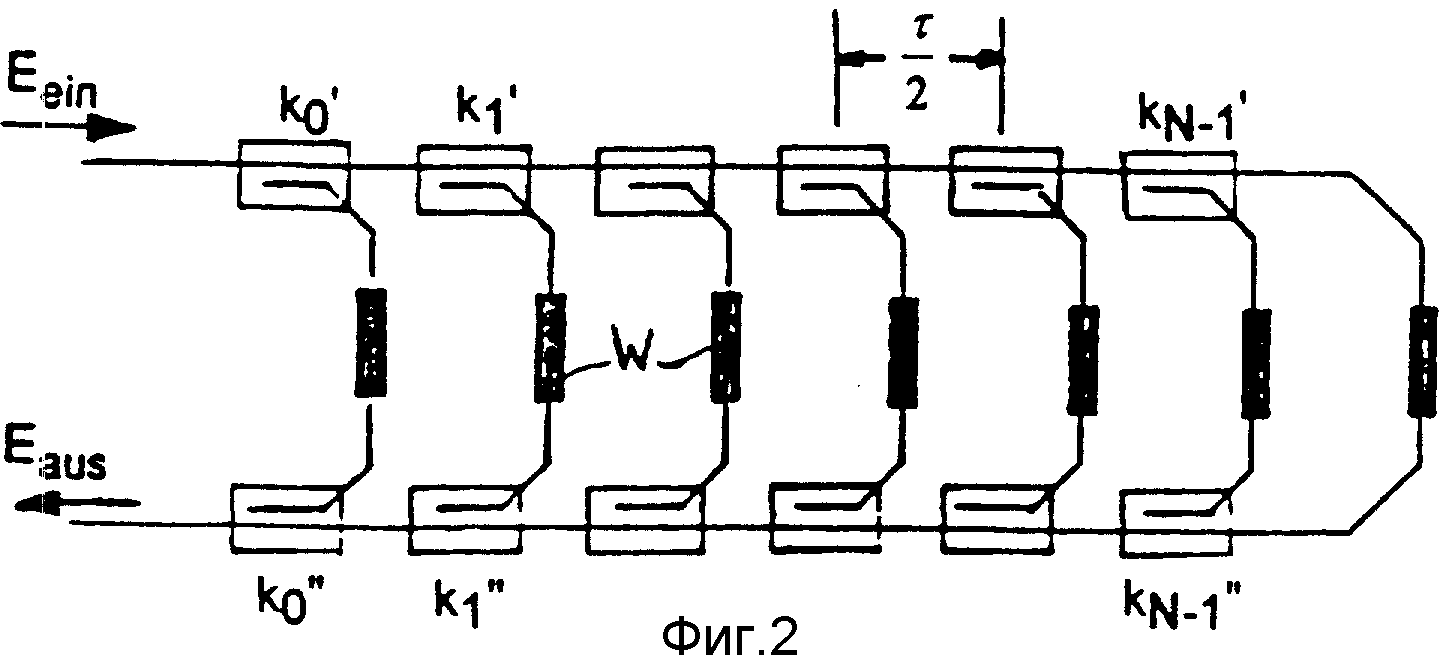
Согласно фиг. 2 оптический трансверсальный фильтр имеет ряд соответственно следующих друг за другом на расстоянии τ 2 эксплуатируемых в качестве разветвителей направленных ответвителей k'₀, k'₁,...,k'_N-1 и ряд также следующих друг за другом на расстоянии τ 2 эксплуатируемых в качестве объединителей направленных ответвителей k''₀,k''₁,...,k''_N-1, причем соответственно второй выход каждого направленного ответвителя из эксплуатируемых в качестве разветвителей направленных ответвителей k'₀,k'₁,...,k'_N-1 ведет к второму входу соответствующего эксплуатируемого в качестве объединителя направленного ответвителя k''₀,k''₁,...,k''_N-1. В отдельных ветвях оптического трансверсального фильтра могут быть расположены нагревательные элементы W, которые еще будут пояснены ниже.

Амплитуды отдельных коэффициентов фильтров реализуются за счет коэффициентов связи отдельных разветвителей и объединителей, причем при выборе параметров также следует учитывать действие ответвителей, расположенных перед соответствующим разветвителем или соответственно после соответствующего объединителя. Структура фильтра целесообразно является симметричной, то есть предусмотрены одинаковые коэффициенты связи для отбора и ввода, так что могут исключаться дополнительные потери при объединении составляющих мощности.

Для трансверсального фильтра комплексная передаточная функция H(j ω ) для электрической напряженности поля и импульсный ответ h(t) на δ - импульс выглядит следующим образом:

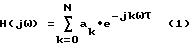
и

где δ (t) является дельта-функцией.

Импульсный ответ фильтра получается с помощью преобразования Фурье H (j ω ) во временную область. Если, как это имеет место согласно уравнения (2) в случае транверсального фильтра, импульсный ответ является дискретным во времени, то получается периодический ход частоты фильтра с периодичностью (Free Spectral Range FSR), равной FSR = 1 τ .

Для пропускания оптической мощности в зависимости от круговой частоты ω тогда справедливо
пропускание

ход фазы ϕ(ω) от ω
ϕ(ω) arg{H(jω)}. (4)
Групповое время задержки T_g ω равно

а дисперсия D ω

откуда с зависимостью с= λf получается

При рассмотрении частотных областей, которые являются малыми по сравнению с оптической частотой, в уравнении (7) для λ могут использоваться средние длины волн.

Если задается передаточная функция по модулю и фазе (или соответственно дисперсия), то отсюда путем преобразования Фурье можно определить импульсный ответ, а из импульсного ответа получается за счет считывания с периодом считывания τ = 1/FSR коэффициенты фильтра a₀...a_N.

Рассмотрим, например, фильтр с дисперсией - 1000 пс/нм на ширине полосы 10 ГГц. Из уравнения (7) видно, что для постоянной дисперсии необходимым является квадратичный ход фазы от ω .

где
λ₀ является длиной волны (например, λ₀ =1,55 мкм), при которой точно должна достигаться желаемая дисперсия D. На фиг. 3 представлены свободно выбираемые в известных границах характеристики модуля и фазы передаточной функции. В случае фазы кроме квадратичной характеристики также обращают внимание на то, чтобы разница фаз на границах области была целочисленным кратным от 360^o, чтобы возникали непрерывные переходы (показанный отрезок передаточной функции периодически повторяется). Характеристика модуля была выбрана так, чтобы область отрицательной дисперсии лежала в области высокого пропускания. Также и здесь следует обращать внимание на возможно непрерывные переходы для того, чтобы поддерживать возможно малой длину соответствующего импульсного ответа.

Относительно периодической характеристики фильтра следует отметить, что она позволяет производить одновременную компенсацию дисперсии при множестве длин волн. Дисперсия следующих друг за другом на расстоянии FSR = 1 τ полезных областей фильтра однако зависит от длины волны. Составляющая

в уравнении (7) имеет с расстояниями FSR = 1 τ всегда одинаковую величину, которая обозначается k. Дисперсия тем самым может быть представлена следующим образом:

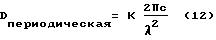
Производная по λ дает

Для компенсации дисперсии стандартного волокна в 1 км при длине волны 1,55 мкм требуется дисперсия порядка - 17 пс/нм. Из уравнения (13) при этом получается нарастание дисперсии следующих друг за другом на расстояниях FSR = 1 τ областей фильтра 0,02 пс/нм². По сравнению с этим стандартное волокно имеет на километр длины нарастание дисперсии порядка 0,06 пс/нм². Это нарастание таким образом не компенсируется; более того, остается значение 0,08 пс/нм²км, так что только для одной длины волны достигается точная компенсация. В частности, при близлежащих длинах волн периодические характеристики фильтров тем не менее являются пригодными также и для частотного уплотнения (WDM).

Применение быстрого преобразования Фурье к показанной на фиг. 3 передаточной функции дает представленный на фиг. 4 импульсный ответ. Разнесенные друг от друга на τ = 1/FSR опорные точки (считываемые значения) являются искомыми коэффициентами фильтра a_k(фиг. 1). Так как каждому считываемому значению соответствует одна ветвь в трансферсальном фильтре (фиг. 1 и 2), то следует стремиться к возможно малому количеству считываемых значений. В основе рассмотренного здесь примера выполнения лежит только тринадцать считываемых значений, которые лежат в ограниченной на фиг. 4 штриховкой временной области.

Как видно из фиг. 4, фазы считываемых значений являются в значительной степени не равными 0 или 180^o, то есть являются комплексными, таким образом справедливо

Импульсный ответ реализуемой передаточной функции может тем временем не иметь считываемых значений с любыми фазами, однако должен быть реальным; если, как здесь, желаемая передаточная характеристика нужна только внутри ширины полосы, которая мала по сравнению с абсолютным (оптическим) положением частоты, фильтр может быть реализован. При этом фазы считываемых значений реализуются за счет соответствующих времен задержки:



При этом ω = 2πc/λ₀ является круговой частотой, при которой фаза должна точно достигаться (например, при λ₀ = 1,55 мкм).

С использованием ограниченных на фиг. 4 тринадцати считываемых значений для пропускания и дисперсии получаются показанные на фиг. 5 характеристики. Дисперсия имеет при этом относительно большую волнистость, что объясняется тем, что был рассмотрен не полный импульсный ответ, а только тринадцать считываемых значений в нем.

Для достижения с ограниченным числом считываемых значений лучших характеристик может производиться оптимизация с помощью вычислений, при которой амплитуды (модули) и фазы (аргументы) считываемых значений варьируют. Фиг. 6 показывает результат такой оптимизации, на основе которой фильтр получает относительно постоянную дисперсию в - 1000 пс/нм в ширине полосы 10 ГГц, причем в этой области пропускание имеет также широкий выраженный максимум.

В основе рассмотренного здесь примера лежит Free Spectral Range FSR = 31,6 ГГц.

Как показывает масштаб на кривой пропускания (фиг. 5 и 6), фильтр имеет ослабление порядка 5,5 дБ. Возможным является также при одинаковой дисперсии выполнять фильтр с зависящим от частоты пропусканием, причем ослабление может составлять около 7,5 дБ.

Для понимания принципиально имеющегося в трансверсальных фильтрах ослабления следует заметить следующее: сумма модулей всех считываемых значений идеального, не имеющего потерь трансверсального фильтра равна единице. Пропускание, однако, будет равно единице только тогда, если при объединении отдельных составляющих мощности всей волны суммируются с одинаковой фазой. Вследствие разниц времен прохождения отдельных составляющих это может быть возможным только в очень узкой полосе. Фильтры для компенсации дисперсии, однако, должны быть возможно широкополосными, причем тогда по всей ширине полосы все фазы составляющих мощности не будут совпадать друг с другом ни на какой частоте.

Как уже было сказано выше, в примере выполнения согласно фиг. 2 амплитуды отдельных коэффициентов фильтра реализуются за счет коэффициентов связи отдельных разветвителей и объединителей, причем при выборе параметров следует учитывать также действие расположенных перед соответствующим разветвителем или соответственно после объединителя ответвителей, и причем структура фильтра целесообразно является симметричной, то есть предусматриваются одинаковые коэффициенты связи для ввода и вывода, так что избегаются дополнительные потери при объединении составляющих мощности. Для выше поясненных трансверсальных фильтров получаются следующие коэффициенты связи:
k₀= - 22,97 дБ, k₁= -20,28 дБ, k₂ = - 17,91 дБ, k₃ = - 13,45 дБ, k₄=-9,77 дБ, k₅= -5,68 дБ, k₆= -4,63 дБ, k₇= -2,54 дБ, k₈= -2,46 дБ, k₉= -2,57 дБ, k₁₀= -2,85 дБ, k₁₁= -1,99 дБ.

Соответствующая необходимой при FSR = 31,6 ГГц разнице времен прохождения τ = 31,64 пс длина волны составляет 6,3 мм (при коэффициенте преломления n = 1,5).

За счет изменения времени задержки τ может достигаться, таким образом, обмен между шириной полосы В и дисперсией D, когда произведение B²D для соответствующего фильтра остается постоянным. С изменением задержки τ в некоторой степени достигается расширение или сжатие масштаба частоты в остальном неизменной характеристики фильтра; удвоение ширины полосы В проявляется в уменьшении дисперсии D на коэффициент 4. Принципиально можно предусматривать любые значения для B и D. При больших значениях B²D, однако, требуется большее количество считываемых значений, что ставит соответствующие границы для реализации. На практике оказывается, что считываемые значения, которые являются меньшими, чем 2,5% от максимального считываемого значения, не могут быть реализованы. Это краевое условие имеет место также в поясненном здесь примере выполнения.

В то время как при постоянной ширине полосы дисперсия увеличивается примерно линейно с количеством считываемых значений, рост необходимого за счет принципа фильтра ослабления уменьшается с увеличением количества считываемых значений, так что отношение дисперсии к ослаблению улучшается. Так это соотношение составляет примерно 709 пс/нм/дБ при ширине полосы 10 ГГц и пятидесяти семи считываемых значениях; при 250 пс/нм/дБ, как это достигается в настоящее время в случае дисперсионно-компенсированных волокон, этот трансверсальный фильтр должен бы вносить еще дополнительное ослабление порядка 26 дБ, чтобы тем не менее достигнуть в целом лучшие результаты, чем в случае дисперсионно-компенсированных волокон. Следует вспомнить, что эти свойства трансверсального фильтра по сравнению с волокном связаны с не слишком большой шириной полосы, при ширине полосы в 20 ГГц дисперсия имела бы в расчете на принципиальное ослабление значение в примере 177 пс/нм/дБ.

Для тонкого согласования фаз ( аргументов) отдельных (комплексных) считываемых значений в ветвях оптического трансверсального фильтра могут быть размещены нагревательные элементы W, как это также намечено на фиг. 2. Можно предусматривать также настраиваемые направленные ответвители, которые также позволяют настройку модулей считываемых значений. Предусматривать в оптических трансверсальных фильтрах нагревательные элементы или настраиваемые ответвители является само по себе уже известным (J. Lightwave Technol., т. 12, 1994, с. 664 - 69), так что более подробные пояснения здесь не нужны.

Для стабилизации фильтра на длину волны передающего лазера при соответствующем выборе параметров фильтра может служить пропускание (фиг. 6). Сдвиг кривой фильтра является возможным путем равномерного изменения времен задержки всех ветвей с помощью нагревательных элементов. Наоборот, является возможной также стабилизация длины волны передатчика на кривую фильтра, что, в частности, принимается во внимание при больших фильтрах. В этом случае, при необходимости, была бы достаточной одноразовая настройка фильтра, и в процессе эксплуатации должна только поддерживаться постоянной температура фильтра.

Реферат

Схема для компенсации дисперсии может быть использована в волоконно-оптических линиях связи. Оптический фильтр отрицательной дисперсии выполнен в виде трансверсального фильтра, который содержит ряд следующих друг за другом с расстоянием, равным половине времени задержки элемента фильтра, разветвителей и ряд следующих друг за другом на таком же расстоянии объединителей. Второй выход каждого разветвителя соединен с вторым входом соответствующего объединителя. Схема позволяет свободно выбирать процессы пропускания и дисперсии. 4 з.п. ф-лы, 6 ил.

Формула