Лопатка газовой турбины - RU2178086C2
Код документа: RU2178086C2
Чертежи
Описание
Изобретение относится к области турбостроения и может быть использовано в конструкциях лопаток рабочих колес и сопловых аппаратов осевых газовых турбин различного назначения.
Известны конструкции рабочих и сопловых лопаток, профильные поверхности которых образованы сочетанием дуг окружностей и гиперболических спиралей (Аронов Б. М. Авторские свидетельства "Лопатка реактивной газовой турбины" 266475 от 5.01.70 и 332074 от 3.09.71), по методу доминирующей кривизны (Мамаев Б. И. , Рябов Е. К. Построение решетки турбинных профилей методом доминирующей кривизны//Теплоэнергетика. 1979. 2. С. 52-55), сочетанием дуг окружностей и отрезков прямых (патент: Россия 2053370, кл. F 01 D 5/14).
Контуры профилей, образованные разными кривыми, по-разному влияют на потери энергии и, следовательно, на экономичность турбины, а также на ее прочность и технологичность. Даже при наличии средств автоматизированного проектирования образование поверхностей пера разными кривыми отражается и на времени разработки конструкции лопаток и, следовательно, на фактической стоимости каждого комплекта турбины. Кроме того, каждый метод имеет свои границы области допустимых сочетаний параметров решеток, что ограничивает область реализуемых конструкций лопаток и параметров турбин.
Наиболее близкими по технической сущности к заявляемой конструкции являются лопатки, профильные части которых образованы лемнискатами Бернулли (Основы проектирования турбин авиадвигателей. А. В. Деревянко, В. А. Журавлев, В. В. Зикеев и др. Под ред. С. З. Копелева. - М. : Машиностроение, 1988. 328с. ) При определенных сочетаниях конструктивных параметров построение контуров строится быстро, и сформированное перо удовлетворяет требованиям газовой динамики и прочности.
Турбинные лопатки, профильные части которых образованы лемнискатами Бернулли, обладают тремя
недостатками:
1) диапазон
параметров, в пределах которого можно с помощью лемнискат Бернулли построить контуры профилей, удовлетворяющих требованиям газовой динамики и прочности, не
охватывает всех практически важных значений,
особенно характерных для больших градиентов кривизн контуров спинки и корыта, что важно при проектировании высокотемпературных высоконагруженных турбин;
2) очень сложно построить профили
сечений в единой связке профилей пера лопатки (следствие первого недостатка);
3) контуры профилей во многих случаях строятся лишь при отказе от
оптимальных значений параметров, при которых
достигаются минимальные потери энергии, т. е. имеет место недобор КПД ступени турбины (следствие предыдущих пунктов).
В основу изобретения поставлены задачи: расширить область надежного построения профилей лопаток турбин; сократить время профилирования лопаток; снизить потери энергии в лопаточных венцах и, следовательно, повысить КПД турбин.
Решение поставленных задач
достигается тем, что контуры спинки и корыта образованы синусоидальными спиралями, каждая точка которых определена выражением:
x = x0+ρ•cosϕ;
y =
y0+ρ•sinϕ;
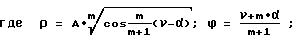
(x0, y0) - координаты полюса спирали;
А - полюсное расстояние;
α - угол между полярной осью и осью ОХ;
ν - угол между перпендикуляром, восстановленным в произвольной точке лемнискаты, и осью ОХ;
ρ - радиус-вектор точки;
ϕ - угол между радиусом-вектором и осью ОХ;
m - параметр, определяющий вид кривой.
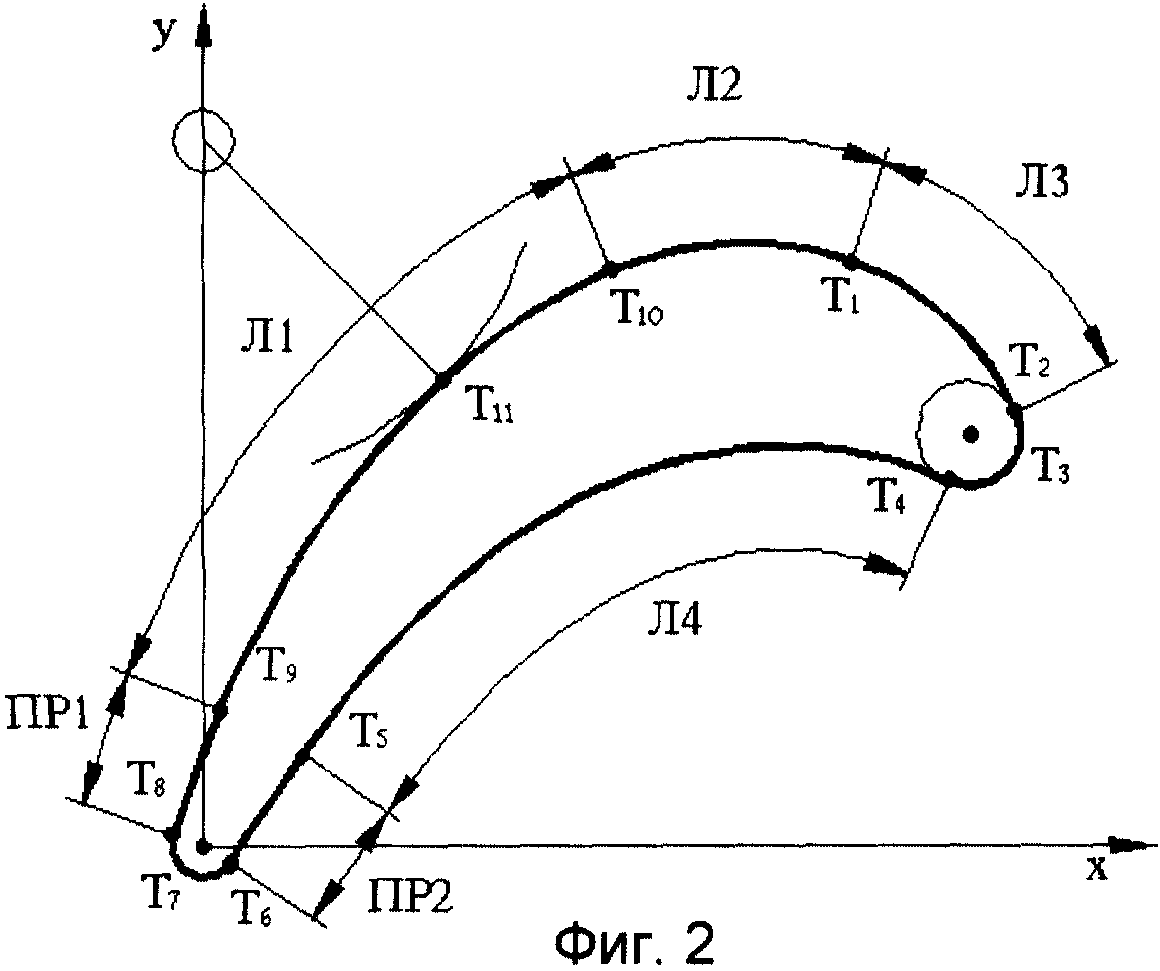
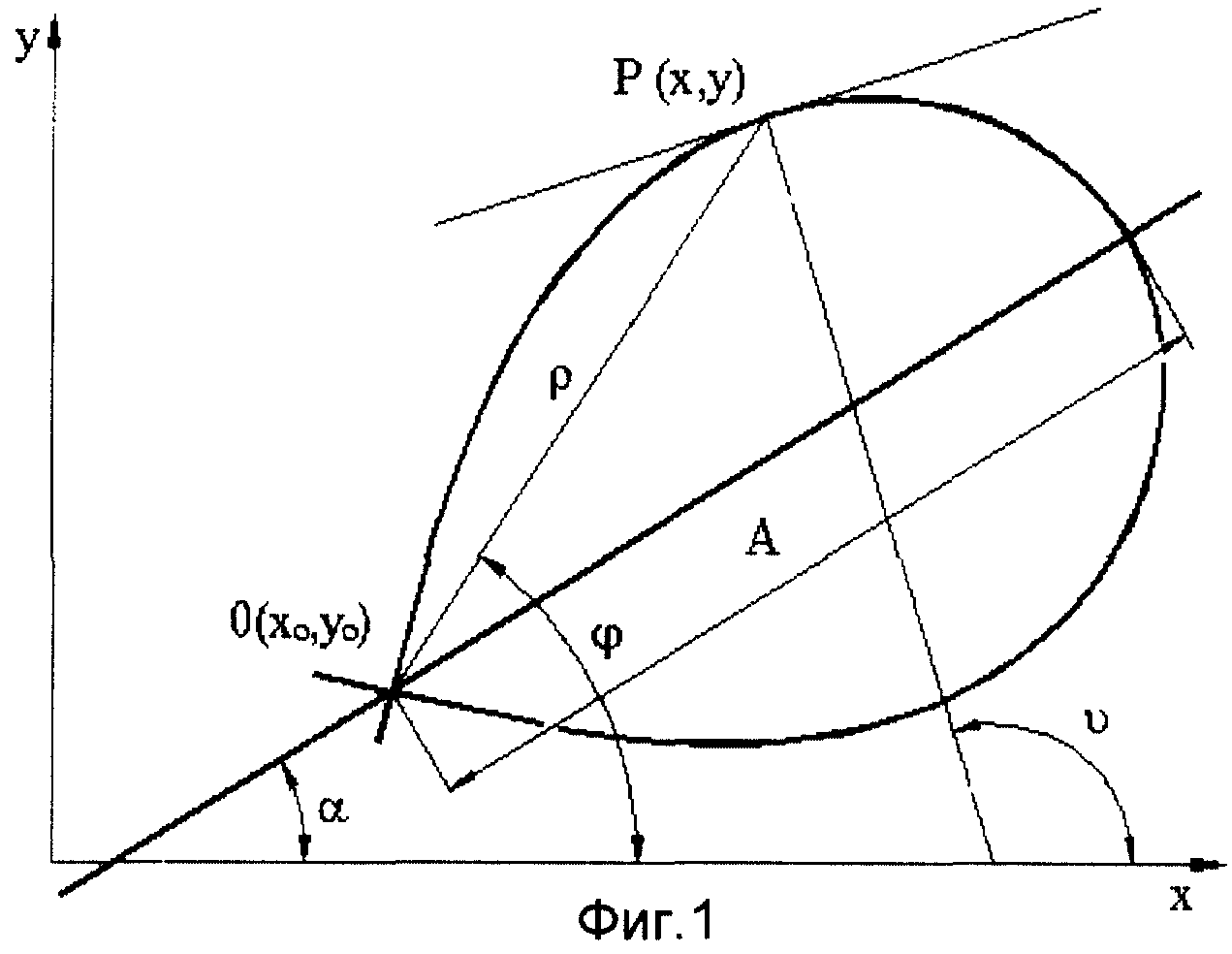
На фиг. 1 изображена синусоидальная спираль. На фиг. 2 - контур профиля турбинной лопатки по предлагаемому изобретению: контур спинки образован тремя спиралями, корыта - одной спиралью. Входная и выходная кромки образованы дугами окружностей. На этой фигуре показана схема разбиения контура профиля с обозначением кривых, образующих участки профиля, и характерных точек. Здесь Кр1, Кр2, Кр3 - кривые, описывающие спинку; Кр4 - спираль, описывающая корыто. В некоторых случаях (в периферийных сечениях) возможно применение в районе выходной кромки участков прямых как на спинке Пр1, так и на корыте Пр2 соответственно.
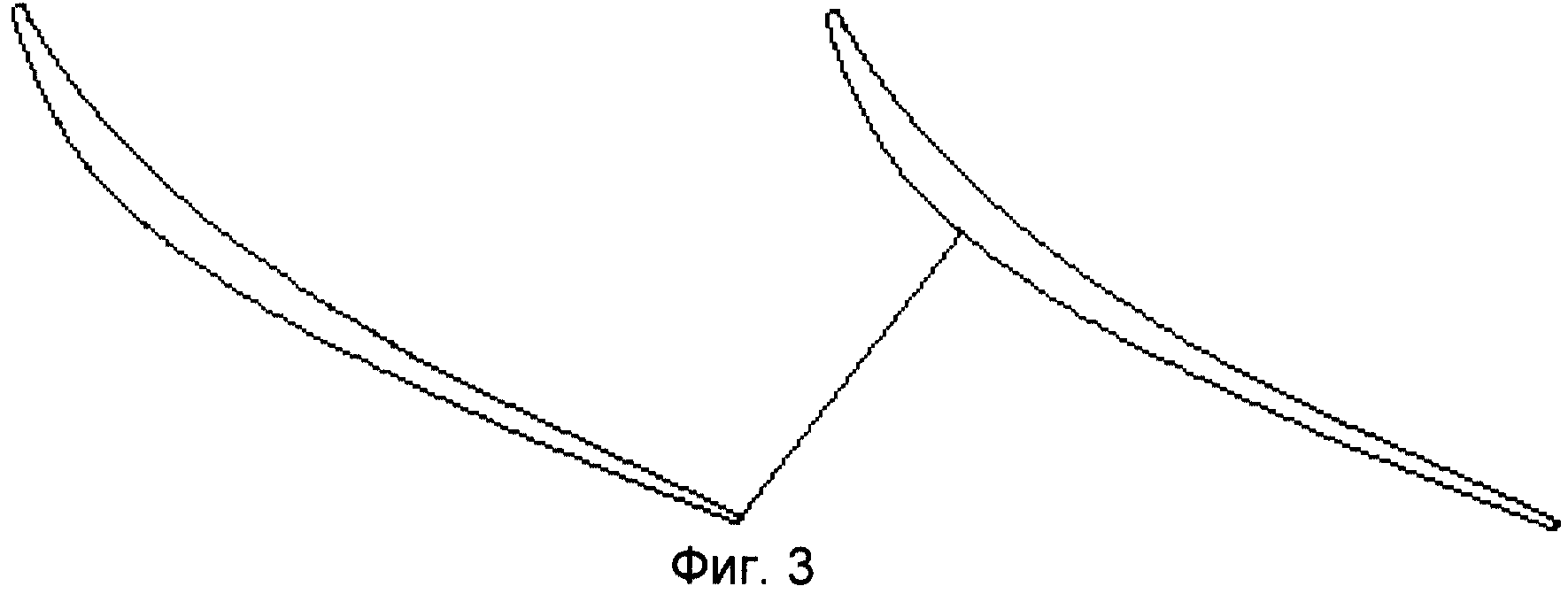
На фиг. 3,4 приведены результаты профилирования решеток турбин на такие геометрические параметры, при которых с помощью лемнискат
Бернулли профили нельзя построить. На
фиг. 3 решетка построена на следующие исходные данные: угол входа потока β1== 130°; угол выхода потока β2=
26,5°; приведенная
адиабатическая скорость на выходе λ2S= 0,0992. Она имеет геометрические параметры:
β1k= 115°;
β2k= 22,9°;ω1= 9°,ω2= 1,8°; r1= 0,28 мм; r2= 0,2 мм; δ= 17o; γ= 35o; b= 44
мм; S= 25,47 мм; t= 40,02 мм; βэф= 26,06°.
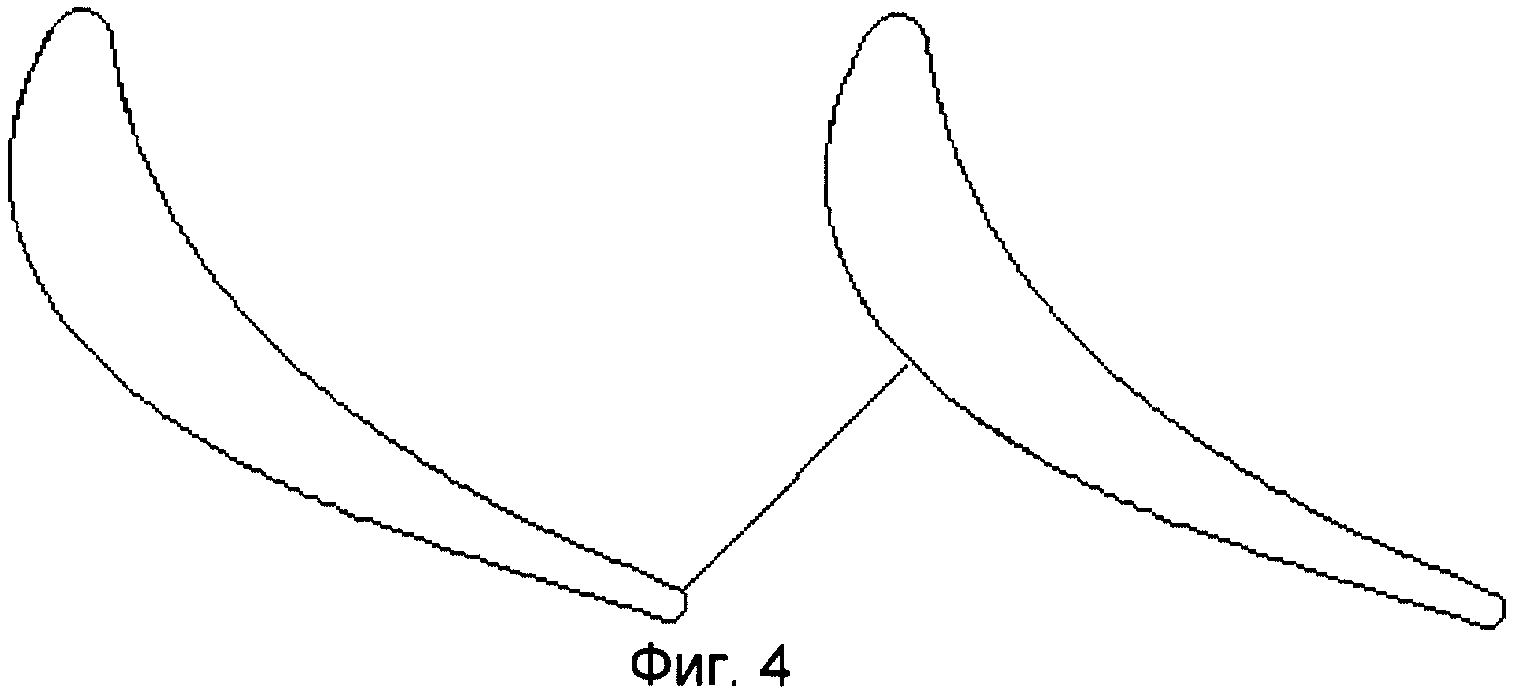
На фиг. 4 решетка построена на следующие исходные данные: угол входа
потока β1= 78°; угол выхода потока β2= 24,5°; приведенная адиабатическая скорость на выходе λ2S= 0,75. Она
имеет геометрические характеристики: β1k= 78,8°;β2k= 19,9°,ω1= 37,5°,ω2=
6°; r1= 1,6 мм;
r2= 0,9 мм; δ= 28,2o; γ= 43,25o; b= 45,51 мм; S= 32,0 мм; t= 43,25 мм; βэф= 23,49°.
Данное изобретение позволит проектировать лопатки, геометрические параметры профильной части которых принадлежат более широкой области сочетаний параметров, вследствие чего становятся шире границы возможных решений при газодинамическом проектировании турбин, а следовательно, и газотурбинного двигателя в целом.
Реферат
Лопатка газовой турбины имеет профильную часть, состоящую из контуров спинки, корыта и кромок. Контуры спинки и корыта образованы синусоидальными спиралями, каждая точка которых определена выражением: x = x0+ρ•cosϕ; y = y0+ρ•sinϕ, где
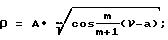
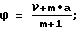
(х0, у0) - координаты полюса спирали; А - полюсное расстояние ; α - угол между полярной осью и осью ОХ; ν - угол между перпендикуляром, восстановленным в произвольной точке лемнискаты, и осью ОХ; ρ - радиус-вектор точки; ϕ - угол между радиусом-вектором и осью ОХ; m - параметр, определяющий вид кривой. Изобретение позволяет снизить потери энергии в лопаточных венцах, сократить время профилирования лопаток и расширить область надежного построения профилей лопаток. 4 ил.
Формула
x = x0+ρ•cosϕ;
y = y0+ρ•sinϕ,
где
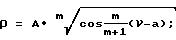
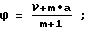
(х0, у0 ) - координаты полюса спирали;
А - полюсное расстояние;
α - угол между полярной осью и осью ОХ;
ν - угол между перпендикуляром, восстановленным в произвольной точке лемнискаты, и осью ОХ;
ρ - радиус-вектор точки;
ϕ - угол между радиус-вектором и осью ОХ;
m - параметр, определяющий вид кривой.

Комментарии