Способ неинвазивного электрофизиологического исследования сердца - RU2409313C2

Чертежи

Показать все 28 чертежа(ей)

Описание

Область техники, к которой относится изобретение

Изобретение относится к медицине, а именно к кардиологии, сердечно-сосудистой хирургии и функциональной диагностике (клинической физиологии), и предназначено для проведения диагностической процедуры - неинвазивного электрофизиологического исследования сердца. Более точно, изобретение предназначено для реконструкции динамики электрического поля сердца во внутренних точках грудной клетки, в частности, для получения внутрипищеводных и эпикардиальных электрограмм, а также для осуществления активационного эпикардиального картирования - получения эпикардиальных изопотенциальных и изохронных карт (паттернов активации миокарда) неинвазивным путем, т.е. без введения регистрирующих устройств в камеры сердца, полость перикарда, полость пищевода и т.п.

Уровень техники

Основным методом диагностики электрофизиологических процессов сердца, рутинно использующимся в клинической практике, является электрокардиография в 12 стандартных отведениях. Простота и низкая себестоимость в сочетании с относительно высокой информативностью стандартного элетрокардиографического исследования привела к чрезвычайно широкому его использованию в повседневной практике.

Однако электрокардиографический метод имеет принципиальные ограничения. Активность определенных отделов миокарда незначительно отражается в электрокардиографических сигналах, зарегистрированных в стандартных отведениях. Примером является трудность ЭКГ-диагностики инфаркта миокарда задне-базальных отделов левого желудочка. Кроме того, согласно принципу суперпозиции в электродинамике, электрокардиограмма является суммой электрических потенциалов, возникающих от источников во множестве точек миокарда. Так как электрофизиологические процессы в различных участках сердечной мышцы протекают одновременно, по стандартным ЭКГ-отведениям весьма сложно определить локальную электрическую активность миокарда. Например, волна реполяризации предсердий у человека в условиях нормального ритма не выявляется на ЭКГ, так как она "скрыта" высокоамплитудным комплексом QRS, отражающим деполяризацию желудочков. Аналогичными ограничениями характеризуется и метод векторэлектрокардиографии.

Более широкими возможностями обладает метод поверхностного электрокардиографического картирования грудной клетки. Метод заключается в синхронной регистрации множества (от 40 до 250 и более) однополюсных ЭКГ-отведений с поверхности грудной клетки и построении путем интерполяции для каждого момента времени кардиоцикла карт распределения электрического потенциала на поверхности грудной клетки.

Однако указанный метод не позволяет точно определять локальную электрическую активность миокарда. Если электрод расположен на поверхности грудной клетки, вклады в ЭКГ-сигнал от ближайшего и наиболее удаленного по отношению к регистрирующему электроду сегмента миокарда отличаются примерно на один порядок. Для электрода, помещенного на поверхность сердца, это различие составляет три порядка. В связи с этим для выявления локальной электрической активности сердца используют методы инвазивной регистрации ЭКГ, стремясь максимально приблизить электроды к поверхности сердца.

Чреспищеводное электрофизиологическое исследование сердца основано на введении зонда с регистрирующими электродами в полость пищевода. Пищевод на определенном участке достаточно плотно прилежит к задней стенке левого предсердия и задней стенке левого желудочка, поэтому внутрипищеводные ЭКГ-сигналы избирательно регистрируют активность этих отделов сердца. Внутрипищеводная электрокардиография применяется, в частности, для дифференциальной диагностики наджелудочковых и желудочковых аритмий (Чреспищеводная электрическая стимуляция сердца / Под ред. В.А.Сулимова, В.И.Маколкина. - М.: Медицина, 2001. - 208 с.).

Однако указанные методы позволяют выявить локальную электрическую активность лишь отдельных сердечных структур.

Для комплексной оценки электрофизиологических процессов сердца и топической диагностики нарушений сердечного ритма используется инвазивное электрофизиологическое исследование сердца, основанное на прямой регистрации комплекса электрограмм с эпикардиальной или эндокардиальной поверхности сердца. Указанные методы могут применяться на «открытом сердце» в условиях торакотомии, а также на основе интервенционных технологий введения регистрирующих устройств (катетеров) в полости сердца чрессосудистым доступом или в полость перикарда путем его чрескожной пункции под флюороскопическим контролем.

Современные реализации указанных методов предусматривают точное определение трехмерных координат регистрирующих электродов нефлюороскопическими методами и визуализацию результатов в виде изопотенциальных и изохронных карт на моделях отделов сердца средствами компьютерной графики. Компьютерные модели отделов сердца строятся по множеству точек регистрации электрограмм с известными координатами, а также на основе данных КТ или МРТ сердца (Ревишвили А.Ш., Рзаев Ф.Г., Джетыбаева С.К. Электрофизиологическая диагностика и интервенционное лечение сложных форм нарушения ритма сердца с использованием системы трехмерного электроанатомического картирования. - Вестник аритмологии 2004; 34: 32-37; Покушалов Е.А., Туров А.Н., Шугаев П.Л., Артеменко С.Л. Радиочастотная аблация желудочковой тахикардии трансперикардиальным доступом. - Вестник аритмологии. 2006; 44: 58-62).

К этой же группе относятся способы бесконтактного эндокардиального картирования, основанные на введении в полости сердца «плавающего» баллонного катетера, регистрации комплекса электрограмм на его поверхности и реконструкции вычислительным путем по полученным данным эндокардиальных электрограмм (Schilling R.J., Kadish А.Н., Peters N.S. et al. Endocardial mapping of atrial fibrillation in the human right atrium using a non-contact catheter. - European Heart Journal. 2000; 21: 550-564).

Недостатком указанных способов, преодолеваемым в настоящем изобретении, является их инвазивный характер.

Аналогами изобретения являются способы реконструкции электрограмм во внутренних точках грудной клетки вычислительным путем по данным синхронной регистрации комплекса ЭКГ на поверхности грудной клетки.

Указанные способы основаны на решении обратной задачи электрокардиографии. Постановка обратной задачи электрокардиографии (ОЗ ЭКГ) сформулирована в работах (Барр Д., Спек М. Решения обратной задачи, выраженные непосредственно в форме потенциала // Теоретические основы электрокардиологии: Пер. с англ. / Под ред. К.В.Нельсона и Д.В.Гезеловица. - М.: Медицина, 1979. - С.341-352; MacLeod R.S., Brooks D.H. Recent progress in inverse problem in electrocardiology // IEEE Eng. in Med. Bio. Mag. 17:1, pp.78-83, Jan. 1998; Rudy Y., Messinger-Rapport B.J. The inverse problem in electrocardiography: Solutions in terms of epicardial potentials. CRC Crit. Rev. Biomed. Eng. 1988; 16: 216-268).

ОЗ ЭКГ с математической точки зрения является задачей гармонического продолжения потенциала в сторону источников, т.е. задачей Коши для уравнения Лапласа. Расчетной областью, в которой задается уравнение Лапласа, является часть грудной клетки, ограниченная внешней поверхностью сердца, поверхностью грудной клетки, на которой доступна регистрация ЭКГ, и воображаемыми поперечными сечениями грудной клетки на уровне диафрагмы и ключиц.

На части поверхности грудной клетки, где доступна регистрация ЭКГ, задаются полученные в результате ЭКГ-картирования значения электрического потенциала, а также условие равенства нулю нормальной производной потенциала. Эти данные составляют условия Коши.

Задача Коши заключается в нахождении потенциала электрического поля в указанной области и его следа на поверхности сердца и поперечных сечениях грудной клетки таким образом, чтобы потенциал в расчетной области удовлетворял уравнению Лапласа, а на поверхности торса, где доступна регистрация ЭКГ, - условиям Коши.

Задача Коши для уравнения Лапласа является некорректно поставленной по Адамару: сколь угодно малые погрешности условия могут привести к произвольно большим погрешностям решения. Для решения задачи Коши для уравнения Лапласа необходимо применять специальные, т.н. регуляризирующие алгоритмы решения (Денисов A.M. Введение в теорию обратных задач. - М.: Изд-во Моск. ун-та, 1994; Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. - М.: Наука, 1986. - 312 с.).

Решить задачу Коши для уравнения Лапласа в указанной постановке (обратную задачу электрокардиографии) аналитическим способом не представляется возможным. Поэтому обратная задача электрокардиографии решается численно средствами вычислительной математики с использованием компьютерной техники.

Один из способов решения обратной задачи электрокардиографии - метод реконструкции электрического поля на «квазиэпикарде» - условной сферической поверхности, окружающей сердце. С математической точки зрения метод основан на представлении потенциала электрического поля сердца в виде гармонического полинома (шаровой функции), коэффициенты которого находятся из условия равенства (или минимума среднеквадратичного отклонения) значений полинома и значений ЭКГ-сигнала в точках его регистрации с учетом равенства нулю нормальной производной потенциала на поверхности грудной клетки. Для обеспечения устойчивости решения используется полином не выше 4 степени. Способ обладает существенным недостатком: при уменьшении радиуса сферы, т.е. по мере приближения поверхности «квазиэпикарда» к реальной поверхности сердца точность реконструкции потенциала резко падает. При приближении поверхности квазиэпикарда к поверхности грудной клетки снижается разрешающая способность метода в плане выявления локальной электрической активности миокарда (Титомир Л.И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. - М.: Наука. Физматлит, 1999. - 448 с.; Титомир Л.И., Трунов В.Г., Аиду Э.А.И. Неинвазивная электрокардиотопография. - М.: Наука, 2003. - 198 с.).

Для решения граничных задач для уравнения Лапласа широко используются методы интегральных уравнений теории потенциала, в англоязычной литературе более известные как методы граничных элементов (Бреббия К., Теллес Ж., Вроубел Л. Методы граничных элементов - Пер. с англ. М.: Мир, 1987). Данный подход для решения ОЗ ЭКГ предложен в работах Е.Таккарди, Р.Плонзи, Р.Барра (Барр Д., Спек М. Решения обратной задачи, выраженные непосредственно в форме потенциала // Теоретические основы электрокардиологии: Пер. с англ.). Указанные методы, в частности, предполагают представление поверхностей сердца и торса в виде полигональных поверхностей, т.е. разбиение граничных поверхностей на множество треугольных элементов. Согласно методу граничных элементов, ОЗ ЭКГ для однородной модели грудной клетки сводится к решению системы двух интегральных уравнений Фредгольма I и II рода, которая приближенно заменяется системой матрично-векторных уравнений:

где A_i,j - известные матрицы, х₁, х₂ - неизвестные векторы, имеющие смысл искомых значений потенциала и его нормальных производных в узлах триангуляционых сеток, аппроксимирующих поверхности сердца и поперечных сечений торса, с₁, с₂ - известные векторы, рассчитываемые по известным данным задачи.

В способе неинвазивного эпикардиального картирования, предложенном В.В.Шакиным и соавт., использовался следующий алгоритм решения ОЗ ЭКГ.

Система матрично-векторных уравнений (1) путем элементарных преобразований сводилась к системе линейных алгебраических уравнений, которая разрешалась в явном виде:

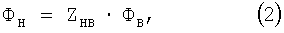
где Ф_Н - неизвестный вектор, имеющий смысл искомых значений потенциала в узлах триангуляционных сеток, аппроксимирующих поверхности сердца и поперечных сечений торса, Z_HB - известная матрица, Ф_В - известный вектор. Для вычисления матрицы Z_HB необходимо использовать процедуру обращения матриц, входящих в систему (1), причем одна из обращаемых матриц является неквадратной и плохо обусловленной. Для выполнения указанной процедуры использовалось построение псевдообратной матрицы Мура-Пенроуза на основе SVD-разложения исходной матрицы и замена нулями малых сингулярных чисел.

Поверхности сердца торса представлялись упрощенными моделями в виде цилиндрической и эллипсоидальной поверхностей, строившихся на основе рентгенографии грудной клетки в двух проекциях. Результаты картирования в виде изопотенциальных и изохронных карт накладывались на модельные схемы-развертки отделов сердца. Методика применялась для выявления локализации ДПП при манифестирующем синдроме WPW и эктопических источников при желудочковой экстрасистолии (Шакин В.В. Вычислительная электрокардиография. - М.: Наука, 1980).

В работах В.В.Шакина указывалось на перспективность применения компьютерно-томографических методик для точного построения поверхностей торса и сердца, однако из-за недостаточного развития методов компьютерной томографии сердца этот подход не применялся.

Наиболее близким к заявляемому способу (прототип) является методика неинвазивного электрокардиографического картирования (Noninvasive Electrocardiographic imaging, ECGI).

В указанном способе поверхностное картирование осуществляется с использованием 240 однополярных электродов, размещенных на специальном жилете, который надевается на пациента во время исследования. Поверхности торса и сердца определяются на основе компьютерной или МРТ-томографии грудной клетки. Алгоритм реконструкции основан на решении обратной задачи электрокардиографии методом граничных элементов.

Поверхности сердца и торса приближенно представляются в виде полигональных поверхностей. Для решения ОЗ ЭКГ также используется система матрично-векторых уравнений (1), которая путем тождественных преобразований сводится к системе линейных алгебраических уравнений

где х - неизвестный вектор, имеющий смысл искомых значений потенциала в узлах триангуляционных сеток, аппроксимирующих поверхности сердца и поперечных сечений торса, А - известная матрица, с - известный вектор.

Система линейных алгебраических уравнений (3) является плохообусловленной. Для ее решения используется метод регуляризации А.Н.Тихонова и метод итерационной регуляризации на основе GMRes-алгоритма. Метод Тихонова основан на решении вместо системы (3) системы:

(A^T·A+αE)x=A^Tc,

где A^T - матрица, транспонированная по отношению к матрице А, Е - единичная матрица, α - параметр регуляризации (малое положительное действительное число).

Метод итерационной регуляризации основан на решении системы (3) методом последовательных приближений с ограничением числа итераций на основе GMRes-алгоритма, относящегося к группе методов подпространств Крылова (Ramanathan, С., Ghanem, R.N., Jia P., Ryu К., Rudy У. Electrocardiographic Imaging (ECGI): A Noninvasive Imaging Modality for Cardiac Electrophysiology and Arrhythmia // Nature Medicine, 2004; 10: 422-428; Rudy Y, Ramanathan, C., Ghanem, R.N., Jia P. System and method for noninvasive electrocardiographic imaging (ECGI) using generalized minimum residual (GMRES) // United states patent № 7016719 B2, 2006).

Аналогичный способ использовался в работе (Berger Т., Fisher G., Pfeifer В. et al. Single-Beat Noninvasive Imaging of Cardiac Electrophysiology of Ventricular Pre-Exitation // J. Am. Coll. Cardiol., 2006; 48: 2045-2052).

Способ применялся для выявления локализации ДПП при манифестирующем синдроме WPW, эктопических источников при желудочковой экстрасистолии и тахикардии, реконструкции динамики активации миокарда при трепетании предсердий.

Существенным недостатком рассмотренного способа является использование модели грудной клетки с постоянным коэффициентом удельной электропроводности. Удельная электропроводность различных органов и тканей грудной клетки существенно различается. Переменный коэффициент электропроводности биологических тканей оказывает достаточно большое влияние на электрическое поле сердца в грудной клетке, что подтверждается данными экспериментальных исследований (Rudy Y., Wood R., Plonsey R., Liebman J. The effect of high lung conductivity on electrocardiographic potentials. Results from human subjects undergoing bronchopulmonary lavage // Circulation 1982; 65: 440-445). Наибольшую роль играет различие электропроводности легких и окружающих мягких тканей (в 4-5 раз). Потенциалы электрического поля сердца модельных источников, рассчитанные для однородной и неоднородной моделей грудной клетки, различаются на 15-20% (Титомир Л.И., Кнеппо П. Математическое моделирование биоэлектрического генератора сердца. - М.: Наука. Физматлит, 1999. - 448 с). Таким образом, пренебрежение электрической неоднородностью тканей грудной клетки приводит к большим погрешностям реконструкции электрического поля сердца.

Целью настоящего изобретения является повышение точности неинвазивного электрофизиологического исследования сердца за счет учета различного коэффициента электропроводности тканей грудной клетки.

Сущность изобретения

Для проведения электрофизиологического исследования сердца необходима регистрация комплекса электрограмм с поверхности сердца, на основе которых строятся изопотенциальные, изохронные карты и осуществляется диагностика электрофизиологических процессов в сердечной мышце. Для получения электрограмм используется инвазивный путь - введение специальных регистрирующих устройств в камеры сердца или полость перикарда.

Сущность настоящего изобретения состоит в том, что электрограммы, экспериментальная регистрации которых требует инвазивного доступа, реконструируются вычислительным путем по однополюсным ЭКГ, записанным в 80 и более точках поверхности грудной клетки. По набору поверхностных электрокардиограмм для каждого дискретного момента времени кардиоцикла определяются значения потенциала электрического поля сердца в точках записи ЭКГ и путем интерполяции рассчитывается значение потенциала электрического поля в каждой точке поверхности грудной клетки. По данным какой-либо визуализационной методики (компьютерная томография, магнитно-резонансная томография) определяются границы поверхностей грудной клетки и эпикардиальной поверхности сердца, а также значения удельной электропроводности ткани в каждой точке грудной клетки.

Далее вычислительным путем на основе решения задачи Коши для уравнения Лапласа в неоднородной среде осуществляется продолжение потенциала электрического поля на всю область грудной клетки вплоть до эпикардиальной поверхности сердца. Решение задачи Коши для уравнения Лапласа сводится к численному решению операторного уравнения первого рода в пространстве L₂. Решение операторного уравнения осуществляется путем решения эквивалентной задачи минимизации выпуклого положительного квадратичного функционала. Указанная вариационная задача решается путем численной минимизации на основе градиентных методов или путем численного решения уравнения Эйлера. Все указанные методы носят итерационный характер. На каждом шаге итерационной процедуры осуществляется решение смешанных граничных задач для уравнения Лапласа в неоднородной среде методом конечных элементов. Регуляризация в вычислительных процедурах обеспечивается за счет ограничения количества итераций или использования метода Тихонова. Параметры регуляризации определяются согласно принципу невязки.

Описанную выше последовательность процедур повторяют для каждого момента времени кардиоцикла. По полученным значениям потенциала в заданных внутренних точках грудной клетки путем интерполяции реконструируют требуемые электрограммы. На основе реконструированных электрограмм строятся изопотенциальные, изохронные карты на реалистичных моделях сердца, реконструируется динамика возбуждения миокарда и осуществляется диагностика электрофизиологических процессов в сердечной мышце.

Краткое описание чертежей

Фиг.1 иллюстрирует общую схему способа.

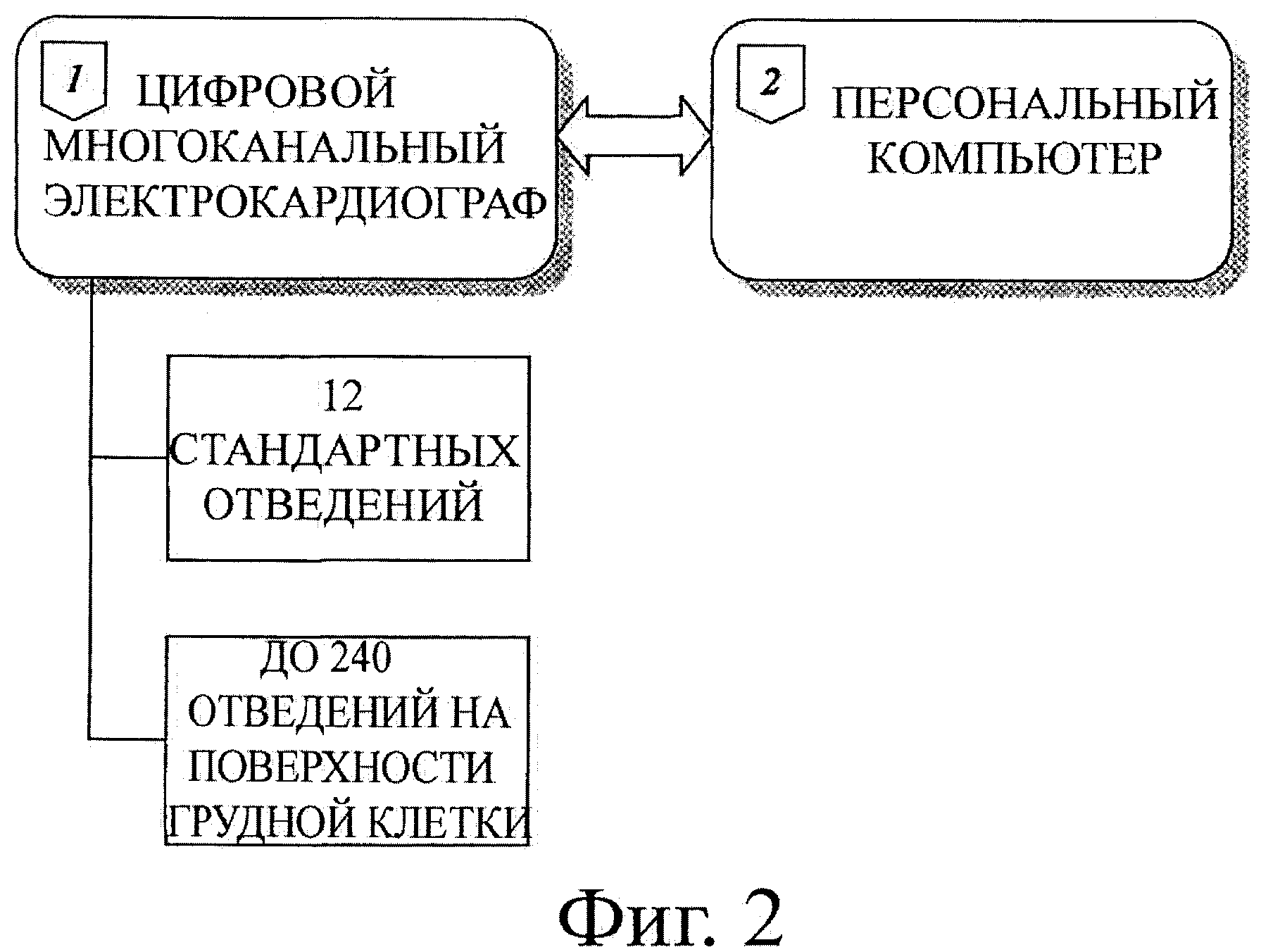
На фиг.2 представлена схема методики поверхностного картирования ЭКГ.

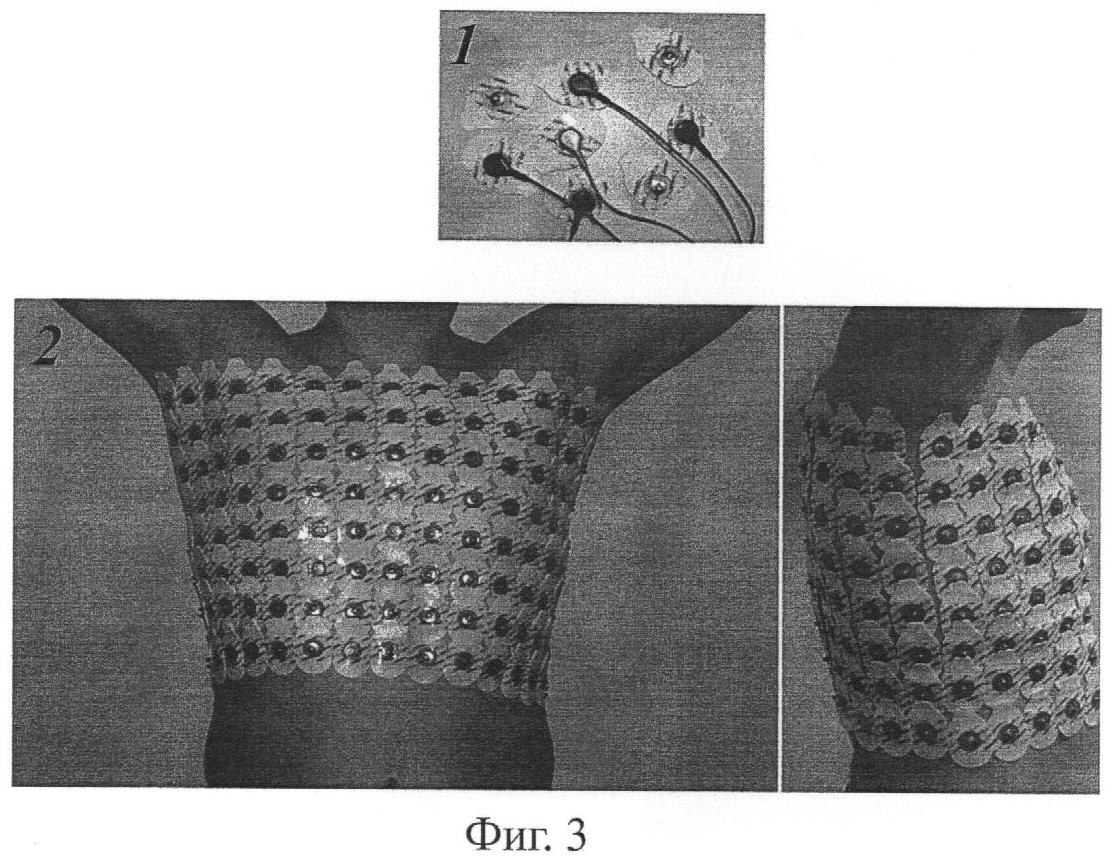
Фиг.3 иллюстрирует схему наложения электродов на поверхность грудной клетки.

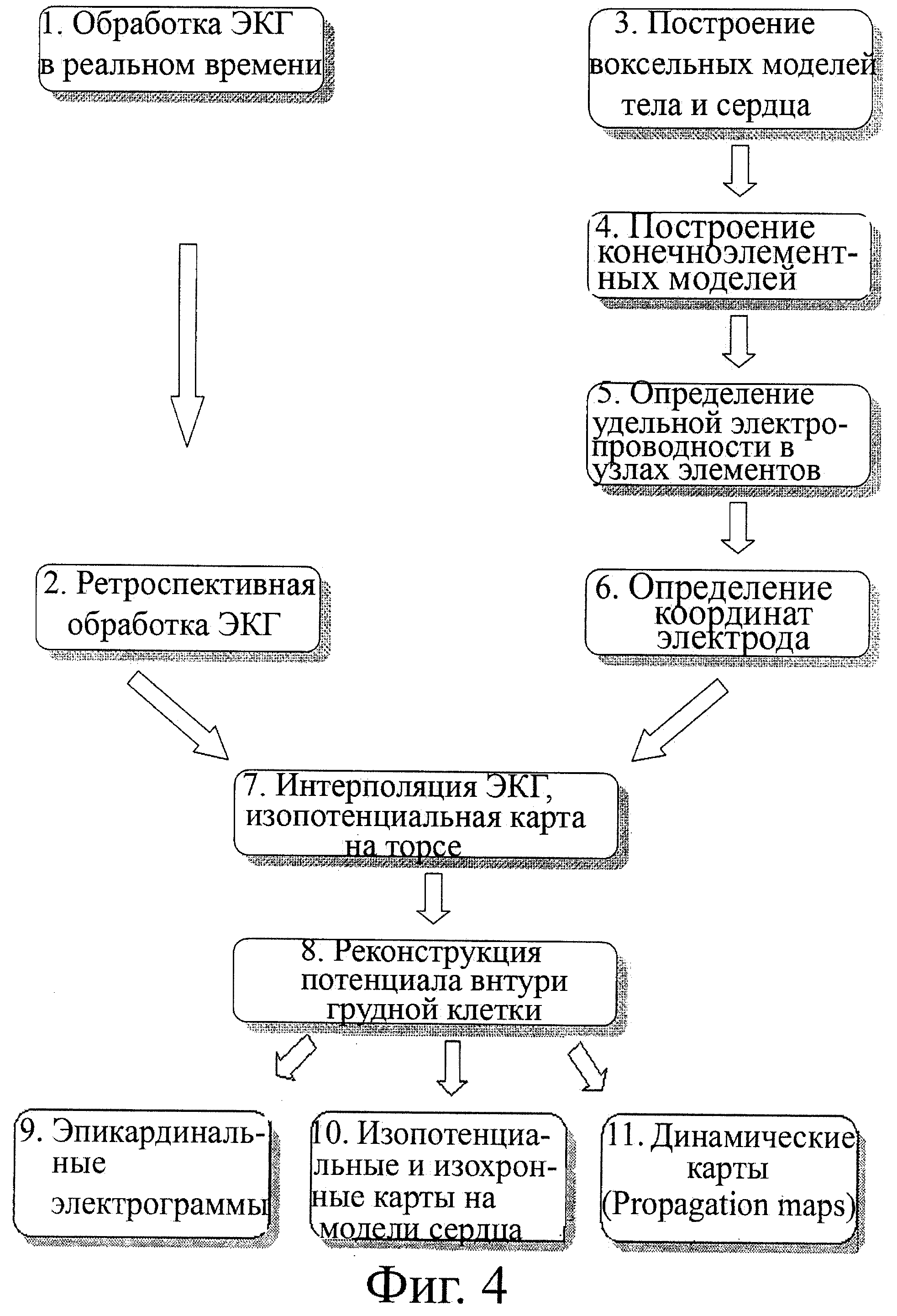
На фиг.4 представлены основные этапы компьютерной обработки информации.

Фиг.5 иллюстрирует обработку ЭКГ-сигналов в процессе ЭКГ картирования в режиме реального времени. Сверху показаны сетевые наводки, снизу - мышечные наводки. Фиг 5 (продолжение). Сверху показан дрейф изолинии, снизу - результирующий отфильтрованный сигнал.

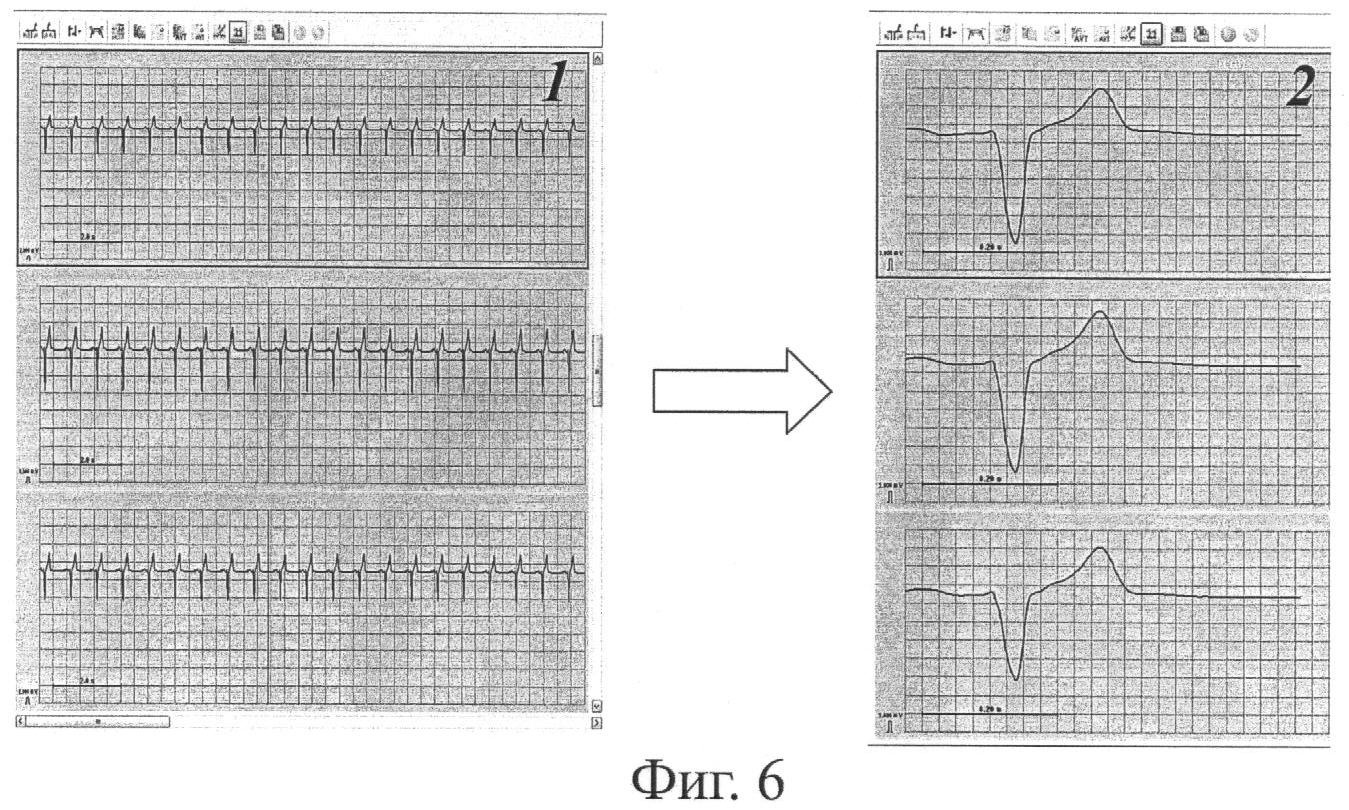
Фиг.6 иллюстрирует ретроспективную обработку ЭКГ-сигналов.

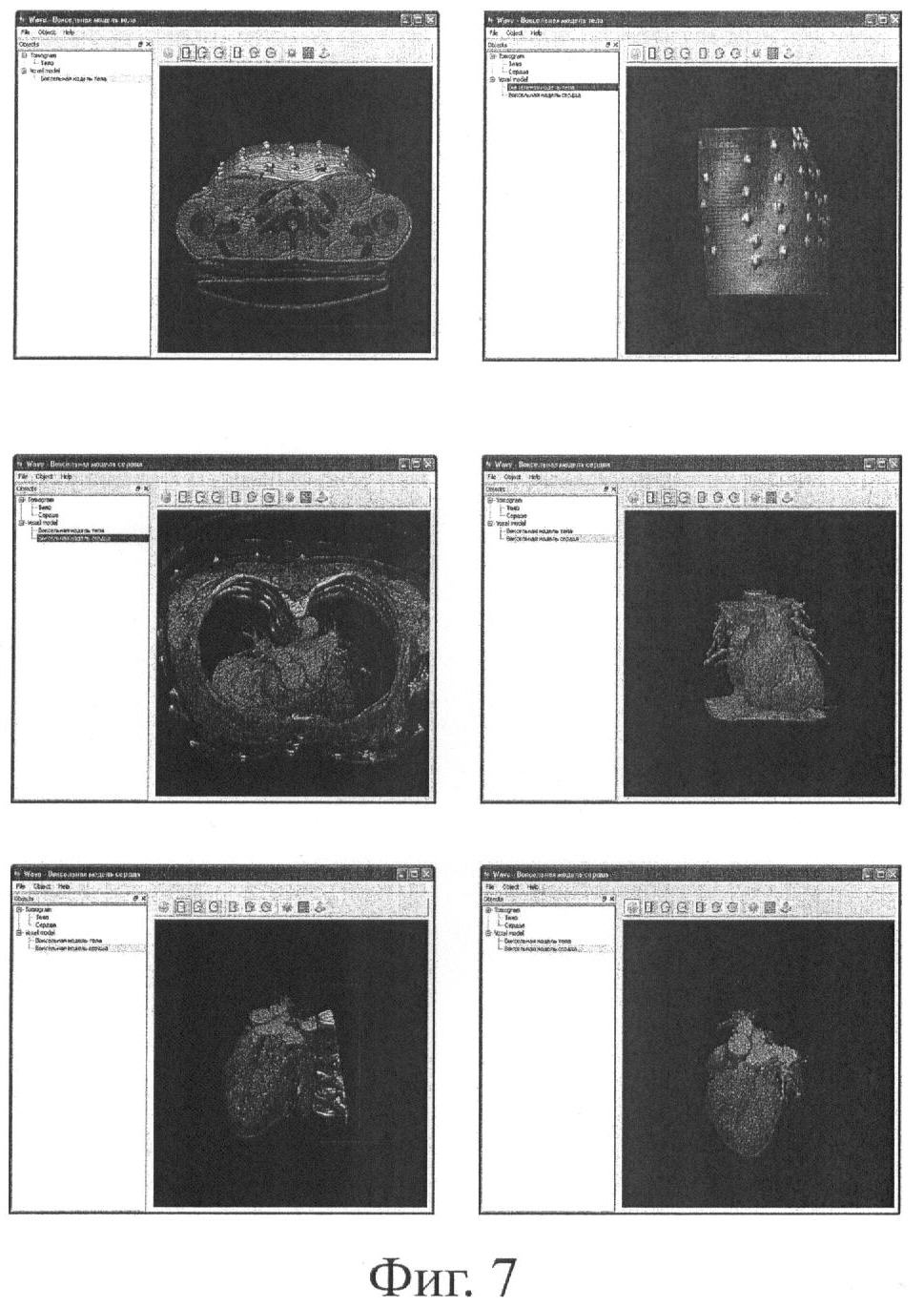
На фиг.7 показано построение вексельной модели торса и сердца в редакторе вексельной графики.

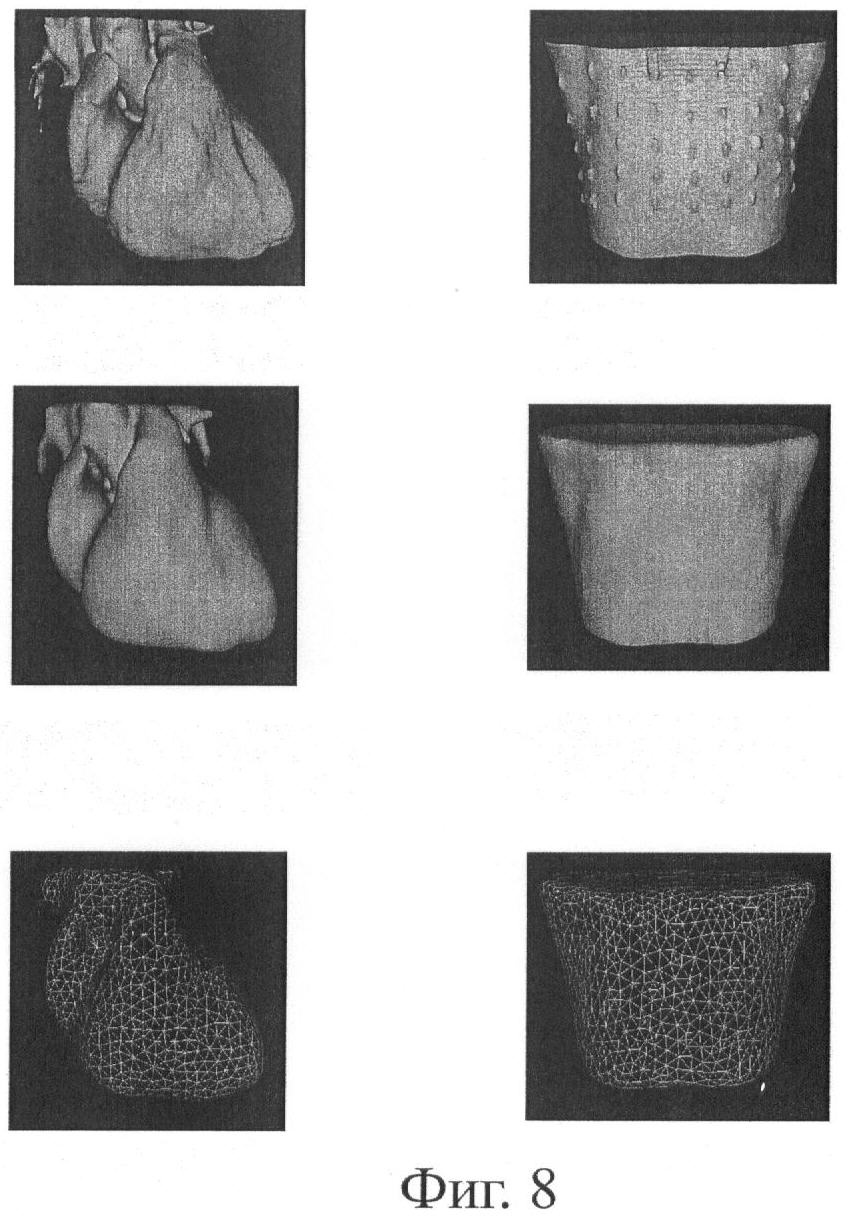
Фиг.8 иллюстрирует построение полигональных поверхностей (триангуляционных сеток) торса и сердца и конечно-элементной сетки на основе вексельных моделей. В левом столбце показаны этапы построения полигональной сетки сердца: исходная сетка (350 тыс. элементов), реконструированная сетка (20 тыс. элементов), разреженная сетка (3 тыс. элементов). В правом столбце показаны этапы построения полигональной сетки торса: исходная сетка (900 тыс. элементов), реконструированная сетка (20 тыс. элементов) и разреженная сетка (3 тыс. элементов).

На фиг.9 показано автоматическое определение координат электродов по данным КТ или МРТ грудной клетки.

На фиг.10 представлены изопотенциальные карты на поверхности торса.

На фиг.11 приведена блок-схема вычислительного алгоритма решения обратной задачи электрокардиографии на основе метода сопряженных градиентов.

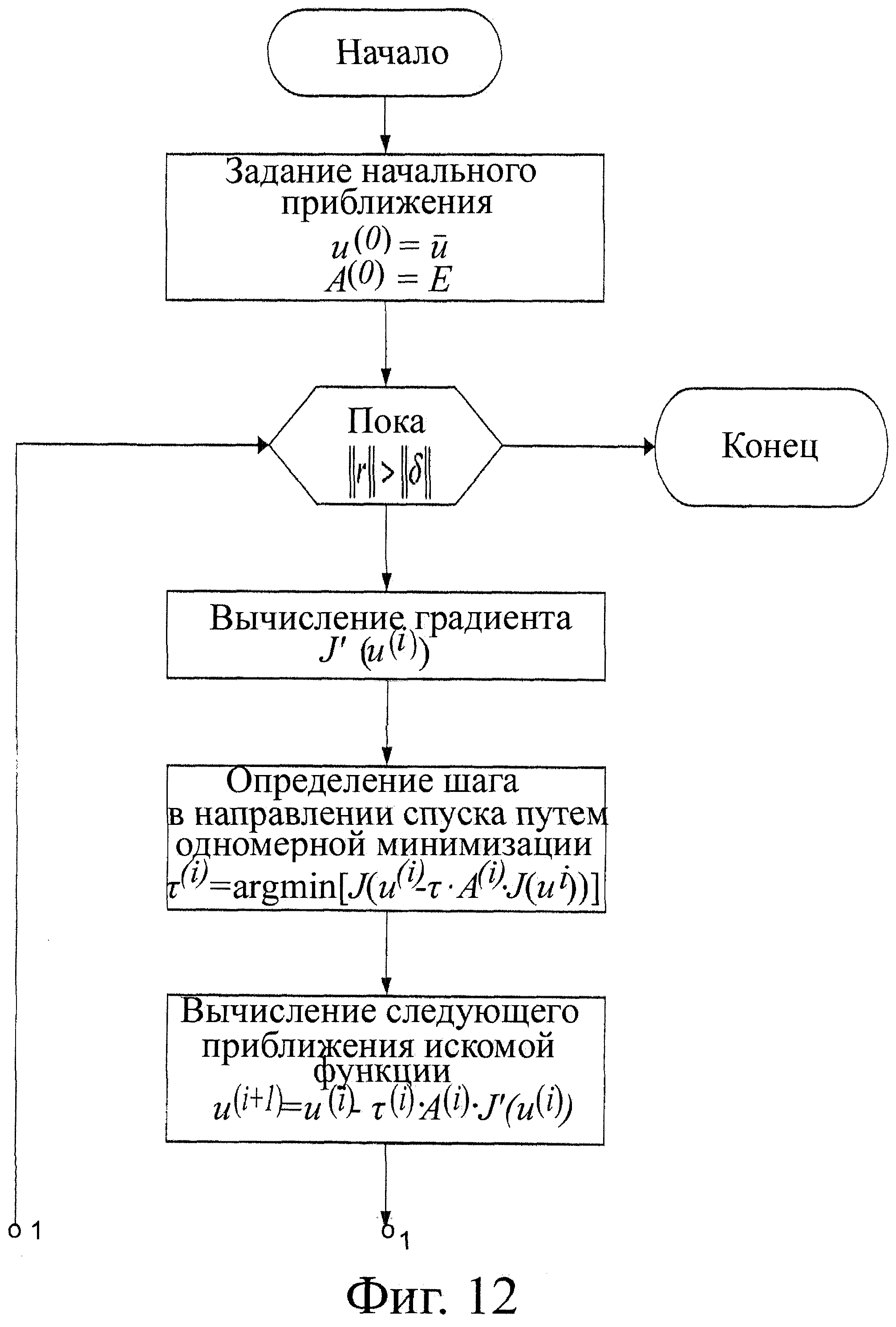
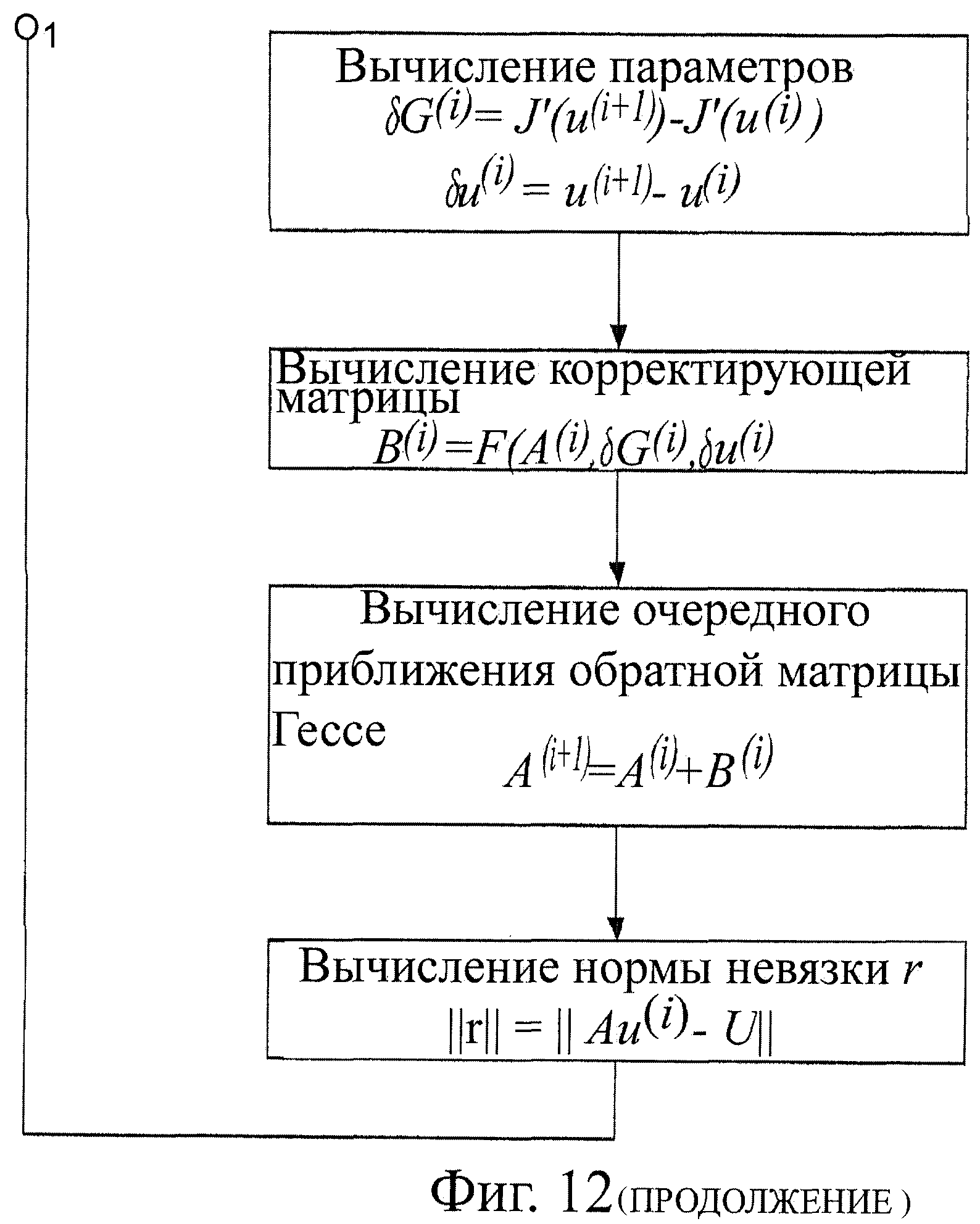
На фиг.12 приведена блок-схема вычислительного алгоритма решения обратной задачи электрокардиографии на основе квазиньютоновских методов.

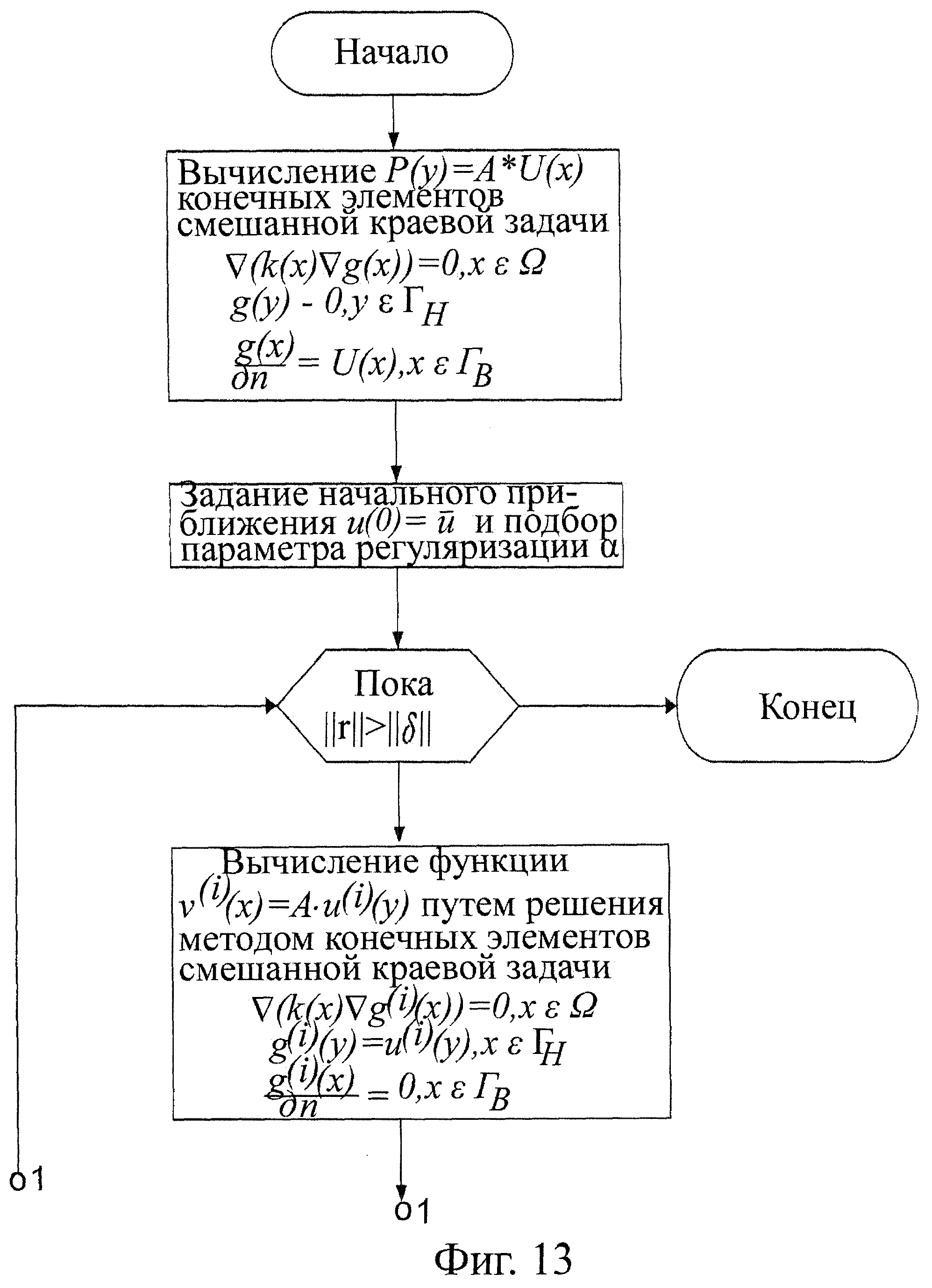
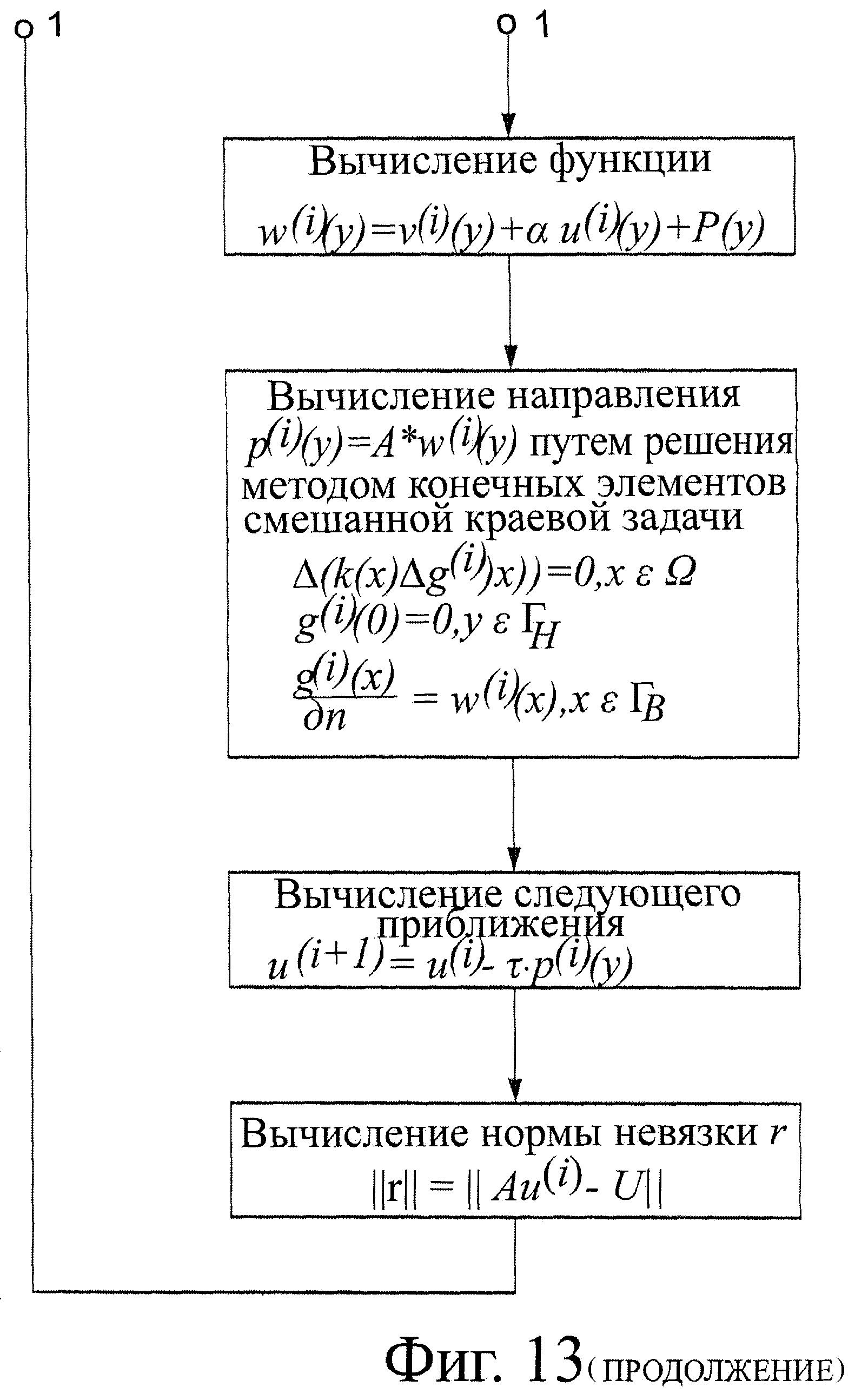
На фиг.13 приведена блок-схема вычислительного алгоритма решения обратной задачи электрокардиографии на основе итерационного решения уравнения Эйлера.

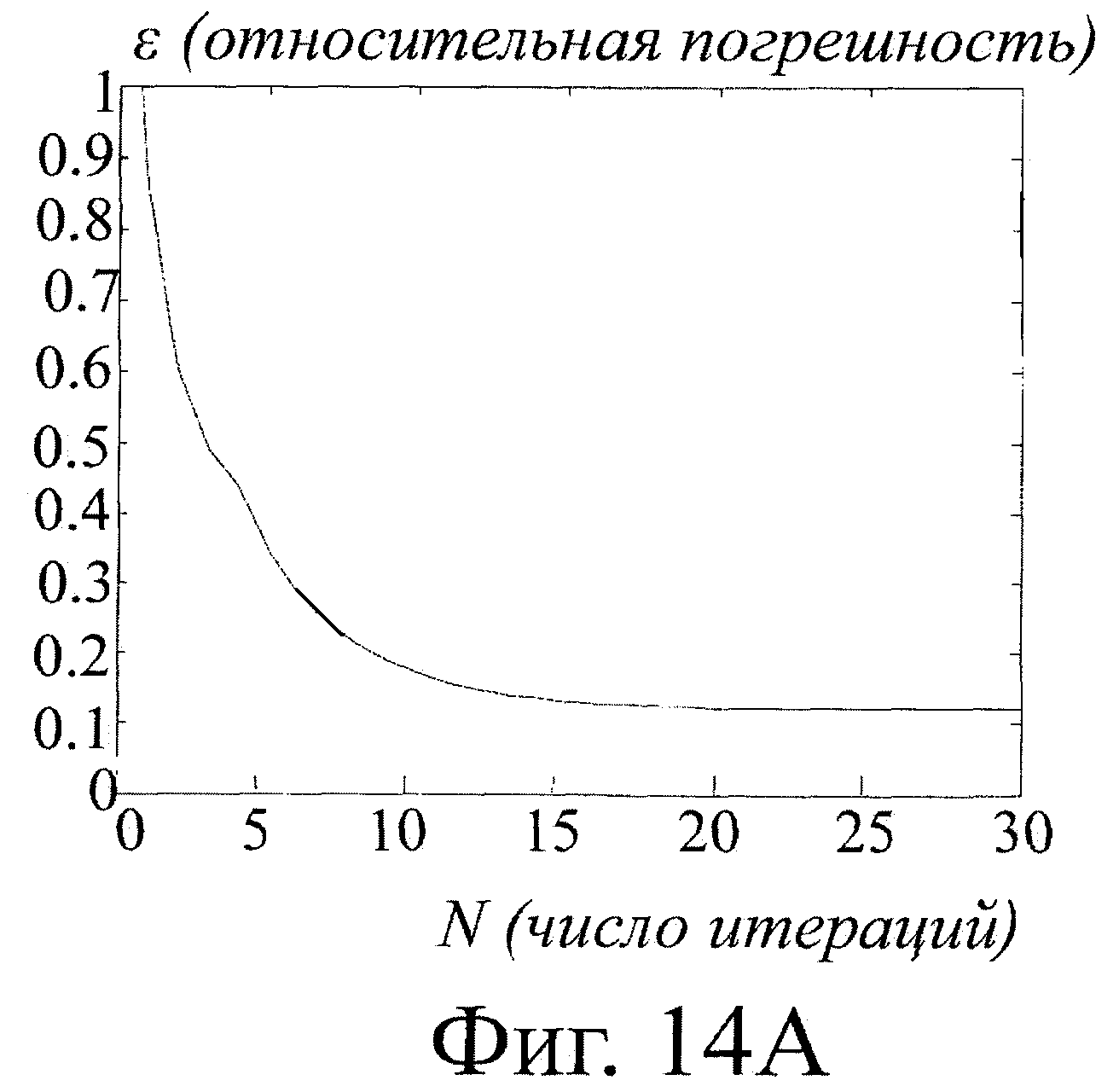
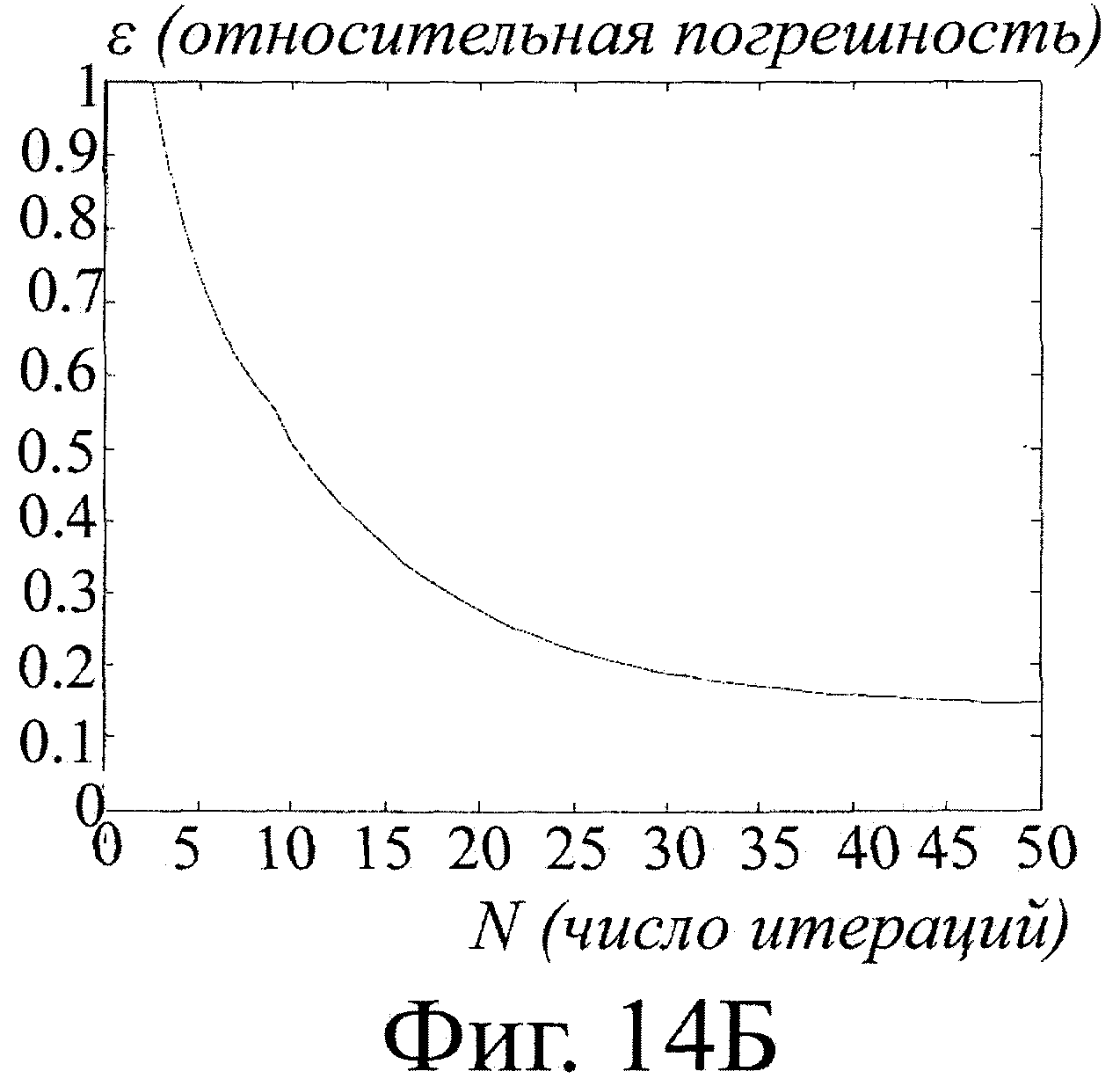
На фиг.14 приведен график сходимости итерационной процедуры для метода Девидона-Флетчера-Пауэла (а) и итерационного метода решения уравнения Эйлера (b).

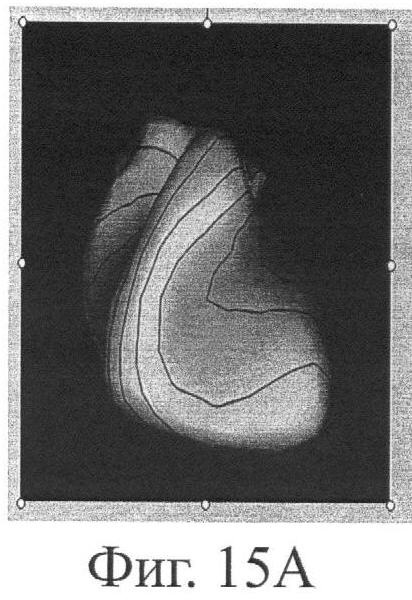
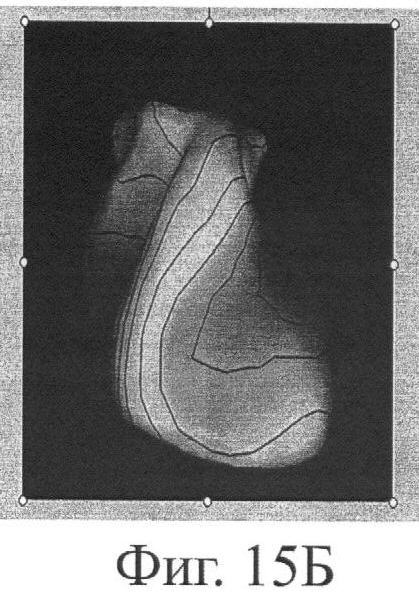
На фиг.15 приведены результаты реконструкции электрического поля на поверхности сердца для неоднородной модели (b) и однородной модели (с). Эталонная реконструкция показана на фиг.(а).

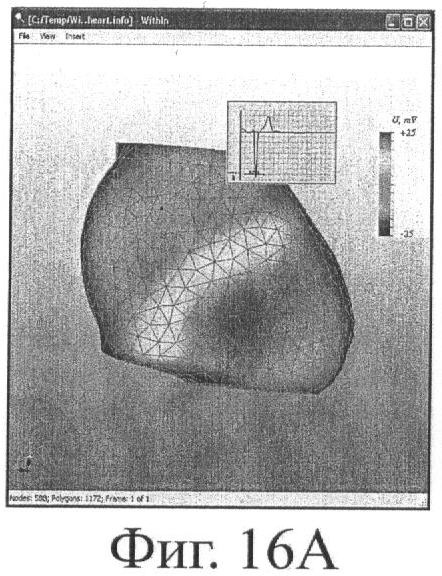
На фиг.16 представлены примеры визуализации результатов неинвазивного электрофизиологического исследования сердца.

На фиг.17 представлен пример топической диагностики аритмогенного источника.

Описание

Чтобы обеспечить полное понимание изобретения, далее будут описаны конкретные иллюстративные его воплощения, однако специалисту в данной области должно быть ясно, что системы и методы могут быть модифицированы в пределах, не выходящих за рамки описанных в формуле изобретения.

Раскрытые методы и системы используют устройство поверхностного картирования ЭКГ, визуализационную технику компьютерной (КТ) или магнитно-резонансной (МРТ) томографии, вычислительную технику, а также математические алгоритмы решения обратной задачи электрокардиографии для неинвазивной реконструкции электрограмм во внутренних точках грудной клетки и на эпикардиальной поверхности сердца и для построения изопотенциальных и изохронных эпикардиальных карт на реалистичной трехмерной компьютерной модели сердца.

Фиг.1 иллюстрирует общую схему способа. Способ включает регистрацию 240 однополярных ЭКГ на поверхности грудной клетки (1), проведение КТ или МРТ грудной клетки (2), обработку данных поверхностного картирования ЭКГ и компьютерной (МРТ) томографии средствами вычислительной техники (3) и представление полученной электрофизиологической информации средствами компьютерной графики (4).

Фиг.2 иллюстрирует схему методики поверхностного картирования ЭКГ. Устройство картирования включает цифровой многоканальный электрокардиограф (1), соединенный с персональным компьютером (2). Цифровой многоканальный электрокардиограф позволяет регистрировать ЭКГ-сигналы в 12 стандартных отведениях и до 240 однополюсных отведениях с поверхности грудной клетки.

Фиг.3 иллюстрирует схему наложения электродов. Для поверхностного картирования ЭКГ используются одноразовые хлор-серебряные электроды (1). Электроды накладываются в виде 5-8 горизонтальных поясов, расположенных на одинаковых расстояниях по вертикали. Верхний пояс располагается на уровне грудинно-ключичного сочленения, нижний пояс - на уровне нижнего края реберной дуги. Каждый пояс включает от 16 до 30 электродов, расположенных на одинаковых расстояниях по окружности грудной клетки (2). При использовании рентгеновской в качестве визуализационной методики компьютерной томографии применяются одноразовые металлические хлор-серебряные электроды, хорошо визуализируемые на рентгеновских томографических изображениях и дающие минимальный уровень артефактов. При использовании в качестве визуализационной методики магнитно-резонансной терапии применяются графитовые одноразовые электроды, обладающие аналогичными свойствами для данной томографической техники.

Фиг.4 иллюстрирует основные этапы компьютерной обработки информации.

Первый этап (1) - обработка ЭКГ-сигналов в режиме реального времени в процессе многоканальной регистрации ЭКГ с поверхности грудной клетки. Второй этап (2) - ретроспективная обработка ЭКГ-сигналов. Третий этап (3) - построение вексельных моделей грудной клетки, сердца и его отделов по данным КТ или МРТ. Четвертый этап (4) - построение полигональных поверхностей грудной клетки, сердца и его отделов. Пятый этап (5) - автоматическое определение координат регистрирующих электродов на поверхности грудной клетки по данным КТ или МРТ. На шестом этапе (6) осуществляется поверхностная интерполяция значений ЭКГ-сигналов поверхностного картирования в каждый момент времени и построение изопотенциальных карт на поверхности грудной клетки. Седьмой этап (7) включает вычислительную реконструкцию потенциала электрического поля сердца во внутренних точках грудной клетки и на эпикардиальной поверхности сердца. На последнем этапе осуществляется реконструкция эпикардиальных электрограмм (8) и построение средствами компьютерной графики эпикардиальных изопотенциальных, изохронных карт (9) на реалистичной компьютерной модели сердца и визуализация динамики электрофизиологических процессов миокарда в анимационном режиме (propagation mapping) (10).

Фиг.5 иллюстрирует обработку ЭКГ - сигналов в процессе ЭКГ картирования в режиме реального времени. Регистрируемые ЭКГ-сигналы отображаются на дисплее компьютера. Оператор контролирует качество ЭКГ-сигнала в каждом из отведений, при необходимости используется программное подавление сетевых (1) и мышечных (2) наводок и дрейфа изолинии (3). Также осуществляется автоматический контроль контакта электрода с кожей и правильности наложения электродов на основе спектрального и взаимно-корреляционного анализа сигналов ЭКГ. Результатом первого этапа являются оцифрованные и отфильтрованные значения ЭКГ-сигналов в 240 монополярных отведений с поверхности грудной клетки и в 12 стандартных отведениях длительностью до 3 минут.

Фиг.6 иллюстрирует ретроспективную обработку ЭКГ-сигналов.

Оператор просматривает зарегистрированные ЭКГ-сигналы и выбирает для дальнейшей обработки один или несколько кардиоциклов (1, 2). Далее осуществляется приведение ЭКГ к единой изолинии (3, 4): оператор на одной из ЭКГ выбирает интервал времени τ, в пределах которого ЭКГ-сигнал совпадает с изолинией (как правило, этот интервал принадлежит сегменту PQ). Коррекция ЭКГ-сигналов осуществляется по формуле:

U₀(t)=U(t)-u₀,

где U₀(t) - корригированный ЭКГ-сигнал, U(t) - исходный ЭКГ-сигнал, u₀ - среднее значение исходного ЭКГ-сигнала на интервале времени τ.

После чего оператор выбирает интересующий фрагмент кардиоцикла для дальнейших расчетов.

Фиг.7 иллюстрирует построение вексельной модели торса и сердца в редакторе вексельной графики.

По данным КТ или МРТ грудной клетки и сердца осуществляется вексельный рендеринг анатомических структур грудной клетки. Для этой цели используются алгоритм «факторизации сдвиг-деформации» для преобразования просмотра (Shear-Warp Factorization of the Viewing Transformation), относящийся к группе методов преобразования растровой строки (a scanline-order volume rendering algorithm).

Концепция используемого метода вексельного рендеринга заключается в трех основных шагах (Philippe Lacroute Fast Volume Rendering Using a Shear-Warp Factorization of the Viewing Transformation. - Ph.D. dissertation. Technical Report CSL-TR-95-678, Stanford University, 1995).

На первом шаге объемные данные преобразуются сдвиговой матрицей в соответствующее объектное пространство. При этом каждый параллельный срез объемных данных после преобразования проходит через специальный фильтр для снижения искажений.

На втором шаге из набора отфильтрованных и сдвинутых срезов совместно путем их наложения в прямом порядке формируется промежуточное 2D изображение в том же сдвиговом пространстве.

На третьем шаге полученное промежуточное 2D изображение переводится в нормальное пространство изображения с использованием матрицы деформации и далее проходит опять через фильтр для формирования финального изображения.

Оператор, пользуясь инструментами воксельного редактирования, подготавливает вексельную модель торса, сердца или одну из его структур.

Фиг.8 иллюстрирует построение полигональных поверхностей (триангуляционных сеток) торса и сердца на основе вексельных моделей.

На основе полученных вексельных моделей автоматически строятся полигональные поверхности, состоящие из объединения плоских треугольников, и объемные тетраэдерные конечно-элементные сетки.

Исходные данные представляют собой трехмерное скалярное поле плотностей в вексельном представлении, т.е. трехмерную прямоугольную сетку, в узлах которой заданы значения условных плотностей тканей грудной клетки. Построение триангуляционных сеток торса и сердца представляет собой построение полигональных поверхностей, которые наиболее близким образом повторяют поверхности указанных структур, заданные определенным уровнем плотности.

Процедура построения полигональных поверхностей включает следующие этапы:

- фильтрация исходных вексельных моделей для уменьшения уровня случайного шума;

- построение конечно-элементной объемной и поверхностной сетки на основе «метода исчерпывания», в англоязычной литературе более известного как алгоритм «распространяющегося фронта» («advancing front method»).

Подробное описание алгоритма «распространяющегося фронта» см.: (S.H.Lo. Volume Discretization into Tetrahedra - II. 3D Triangulation by Advancing Front Approach // Computers and Structures, Pergamon, Vol.39, №5, p.p.501-511, 1991. A. Rassineux Generation and Optimization of Tetrahedral Meshes by Advancing Front Technique // International Journal for Numerical Methods in Engineering, Wiley, Vol.41, p.p.651-674, 1998. Гольник Э.Р., Вдовиченко А.А., Успехов А.А. Построение и применение препроцессора генерации, управления качеством и оптимизации сеток триангуляции контактных систем // Информационные технологии. - 2004. - №4. - С.2-10).

На следующем этапе для каждого узла конечно-элементной сетки определялся коэффициент удельной электропроводности биологической ткани. Вначале на основе чисел Хаунсфилда на компьютерных томограммах или значений МР-сигнала на магнитно-резонансных томограммах определялся тип биологической ткани. После чего каждому типу биологической ткани приписывался на основе литературных данных коэффициент удельной электропроводности.

Приведем пример соответствия чисел Хаунсфилда и удельной электропроводности тканей грудной клетки (М.Хофер Компьютерная томография. Базовое руководство. / Пер с англ. М.: Медицинская литература, 2006. Э.Г.Мартиросов, Д.В.Николаев, С.Г.Руднев. Технологии и методы определения состава тела человека. - М.: Наука, 2006).

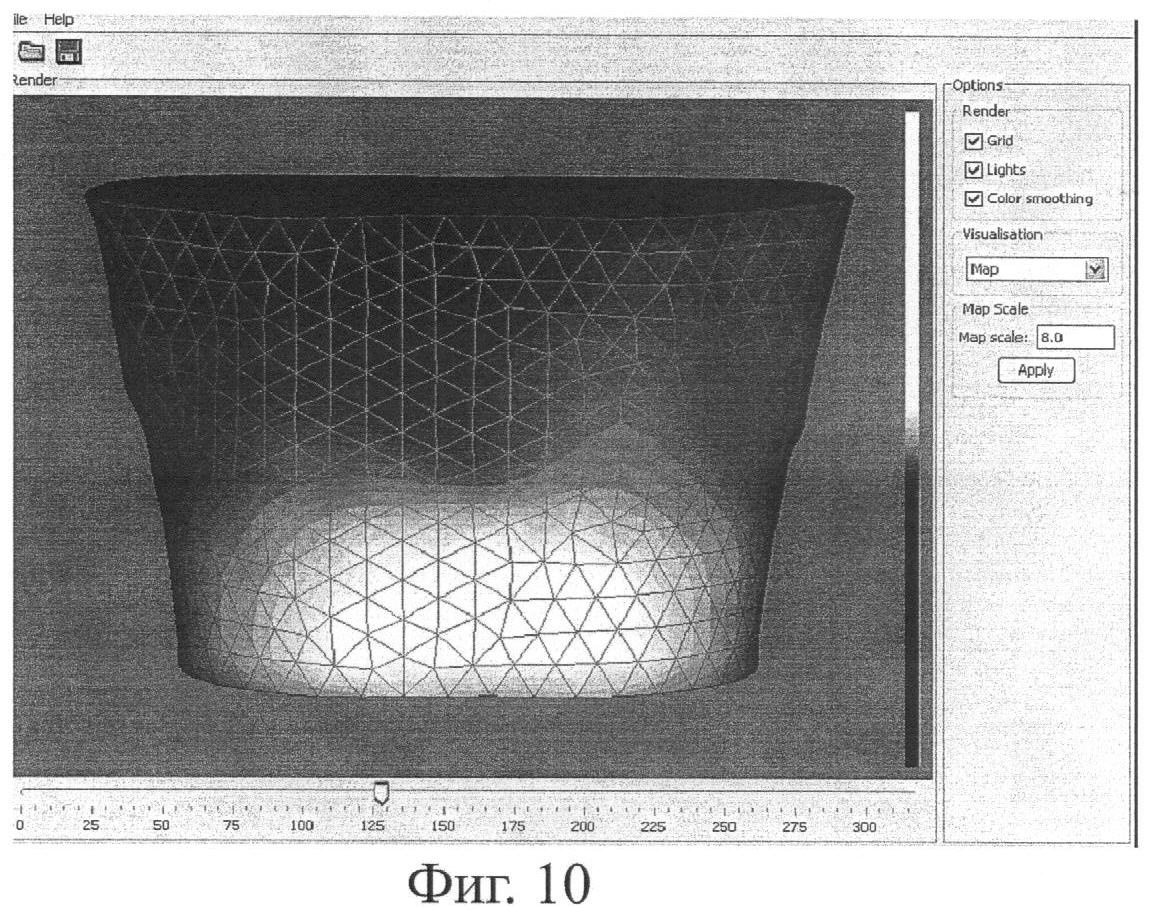
Фиг.10 иллюстрирует построение изопотенциальных карт на поверхности торса.

Построение изопотенциальных карт осуществляется путем поверхностной интерполяции значений ЭКГ-сигналов в каждый момент времени с использованием радиальных базисных функций.

Потенциал электрического поля на поверхности грудной клетки S представляется в виде разложения по системе радиальных базисных функций (РБФ):

U(x)=Σa_j·f_j(x), x∈S,

где U(x) - потенциал электрического поля, f_i(x) - радиальные базисные функции, а_i - неопределенные коэффициенты.

В качестве РБФ используются функции следующего вида, заданные в точках регистрации ЭКГ

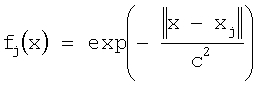
где х - произвольная точка на поверхности тела, x_j - точки регистрации ЭКГ,

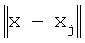
Коэффициенты a_j находятся из условия минимума функционала J:

при условии

где U(x_i) - значения потенциала электрического поля в x_i точках регистрации ЭКГ на поверхности грудной клетки, N - число точек регистрации ЭКГ.

Для нахождения коэффициентов a_j решается соответствующая система линейных алгебраических уравнений с матрицей размерностью N×N.

Потенциал U(x_i) рассчитывается в узлах триангуляционной поверхности торса x_i по формуле:

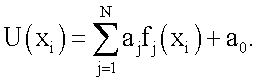
Для расчета потенциала в каждой точке поверхности торса используется билинейная интерполяция по значениям в вершинах треугольника сетки, которому принадлежит точка.

Заявляемый способ включает метод неинвазивной реконструкции потенциала электрического поля сердца во внутренних точках грудной клетки по измеренным значениям потенциала электрического поля на поверхности грудной клетки путем численного решения обратной задачи электрокардиографии для модели грудной клетки с переменным коэффициентом электропроводности методом конечных элементов на основе итерационных алгоритмов.

Для реализации метода используется следующая модель. Пусть Ω∈R³ - часть грудной клетки, ограниченная достаточно гладкой границей ∂Ω, включающей поверхность торса, контактирующую с внешней средой Г_В, поперечные сечения грудной клетки на уровне диафрагмы и ключиц Г_Т1 и Г_Т2, а также эпикардиальную поверхность сердца Г_Е. Допускается, что ткани грудной клетки в области Ω имеют переменный непрерывный положительный ограниченный коэффициент удельной электропроводности k(x), x∈Ω∪∂Ω.

Допускается, что потенциал электрического поля сердца в области Ω удовлетворяет уравнению Лапласа в неоднородной среде:

где Х=(x₁,x₂,x₃)^T∈Ω⊂R³ - точка в трехмерном пространстве,

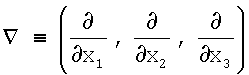
На части границы Г_В области Ω считается известным условие Дирихле - потенциал электрического поля (измеренный в результате поверхностного картирования ЭКГ):

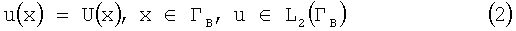
Условие Дирихле как результат экспериментальных измерений, содержит шумовую составляющую:

где u₀(x) - точное значение потенциала на поверхности грудной клетки, ξ(х) - погрешность измерения, для которой известна оценка:

На этой же части границы известно условие Неймана:

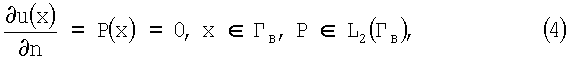
где

Решение обратной задачи электрокардиографии заключается в нахождении в классе функций L₂(Г_Н) следа потенциала u(у) на поверхности Г_Н, удовлетворяющего в области Ω уравнению Лапласа (4), а на границах областей - граничным условиям (5)-(7).

Поставим следующие вспомогательные задачи.

1. Требуется найти потенциал u(Х), такой, что:

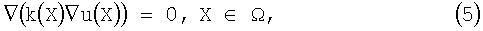
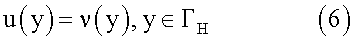
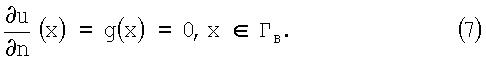
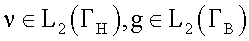
Данную задачу назовем прямой по отношению к изучаемой обратной граничной задаче.

2. Требуется найти потенциал u(Х), такой, что:

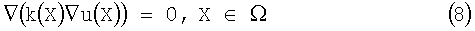
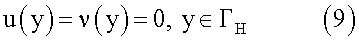
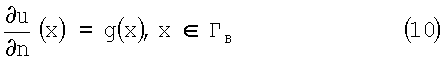
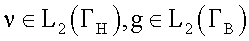
Данную задачу назовем сопряженной по отношению к прямой задаче.

Пусть u(y) - след решения прямой задачи (5)-(7) на поверхности Г_В. Введем оператор прямой задачи А, отображающий заданное на поверхности Г_Н условие Дирихле ν(y) в след решения прямой задачи u(х) на поверхности Г_В, умноженный на коэффициент электропроводности k(x), x∈Г_В, при фиксированном и равном нулю условии Неймана на Г_В:

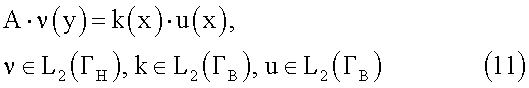
Тогда решение обратной задачи сведется к решению операторного уравнения относительно неизвестной функции ν(у):

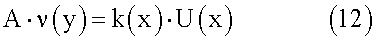
Введем квадратичный функционал:

Данный функционал является положительным, строго выпуклым и его точная нижняя грань равна нулю. Поэтому задаче решения уравнения (12) эквивалентна вариационная задача нахождения функции ν, на которой данный функционал достигает минимума:

ν=arg min J(ν).

Заявляемый способ включает алгоритмы решения обратной задачи электрокардиографии путем численной минимизации функционала (13) на основе методов градиентной оптимизации или итерационного решения уравнения Эйлера, являющегося необходимым условием минимума функционала. Указанные алгоритмы являются итерационными, причем на каждой итерации выполняется решение прямой и сопряженной задач методом граничных элементов.

Задача минимизации функционала (13) является некорректно поставленной по Адамару в силу некорректности обратной задачи электрокардиографии.

Заявляемый способ включает алгоритмы решения обратной задачи электрокардиографии путем численной минимизации функционала (13) с использованием методов регуляризации, основанных на ограничении числа итераций и методе Тихонова.

Вычислительный алгоритм включает следующие этапы:

1. Проводится конечно-элементная дискретизация расчетной области: область Ω разбивается на тетраэдерные элементы, границы области Г_В и Г_Н - на треугольные элементы. При этом функции u(x), x∈Г_Н,

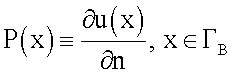
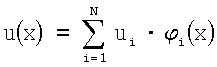
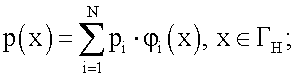
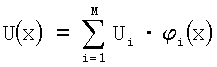
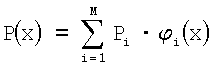
2. Вычисляется вектор u={u₁, u₂, …, u_n} на основе итерационной процедуры численной минимизации функционала (21).

3. Находится функция u(х), х∈Г_Н, являющаяся итоговым решением задачи, по формуле:

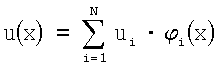
Способ включает следующие итерационные методы для нахождения вектора u={u₁, u₂, …, u_n}. См.: (Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Пер. с англ. - М.: Мир, 1985).

1. Метод сопряженных градиентов (метод Флетчера-Ривса).

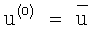
S⁽⁰⁾=-J'(u⁽ⁱ⁾),

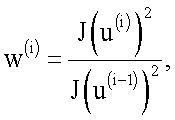
S⁽ⁱ⁾=-J'(u⁽ⁱ⁾)+ω⁽ⁱ⁾·S^(i-1),

τ⁽ⁱ⁾=arg min(J(u⁽ⁱ⁾+τ·S⁽ⁱ⁾)),

u⁽ⁱ⁺¹⁾=u⁽ⁱ⁾+τ·S⁽ⁱ⁾,

где i=1, 2 …, N - номер итерации,

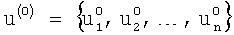
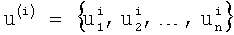
Выход итерационной процедуры осуществляется по принципу невязки (принцип Морозова): итерационный процесс останавливается при достижении условия:

При достижении номера итерации, кратного m, полагается:

S^(im)=S⁽⁰⁾, где m - целочисленный параметр, подбираемый экспериментально.

2. Квазиньютоновские методы, объединяющие метод градиентного спуска (метод Коши) и метод Ньютона, но использующие итерационные способы вычисления обратной матрицы Гессе.

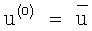
А⁽⁰⁾=Е,

τ=arg min[J(u⁽ⁱ⁾-τ⁽ⁱ⁾·A⁽ⁱ⁾·J'(uⁱ))],

u⁽ⁱ⁺¹⁾=u⁽ⁱ⁾-τ⁽ⁱ⁾·A⁽ⁱ⁾·J(u⁽ⁱ⁾),

δG⁽ⁱ⁾=J'(u⁽ⁱ⁺¹⁾)-J'(u⁽ⁱ⁾),

δu⁽ⁱ⁾=u⁽ⁱ⁺¹⁾-u⁽ⁱ⁾,

A⁽ⁱ⁺¹⁾=A⁽ⁱ⁾+B⁽ⁱ⁾,

где A⁽ⁱ⁾ - очередное приближение обратной матрицы Гессе функционала J(u),

Е - единичная матрица, B⁽ⁱ⁾ - корректирующая матрица, вычисляемая различными способами, описанными ниже.

2.1. Метод Девидона - Флетчера - Пауэлла.

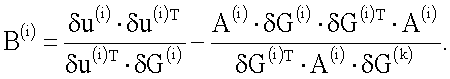
2.2. Метод Бройдена - Флетчера - Шэнно.

2.3. Методы Пирсона.

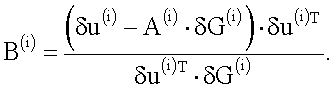
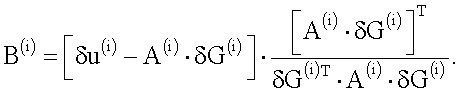
Выход итерационной процедуры осуществляется по принципу невязки (принцип Морозова): итерационный процесс останавливается при достижении условия:

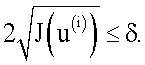
При достижении номера итерации, кратного m, полагается:

A^(im)=A⁽⁰⁾, где m - целочисленный параметр, подбираемый экспериментально.

В описанных итерационных процедурах необходимо вычислять функционал J(uⁱ) и его градиент J'(u⁽ⁱ⁾).

Способ включает вычисление указанных объектов следующими методами.

1. Вычисление J(uⁱ).

1.1. Находится функция ν⁽ⁱ⁾(х), x∈Ω путем решения методом граничных элементов следующей смешанной граничной задачи для уравнения Лапласа в неоднородной среде (прямой задачи (5)-(7)):

∇(k(x)∇ ν⁽ⁱ⁾(x))=0, x∈Ω,

ν⁽ⁱ⁾(x)=u⁽ⁱ⁾(x),x∈Г_Н.

Находится след решения ν⁽ⁱ⁾(х) на границе Г_В.

Путем численного интегрирования вычисляется J(u⁽ⁱ⁾) по формуле:

2. Вычисление J'(u⁽ⁱ⁾).

2.1. Находится функция g⁽ⁱ⁾(x), x∈Ω путем решения методом граничных элементов следующей смешанной граничной задачи для уравнения Лапласа в неоднородной среде (сопряженной задачи (8)-(10)):

∇(k(X)∇g⁽ⁱ⁾(X))=0, X∈Ω,

g⁽ⁱ⁾(y)=0, x∈Г_Н,

2.2. Путем численного дифференцирования найденного решения g⁽ⁱ⁾(x) вычисляется нормальная производная решения на границе

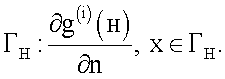
2.3. Полученная нормальная производная умножается на коэффициент электропроводности k(y) с обратным знаком на поверхности Г_н:

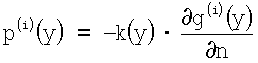
2.4. В качестве значений вектора J'(u⁽ⁱ⁾) принимаются значения полученной функции р⁽ⁱ⁾(х), х∈Г_н в поверхностных узлах гранично-элементной сетки:

Способ включает минимизацию функционала (13) на основе численного решения уравнения Эйлера, являющегося необходимым условием минимума функционала (13):

где А^* - оператор, сопряженный к оператору А.

Решение уравнения (11) осуществляется на основе следующего итерационного алгоритма:

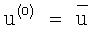
u⁽ⁱ⁺¹⁾=u⁽ⁱ⁾-τ·(А^*·A·u⁽ⁱ⁾-А^*·U),

где

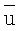
Выход итерационной процедуры осуществляется по принципу невязки:

Итерационный процесс останавливается при достижении условия:

В более подробном виде алгоритм можно записать:

Р(y)=A^*U(x),

ν⁽ⁱ⁾(x)=A·u⁽ⁱ⁾(y),

pⁱ(y)=A*·ν⁽ⁱ⁾(x)

u⁽ⁱ⁺¹⁾(y)=u⁽ⁱ⁾(y) -τ(pⁱ(y)-P(y)),

х∈Г_В, у∈Г_Н.

Вычисление функции Р(y)=A^*U(x) осуществляется следующим образом.

1. Методом конечных элементов решается следующая смешанная граничная задача для уравнения Лапласа в неоднородной среде (сопряженная задача (8)-(10)):

∇(k(X)∇g(X))=0, X∈Ω,

g(y)=0, y∈Г_Н,

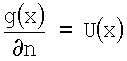
2. Путем численного дифференцирования найденного решения g(y) вычисляется нормальная производная решения на границе Г_Н:

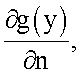
3. Полученная нормальная производная умножается на коэффициент электропроводности k(y) с обратным знаком на границе Г_Н:

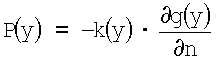
Вычисление функций р(y)=A^*ν⁽ⁱ⁾(x) осуществляется аналогичным образом.

1. Методом конечных элементов на каждой итерации решается следующая смешанная граничная задача для уравнения Лапласа в неоднородной среде (сопряженная задача (8)-(10)):

∇(k(X)∇g⁽ⁱ⁾(X))=0, X∈Ω,

g⁽ⁱ⁾(0)=0, y∈Г_Н,

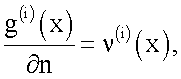
2. Путем численного дифференцирования найденного решения g(y) вычисляется нормальная производная решения на границе Г_Н:

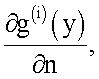
3. Полученная нормальная производная умножается на коэффициент электропроводности k(y) с обратным знаком на границе Г_Н:

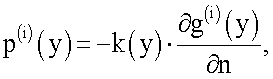
Вычисление функции

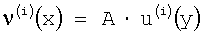
1. Находится функция ν⁽ⁱ⁾(x), x∈Ω путем решения методом граничных элементов следующей смешанной граничной задачи для уравнения Лапласа в неоднородной среде (прямой задачи (5)-(7)):

∇(k(X)∇ν⁽ⁱ⁾(X))=0, X∈Ω,

ν⁽ⁱ⁾(y)=u⁽ⁱ⁾(y), x∈Г_Н,

2. След полученного решения на границе умножается на коэффициент электропроводности k(x) на границе Г_В:

ν⁽ⁱ⁾(x)=k(x)·u(x), x∈Г_В.

Способ включает минимизацию функционала (13) использованием регуляризации Тихонова на основе решения соответствующего уравнения Эйлера:

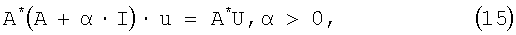
где α - параметр регуляризации, I - единичный оператор.

Решение уравнения (15) осуществляется на основе итерационной процедуры:

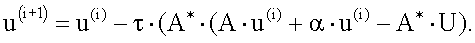
Выход из итерационной процедуры осуществляется при достижении условия:

|u_i+1-u_i|<ε, где ε - малый положительный параметр, зависящий от машинной точности.

Выбор параметра регуляризации α осуществляется по принципу невязки: α выбирается таким, при котором наиболее точно выполняется равенство:

где u(α) - полученное в результате выполнения итерационной процедуры решение, зависящее от параметра α.

Блок-схемы алгоритмов приведены на фиг.1, 12, 13.

На фиг.14 приведены графики сходимости квазиньютоновской итерационной процедуры Девидона-Флетчера-Пауэлла (14а) и итерационного решения уравнения Эйлера (14б).

В расчетах использовалась модель торса и сердца реального пациента. Для моделирования эталонного электрического поля сердца использовался квадрупольный источник, помещенный в геометрический центр сердца.

На фиг.15 приведены наложенные на реалистичные модели сердца изопотенциальные карты точного электрического потенциала (14.а), рассчитанного раскрываемым в настоящем патенте алгоритмом с учетом электрической неоднородности грудной клетки (14.б) и алгоритмом на основе однородной модели грудной клетки, раскрытым в патенте-прототипе изобретения (14.в).

На фиг.16 представлены примеры визуализации результатов неинвазивного электрофизиологического исследования сердца.

Используются следующие типы визуального отображения:

1. Построение электрограмм в интерактивно выбранных точках эпикардиальной поверхности сердца, эндокардиальных поверхностей межжелудочковой и межпредсердной перегородок, а также внутренних точках грудной клетки на поперечных томографических срезах (фиг.16а).

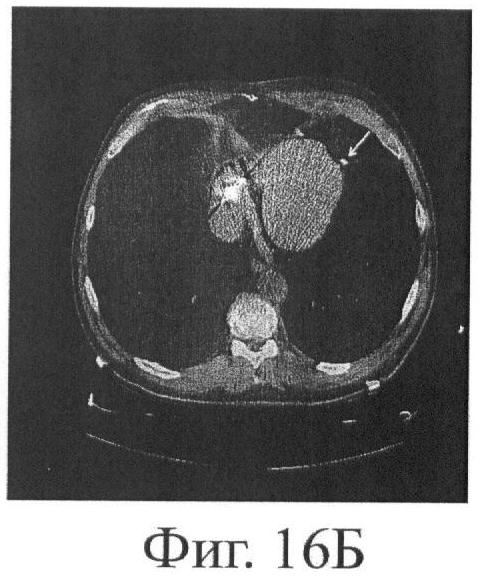
2. Построение изопотенциальных карт на поперечных томографических срезах грудной клетки (фиг.16б).

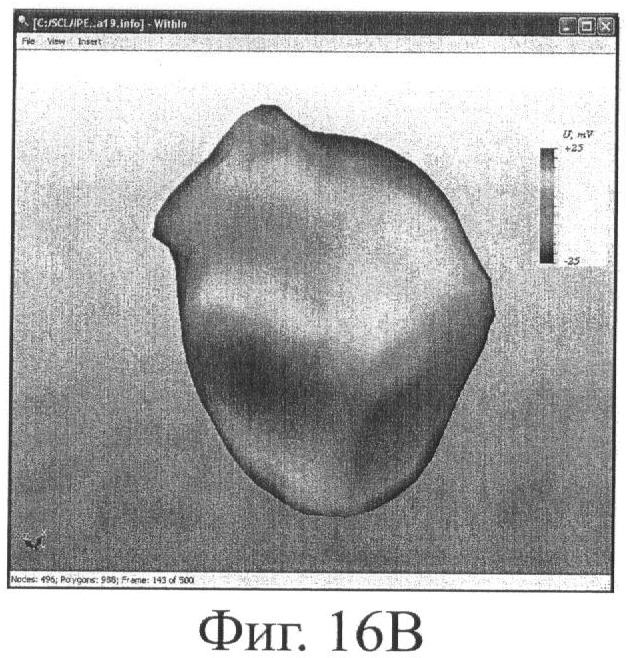
3. Построение изопотенциальных и изохронных карт на эпикардиальной поверхности сердца, эндокардиальных поверхностей межжелудочковой и межпредсердной перегородок (фиг.16в).

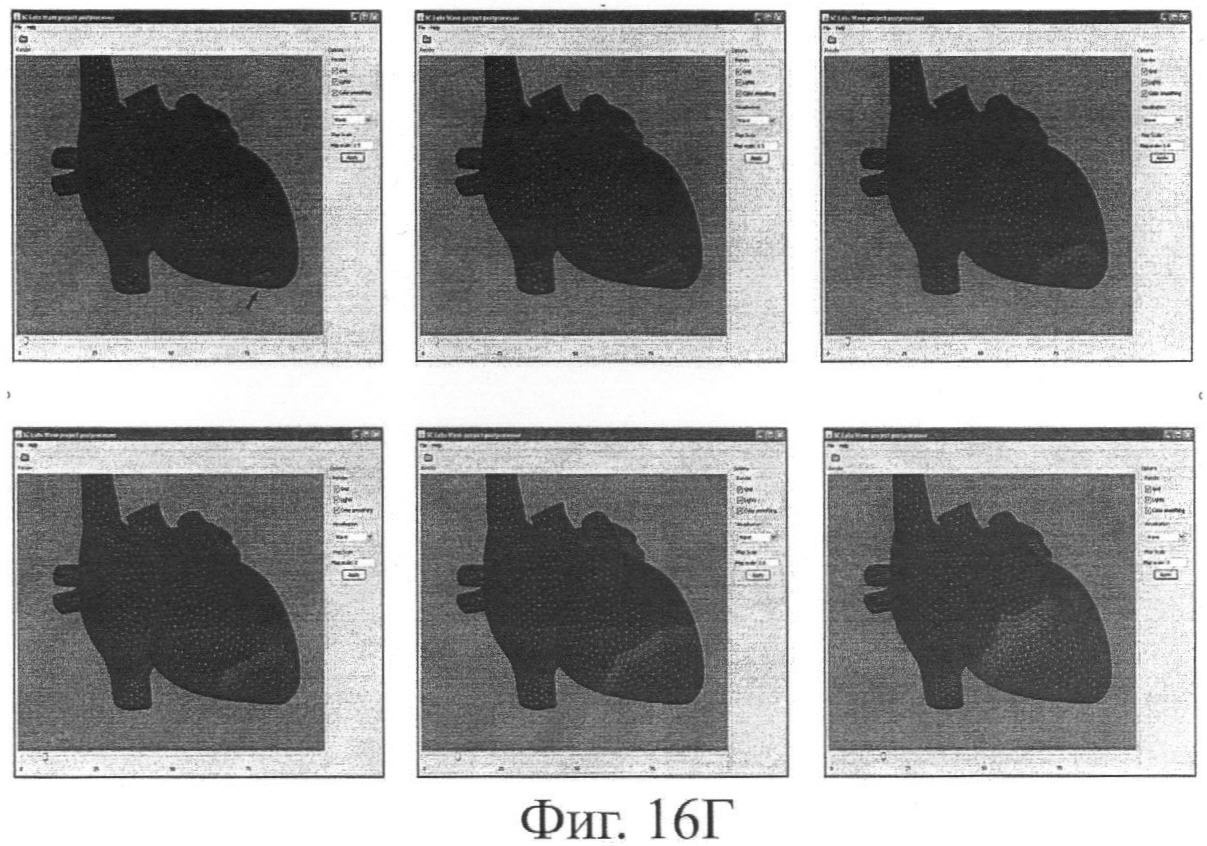
4. Визуализация динамики возбуждения миокарда на эпикардиальной поверхности сердца, эндокардиальных поверхностей межжелудочковой и межпредсердной перегородок в анимационном режиме (propagation maps) (фиг.16г).

Монополярные электрограммы строятся путем интерполяции вычисленных значений потенциала электрического поля сердца для всех моментов времени кардиоцикла в заданной точке. Биполярные электрограммы строятся как разность электрограмм в выбранном узле и в точке, находящейся в окрестности узла на расстоянии Δl по направлению I. Параметры Δl и I задаются интерактивно.

Изопотенциальные карты строятся на основе билинейной интерполяции вычисленных значений потенциала электрического поля сердца в узлах сетки в заданный момент времени кардиоцикла методом градиентной закраски или построения изопотенциальных линий.

Для построения изохронных карт предусмотрены два режима: ручной и автоматический. В ручном режиме в интерактивно выбранном узле сетки реконструируются: монополярная электрограмма U(t), биполярная электрограмма U_b=U₁(t)-U₂(t), а также дифференциальная электрограмма

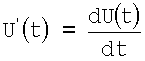
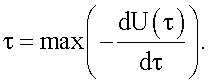
На основе билинейной интерполяции значений τ в узлах сетки визуализируются изохронные карты путем градиентной закраски или построения изохронных линий. Эти же данные представляются в анимационном режиме в виде т.н. карт распространения возбуждения (propagation maps).

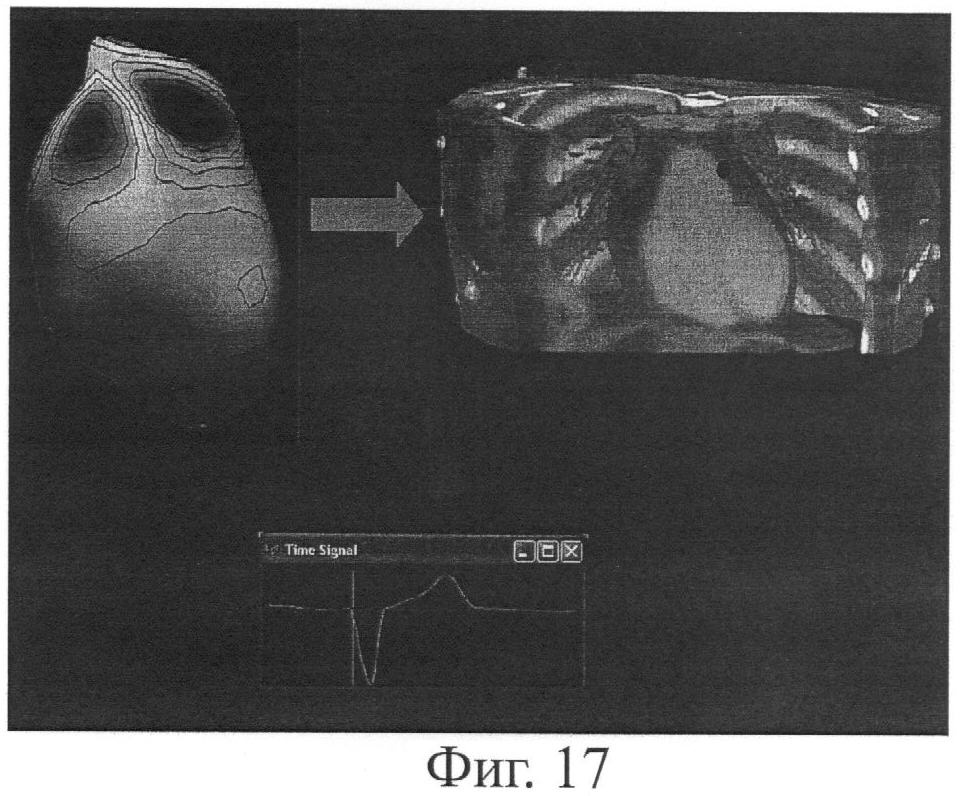
На фиг.17 представлены реконструированные описанным способом эпикардиальные изохронные карты экстрасистолии, вызванной эктопическим источником в области выводного тракта правого желудочка. Кружком указана локализация аблационного электрода, при помощи которого была выполнена успешная радиочастотная аблация эктопического источника.

Реферат

Изобретение относится к кардиологии, сердечно-сосудистой хирургии, функциональной диагностике и клинической электрофизиологии сердца. Способ неинвазивного электрофизиологического исследования сердца включает следующие стадии: закрепление регистрирующих электродов на поверхности грудной клетки; регистрация ЭКГ; обработка ЭКГ-сигналов; КТ или МРТ грудной клетки; построение и редактирование компьютерных вексельных моделей органов грудной клетки и сердца; построение полигональных моделей торса и сердца; построение конечно-элементной сетки области грудной клетки; определение коэффициента удельной электропроводности для каждой точки грудной клетки; определение координат регистрирующих электродов на поверхности грудной клетки; получение изопотенциальных карт на полигональной модели торса; реконструкция потенциала электрического поля в заданных точках с учетом найденных значений коэффициентов удельной электропроводности; визуализация результатов реконструкции электрического поля сердца; клиническая оценка результатов. Для определения коэффициентов удельной электропроводности в каждой точке томографических данных определяется тип биологической ткани, соответствующий числу Хаунсфилда при КТ или значению интенсивности МР-сигнала при МРТ, после чего найденному типу биологической ткани сопоставляется значение удельной электропроводности. Использование способа позволит повысить точность неинвазивной диагностики нарушений сердечного ритма и других сердечно-сосудистых заболеваний. 13 з.п.ф-лы, 17 ил., 1 табл.

Формула