Быстрая вязкоакустическая и вязкоупругая инверсия полного волнового поля - RU2016150545A

1. Способ, содержащий этапы, на которых:

получают, с помощью компьютера, начальную геофизическую модель;

моделируют, с помощью компьютера, прямое волновое поле с помощью вязкоакустических или вязкоупругих волновых уравнений, при этом прямое волновое поле с вязкоакустическими волновыми уравнениями основано на первой вспомогательной переменной, которая является функцией как от давления, так и от переменной запоминающего устройства, либо прямое волновое поле с вязкоупругими волновыми уравнениями основано на второй вспомогательной переменной, которая является функцией как от механического напряжения, так и переменной запоминающего устройства, соответственно, и первая и вторая вспомогательные переменные выбираются с возможностью исключать член сейсмической скорости из прямого волнового поля с помощью вязкоакустических или вязкоупругих волновых уравнений;

моделируют, с помощью компьютера, сопряженное волновое поле с помощью сопряженных вязкоакустических или сопряженных вязкоупругих волновых уравнений, которые извлекаются из прямых вязкоакустических или прямых вязкоупругих волновых уравнений, соответственно, и основаны на сопряженном операторе первой или второй вспомогательной переменной, соответственно, при этом моделирование включает в себя этап, на котором инструктируют пространственной производной переменной запоминающего устройства выпадать из сопряженных вязкоакустических или вязкоупругих волновых уравнений вследствие сопряженной первой или второй вспомогательной переменной;

получают, с помощью компьютера, градиент функции затрат на основе комбинации модели прямого волнового поля и модели сопряженного волнового поля; и

используют, с помощью компьютера, градиент функции затрат для того, чтобы обновлять начальную геофизическую модель и получать обновленную геофизическую модель.

2. Способ по п. 1, в котором получение начальной геофизической модели включает в себя этап, на котором получают релаксационные параметры для данного коэффициента качества с использованием обобщенной реологической модели Максвелла и параметров акустической или упругой среды.

3. Способ по п. 1, в котором получение начальной геофизической модели включает в себя этап, на котором получают релаксационные параметры для данного коэффициента качества с использованием начальной реологической модели и параметров акустической или упругой среды.

4. Способ по любому из пп. 1-3, в котором сопряженное волновое поле моделируется с использованием сопряженных вязкоакустических уравнений.

5. Способ по любому из пп. 1-4, в котором вспомогательная переменная является , где p является давлением, является переменной запоминающего устройства для механизма l, где l является целым числом, большим или равным 1, и является параметром инверсии для механизма l.

6. Способ по любому из пп. 1-5, в котором сопряженные вязкоакустические уравнения являются следующими:

,

,

,

,

где является оператором дивергенции,

t является временем,

является нерелаксированным модулем объемной деформации ( ),

является массовой плотностью,

является сейсмической скоростью ( в трехмерном пространстве),

является сопряженным давлением,

является функцией затрат, где является параметрами модели (т.е. некоторой комбинация или , и )

является сопряженной сейсмической скоростью, и

является частотой релаксации для механизма l,

и являются производными целевой функции относительно давления и сейсмической скорости, соответственно.

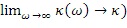
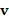
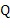
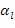
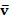
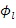
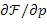
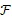
7. Способ по любому из пп. 1-6, в котором сопряженное волновое поле моделируется с использованием сопряженных вязкоупругих уравнений.

8. Способ по п. 7, в котором вспомогательная переменная является , где является механическим напряжением, является переменной запоминающего устройства для механизма l, где l является целым числом, большим или равным 1, является упругим конститутивным соотношением для изотропной нерелаксированной системы, и 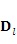является конститутивным соотношением для запоминающей системы.

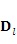
9. Способ по п. 8, в котором сопряженные вязкоупругие уравнения являются следующими:

,

,

,

,

где t является временем,

является сопряженным механическим напряжением, ,

является сопряженной сейсмической скоростью,

является сопряженным полем запоминающего устройства для механизма l, ,

является переменной, заданной для ясности для механизма l, ,

является массовой плотностью,

и являются производными целевой функции относительно механического напряжения и сейсмической скорости, соответственно

= ,

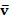
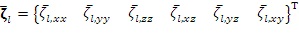
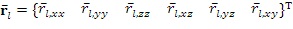
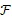
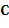
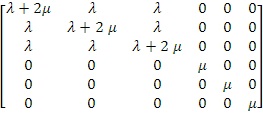
что является упругим конститутивным соотношением для изотропной нерелаксированной системы с точки зрения постоянных и Ламе,

= ,

что является конститутивным соотношением для запоминающей системы ( 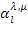вычисляются из коэффициента качества продольных и поперечных сейсмоволн с использованием уравнения (9)), и является оператором относительной деформации, ,

является функцией затрат, где является параметрами модели (т.е. некоторой комбинацией , или , , и ).

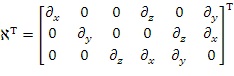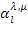
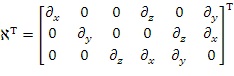
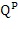
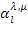
10. Способ по любому из пп. 1-9, дополнительно содержащий этап, на котором используют обновленную подповерхностную модель для того, чтобы управлять углеводородами.

11. Способ по любому из пп. 1-10, в котором начальная геофизическая модель включает в себя модель на основе сейсмической скорости.

12. Способ по любому из пп. 1-11, в котором начальная геофизическая модель включает в себя модель на основе коэффициента качества.