Способ q томографии - RU2558013C2

Код документа: RU2558013C2

Чертежи

Показать все 11 чертежа(ей)

Описание

Перекрестная ссылка на родственную заявку

По этой заявке испрашивается преимущество приоритета предварительной заявки № 61/331694 на патент США, поданной 5 мая 2010 года, под названием “Q tomography method”, которая полностью включена в эту заявку путем ссылки.

Область техники, к которой относится изобретение

В общем настоящее изобретение относится к области геофизических исследований, а более конкретно к обработке сейсмических данных. В частности, изобретение относится к области Q томографии.

Предпосылки создания изобретения

Эффект затухания сейсмических волн необходимо учитывать при определении свойств породы и соответствующем анализе зависимости амплитуды отражения от удаления. При миграции информация о затухании сейсмических волн необходима для компенсации эффекта поглощения, чтобы повышать качество мигрированного изображения. Поэтому оценивание затухания сейсмических волн является важным при обнаружении и мониторинге коллектора.

Затухание сейсмических волн можно численно описать добротностью Q. Простое предположение заключается в том, что затухание сейсмических волн является частотно-зависимым, но добротность является частотно-независимой. Это предположение является справедливым в диапазоне частот применений разведочной геофизики. Q томография является способом оценивания Q. В этом способе стараются перестраивать двумерные или трехмерные модели Q геологической среды на основании сейсмических данных. Обычно алгоритмы Q томографии подразделяют на две основные категории. К одной категории относится лучевая томография (Quan and Harris, 1997; Plessix, 2006; Rossi et al., 2007). К другой категории относится томография на основе решения волнового уравнения (Liao and McMechan, 1996; Hick and Pratt, 2001, Pratt et al., 2003; Watanabe et al., 2004; Gao et al., 2005). Томография на основе решения волнового уравнения физически является более точной, но требующей больших затрат на вычисление и непрактичной в трехмерных случаях. Настоящее изобретение относится к категории лучевой Q томографии.

Одна основная проблема, связанная с Q томографией, заключается в способе установления связи между моделями Q и сейсмическими данными при минимальных приближениях и с максимальной гибкостью. Широко используемый способ основан на зависимости между Q и ослаблением амплитуд сейсмических волн. В другом способе используют сдвиг вниз центроидных частот сейсмических волн для оценивания добротности Q. Этот последний способ считают более робастным, поскольку этот способ не зависит от эффекта геометрического расхождения и потерь на отражение/прохождение. Однако в обычном способе сдвига центроидных частот можно использовать только Гауссову, прямоугольную или треугольную функцию для аппроксимации амплитудного спектра источника, что вносит значительную погрешность, поскольку в большинстве случаев спектр источника нельзя аппроксимировать этими функциями. Настоящее изобретение включает в себя частотно-взвешенную экспоненциальную функцию, которая предназначена для аппроксимации различных асимметричных амплитудных спектров источника, для повышения точности Q томографии при значительно сниженной погрешности аппроксимации амплитудного спектра источника.

В большей части существующих алгоритмов Q томографии относящаяся к оптимизации часть основана на способах оптимизации без ограничений или основана на простых способах оптимизации с неотрицательными ограничениями. В результате для этих алгоритмов Q томографии требуется большое время вычислений или получаются многочисленные артефакты и нереалистичные модели Q (например, отрицательные значения Q или экстремально низкие значения Q), особенно в случае, когда сейсмические данные загрязнены шумом. Настоящее изобретение, включающее в себя эффективный алгоритм оптимизации с боксовыми ограничениями, обеспечивает возможность повышения качества и надежности перестроенных моделей Q. Более подробное рассмотрение предшествующего уровня техники следует ниже.

Томография затухания сейсмических волн (Q томография) исследовалась в течение многих лет и был достигнут значительный прогресс. Двумя основными компонентами алгоритма лучевой Q томографии являются 1) простая, но точная зависимость между сейсмическими данными и моделями Q, предназначенная для построения математической модели Q томографии; 2) надежный и робастный алгоритм оптимизации, предназначенный для решения этой математической задачи. Многочисленные способы были разработаны или предложены для создания этих двух компонентов. Эти способы рассматриваются ниже.

Установление связи между сейсмическими данными и моделями Q

Наиболее простой и прямой способ оценивания Q представляет собой способ спектрального отношения (Spencer et al., 1982; Tonn, 1991), в котором логарифм отношения спектров двух сейсмических волновых сигналов вычисляют в виде функции частоты и эту функцию аппроксимируют линейной функцией частоты, наклон которой трактуют как накопленное затухание сейсмической волны и в конечном итоге связывают со значениями Q вдоль пути пробега волны. В идеальном случае этим способом исключают эффект геометрического расхождения и потери на отражение/прохождение в предположении, что эти эффекты являются частотно-независимыми. При практических применениях этот способ является относительно ненадежным вследствие наложения сейсмических импульсов, неопределенности при линейной аппроксимации и наличия многих других факторов.

Rickett (2006) предложил томографическое расширение способа спектрального отношения через посредство технологии частотно-временного анализа. Этот способ был заявлен как нечувствительный к абсолютному шкалированию и был применен при оценивании профиля Q с использованием вертикального сейсмического профиля (ВСП). В этом способе скаляры логарифмических амплитуд, описывающие частотно-независимое изменение амплитуд, включают в неизвестные величины, при этом значительно возрастает количество неизвестных величин и снижается эффективность алгоритма. Кроме того, при двумерной/трехмерной Q томографии с использованием данных об отражении сейсмических волн от поверхности скаляры логарифмических амплитуд являются не только функцией положения, но также и функцией луча, что серьезно усложняет процедуру.

Основываясь на том, что изменение времени нарастания сейсмического импульса линейно связано с профилем 1/Q вдоль пути пробега волны, Wu и Lees (1996) описали способ томографии на основе затухания сейсмических волн с использованием времени нарастания, предназначенный для сейсмологических исследований. К сожалению, этот способ является непрактичным для разведочной геофизики вследствие неизбежного загрязнения сейсмических импульсов шумом, эффекта рассеяния, наложения и т.д.

Было замечено, что на форму амплитудного спектра сейсмического импульса едва ли не исключительно влияет добротность Q, и был разработан способ изменения пиковой частоты для оценивания Q (Zhang, 2008). Этот способ является привлекательным, но на практике имеются трудности, заключающиеся в неточности измерения изменения пиковой частоты. Кроме того, поскольку используется только информация на индивидуальной частоте, неопределенность оценивания Q может быть большой.

Более робастный способ выдвинули Quan и Harris (1997), в котором информацию в пределах всего диапазона частот сейсмических волновых сигналов используют для вычисления сдвига вниз центроидных частот и затем связывания сдвига центроидных частот с профилем Q вдоль траектории луча с помощью простой формулировки в замкнутой форме. Этот способ по своей сущности невосприимчив к геометрическому расхождению и потерям на отражение/прохождение. Ограничение этого способа заключается в том, что амплитудный спектр источника должен представляться Гауссовой, прямоугольной или треугольной функцией. Хорошо известно, что амплитудный спектр сейсмических волн никогда не представляется прямоугольной или треугольной функцией. Кроме того, обычно он является асимметричным и может очень отличаться от Гауссовой функции. Если этот асимметричный амплитудный спектр аппроксимировать Гауссовой функцией, значительные погрешности будут вноситься при перестраивании моделей Q. Поэтому, если имеется функция, которую можно использовать для более точной аппроксимации различных частотных спектров сейсмических волн без потери простого характера зависимости между центроидной частотой регистрируемых сейсмических данных и профилем Q вдоль траектории луча, то этот робастный способ может быть более точным при практических применениях Q томографии.

Алгоритмы оптимизации с ограничениями для Q томографии

Когда зависимость между сейсмическими данными и моделями Q установлена, задачу лучевой Q томографии можно описывать с помощью линейной задачи оптимизации. В большей части существующих алгоритмов Q томографии эта линейная задача оптимизации решается итеративно с использованием способов подпространства Крылова, таких как способ сопряженных градиентов и способ LSQR, без применения каких-либо ограничений (Quan and Harris, 1997; Plessix, 2006, Rossi et al., 2007). Эти алгоритмы хорошо работают при условии, что сейсмические данные имеют высокое отношение сигнала к шуму. Однако сейсмические данные никогда не являются чистыми; при обработке реальных полевых данных эти алгоритмы оптимизации без ограничений всегда приводят к некоторому количеству отрицательных значений Q или экстремально низких значений Q, которые являются физически нереальными. Кроме того, при некоторых обстоятельствах является известной априорная информация относительно диапазона значений Q. В этих случаях эту информацию необходимо включать в алгоритм томографии через посредство боксовых ограничений, чтобы получать более надежные результаты Q томографии.

Rickett (2006) разработал алгоритм оценивания Q с ограничением. Но в его алгоритме принято неотрицательное ограничение вместо боксового ограничения, что означает исключение отрицательных значений Q, но экстремально низкие положительные значения Q все же могут существовать. Rickett (2006) описал два способа применения неотрицательного ограничения. Первый способ представляет собой нелинейный способ преобразования. В этом нелинейном способе преобразования переменную Q заменяют на e^y и находят решение относительно y вместо 1/Q. Выполняя это, принуждают значение Q быть положительным, но вся система может быть сильно нелинейной. Для достижения этой цели результирующую систему оптимизации решают способом Гаусса-Ньютона, что может быть очень затратным. Другой недостаток этого способа заключается в том, что во время оптимизации, когда значения Q являются очень большими, алгоритм оптимизации на градиентной основе является инертным или сходится очень медленно, то есть значения Q остаются неизменными и больше не изменяются. В тяжелом случае, если значения y в исходной модели являются бесконечными, то градиент функции стоимости равен 0 и алгоритм оптимизации не выполняет поиска. Второй способ применения неотрицательного ограничения, который предложил Rickett (2006), заключается в повышении монотонности возрастания характеристики затухания сглаживанием. Этот способ эффективно работает при оценивании Q с использованием данных вертикального сейсмического профилирования, но может перестать действовать при двумерной Q томографии с использованием сейсмических данных об отражениях от поверхности.

Изобретателям настоящего изобретения известно об отсутствии алгоритма Q томографии с боксовыми ограничениями для улучшения оцениваемых значений Q в пределах диапазонов, точно определяемых верхними границами и нижними границами. Однако алгоритмы оптимизации с боксовыми ограничениями используют при некоторых других геофизических применениях, таких как томография скорости. Например, Delbos и соавторы (2006) разработали алгоритм томографии сейсмического отражения с боксовыми ограничениями. В их алгоритме задача оптимизации с ограничениями решается способом Гаусса-Ньютона, дополненным Лагранжем, а связанная задача Лагранжа, еще одна задача оптимизации с ограничениями, решается сочетанием способа проекции градиента, способа активных множеств и способа сопряженных градиентов. Способ активных множеств используется обычным образом и это неэффективно, поскольку в алгоритме обновляется активное множество в соответствии с одним ограничением за один раз (Bierlaire et al., 1991; Löstedt, 1984; Nocedal and Wright, 1999). Когда количество боксовых ограничений очень большое, скорость сходимости алгоритма может быть очень низкой.

В настоящем изобретении последние достижения в области математики, к которым можно отнести многоиндексный способ активных множеств (Morigi et al., 2007), используются для осуществления Q томографии с боксовыми ограничениями, что значительно улучшает характеристики алгоритма Q томографии в части качества перестроения Q и эффективности алгоритма по сравнению с характеристиками алгоритма Q томографии без ограничений и алгоритмом с ограничениями при использовании обычного способа активных множеств.

Краткое изложение изобретения

Согласно одному осуществлению изобретением является лучевой способ сдвига центроидных частот Q томографии для перестроения глубинных моделей 1/Q геологической среды на основании сейсмических данных, измеряемых приемниками при исследовании с использованием сейсмического источника, содержащий выбор математической функции для аппроксимации амплитудного спектра сейсмического источника, чтобы вычислить сдвиг центроидных частот спектра вследствие затухания в земле и связывание указанного сдвига центроидных частот с затуханием, представленным обратной величиной добротности Q, и нахождение решения относительно Q или 1/Q путем итеративной линейной оптимизации, в котором оптимизация имеет боксовые ограничения для поддержания оцениваемых значений Q в пределах зависимых от положения диапазонов, точно определяемых верхними границами и нижними границами. Оптимизация с ограничениями может быть разрешена многоиндексным способом активных множеств, который позволяет обновлять активное множество в соответствии с многочисленными индексами сетки за один раз, при этом индекс сетки обозначает расположение геологической среды. Выбираемая математическая функция может быть частотно-взвешенной экспоненциальной функцией частоты. Использование этой функции для аппроксимации амплитудного спектра сейсмического источника предпочтительно независимо от того, используются или нет боксовые ограничения при оптимизации.

Перестроенную модель Q геологической среды, образуемую способом настоящего изобретения, можно выгодно использовать, в частности, при построении сейсмических изображений для компенсации ослабления амплитуд, потери частот и эффекта фазовых искажений, обусловленных вязкоакустической перекрывающей породой, такой как газовый коллектор. Путем включения более точной модели Q, предоставляемой настоящим изобретением, в процедуру построения сейсмических изображений можно существенно повышать качество изображения геологической структуры. В дополнение к этому перестроенная модель Q будет полезной в применениях, связанных с определением характеристик коллектора, поскольку значение Q является очень чувствительным к некоторым свойствам породы и флюида, таким как насыщение флюидом и пористость. При таких применениях изобретение становится способом разведки, разработки или добычи углеводородов.

Специалист в области Q томографии должен осознавать, что по меньшей мере некоторые из этапов способа настоящего изобретения предпочтительно осуществлять на компьютере, программируемом в соответствии с идеями, изложенными в этой заявке, то есть изобретение осуществляется компьютером в большей части практических применений или при всех.

Краткое описание чертежей

Настоящее изобретение и его преимущества станут более понятными при обращении к нижеследующему подробному описанию и сопровождающим чертежам, на которых:

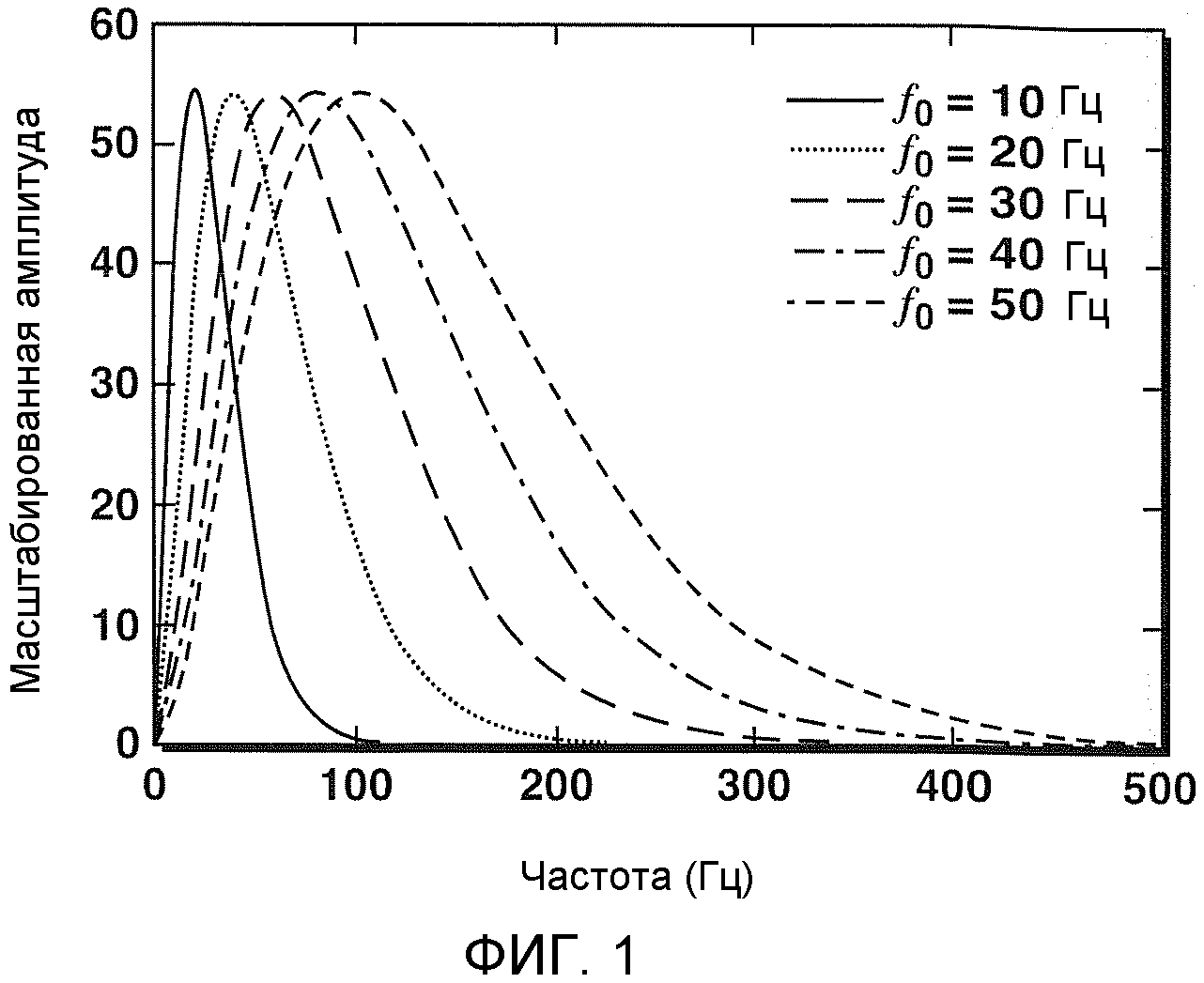
фиг.1 - иллюстрация изменения ширины полосы частот частотно-взвешенной экспоненциальной функции, предназначенной для аппроксимации различных асимметричных амплитудных спектров источника в по меньшей мере некоторых осуществлениях изобретения, при различных значениях параметра характеристической частоты и выбранном значении n=2 для второго параметра, называемого индексом симметрии;

фиг.2 - вид кривых частотно-взвешенной экспоненциальной функции $F (f) = A f^{n} \exp (- \frac{f}{f_{0}})$

при n=1, 2, 3, 4 и 5, при этом центроидная частота (n+1)f₀ является фиксированной, 30 Гц;

фиг.3 - блок-схема последовательности действий, показывающая основные этапы осуществления настоящего изобретения при Q томографии;

фиг.4 - 8А-В относятся к применению синтетических примеров, при этом на

фиг.4 - вид амплитудного спектра источника;

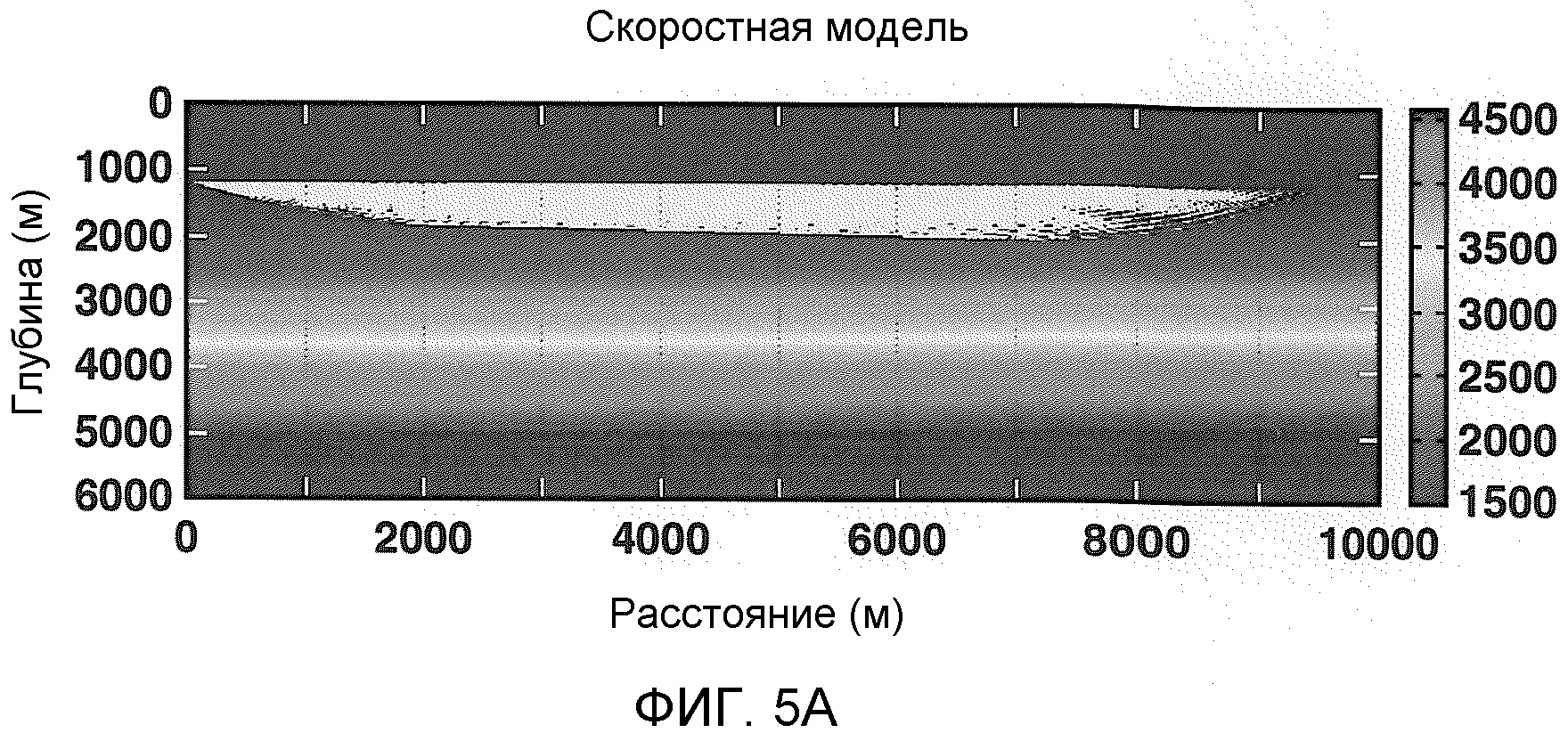
фиг.5А-В - иллюстрация скоростной модели, траекторий лучей (5А) и истинной модели 1/Q (5B);

фиг.6А - вид модели 1/Q, перестроенной с использованием обычного способа сдвига центроидных частот Q томографии при аппроксимации Гауссовой функцией и без боксовых ограничений; фиг.6В - иллюстрация различий между перестроенной моделью 1/Q из фиг.6А и истинной моделью 1/Q из фиг.5В;

фиг.7А - вид модели 1/Q, перестроенной с использованием способа сдвига центроидных частот Q томографии при аппроксимации частотно-взвешенной экспоненциальной функцией согласно настоящему изобретению, но без боксовых ограничений; фиг.7В - иллюстрация различий между перестроенной моделью 1/Q из фиг.7А и истинной моделью 1/Q из фиг.5В;

фиг.8А - вид модели 1/Q, перестроенной с использованием способа сдвига центроидных частот Q томографии при аппроксимации частотно-взвешенной экспоненциальной функцией согласно настоящему изобретению и боксовыми ограничениями согласно настоящему изобретению; фиг.8В - иллюстрация различий между перестроенной моделью 1/Q из фиг.8А и истинной моделью 1/Q из фиг.5В.

Вследствие ограничений, накладываемых патентным законом на чертежи, фиг.5А-В - 8А-В являются черно-белыми репродукциями цветных изображений. Копии цветных чертежей могут быть получены при запросе копии экземпляра заявки США от Ведомства США по патентам и товарным знакам и уплате сбора.

Изобретение будет описано применительно к примерам осуществлений. Однако в той части, в какой нижеследующее подробное описание является специфическим для конкретного осуществления или конкретного использования изобретения, оно предназначается только для иллюстрации и не предполагается ограничивающим объем изобретения. И, наоборот, оно предполагается охватывающим все варианты, модификации и эквиваленты, которые могут быть включены в объем изобретения, определенный прилагаемой формулой изобретения.

Подробное описание примеров осуществлений

Настоящее изобретение включает в себя способ перестроения двумерных или трехмерных сейсмических моделей добротности (Q) на основании сейсмических данных, в данной области техники известный как Q томография.

Основными признаками настоящего изобретения согласно по меньшей мере некоторым осуществлениям являются следующие. Амплитудный спектр сейсмического импульса источника анализируют и аппроксимируют специально синтезированной функцией, частотно-взвешенной экспоненциальной функцией. Аппроксимацию амплитудного спектра сейсмического импульса источника осуществляют путем подбора двух параметров частотно-взвешенной экспоненциальной функции. Сдвиги центроидных частот принимаемых сейсмических волновых сигналов относительно центроидной частоты сейсмического импульса источника вычисляют и вводят в алгоритм оптимизации с боксовыми ограничениями для построения модели Q, при этом диапазоны значений Q заранее определяют в соответствии с априорной информацией. В отличие от первоначального способа сдвига центроидных частот (Quan and Harris, 1997) со специально синтезированной функцией аппроксимации амплитудного спектра этим алгоритмом Q томографии можно обрабатывать негауссовские и асимметричные амплитудные спектры источника, чтобы снижать погрешность, вносимую рассогласованием при аппроксимации амплитудного спектра источника. При наличии такой специально синтезированной функции аппроксимации спектра источника задача Q томографии сводится к задаче условной оптимизации с боксовыми ограничениями. Эту задачу оптимизации с ограничениями решают, используя многоиндексный способ активных множеств (Morigi et al., 2007), с помощью которого дополнительно повышают точность и робастность этого алгоритма Q томографии без ухудшения высокоэффективных характеристик. Термин «активное множество» относится к такому подмножеству из множества оптимизируемых неизвестных, которое, как будет показано, не может быть обновлено в конце итерационного цикла, поскольку для него присуще ограничение верхнего предела или нижнего предела.

Далее поясняются несколько основополагающих теорий изобретения.

Если амплитудный спектр сейсмического импульса источника представить как S(f), то амплитудный спектр R(f) принимаемого сейсмического волнового сигнала можно выразить как (Quan and Harris, 1997)

R(f)=GH(f)S(f), $\begin{array}{c} \end{array}$

(1)

где G представляет собой частотно-независимый множитель, учитывающий эффекты геометрического расхождения, коэффициенты отражения/прохождения и т.д., H(f) представляет собой функцию импульсного отклика, описывающую эффект затухания сейсмических волн, которая формулируется следующим образом

$H (f) = \exp (- f \int_{п о л у ч у} \frac{π}{Q v} d l)$

\begin{array}{c}  \end{array}

(2)

где Q является добротностью и v является скоростью сейсмических (акустических) волн.

В способе сдвига центроидных частот при оценивании Q ключевая часть заключается в использовании аналитической функции для аппроксимации амплитудного спектра S(f) источника и затем в получении явно выраженной зависимости между центроидной частотой принимаемого сейсмического волнового сигнала и профилем Q вдоль пути пробега волны. В первоначальном способе сдвига центроидных частот эту явно выраженную зависимость можно было получать только в предположении, что амплитудный спектр источника является Гауссовой функцией, или прямоугольной функцией (функцией, которая равна нулю на протяжении всей вещественной линии за исключением единственного интервала, где она равна постоянной величине), или треугольной функцией. Это является основным недостатком традиционного способа сдвига центроидных частот, который может приводить к большим погрешностям при оценивании Q (Rickett, 2006; Zhang, 2008).

Одна из основных особенностей по меньшей мере некоторых осуществлений изобретения заключается в том, что частотно-взвешенную экспоненциальную функцию синтезируют, чтобы более точно аппроксимировать различные асимметричные амплитудные спектры источника без потери простой зависимости в замкнутой форме между сдвигом центроидной частоты и профилем Q вдоль траектории луча. Кроме того, очень удобно осуществлять аппроксимацию амплитудного спектра источника с использованием этой специально синтезированной функции, поскольку форма и ширина полосы частот функции определяются по отдельности двумя параметрами. Формулировка частотно-взвешенной экспоненциальной функции имеет вид

$F (f) = A f^{n} \exp (- \frac{f}{f_{0}})$

\begin{array}{c}  \end{array}

(3)

где А является постоянной для масштабирования амплитуды, f₀ называют характеристической частотой и n называют индексом симметрии. Характеристическая частота f₀ является параметром при управлении шириной полосы частот. Если индекс n симметрии является фиксированным, ширина полосы частот этой функции увеличивается с повышением характеристической частоты. Фактически центроидная частота функции F(f) имеет очень простую форму, приведенную ниже:

$f_{F} = \frac{\int_{0}^{+ \infty} f F (f) d f}{\int_{0}^{+ \infty} F (f) d f} = (n + 1) f_{0}$

\begin{array}{c}  \end{array}

(4)

На фиг.1 показано изменение ширины полосы частот функции F(f) при n=2 для пяти различных характеристических частот в пределах от 10 Гц до 50 Гц с размером шага 10 Гц. На фиг.1 при изменении f₀ от 50 Гц до 10 Гц форма F(f) остается относительно неизменной, тогда как ширина полосы частот сокращается, как и ожидалось. С другой стороны, индекс n симметрии используют для управления свойством симметрии F(f). Как показано на фиг.2, чем больше индекс n симметрии, тем более симметрична форма функции F(f), при этом центроидная частота фиксирована на уровне 30 Гц, тогда как индекс n симметрии изменяется от 1 (наименьшая симметрия) до 5 (наибольшая симметрия). Нет необходимости в том, чтобы n было целым числом. Теоретически для точности аппроксимации n может быть любым вещественным числом. Однако на практике обычно n не должно превышать 5. Как упоминалось ранее, поскольку управление центроидной функцией и свойством симметрии этой специально синтезированной функции осуществляют раздельно с помощью двух различных параметров, пользователям очень легко точно аппроксимировать различные асимметричные амплитудные спектры источника этой функцией.

В соответствии с лучевой теорией, если амплитудный спектр источника аппроксимируют частотно-взвешенной экспоненциальной функцией, то есть S(f)=F(f), то после подстановки уравнений (2) и (3) в уравнение (1) амплитудный спектр принимаемого сейсмического волнового сигнала можно записать в форме

$R (f) = G H (f) S (f) = A G f^{n} \exp [- f (\int_{п о л у ч у} \frac{π}{Q v} d l + \frac{1}{f_{0}})]$

\begin{array}{c}  \end{array}

(5)

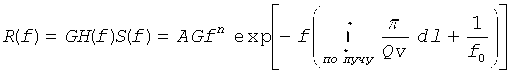
Центроидная частота принимаемого сейсмического волнового сигнала может быть вычислена как

$f_{R} = \frac{\int_{0}^{+ \infty} f R (f) d f}{\int_{0}^{+ \infty} R (f) d f} = \frac{n + 1}{\int_{п о л у ч у} \frac{π}{Q v} d l + \frac{1}{f_{0}}}$

\begin{array}{c}  \end{array}

(6)

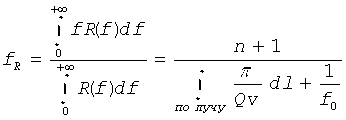
Поскольку центроидная частота амплитудного спектра f_S источника равна (n+1)f₀, сдвиг центроидной частоты между амплитудным спектром источника и амплитудным спектром принимаемого сигнала можно легко получить в виде

$Δ f = f_{S} - f_{R} = (n + 1) (f_{0} \frac{1}{\int_{п о л у ч у} \frac{π}{Q v} d l + \frac{1}{f_{0}}})$

\begin{array}{c}  \end{array}

(7)

Теперь путем решения уравнения (7) суммарное затухание $\int_{п о л у ч у} \frac{π}{Q v} d l$

вдоль траектории луча можно получить на основании сдвига центроидной частоты:

$\int_{п о л у ч у} \frac{π}{Q v} d l = \frac{Δ f}{f_{0} [(n + 1) f_{0} - Δ f]} = \frac{Δ f}{f_{0} (f_{S} - Δ f)} = \frac{Δ f}{f_{0} f_{R}} = \frac{(n + 1) Δ f}{f_{S} f_{R}}$

\begin{array}{c}  \end{array}

(8)

Уравнение (8) показывает, что 1/Q связано со сдвигом центроидной частоты через очень простую линейную зависимость с частотно-взвешенной экспоненциальной функцией.

Дискретная форма уравнения (8) для i-го измерения (i-го луча) имеет вид

$\sum_{j} \frac{π l_{j}^{i}}{Q_{j} v_{j}} = \frac{Δ f^{i}}{f_{0} f_{R}^{i}}$

\begin{array}{c}  \end{array}

(9)

где верхний индекс i является индексом измерения и нижний индекс j является индексом сетки, а $l_{j}^{i}$

является длиной луча на j-й сетке при i-ом измерении.

После сбора всех измерений уравнение (9) можно записать в матричной форме

Ax=d. $\begin{array}{c} \end{array}$

(10)

В уравнении (10) А является матрицей ядра, элементы которой определяются в соответствии с

$A_{i j} = \frac{π l_{j}^{i}}{v_{j}}$

\begin{array}{c}  \end{array}

(11)

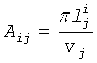
x является вектором неизвестных величин, то есть

x_j=1/Q_j, $\begin{array}{c} \end{array}$

(12)

и d является вектором измерения, определяемым в соответствии с

$d_{i} = \frac{Δ f^{i}}{f_{0} f_{R}^{i}}$

\begin{array}{c}  \end{array}

(13)

Оставшейся задачей является решение уравнения (10) относительно Q. Поскольку измеряемые данные неизбежно загрязнены шумом, линейная система уравнений (10) является плохо обусловленной и имеет неоднозначные решения. Поэтому эту систему можно трактовать как задачу наименьших квадратов и находить решение в виде приближенного решения задачи квадратичного программирования

$\min ‖ A x - d ‖$

\begin{array}{c}  \end{array}

(14)

где $‖ ... ‖$

означает Евклидов вектор.

Как рассматривалось ранее, для исключения нереалистичных отрицательных значений Q и включения априорной информации относительно диапазонов Q в представляющих интерес областях задачу (14) можно преобразовать в задачу минимизации с боксовыми ограничениями

$m i n ‖ A x - d ‖$

при условии l<x<u,

\begin{array}{c}  \end{array}

(15)

где l и u представляют собой векторы, сохраняющие нижние границы и верхние границы значений Q. Алгоритм предпочтительного типа, который можно использовать для решения задачи (15) оптимизации, представляет собой многоиндексный способ активных множеств, такой какой был раскрыт Morigi et al. (2007). Статья Morigi et al. (2007) полностью включается в эту заявку, когда патентными ведомствами позволяется делать это. По сравнению с другими алгоритмами томографии с ограничениями (Rickett, 2008, Delbos et al., 2006) этим алгоритмом можно справляться с боксовыми ограничениями более эффективно и более действенно. Основная особенность этого способа активных множеств нового типа заключается в том, что он позволяет обновлять активное множество в соответствии с многочисленными индексами за один прием.

Двухуровневая структурированная процедура этого алгоритма оптимизации с ограничениями может быть описана в следующем виде.

1. Инициализация: при заданной исходной модели x⁰ и допустимой погрешности ε итеративно решают задачу оптимизации без ограничений

$‖ A x - d ‖ < ε$

\begin{array}{c}  \end{array}

(16)

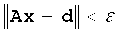
для получения решения ${\hat{x}}^{1}$

без ограничений, где

‖ ... ‖

означает норму евклидова вектора, то есть

‖ x ‖ = \sqrt{(x_{1}^{2} + x_{2}^{2} + ... + x_{n}^{2})}

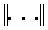
2. Начало k-й внешней итерации, начиная с k=1: ортогональное проецирование ${\hat{x}}^{k}$

на допустимый вектор, задаваемый для получения приближенного решения с ограничениями при первой внешней итерации x^k. Ортогональную проекцию выражают как

$x_{i}^{k} = {\begin{array}{c} l_{i} & {\hat{x}}_{i}^{k} < l_{i} \\ u_{i} & {\hat{x}}_{i}^{k} > u_{i} \\ {\hat{x}}_{i}^{k} & l_{i} \leq {\hat{x}}_{i}^{k} \leq u_{i} \end{array}$

\begin{array}{c}  \end{array}

(17)

где верхний индекс является индексом внешней итерации и нижний индекс является индексом сетки. Те $x_{i}^{k}$

, которые удовлетворяют каждому из первых двух условий уравнения (17), называют активным множеством переменных для текущей итерации или их индексы называют активным множеством индексов. То есть они являются переменными (индексами), которые связаны тем или иным боксовым ограничением.

3. Оценивание остатка r^k=Ax^k-d. Если 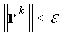$‖ r^{k} ‖ < ε$

, то приближенное решение x^k с ограничениями удовлетворяет критерию остановки. Завершают итерацию и x^k является конечным решением. Если не удовлетворяет, то переходят к этапу 4.

4. Вычисление множителей λ^k=A^T(Ax^k-d) Лагранжа и обновление активного множества путем образования диагональной матрицы C^k, диагональные элементы $c_{i i}^{k}$

которой определяют в соответствии с

$c_{i i}^{k} = {\begin{array}{c} 0 & x_{i}^{k} = l_{i}, λ_{i}^{k} > 0 \\ 0 & x_{i}^{k} = u_{i}, λ_{i}^{k} < 0 \\ 1 & в иных случаях \end{array}$

\begin{array}{c}  \end{array}

(18)

5. Итеративное (это является внутренней итерацией) решение следующей задачи минимизации без ограничений при использовании способа сопряженных градиентов для получения вектора y^k корректировки.

$‖ B^{k} y^{k} + r^{k} ‖ < ε$

\begin{array}{c}  \end{array}

(19)

где

B^k=AC^k.

6. Корректировка решения x^k для получения решения ${\hat{x}}^{k + 1}$

без ограничений для следующей внешней итерации в соответствии с

${\hat{x}}^{k + 1} = x^{k} + C^{k} y^{k}$

\begin{array}{c}  \end{array}

(20)

Затем переход к этапу 2 и вход в следующую внешнюю итерацию.

При практическом использовании изобретения некоторые или все (обычно все) шесть этапов изложенного выше способа выполняют с использованием компьютера.

Изложенный выше алгоритм отличается от обычных способов активных множеств (Bierlaire et al., 1991; Löstedt, 1984; Nocedal and Wright, 1999) в следующих двух отношениях: в способе настоящего изобретения предполагается выполнение этапа 1 и этапа 5 до удовлетворения условий (16) и (19) оптимальности; а затем на этапе 4 совокупность активных множеств обновляют путем удаления или добавления одного или нескольких индексов (сетки) в соответствии с тем, удовлетворяет ли ${\hat{x}}_{i}^{k}$

из предшествующего цикла внутренней итерации без ограничений одному из двух условий

${\hat{x}}_{i}^{k} < l_{i}$

${\hat{x}}_{i}^{k} > u_{i}$

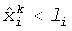
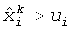
В противоположность этому в обычных способах активных множеств только один индекс в активном множестве обновляют за один раз. Иначе говоря, в обычных способах активных множеств осуществляют обновление активного множества, как только обнаруживают верхние или нижние границы приближенного решения, а в способе настоящего решения активное множество не обновляют до тех пор, пока в алгоритме не достигается сходимость к допустимой погрешности. Обычным алгоритмом активных множеств гарантируется монотонное снижение остатка; при практических применениях он показывает очень низкую скорость сходимости, поскольку он часто вырождается в повторно запускаемый способ скорейшего спуска, особенно в случае, когда матрица является плохо обусловленной. Алгоритмом активных множеств этого нового типа не гарантируется монотонное снижение несоответствия данных. Однако опыт показывает, что, если допустимая погрешность выбрана надлежащим образом, этот алгоритм работает очень хорошо в части высокой скорости сходимости и приводит к возможному решению, удовлетворяющему допустимой погрешности.

Другое преимущество алгоритма активных множеств согласно настоящему изобретению, представленного в качестве примера этапами 1-6, изложенными выше, заключается в том, что исходная модель Q, используемая для начала осуществления оптимизации, может быть произвольной, что означает возможность задания исходной модели Q на верхней или нижней границе или даже вне границы. При некоторых обстоятельствах эта особенность может быть очень полезной.

Настоящее изобретение может быть реализовано в соответствии с блок-схемой последовательности действий, показанной на фиг.3. Как и в случае обычных алгоритмов лучевой томографии, на этапе 60 скоростную модель 20 и положения 30 источника/приемника вводят в код трассирования лучей для вывода информации о траекториях лучей, которую используют для построения матрицы ядра (А из уравнений 10 и 11) на этапе 70. Сейсмические данные анализируют и амплитудный спектр источника аппроксимируют частотно-взвешенной экспоненциальной функцией (уравнение 3) на этапе 40, во время выполнения которого определяют индекс n симметрии и характеристическую частоту f₀. Затем на этапе 50 центроидные частоты всех сейсмических трасс вычисляют для получения сдвигов центроидных частот (уравнение 7). На этапе 80 и этапе 90 априорную информацию собирают для построения исходной модели Q и карты диапазонов изменений Q. После этого на этапе 100 сдвиги центроидных частот всех сейсмических трасс, матрицу ядра, исходную модель Q и карту диапазонов изменений Q вводят в код оптимизации с ограничениями многоиндексного активного множества (6-этапный алгоритм, изложенный выше) для выполнения перестроения модели Q. На этапе 110 перестроенную модель Q оценивает пользователь. Если перестроенная модель Q является приемлемой, процесс Q томографии заканчивают. В ином случае пользователь вновь выполняет построение исходной модели Q и/или карты диапазонов изменений Q и снова осуществляет оптимизацию с ограничениями до тех пор, пока перестроенная модель Q не будет удовлетворительной. Заключенное выше в круглые скобки относится к примерам осуществлений изобретения. Описание в этой заявке сосредоточено на этапах 40 и 100, которые представляют основную суть изобретения. За исключением случаев, на которые обращено внимание, другие этапы, показанные на фиг.3, являются хорошо известными в области Q томографии и для задач этого изобретения могут выполняться любым известным или позднее разработанным способом. Кроме того, хотя предпочтительно осуществлять настоящее изобретения на этапе 40 и его усовершенствования на этапе 100, одно можно осуществлять без другого, то есть стандартный способ можно использовать для выполнения действия согласно этапу 40 или этапу 100.

Различные выполняемые по желанию этапы или уточнения могут быть добавлены к основным этапам, показанным на фиг.3. Например:

1) Все сейсмические трассы можно предварительно обрабатывать до этапа 40: Первые вступления обрабатывают методом окна и разделяют, амплитудные спектры разделенных сейсмических импульсов вычисляют и осуществляют полиномиальную аппроксимацию амплитудных спектров. (Часто исходные сейсмические данные сильно зашумлены. Поэтому вместо попытки аппроксимации амплитудного спектра исходных сейсмических данных с использованием Гауссовой функции на практике первый этап может быть полиномиальной аппроксимацией амплитудного спектра исходных сейсмических данных для преобразования его в гладкую кривую. Этот же самый промежуточный этап может быть полезным при применении способа настоящего изобретения, после которого может быть легче аппроксимировать гладкую полиномиальную кривую частотно-взвешенной экспоненциальной функцией).

2) Регуляризацию матрицы можно добавлять для стабилизации процесса оптимизации из этапа 100.

3) Исходную модель Q можно построить (этап 80) на основании одной или нескольких аномалий скорости.

4) Когда количество сейсмических трасс очень небольшое, можно использовать способы регуляризации данных.

5) Во время этапа 100 внутреннюю итерацию алгоритма оптимизации с ограничениями можно осуществлять с использованием способа сопряженных градиентов или способа LSQR (разновидности способа сопряженных градиентов; см. Paige and Saunders, 1982).

6) Если спектр источника не имеется во время этапа 40, его можно оценивать на основании принимаемых сейсмических волновых сигналов, связанные лучи которых не проходят сквозь области с возможными аномалиями Q.

Примеры

В этом разделе представлен синтетический пример Q томографии. Сделано сравнение характеристик алгоритма Q томографии согласно настоящему изобретению с характеристиками обычных алгоритмов сдвига центроидных частот Q томографии с использованием Гауссовой функции с боксовыми ограничениями и без них. На фиг.4 показан амплитудный спектр источника, который является асимметричным. Вычисленная численно-центроидная частота амплитудного спектра источника составляет 55,7 Гц, а пиковая частота составляет 33 Гц. При аппроксимации амплитудного спектра источника Гауссовой функцией пиковая частота Гауссовой функции составляет 55,7 Гц и дисперсия составляет 1246 Гц². При аппроксимации частотно-взвешенной экспоненциальной функцией параметры n и f₀ в уравнении (3) составляют 1,45 и 22,7 Гц соответственно. На фиг.5А представлены скоростная модель и траектории лучей, полученные при выполнении кода трассирования лучей, тогда как на фиг.5В представлена истинная модель 1/Q. При этом исследовании синтетических данных использовались 50 источников. Для каждого источника имелось 90 приемников. Поэтому в сумме было 4500 трасс. На фиг.5А-В - 8А-В представлены черно-белые репродукции изображений, на которых величина, нанесенная в зависимости от глубины и расстояния, представлена цветом в соответствии с цветовой шкалой, показанной на чертежах.

На фиг.6А представлена модель 1/Q, перестроенная с использованием обычного способа сдвига центроидных частот Q томографии, при этом использовались аппроксимация Гауссовой функцией и оптимизация без ограничений. Вследствие этого перестроенная модель 1/Q существенно отклоняется от истинной модели 1/Q вследствие большой погрешности, вносимой аппроксимацией амплитудного спектра источника Гауссовой функцией. На фиг.6В показано различие между перестроенной моделью 1/Q и истинной моделью 1/Q. После этого Гауссову функцию заменяли частотно-взвешенной экспоненциальной функцией согласно настоящему изобретению, чтобы аппроксимировать амплитудный спектр источника, и модель 1/Q, перестроенная с использованием алгоритма оптимизации без ограничений, показана на фиг.7А. Результат значительно улучшился по сравнению с результатом, полученным с использованием Гауссовой аппроксимации. Однако имеются многочисленные артефакты в перестроенной модели 1/Q, а значения Q в некоторых областях являются отрицательными, что физически нереально. И в этом случае на фиг.7В представлено различие между перестроенной моделью 1/Q и истинной моделью 1/Q. На фиг.8А показан результат Q томографии, полученный с использованием аппроксимации частотно-взвешенной экспоненциальной функцией согласно настоящему изобретению, и на этот раз также с использованием алгоритма оптимизации с боксовыми ограничениями согласно настоящему изобретению, которым перестроенные значения 1/Q вводятся в диапазон от 0 до 0,05. На фиг.8В представлено различие между перестроенной моделью 1/Q и истинной моделью 1/Q. Этот результат лучше предшествующих двух, поскольку в результате отсутствует отрицательное значение Q и артефакты присутствуют в меньшем количестве.

В некоторых осуществлениях изобретения оценивание амплитудного спектра источника выполняют путем вычисления усредненного амплитудного спектра сейсмических трасс, которые не проходят через подземные области, проявляющие аномалии Q. Сглаживание может быть применено к усредненному амплитудному спектру, что может быть сделано при использовании способа полиномиального приближения.

В некоторых осуществлениях изобретения амплитудный спектр принимаемых сигналов может быть вычислен по первым приходам трасс сейсмических данных, которые могут быть разделены обработкой методом окна.

В некоторых осуществлениях изобретения исходная модель 1/Q может быть построена на основании акустической скоростной модели геологической среды. Исходная модель 1/Q может быть построена на основании одной или нескольких аномалий в акустической скоростной модели геологической среды путем линейного картирования.

В некоторых осуществлениях изобретения карта диапазонов изменений 1/Q может иметь нижние границы, которые все больше 0.

Приведенное выше описание обращено к конкретным осуществлениям настоящего изобретения с целью иллюстрации их. Однако специалисту в данной области техники должно быть понятно, что возможны многочисленные модификации и варианты осуществлений, описанных в этой заявке. Все такие модификации и варианты предполагаются находящимися в рамках объема настоящего изобретения, определяемого прилагаемой формулой изобретения.

Список литературы

Bierlaire, M., Ph. L. Toint, and D. Tuyttens, "On iterative algorithms for linear least squares problems with bound constraints," Linear Algebra Appl 143, 111-143 (1991).

Delbos, D., J. Ch. Gilbert, R. Glowinski, and D. Sinoquet, "Constrained optimization in seismic reflection tomography: a Gauss-Newton augmented Lagrangian approach," Geophysics 164, 670-684 (2006).

Gao, F., G. Fradelizio, A. Levander, G. Pratt, and C. Zelt, "Seismic velocity, Q, geological structure and lithology estimation at a ground water contamination site," 75th SEG, Expanded Abstracts, 1561-1564, Soc. of Expl. Geophys (2005).

Hicks, G. J. and R. G. Pratt, "Reflection waveform inversion using local descent methods: Estimating attenuation and velocity over a gas-sand deposit," Geophysics 66, 598-612 (2001).

Liao, Q. and G. A. McMechan, "Multifrequency viscoacoustic modeling and inversion," Geophysics 61, No. 5, 1371-1378 (1996).

Lötstedt, P., "Solving the minimal least squares problem subject to bounds on the variables," BIT 24(1984).

Morigi, S., L. Reichel, F. Sgallari, and F. Zama, "An iterative method for linear discrete ill-posed problems with box constraints," Journal of Computational and Applied Mathematics 198, 505-520 (2007).

Nocedal, J. and S. J. Wright, Numerical Optimization, Springer, New York (1999).

Paige, С. C. and M. A. Saunders, "LSQR: An algorithm for sparse linear equations and sparse least squares," A CM Trans. Math. Software 8, 43-71 (1982).

Plessix, R.-E., "Estimation of velocity and attenuation coefficient maps from crosswell seismic data," Geophysics 71, S235-S240 (2006).

Pratt, R. G., К. Bauer, and M. Weber, "Crosshole waveform tomography velocity and attenuation images of arctic gas hydrates," 73rd SEG, Expanded Abstracts, Society of Exploration Geophysics, 2255-2258 (2003).

Rickett, J. E., "Method for estimation of interval seismic quality factor," U.S. Patent No. 5 7,376,517 (2006).

Rossi, G., D. Gei, G. Böhm, G. Madrussani, and J. M. Carcione, "Attenuation tomography: An application to gas-hydrate and free-gas detection," Geophysics 55, 655-669 (2007).

Spencer, T. W., J. R. Sonnad, and T. M. Butler, "Seismic Q-stratigraphy or dissipation," Geophysics 47, 16-24(1982).

Tonn, R., "The determination of the seismic quality factor Q from VSP data: A comparison of different computational method," Geophysical Prospecting 39, 1-27 (1991).

Quan, Y. and J. M. Harris, "Seismic attenuation tomography using the frequency shift method," Geophysics 62, 895-905 (1997).

Watanabe, Т., К. T. Nihei, S. Nakagawa, and L. R. Myer, "Viscoacoustic waveform inversion of 15 transmission data for velocity and attenuation," J. Acoust. Soc. Am. 115, 3059-3067 (2004).

Wright, S. J., "Primal-Dual Interior Point Methods," SIAM (1997).

Wu, H., and J. M. Lees, "Attenuation structure of Coso geothermal data, California from wave pulse widths," Bulletin of the Seismological Society of America 86, 1574-1590 (1996).

Zhang, C., "Seismic Absorption Estimation and Compensation," PhD thesis, University of 20 British Columbia (2008).

Реферат

Изобретение относится к области геофизики и может быть использовано при обработке данных сейсмических исследований. Заявлен способ перестроения моделей (110) Q геологической среды на основании сейсмических данных (10) путем осуществления лучевой Q томографии сдвига центроидных частот. Амплитудный спектр волнового сигнала сейсмического источника аппроксимируют (40) частотно-взвешенной экспоненциальной функцией частоты, имеющей два подбираемых параметра для приведения в соответствие данным о сдвиге частот. В результате чего обеспечивают лучшее соответствие различным асимметричным амплитудным спектрам источника. Боксовые ограничения могут использоваться при выполнении процедуры оптимизации, а многоиндексный способ активных множеств, используемый при томографии скорости, является предпочтительным способом для реализации (100) боксовых ограничений. Технический результат - повышение точности данных сейсмических исследований. 2 н. и 18 з.п. ф-лы, 12 ил.

Формула

1. Лучевой способ сдвига центроидных частот Q томографии для перестроения модели Q геологической среды на основании сейсмических данных, измеряемых приемниками при исследовании с использованием сейсмического источника, содержащий выбор математической функции для аппроксимации амплитудного спектра сейсмического источника, чтобы вычислить сдвиг центроидных частот спектра вследствие затухания в земле, и связывание указанного сдвига центроидных частот с затуханием, представленным обратной величиной добротности Q, и нахождение решения относительно Q или 1/Q путем итеративной линейной оптимизации с использованием компьютера, в котором оптимизация имеет боксовые ограничения для поддержания оцениваемых значений Q в пределах зависимых от положения диапазонов, точно определяемых верхними границами и нижними границами.

2. Способ по п. 1, в котором оптимизация с боксовыми ограничениями разрешается многоиндексным способом активных множеств, который позволяет обновлять активное множество в соответствии с многочисленными индексами сетки за один раз, при этом индекс сетки обозначает расположение геологической среды.

3. Способ по п. 1, в котором выбираемая математическая функция представляет собой частотно-взвешенную экспоненциальную функцию частоты.

4. Способ по п. 3, в котором частотно-взвешенная экспоненциальная функция частоты имеет два параметра, которые подбирают, чтобы обеспечивать соответствие амплитудному спектру сейсмического источника.

5. Способ по п. 4, в котором два параметра представляют собой характеристическую частоту для управления шириной полосы частот и индекс симметрии, при этом каждый является положительным вещественным числом.

6. Способ по п. 5, в котором частотно-взвешенная экспоненциальная функция частоты может быть выражена в форме

F (f) = A f^{n} \exp (- \frac{f}{f_{0}})

,
где f является частотой, А является постоянной при масштабировании амплитуды, f₀ является характеристической частотой и n является индексом симметрии.

7. Способ по п. 1, дополнительно содержащий:
(а) оценивание амплитудного спектра источника и вычисление его центроидной частоты;
(b) аппроксимацию амплитудного спектра источника частотно-взвешенной экспоненциальной функцией частоты;
(с) вычисление амплитудных спектров первых вступлений трасс сейсмических данных;
(d) вычисление сдвигов центроидных частот, являющихся разностями между центроидными частотами амплитудных спектров, вычисленных на этапе (с), и вычисленной центроидной частотой амплитудного спектра источника;
(е) построение вектора d измерения в значениях сдвигов центроидных частот и центроидных частот амплитудных спектров, вычисленных на этапе (с);
(f) выполнение кода трассирования лучей на компьютере при использовании акустической скоростной модели геологической среды и информации о расстоянии источник-приемник из исследования;
(g) построение матрицы А ядра в значениях длин отрезков лучей и соответствующих скоростей акустических волн;
(h) построение исходной модели Q геологической среды на основании имеющейся информации, при этом указанная исходная модель точно определяет значение 1/Q для каждой ячейки в исходной модели;
(i) образование карты диапазонов изменений 1/Q, обеспечивающей боксовые ограничения для 1/Q на всем протяжении модели, при этом указанные боксовые ограничения основаны на имеющейся информации;
(j) выполнение итеративной оптимизации, при которой компьютер решает задачу

m i n ‖ A x - d ‖

для компонентов вектора x при условии соблюдения боксовых ограничений, при этом x_j=1/Q_j, индекс j обозначает j-тую ячейку в модели, вследствие чего перестраивается объем значений 1/Q в зависимости от глубины и поперечного положения в геологической среде.

8. Способ по п. 7, в котором итеративную оптимизацию при условии соблюдения боксовых ограничений выполняют при использовании способа активных множеств, который обновляет многочисленные индексы активных множеств во время оптимизации.

9. Способ по п. 8, в котором итеративная оптимизация имеет внешний цикл итерации и внутренний цикл итерации, и при внутреннем цикле итерации выполняют оптимизацию без ограничений, которой определяются подборки x_i для минимизации

‖ A x - d ‖

10. Способ по п. 9, в котором после каждого внутреннего цикла итерации получают x_i для каждой ячейки i модели, следующий внешний цикл начинают с проверки x_i относительно боксовых ограничений и связывания тех x_i, которые противоречат этим ограничениям, при этом указанные x_i с ограничениями называют активным множеством, затем проверяют, соблюдается ли

‖ A x - d ‖ < ε

, и если нет, переходят к следующей внутренней итерации.

11. Способ по п. 10, в котором совокупность активных множеств не обновляют до тех пор, пока итерация без ограничений внутреннего цикла не сойдется с удовлетворением выбранного условия оптимальности.

12. Способ по п. 2, в котором в многоиндексном способе активных множеств используют решатель сопряженных градиентов или решатель LSQR (разреженных линейных систем и разреженных задач наименьших квадратов).

13. Способ по п. 6, в котором указанное связывание указанного сдвига Δf центроидной частоты с 1/Q может быть математически выражено в соответствии с

Δ f = f_{S} - f_{R} = (n + 1) (f_{0} \frac{1}{\int_{п о л у ч у} \frac{π}{Q v} d l + \frac{1}{f_{0}}})

,
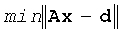
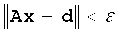
где f_S и f_R - центроидная частота для соответственно амплитудного спектра сейсмического источника и амплитудного спектра, обнаруживаемого приемником, v - скорость акустических волн и dl является приращением траектории луча.

14. Способ по п. 1, дополнительно содержащий использование определяемых решений значений Q или 1/Q в построении сейсмического изображения при поиске углеводородов или при получении характеристик коллектора углеводородов.

15. Лучевой способ сдвига центроидных частот Q томографии для перестроения модели геологической среды для Q или 1/Q на основании сейсмических данных, измеряемых приемниками при исследовании с использованием сейсмического источника, содержащий использование частотно-взвешенной экспоненциальной функции частоты для аппроксимации амплитудного спектра сейсмического источника, чтобы вычислить сдвиг центроидных частот спектра вследствие затухания в земле, и связывание указанного сдвига центроидных частот с затуханием, представленным обратной величиной добротности Q, и нахождение решения относительно Q или 1/Q путем итеративной линейной оптимизации, выполняемой с использованием компьютера.

16. Способ по п. 15, в котором оптимизация имеет боксовые ограничения для поддержания оцениваемых значений Q в пределах зависимых от положения диапазонов, точно определяемых верхними границами и нижними границами.

17. Способ по п. 15, в котором оптимизация с боксовыми ограничениями разрешается многоиндексным способом активных множеств, который позволяет обновлять активное множество в соответствии с многочисленными индексами сетки за один раз, при этом индекс сетки обозначает расположение геологической среды.

18. Способ по п. 15, в котором частотно-взвешенная экспоненциальная функция частоты имеет два параметра, которые подбирают, чтобы обеспечивать соответствие амплитудному спектру сейсмического источника, указанные два параметра представляют собой характеристическую частоту для управления шириной полосы частот и индекс симметрии, при этом каждый является положительным вещественным числом.

19. Способ по п. 18, в котором частотно-взвешенная экспоненциальная функция частоты может быть выражена в форме

F (f) = A f^{n} \exp (- \frac{f}{f_{0}})

20. Способ по п. 15, дополнительно содержащий использование определяемых решением значений Q или 1/Q в построении сейсмического изображения при поиске углеводородов или при получении характеристик коллектора углеводородов.

Патенты аналоги

Авторы

ХУ Вэньи (US)

KHU VEHN I

KHU VEHN'I

Патентообладатели

EHKSONMOBIL APSTRIM RISERCH KOMPANI

Заявители

EHKSONMOBIL APSTRIM RISERCH KOMPANI

СПК: G01V1/282 G01V1/306 G01V2210/671

Публикация: 2015-07-27

Дата подачи заявки: 2011-03-21

РОССТИП

Поиск по товарам

Добавить свой товар

Сообщества

Товары

Участники

Патенты

Запросов

Поставщикам

О сервисе

Блогерам

Помощь