Способы оценивания параметров геологической среды при инверсии полного волнового поля и обратной миграции во временной области - RU2545487C2

Чертежи

Описание

Описание

Перекрестная ссылка на родственную заявку

По этой заявке испрашивается приоритет предварительной заявки № 61/303148 на патент США, поданной 10 февраля 2010 года, под названием “Methods for subsurface parameter estimation in full wavefield inversion and reverse-time migration”, которая для всех целей полностью включена в эту заявку путем ссылки.

Область техники, к которой относится изобретение

В общем, это изобретение относится к области геофизических исследований, а более конкретно к обработке сейсмических данных. В частности, изобретением является способ оценивания параметров геологической среды при инверсии полного волнового поля и обратной миграции во временной области.

Предпосылки создания изобретения

Инверсия полного волнового поля при обработке разведочных сейсмических данных основана на вычислении градиента целевой функции относительно параметров модели геологической среды [12]. Целевую функцию Е обычно определяют как норму L₂ в виде

где p и p_b являются измеряемым давлением, то есть амплитудой сейсмической волны, и моделируемым давлением в модели вмещающей геологической среды на месте r_g нахождения приемника при взрыве, локализованном в r_s. В процессах итеративной инверсии вмещающая среда обычно представляет собой среду, являющуюся результатом предшествующего цикла инверсии. При выполнении процессов неитеративной инверсии или миграций вмещающую среду обычно получают с использованием обычных способов обработки сейсмических данных, таких как анализ скорости миграции. Целевую функцию интегрируют по всему времени t и поверхностям S_g и S_s, которые определяются разносом приемников и взрывов. Зададим K_d(r)=K(r)-K_b(r) и ρ_d(r)=ρ(r)-ρ_b(r), где K(r) и ρ(r) являются истинным объемным модулем упругости и плотностью, а K_b(r) и ρ_b(r) являются объемным модулем упругости и плотностью из модели вмещающей среды в точке r геологической среды. Также зададим разность между измеряемым и моделируемым давлениями в виде p_d(r_g,r_s;t)=p(r_g,r_s;t)-p_b(r_g,r_s;t).

Измеряемое давление p удовлетворяет волновому уравнению

или

где q(t) является сигнатурой источника. Разлагая в ряд члены возмущения и учитывая только члены приближения Борна первого порядка, можно получить уравнение рассеяния Борна для давления p_d,

и поэтому p_d удовлетворяет

где V' является объемом, охватывающим r', и g_b является функцией Грина во вмещающей среде.

Можно получить уравнения для градиентов p_b, используя уравнение (5) и учитывая относительное изменение δp_b вследствие относительных изменений δK_b и δρ_b на протяжении бесконечно малого объема dV,

и

где P_b=F{p_b}, P_d=F{p_d}, G_b=F{g_b}, и при этом F и F^-1 являются операторами преобразования Фурье и обратного преобразования Фурье.

Используя уравнения (6) и (7) и используя соотношение взаимности ρ_b(r)G_b(r_g,r)=ρ_b(r_g)G_b(r,r_g), получаем

и

После этого уравнения (8) и (9) можно использовать для выполнения инверсии полного волнового поля итерационным способом.

Обратная миграция во временной области основана на способах, аналогичных вычислению градиента при инверсии полного волнового поля, когда распространяющееся вперед поле взаимно коррелировано с обращенным во времени принимаемым полем. При этом в процессе обратной миграции во временной области отсутствуют ограничения способов миграции на основе лучевого подхода, таких как миграция Кирхгофа. При обратной миграции во временной области уравнение поля М мигрированных изображений в точке r геологической среды имеет вид

и оно очень похоже на градиентное уравнение (8) инверсии полного волнового поля.

Хотя уравнения (8) и (9) обеспечивают основу для обращения данных в моделях геологической среды, сходимость процесса инверсии часто является очень медленной. Кроме того, при обратной миграции во временной области с использованием уравнения (10) слабая амплитуда в глубинном разрезе претерпевает изменения вследствие расходимости волнового поля. Делались многочисленные попытки улучшить сходимость инверсии полного волнового поля или повысить амплитуду обратной миграции во временной области путем использования гессиана целевой функции [9], то есть второй производной целевой функции. Однако для вычисления гессиана требуются не только большие затраты вычислительных ресурсов, но также требуется чрезмерно большой объем запоминающего устройства для решения реальной задачи трехмерной инверсии. Кроме того, инверсия полного волнового поля с использованием полной матрицы Гесса может сводиться к субоптимальной инверсии [2].

Более устойчивую инверсию можно выполнять путем перевода недиагональных членов гессиана в диагональные члены [2]. Однако для этого все же требуется вычисление полной матрицы Гесса или по меньшей мере нескольких недиагональных членов матрицы Гесса, что может быть затратным в вычислительном отношении. Хотя можно выбирать использование только диагонали гессиана [11], это является справедливым только в высокочастотном асимптотическом режиме при бесконечной апертуре [1, 7].

Plessix и Mulder пытались преодолеть эти трудности, сначала вычисляя приближенный диагональный гессиан, а затем масштабируя на

Краткое изложение изобретения

В одном осуществлении изобретение представляет собой способ определения модели физического свойства в подземной области на основании инверсии сейсмических данных, зарегистрированных в результате сейсмического исследования подземной области, или на основании обратной миграции во временной области сейсмических изображений из сейсмических данных, при этом указанный способ содержит определение объема сейсмического разрешения для физического свойства и использование его в качестве мультипликативного масштабного коэффициента при вычислениях, выполняемых на компьютере, для

(а) преобразования градиента несоответствия данных при инверсии или

(b) компенсации обратно мигрированных во временной области сейсмических изображений,

чтобы получить модель физического свойства или обновить предполагаемую модель.

В некоторых осуществлениях способа изобретения градиент несоответствия данных или обратно мигрированные во временной области изображения умножают на дополнительные масштабные коэффициенты, помимо объема сейсмического разрешения, при этом дополнительные масштабные коэффициенты включают в себя коэффициент освещения источником, коэффициент освещения приемника и коэффициент свойств вмещающей среды. Это приводит к модели физического свойства или обновлению предполагаемой модели, имеющей корректные единицы измерения.

Для специалистов в данной области техники должно быть очевидно, что при любом практическом применении изобретения, инверсия или миграция сейсмических данных должна выполняться на компьютере, специально программируемом для выполнения этой операции.

Краткое описание чертежей

Настоящее изобретение и его преимущества станут более понятными при обращении к нижеследующему подробному описанию и сопровождающим чертежам, на которых:

Фиг.1 - блок-схема последовательности действий, показывающая основные этапы в одном осуществлении способа настоящего изобретения;

Фиг.2-5 - иллюстрации первого применения настоящего изобретения, где на фиг.2 показан градиент целевой функции относительно объемного модуля упругости в Па·м⁴·с, вычисленный с использованием уравнения (8);

Фиг.3 - иллюстрация обновления 〈K_d(r)〉 объемного модуля упругости в Па, вычисленного с использованием уравнения (18) и градиента из фиг.2;

Фиг.4 - иллюстрация обновления 〈K_d(r)〉 объемного модуля упругости в Па, вычисленного с использованием уравнения (24) и градиента из фиг.2;

Фиг.5 - иллюстрация градиента целевой функции относительно плотности в Па²·м⁷·с/кг, вычисленного с использованием уравнения (9);

Фиг.6 и 7 - иллюстрации второго примера применения настоящего изобретения, где на фиг.6 показано обновление 〈ρ_d(r)〉 плотности в кг/м³, вычисленное с использованием уравнения (28) и градиента из фиг.5; и

Фиг.7 - иллюстрация обновления 〈ρ_d(r)〉 плотности в кг/м³, вычисленного с использованием уравнения (34) и градиента из фиг.5.

Изобретение будет описано применительно к примерам осуществлений. Однако в тех случаях, когда нижеследующее подробное изобретение является характерным для конкретного осуществления или конкретного использования изобретения, оно предполагается только иллюстративным и не должно толковаться как ограничивающее объем изобретения. Наоборот, оно предполагается охватывающим все варианты, модификации и эквиваленты, которые могут быть включены в объем изобретения, определяемый прилагаемой формулой изобретения.

Подробное описание примеров осуществлений

В настоящем изобретении для получения уравнений инверсии для K_d и ρ_d используются уравнения (8) и (9). Сначала это делается с использованием того, что p_d в уравнениях (8) и (9) также можно разложить в ряд, используя приближение Борна из уравнения (5). Пренебрегая перекрестными компонентами между K_d и ρ_d, уравнения (8) и (9) можно аппроксимировать как

и

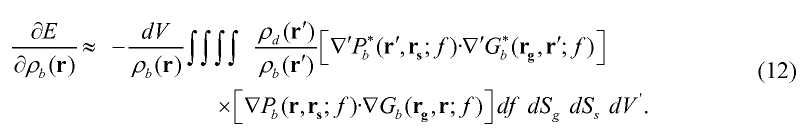
Изменяя порядки интеграла, уравнение (11) можно перезаписать в частотной области в виде

Первый член интеграла

в уравнении (13) представляет собой приближение для обратного распространения с обращением времени поля, создаваемого импульсным источником в точке r', измеряемой на поверхности S_g, и затем распространяющегося обратно в r (см., например, список литературы [8, 3]). Волновое поле, обусловленное этим членом, распространяется обратно к импульсному источнику в точке r' и ведет себя аналогично пространственной дельта-функции δ(r-r') при t=0, если интегральная поверхность S_g включает в себя точку r'. Корреляцию этого волнового поля осуществляют с волновым полем, обусловленным вторым членом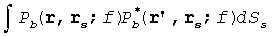

где

а V_k(r) является сейсмическим разрешением в точке r геологической среды. Уравнение (15) эквивалентно сосредоточению масс матрицы Гаусса-Ньютона-Гесса в предположении что недиагональные элементы равны диагональным элементам, когда недиагональные элементы находятся в объеме сейсмического разрешения диагонального элемента и вне нуля объема разрешения. Иначе говоря, уравнение (15) эквивалентно косвенному подсчету количества недиагональных элементов N_i матрицы Гаусса-Ньютона-Гесса в каждой i-той строке, которые являются значимыми для амплитуды, путем использования объема сейсмического разрешения исследования и затем умножения диагонального элемента i-той строки на N_i.

Объем сейсмического разрешения можно представить себе как минимальный объем в r, который система построения сейсмического изображения может разрешать при данных параметрах регистрации сейсмических данных. Два небольших объекта исследований, которые находятся в одном объеме сейсмического разрешения, обычно не разрешаются и проявляются как один объект исследований в системе построения сейсмического изображения. Объемы разрешения при различных параметрах среды являются разными вследствие различий в характеристиках излучения. Например, объекты исследований, обусловленные возмущением объемного модуля упругости, создают монопольную характеристику излучения, тогда как объекты, обусловленные возмущением плотности, создают дипольную характеристику излучения. Объем V_K(r) сейсмического разрешения для случая объемного модуля упругости можно вычислять, например, используя относительно экономичное лучевое приближение [6, 4]. Специалистам в данной области техники могут быть известны другие способы оценивания объема разрешения. Например, можно эмпирически оценивать объем разрешения в соответствии с распределением точечных объектов во вмещающей среде и путем исследования распределения объектов в сейсмическом изображении. Если вмещающая среда содержит скоростную границу, обусловленную итерационным характером инверсии, может возникать необходимость сглаживания вмещающей среды трассированием лучей. Можно также делать упрощающее предположение, заключающееся в том, что охват по волновым числам является равномерным. В этом случае объем сейсмического разрешения является сферой с радиусом σ≈(5/18π)^0,5v_p(r)/f_p, где f_p является пиковой частотой [6]. Можно также использовать приближение σ≈v_p(r)T/4=v_p(r)/4B, где Т и В являются эффективной длительностью и эффективной полосой частот волнового сигнала источника, вытекающее из уравнения разрешающей способности радиолокатора [5].

В таком случае уравнение (11) можно упростить, используя уравнение (15), до следующей формы

и поэтому

где 〈K_d(r)〉 представляет собой пространственное среднее K_d по сейсмическому разрешению в пространственной точке r.

Уравнение (16) можно дополнительно упростить, если использовать функцию Грина для свободного пространства

и предположить, что S_g противолежит половине телесного угла. В таком случае уравнение (16) упрощается до

I_K(r)≈I_K,s(r)I_K,s(r),

где

и

Член I_K,s(r) можно признать освещением источником в модели вмещающей среды и под I_K,g(r) можно понимать освещение приемника. Кроме того, можно изменять телесный угол интеграла в каждой точке r геологической среды, следуя геометрии исследования. В таком случае уравнение (11) становится

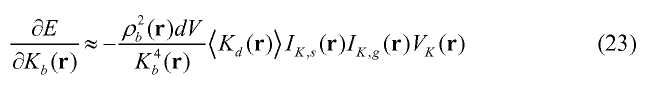
и

Из уравнений (18) и (24) видно, что градиент ∂E/∂K_b(r) можно преобразовать в параметр 〈K_d(r)〉 среды путем масштабирования градиента в соответствии с освещениями источником и приемника, объемом разрешения и свойствами вмещающей среды. Если процесс инверсии не является итерационным, уравнение (24) можно использовать для инверсии параметра. Если процесс инверсии является итерационным, можно использовать 〈K_d(r)〉 из уравнения (24) в качестве предобусловленного градиента для способов оптимизации, таких как способ скорейшего спуска, сопряженных градиентов или сопряженных градиентов Ньютона. Важно отметить, что уравнениями (18) и (24) дается объемный модуль упругости в корректных единицах измерения, то есть являющихся корректными по размерности, поскольку все члены приняты в расчет без пренебрежения для упрощения вычисления, как в случае некоторых опубликованных способов. Опубликованные способы, в которых пренебрегают одним или несколькими членами освещения источником, освещения приемника, свойств вмещающей среды и объема сейсмического разрешения, не приводят к корректным единицам измерения, и поэтому необходимо некоторое упорядочение по ситуации для приведения в соответствие до того, как их можно будет использовать для итеративной или неитеративной инверсии.

Для градиента плотности сделаем предположение, подобное предположению из уравнения (15),

где

а V_ρ(r) является сейсмическим разрешением для плотности ρ в точке r геологической среды. Объем V_ρ(r) разрешения отличается от V_K(r), поскольку волновые числа теряются, когда падающее и рассеиваемое поля почти ортогональны по отношению друг к другу. Как рассматривалось ранее, это обусловлено дипольной характеристикой излучения вследствие возмущения плотности. Трассирование лучей, сделанное для V_K(r), можно использовать для вычисления объема V_ρ(r) разрешения при учете этих недостающих почти ортогональных волновых чисел. В качестве варианта можно предположить V_K(r)≈V_ρ(r), пренебрегая различием в охвате по волновым числам.

В таком случае градиентное уравнение (12) можно перезаписать как

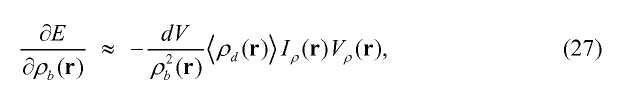
и поэтому

где 〈ρ_d(r)〉 является пространственным средним ρ_d(r) по объему V_ρ(r) сейсмического разрешения.

Можно дополнительно упростить уравнение (25), используя векторное тождество (a·b)(c·d)=(a·d)(b·c)+(a×c)·(b×d), чтобы получить

Второй член в правой части уравнения (29) представляет собой поправочный член для дипольной характеристики излучения рассеянного поля и поэтому он достигает максимума, когда ∇P_b и ∇G_b ортогональны по отношению друг к другу. В пренебрежении этим поправочным членом

В таком случае уравнение (12) можно аппроксимировать как

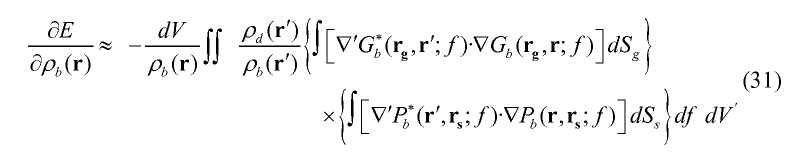
Используя функцию Грина для свободного пространства, можно аппроксимировать интеграл по S_g из уравнения (26)

Интегрирование выполнялось по половине телесного угла в предположении, что ∇(ρ_b(r_g)/ρ_b(r))≈0 и ρ_b(r_g) является постоянной по S_g.

В таком случае градиентное уравнение, приведенное выше, можно перезаписать в виде

и поэтому

где

и

Как и применительно к 〈K_d(r)〉, уравнение (28) или (34) можно использовать в качестве формулы инверсии для неитеративной инверсии или в качестве предобусловленного градиентного уравнения для итеративной инверсии. Важно отметить, что этими уравнениями плотность дается в корректных единицах измерения, то есть являющихся корректными по размерности, поскольку все члены приняты в расчет без пренебрежения для упрощения вычисления, как в случае некоторых опубликованных способов. То же самое справедливо в отношении уравнений (18) и (24) для объемного модуля упругости. Опубликованные способы, в которых пренебрегают одним или несколькими членами освещения источником, освещения приемника, свойств вмещающей среды и объема сейсмического разрешения, не приводят к корректным единицам измерения, и поэтому необходимо некоторое упорядочение по ситуации для приведения в соответствие до того, как их можно будет использовать для итеративной или неитеративной инверсии.

Поскольку первая итерация инверсии полного волнового поля аналогична обратной миграции во временной области, способ, предлагаемый в этой заявке, при небольшой модификации можно применять для анализа амплитудного члена при обратной миграции во временной области. Сейсмическую миграцию, включая обратную миграцию во временной области, обычно используют для построения изображения структуры геологической среды и поэтому информацию об амплитуде в мигрированном изображении часто отбрасывают. Заявитель обнаружил, что амплитуда обратной миграции во временной области при надлежащем масштабировании с использованием способа, предлагаемого в этой заявке, представляет разность между истинной скоростью продольной волны в геологической среде и скоростью из модели вмещающей среды.

Заметим, что в уравнении (10) обратной миграции во временной области отсутствует вторая производная падающего поля из уравнения (8). Вторая производная означает, что в режиме классического рассеяния Релея высокочастотные составляющие рассеиваются более эффективно, чем низкочастотные составляющие (см. список литературы [10, 13]). Поэтому уравнение (10) можно рассматривать как операцию вычисления градиента в уравнении (8) при частичном пренебрежении частотной зависимостью рассеиваемого поля,

где f_c является центральной частотой волнового сигнала источника. Частотная зависимость является частично пренебрежимой, поскольку при пренебрежении частотной зависимостью прямого поля p_b частотной зависимостью, присущей принимаемому полю p_s, пренебрегать нельзя. Пространственная вариация плотности обычно не учитывается при обратной миграции во временной области и поэтому в уравнении (37) ρ_b предполагается постоянной величиной.

Теперь к уравнению (10) можно применить такое же приближение, которое использовалось для получения уравнений (17) и (23),

что совместно с уравнением (37) дает

Уравнение (39) позволяет осуществлять численный анализ обратно мигрированного во временной области изображения. Более конкретно, оно позволяет осуществлять обращение амплитуды в разностный объемный модуль упругости геологической среды.

На фиг.1 представлена блок-схема последовательности действий, показывающая основные этапы одного осуществления способа настоящего изобретения. На этапе 103 вычисляют градиент целевой функции, используя входную сейсмическую запись (101) и информацию о вмещающей геологической среде (102). На этапе 104 освещения источником и приемника вычисляют из модели вмещающей среды. На этапе 105 вычисляют объем сейсмического разрешения, используя скорости из модели вмещающей среды. На этапе 106 градиент из этапа 103 преобразуют в разностные параметры модели геологической среды, используя освещения источником и приемника из этапа 104, объем сейсмического разрешения из этапа 105 и модель (102) вмещающей геологической среды. Если на этапе 107 должен выполняться процесс итеративной инверсии, используют разностные параметры модели геологической среды из этапа 106 в качестве предобусловленных градиентов для процесса итеративной инверсии.

Примеры

Рассмотрим случай идеального рассеивателя Борна с размерами 30 м×30 м×30 м в однородной среде с K_b=9 МПа и ρ_b=1000 кг/м³. Объект исследований центрирован в (x, y, z)=(0, 0, 250 м), где x и y являются двумя горизонтальными координатами, а z является глубиной. Объект исследований можно видеть на фиг.2-7 в виде матрицы размера 3×3 из небольших квадратов, расположенной в центре каждой диаграммы. Источники и приемники считались расположенными на интервалах -500 м≤x≤500 м и -500 м≤y≤500 м при разносе на 10 м в обоих направлениях, x и y. Предполагалось, что сейсмический импульс источника имеет на расстоянии 1 м равномерную амплитуду 1 Па/Гц в диапазоне частот от 1 до 51 Гц.

В первом примере предполагалось, что объект исследований имеет возмущение объемного модуля упругости, задаваемое как K_d=900 кПа. На фиг.2 показан градиент ∂E/∂K_b(r) вдоль плоскости y=0, полученный с использованием уравнения (8). Рассеиваемое поле p_d из уравнения (8) вычислялось с использованием уравнения (5). Градиент на фиг.2 имеет единицы измерения Па·м⁴·с и поэтому не может быть непосредственно связан с K_d. Как описывалось в разделе «Предпосылки», приведенном выше, это является трудностью, встречающейся в некоторых опубликованных попытках вычисления обновления модели на основании градиента целевой функции.

На фиг.3 показано среднее 〈K_d(r)〉, полученное с использованием уравнения (18) настоящего изобретения. Предполагалось, что объем V_K(r) сейсмического разрешения является сферой с радиусом σ=v_p(r)/4B=15 м. Можно видеть, что на фиг.3 представлено размытое изображение объекта исследований, поскольку 〈K_d(r)〉 является усредненным свойством по объему сейсмического разрешения. На фиг.4 показано 〈K_d(r)〉, полученное при использовании менее строгого уравнения (24). Можно видеть, что 〈K_d(r)〉 на фиг.3 и 4 находятся в хорошем согласии друг с другом. Значение 〈K_d(r)〉 в центре объекта исследований на фиг.3 составляет 752 кПа, а на фиг.4 составляет 735 кПа, оба значения находятся в пределах 20% истинного значения 900 кПа.

Вторым примером является случай, когда объект исследований имел возмущение плотности ρ_d=100 кг/м³. На фиг.5 показан градиент ∂E/∂ρ_b(r) вдоль плоскости y=0, полученный с использованием уравнения (9). Рассеянное поле из уравнения (9) вычислялось с использованием уравнения (5). Градиент на фиг.5 имеет единицы измерения Па²·м⁷·с/кг. Как и в первом примере, разные единицы измерения препятствуют установлению непосредственной связи градиента с обновлением плотности, и этим опять иллюстрируется проблема, встречающаяся в опубликованных способах.

На фиг.6 показано среднее 〈ρ_d(r)〉, полученное с использованием уравнения (28). Объем V_ρ(r) сейсмического разрешения предполагался идентичным V_K(r). На фиг.7 показано 〈ρ_d(r)〉, полученное с использованием уравнения (34). Оценивание 〈ρ_d(r)〉 с использованием уравнения (34) приводит к менее точной инверсии по сравнению с использованием уравнения (28) вследствие пренебрежения членом дипольного освещения из уравнения (31).

Изложенная выше патентная заявка касается иллюстрации конкретных осуществлений настоящего изобретения. Однако специалисту в данной области техники должно быть понятно, что возможны многочисленные модификации и варианты осуществлений, описанных в этой заявке. Все такие модификации и варианты предполагаются находящимися в объеме настоящего изобретения, определяемого прилагаемой формулой изобретения. Специалисты в данной области техники должны осознавать, что при практических применениях изобретения по меньшей мере некоторые этапы способов настоящего изобретения выполняются на компьютере или с помощью его, то есть изобретение является реализуемым компьютером.

Список литературы

[1] G. Beylkin, "Imaging of discontinuities in the inverse scattring problem by inversion of a causal generalized Radon transform," J. Math. Phys. 26, 99-108 (1985).

[2] G. Chavent and R.-E. Plessix, "An optimal true-amplitude least-squares prestack depth-migration operator," Geophysics 64(2), 508-515 (1999).

[3] D. R. Jackson and D. R. Dowling, "Phase conjugation in underwater acoustics," /. Acoust. Soc. Am. 89(1), 171-181(1991).

[4] I. Lecomte, "Resolution and illumination analyses in PSDM: A ray-based approach," The Leading Edge, pages 650-663 (May 2008).

[5] N. Levanon, Radar Principles, chapter 1, pages 1-18, John Wiley & Sons, New York (1988).

[6] M. A. Meier and P. J. Lee, "Converted wave resolution," Geophysics 74(2), Q1-Q16 (2009).

[7] R. E. Plessix and W. A. Mulder, "Frequency-domain finite-difference amplitude-preserving migration," Geophys. J. Int. 157, 975-987 (2004).

[8] R. P. Porter, "Generalized holography with application to inverse scattering and inverse source problems," Progress in Optics XXVII, E. Wolf, editor, pages 317-397, Elsevier (1989).

[9] R. G. Pratt, С Shin, and G. J. Hicks, "Gauss-Newton and foil Newton methods in frequency-space seismic waveform inversion," Geophys. J. Int. 133, 341-362 (1998).

[10] J. W. S. Rayleigh, "On the transmission of light through an atmosphere containing small particles in suspension, and on the origin of the blue of the sky," Phil. Mag. 47, 375-384 (1899).

[11] С Shin, S. Jang, and D.-J. Min, "Waveform inversion using a logarithmic wavefield," Geophysics 49, 592-606 (2001).

[12] A. Tarantola, "Inversion of seismic reflection data in the acoustic approximation," Geophysics 49, 1259-1266(1984).

[13] R. J. Urick, Principles of Underwater Sound, chapter 9, pages 291-327, McGraw-Hill, New York, 3rd edition (1983).

Реферат

Изобретение относится к области геофизики и может быть использовано для обработки данных сейсморазведки. Заявлен способ преобразования сейсмических данных для получения модели объемного модуля упругости или плотности геологической среды. Градиент целевой функции вычисляют (103), используя сейсмические данные (101) и модель (102) вмещающей геологической среды. Коэффициент освещения источником и коэффициент освещения приемника вычисляют (104) в модели вмещающей среды. Объем сейсмического разрешения вычисляют (105), используя скорости из модели вмещающей среды. Градиент преобразуют (106) в разностные параметры модели геологической среды, используя коэффициент освещения источником, коэффициент освещения приемника, объем сейсмического разрешения и модель вмещающей геологической среды. Указанные величины являются масштабными коэффициентами, используемыми для компенсации сейсмических данных после миграции путем обратной миграции во временной области, которые затем можно связать с моделью объемного модуля упругости геологической среды. В случае итерационной инверсии разностные параметры (106) модели геологической среды используют (107) в качестве предобусловленных градиентов. Технический результат - повышение точности получаемых данных. 20 з.п. ф-лы, 7 ил.

Формула

8. Способ по п.4, в котором коэффициент освещения приемника, когда физическим свойством является объемный модуль упругости, аппроксимируют в соответствии с (1/8π)(ρ_b(r_g)/ρ_b(r), где ρ_b(r) является плотностью вмещающей среды в точке r и r_g является местом нахождения приемника; а коэффициент I_ρ,g(r) освещения приемника, когда физическим свойством является плотность, аппроксимируют в соответствии с

,
где v_p(r) является скоростью в точке r.