Инверсия одновременных источников для данных сейсмоприемной косы с взаимнокорреляционной целевой функцией - RU2587498C2

Чертежи

Описание

ПЕРЕКРЕСТНАЯ ССЫЛКА НА РОДСТВЕННУЮ ЗАЯВКУ

Эта заявка испрашивает приоритет по предварительной патентной заявке США 61/418,694, поданной 1 декабря 2010 г., озаглавленной Simultaneous Source Inversion for Marine Streamer Data with Cross-Correlation Objective Function, и предварительной патентной заявке США 61/509,904, поданной 20 июля 2011 г., имеющей такое же название, обе из которых полностью включены в настоящий документ посредством ссылки.

ОБЛАСТЬ ТЕХНИКИ, К КОТОРОЙ ОТНОСИТСЯ ИЗОБРЕТЕНИЕ

Изобретение относится, в общем, к области геофизической разведки, и более конкретно, к обработке геофизических данных. Конкретно, изобретение является способом для инверсии данных, полученных от множественных геофизических источников, таких как сейсмические источники, включая геофизическое моделирование, которое вычисляет данные от многих одновременно активных геофизических источников при одном выполнении моделирования.

УРОВЕНЬ ТЕХНИКИ

Даже при современных вычислительных возможностях, инверсия сейсмического полного волнового поля все еще является вычислительно дорогостоящим предприятием. Однако ожидается, что преимущество получения детального представления геологической среды с использованием этого способа перевесит это препятствие. Разработка алгоритмов и технологических процессов, которые ведут к более быстрой производительности по времени, является ключевым этапом в направлении к тому, чтобы эту технологию можно было реализовывать для масштаба данных полевых наблюдений. Инверсия сейсмической полной волновой формы включает в себя несколько итераций прямого и сопряженного моделирования данных. Поэтому способы, которые уменьшают затраты проходов прямого и сопряженного вычислений, обеспечивают возможность пользователям решать проблемы более большого масштаба за разумное время.

Геофизическая инверсия [1, 2] пытается найти модель свойств геологической среды, которая оптимально объясняет наблюдаемые данные и удовлетворяет геологическим и геофизическим ограничениям. Имеется большое количество хорошо известных способов геофизической инверсии. Эти хорошо известные способы попадают в одну из двух категорий: итеративная инверсия и неитеративная инверсия. Последующее является определениями того, что обычно предполагается под каждой из двух категорий:

Неитеративная инверсия - инверсия, которая выполняется при предположении некоторой простой фоновой модели и обновлении модели на основе входных данных. Этот способ не использует обновленную модель в качестве входа на другой этап инверсии. Для случая сейсмических данных эти способы обычно указываются как формирование изображений, миграция, дифракционная томография или инверсия Борна.

Итеративная инверсия - инверсия, включающая в себя повторяющееся улучшение модели свойств геологической среды, в результате чего находится модель, которая удовлетворительно объясняет наблюдаемые данные. Если инверсия сходится, то конечная модель будет лучше объяснять наблюдаемые данные и будет более близко приближать фактические свойства геологической среды. Итеративная инверсия обычно вырабатывает более точную модель, чем неитеративная инверсия, но является намного более дорогостоящей для вычислений.

Итеративная инверсия является, в общем, предпочтительной по сравнению с неитеративной инверсией, так как она дает более точные модели параметров геологической среды. К сожалению, итеративная инверсия является настолько вычислительно дорогостоящей, что является непрактичным применять ее ко многим интересующим проблемам. Эти высокие вычислительные затраты являются результатом того, что все способы инверсии требуют большого количества вычислительно интенсивных моделирований. Время вычислений любого индивидуального моделирования является пропорциональным количеству источников, подлежащих инвертированию, и обычно в геофизических данных имеется большое количество источников, при этом признак источник, используемый в предшествующем, указывает на местоположение активации устройства источника. Для итеративной инверсии проблема осложняется, так как количество моделирований, которые должны вычисляться, является пропорциональным количеству итераций в инверсии, и требуемое количество итераций имеет обычно порядок от сотен до тысяч.

Наиболее распространенным способом итеративной инверсии, применяемым в геофизике, является оптимизацией функции затрат. Оптимизация функции затрат включает в себя итеративную минимизацию или максимизацию значения, по отношению к модели M, функции затрат S(M), которая является мерой несоответствия между вычисленными и наблюдаемыми данными (она также иногда указывается как целевая функция), где вычисленные данные моделируются с помощью компьютера с использованием текущей модели геофизических свойств и физики, определяющей распространение сигнала источника в среде, представленной заданной моделью геофизических свойств. Вычисления моделирования могут делаться посредством любого из нескольких численных методов, включающих в себя, но не ограниченных этим, конечную разность, конечный элемент или трассировку лучей. Вычисления моделирования могут выполняться либо в частотной, либо во временной области.

Способы оптимизации функции затрат являются либо локальными, либо глобальными [3]. Глобальные способы просто включают в себя вычисление функции затрат S(M) для совокупности моделей {M₁, M₂, M₃,...} и выбор набора одной или более моделей из этой совокупности, которые приближенно минимизируют S(M). Если требуется дополнительное улучшение, этот новый выбранный набор моделей может тогда использоваться в качестве основы, чтобы генерировать новую совокупность моделей, которая может снова тестироваться в отношении функции затрат S(M). Для глобальных способов каждая модель в тестовой совокупности может рассматриваться как итерация, или на более высоком уровне каждый набор протестированных совокупностей может рассматриваться как итерация. Хорошо известные глобальные способы инверсии включают в себя Монте-Карло, искусственный аннилинг, генетические и эволюционные алгоритмы.

К сожалению, глобальные способы оптимизации обычно сходятся в высшей степени медленно и, поэтому, большинство геофизических инверсий основываются на локальной оптимизации функции затрат. Алгоритм 1 подытоживает локальную оптимизацию функции затрат.

Эта процедура повторяется посредством использования новой обновленной модели в качестве начальной модели для другого градиентного поиска. Процесс продолжается до тех пор, когда находится обновленная модель, которая удовлетворительно объясняет наблюдаемые данные. Распространенно используемые способы локальной инверсии функции затрат включают в себя градиентный поиск, сопряженные градиенты и способ Ньютона.

Локальная оптимизация функции затрат сейсмических данных в акустическом приближении является общей задачей геофизической инверсии, и является, в общем, иллюстрацией других типов геофизической инверсии. При инвертировании сейсмических данных в акустическом приближении функция затрат может быть записана как:

где

S = функция затрат,

M = вектор N параметров, (m₁, m₂,...m_N), описывающих модель геологической среды,

g = индекс сейсмограммы,

w_g = функция источника для сейсмограммы g, которая является функцией пространственных координат и времени, для точечного источника она является дельта функцией пространственных координат,

N_g = количество сейсмограмм,

r = индекс приемника в сейсмограмме,

N_r = количество приемников в сейсмограмме,

t = индекс временной выборки внутри трассы,

N_t = количество временных выборок,

W = функция критерия минимизации (мы обычно выбираем W(x)=x², которая является критерием наименьших квадратов (L2)),

ψ_вычисл = вычисленные сейсмические данные давления для модели M,

ψ_набл = измеренные сейсмические данные давления.

Сейсмограммы могут быть любым типом сейсмограммы, которая может моделироваться в одном проходе программы сейсмического прямого моделирования. Обычно сейсмограммы соответствуют сейсмическому взрыву, хотя взрывы могут быть более общими, чем точечные источники. Для точечных источников индекс сейсмограммы g соответствует местоположению индивидуальных точечных источников. Для источников плоской волны g соответствует разным направлениям распространения плоской волны. Эти данные обобщенного источника, ψ_набл, могут либо получаться в полевых условиях, либо могут синтезироваться из данных, полученных с использованием точечных источников. Вычисленные данные ψ_вычисл, с другой стороны, могут обычно вычисляться напрямую посредством использования функции обобщенного источника при прямом моделировании. Для многих типов прямого моделирования, включающих в себя моделирование конечных разностей, время вычисления, необходимое для обобщенного источника, грубо равняется времени вычисления, необходимому для точечного источника.

Уравнение (1) может быть упрощено до

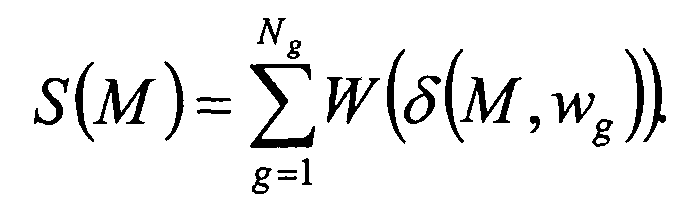
где сумма по приемникам и временным выборкам теперь подразумевается, и

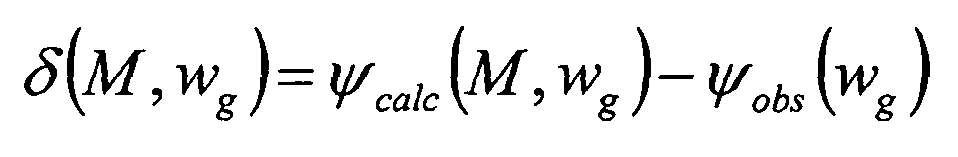
Инверсия пытается обновить модель M так, что S(M) является минимумом. Это может выполняться посредством локальной оптимизации функции затрат, которая обновляет заданную модель

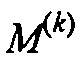
где k является номером итерации,

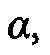
Из уравнения (2) для градиента функции затрат может быть выведено следующее уравнение:

Таким образом, чтобы вычислить градиент функции затрат, необходимо отдельно вычислить градиент каждого вклада сейсмограммы в функцию затрат, затем сложить эти вклады. Поэтому вычислительные затраты, требуемые для вычисления

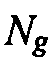
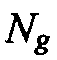
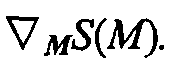
Отметим, что вычисление

В то время как вычисление градиентов с использованием метода сопряженных уравнений является эффективным относительно других способов, оно является все же очень дорогостоящим. В частности метод сопряженных уравнений требует два моделирования, одно прямое во времени и одно обратное во времени, и для геофизических проблем эти моделирования являются обычно очень вычислительно интенсивными. Также, как описано выше, это вычисление метода сопряженных уравнений должно выполняться для каждой измеренной сейсмограммы данных индивидуально, что увеличивает вычислительный затраты на коэффициент N_g.

Вычислительные затраты всех категорий инверсии могут быть уменьшены посредством инвертирования данных из комбинаций источников, нежели инвертирования источников индивидуально. Это может быть названо как инверсия одновременных источников. Являются известным несколько типов комбинирования источников, включающие в себя: когерентное суммирование близко расстановленных источников, чтобы порождать эффективный источник, который вырабатывает волновой фронт некоторой требуемой формы (например, плоской волны), суммирование широко расстановленных источников, или полное или частичное суммирование данных до инверсии.

Уменьшение вычислительных затрат, достигаемое посредством инвертирования комбинированных источников, по меньшей мере, частично возмещается тем фактом, что инверсия комбинированных данных обычно вырабатывает менее точную инвертированную модель. Эта потеря в точности происходит вследствие того факта, что информация теряется, когда индивидуальные источники суммируются, и, поэтому, суммированные данные не ограничивают инвертированную модель также жестко, как несуммированные данные. Эта потеря информации во время суммирования может быть минимизирована посредством кодирования каждой записи взрыва до суммирования. Кодирование до комбинирования сохраняет значительно больше информации в данных одновременных источников, и, поэтому, лучше ограничивает инверсию [4]. Кодирование также обеспечивает возможность комбинирования близко расстановленных источников, таким образом, обеспечивая возможность комбинировать большее количество источников для заданной вычислительной области. С этим способом могут использоваться различные схемы кодирования, включающие в себя кодирование с временным сдвигом и кодирование со случайной фазой. В оставшейся части этого раздела Уровень техники кратко рассматриваются различные опубликованные способы геофизических одновременных источников, как с кодированием, так и без кодирования.

Ван Манен [6] предлагает использование способа сейсмической интерферометрии для ускорения прямого моделирования. Сейсмическая интерферометрия работает посредством размещения источников повсюду на границе области интереса. Эти источники моделируются индивидуально и волновое поле записывается во всех местоположениях, для которых требуется функция Грина. Функция Грина между любыми двумя записанными местоположениями может затем вычисляться посредством взаимного коррелирования трасс, полученных в двух записанных местоположениях, и суммирования по всем граничным источникам. Если данные, подлежащие инвертированию, имеют большое количество источников и приемников, которые находятся внутри области интереса (в противоположность наличию одного или другого на границе), то это очень эффективный способ для вычисления требуемых функций Грина. Однако для случая сейсмических данных является редким, что как источник, так и приемник для данных, подлежащих инвертированию, находятся внутри области интереса. Поэтому, это улучшение имеет очень ограниченную применимость к проблеме сейсмической инверсии.

Беркхаут [7] и Жанг [8] предлагают, что инверсия, в общем, может быть улучшена посредством инвертирования некодированных одновременных источников, которые когерентно суммируются, чтобы вырабатывать некоторый требуемый волновой фронт внутри некоторой области геологической среды. Например, данные точечного источника могут суммироваться с временными сдвигами, которые являются линейной функцией местоположения источника, чтобы вырабатывать идущую вниз плоскую волну при некотором конкретном угле по отношению к поверхности. Этот способ может применяться ко всем категориям инверсии. Проблема с этим способом состоит в том, что когерентное суммирование сейсмограмм источников обязательно уменьшает количество информации в данных. Таким образом, например, суммирование для создания плоской волны удаляет всю информацию в сейсмических данных, связанных с временем прохода по отношению к удалению источник-приемник. Эта информация является критической для обновления медленно изменяющейся фоновой скоростной модели, и, поэтому, способ Беркхаута не является хорошо ограниченным. Чтобы преодолевать эту проблему, может инвертироваться много разных когерентных сумм данных (например, много плоских волн с разными направлениями распространения), но тогда потеряется эффективность, так как затраты на инверсию пропорциональны количеству разных инвертированных сумм. Здесь, такие когерентно суммированные источники называются обобщенными источниками. Поэтому обобщенный источник может либо быть точечным источником, либо суммой точечных источников, которая вырабатывает волновой фронт некоторой требуемой формы.

Ван Риел [9] предлагает инверсию посредством некодированного суммирования или частичного суммирования (по отношению к удалению источник-приемник) входных сейсмических данных, затем определяя функцию затрат по отношению к этим суммированным данным, которые оптимизируются. Таким образом, эта публикация предлагает улучшение основывающейся на функции затрат инверсии с использованием некодированных одновременных источников. Как имело место для способа инверсии одновременных источников Беркхаута [6], суммирование, предложенное этим способом, уменьшает количество информации в данных, подлежащих инвертированию, и, поэтому, инверсия является менее хорошо ограниченной, чем она была бы с исходными данными.

Мора [10] предлагает инвертирование данных, которые являются суммой широко расстановленных источников. Таким образом, эта публикация предлагает улучшение эффективности инверсии с использованием моделирования некодированных одновременных источников. Суммирование широко расстановленных источников имеет преимущество сохранения намного большего количества информации, чем когерентное суммирование, предложенное Беркхаутом. Однако суммирование широко расстановленных источников имеет следствием, что апертура (инвертируемая область модели), которая должна использоваться в инверсии, должна быть увеличена, чтобы вмещать все широко расстановленные источники. Так как время вычислений является пропорциональным области этой апертуры, способ Мора не обеспечивает такого прироста эффективности, как мог бы быть достигнут, если бы суммируемые источники были рядом друг с другом.

Обер [11] предлагает ускорение сейсмической миграции, специальный случай неитеративной инверсии, посредством использования одновременных кодированных источников. После тестирования различных способов кодирования, Обер обнаружил, что результирующие мигрированные изображения имели значительно уменьшенное отношение сигнала к шуму вследствие того факта, что широкополосные кодирующие функции необходимо являются только приближенно ортогональными. Таким образом, при суммировании более чем 16 взрывов, качество инверсии не было удовлетворительным. Так как неитеративная инверсия не является очень дорогостоящей, чтобы с нее начинать, и так как инверсия высокого отношения сигнала к шуму является желательной, этот способ не является широко используемым в геофизических методах разведки.

Икелле [12] предлагает способ для быстрого прямого моделирования посредством одновременного моделирования точечных источников, которые активированы (в моделировании) в изменяющиеся временные интервалы. Также описывается способ для декодирования этих сдвинутых по времени смоделированных данных одновременных источников назад в отдельные моделирования, которые были бы получены от индивидуальных точечных источников. Эти декодированные данные могут затем использоваться как часть любой стандартной процедуры инверсии. Проблема со способом Икелле состоит в том, что предложенный способ декодирования вырабатывает разделенные данные, имеющие уровни шума, пропорциональные различию между данными от смежных источников. Этот шум становится значительным для моделей геологической среды, которые не являются латерально постоянными, например, для моделей, содержащих наклонные отражающие границы. Дополнительно, этот шум будет расти в пропорции к количеству одновременных источников. Вследствие этих трудностей, подход одновременных источников Икелле может давать результатом неприемлемые уровни шума, если используется в инвертировании геологической среды, которая не является латерально постоянной.

Кодирование источника, предложенное Кребсом и др. в публикации патентной заявки PCT номер WO 2008/042081, которая включается сюда по ссылке во всех юрисдикциях, которые это позволяют, является очень эффективным в отношении затрат способом для инвертирования данных полного волнового поля. (Такой же подход одновременной инверсии кодированной сейсмограммы будет работать для приемников, либо за счет взаимности источник-приемник, либо за счет кодирования фактических местоположений приемников в сейсмограммах общих источников данных.) Для фиксированных приемников, прямые и сопряженные вычисления должны выполняться только для одиночного эффективного источника; см. публикацию патентной заявки PCT номер WO 2009/117174, которая включается сюда по ссылке во всех юрисдикциях, которые это позволяют. Притом, что для обычных геометрий систем регистрации 2D записываются сотни взрывов, и тысячи в случае обследований 3D, этот способ обеспечивает достаточно значительные сокращения вычислений. На практике, предположение фиксированных приемников не является строго действительным для большинства общих эксплуатационных геометрий систем регистрации данных. В случае данных сейсмоприемной косы, как источники, так и приемники перемещаются для каждого нового взрыва. Даже в обследованиях, где местоположения приемников являются фиксированными, практика часто состоит в том, что не все приемники "слушают" каждый взрыв, и приемники, которые слушают, могут изменяться от взрыва к взрыву. Это также нарушает "предположение фиксированных приемников". В дополнение, вследствие логистических проблем, является трудным записывать данные, близкие к источнику, и это означает, что данные близкого удаления обычно отсутствуют. Это верно для обследований как на море, так и на земле. Оба этих фактора означают, что для сейсмограммы одновременных источников, для каждого местоположения приемника будут отсутствующие данные для некоторых взрывов источников. В итоге, в инверсии одновременных кодированных источников, для заданной одновременной кодированной сейсмограммы, требуются данные во всех местоположениях приемников для каждого взрыва, и это может указываться как предположение фиксированных приемников инверсии одновременных кодированных источников. В WO 08/042081, некоторые из раскрытых вариантов осуществления могут работать более хорошо, чем другие, когда предположение фиксированных приемников не удовлетворяется. Поэтому, будет предпочтительным иметь размещение или настройку для непосредственного применения инверсии одновременных кодированных источников (и/или приемников), которая обеспечит увеличение ее производительности, когда предположение фиксированных приемников нарушено. Настоящее изобретение обеспечивает способы делать это. Хабер и др. [15] также описывает подход к проблеме перемещения приемников в инверсии одновременных кодированных источников с использованием способа стохастической оптимизации, и применяет его к проблеме удельного сопротивления постоянному току.

СУЩНОСТЬ ИЗОБРЕТЕНИЯ

В одном варианте осуществления изобретение является компьютерно-реализуемым способом для инверсии полного волнового поля, с использованием кодирования одновременных источников, измеренных геофизических данных из обследования, которое не удовлетворяет предположению фиксированных приемников инверсии одновременных кодированных источников, чтобы определять модель физических свойств для области геологической среды, содержащий следующие этапы, описанные со ссылкой на блок-схему последовательности операций из Фиг.2, при этом все суммирование, моделирование, вычисление и обновление выполняется на компьютере:

(a) получение группы двух или более кодированных сейсмограмм измеренных геофизических данных (40), полученных при условиях, где предположение фиксированных приемников не является действительным, при этом каждая сейсмограмма ассоциирована с одиночным обобщенным источником, или альтернативно с одиночным приемником, и при этом каждая сейсмограмма кодируется (60) с помощью разной кодирующей функции, выбранной из набора неэквивалентных кодирующих функций (30);

(b) суммирование кодированных сейсмограмм в группе посредством суммирования всех, или выбранных, записей данных в каждой сейсмограмме, которые соответствуют одиночному приемнику (60) или альтернативно одиночному источнику, и повторение для каждого другого приемника или альтернативно для каждого другого источника, что дает результатом одновременную кодированную сейсмограмму (80); или альтернативно получение кодированных данных в полевом обследовании (90), где кодирующие функции являются измеренными формами (50) импульсов источников;

(c) предположение модели (10) физических свойств области геологической среды, при этом упомянутая модель обеспечивает значения, по меньшей мере, одного физического свойства в местоположениях всюду по области геологической среды;

(d) моделирование синтетической одновременной кодированной сейсмограммы данных, с использованием предполагаемой модели физических свойств, при этом моделирование использует кодированные формы (70) импульсов источников, и при этом полная одновременная кодированная сейсмограмма моделируется в одиночной операции моделирования;

(e) вычисление целевой функции, измеряющей взаимную корреляцию между одновременной кодированной сейсмограммой измеренных данных и смоделированной одновременной кодированной сейсмограммой (100);

(f) обновление (110) модели физических свойств посредством оптимизации целевой функции (100);

(g) повторение этапов (a)-(f), по меньшей мере, еще один раз с использованием обновленной модели (20) физических свойств из предыдущей итерации в качестве предполагаемой модели физических свойств в этапе (c), что дает результатом дополнительную обновленную модель физических свойств; и

(h) после схождения (120), загрузка, отображение, или сохранение дополнительной обновленной модели физических свойств в компьютерное хранилище (130).

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Вследствие ограничений патентного законодательства, один или более из чертежей должны быть черно-белыми воспроизведениями цветных оригиналов. Цветные оригиналы были поданы в соответствующей заявке США. Копии публикации этого патента или патентной заявки с цветными чертежами могут быть получены от Патентного ведомства США при запросе и оплате необходимой пошлины.

Настоящее изобретение и его преимущества будут более хорошо пониматься с помощью ссылки на последующее подробное описание и прилагаемые чертежи, на которых:

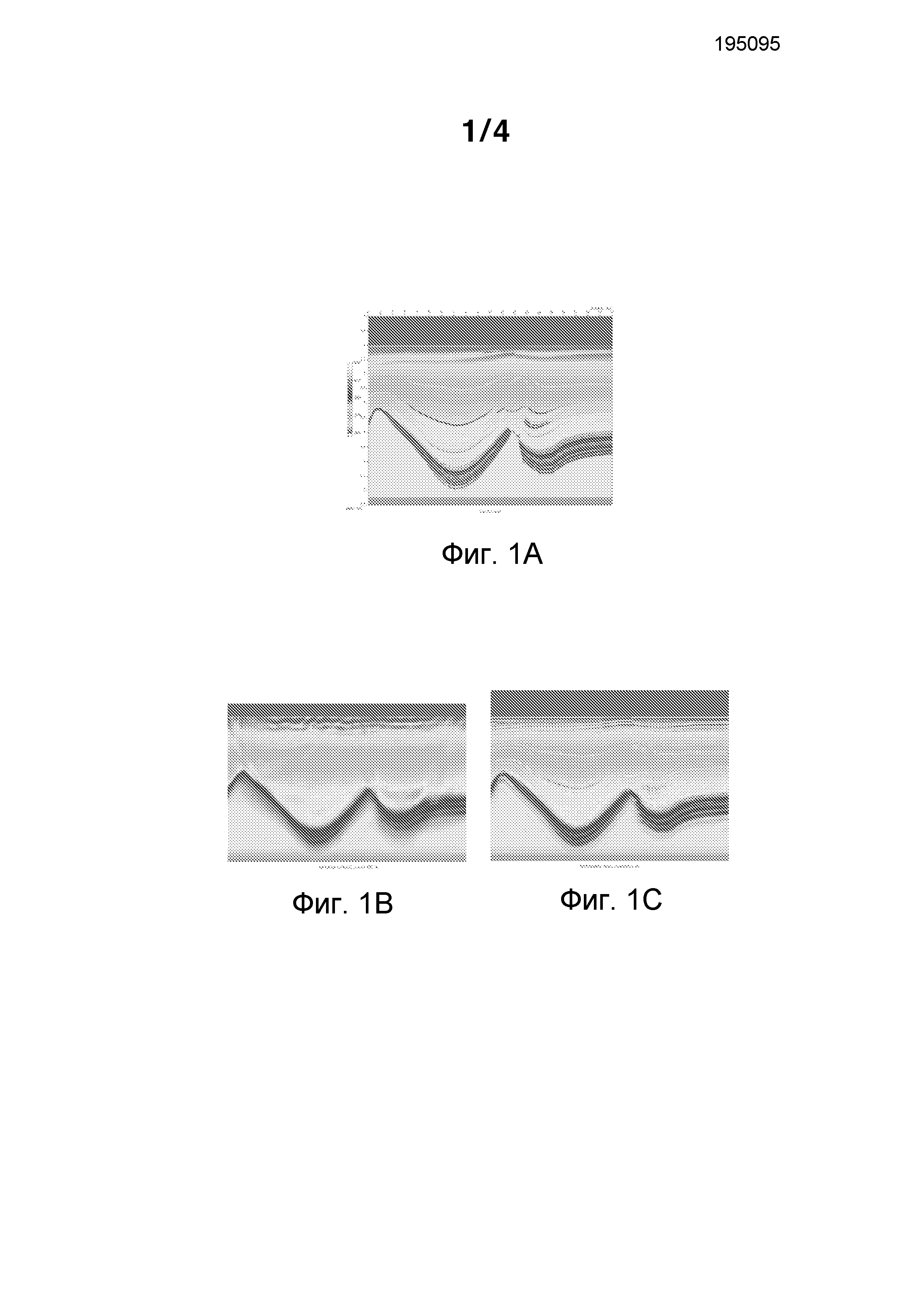
Фиг.1A-1C являются данными тестового примера, при этом Фиг.1A показывает "истинную" скоростную модель для использования, т.е. модель, используемую, чтобы моделировать синтетические данные обследования; Фиг.1B показывает скоростную модель, полученную посредством инверсии моделированных данных обследования с использованием стандартной целевой функции L2; и Фиг.1C показывает скоростную модель, полученную посредством инверсии с использованием взаимнокорреляционной целевой функции представленного нового способа;

Фиг.2 является блок-схемой последовательности операций, показывающей базовые этапы в одном иллюстративном варианте осуществления представленного нового способа;

Фиг.3 является поперечным сечением моделированных сейсмических данных, показывающих сумму четырех взрывов, расстановленных на расстоянии 20 м;

Фиг.4 является поперечным сечением моделированных сейсмических данных, показывающих сумму четырех взрывов, расстановленных на расстоянии 100 м; и

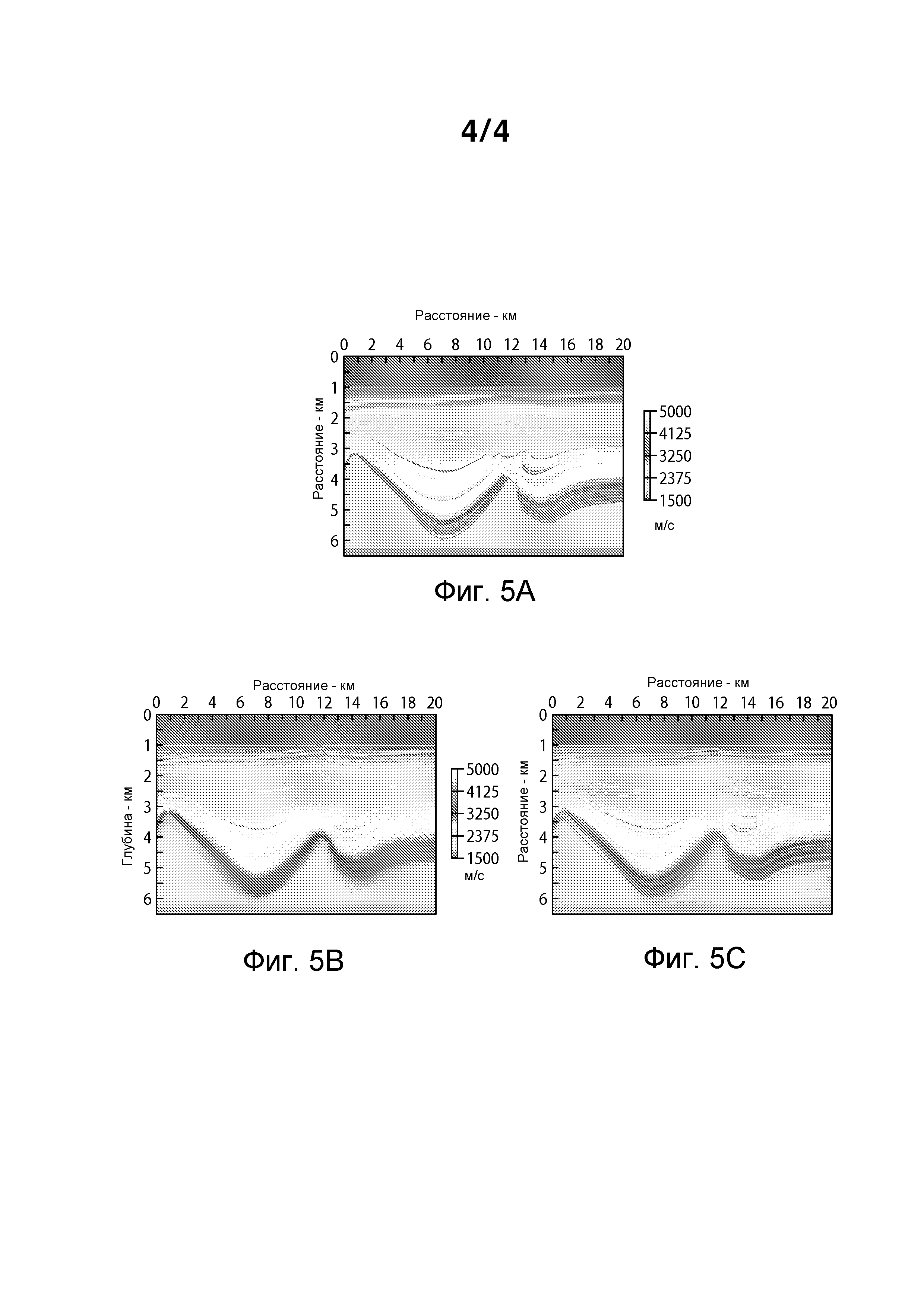
Фиг.5A-5C отображают результаты модельного изучения, показывающего преимущества одного варианта осуществления представленного нового способа, который уменьшает проблему локального минимума, которая оказывает влияние на сходимость в процессе итеративной инверсии с использованием взаимнокорреляционной целевой функции.

Изобретение описывается в связи с иллюстративными вариантами осуществления. Однако в той степени, в которой последующее подробное описание является специальным для конкретного варианта осуществления или конкретного использования изобретения, предполагается, что оно является только иллюстративным, и не должно толковаться как ограничивающее объем изобретения. Напротив, предполагается, что охватываются все альтернативы, модификации и эквиваленты, которые могут содержаться в объеме изобретения, как определено посредством прилагаемой формулы изобретения.

ПОДРОБНОЕ ОПИСАНИЕ ИЛЛЮСТРАТИВНЫХ ВАРИАНТОВ ОСУЩЕСТВЛЕНИЯ

Способ, предложенный в этой патентной заявке, использует взаимнокорреляционную целевую функцию, чтобы инвертировать данные кодированных одновременных источников. Исходные сейсмограммы взрывов, которые кодируются, чтобы формировать данные одновременных источников, имеют отсутствующие ближние и дальние удаления, что является обычным в обследовании сейсмоприемной косы. Интуитивное понимание того, как эта взаимнокорреляционная целевая функция работает для инверсии полного волнового поля ("FWI") для данных нефиксированных приемников, может получаться при рассмотрении проблемы формирования изображений. В FWI, один или много режимов сейсмических волновых полей инвертируются, чтобы получать модель физических свойств Земли. Сначала рассмотрим проблему формирования изображений для миграции обратного времени одновременных источников ("RTM").

Предположим, что имеются два измеренных волновых поля d₁, d₂ в геологической среде, обусловленные двумя источниками, и они кодируются согласно

где P является оператором проекции, который проецирует данные на все приемники, требуемые для геометрии фиксированных приемников. Таким образом, если оператор P является одним и тем же для всех взрывов, то это является геометрией фиксированных приемников. Кодированный источник задается посредством

S=a₁S₁+a₂S₂

Пусть прямая задача обозначается посредством Ld=S, где L является дифференциальным оператором в частных производных, d является моделированным откликом и S является функцией кодированного источника. Если обозначить прямой оператор посредством L^-1, так что смоделированные данные d=L^-1S, и обозначить оператор обратного распространения посредством

Изображение

где P является оператором проекции, который преобразовывает данные, вычисленные во всей области, в набор фиксированных приемников. Для случая фиксированных приемников, P будет одним и тем же для всех источников, так как каждый без исключения приемник слушает все источники.

Для геометрии нефиксированных приемников, предположим, что P_k является оператором проекции на поднабор приемников для k-го источника. Тогда кодированные данные задаются посредством

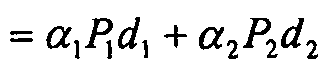
Изображение тогда задается посредством

Изображение

Если используются несколько реализаций кодирования, второй член вследствие перекрестной помехи аннулируется и его вклад в изображение убывает, тем самым, увеличивая отношение сигнала к шуму. Имеется близкая связь между формированием изображений и формированием градиента для FWI. Если рассматривать целевую функцию (часто называемую функция затрат) в FWI, которая является L2, т.е. наименьших квадратов, нормой между измеренными и смоделированными данными, то градиент целевой функции L2 является просто взаимной корреляцией остатка обратно распространенных данных с моделированным волновым полем. Для геометрии фиксированных приемников это является хорошей мерой, так как конкретный приемник слушает все источники. Для нефиксированных приемников это является проблематичным, так как кодированные измеренные данные являются недостаточными по сравнению с кодированными смоделированными данными. Этот недостаток в конечном счете преобразовывается в артефакты модели.

Однако понимание, приобретенное из ситуации формирования изображений, где приемники являются нефиксированными, может восприниматься как намек, что использование взаимнокорреляционной целевой функции для FWI может помочь ослабить эту проблему. Таким образом, вместо L2, рассмотрим взаимнокорреляционную целевую функцию, заданную посредством:

где

Трассы, которые вносят вклад в

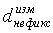
Также, если для некоторых итераций используется разное кодирование, предпочтительно на каждой итерации, как указано Кребсом и др. в публикации патентной заявки PCT номер WO 2008/042081, второй член в конечном счете будет убывать. В дополнение к изменению кодирования каждую итерацию, дополнительный вариант выбора состоит в том, чтобы использовать набор кодирований на каждой итерации с целью получать средний градиент целевой функции, т.е. градиенты, полученные из каждого из кодирований, когда суммируются, дают средний градиент. Поэтому на каждой итерации эта обработка усреднения уменьшает перекрестную помеху - идея, которая является очень похожей на формирование изображений RTM одновременных источников, где изображения, полученные с разными кодированиями, суммируются, чтобы аннулировать шум перекрестных помех. Усреднение градиента также рекомендуется в способах стохастической оптимизации (Хабер и др. [15]).

Общая цель в предпочтительных вариантах осуществления представленного нового способа состоит в том, чтобы максимизировать, не минимизировать, взаимнокорреляционную целевую функцию. Однако можно переформулировать целевую функцию, например, заменить ее на ее отрицательную, таким образом, что можно фактически решать проблему минимизации. Общее выражение этого этапа в представленном новом способе состоит, поэтому, в том, чтобы оптимизировать целевую функцию. В зависимости от выбора алгоритма оптимизации, т.е. осуществляется ли поиск решения согласно алгоритму максимизации или минимизации, целевая функция может выбираться так, что она сохраняет главные характеристики взаимнокорреляционного свойства, которые являются нечувствительными к любому произвольному масштабу данных. Преимущество взаимнокорреляционной целевой функции состоит в том, что она делает FWI нечувствительной к масштабу вейвлета. Фактически составляющие времени прохода волновой формы соответствуют этой целевой функции. Это может быть легко видно, если целевая функция записана в частотной области, где фаза является функцией времени прохода.

Синтетический пример

Осуществимость представленного нового способа была продемонстрирована с синтетическим примером с использованием скоростной модели, показанной на Фиг.1A. В примере, 383 взрыва генерировались с расстановкой взрывов 80 м и приемники были расположены каждые 20 м. Чтобы моделировать геометрию нефиксированных приемников, для каждого взрыва удалили ближние и дальние удаления и использовали удаления от положительных 200 м до 3 км. Как предполагалось, отсутствующие данные приемников на ближних и дальних удалениях нарушают предположение фиксированных приемников. Эти взрывы кодировались, чтобы формировать измеренные кодированные данные. На каждой итерации в нелинейной инверсии, использовались все последовательные взрывы в обследовании и кодировали их 8 раз с использованием разных кодирующих функций, чтобы формировать 8 одновременных источников, чтобы вычислять средний градиент. В зависимости от того, сколько перекрестных помех присутствует в среднем градиенте, можно увеличивать количество кодирований. Это осуществлено как для целевой функции L2, так и для взаимнокорреляционной целевой функции.

Чтобы выполнять инверсию, использовался способ переменной разрешающей способности с временной оконной обработкой. В способе переменной разрешающей способности, данные подвергались оконной обработке посредством частотных диапазонов, чтобы стабилизировать проблему инверсии. Обычно сначала инвертируются данные на нижнем частотном диапазоне и модель, полученная из низкочастотной инверсии, используется в качестве начальной модели для следующего более высокого частотного диапазона. Этот способ используется, чтобы избегать схождения к неверному решению, часто указываемому как решения локальных минимумов. Фиг.1B показывает модель, полученную с использованием целевой функции L2. Ясно, артефакты могут быть видны как в поверхностной, так и в глубокой части модели. Модель на Фиг.1C является результатом использования взаимнокорреляционной целевой функции. Модель ясно показывает значительное улучшение по сравнению с моделью из Фиг.1B, подкрепляющее наблюдение, что взаимнокорреляционная мера является намного более подходящей, чтобы обрабатывать данные одновременных источников геометрии нефиксированных приемников.

Инверсия с взаимнокорреляционной целевой функцией может наталкиваться на локальные минимумы, когда записи источников, которые добавлены, расстановлены слишком близко. Расстановка записей взрывов дополнительно дальше решает эту проблему, но уменьшает количество информации, переходящей в инверсию, тем самым, ухудшая качество конечной инвертированной модели. Способ, чтобы решать этот конфликт состоит в том, чтобы разбивать все доступные записи взрывов на несколько групп, где записи взрывов, принадлежащие одной и той же группе, расстановлены дополнительно дальше. Разная группа взрывов может тогда выбираться в каждой итерации нелинейной инверсии, до тех пор, когда все группы будут использованы. Обработка может повторяться до схождения. Один способ, посредством которого это может делаться, состоит в применении кодирующих функций, которые умножают формы импульсов источников и измеренные сейсмограммы данных. Все кодирующие функции для записей данных не в выбранной группе для конкретной итерации могут устанавливаться равными нулю. Фактически, кодирующие функции могут использоваться, чтобы случайным образом выбирать взрывы в каждой группе, что будет давать результатом увеличенную расстановку взрывов, следуя идее, представленной авторами Boonyasiriwat and Schuster, 2010, где они применяют ее к разнесению фиксированных приемников и для другой цели. Это может делаться с использованием случайной кодирующей последовательности [-1,0,+1]. Этот способ для увеличения расстановки взрывов может использоваться в представленном новом способе для уменьшения шума перекрестных помех для нестационарных приемников. Могут разрабатываться другие способы для достижения большего разделения взрывов в меньших группах записей взрывов.

Последующее является примером применения стратегии, описанной выше.

Осуществимость этого подхода демонстрируется с помощью синтетического примера. Имеются 383 взрыва, сгенерированные с расстановкой взрывов 20 м, и приемники помещаются каждые 10 м. Чтобы моделировать геометрию нефиксированных приемников, для каждого взрыва используются удаления от положительных 200 м до 3 км. Эти взрывы кодируются, чтобы формировать измеренные кодированные данные. На каждой итерации в нелинейной инверсии, используются 8 одновременных источников, чтобы вычислять средний градиент. Фиг.3 показывает сумму 4 взрывов, которые близко расстановлены (здесь 20 м), тогда как Фиг.4 показывает сумму 4 взрывов, которые находятся более далеко (здесь 100 м). Базовая идея состоит в том, что увеличение разделения взрывов уменьшает компоненту перекрестных помех в целевой функции; однако слишком большое разделение ведет к разрывам в данных, которые уменьшают возможность обновлять модель. Как указано выше, эта ситуация может смягчаться посредством выбора нескольких групп, чтобы формировать кодированные взрывы. Каждая группа имеет хорошо разделенные взрывы, но использование нескольких из этих групп заполняет пространственные разрывы, которые бы в противном случае оставались, если выбирается только одна группа. Для примера, представленного здесь, на каждой итерации выбираются 4 группы и для каждой группы используются 2 реализации, при этом реализация является моделированием одновременных источников с различным набором кодирующих функций. Таким образом, в целом, имеется 8 кодированных одновременных взрывов в расчете на итерацию. Для сравнения, инверсия была выполнена с кодированными взрывами, которые были близко расстановлены, с 8 реализациями в расчете на итерацию. Фиг.5A является истинной моделью, используемой в этом примере. Фиг.5B показывает результаты из инверсии одновременных источников, когда источники являются близко расстановленными. Вследствие присутствия перекрестных помех в модели, инверсия не смогла найти подходящее обновление после 50 итераций. Графическое изображение модели на 50^ой итерации приведено на Фиг.5B. Для сравнения, графическое изображение модели от 50^ой итерации, когда взрывы являются хорошо разделенными, представлено на Фиг.5C. Не было никакой проблемы схождения в процессе инверсии. Имеется намного более хорошее согласие между Фиг.5C и 5A, чем между Фиг.5B и 5A.

Вышеизложенная заявка направлена на конкретные варианты осуществления настоящего изобретения с целью ее иллюстрации. Однако специалисту в данной области техники, должно быть ясно, что являются возможными многие модификации и изменения с вариантами осуществления, здесь описанными. Предполагаются, что все такие модификации и изменения находятся в объеме настоящего изобретения, как определяется в прилагаемой формуле изобретения. Специалисты в данной области техники должны легко распознать, что в предпочтительных вариантах осуществления изобретения, по меньшей мере, некоторые из этапов в представленном новом способе выполняются на компьютере, т.е. изобретение является компьютерно-реализуемым. В таких случаях, результирующая обновленная модель физических свойств может либо загружаться, отображаться, либо сохраняться в компьютерном хранилище.

ССЫЛКИ

1. Tarantola, A., "Inversion of seismic reflection data in the acoustic approximation," Geophysics 49, 1259-1266 (1984).

2. Sirgue, L., and Pratt G. "Efficient waveform inversion and imaging: A strategy for selecting temporal frequencies," Geophysics 69, 231-248 (2004).

3. Fallat, M. R., Dosso, S. E., "Geoacoustic inversion via local, global, and hybrid algorithms," Journal of the Acoustical Society of America 105, 3219-3230 (1999).

4. Hinkley, D. and Krebs, J., "Gradient computation for simultaneous source inversion", публикация патентной заявки PCT номер WO 2009/117174.

5. Krebs, J. R., Anderson, J. A., Neelamani, R., Hinkley, D., Jing, C., Dickens, T., Krohn, C., Traynin, P., "Iterative inversion of data from simultaneous geophysical sources," PCT Patent Application Publication No. WO 2008/042081.

6. Van Manen, D. J., Robertsson, J.O.A., Curtis, A., "Making wave by time reversal," SEG International Exposition and 75th Annual Meeting Expanded Abstracts, 1763-1766 (2005).

7. Berkhout, A. J., "Areal shot record technology," Journal of Seismic Exploration 1, 251-264(1992).

8. Zhang, Y., Sun, J., Notfors, C., Gray, S. H., Cherris, L., Young, J., "Delayed-shot 3D depth migration," Geophysics 70, E21-E28 (2005).

9. Van Riel, P., and Hendrik, W. J. D., "Method of estimating elastic and compositional parameters from seismic and echo-acoustic data", Патент США номер 6,876,928 (2005).

10. Mora, P., "Nonlinear two-dimensional elastic inversion of multi-offset seismic data," Geophysics 52, 1211-1228(1987).

11. Ober, C. C., Romero, L. A., Ghiglia, D. C., "Method of Migrating Seismic Records", Патент США номер 6,021,094 (2000).

12. Ikelle, L. T., "Multi-shooting approach to seismic modeling and acquisition", Патент США номер 6,327,537(2001).

13. Romero, L. A., Ghiglia, D. C., Ober, C. C., Morton, S. A., "Phase encoding of shot records in prestack migration," Geophysics 65,426-436 (2000).

14. Jing X., Finn, C. J., Dickens, T. A., Willen, D. E., "Encoding multiple shot gathers in prestack migration," SEG International Exposition and 70th Annual Meeting Expanded Abstracts, 786-789 (2000).

15. Haber, E., Chung M. and Herrmann, "An effective method for parameter estimation with PDE constraints with multiple right hand sides," Preprint - UBC http://www.math.ubc.ca/~haber/pubs/PdeOptStochV5.pdf (2010).

16. Jerome R. Krebs, John E. Anderson, David Hinkley, Ramesh Neelamani, Sunwoong Lee, Anatoly Baumstein, and Martin-Daniel Lacasse, "Full-wavefield seismic inversion using encoded sources," Geophysics 74-6, WCC177-WCC188 (2009).

17. Boonyasiriwat, C., and Schuster, G., "3D Multisource full-waveform inversion using dynamic random phase encoding," SEG Expanded Abstracts 29, 1044-1049 (2010).

Реферат

Изобретение относится к области геофизики и может быть использовано при обработке сейсмических данных. Предложен способ для одновременной инверсии полного волнового поля сейсмограмм кодированных (30) геофизических данных (80) источников (или приемников), чтобы определять модель (20) физических свойств для области геологической среды, особенно подходящий для обследований, где условия геометрии фиксированных приемников не были удовлетворены при регистрации данных (40). Инверсия включает в себя оптимизацию взаимнокорреляционной целевой функции (100). Технический результат - повышение точности получаемых данных. 4 н. и 23 з.п. ф-лы, 9 ил.

Формула

2. Способ по п. 1, в котором целевая функция φ задается посредством или является математически эквивалентной следующему:

где

являются одновременной кодированной сейсмограммой
измеренных данных, и

являются смоделированной одновременной кодированной сейсмограммой, включающей в себя трассы смоделированных данных для всех местоположений приемников, активных или неактивных в течение конкретного взрыва, и ||…|| обозначает выбранную норму.

3. Способ по п. 2, дополнительно содержащий аппроксимацию целевой функции посредством:

где

являются смоделированной одновременной кодированной сейсмограммой, такой что трассы, соответствующие приемникам, которые являются неактивными в течение конкретного взрыва, заменяются нулями до кодирования.