Способ индивидуального определения в организме функции эластичности и непрерывного определения системного кровотока живого существа - RU2179408C2
Код документа: RU2179408C2
Чертежи





Описание
Изобретение касается способа индивидуального определения в организме функции эластичности С(р)=dV/dp сосудистой системы после желудочка сердца живого существа по кровяному давлению р(t) и эталонному минутному объему сердца СОref.
Кроме того, изобретение касается способа непрерывного определения системного кровотока q(t), в котором непрерывно измеряется кровяное давление р(t) в аорте или около нее.
Известны способы и устройства вышеупомянутого типа. В прошлом было разработано множество способов вычисления минутного объема сердца (СО) по артериальному кровяному давлению. С одной стороны, предложены способы, при которых СО определяют по нескольким характерным показателям, как например среднему артериальному давлению (МАР), систолическому и диастолическому давлению (АРsys АPdia), времени выброса (ЕТ) и данным о пациенте (возраст, пол, вес, рост) [4, 6, 7], а с другой стороны, применяют алгоритмы, при которых для вычисления минутного сердечного выброса используют полный контур кривой пульсового кровяного давления [1, 5, 20]. В последних методах, которые называют также анализом контура пульсаций, до сих пор применяли два разных подхода. Во-первых, СО определяют непосредственно по артериальному кровяному давлению с помощью некоторых поправочных коэффициентов [19, 20], в то время как в другой работе [5, 25] кровоток вычисляют по давлению при определенных допущениях, полагая, что он соответствует действительному кровотоку в аорте и, следовательно, может быть использован для определения минутного объема сердца.
В классической модели Уиндкесселя, которая впервые была предложена Хэйлзом [26] и использована Франком [27] для определения ударного объема крови (SV), для моделирования исследуемой сердечно-сосудистой системы наряду с частотой сердечных сокращений и минутным объемом сердца используют только периферическое сопротивление сосудов R и эластичность С. В этой модели артериальный кровоток, определяемый как q(t), может быть вычислен для данных С и R с помощью показателя кровяного давления р(t), который подлежит измерению. Однако, как показывает более тщательная проверка, эта простая модель лишь неполностью воспроизводит физиологическое состояние, в результате чего было предложено много модификаций первоначальной модели; для общего ознакомления можно сослаться на [24, 28].
Точность этих методов зависит, главным образом, от того, насколько хорошо допущения, т.е. используемая модель, отражают состояние исследуемой сердечно-сосудистой системы, и в [5], таким образом, применяется нелинейная модель Уиндкесселя, чьи параметры диктуются возрастом и полом пациента. Однако, как показывают поздние исследования [21], модель, применяемая в [5], не воспроизводит точные основные физиологические параметры; в частности, эластичность (растяжимость) сосудов не всегда может быть охарактеризована зависимостью эластичность/давление, приведенной в [5]. Возможно, существует несколько причин этого противоречия. Во-первых, в [5] учитывается только зависимость определенного в организме поперечного сечения аорты от кровяного давления, и, как описывается в [22, 23], не принимается во внимание изменение длины; кроме того, учитывается только плотность крови, а не сильно зависящая от гематокрита вязкость и, вероятно, игнорируется эластичность периферической системы. Во-вторых, в способе, описанном в [5], помимо возраста и пола невозможно использовать функцию эластичности С(р) конкретного индивидуума. Однако, как точно установлено при исследовании патофизиологических случаев заболевания, например артериосклероза, невозможно предположить, что С(р) изменяется в соответствии с возрастом и полом, так что основная модель лишь неполностью характеризует физиологические параметры [25]. И, наконец, как было показано в [24], следует предположить, что модифицированная модель Уиндкесселя может точнее воспроизводить основные физиологические параметры.
Однако общей особенностью всех вышеописанных моделей является то, что параметры модели, будучи однажды определенными, больше не зависят от состояния исследуемой сердечно-сосудистой системы. Тем не менее, почти все параметры могут изменяться со временем, и, например, системное сопротивление R может изменяться в результате лекарственной терапии. Другие параметры, включая расширяемость и длину аорты, настолько сильно изменяются с давлением, что они в действительности должны рассматриваться как переменные величины в пределах даже одного сердечного сокращения.
Тот факт, что аортальный импеданс и эластичность нельзя считать постоянными
величинами, продемонстрировано как при экспериментах на животных [22], так и в отношении людей [29]. Главными причинами этого являются расширяемость, изменение длины и изменение объема аорты и сосудов
вблизи аорты. Типичное изменение аортального объема V как функции давления, между прочим, описано в [30]. Вследствие того что эластичность системы определяется как
C(p)=dv/dp, (4)
из-за ограниченного объема эластичность стремится к нулю для очень высоких давлений и не может быть постоянной величиной. Так как изменение объема вызывается изменениями в длине и поперечном сечении
сосудов, то существует также изменение в аортальном импедансе, который согласно уравнению Навье-Стокса определяется, с одной стороны, поперечным сечением и плотностью жидкости, а с другой стороны,
длиной, вязкостью и плотностью крови.
Зависимые от давления аортальный импеданс и эластичность обсуждаются в [5, 21] и используются в них для исследования нелинейных моделей Уиндкесселя. В [5], в частности, предполагается, что С(р) может быть установлена по возрасту и полу пациента. При этом подходе также игнорируется импеданс Z(p). Более того, как следует из результатов, полученных в [21], модель, используемая в [5], может в какой-то степени противоречить истинному физиологическому состоянию. Одной причиной этого является то, что эластичность и аортальный импеданс являются заранее заданными. Подход этого типа не годится для учета характерных особенностей пациента. Кроме того, метод, предложенный в [5] , невозможно без модификаций применять к другим видам. Более того, в [5] принимается во внимание только типичный аортальный диаметр, заранее исследованный в организме, и плотность крови. При моделировании условий, существующих в организме, игнорируются влияние изменений аортальной длины, динамическое поведение сосудов вблизи аорты и периферических сосудов и вязкость крови.
Следовательно, еще не существует никакого способа, при котором для индивидуального определения в организме зависимости эластичность/давление применяются измеренные переменные величины, используемые здесь.
Этот недостаток устраняется с помощью устройства согласно настоящему изобретению и посредством определения всех представляющих интерес параметров модели по измерениям на исследуемой физиологической системе, т.е. человеке или животном. С этой целью, в частности, подлежит непрерывному измерению кровяное давление р(t) в аорте и вблизи нее и требуется по крайней мере одноразовое измерение эталонного минутного объема сердца (СОref). С помощью этих величин могут быть установлены все параметры с последующим их использованием для гемодинамического исследования.
Задачей изобретения является создание устройства для индивидуального определения в организме функции эластичности живого существа, которое как можно более верно воспроизводит физиологические условия.
Другой задачей изобретения является создание устройства для непрерывного определения системного кровотока пациента, которое имеет низкую степень инвазивности и как можно более точно описывает действительный кровоток в любой данный момент времени.
Путь, которым решаются эти задачи, описан в независимых пунктах формулы изобретения. В зависимых пунктах формулы изобретения можно найти полезные усовершенствования.
Согласно изобретению используется т.н. модель Уиндкесселя, чьи параметры могут быть идентифицированы с помощью эталонного измерения в организме. Затем посредством этого определяют системный кровоток и другие гемодинамические параметры. Модель Уиндкесселя, принятая и модифицированная таким образом, более точно описывает сердечно-сосудистую систему исследуемого индивидуума и, следовательно, может быть использована для еще более точного вычисления системного кровотока и гемодинамических параметров, производных от него. Этот способ может быть также применен непосредственно к другим видам без необходимости в том, чтобы для этого заранее определять гипотетические характеристики. Дополнительные издержки нового разработанного способа заключаются в том, что для вычисления индивидуальной функции эластичности помимо непрерывного измерения кровяного давления требуется по меньшей мере один раз определять минутный объем сердца, используя другой способ, например артериальное терморазведение.
Ниже изобретение будет подробнее объяснено со ссылкой на иллюстративный вариант его осуществления, схематически представленный на чертежах, на которых:
фиг. 1
показывает предпочтительную электрическую схему модели исследуемой сердечно-сосудистой системы;
фиг. 2 показывает блок-схему вычисления аортального импеданса Z(р), функции эластичности С(р) и
кровотока q(t);
фиг. 3: а) показывает график, иллюстрирующий зависимость кровяного давления р(t) от времени, где t0 обозначает время, в которое открывается аортальный клапан, tS - время, в которое закрывается аортальный клапан, и tD - время окончания диастолы; b) показывает график, объясняющий зависимость кровяного давления р(t) и получающегося кровотока
q(t) от времени;
фиг. 4 показывает типичную функцию эластичности С(р) аорты человека;
фиг. 5 показывает блок-схему устройства согласно изобретению.
На фиг. 1 показана нелинейная модифицированная модель Уиндкесселя, которая предпочтительно используется согласно изобретению и в которой учитываются функции аортального импеданса Z(р) и Z0(р), функция эластичности С(р) и системное сопротивление R.
Сопротивление R на фиг. 1 соответствует сопротивлению переменного во времени периферического кровотока в организме. Z0(р) и Z(р) нелинейные имледансы, которые зависят от давления р(t) и наряду с нелинейной зависящей от давления емкостью С(р) предназначены для моделирования поведения аорты и кровеносных сосудов вблизи аорты.
Результат, полученный для изображенной на фиг. 1 модели посредством преобразования Фурье

и функции


так что для R>>Z следует, что

Кроме того, для эластичности С удовлетворяет следующее уравнение
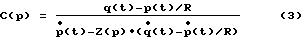
в котором

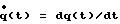
На фиг. 2 в общих чертах показан усовершенствованный метод.
i) Вначале по давлению р(t) определяют среднее артериальное кровяное давление МАР и частоту сердечных сокращений НR.
ii) Наряду с эталонным минутным объемом сердца СОref, который предпочтительно определяют артериальным термодилюционным методом и для которого
удовлетворяется следующее уравнение
COref = HR•∫q(t)dt (5)
вычисляют системное сопротивление по R=(МАР-СVР)/СОref. В этом выражении СVР - центральное венозное
давление, которое, если оно неизвестно, может приближенно равняться подходящему постоянному давлению, например 0 мм рт.ст.
iii) Следующая стадия - это установление кровотока q(t),
который следует выбирать соответствующим образом и который используется в качестве начальной функции при последующей итерации и удовлетворяет основным физиологическим условиям. Кровоток q(t)
характеризует кровоток, который проходит прямо из левых отделов сердца в аорту. Следовательно, требуется q(t) чтобы подусловия
q(to)=q(ts)=0 и
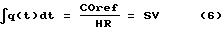
удовлетворяли всем сердечным сокращениям, зарегистрированным во время измерения эталонного минутного объема сердца СОref. В этом выражении время t0 - начало систолы, и tS - конец систолы. Ниже конец диастолы обозначен как tD. Соответствующие кровотоки q(t) были бы q(t)=0 для ts < t ≤ tD и для t0 < t ≤ tS, например,

или предпочтительно

В последнем случае k должно быть определено из условия ∫q(t)dt = COref/HR. Однако, кроме кровотоков, показанных в уравнениях (7) и (8), возможны другие начальные условия, например постоянный или параболический кровоток.
iv) Устанавливают Z(р)= 0 и вводят дополнительные переменные qold(t) и Eold, которые инициализируют при qold(t)=q(t) и Eold=∞.
v) По кровяному давлению р(t),
измеренному в аорте или вблизи нее, кровотоку q(t) и его производным по времени вычисляют функцию эластичности согласно

vi) Затем аппроксимируют обратную величину функции эластичности посредством многочлена соответствующего порядка в p, т.е. в

где коэффициенты разложения определяют таким образом, чтобы тождество

было оптимально удовлетворяемым. В качестве подходящего критерия для этого среднеквадратичная ошибка

может быть минимизирована, так что можно использовать р(t) и q(t) всегда или, с другой стороны, только в предпочтительных интервалах времени. В этом случае и ниже обозначение <•> указывает на вычисление среднего значения.
vii) Если Е < Еold, то тогда устанавливают qold(t) = q(t) и Еold = Е и продолжают со стадией (viii), а в противном случае переходят к пункту (x).
viii) Вычисляют Z(р). С одной стороны, принятой для этого методикой может быть определение Z(р) согласно уравнениям (1) и (2). В этом случае принимается, что эти уравнения, которые первоначально были справедливы только для модели на фиг.1b, в которой параметры не зависят от времени, для достаточно коротких интервалов времени Δt применимы также к нелинейному методу, предложенному согласно фиг.1. Для последнего затем может быть установлена функция импеданса согласно уравнению (2) посредством


даже непосредственно по зависящим от времени кровяному давлению р(t) и кровотоку q(t) без предшествующего преобразования Фурье.
С другой стороны, Z(р) можно еще проще вычислить по

как можно видеть из следующего обсуждения. Аортические диаметр d и длина l увеличиваются с повышением давления, так что в первом приближении можно принять d l. Согласно закону Хагена-Пуазейля это приводит к Z(p) α η/V, где η обозначает вязкость крови и V - аортический объем. При С(р)=dV/dp это дает C(p) α d(1/Z)/dp, из которого непосредственно следует уравнение (13). Коэффициент пропорциональности А, который содержится в нем, может быть, например, определен путем установления функции Z(р) для по меньшей мере одного давления р согласно уравнению (12).
ix) Если ошибка Е достаточно мала, то здесь оканчивают идентификацию параметров модели. В противном случае, ее продолжают с (x).
x) Предполагаемый кровоток, наконец, должен
изменяться таким образом, чтобы ударный объем крови еще более соответствовал ударному объему крови SV = СОref/НR, который следует из эталонного минутного объема сердца. Так как на этот раз qold(t) всегда характеризует оптимальный до сих пор кровоток, то устанавливается q(t) = qold(t)+δq(t) при ∫δq(t)dt = 0.
xi) Продолжение со стадии (v).
Алгоритм, показанный в (i)-(xi), характеризует предпочтительный способ, при котором эталонный минутный объем сердца СОref и непрерывно измеряемую артериальную пульсовую кривую p(t) используют для определения всех других параметров. Это гарантирует, что функция эластичности и функция аортального импеданса определяются так, как это требуют взаимодействия, действительно происходящие в исследуемой сердечно-сосудистой системе. В частности, С(р), тем самым, учитывает не только изменение в аортальном поперечном сечении, но и действительное изменение в объеме аорты и периферических сосудов; подобным же образом изменение в длине аорты и плотность и вязкость крови характеризуются посредством Z(р). С помощью приема, который представлен на стадии (vi), и может воспроизводить любую физиологически возможную зависимость эластичность/давление, становится также возможной экстраполяция С(р) и Z(р), так что эти функции могут быть применены даже за пределами давлений, наблюдавшихся во время тарирования, т.е. во время измерения эталонного минутного объема сердца.
Указанный алгоритм характеризует предпочтительный метод. Из него могут быть легко выведены другие способы, которые охватываются прилагаемой формулой изобретения. В частности, в (vi) вместо обратного значения функции эластичности эта функция С(р) может быть также описана конечным рядом Тэйлора, т. е. многочленом. Кроме того, возможна взаимная замена стадий (viii) и (ix) друг с другом или изменение на стадии (vi) критерия оптимизации. Например, вместо минимизации среднеквадратичной ошибки возможна также максимизации математического ожидания.
Для того чтобы ускорить способ, можно, в частности, сделать выбор начального кровотока q(t) на стадии (iii) таким образом, чтобы первоначально определять С(р) только по диастолам, т.е. для tS < t ≤ tD. Согласно уравнению (9) тогда удовлетворяется

q(t) = Σkqksin(k•π•(t-to )/(ts-to)) (14)
В этом случае коэффициенты qk определяют посредством минимизации выражения

Вышеуказанную ошибку вычисляют при всех р(t) < р(tS), включая и те, которые имеют место в начале систолы. Если при этом выборе кровотока сердечно-сосудистая система будет находиться в достаточно хорошем состоянии, то для вычисления параметров модели с использованием описанного алгоритма будет как раз достаточна одна или несколько итераций.
Способ может быть еще более ускорен в случае, в котором на стадии (vi) используют только значения давления из интервалов диастолы и аппроксимируют 1/С(р)
посредством многочлена второй степени. Во время первой итерации для этого применения получают следующий результат

После определения параметров модели на фиг.1 по кровяному давлению р(t) в аорте или вблизи нее и по эталонному минутному объему сердца СОref можно затем непосредственно по кровяному давлению непрерывно по сокращениям вычислять минутный объем сердца. Для этой цели требуется вычислять начало сердечного сокращения, которое ниже вновь обозначается как t0, и необходимо решать уравнение (11) для начального состояния

SV = γ∫q(t)dt (17)
так что для непрерывно определяемого минутного объема сердца СО получают следующее
CO = HR•SV = HR•γ•∫q(t)dt (18)
В вышеприведенном выражении HR обозначает частоту сердечных сокращений, которая также вычисляется по пульсовой кривой р(t) и показывает количество сокращений в минуту. В этом случае интегрирование в уравнениях (16) и (17) может быть выполнено по всему сердечному сокращению или, с другой стороны, только по протяженности систолы, так как во время диастолы удовлетворяется q(t)=0. Если ударный объем крови SV и, следовательно, СО вычисляют в течение всего сердечного сокращения, то тогда не обязательно определять конец систолы. Для выполнения этого (см., например, [31]) или был бы необходим точный анализ кривой давления для того, чтобы определить положение т.н. дихротического углубления и, следовательно, конец систолы по р(t), или потребовались бы дополнительные измерительные приборы, как например электрокардиограф. Следовательно, интегрирование по всему периоду является более надежным и менее сложным способом, чем те способы, которые оценивают только определенный период сердечного сокращения. Кроме того, если непрерывно определяемый минутный объем сердца СО также вычисляют по тем измерениям кровяного давления, которые наряду с эталонным минутным объемом сердца СОref использовали для идентификации модели с применением вышеописанного метода, то тогда можно еще более увеличить точность метода непрерывного вычисления СО тем, что должно удовлетворяться СO=СОref, и, следовательно, тарировочный коэффициент γ определяется согласно

Для того чтобы использовать описанный способ, необходимо иметь устройство, основная конструкция которого представлена на фиг. 5. На этой фигуре составные части, обведенные пунктирной линией, являются необязательными, и по меньшей мере некоторые из них могут отсутствовать в минимальной компоновке устройства. Устройство этого типа состоит по меньшей мере из узла оценки, обычно центрального процессора, в котором реализован способ определения индивидуальной функции эластичности С(р) сам по себе или вместе с другими способами; в частности, в том же самом устройстве может быть реализован способ непрерывного вычисления минутного объема сердца. Кроме того, необходимо иметь датчик для измерения кровяного давления р(t) в аорте или вблизи нее, устройство для обработки и преобразования сигнала, запоминающее устройство программ, запоминающее устройство данных, а также устройство для определения эталонного минутного объема сердца СОref. Если СОref определяется артериальным термодилюционным методом, то тогда это устройство состоит по меньшей мере из датчика температуры крови и датчика для измерения температуры инъекционной дозы, применяемой при этом методе (см. [8]). Однако так как СОref может быть также получен другими способами, то этот модуль может также иметь другой вид или ввод может осуществляться через вспомогательную клавиатуру, которая в устройстве может, кроме того, применяться пользователем для ввода команд. Кроме того, будет иметься по меньшей мере один из вариантов получения результатов оценки в виде изображения, распечатки или хранения в объемном запоминающем устройстве (не показано).
Реферат
Изобретение направлено на индивидуальное определение в организме функции эластичности С(р)-dV/dp сосудистой системы после желудочка сердца и/или системного кровотока живого существа по кровяному давлению р(t) и эталонному минутному объему сердца COref. Согласно изобретению непрерывно определяют давление р(t) аорты или вблизи аорты, вычисляются среднее кровяное давление МАР по кровяному давлению р(t), вычисляются системное сопротивление R организма как R = (MAP-CVP)/COref, где СVР - произвольное центральное венозное давление, которое установлено или определено, и COref - эталонное значение минутного объема сердца, берется по меньшей мере первый дифференциал кровяного давления по времени р(t)=dp/dt, а затем вычисляют функцию эластичности С(р) по меньшей мере по р(t),
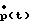

Формула

где СVР - произвольное центральное венозное давление, которое установлено или рассчитано, и СОref - эталонное значение минутного объема сердца, берут, по меньшей мере, первый дифференциал кровяного давления по времени р(t)= dp/dt, и вычисляют функцию эластичности С(р) и кровоток р(t),

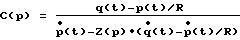
для произвольных функций аортального импеданса Z(р) и произвольных моментов времени t таким образом, что

является оптимально удовлетворяемым.
p(t)≤p(ts),
где ts - время, когда закрывается аортальный клапан.
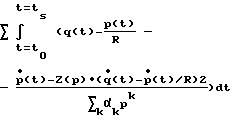
и затем вычисляют индивидуальную функцию эластичности С(р) как

8. Способ по одному из пп. 4 или 6, отличающийся тем, что определяют обратную величину функции эластичности С(р) посредством многочлена второго порядка и аппроксимируют С(р) посредством следующей функции:
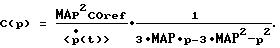
9. Способ по одному из предшествующих пунктов, отличающийся тем, что аппроксимируют функцию эластичности С(р) посредством многочлена конечного порядка и используют этот многочлен для экстраполяции С(р) за пределы интервала давления, зарегистрированного при определении эталонного минутного объема сердца.

и затем вычисляют индивидуальную функцию эластичности С(р) как
C(p)-∑kβkpk.
11. Способ по п. 2 или 4, отличающийся тем, что используют функцию эластичности С(р), вычисленную при р(t)≤р(ts), для увеличения объема кровотока q(t) в виде полной функциональной системы и, в частности, описывают q(t) в виде ряда Фурье посредством следующего уравнения

где коэффициент qk определен посредством минимизации среднеквадратичной ошибки, а величины tо и ts обозначают моменты времени, когда открывается и закрывается аортальный клапан.

где А - коэффициент пропорциональности.
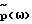
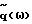

или при R>>Z

15. Способ по п. 1, отличающийся тем, что определяют кровоток q(t) на основании давления р(t) и первой производной по времени dp/dt и вычисляют функцию импеданса

согласно

16. Способ по одному из пп. 2, 6, 7, 9, 13, 14, 15, отличающийся тем, что аппроксимируют функцию аортального импеданса Z(р) посредством многочлена конечного порядка и используют этот многочлен для экстраполяции Z(р) за пределы интервала давления, зарегистрированного во время тарирования.
SV = ∫q(t)dt,
при этом соответствующий период времени соответствует времени сердечного сокращения или времени выброса во время сердечного сокращения.
SV = γ-∫q(t)dt/
c

19. Способ по одному из п. 1 или 16, отличающийся тем, что вычисляют изменение ударного объема крови согласно

и используют его само по себе или с другими параметрами, например, средним кровяным давлением МАР, систолическим кровяным давлением АРsys, диастолическим кровяным давлением и АРDIA и частотой сердечных сокращений НR для корректирования ударного объема крови.
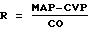
по произвольному центральному венозному давлению СVР, которое было измерено или рассчитано.


Комментарии