Способ определения курса объекта на линейной траектории с использованием измерений его радиальной скорости - RU2714884C1
Код документа: RU2714884C1
Чертежи



Описание
Изобретение относится к радиолокации и может быть использовано для определения курса неманеврирующих объектов, движущихся по линейной траектории, в том числе аэродинамических и надводных морских целей, преимущественно в РЛС с большими ошибками измерения азимута.
Известен способ, в котором текущий курс определяют как сумму курсового угла qn и азимута объекта βn-1 в предыдущем обзоре Q=qn+βn-1. Для определения курсового угла, то есть угла между линией визирования объекта (между направлением «РЛС - объект») и направлением вектора скорости, вычисляют несколько вспомогательных величин: разность азимутов в соседних обзорах δβn; произведение дальности в последнем обзоре на синус разности азимутов bn=rnsinδβn; разность между дальностью в предыдущем обзоре и произведением дальности в последнем обзоре на косинус разности азимутов an=rn-1-rncosδβn; вспомогательный угол

Недостаток способа: низкая точность определения курса при больших ошибках измерения азимута.
Известен способ, в котором для определения курса объекта находят оценки (сглаженные значения) скорости изменения горизонтальных прямоугольных координат
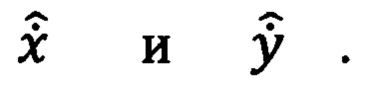

Для устранения неоднозначности определения курса используют информацию о знаке оценок скорости изменения горизонтальных прямоугольных координат [2, С. 314].
Недостаток способа: низкая точность определения курса при больших ошибках измерения азимута.
Наиболее близким аналогом заявленному способу (прототипом) является способ, в котором для определения курса неманеврирующего объекта, движущегося по линейной траектории, вычисляют оценку курсового угла


При этом оценку радиальной скорости


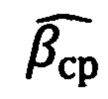
Далее вычисляют значения курса, как алгебраическую сумму оценок азимута



Недостаток прототипа: низкая точность определения курса при больших ошибках измерения дальности, достигающих значений до нескольких сотен метров и более. Для получения выигрыша в точности определения курса по сравнению с другими способами необходимо уменьшить ошибки измерения дальности до нескольких десятков метров. Это требование сложно реализовать в РЛС метрового и декаметрового диапазонов с относительно узкополосными зондирующими сигналами. Ширина полосы частот зондирующих сигналов этих РЛС ограничена требованиями электромагнитной совместимости с системами связи, навигации, телевидения и другими радиоэлектронными средствами.
Техническим результатом заявленного изобретения является повышение точности определения курса неманеврирующего объекта, движущегося по линейной траектории, за счет использования выборок произведений дальности на радиальную скорость и уменьшения вследствие этого влияния ошибок измерения дальности и азимута объекта.
Для достижения этого технического результата в заявленном изобретении так же, как в прототипе, в РЛС измеряют полярные координаты объекта (дальность ri и азимут βi) и преобразуют их в цифровые сигналы. Далее производят преобразование этих координат в горизонтальные прямоугольные координаты: xi=risinβi, yi= ricosβi.
Путем оптимального взвешенного суммирования фиксированной выборки этих координат определяют оценки скорости изменения прямоугольных координат




Далее определяют значения радиальной скорости



После этого определяют два значения курса, как алгебраическую сумму сглаженных значений оценок азимута

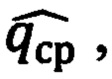

В отличие от прототипа, согласно заявленного изобретения, радиальную скорость


Для измерения путевой скорости


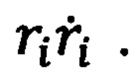




Азимут объекта в середине интервала наблюдения оценивают путем взвешенного суммирования измеренных значений азимута βi:

где N - число измерений азимута или значений произведений дальности на радиальную скорость в выборке;
i - номер измерения азимута или значения произведения дальности на радиальную скорость в выборке.
Далее определяют две оценки курса




Для определения другой оценки курса


Затем вычисляют абсолютные значения разностей двух полученных оценок и однозначной оценки, полученной во втором аналоге


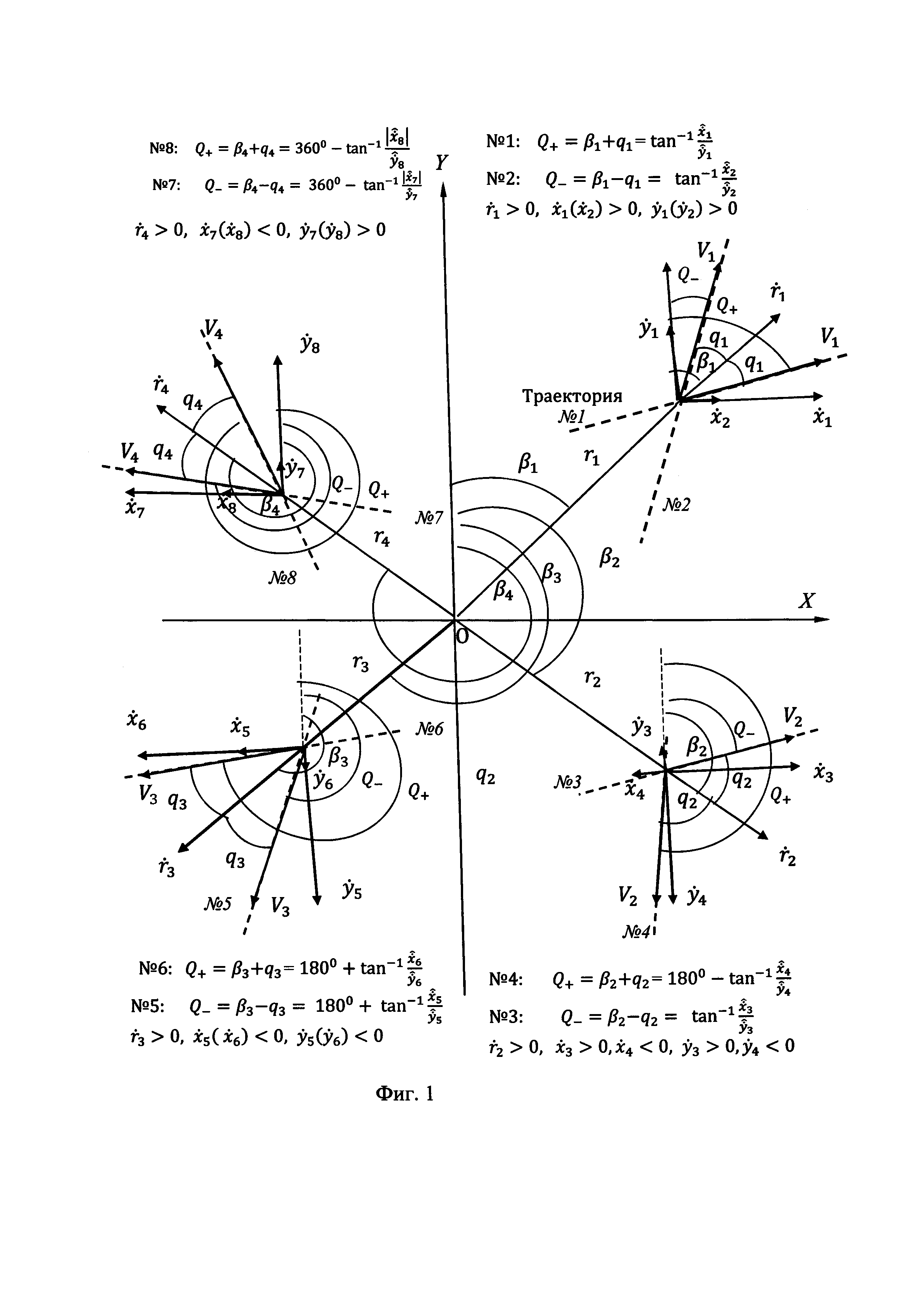
Достоверность формул (3), (6) и (7) подтверждается схемами траекторий, приведенными в фиг. 1 - фиг. 4. В фиг. 1 и фиг. 2 приведены схемы восьми траекторий в точках с координатами ri и βi. Для удаляющихся от РЛС объектов (фиг. 1), то есть при положительной радиальной скорости



В фиг. 3 приведены параметры траектории в двух точках, то есть вблизи траверза (точка А) и на краю зоны обнаружения (точка В), удаляющегося от РЛС объекта. При этом курс равен разности между азимутом и курсовым углом:

В фиг. 4 также приведены параметры траектории в двух точках, но курс равен сумме азимута и курсового угла:

Во всех приведенных случаях при истинном курсе разность теоретически равна нулю, а при ложном курсе - удвоенному курсовому углу

Для доказательства реализуемости заявленного технического результата вычислим среднеквадратические ошибки (СКО) определения курса объекта, то есть аэродинамической цели (АЦ), в РЛС «Резонанс-Н» тремя способами по фиксированным выборкам из 13 значений дальности, радиальной скорости и азимута при СКО измерения азимута σβ=1,5° радиальной скорости
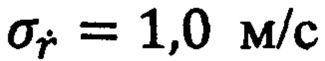
В приведенном примере, как показано на схеме фиг. 3, АЦ летит с курсом Q=20°, скоростью 250 м/с и курсовым параметром (траверзным расстоянием) Р=25 км. Автосопровождение АЦ и оценивание параметров ее движения, то есть курса Q, путевой скорости V, азимута

СКО определения курса в заявленном изобретении и в прототипе


СКО определения путевой скорости в прототипе




Прототип нельзя использовать в РЛС «Резонанс-Н» для определения курса объекта, так как из-за больших ошибок измерения дальности в соответствии с (9) СКО оценивания путевой скорости

Результаты анализа точности определения курса в заявленном изобретении


В заявленном изобретении большие ошибки измерения дальности (σr = 300 м) в соответствии с (10) несущественно (до 17%) снижают точность оценивания путевой скорости на дальностях до 100 км, а на дальностях более 200 км практически не оказывают влияния. Ошибки измерения азимута на дальностях более 100 км также практически не оказывают влияния на точность определения курса.
В способе-аналоге (3), то есть при оценивании курса по выборкам прямоугольных координат, ошибки определения курса зависят от СКО измерения азимута и вычисляются по формуле [3]:

Эффективность заявленного технического результата характеризуется выигрышем в точности оценивания курса заявленным способом по сравнению с аналогом, то есть отношением их СКО
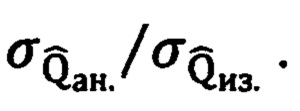

Как видно из нижней строки таблицы 1, этот выигрыш в точности оценивания курса заявленным способом по сравнению с аналогом на дальностях до 200 км достигает значений от 1,75 до 4,2. На дальности 350 км выигрыш отсутствует, а на дальностях больше 350 км заявленный способ уступает в точности второму аналогу.
В общем виде этот выигрыш вычисляется по формуле:

В соответствии с (12) этот выигрыш возрастает при увеличении путевой скорости V, курсового угла


Как видно из таблицы 1 и фиг. 5, на дальности 175 км курсовой угол становится равным СКО его определения заявленным способом


Поэтому во втором пункте формулы изобретения предлагается вычислять СКО определения курса заявленным способом по формуле:

Где

Далее вычисляют отношение курсового угла к СКО его определения

Если это отношение меньше единицы, то есть


В приведенном в таблице 1 примере на дальности 350 км положительное смещение оценки курса, равное курсовому углу qcp=4,1°, в 8 (восемь) раз меньше СКО определения курсового угла

На графиках фиг. 6 показана зависимость значений среднеквадратических ошибок определения курса от дальности до объекта в заявленном изобретении

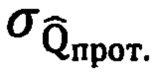
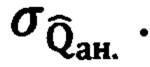
Таким образом, доказана промышленная реализуемость технического результата заявленного изобретения: повышение точности определения курса неманеврирующего объекта, движущегося по линейной траектории, за счет использования выборок произведений дальности на радиальную скорость и уменьшения вследствие этого влияния ошибок измерения дальности и азимута объекта.
Список использованных источников
1. Кузьмин С.З. Цифровая обработка радиолокационной информации. - М.: «Радио и связь», 1967 с.
2. Кузьмин С.З. Основы теории цифровой обработки радиолокационной информации. - М.: «Советское радио», 1974.
3. Способ и устройство определения курса неманеврирующей аэродинамической цели с использованием выборки квадратов дальности. Патент на изобретение №2621692 от 07.06.17.
4. Способ определения модуля скорости аэродинамической цели. Патент на изобретение №2559296 от 14.07.15.
5. Устройство радиолокационного определения путевой скорости неманеврирующей воздушной цели. Патент на полезную модель №152617 от 18.05.15.
6. Радиолокационный измеритель путевой скорости неманеврирующей аэродинамической цели по выборке квадратов дальности. Патент на полезную модель №158491 от 11.12.15.
7. Способ радиолокационного определения путевой скорости неманеврирующей аэродинамической цели по выборке произведений дальности на радиальную скорость и устройство для его реализации. Патент на изобретение №2644588 от 13.02.1.
8. Вооружение ПВО и РЭС России. Альманах. М.: Издательство НО «Лига содействия оборонным предприятиям», 2011, 504 с.
Реферат
Изобретение относится к области радиолокации и предназначено для определения курса неманеврирующих объектов. Технический результатом изобретения заключается в повышении точности определения курса неманеврирующего объекта. Указанный результат достигается за счет использования выборки произведений измеренных значений дальности rна радиальную скоростьи уменьшения вследствие этого влияния ошибок измерения дальности и азимута. Для этого оценивают путевую скоростьпо выборке произведений дальности на радиальную скорость и вычисляют курсовой угол в середине интервала наблюденияКурс вычисляют как алгебраическую сумму сглаженных значений оценок азимутакурсового углаа также углов 0° или 180°. С помощью известного способа определения курса по выборкам прямоугольных координат устраняют неоднозначность определения курса в заявленном изобретении. 1 з.п. ф-лы, 6 ил., 1 табл.
Формула



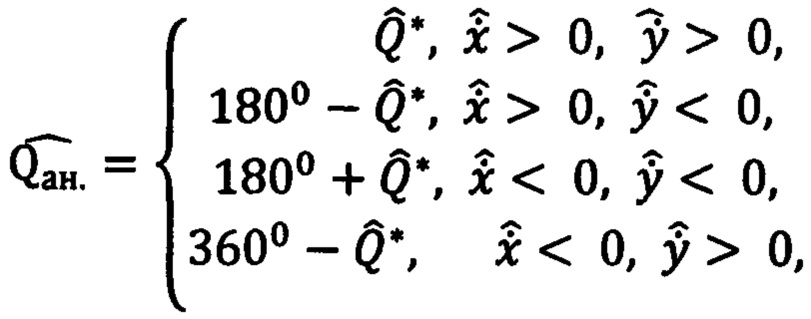




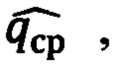







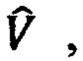







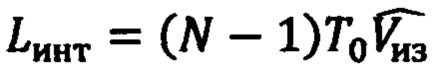



Документы, цитированные в отчёте о поиске
Способ и устройство определения курса неманеврирующей аэродинамической цели с использованием выборки квадратов дальности

Комментарии