Способ определения высоты полета низколетящей цели моноимпульсной рлс сопровождения - RU2761955C9

Чертежи

Описание

Изобретение относится к радиолокации и может быть использовано в радиолокационной станции (РЛС) сопровождения низколетящих целей под малыми углами места при наличии мешающих отражений от подстилающей поверхности.

В практической работе современных РЛС одной из важнейших задач является обнаружение и сопровождение низколетящих целей (НЛЦ). При сопровождении низколетящей цели важно как можно раньше правильно определить ее угломестную координату (оценить высоту ее полета), чему мешают значительные угломестные ошибки из-за многопутного распространения (явления многолучевости), иначе говоря, из-за сигнала так называемого «антипода».

В результате появления сигнала «антипода» в угломестном разностном канале появляется ложный сигнал ошибки, из-за чего следящая система по углу места сдвигает луч антенны РЛС до тех пор, пока этот ложный сигнал не будет скомпенсирован. При сопровождении на малых углах места ошибка из-за многопутного распространения очень велика, так как сигнал «антипода» попадает в главный лепесток ДН антенны РЛС. При этом реальная цель и сигнал «антипода» образуют двухточечную цель с изменяющейся разностью фаз и амплитудами сигналов, которые сравнимы по величине. Под воздействием сигнала ошибки следящей системы луч антенны РЛС периодически то устремляется к нулевому углу места, то, при достижении сдвига фаз между сигналами в 180°, снова движется вверх по направлению к цели [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.]. При этом сигнал следящей системы (СС) образует локальные максимумы, так называемые «колокола».

Для борьбы с явлением многопутного распространения при сопровождении низколетящих целей используются различные методы, которые можно условно разделить на две группы.

К первой относятся методы, направленные на создание узконаправленных по углу места диаграмм направленности антенн с целью уменьшения (или исключения) проникновения сигнала «антипода» в главный луч диаграммы направленности антенны. Практическая реализация этих способов подразумевает увеличение апертуры антенной системы по вертикали и по горизонтали. Повышение угловой разрешающей способности лежит в основе этих способов. Реализация крупногабаритных антенн затруднительна для большинства передвижных радиолокаторов, предназначенных для обнаружения и сопровождения низколетящих целей, так как повышается конструктивно-технологическая сложность систем и снижается их мобильность.

Вторая группа способов определения угла места (высоты цели) основана на использовании дополнительной информации о влиянии отражений от подстилающей поверхности и устранении или уменьшении этого влияния на оценку угла места (высоты) цели. К этому подклассу относится большое число методов, основанных на моноимпульсном методе измерения угломестной координаты. Моноимпульсные способы измерения угла места целей имеют преимущества, как наиболее устойчивые к шумовым и динамическим ошибкам измерения.

В работе [А.И. Леонов, К.И. Фомичев. «Моноимпульсная радиолокация». Москва, «Радио и связь», 1984 г.] описан способ определения угла места цели, при котором используются две антенны в вертикальной плоскости, расположенные на разной высоте. Антенны имеют идентичные диаграммы направленности и одинаковую ориентацию по углу места. Расстояние между антеннами регулируется так, чтобы разность фаз между сигналами от «антипода», принимаемых двумя антеннами, равнялась π. При этом разность фаз между сигналами от цели должна быть отлична от π. В зависимости от амплитуды и фазы сигналов (от цели и «антипода»), принятых антеннами, вырабатываются сигналы управления сдвигом фазы сигнала (от цели и антипода) и разнесением антенн по высоте. Если сигнал ошибки от цели и управляющий сигнал разнесения антенн одновременно равняются нулю, то система отслеживает направление на цель со сравнительно малыми ошибками. Указанный способ, несмотря на высокую точность определения угла места НЛЦ, весьма сложен в конструктивном отношении, требует использования дополнительной антенны.

Наиболее близким по технической сущности к заявляемому способу является способ вычисления высоты полета низколетящей цели, описанный в [патент RU №2080619 С1, МПК G01S 13/44. Способ определения угла места и дальности низколетящей цели моноимпульсным радиолокатором при многолучевом распространении отраженного от цели сигнала. 1994 г.], характеризующийся формированием и излучением зондирующих радиолокационных сигналов, приемом отраженных эхо-сигналов от низколетящей цели (НЛЦ) и от подстилающей поверхности (сигнала «антипода») и их обработкой с помощью ЭВМ РЛС для определения угла места низколетящей цели без размыкания контура следящей системы по углу места.

Недостатком прототипа является то, что этот способ работает тогда, когда известно, что рассматривается 1-ый нуль мнимой функции (Im), то есть набег фаз в 180° между прямым сигналом от цели и сигналом «антипода» произошел только один раз. Для последующих нулей мнимой функции (Im) этот способ работать не будет из-за неоднозначности вычислений. Кроме того, для реализации этого способа необходимо организовывать дополнительную квадратурную обработку принимаемого сигнала в угломестном канале, и возникает необходимость изменения высоты антенны РЛС.

Техническим результатом изобретения является устранение недостатков прототипа - более точное определение высоты полета НЛЦ за счет того, что высота цели определяется по измерениям дальности до цели R₁ и R₂, которые соответствуют центрам любых 2-х соседних максимумов («колоколов») сигнала следящей системы по углу места (см. фиг.1). То есть, заранее неизвестны номера этих «колоколов» с момента выхода цели из-за радиогоризонта, неизвестно, сколько раз произошел набег разности фаз в 180° между прямым сигналом и сигналом «антипода». В заявляемом способе точность определения высоты полета НЛЦ приблизительно равна точности определения дальностей до цели R₁ и R₂, которые поступают от РЛС при сопровождении НЛЦ. Кроме того, в заявляемом способе не требуется проведение каких-либо конструктивных или аппаратурных изменений в РЛС, введения дополнительной квадратурной обработки, изменения высоты антенны РЛС и т.д.

Указанный технический результат достигается тем, что используется способ определения высоты полета низколетящей цели моноимпульсной РЛС сопровождения, характеризующийся формированием и излучением зондирующих радиолокационных сигналов, и приемом отраженных эхо-сигналов от низколетящей цели (НЛЦ) и от подстилающей поверхности (сигнала «антипода») и их обработкой с помощью ЭВМ РЛС для определения угла места низколетящей цели без размыкания контура следящей системы по углу места. Особенностью этого способа является повышение точности определения высоты полета НЛЦ за счет использования многоволнового принципа радиолокации, при котором в процессе сопровождения НЛЦ РЛС на каждом такте зондирования работает на одной из n (n=3 и более) различных значениях рабочих длин волн λ₁, λ₂, …, λ_n метрового, дециметрового или сантиметрового диапазона, причем значения λ потактно изменяются на 10%-50% в сторону увеличения или уменьшения. Указанная последовательность рабочих длин волн циклически повторяется при работе РЛС. В процессе работы РЛС выполняется следующая очередность действий: на 1-м такте при использовании длины волны λ₁ РЛС принимает суммарный отраженный сигнал (смесь прямого сигнала от цели и сигнала «антипода»), и в ЭВМ РЛС запоминается соответствующее значение модуля сигнала угломестного разностного канала, на 2-м такте при использовании длины волны λ₂ РЛС принимает суммарный отраженный сигнал, и в ЭВМ РЛС запоминается соответствующее значение модуля сигнала угломестного разностного канала, …, на n-м такте при использовании длины волны λ_n РЛС принимает суммарный отраженный сигнал, и в ЭВМ РЛС запоминается соответствующее значение модуля сигнала угломестного разностного канала для длины волны λ_n. То есть для каждой длины волны λ потактно формируются n числовых массивов, состоящих из модулей сигналов угломестного разностного канала для этой длины волны λ. Причем в каждом из этих массивов каждый такт выполняется скользящий поиск минимума путем сравнения сигналов по величине друг с другом. Затем, при накоплении n последовательных минимумов модулей сигнала угломестного разностного канала, соответствующих разным длинам волн, для каждой пары этих минимумов определяются соответствующие им дальности от РЛС до цели R₁ и R₂, и определяется s целевых функций F₁(Н_Ц, N_x), F₂(Н_Ц, N_x), …, F_s(Н_Ц, N_x), где s равно числу сочетаний из и по 2. Эти функции имеют вид:

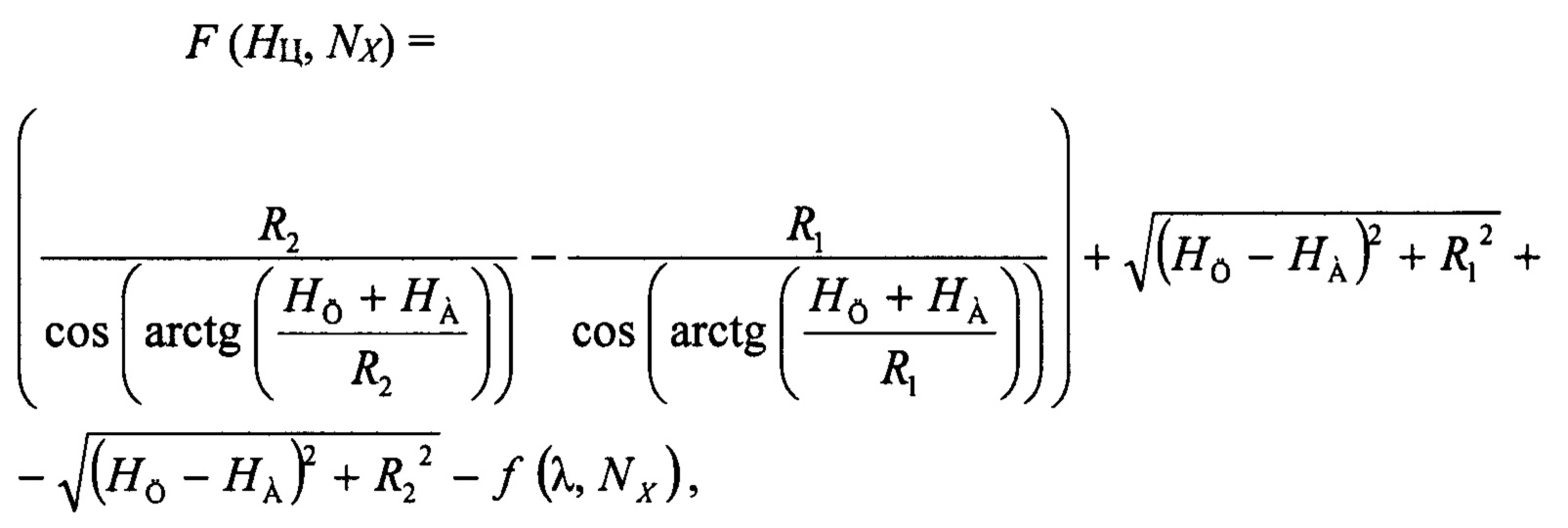
где Н_А - высота фазового центра антенны РЛС;

Н_Ц - высота полета цели;

R₁ и R₂ - дальности от РЛС до цели, соответствующие рассматриваемым моментам минимумов модулей сигнала угломестного разностного канала РЛС;

ƒ/(λ, N_x) - функция разности хода, вычисляющая разность хода сигналов между рубежами R₁ и R₂, зависящая от рабочих длин волн λ₁, λ₂, …, λ_n, и действительного коэффициента коррекции N_x. Затем в процессе двумерного поиска нулей указанных целевых функций F₁(Н_Ц, N_x), F₂(Н_Ц, N_x),…, F_s(Н_Ц, N_x) по переменным Н_Ц и N_x определяется искомая высота полета низколетящей цели Н_Ц. Предложенный многоволновый принцип работы РЛС позволяет регулярно определять высоту полета НЛЦ и постоянно уточнять получаемую оценку высоты на всем интервале сопровождения НЛЦ.

На фиг.1, 2, 3, …, 9 соответственно представлены:

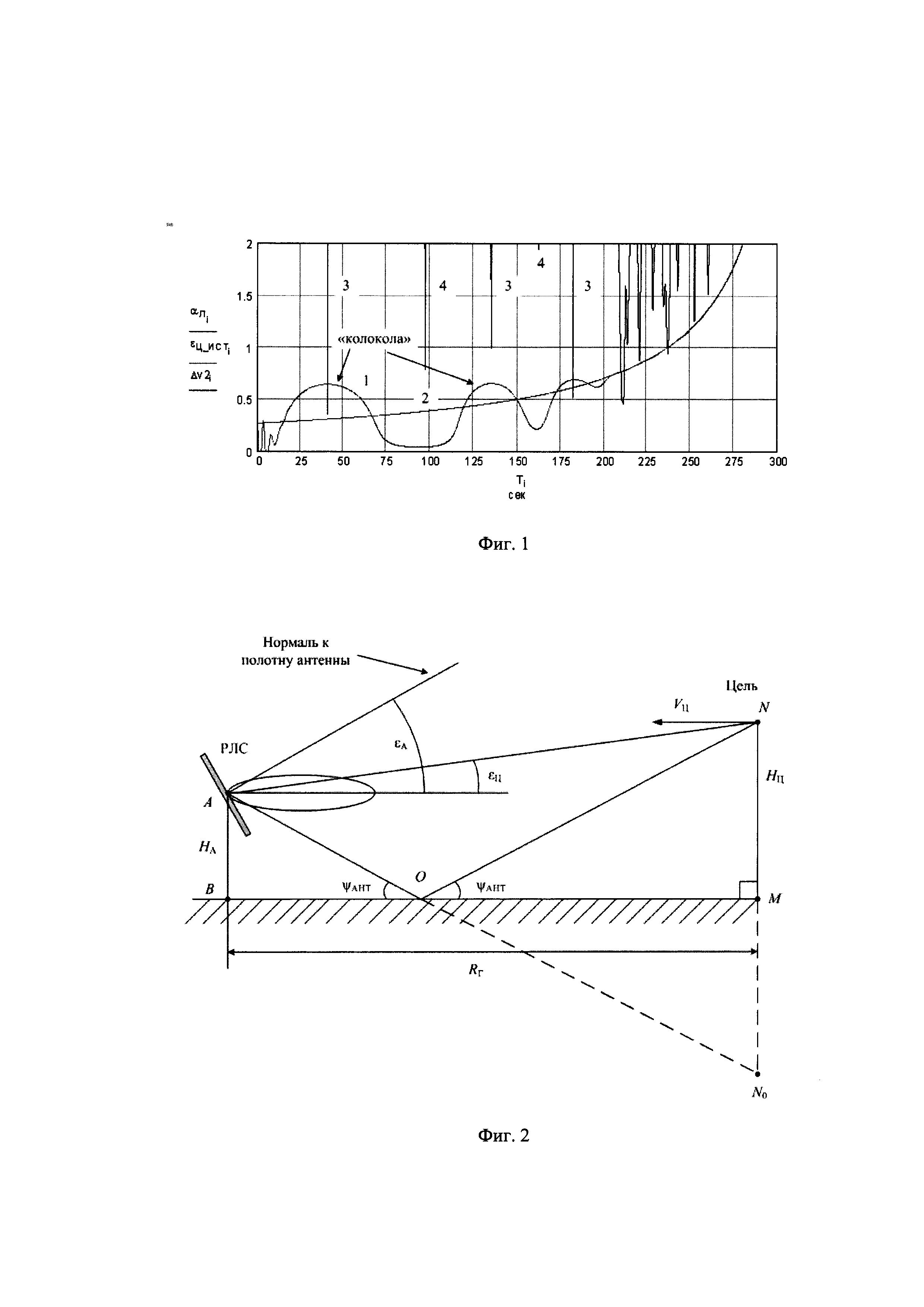
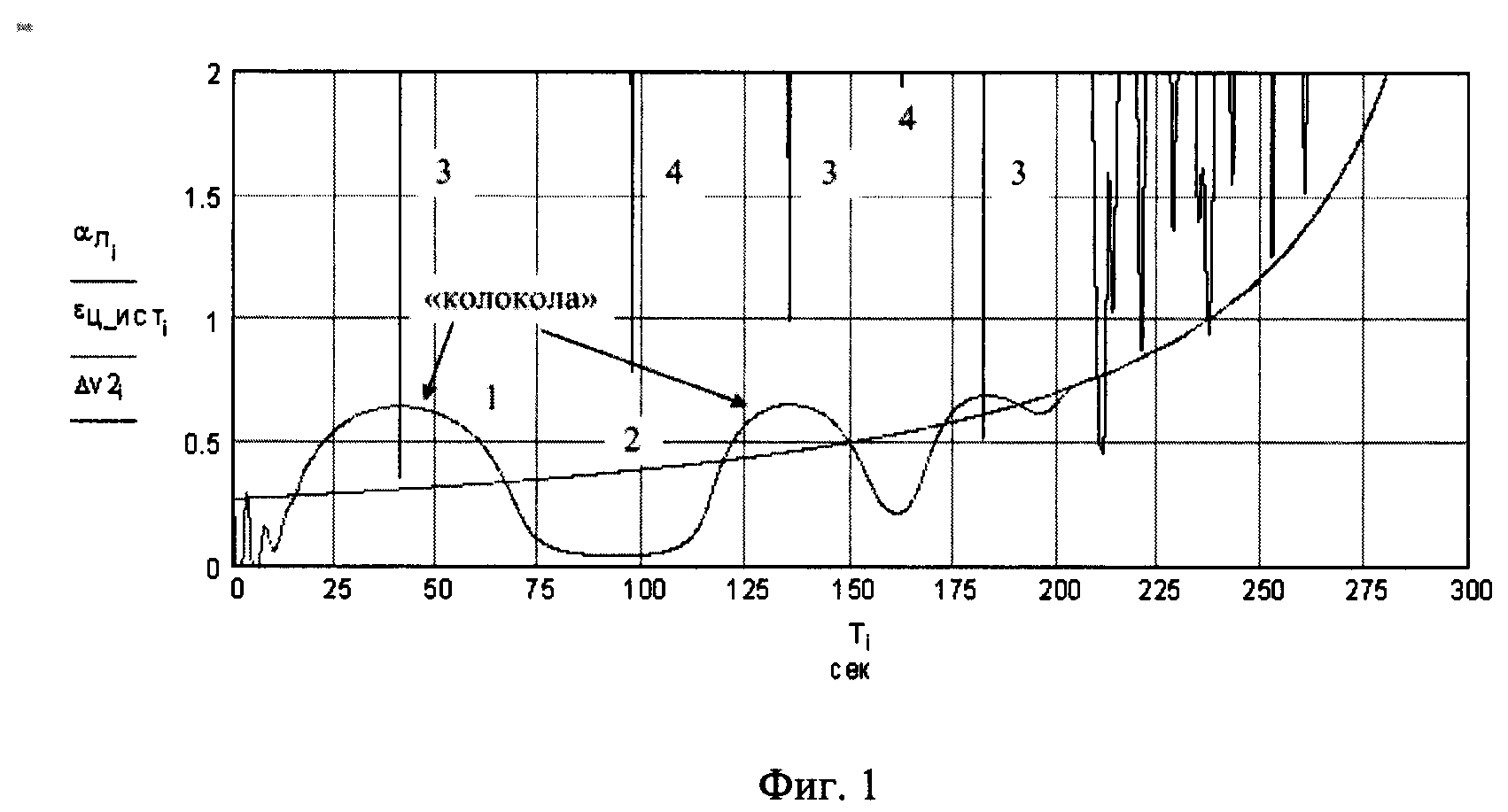
фиг.1 - характерный вид сигнала следящей системы («колокола» сигнала следящей системы);

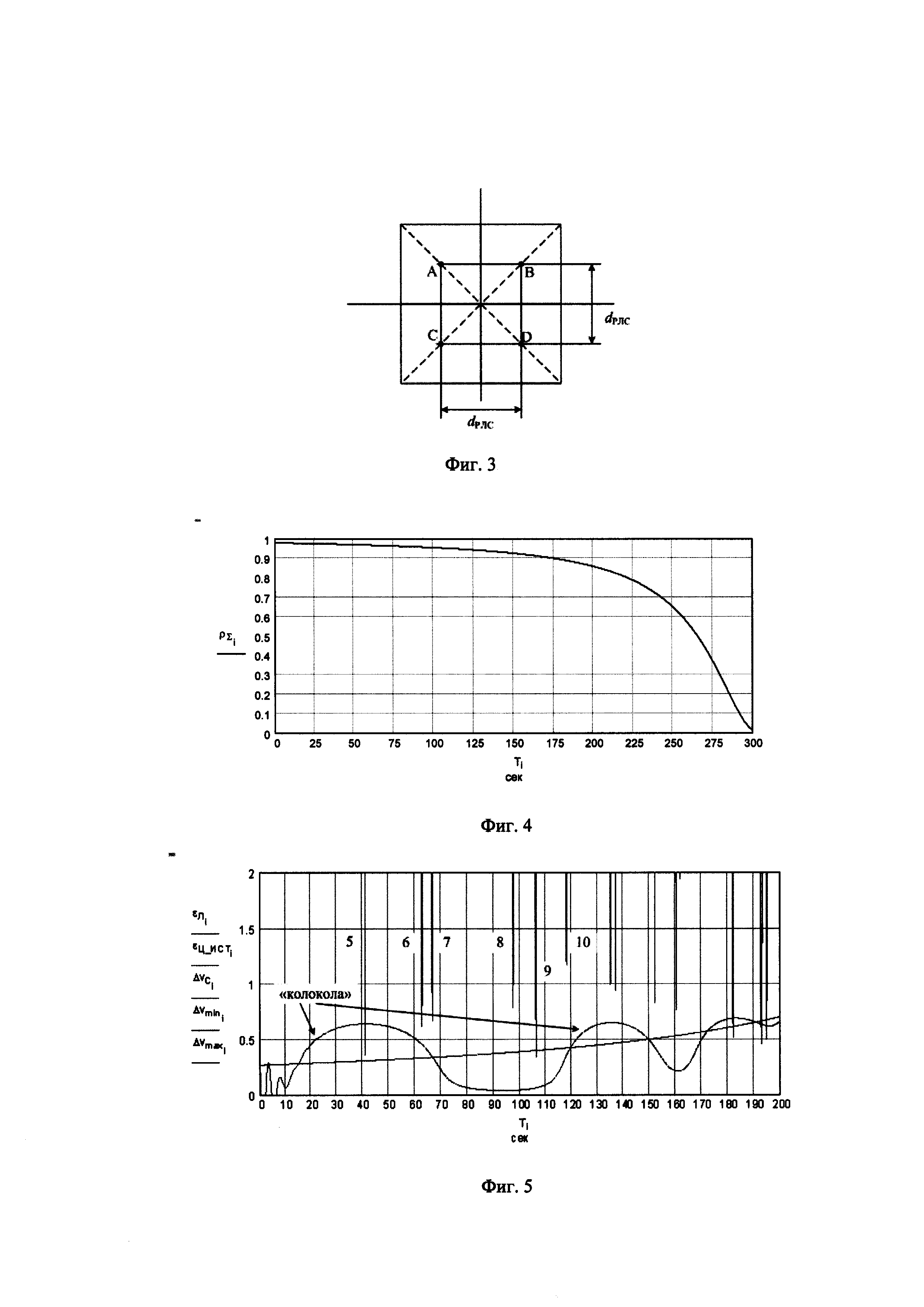
фиг. 2 - геометрия распространения прямого луча и луча, отраженного от Земли для «плоской» Земли;

фиг. 3 - классический вид квадратного полотна антенны моноимпульсной РЛС;

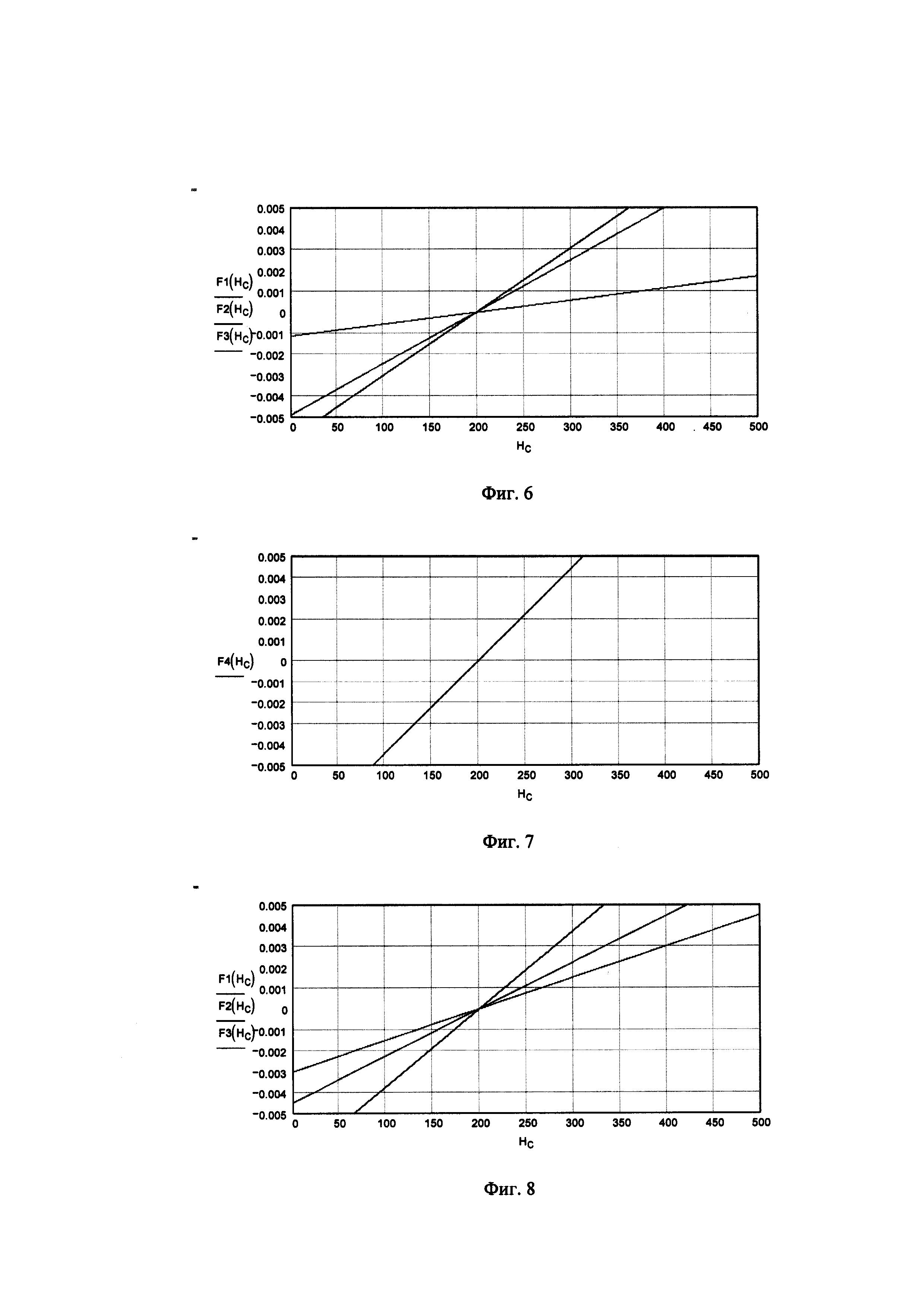
фиг. 4 - кривая изменения коэффициента зеркального отражения ρ_∑ в зависимости от времени наблюдения низколетящей цели;

фиг. 5 - процессы на начальном отрезке интервала сопровождения НЛЦ от 0 с до 200 с;

фиг. 6 - графический результат двумерного поиска нулей целевых функций для минимумов 5, 6 и 7 на фиг.5;

фиг. 7 - графический результат одномерного поиска нуля целевой функции для минимумов 7 и 8 на фиг.5;

фиг. 8 - графический результат двумерного поиска нулей целевых функций для минимумов 8, 9 и 10 на фиг.5;

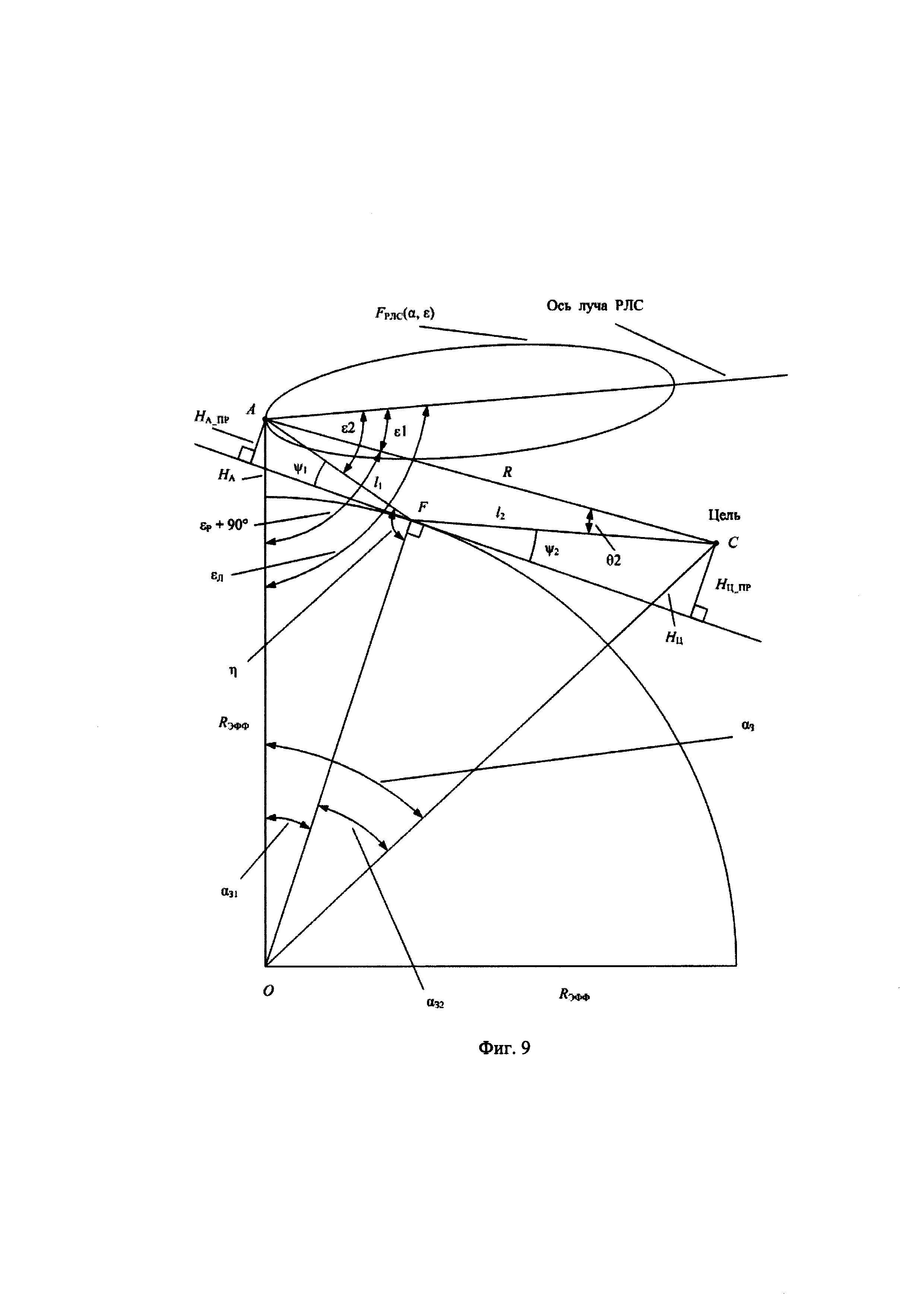
фиг. 9 - геометрическое построение распространения прямого луча и луча, отраженного от Земли для «сферической» Земли.

На фиг.1 обозначено: кривая 1 - сигнал следящей системы по углу места в градусах; кривая 2 - изменение истинного угла места цели в градусах; кривые 3 - минимумы модуля сигнала в угломестном разностном канале, соответствующие центрам «колоколов» и разности фаз между сигналами в 180°; кривые 4 - минимумы модуля сигнала в угломестном разностном канале, соответствующие разности фаз между сигналами в 0°. По оси абсцисс отложено время в секундах. По оси ординат отложены градусы.

На фиг.2 обозначено: Н_А - высота фазового центра антенны РЛС; ε_A - угол поднятия нормали к полотну антенны РЛС относительно горизонта; ε_Ц - истинный угол места цели; Н_Ц - высота полета цели; V_Ц - скорость полета цели; ψ_АНТ - угол скольжения сигнала «антипода»; R_Г - горизонтальная дальность до цели; А - положение фазового центра антенны РЛС; О - точка отражения сигнала «антипода»; N - положение цели; N₀ - зеркальное положение цели.

На фиг.3 обозначено: А, В, С, D - квадранты полотна антенны моноимпульсной РЛС; d_рлс - база антенны РЛС.

На фиг.4 по оси абсцисс отложено время в секундах. Ось ординат безразмерная.

На фиг.5 обозначено: кривые 5 и 8 - минимумы модуля сигнала угломестного разностного канала, соответствующие центральной длине волны λ₀=0,03 м; кривые 6 и 9 - минимумы модуля сигнала угломестного разностного канала для минимальной длины волны λ_MIN=0,026 м; кривые 7 и 10 - минимумы модуля сигнала угломестного разностного канала для максимальной длины волны λ_МАХ=0,033 м. По оси абсцисс отложено время в секундах. По оси ординат отложены градусы.

На фиг.6 по оси абсцисс отложена высота цели в метрах. Ось ординат безразмерная.

На фиг.7 по оси абсцисс отложена высота цели в метрах. Ось ординат безразмерная.

На фиг.8 по оси абсцисс отложена высота цели в метрах. Ось ординат безразмерная.

На фиг.9 обозначено: R_ЭФФ - эффективный радиус Земли; О - центр Земли; F - точка отражения сигнала «антипода»; Н_А - высота фазового центра антенны РЛС; Н_Ц - истинная высота полета цели (высота цели над местным горизонтом); Н_{Ц_ПР} - приведенная высота цели; Н_{А_ПР} - приведенная высота РЛС; R - наклонная дальность РЛС-цель; ψ₁, ψ₂ - углы скольжения; l₁₁, l₂₁ - расстояния от точки отражения F до фазового центра антенны РЛС А и цели С соответственно.

Способ осуществляется следующим образом.

На фиг.1 приведен типичный вид «колоколов» для плоской Земли - кривая 1 (в градусах), истинный угол места - кривая 2 (в градусах). Высота полета цели Н_Ц=200 м, скорость цели V_Ц=130 м/с, полетное время в секундах отложено по оси абсцисс, коэффициент отражения от подстилающей поверхности ρ ≈ 0,9, длина рабочей волны РЛС λ=0,03 м.

В моменты максимумов «колоколов» (см. фиг.1, кривая 1) разность фаз между сигналом цели и сигналом «антипода» становится равной 180°. Между каждыми соседними максимумами («колоколами») разность хода между сигналами ΔL возрастает на длину волны λ, или, что то же самое, разность фаз сигналов увеличивается на 2-я.

Эти максимумы («колокола») обычно хорошо различимы при сопровождении НЛЦ, поэтому, пользуясь этой информацией, можно вычислить высоту полета НЛЦ Н_Ц.

На фиг.2 представлена геометрия распространения прямого луча и луча, отраженного от земной поверхности («антипода») для «плоской» Земли.

На фиг.3 приведено классическое квадратное полотно антенны радиолокатора (А, В, С, D - квадранты полотна), которое используется при моделировании сопровождения НЛЦ. Суммарно-разностная обработка выполняется по схеме Пейджа. Угломестный разностный канал формируется стандартным образом: (А+В) - (С+D).

Очередной «колокол» начинает формироваться, когда разность фаз между сигналом цели и сигналом «антипода» приближается к 180°. В моменты максимумов «колоколов» (см. фиг.1, кривая 1) разность фаз между сигналом цели и сигналом «антипода» становится равной 180°. Так как сигналы близки по мощности, то сигнал суммарного канала стремится к нулю. Модуль сигнала в угломестном разностном канале Δν также стремится к нулю. Поэтому при вычислении сигнала ошибки Δε фазового дискриминатора выполняется деление на ноль, то есть возникает сингулярность.

В простейшем варианте работы следящей системы положение центра луча радиолокатора ε_л на i+1-м шаге описывается формулой:

ε_лi+1=ε_{л i}+Δε_i⋅D_ε⋅Δt,

где D_ε - добротность следящей системы (коэффициент усиления сигнала ошибки);

ε_{л i} -положение луча на i-м шаге;

Δε_i - сигнал ошибки фазового дискриминатора на i-м шаге;

Δt - величина дискрета счета.

Из-за явления сингулярности вычисляемая угловая ошибка Δε может достигать очень большой величины, которую будет ограничивать только собственный шум суммарного канала. Следящая система резко увеличивает угол подъема луча ε_л, и образуются «колокола» (см. фиг.1).

С течением времени период следования «колоколов» уменьшается, так как при увеличении угла места цели ε_ц разность хода ΔL (и разность фаз) между прямым сигналом и сигналом «антипода» возрастает все быстрее (см. фиг.2). Между каждыми двумя соседними «колоколами» разность хода между сигналами возрастает на длину рабочей волны радиолокатора λ, или, иначе, разность фаз сигналов увеличивается на 2⋅π (360°).

В наиболее простом случае для получения оценки высоты достаточно взять два соседних «колокола» сигнала ошибки ε_л. В моменты времени t₁ и t₂, которые соответствуют первому и второму «колоколу» сигнала СС (см. фиг.1, кривая 1, считать слева направо), используются значения горизонтальной дальности R_Г - R₁ и R₂, поступающие от РЛС. Углы ψ₁ и ψ₂ - углы скольжения в моменты времени t₁ и t₂. Для повышения точности определения временных отметок t₁ и t₂ берутся значения минимумов модуля сигнала в угломестном разностном канале Δν (см. фиг.1, кривые 3), соответствующие этим двум соседним «колоколам». Этим достигается точное соответствие разности фаз между сигналами в 360°.

Для «плоской» Земли записываются следующие уравнения (см. фиг.2):

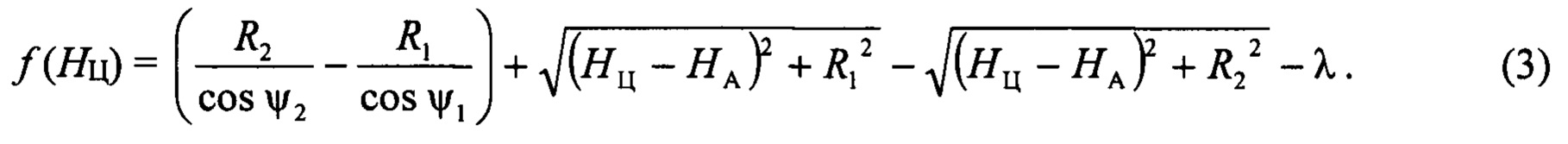
Для получения величины высоты полета цели необходимо найти значение переменной Н_Ц, при котором целевая функция (Н_Ц) (3) обращается в нуль. Строгого решения здесь нет, так как получается уравнение 4-ой степени.

Производная функции (3)

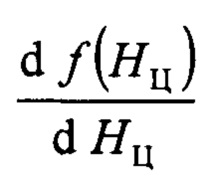
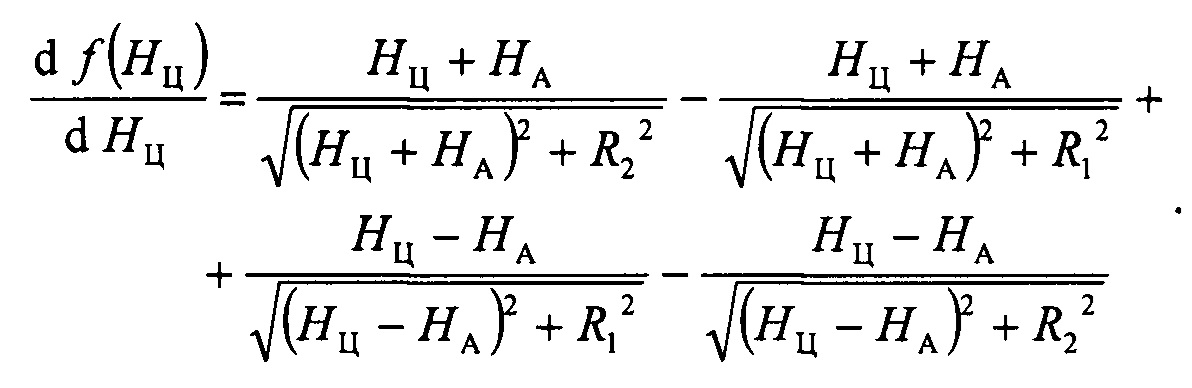
При R₁>R₂ производная

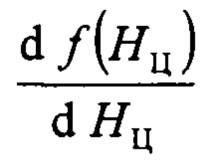
Предлагаемый алгоритм был усовершенствован. Минимумы модуля сигнала угломестного разностного канала Δν (см. фиг.1, кривые 3 и 4) имеют ярковыраженный характер и наблюдаются в 2 раза чаще «колоколов» сигнала СС, причем разность хода ΔL между соседними минимумами модуля сигнала Δν возрастает на половину длины волны, то есть на λ/2. Минимумам модуля сигнала угломестного разностного канала Δν, расположенным между «колоколами» (см. фиг.1, кривые 4 - «промежуточные» минимумы) соответствует синфазность прямого сигнала и сигнала «антипода», то есть в этих точках разность фаз между сигналами равна 0°. Это существенно ускоряет получение оценки высоты полета НЛЦ. При этом в формуле (3) вместо длины волны λ ставится значение λ/2.

При изменении длины рабочей волны РЛС λ «колокола» изменяют свое положение на временной шкале. Изменение длины волны на 10%-20% позволяет существенно изменять положение очередного «колокола» во времени. Уменьшение длины волны вызывает более раннее появление «колоколов». При увеличении длины волны «колокола» запаздывают по времени.

Коэффициент зеркального отражения ρ_∑ вычисляется по формуле [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.]:

ρ_∑=ρ₀(ψ)⋅ρ_S,

где ρ₀ (ψ) - коэффициент отражения для гладкой поверхности, зависит от угла ψ;

ρs - коэффициент отражения от неровной поверхности.

Сферическая расходимость радиоволн не учитывается, то есть К_сф=1 [«Теоретические основы радиолокации», под ред. В.Е. Дулевича, Москва, «Советское радио», 1978 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V. Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C, 1970].

Коэффициент отражения от неровной поверхности ρs вычисляется по формуле [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V. Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D.C., 1970]:

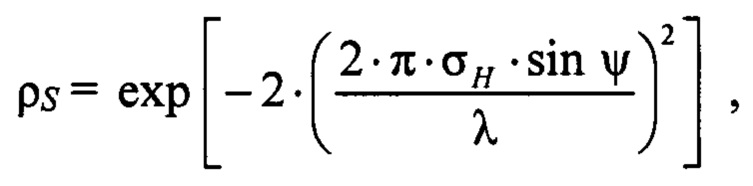
где σ_H - среднеквадратичное значение отклонения высоты поверхности;

ψ - угол скольжения.

Характер изменения коэффициента отражения от гладкой поверхности ρ₀(ψ) [«Справочник по радиолокации в 4 томах, т.1», под. ред. М.И. Сколника. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V. Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C., 1970] аппроксимируется выражением:

ρ₀(ψ)=a⋅ψ₂+b⋅ψ+с if ψ≤10°,

где a=0,0108642; b=-0,19555556; с=1,0.

Фаза при отражении равна ϕ_ОТР=180°, так как угол скольжения ψ_АНТ≤5° [«Справочник по радиолокации в 4 томах, т.1», под. ред. М.И. Сколника. Москва, «Советское радио», 1976 г., «Справочник по радиолокации в 2 книгах», под. ред. М.И. Сколника. Москва, «Техносфера», 2014 г., Lamont V.Blake, "Machine Plotting of Radio/Radar Vertical-Plane Coverage Diagrams". Naval Research Laboratory, Washington, D. C, 1970].

На фиг.4 приведена кривая изменения коэффициента зеркального отражения ρ_∑ при высоте полета цели Н_Ц=100 м и скорости полета V_Ц=130 м/с, полученная при значении σ_H=0,2 м, которое соответствует волнению моря в 2 балла [«Справочник по радиолокационным измерениям». Д. Бартон, Г. Вард. Москва, «Советское радио», 1976 г.].

Изменение рабочей длины волны РЛС λ обеспечивает существенное увеличение эффективности алгоритма, так как позволяет постоянно корректировать вычисляемую оценку высоты полета цели, причем для разных условий отражения эхо-сигнала от подстилающей поверхности, поскольку отражения в этом случае происходят при различных значениях рабочей длины волны РЛС.

Рассмотрим на следующем примере, как достигается более точная оценка высоты полета цели Н_Ц при работе РЛС на 3-х значениях рабочей длины волны λ.

Рассматривается «плоская» Земля. Высота полета цели Н_Ц=200 м, скорость цели V_Ц=130 м/с.Начальная горизонтальная дальность R_{г_нач}=42 км. Конечная горизонтальная дальность R_{г_кон}=3000 м. Эффективная поверхность рассеяния (ЭПР) цели σ_ц≈2 м². Высота фазового центра антенны РЛС HA=5,5 м. Ширина ДН одного квадранта равна θ_0,5=1,342° (см. фиг.3), ширина суммарной ДН θ_0,5=0,8553°. База антенны РЛС d_рлс=0,838 м, крутизна пеленгационной характеристики угломестного канала К_а=1,056 1/градус. Временной интервал наблюдения T_набл=300 с. РЛС работает на 3-х значениях рабочих длин волн: λ₀=0,03 м (центральная длина волны); λ_MIN=0,026 м, Δλ_MIN=0,004 м; λ_мах=0,033 м, Δλ_мах=0,003 м. Отношение сигнал/шум на дальности 42 км ρ_сш ≈ 40 дБ м (для центральной длины волны λ₀). Добротность следящей системы D_ε=5. Общая тактовая частота РЛС F_t=30 Гц. РЛС каждый такт меняет рабочую длину волны по схеме λ_MIN, λ₀, λ_мах, λ_MIN, λ₀, λ_мах,…. Дискрет счета программы для каждого значения рабочей частоты Δt=0,1 с. Волнение моря 2 балла, ему соответствует с.к.о. высоты поверхности σ_H=0,2 м.

Анализ начинается с 1-го «колокола» сигнала следящей системы (см. фиг.1), которому соответствует отрезок времени приблизительно от 15 с до 65 с. Для наглядности на фиг.5 приведен начальный временной интервал наблюдения НЛЦ от 0 с до 200 с.

Минимумы модуля сигнала угломестного разностного канала Δν, соответствующие центральной длине волны λ₀=0,03 м - это кривые 5 и 8 (см. фиг.5). Минимумы модуля сигнала разностного канала для минимальной длины волны λ_MIN=0,026 м - кривые 6 и 9 (см. фиг.5), минимумы модуля сигнала разностного канала для максимальной длины волны λ_мах=0,033 м - кривые 7 и 10 (см. фиг.5). Чтобы не загромождать график, на фиг.5 приведены «колокола» только для центральной длины волны λ₀=0,03 м. Первый «колокол» сигнала с минимальной длиной волны λ_MIN скрывается слева за нулевым отсчетом временной шкалы, центр 1-го «колокола» сигнала с максимальной длиной волны λ_мах отмечен минимумом модуля сигнала разностного канала - кривая 7 (см. фиг.5).

Разность хода между кривыми 5 и 8 равна ΔL=λ₀/2, разность хода между кривыми 6 и 9 равна ΔL=λ_MIN/2, разность хода между кривыми 7 и 10 равна ΔL=λ_мах/2.

Анализируются первые три минимума модулей сигнала разностного канала - кривые 5, 6, 7 (см. фиг.5), которым соответствуют моменты времени Т₁ ≈ 41 с, Т₂ ≈ 62,5 с, T₃ ≈ 67 с. Соответствующие дальности до цели: R₁ ≈ 36670 м, R₂ ≈ 33875 м, R₃ ≈ 33290 м.

Минимум модуля сигнала разностного канала Δν, соответствующий центру первого «колокола» - кривая 7 (см. фиг.5), но запаздывающего первого «колокола» по временной шкале из-за увеличенной длины волны λ_мах. Кривая 6 - минимум модуля сигнала разностного канала (см. фиг.5), находится на разности хода λ_MIN/2 также от первого «колокола», но этот «колокол» опережает первый «колокол» (см. фиг.5), который соответствует центральной длине волны λ₀ (кривая 5).

Учитывая разности хода между соответствующими минимумами модулей сигнала разностного канала, можно записать систему из следующих 3-х целевых функций.

Целевая функция для оценки высоты полета цели на промежутке 5-6 (см. фиг.5):

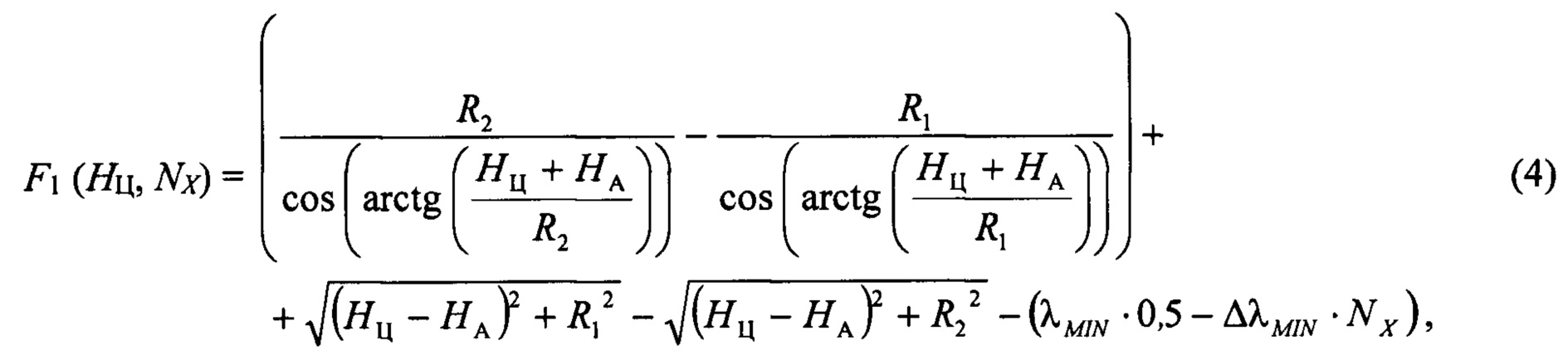
где λ_MIN⋅0,5 - Δλ_MIN⋅N_x - разность хода на промежутке 5-6.

Целевая функция для оценки высоты полета цели на промежутке 5-7 (см. фиг.5):

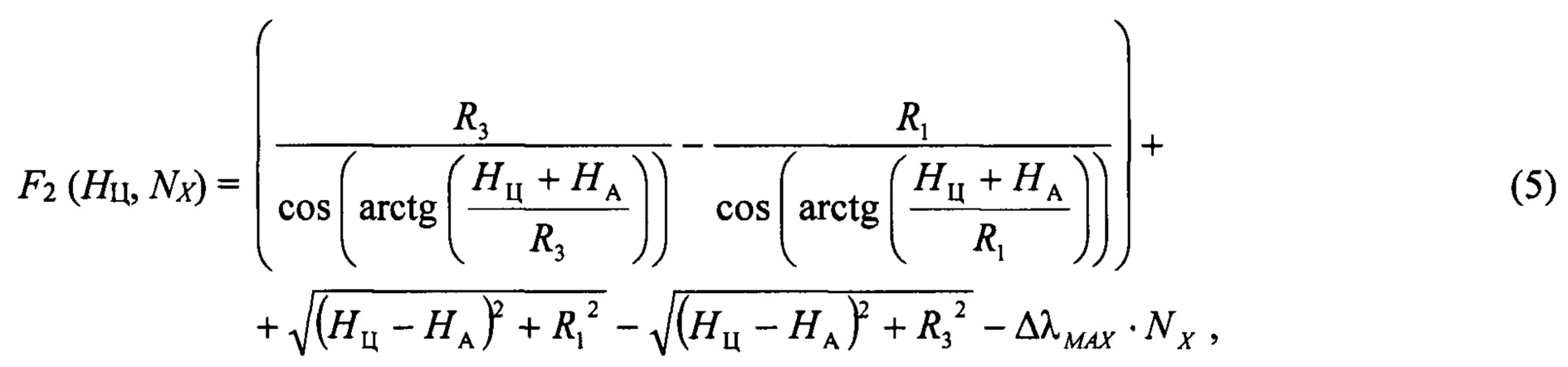
где Δλ_мах⋅N_x - разность хода на промежутке 5-7.

Целевая функция для оценки высоты полета цели на промежутке 6-7 (см. фиг.5):

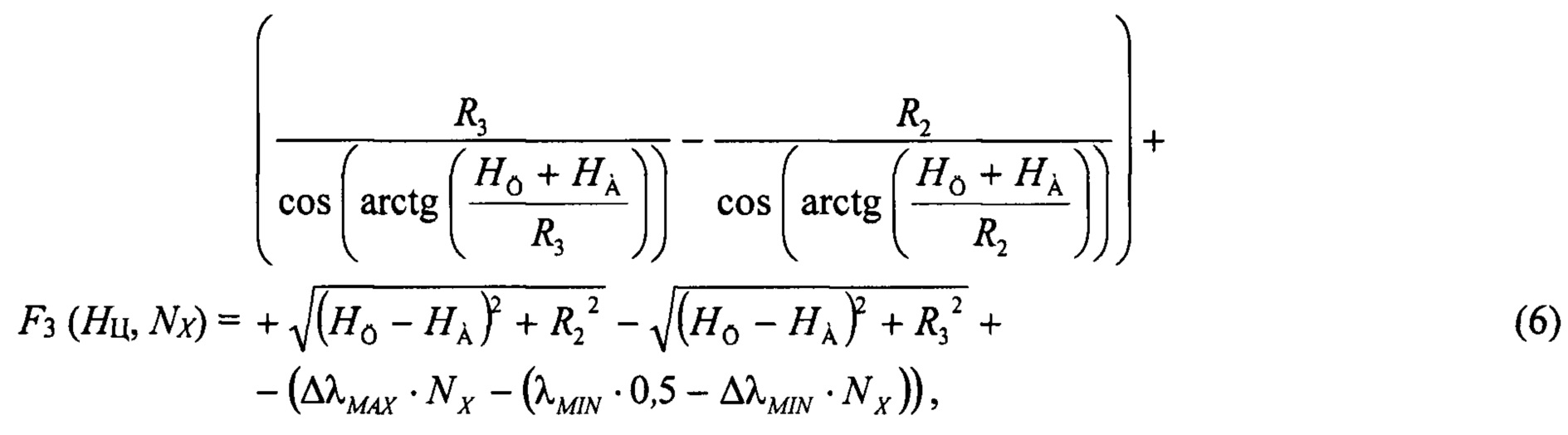
где Δλ_мах⋅N_x-(λ_min⋅0,5 - Δλ_min⋅N_x) -разность хода на промежутке 6-7;

N_x - действительная переменная (коэффициент коррекции), участвующая в двумерном поиске.

Разность хода на промежутке 5-7 для запаздывающего «колокола» (5) равна произведению разницы в длинах волн Δλ_мах на неизвестный коэффициент N_x: Δλ_MIN⋅N_x. Разность хода на промежутке 5-6 для опережающего «колокола» (4) равна разности половины минимальной длины волны λ_MIN и произведения текущей разницы в длинах волн Δλ_MIN на неизвестный коэффициент N_x: λ_MIN⋅0,5 - Δλ_MIN⋅N_x. Разность хода на промежутке 6-7 (6) равна разности ходов на промежутках 5-7 и 5-6: Δλ_мах⋅N_x-(λ_MIN⋅0,5 - Δλ_min⋅N_x).

Затем выполняется двумерный поиск нулей целевых функций F₁(Н_Ц, N_x), F₂(Н_Ц, N_x) и F₃(Н_Ц, N_x) по переменным Н_Ц и N_x. В процессе поиска все 3 прямые пересекаются в единственной точке с ординатой равной 0, абсциссой которой является искомая высота полета цели: Н_Ц ≈ 200 м (см. фиг.6). Значение переменной N_x при этом составляет N_x ≈ 2,02.

Так как известно вычисленное на предыдущем этапе значение переменной N_x ≈ 2,02 для промежутка 5-7, одномерным поиском нуля аналогичной целевой функции по переменной Н_Ц вычисляется высота полета на промежутке минимумов модулей сигнала Δν 7-8 при N_x≈2,02 (см. фиг.5). Кривой 8 - минимуму модуля сигнала угломестного разностного канала Δν соответствует момент времени Т₄ ≈ 97,5 с и дальность R₄ ≈ 29325 м.

Целевая функция для оценки высоты полета цели на промежутке 7-8:

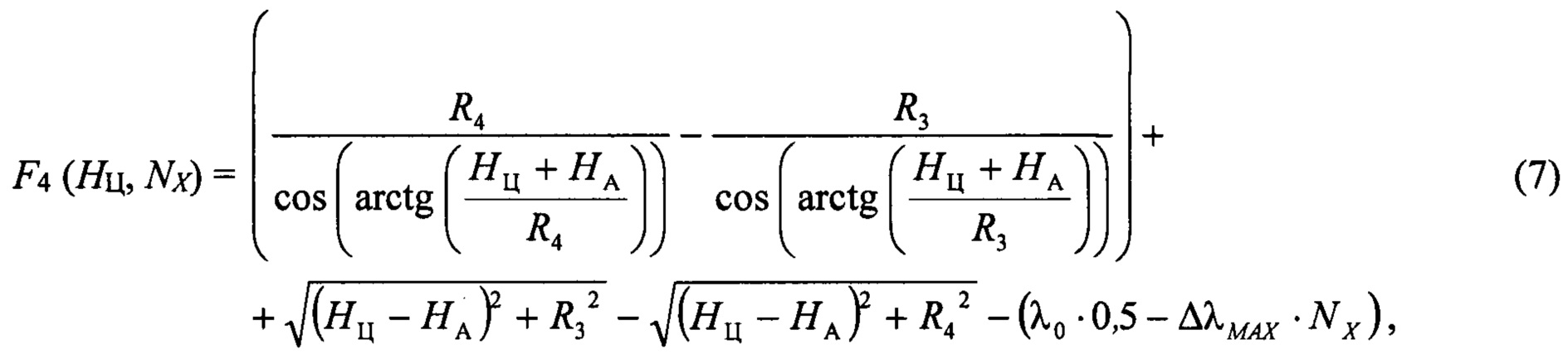
где λ₀⋅0,5 - Δλ_мах⋅N_x - разность хода на промежутке 7-8.

Результат проведения одномерного поиска нуля функции F₄(Н_Ц, N_x) (7) на промежутке 7-8 попеременной Н_Ц при известном значении N_x≈ 2,02 (для промежутка 7-8) приведен на фиг.7. В результате получена искомая высота полета НЛЦ Н_Ц≈ 200 м.

Затем анализируются следующие три минимума модулей сигнала разностного канала - кривые 8, 9, 10 (см. фиг.5), которым соответствуют моменты времени Т₄ ≈ 97,5 с, T₅ ≈ 106,2 с, T₆ ≈ 118 с. Соответствующие дальности до цели: R₄ ≈ 29325 м, R₅ ≈ 28194 м, R₆ ≈ 26660 м.

Целевые функции (4-6) не меняются, формулы для записи разностей ходов в них остаются теми же, так как последовательность минимумов модулей сигнала Δν - кривые 8, 9, 10 такая же, как и рассмотренная выше последовательность минимумов модулей сигнала разностного канала - кривые 5, 6, 7 (см. фиг.5), только в формулах необходимо учесть: R₁=R₄, R₂=R₅, R₃=R₆.

Результат выполнения двумерного поиска нулей по переменным Н_Ц и N_x (для кривых 8, 9, 10) приведен на фиг.8. Все 3 прямые пересекаются в одной точке с нулевой ординатой и абсциссой, равной искомой высоте полета НЛЦ: Н_Ц ≈ 200 м (см. фиг.8). Значение переменной N_x при этом составляет N_x ≈ 2,499.

Аналогично выполняется анализ последующих минимумов модулей сигнала разностного канала Δν (см. фиг.5).

Если из-за других значений разниц между длинами волн Δλ_MIN и Δλ_мах изменится порядок следования минимумов модулей сигнала разностного канала для волн с длинами λ_MIN, λ₀, λ_мах (см. фиг.5, кривые 5, 6, 7, 8, 9,…), то разности ходов на соответствующих промежутках в целевых функциях (4 - 6) должны быть записаны иначе.

Важно отметить, что в целевых функциях (4 - 6) необходимо использовать те минимумы модулей сигнала разностного канала Δν, которые относятся не к одному и тому же «колоколу», а к различным. При этом целесообразнее брать соседние «колокола». Тогда прямые, описываемые функциями (4-6) будут иметь разный коэффициент наклона (они будут непараллельны), и двумерный поиск нулей по переменным Н_Ц и N_x обеспечит определение искомого значения высоты полета НЛЦ - то есть, будет исключена неоднозначность при вычислении высоты полета цели.

Оценка высоты полета может выполняться и по 2-м парам минимумов модулей сигнала разностного канала, лишь бы они относились к различным «колоколам».

В общем случае при использовании n значений рабочих длин волн максимальное количество целевых функций достигает величины:

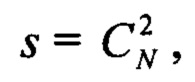
где

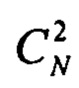
Теперь рассмотрим сопровождение НЛЦ в случае «сферической» Земли.

В случае оценки высоты полета НЛЦ для «сферической» Земли ничего принципиально не изменяется, но алгоритм вычислений немного усложняется (см. фиг.9).

Геометрическая задача нахождения точки отражения F прямого решения не имеет, поэтому применяется приближенный метод решения. Здесь R_эфф=8500 км - это эффективный радиус Земли (при нормальной рефракции).

Задается начальное значение отрезка l₁≥Н_а+1, l₁=

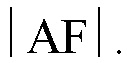
Пусть, например, РЛС работает на 3-х значениях рабочей длины волны λ-λ₁, λ₂, λ₃. В процессе сопровождения НЛЦ в ЭВМ РЛС потактно запоминаются значения модулей сигналов угломестного разностного канала для каждого значения рабочей длины волны. При накоплении 3-х последовательных минимумов модулей сигнала угломестного разностного канала, соответствующих разным длинам волн, для моментов времени наступления этих минимумов используются данные измерений РЛС наклонной дальности R - рубежи R₁, R₂, R₃. Для некоторого заданного значения высоты цели Н_Ц и для каждого рубежа R₁, R₂, R₃ проводится интерполяция, вычисляется положение точки отражения F и решаются треугольники AOF и COF (см. фиг.9).

С помощью полученных значений длин отрезков l₁₁, l₂₁ (рубеж R₁) и l₁₂, l₂₂ (рубеж R₂) и углов скольжения ψ₁ (рубеж R₁) и ψ₂ (рубеж R₂) вычисляются, так называемые, приведенные высоты цели и РЛС Н_{ц_пр} и Н_{а_пр} для рубежей R₁ и R₂ (см. фиг.9):

Н_{ц_пр1}=l₂₁⋅sinψ₁; Н_{а_пр1}=l₁₁⋅sinψ₁; - рубеж R₁;

Н_{ц_ПР2}=l₂₂⋅sin ψ₂; H_{A_пР2}=l₁₂⋅sinψ₂; - рубеж R₂.

Целевая функция F_СФ (Н_Ц, N_x) для «сферической» Земли и рубежей R₁ и R₂ имеет вид:

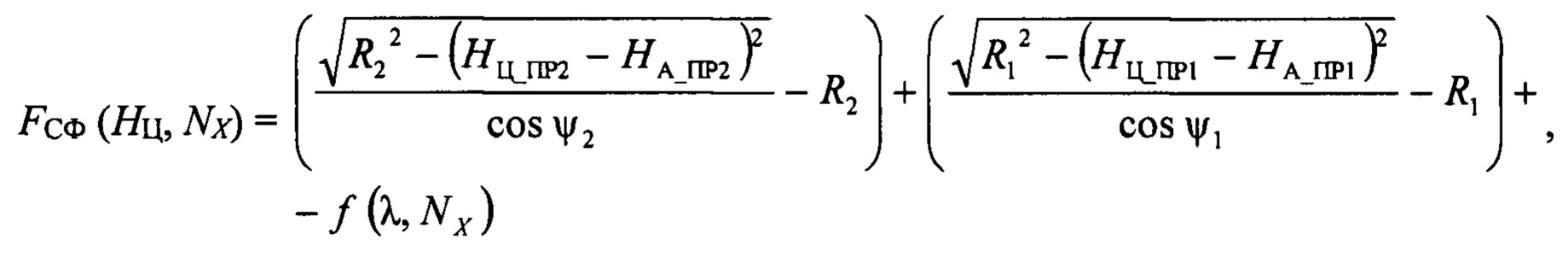
где ƒ(λ, N_x) - значение разности хода (функция разности хода) между рубежами Ri** и R₂.

Таким образом, для анализа соответствующих минимумов модулей сигнала разностного канала Δν записываются целевые функции для «сферической» Земли аналогично формулам (4-6), и затем выполняется двумерный поиск нулей этих функций по переменным Н_Ц (высота цели над местным горизонтом) и коэффициенту коррекции N_x. Так вычисляется искомое значение высоты полета цели Н_Ц (высоты цели над местным горизонтом, см. фиг.9) и приведенные значения высоты цели Н_{ц_пр} для соответствующих дальностей (рубежей). Таким образом, высота полета НЛЦ Н_Ц при рассмотрении модели «сферической» Земли также вычисляется со сколь угодно высокой точностью.

При этом многоволновой (многочастотный) принцип работы РЛС, то есть работа РЛС на нескольких значениях рабочих длин волн (3-4 и более) позволяет регулярно проводить определение высоты полета НЛЦ и постоянно уточнять получаемую оценку высоты на всем интервале сопровождения НЛЦ.

Изменение длины рабочей волны РЛС может выполняться в достаточно широком диапазоне, поэтому оценки высоты будут вычисляться для различных условий отражения сигнала «антипода» от земной поверхности. Это позволит лучше сглаживать влияние различных неровностей подстилающей поверхности на правильность получаемой оценки высоты полета НЛЦ.

Предложенный многоволновой принцип работы РЛС (3-4 значения рабочих длин волн и более) для вычисления высоты полета НЛЦ позволяет значительно быстрее и точнее получать оценку высоты по сравнению с более простым способом использования только одного значения длины волны (3). Например, на промежутке 5-7 (см. фиг.5) оценка высоты НЛЦ при скорости цели V_ц=130 м/с будет получена приблизительно за 25 с, если же использовать только одно значение длины волны λ₀, то оценка высоты будет получена приблизительно за 56 с.

В предложенном способе точность определения высоты полета НЛЦ приблизительно равна точности определения дальностей до цели R₁ и R₂ (для каждой целевой функции), которые поступают от РЛС при сопровождении НЛЦ. Кроме того, в заявляемом способе не требуется проведение каких-либо конструктивных или аппаратурных изменений в РЛС, введения дополнительной квадратурной обработки, изменения высоты антенны РЛС и т.д.

Предложенный способ не требует знания номеров «колоколов» сигнала следящей системы по углу места с момента выхода цели из-за радиогоризонта, то есть не нужна информация о количестве набегов разности фаз в 180° между прямым сигналом и сигналом «антипода».

Надо отметить, что в предлагаемом способе при вычислении высоты полета НЛЦ контур сопровождения следящей системы по углу места не разрывается, что позволяет увеличить дальность сопровождения НЛЦ.

Для корабельных РЛС, а также береговых РЛС, или при наличии другой, относительно ровной подстилающей поверхности, предлагаемый способ особенно эффективен. При волнении моря не выше 2-3 баллов можно считать, что поверхность моря представляет собой практически идеальную сферу. При малых углах места коэффициент отражения ρ₀ близок к 1, влияние неровностей поверхности сводится к минимуму, поэтому локальные максимумы сигнала СС по углу места («колокола») и минимумы модулей сигнала угломестного разностного канала Δν хорошо акцентированы.

Реферат

Изобретение относится к радиолокации и может быть использовано в радиолокационной станции (РЛС) сопровождения низколетящих целей под малыми углами места при наличии мешающих отражений от подстилающей поверхности. Техническим результатом изобретения является более точное определение высоты полета НЛЦ. В заявленном способе осуществляется формирование и излучение зондирующих радиолокационных сигналов, прием отраженных эхо-сигналов от низколетящей цели (НЛЦ) и от подстилающей поверхности (сигнала «антипода») и их обработка с помощью ЭВМ РЛС для определения угла места низколетящей цели без размыкания контура следящей системы по углу места. В процессе сопровождения НЛЦ на каждом такте зондирования РЛС работает на одной из n различных рабочих длин волн λ₁, λ₂, …, λ_n, причем значения λ потактно изменяются на 10%-50% в сторону увеличения или уменьшения, а последовательность рабочих длин волн циклически повторяется. На каждом такте при использовании одной из длин волн λ РЛС принимает суммарный отраженный сигнал (смесь прямого сигнала от цели и сигнала «антипода») и ЭВМ РЛС запоминает значение модуля сигнала угломестного разностного канала. Т.о. для каждой длины волны λ потактно формируются n числовых массивов, состоящих из модулей сигналов угломестного разностного канала для этой длины волны λ. В этих массивах каждый такт выполняется скользящий поиск минимума, а при накоплении n последовательных минимумов модулей сигнала угломестного разностного канала для каждой пары этих минимумов определяются соответствующие им дальности от РЛС до цели R₁ и R₂ и определяется s целевых функций F₁(Н_Ц, Ν_Х), F₂(Н_Ц, Ν_Х), …, F_s(Н_Ц, Ν_Х), где s равно числу сочетаний из n по 2, где Ν_Х – коэффициент коррекции, Н_Ц – высота полета цели. Затем в процессе двумерного поиска нулей указанных целевых функций F₁(Н_Ц, Ν_Х), F₂(Н_Ц, Ν_Х), …, F_s(Н_Ц, Ν_Х) по переменным Н_Ц и Ν_Х определяется искомая высота полета низколетящей цели Н_Ц. 9 ил.

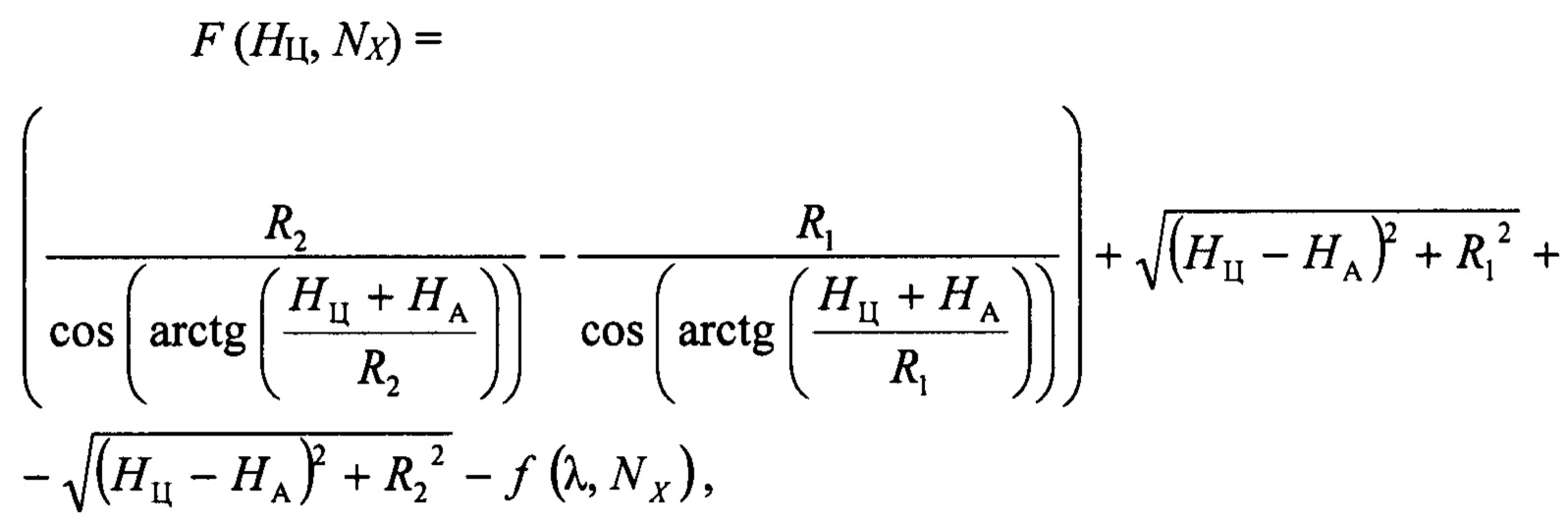
Формула