Двигатель со стоячей детонационной волной - RU2616143C2
Код документа: RU2616143C2
Чертежи







Описание
ИСПРАШИВАНИЕ ПРИОРИТЕТА
В этой заявке испрашивается приоритет согласно ранее поданной предварительной заявке № 61/712972 на патент США от 12 октября 2012 г., которая полностью включена сюда посредством ссылки.
ОБЛАСТЬ ТЕХНИКИ
Настоящее изобретение относится к двигателю со стоячей детонационной волной.
ПРЕДПОСЫЛКИ СОЗДАНИЯ ИЗОБРЕТЕНИЯ
Детонационные волны в газах могут распространяться в разных геометрических конфигурациях и подвергаться их влиянию. В цилиндрических жестких трубах это распространение может происходить в форме многоячеистой детонации в трубах большого диаметра, спиновой детонации в трубах умеренного диаметра и/или галопирующей детонации в трубах очень малого диаметра. В каналах с прямоугольными поперечными сечениями, имеющими разные коэффициенты формы (отношения высоты к ширине), также возможно достижение режимов, аналогичных режимам ячеистой или галопирующей детонации. В промежутке между параллельными пластинами, когда зазор между пластинами гораздо меньше, чем поперечная протяженность пластин, можно достичь двумерной ячеистой детонации из-за подавления поперечных волн в направлении, перпендикулярном пластинам. Другими конфигурациями являются те, в которых детонации стабилизированы в сверхзвуковых потоках и которые могут оказаться уместными для решения проблемы детонационной тяги и детонационных двигателей.
Детонационное горение - это эффективный способ сжигания смеси топлива и воздуха для высвобождения химической энергии. Теоретический кпд детонационного горения, вычисляемый путем деления полезной работы на подводимое тепло, составляет приблизительно 49%. С этим можно сравнить более традиционные процессы, такие как горение при постоянном объеме и горение при постоянном давлении, которые имеют теоретические кпд 47% и 27% соответственно. Повышенный кпд детонационного горения обусловлен присущим ему особым процессом тепловыделения, при котором сгорание топливовоздушной смеси происходит в десятки тысяч раз быстрее, чем при традиционном горении, которое основано на фронте распространения пламени. Хотя оно и эффективнее, детонационным горением может быть и труднее управлять. Например, трудности возникают при инициировании и поддержании детонационного горения. Вместе с тем, недавние достижения в технологиях управления двигателями позволяют преодолеть эти трудности.
КРАТКОЕ ИЗЛОЖЕНИЕ СУЩНОСТИ ИЗОБРЕТЕНИЯ
Предложены детонационный двигатель и способ детонации. Детонационный двигатель может создавать стабилизированную стоячую детонационную волну. Течение нагретых продуктов сгорания, возникающих за счет стабилизированной детонации, можно преобразовывать в механическую энергию. Например, детонационный двигатель может иметь камеру сгорания, в которой стабилизируется детонационная волна. Камера может быть частично окружена, например, лопатками турбины, которые обеспечивают препятствия для ограничения свободного расширения детонационной волны и поэтому способствуют формированию стабилизированной стоячей волны.
В одном аспекте детонационный двигатель может включать в себя первый впуск, имеющий первый конец, соединенный по текучей среде с первой емкостью, и второй конец, соединенный по текучей среде с детонационным двигателем, второй впуск, имеющий первый конец, соединенный по текучей среде со второй емкостью, и второй конец, соединенный по текучей среде c детонационным двигателем, напротив первого впуска. Первый и второй впуски можно выровнять по общей оси. Детонационный двигатель может дополнительно включать в себя первое сопло, соединенное с первым впуском, второе сопло, соединенное со вторым впуском, и сепаратор, расположенный между вторым концом первого впуска и вторым концом второго впуска. Первый впуск, второй впуск и сепаратор могут быть расположены вдоль общей оси.
В некоторых вариантах осуществления детонационный двигатель может включать в себя препятствия, конфигурация которых обеспечивает стабилизацию детонации в детонационном двигателе. Детонационный двигатель может включать в себя одну или несколько турбин, прикрепленных с возможностью вращения к детонационному двигателю. Турбина может дополнительно включать в себя лопатки, конфигурация которых обеспечивает стабилизацию детонации в детонационном двигателе. Конфигурация первой емкости может обеспечивать прием окислителя. Конфигурация второй емкости может обеспечивать прием топлива. Первое сопло может находиться вблизи второго конца первого впуска. Второе сопло может находиться вблизи второго конца второго впуска. Первое сопло может быть расположено внутри первого впуска. Второе сопло может быть расположено внутри второго впуска.
В еще одном аспекте способ детонации смеси топлива и окислителя может предусматривать введение окислителя в детонационный двигатель через первый впуск, введение топлива в детонационный двигатель через второй впуск, причем первый и второй впуски можно выровнять по общей оси, и детонацию смеси топлива и окислителя на некотором расстоянии от общей оси в пределах цилиндрической области детонации. Способ может предусматривать ускорение окислителя через первое сопло и ускорение топлива через второе сопло. Способ может предусматривать направление окислителя к первой стороне сепаратора и радиально наружу от общей оси и направление топлива ко второй стороне сепаратора, которая противоположна первой стороне, и радиально наружу от общей оси.
В некоторых вариантах осуществления первый впуск может иметь первый конец, соединенный по текучей среде с первой емкостью, и второй конец, соединенный по текучей среде с детонационным двигателем. Второй впуск может иметь первый конец, соединенный по текучей среде со второй емкостью, и второй конец, соединенный по текучей среде с детонационным двигателем. Первый и второй впуски можно выровнять по общей оси. Ускорение окислителя через первое сопло может создавать сверхзвуковой поток, и ускорение топлива через второе сопло может создавать сверхзвуковой поток. Способ может предусматривать расширение продуктов сгорания, являющихся результатом детонации смеси, через турбину для совершения работы. Способ может предусматривать обеспечение препятствий, препятствуя расширению продуктов сгорания, являющихся результатом детонации смеси. Способ предусматривать стабилизацию детонации смеси в детонационном двигателе. Конфигурация препятствий в детонационном двигателе может обеспечивать достижение стабилизации детонации. Препятствия могут быть лопатками турбины, которые могут, например, преобразовывать кинетическую энергию продуктов сгорания в механическую энергию.
Другие аспекты, варианты осуществления и признаки будут очевидны из нижеследующего описания, чертежей и формулы изобретения.
КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ
На фиг.1 представлено сечение детонационного двигателя.
На фиг.2 представлено сечение детонационного двигателя, иллюстрирующее пример цилиндрической области детонации.
На фиг.3 представлена моделируемая стоячая волна при детонации, выраженная терминами давления.
На фиг.4 представлена моделируемая стоячая волна при детонации, выраженная терминами температуры.
На фиг.5 изображена геометрия стоячей детонации в радиально расширяющемся потоке.
На фиг.6 изображены кривые зависимости положения от скорости адиабатического расширения и детонационной ударной волны.
На фиг.7a)-i) изображены радиусы детонаций как функция набегающего потока, заданного в числах Маха.
На фиг.8 изображены возможные профили стационарной детонации.
На фиг.9 изображен радиус возможной детонации как функция начального потока.
На фиг.10 изображен минимальный радиус детонации как функция E и Q.
На фиг.11 изображена потеря устойчивости детонации, которая начинается как стационарное решение, подобное прямоугольной волне.
На фиг.12 изображено расширение детонации, которая начинается как стационарное решение, подобное непрямоугольной волне.
На фиг.13 изображена стабилизация расширяющейся детонации.
На фиг.14 изображено расширение детонационной волны в присутствии препятствия.
На фиг.15 изображена подробная структура зоны реакции.
ПОДРОБНОЕ ОПИСАНИЕ
Достижение стоячей детонационной волны может оказаться трудно осуществимым, но использование вычислительных моделей может резко повысить вероятность успеха. Например, посредством итеративного подхода вычислительная модель может позволить исследователю идентифицировать эффективные геометрии и граничные условия без сооружения серии прототипов. Вычислительная модель должна учитывать законы сохранения, механизмы химических реакций и соображения устойчивости. Детонационную волну можно моделировать как ударную волну, за которой следует зона реакции. Чтобы упростить вычисления и сократить время вычислений, детонационную волну можно моделировать как существующую в идеальной текучей среде, в которой изменение молекулярной массы газов отсутствует. Можно предположить, что подвод энергии происходит в ходе одноступенчатой химической реакции. Чтобы дополнительно упростить вычисления, можно пренебречь эффектами теплопроводности и вязкости. Получаемые в результате двумерные реактивные уравнения Эйлера можно эффективно решать, например, на кластере параллельных компьютеров, чтобы протестировать устойчивое присутствие стоячей детонационной волны.
В детонационном двигателе сверхзвуковой поток реактивной смеси может выходить из сопла Лаваля и может образовывать, например, диск Маха. Сжатие газа в диске Маха может инициировать химические реакции ниже по течению, так что на некотором расстоянии от этого диска образуется зона реакции. Об одном из ранее проведенных исследований этой конфигурации потока сообщалось в первоисточнике [10], где сказано, что авторы смогли достичь образования комплекса стоячей волны и зоны реакции. Несмотря на то, что эта конфигурация напоминает конфигурацию детонации, более уместным, возможно, было бы назвать ее «горением, обуславливаемым ударным воздействием», а не «детонацией», потому что диск Маха может устойчиво существовать в таком потоке независимо от химических реакций. Насколько нам известно, степень важности роли, которую зона реакции играет в существовании и свойствах диска Маха, в упомянутом первоисточнике не уточняется.
Сверхзвуковой поток топливовоздушной смеси можно генерировать с помощью питающих емкостей высокого давления, позволяющих нагнетать топливо и окислитель, например, через суживающееся-расширяющееся сопло в контрольный канал. Изучались детонации, происходящие по потоку и против потока, и исследовалось влияние пограничных слоев потока в канале на скорости детонации. В документе [21] рассмотрена стабилизация путем изменения геометрии канала численными методами, пользуясь моделью с многоэтапной кинетикой для смеси азот-воздух. Авторы того документа сделали вывод, что для стабилизации детонационной волны в канале можно использовать изменения поперечного сечения канала.
Детонацию в сверхзвуковом потоке также можно стабилизировать посредством плохообтекаемого тела. В такой конфигурации детонацию можно стабилизировать на клине в сверхзвуковом потоке реактивного газа. Химические реакции могут начинаться на некотором расстоянии ниже по течению от носа клина и могут влиять на структуру ударной волны, воздействующей на клин. Аналогично случаю реакции ниже по течению от диска Маха в сопле Лаваля, ударная волна в этой конфигурации может существовать даже при отсутствии химических реакций, т.е. возможно горение, обуславливаемое ударным воздействием.
Детонацию в сверхзвуковом потоке можно стабилизировать посредством фиксации ее положения в осевом направлении, но допуская при этом вращение в азимутальном направлении. Такая конфигурация может способствовать достижению непрерывно спиновой детонации. Сверхзвуковой поток воздуха может попадать в тонкий зазор между двумя соосными цилиндрами и смешиваться с топливом. Топливо можно впрыскивать, например, из внутреннего цилиндра. Смесь может непрерывно гореть во вращающейся детонационной волне, которая распространяется в окружном направлении. Эту конфигурацию можно использовать в детонационных двигателях, например, в качестве альтернативы пульсирующим детонационным двигателям.
Как подробнее обсуждается ниже, используя уравнения Эйлера для расчета течения вязких сжимаемых газов применительно к идеальному газу, реагирующему в соответствии с моделью одноступенчатой реакции Аррениуса, можно обнаружить существование детонации в установившемся состоянии, стоячей в сверхзвуковом потоке, истекающем из центрального источника. Условия притока, такие как энтальпия заторможенного потока смеси и число Маха для потока, при существовании и структуре решения для стационарной детонации могут играть роли в устойчивости детонационной волны. В зависимости от параметров, возможно либо отсутствие решения, либо наличие одного или двух решений задачи для установившегося состояния. В случае сосуществования двух стационарных решений, одно из этих решений может соответствовать относительно малому радиусу детонации, а другое - большому ее радиусу. Эти два типа решений могут иметь совершенно разные структуры. Решение, соответствующее малому радиусу, может иметь структуру, подобную прямоугольной волне, с большой зоной индукции, примерно в 100 раз превышающей длину согласно решению типа стационарной плоской волны для установившегося состояния в модели Зельдовича-Неймана-Деринга (ZND). В отличие от этого, решение, соответствующее большому радиусу, не имеет явной зоны индукции.
Кроме того, можно определять устойчивость решений для установившегося состояния и рассчитывать динамику детонации, например, путем численного интегрирования двумерных реактивных уравнений Эйлера. В качестве начальных условий ниже рассматриваются и решения типа прямоугольной волны, и регулярные стационарные решения. Можно получить быстрое сжатие, длящееся десятки промежутков времени длительности установившейся полуреакции, и медленное расширение, длящееся сотни тех же самых промежутков времени. Решение, соответствующее большому радиусу, может привести к очень медленно расширяющейся детонации, при которой ячеистые структуры быстро образуются до того, как происходит сколько-нибудь значительная детонация. Эти расширяющиеся детонации можно стабилизировать, размещая малые жесткие препятствия ниже по течению от радиуса детонации в установившемся состоянии, так что на некотором расстоянии от центра источника устанавливается стабильная ячеистая детонация.
Инициирование детонации посредством препятствий за счет размещения этих препятствий сначала в не реагирующем адиабатическом потоке газа тоже можно определять численно. Скачки уплотнения, которые образуются, например, вокруг препятствий, могут быстро превращаться в детонацию, которая начинает расширяться. С помощью тех же самых препятствий можно получить такую же заключительную структуру детонации, как в случае инициирования.
Вариант осуществления может предусматривать сверхзвуковой поток горючей смеси. Этот сверхзвуковой поток может течь радиально из круглого источника и подвергаться детонационному горению ниже по течению. Поток можно направлять между двумя параллельными пластинами с помощью внешнего источника смеси, обеспечивающего приток из центра. Условия высокоскоростного потока на выходе из источника можно генерировать посредством быстрого расширения, например, через сопло. Детонация в этом варианте осуществления может представлять собой самоподдерживающуюся волну, поскольку существование ударной волны зависит от присутствия химических реакций. Простое адиабатическое расширение могло бы происходить и в отсутствие химической реакции.
Основные реактивные уравнения Эйлера могут допускать решение для установившегося состояния с самоподдерживающейся детонацией, стоячей на некотором конечном расстоянии от источника. Природу такого решения можно изучить, рассматривая роль различных параметров задачи, таких как свойства смеси и условия притока. С помощью вариантов двумерного моделирования можно исследовать линейную динамику детонации, например - ее устойчивость. Детонация обычно неустойчива, и эта неустойчивость проявляется не только в форме образования ячеек, но и в форме общего радиального сжатия и расширения фронта детонации. Предотвратить расширение можно, например, путем установки нескольких жестких препятствий в потоке ниже по течению.
В отсутствие химических реакций двумерный радиально симметричный сверхзвуковой поток идеального горючего газа, истекающий из круглого источника заданного радиуса, - это поток адиабатический, а поскольку он также сверхзвуковой, во время расширения скорость потока и число Маха увеличиваются, а все такие параметры, как давление, температура и плотность, уменьшаются с увеличением расстояния. Эти особенности можно установить из уравнений динамики газов, как будет показано ниже. С помощью анализа, например в рамках теории ZND, можно определить условия, при которых стационарная радиально-симметричная детонационная волна может существовать в адиабатическом радиально расширяющемся потоке. С помощью решений численными методами, например, при помощи двумерных реактивных уравнений Эйлера с одноступенчатой кинетикой Аррениуса, можно показать устойчивость такой стационарной структуры к двумерным возмущениям.
Схематическая геометрия стоячей детонации в радиально расширяющемся потоке показана на фиг.5. Центральный источник имеет радиус r0, от которого реактивный газ истекает при начальных условиях течения, задаваемых давлением p0, плотностью ρ0 и скоростью u0 потока. Поскольку поток во время сверхзвукового расширения ускоряется, на некотором расстоянии rs условия течения могут стать такими, что ниже по течению от rs сможет установиться структура стоячей детонационной волны. Состояние перед детонационной ударной волной определяется параметрами p1, ρ1, u1, а состояние сразу же за ударной волной определяется параметрами p2, ρ2, u2. Для стоячей детонации ее скорость D должна быть такой же, как u1. За ударной волной существует точка перехода через скорость звука, имеющая координату r=r*, где скорость потока равна локальной скорости звука u*=c*.
Как обсуждается ниже, такая структура стоячей детонации может существовать в широком диапазоне условий. Более того, возможно сосуществование нескольких решений в одних и тех же условиях притока.
Если температура газа, истекающего из источника, является достаточно низкой, и поскольку она уменьшается во время расширения, поток из источника можно считать адиабатическим, а реакциями можно пренебречь. Радиус детонации rs априори неизвестен, но может быть определен, например, путем согласования состояния притока с условиями Ренкина-Гюгонио и условиями потока ниже по течению от детонационной ударной волны. Существование точки перехода через скорость звука за ударной волной является важной составляющей такой структуры детонации. Поскольку скорость потока сразу же за ударной волной является дозвуковой, а поток продуктов достаточно далеко от ударной волны является сверхзвуковым, отсюда следует, что на некотором расстоянии от источника, r*>rs, скорость потока равна локальной скорости звука.
Скорость детонации в газах обычно составляет порядка нескольких километров в секунду, и для поддержания такой детонации на некотором фиксированном расстоянии начальную энергию потока можно сделать достаточно высокой. Можно оценить суммарную энергию начального потока, которая необходима для установления стоячей детонации. В предположении отсутствия потерь на трение суммарная энтальпия потока
(1)
есть величина сохраняющаяся. Здесь T - температура потока, u - скорость потока, W - молярная масса смеси, а R - универсальная газовая постоянная. Во время адиабатического расширения температура потока может уменьшаться, и поэтому скорость потока может увеличиваться. Даже если вся потенциальная энергия потока преобразуется в кинетическую энергию, скорость потока не сможет стать больше, чем . С другой стороны, скорость детонации имеет нижний предел, который может быть установлен. В предположении, что радиус сходящейся детонации гораздо больше, чем размер зоны реакции, эффектами кривизны детонации можно пренебречь, а скорость детонации можно приближенно выразить как , где T - температура окружающей среды перед детонационной ударной волной. Таким образом, скорость детонации всегда больше, чем . Чтобы поддержать детонацию на фиксированном расстоянии, поток окружающей среды следует ускорить до скорости детонации, и поэтому условие для начальной энергии потока можно переписать как .
Реактивные уравнения Эйлера
Можно предположить, что двумерный сжимаемый реактивный идеальный газ описывается системой реактивных уравнений Эйлера, состоящих из уравнений сохранения массы, количества движения и энергии, а также химической реакции:
где ω(p, ρ, λ) - скорость реакции, относительно которой можно предположить, что она описывается упрощенной моделью в форме «Реагент→Продукт» и имеет скорость, задаваемую следующим образом:
где Е - энергия активации, ρ - плотность, р – давление, k - постоянная скорости реакции, а λ - переменная протекания реакции. Доля массы реагента составляет 1-λ, а доля массы продукта составляет λ, где λ=0 соответствует свежей смеси, а λ=1 - полностью сгоревшему газу. Уравнение состояния задается следующим образом:
где γ - постоянное отношение удельных теплоемкостей. Тогда суммарная энергия в (4) определяется как .
Условия ударной волны
Условия скачка Ренкина-Гюгонио имеют вид:
где D - нормальная составляющая скорости ударной волны, а un - нормальная составляющая скорости потока. Как обычно, сама ударная волна не реактивна, поэтому выражение (11) удовлетворяется тривиально. Для детонации в установившемся состоянии скорость детонации равна скорости потока окружающей среды, т.е. D=u1, так что в рамках рассмотрения проблемы в лаборатории детонация является стационарной. Для решения в круговых функциях в установившемся состоянии, потоки перпендикулярны поверхности скачка уплотнения, поэтому для идеального газа условия Ренкина-Гюгонио можно переписать в виде:
где ρ1, u1, p1, ρ2, u2, p2 - плотность, скорость и давление перед ударной волной и за ударной волной соответственно. Исходя из этих уравнений, состояние за ударной волной можно переписать в явном виде языком терминов состояния перед ударной волной.
Как обсуждается ниже, систему для установившегося состояния можно сократить до двух обыкновенных дифференциальных уравнений (ОДУ) для u и λ и до двух законов сохранения для суммарной энергии и массы. В предположении, что скорость реакции является нулевой в потоке выше по течению, можно использовать условия Ренкина-Гюгонио только для скорости потока, и они принимают очень простую форму:
(15),
где - суммарная энергия в источнике, которая в установившемся состоянии сохраняется вдоль потока.
Безразмерные уравнения и выбор параметров
В задачах, где детонация распространяется, переходя в состояние покоя с постоянными параметрами, естественным является масштабирование переменных по отношению к постоянному состоянию или по отношению к состоянию за ударной волной. Детонация может стоять или распространяться в неоднородной среде, и поэтому наилучший выбор масштабов не сразу очевиден. Опорное давление pa, опорную плотность ρa, температуру и скорость можно выбрать. Их можно принять соответствующими 0,1 МПа (1 атм) и 300 К. Будучи в общем случае независимыми от конкретного выбора такого опорного состояния, основные уравнения могут сохранять свою форму и с выбором масштабов длины и времени, как поясняется ниже.
Остальными масштабами являются масштаб длины, для которого можно выбрать длину l1/2 зоны полуреакции для плоской детонации, которая распространяется, переходя в вышеупомянутое опорное состояние, и масштаб времени . Для заданного набора параметров реакции - Q, E и γ - задание этих масштабов равносильно фиксации постоянной скорости реакции посредством интеграла
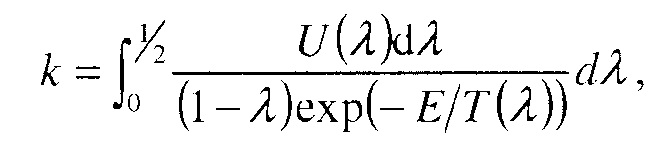
где
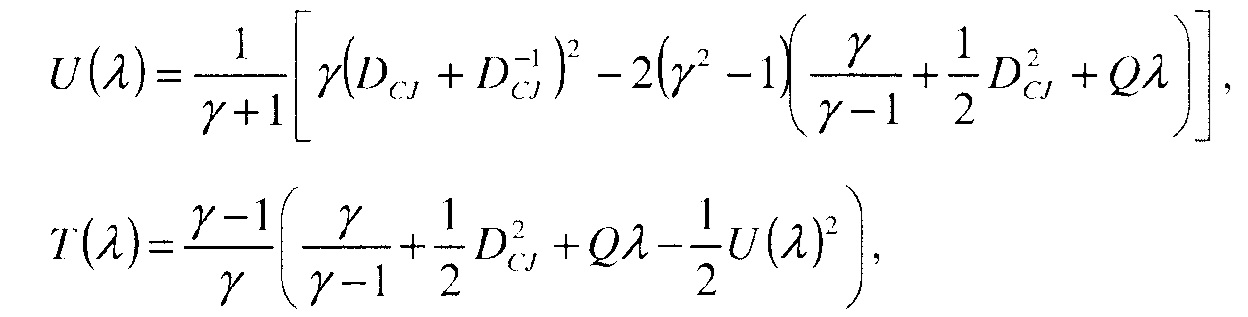
и
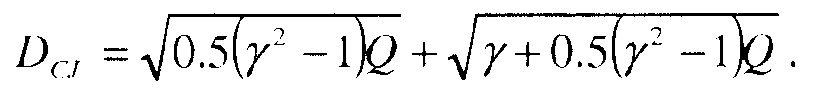
Таким образом, в нижеследующих расчетах масштабы длины и времени можно определить посредством k, а это значение изменяется в зависимости от значений Q, E и γ на основании безразмерного состояния выше по течению, согласно которому p=1, ρ=1 и T=1.
Радиально-симметричное решение для установившегося состояния
В радиально-симметричном случае установившегося состояния уравнения движения принимают вид:
Эти уравнения можно сократить до двух ОДУ для u и λ
а масса и энтальпия являются сохраняемыми величинами:
Здесь - локальная скорость звука, r - радиальная координата, а М - поток массы. В нижеследующих вычислениях уравнения 20 и 21 можно переписать как автономную систему трех уравнений, где неизвестные параметризованы посредством τ
Эта система и два закона сохранения для массы и энтальпии (уравнения 22 и 23) вместе с граничными условиями в источнике и дальнем поле и условием ударной волны (уравнение 15) могут полностью определить структуру стоячей детонации. Состояние окружающей среды, которая находится между источником и детонационной ударной волной, - это состояние адиабатического расширения. Уравнения установившегося состояния можно сократить до одного алгебраического уравнения, например, для скорости потока:
где r0 - радиус источника, а u0 скорость потока у источника.
Форма уравнения (20), в котором представлены вероятность точки перехода через скорость звука в потоке, где u=c, и вероятность регуляризации путем установления числителя уравнения (20) равным нулю в той точке, может задавать условие существования решения. В принципе, процедура решения требует найти всю структуру при заданных условиях притока. Вместе с тем, ни местонахождение ударной волны, ни местонахождение точки перехода через скорость звука нельзя вычислить непосредственно. Для определения последних необходима итеративная процедура.
Поскольку точка перехода через скорость звука является седловой точкой, численно более робастной процедурой может оказаться нахождение решения в окрестности точки перехода через скорость звука как расширения, выражаемого рядом Тейлора, с последующим шагом вбок от него и продолжением итерирования посредством регулярного численного метода. Положение точки перехода через скорость звука может быть неизвестным в явном виде. За счет фиксации условий в источнике, система уравнений (24) имеет один угадываемый параметр в точке перехода через скорость звука. Это может быть радиус r* точки перехода через скорость звука, радиус rs детонации или значение переменной λ* протекания реакции в точке перехода через скорость звука. Чтобы удовлетворить граничным условиям в источнике, можно просканировать один из этих параметров, например, λ*.
Чтобы проиллюстрировать этот алгоритм, допустим, что источник имеет радиус r0, поток в источнике имеет давление p0 и плотность ρ0, а скорость сверхзвукового потока u0>c0. Как только оказывается известным поток в источнике, можно вычислить H и М, которые сохраняются по всей области. Поскольку H - фиксированное значение, можно записать выражение для радиуса r* точки перехода через скорость звука как функцию λ* путем установления числителя уравнения (24)(a) равным нулю и использования c*=u*:
где скорость реакции и скорость звука зависят только от λ* посредством следующих выражений:
Значение λ* может быть угадываемым параметром в этом алгоритме. Путем его сканирования, например между 0 и 1, можно удовлетворить начальным условиям в источнике. Если найти λ* в этом процессе, то, поскольку H известно, можно проинтегрировать систему уравнений (24) до точки перехода через скорость звука в потоке, где смесь становится свежей, λ(τs)=0. Эта точка может определять начало зоны реакции, которая представляет состояние за ударной волной. Следовательно, радиус скачка уплотнения задается следующим образом: rs=r(τs). После этого, применяя условие (15) скачка уплотнения, можно легко получить состояние перед ударной волной и все адиабатические профили путем оценки уравнения (25).
Решение, определяющее детонацию в установившемся состоянии, может существовать только в определенном диапазоне начальных параметров в источнике. Рассматривая процедуру сканирования с другой точки зрения, можно предположить, что H - величина фиксированная. Тогда, решая уравнение (24) для диапазона значений переменной протекания реакции в точке перехода через скорость звука 0<λ*<1, можно задать зависимость скорости потока за ударной волной от радиуса детонации . Эта функция является монотонно убывающей и выпуклой. Такую же зависимость можно вычислить для адиабатического расширения с помощью уравнений (25) и (15). Последняя кривая также является выпуклой и монотонно убывающей, но она содержит один дополнительный параметр - начальную скорость потока в источнике . Регулируя u0, можно переключать адиабатическую кривую относительно кривой детонации . При некоторых значениях начальной скорости потока эти кривые пересекаются, что подразумевает существование нескольких решений в установившемся состоянии для конкретного потока в источнике. Отсутствие точек пересечения означает несуществование установившегося решения задачи.
На фиг.6 показаны три условия. Показаны кривые «положение-скорость» адиабатического расширения и детонационной ударной волны, при этом кривые и имеют два пересечения на виде (a), одно пересечение - на виде (b) и ни одного пересечения - на виде (c). Параметры смеси были выбраны следующими: γ=1,2; E=40; Q=30; H=1,3Hmin; и r0=50. На фиг.6: для вида (a) M0=4,40, для вида (b) M0=4,0, а для вида (c) M0=4,67.
Важным следствием вышеизложенных рассуждений является то, что радиус детонации для конкретной смеси может зависеть только от двух параметров: значения суммарной энтальпии потока и значения начальной скорости потока. При некоторых значениях этих параметров решениz может не существовать, а при других значениях возможно одно или два решения.
Существование и структура решения для установившегося состояния
Может оказаться важным идентифицировать, когда решение существует, а если оно не существует, то идентифицировать, где находится детонация. В структуре решения для установившегося состояния могут играть роль свойства смеси и условия притока.
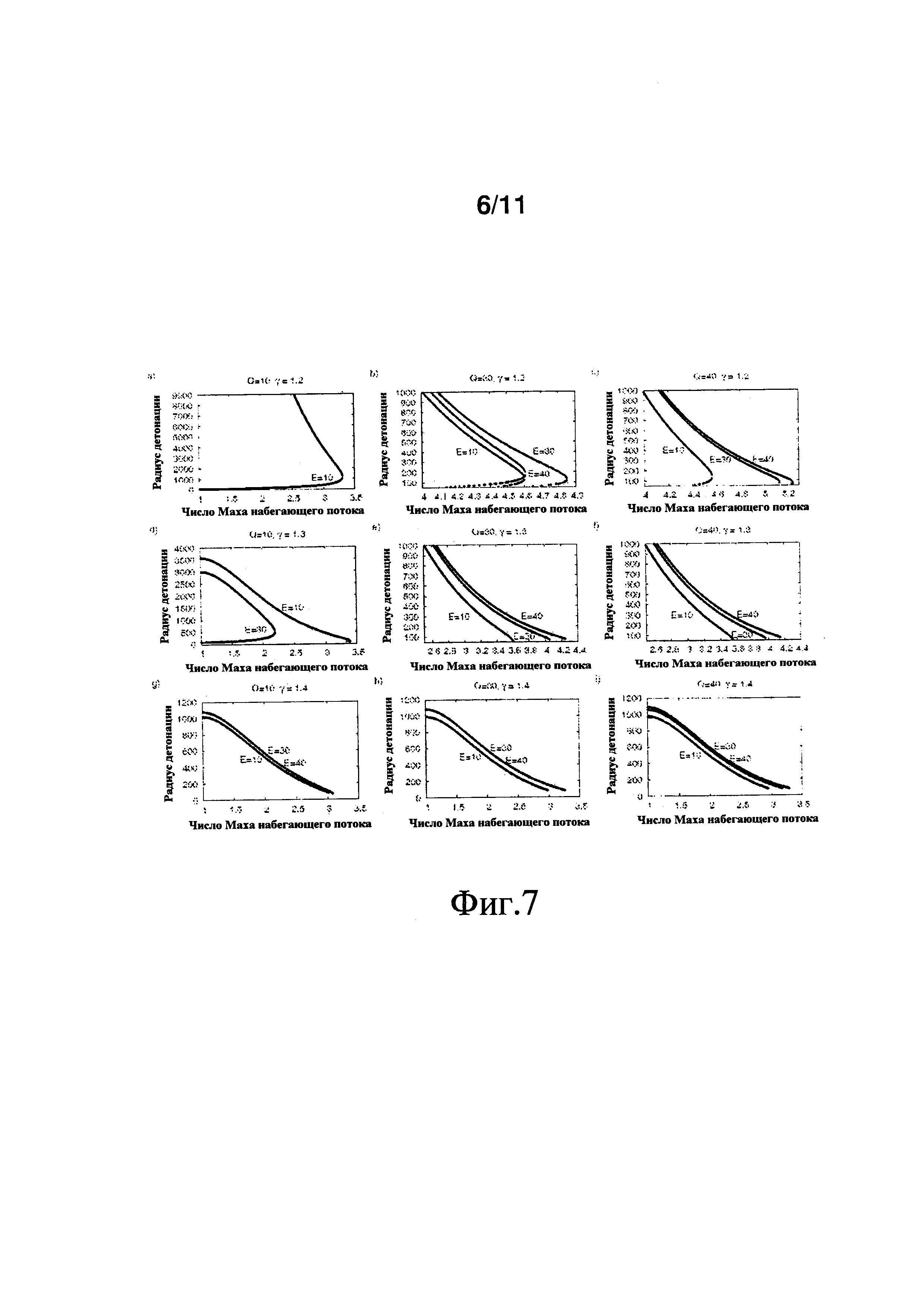
На фиг.7 изображены радиусы детонаций как функция набегающего потока, заданного в числах Маха. Радиус детонации задан как функция числа Маха, M0, потока источника для различных E, Q и γ. Радиус источника r0=50, а энтальпия заторможенного потока H=1,3Hmin=1,3Q(γ2-1). На фиг.7 показано, как число Маха набегающего потока может повлиять на радиус детонации при фиксированном радиусе источника и фиксированном значении энтальпии заторможенного потока. Чертежи также отображают роль, которую играют энергия Е активации, тепловыделение Q и отношение γ удельных теплоемкостей. Существование относительно малого радиуса и относительно большого радиуса на этих чертежах является типичным. При γ=1,2 увеличивающееся Q требует больших значений М0, чтобы достичь стационарного решения. В то же время верхний предел радиуса уменьшается на порядок величины от более чем 9000 до более чем 1000, когда Q изменяется от 10 до 30. Это может указывать, что число Маха набегающего потока достаточно велико; целесообразно иметь детонацию, радиус которой примерно в 1000 раз больше, чем размер зоны реакции. Увеличение γ обладает интересующим воздействием, проявляющимся не только в уменьшении верхнего предела радиуса детонации примерно в те же 1000 раз для зон реакции, но и в значительном уменьшении числа Маха набегающего потока, от примерно 3-5 для γ=1,2 до 1-3. Влияние энергии активации может быть не монотонным, т.е., когда энергия активации увеличивается, радиус детонации может сначала увеличиваться, а потом уменьшаться. Интересный случай представлен посредством фиг.7(d) при E=30. Даже при числе Маха источника, равном 1, существуют два решения, при этом нижний предел радиуса rs составляет примерно 100, а верхний - примерно 3000.
Если энтальпия H смеси мала, т.е. близка к минимальному значению Hmin=Q(γ2-1), то энергия недостаточна для ускорения потока до высоких скоростей даже на расстоянии вплоть до бесконечности. Тогда верхняя ветвь кривой rs(M0) отсутствует, а нижняя по-прежнему существует. Если - с другой стороны - H очень велика, то верхняя ветвь практически осуществима, а нижняя ветвь исчезает по той причине, что соответствующий радиус становится меньше, чем радиус источника. Для отсутствия нижней ветви на некоторых из видов согласно фиг.7 есть свои причины.
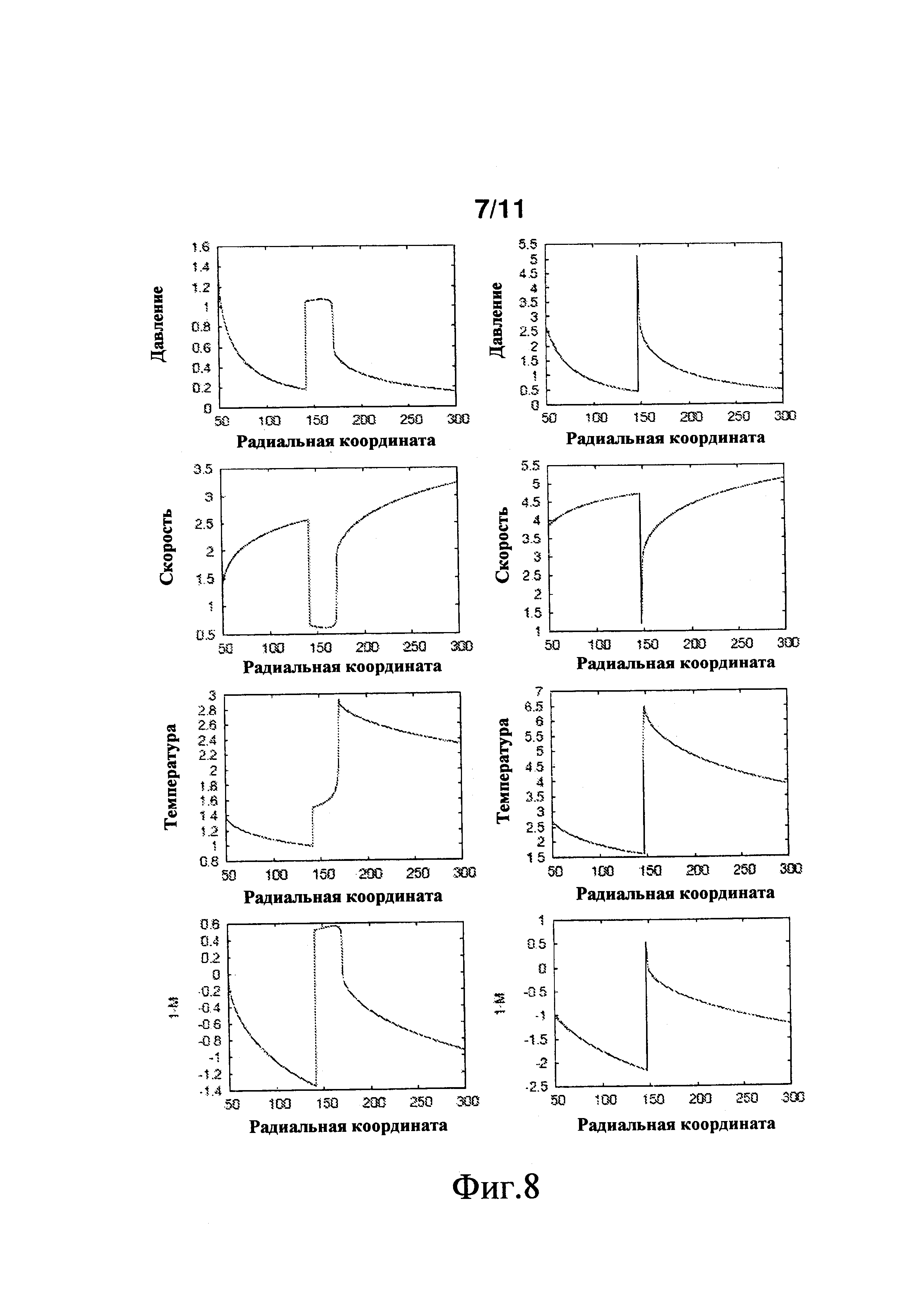
Интересно исследовать структуру решений для установившегося состояния, соответствующую верхним и нижним решениям, показанным на фиг.7. На фиг.8 построены профили p, u, T и 1-M, которые соответствуют нижнему решению (левый столбец) и верхнему решению (правый столбец) при аналогичных условиях потока. Для обоих случаев решение представлено в форме прямоугольной волны.
Левый столбец соответствует детонации типа прямоугольной волны на нижней ветви кривой «rs-M», когда существуют две ветви. Параметры для левого столбца являются следующими: γ=1,2, Q=10, E=30, r0=50, ρ0=1, p0=1,40, u0=1,30, М0=1,0, H=2,1Hmin. Для правого столбца существует только верхняя ветвь. Параметры для правого столбца являются следующими: γ=1,4, Q=10, E=30, r0=50, ρ0=1, р0=2,70, u0=3,90, M0=2,0, H=1,75Hmin.
Отличительным признаком решения, показанного слева, является структура, подобная прямоугольной волне, с довольно длинной зоной реакции. Видно, что профили давления, температуры, скорости и числа Маха демонстрируют почти постоянные состояния за ударной волной до тех пор, пока не высвобождается тонкая область энергии. Имеется зона индукции, которая занимает приблизительно 30 единиц длины. После нее всю энергию можно высвобождать на расстоянии в несколько единиц длины. В отличие от этого структура для верхнего решения не отображает зону индукции, а зона реакции, как отчетливо видно, занимает лишь несколько единиц длины. Свойства смеси для этих двух случаев являются одинаковыми, однако условия притока выбирались по-разному, чтобы детонация имела место примерно на одном и том же расстоянии от начала отсчета. Следовательно, для одной и той же смеси можно изменять условия притока так, что на одном и том же радиусе смогут существовать две весьма разные стоячие детонации. Их устойчивость является решающим фактором, чтобы определить, существуют такие детонации или нет.
В предыдущих вычислениях фиксировали энтальпию притока и исследовали роль параметров смеси и числа Маха притока. Влияние энтальпии притока и числа Маха притока на радиус детонации для заданной смеси обсуждается ниже. Результат отображен на фиг.9.
На фиг.9 радиус детонации показан как функция числа Маха притока для различных значений энтальпии H заторможенного потока. Параметры смеси таковы: γ=1,3, Q=10, E=30. Радиус источника r0=50. За счет увеличения энтальпии смеси можно получить приближение верхнего решения меньшими значениями радиуса детонации. Радиус согласно нижнему решению тоже может уменьшаться по мере увеличения H. Этот результат согласуется с ожиданием, что чем выше энтальпия потока, тем проще ускорить его до скоростей, необходимых для установления стоячей детонации в потоке.
Можно идентифицировать области пространства параметров «Q-E», для которых решение по детонации существует при заданном M0. На фиг.10 минимальный радиус детонации отображен как функция Q и E для двух разных чисел Маха притока, М0=1 и М0=2, при γ=1,2 и γ=1,4. Верхние чертежи соответствуют γ=1,2 а нижние чертежи - γ=1,4. Левые чертежи соответствуют М0=1, а правые - М0=2. Радиус источника r0=50, а H=1,3Hmin. Интересная особенность на этих чертежах заключается в том, что для большего γ диапазон существования решения значительно шире, а минимальный радиус значительно меньше, чем в случае γ=1,2.
Радиус сходящейся детонации может зависеть от потока в источнике и от параметров смеси. Чтобы найти эту зависимость, можно решить полную систему уравнений (24) для диапазона этих параметров. Прежде, чем решать эту задачу, можно сделать некоторые аналитические оценки. Например, скорость потока в некоторой точке должна быть равна скорости детонации, т.е. uСJ=D, для стоячей детонации. Когда радиус детонации велик, скорость детонации можно оценить, например, по формуле Чепмена-Жуге

где T - температура как раз перед детонационной ударной волной. Постольку, поскольку энтальпия фиксирована, температура окружающей среды для адиабатического расширения является функцией только скорости потока

и поэтому можно записать следующее уравнение для скорости адиабатического потока в положении детонационной ударной волны:

Это уравнение можно решить относительно uCJ, и его решение вместе с уравнением (25) дает зависимость радиуса детонации от начальной скорости потока, т.е. rs(u0). Эта функция монотонно убывает: чем быстрее поток в источнике, тем раньше он достигает скорости DCJ Чепмена-Жуге. Эта оценка может дать существенно точное описание верхней ветви кривой «rs-M0».
Двумерные модели
Хотя решения для установившегося состояния существуют для широкого диапазона параметров задачи, может оказаться важным осмыслить их устойчивость. Детонации в газах часто неустойчивы к многомерным возмущениям. Однако два элемента данных конфигураций все же могут играть разъясняемую здесь роль, а именно неоднородный поток выше по течению от детонационной ударной волны и кривизна детонационной ударной волны.
На основании нижеследующего простого аргумента можно было бы сделать вывод, что фактически детонация в нашей конфигурации должна всегда быть неустойчивой даже по отношению к продольным возмущениям. Рассмотрим стационарную радиально-симметричную детонацию, стоячую на некотором расстоянии от центра, и представим, что она подвергается возмущению внутрь к источнику на малом расстоянии. Тогда, поскольку поток выше по течению после возмущения медленнее, чем перед возмущением, и поскольку детонация имеет тенденцию распространяться с постоянной скоростью относительно потока выше по течению, возмущенная ударная волна будет продолжать двигаться внутрь, что подразумевает устойчивость. В противоположной ситуации детонационной волны, подвергающейся возмущению наружу, поток выше по течению от возмущенной ударной волны быстрее, чем поток перед возмущением. Следовательно, по той же причине, по какой детонация имеет тенденцию распространяться с постоянной скоростью относительно состояния выше по течению, возмущенная ударная волна будет продолжать расширяться, что опять подразумевает устойчивость.
Однако эти простые аргументы не учитывают два важных эффекта, которые могут сыграть роль в динамике детонации: влияние кривизны на скорость детонации и поперечную неустойчивость, приводящую к образованию ячеек детонации. С увеличением кривизны скорость детонации может увеличиваться. Таким образом, когда возмущение детонационной ударной волны происходит, например, внутрь, ее скорость в установившемся состоянии будет уменьшаться. Такое уменьшение может оказаться достаточным для компенсации уменьшенной скорости потока выше по течению. Таким образом, сразу же после того, как происходит возмущение детонационной ударной волны внутрь, возможно новое установившееся состояние. Если эффект кривизны доминирует над эффектом сниженной скорости выше по течению, возмущение может фактически уменьшаться, приводя к устойчивости детонации.
Эффект кривизны может быть слабым, когда радиус детонации велик. Гораздо важнее то, что может установиться двумерная неустойчивость, порождая весьма нетривиальную многомерную динамику, при наличии которой ячеистые структуры начинают играть доминирующую роль. Как обсуждается ниже, двумерная эволюция детонации может начинаться решениями для установившегося состояния, которые соответствуют подобным прямоугольной волне, а также регулярным структурам детонации. Радиально-симметричные решения неустойчивы во всех случаях, однако природа неустойчивости является разной для двух видов стационарных решений. Можно найти решения как при сжатии, так и при расширении, а важное различие между ними задается временным масштабом неустойчивости, который гораздо меньше в случае сжатия, чем в случае расширения.
Расширяющуюся детонацию можно стабилизировать посредством нескольких препятствий, размещаемых на некотором расстоянии от центра за точкой перехода через скорость звука. Кроме того, стабилизируемую препятствиями детонацию можно инициировать посредством сверхзвукового потока, наталкивающегося на препятствия. Препятствия могут приводить к скачкам уплотнения, при которых детонация инициируется и может самоустанавливаться за счет соединения индивидуальных фронтов детонации от препятствий в один-единственный фронт, окружающий центральный источник.
Для двумерной модели можно использовать такой метод решения, как разработанный Тейлором, Касимовым и Стюартом. В этом методе решения возможно использование метода конечных объемов, где потоки можно вычислять, например, по взвешенному существенно неколебательному (WENO) алгоритму пятого порядка и можно проводить итерацию во времени, например, методом Рунге-Кутта с убыванием вариации (TVD-методом Рунге-Кутта) третьего порядка. Пространственную область можно дискретизировать как равномерную Декартову сетку с разрешением по меньшей мере 20 точек сетки на длительность полуреакции стационарной детонации. Число Куранта-Фридрихса-Леви (CFL) может составлять 0,5. Для распределенной параллельной архитектуры можно разработать код, например, воспользовавшись методом фиктивных ячеек. Можно задать граничные условия притока из источника, а в конце области можно задать условие оттока путем экстраполирования переменных. Можно сделать допущение о том, что препятствия являются абсолютно жесткими телами, а их границы можно отрабатывать, например, методом погруженных границ.
Неустойчивость стационарной круговой детонации
Чтобы осмыслить неустойчивость стационарных решений, можно проанализировать два случая, как показано на фиг.8 и 11. На фиг.11 показана потеря устойчивости детонации, которая начинается как установившееся решение, подобное прямоугольной волне, показанное на фиг.8. Моменты снимков от (a) до (c), соответственно: t=1, 10 и 40. Размер области составляет 600×600, а количество точек сетки составляет 1280×1280, что соответствует 64-м точкам на полузону реакции. Начальный радиус детонации составляет приблизительно 150. Через короткое время t=40 радиус уменьшился примерно до 100. Внимательный просмотр чертежей выявляет тот факт, что волна подвержена двумерной неустойчивости и что возникают ячейки детонации. Однако эти ячейки слабы и не приводят к заметному изменению круговой формы ударной волны. Ударное давление во время потери устойчивости увеличивается от примерно 1,1 в момент t=0 до 2,3 в момент t=40. Динамика остается, по существу, радиально-симметричной.
В отличие от случая сжатия, рассмотренного выше, на фиг.12 изображена расширяющаяся детонация. Расширение детонации, которая начинается как стационарное решение, подобное прямоугольной волне (как на фиг.8), показано на фиг.12. Моменты снимков от (a) до (c), соответственно: t=0, 150, 400. Размер области составляет 600×600, а количество точек сетки составляет 5120×5120, что соответствует 20-ти точкам на полузону реакции согласно решению для установившегося состояния. Начальное условие является таким же, как начальное условие согласно фиг.8 (правый столбец). Начальный радиус является почти таким же, как в случае сжатия, но структура зоны реакции при детонации весьма отличается, вследствие чего уменьшение давления за набегающей ударной волной является резким, а зона индукции не видна. Двумерная неустойчивость в этом конкретном случае является довольно сильной и быстро приводит к наступлению сильной ячеистой детонации. Наиболее важное отличие этого случая от предыдущего случая - сжатия - заключается в том, что расширение происходит значительно медленнее. Расширение детонации вдвое по сравнению с ее начальным радиусом занимает примерно 400 единиц времени. Это медленное расширение указывает, что можно было бы предотвратить расширение, размещая препятствия, которые замедляют расширяющийся поток продуктов реакции, в потоке ниже по течению от ударной волны.
На фиг.13 показана стабилизация расширяющейся детонации согласно фиг.12 посредством трех препятствий радиуса 10. Моменты снимков от (a) до (c), соответственно: t=10, 50 и 700. Размер области составляет 600×600, а количество точек сетки составляет 2500×2500, что соответствует 10-ти точкам на полузону реакции согласно решению для установившегося состояния.
Стабилизация детонации посредством препятствий
Чтобы увидеть, на самом ли деле можно стабилизировать расширяющуюся детонацию, рассмотренную в предыдущем разделе, можно поместить несколько препятствий в поток как раз ниже по течению от точки перехода через скорость звука в установившемся состоянии. Возникает масса возможностей, зависящих, например, от количества, размера и формы препятствий. Вместе с тем, важно, что для предотвращения расширения достаточно небольшого количества препятствий. Скачки уплотнения, которые образуются перед препятствием, могут замедлять поток продуктов, так что детонационная ударная волна может оставаться стабилизированной в области между источником и препятствиями. Точное положение и форма результирующей детонационной волны могут зависеть от выбора препятствий и особенностей смеси, а также от условий источника.
В качестве примера, на фиг.13(a) показано, что вокруг препятствий может происходить нарастание малых скачков уплотнения, а образование большого скачка уплотнения треугольной формы, как показано на фиг.13(c), может происходить ниже по течению от зоны реакции, обеспечивая стабилизирующую поддержку для стоячей детонации. Использование более трех препятствий, равноотстоящих друг от друга на одном и том же радиусе, в этом конкретном случае может привести к потере устойчивости волны. Является решение сжимающимся или стабилизированным - это может ощутимо зависеть от массы параметров, которые играют роль в этом явлении.
Инициирование детонации
При всех вычислениях можно принимать решение для установившегося состояния в качестве начального условия для двумерных моделей. Такое вычисление может дать понимание свойств устойчивости заданного решения для установившегося состояния. Неустойчивые решения для установившегося состояния могут оказаться труднодостижимыми, например, поскольку такие детонации инициируются источником, что - в случае неустойчивости - может приводить к пульсирующей или ячеистой детонации, не приходящей к решению для установившегося состояния. Таким образом, инициирование стоячей детонации при радиальном оттоке может оказаться важным. Этого можно достичь разными средствами, например, путем инициирования детонации от не реагирующего сверхзвукового потока из источника после того, как такой поток наталкивается на жесткие препятствия.
Такие же препятствия, как рассмотренные выше, можно разместить в потоке, который вначале является не реагирующим и адиабатическим. На фиг.14 показано инициирование детонации посредством трех препятствий такого же типа и положения, как на фиг.13. Виды, показанные на фиг.14, соответствуют моментам времени: (a) - t=10, (b) - t=50, (c) - t=100, (d) - t=200, (e) - t=500 и (f) - t=1500. Размер области составляет 600×600, количество точек сетки составляет 2500×2500. Перед препятствием могут образовываться скачки уплотнения, как показано на фиг.14(a). Быстрое инициирование детонации может облегчить стабилизацию волн посредством препятствий. Однако в некоторый момент эти детонационные волны отделяются друг от друга, образуя независимые структуры, см. фиг.14(b). Вскоре после этого, раздельные фронты детонации сливаются и преобразуются, см. фиг.14(c-e), в такую же заключительную структуру, как показанная на фиг.13.
На фиг.15 показана подробная структура зон реакции согласно фиг.11-13. Фиг.15(a) - сжатие, t=10 - соответствует случаю, показанному на фиг.11(c). Фиг.15(b) - расширение, t=150 - соответствует случаю, показанному на фиг.12(b). Фиг.15(c) - детонация, стабилизируемая препятствиями, t=700 - соответствует случаю, показанному на фиг.13(c).
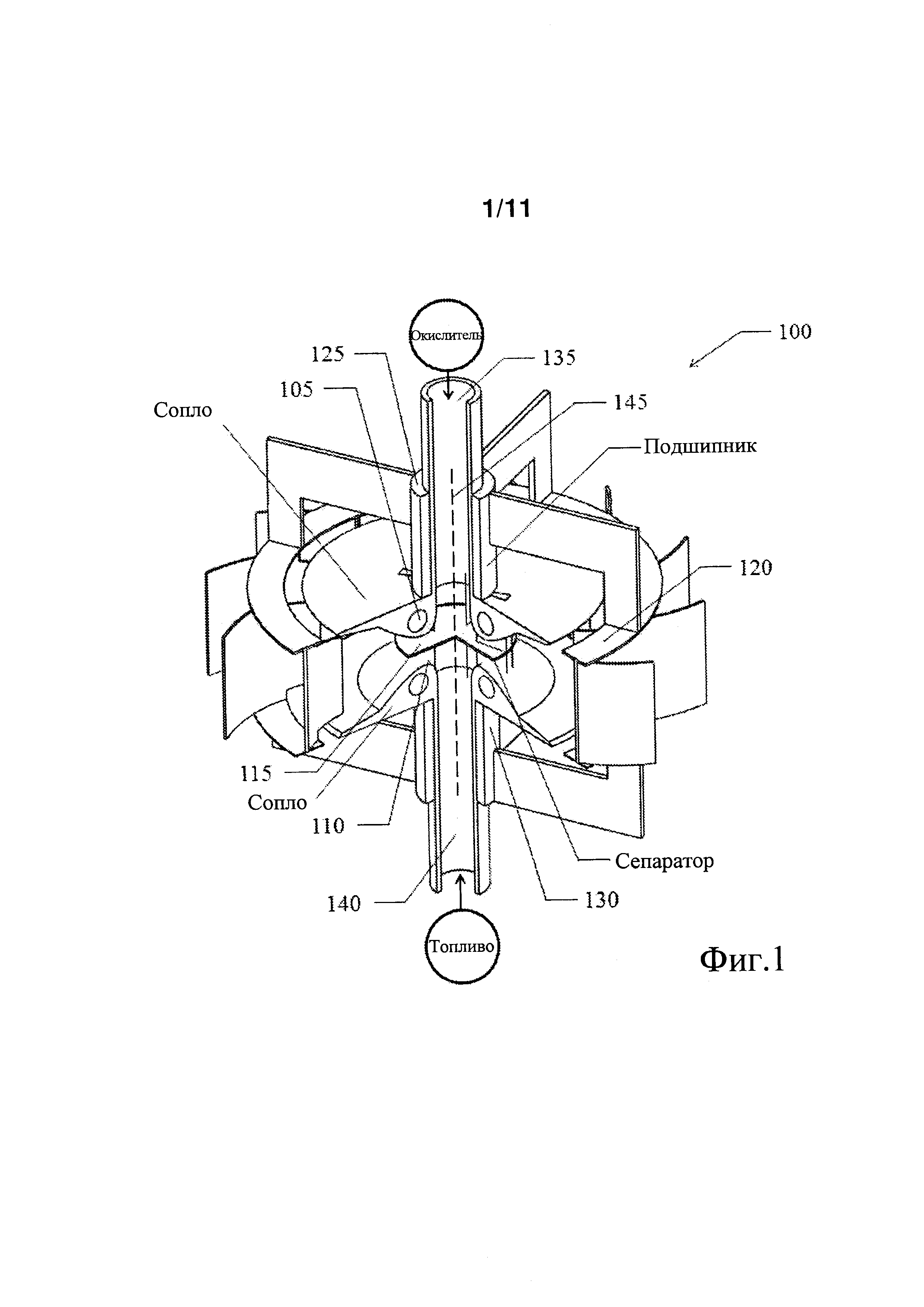
Возможный детонационный двигатель 100 может включать в себя первый впуск 135 для подачи окислителя в двигатель и второй впуск 140 для подачи топлива в двигатель. Первый впуск 135 может быть соединен по текучей среде с первой емкостью (не показана), содержащей окислитель, а второй впуск 140 может быть соединен по текучей среде со второй емкостью (не показана), содержащей топливо. В одном примере, первый и второй впуски (135, 140) могут быть расположены на противоположных сторонах двигателя, как показано на фиг.1. Следовательно, текучую среду и окислитель можно подавать в двигатель 100 в противоположных направлениях вдоль общей оси 145. Первый впуск 135 может включать в себя первое сопло 105, а второй впуск 140 может включать в себя второе сопло 110. Когда окислитель течет через первое сопло 105, сверхзвуковой поток может добираться внутрь двигателя 100. Аналогичным образом, когда топливо течет через второе сопло 110, сверхзвуковой поток может добираться внутрь двигателя 100.
Возможный детонационный двигатель 100 может включать в себя сепаратор 115, расположенный между первым и вторым впусками (135, 140) и вдоль общей оси 145. Первая сторона сепаратора 115 может обеспечивать диффузию первого потока окислителя радиально наружу от общей оси 145. Аналогичным образом, вторая сторона сепаратора 115 может обеспечивать диффузию второго потока топлива радиально наружу от общей оси 145. Когда первый и второй потоки движутся радиально наружу от общей оси 145, эти потоки, в конце концов, вытекают за внешний периметр сепаратора 115. В этот момент первый и второй потоки начинают смешиваться. Смешивание потоков происходит через некоторое время и расстояние, а смешанный поток становится более гомогенным, когда он движется наружу от общей оси 145. Когда смешивание произошло в достаточной степени, может возникнуть детонация.
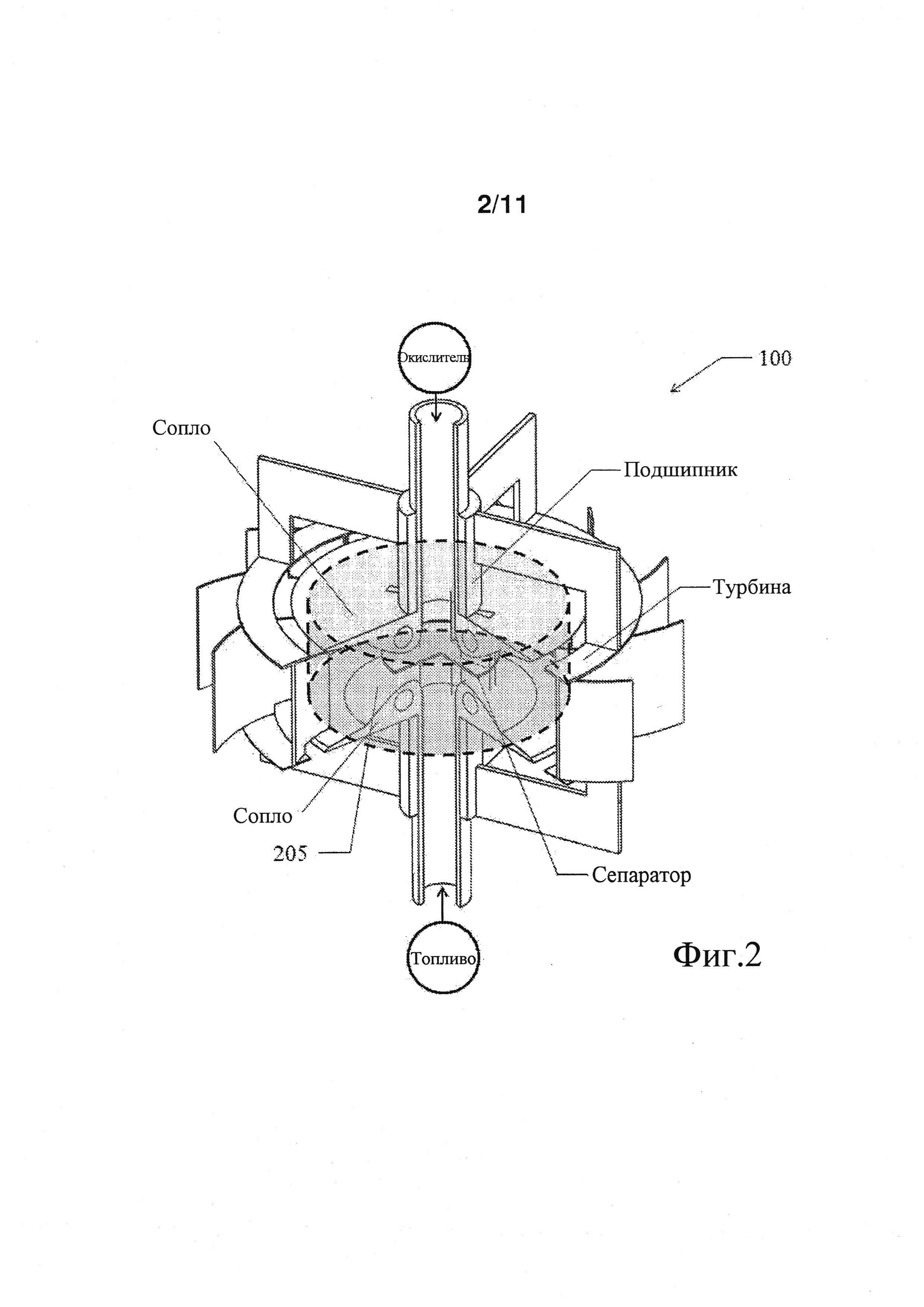
Детонацию можно инициировать в широком диапазоне начальных условий давления, но следует поддерживать определенные температуры и диапазоны химического состава во избежание резкого охлаждения. При ударных волнах в случае детонаций в газах типичными являются температуры порядка 1000 K и давления 3-4 МПа (30-40 бар), а в продуктах детонации типичными являются значения 2500-3000 K и 2-3 МПа (20-30 бар). Предпочтительные диапазоны для этих параметров могут зависеть от конкретных условий и желаемых результатов. Благодаря геометрии детонационного двигателя 100, условия, подходящие для детонации, присутствуют только на определенных расстояниях от общей оси 145. Вследствие этого детонация может возникать в пределах области 205 детонации, имеющей цилиндрическую геометрию, как показано на фиг.2. Область 205 детонации будет включать в себя стоячую детонационную волну.
Типичная область детонации может иметь тонкую ударную волну, за которой следует зона реакции, существование которой весьма зависит от состава смеси и условий горения. Зона реакции в типичном случае может иметь размер от доли миллиметра до нескольких миллиметров или более. Такое быстрое горение может оказаться выгодным в контексте минимизации влияний геометрических факторов и коэффициентов потерь на процесс горения при условии, что размер устройства значительно превышает эти масштабы. Когда смесь проходит через область 205 детонации, возникает детонация, и тепло высвобождается по мере превращения смеси в продукты сгорания. Горячие продукты сгорания продолжают двигаться радиально наружу от области 205 детонации и общей оси 145, а также проходят через турбину 120 и вращают ее, тем самым совершая полезную работу. Когда продукты сгорания проходят через турбину, из продуктов сгорания может выделяться энергия, вызывая уменьшение их температур и давлений.
Конфигурация турбины 120 может обеспечивать свободное вращение независимо от двигателя. В одном примере турбину можно устанавливать на первом и втором подшипниках (125, 130), прикрепленных к первому и второму впускам (135, 140), соответственно, как показано на фиг.1. В альтернативном варианте турбина 120 может вращаться на одном подшипнике или более чем двух подшипниках. В еще одном примере турбина 120 может не быть единым целым с двигателем 100. Например, турбину 120 можно устанавливать в выхлопной трубе, выходящей из двигателя 100, как обычно и бывает в автомобильных приложениях. Хотя показана и описана турбина 120, это не является ограничением; ее можно заменить любым аналогичным компонентом для совершения работы в результате движения продуктов сгорания с повышенными температурами и давлениями.
Чтобы достичь стоячей детонационной волны, окислитель и топливо можно подавать в область 205 детонации со скоростью, равной скорости результирующей детонационной волны. В качестве примера, отметим, что если бы детонационная волна в противном случае распространялась бы со скоростью 2 км/сек при температуре и давлении, обнаруживаемых внутри детонационного двигателя 100, то топливо и окислитель надо было бы подавать в область 205 детонации со скоростью 2 км/сек, чтобы это дало стоячую детонационную волну в области 205 детонации. В одном примере окислитель может покидать первое сопло 105 со сверхзвуковой скоростью примерно 2 км/сек, и топливо может покидать второе сопло 110 со сверхзвуковой скоростью примерно 2 км/сек.
На фиг.3 и 4 представлены возможные вычислительные модели, иллюстрирующие стабилизированные детонационные волны, выраженные терминами давления или температуры. Эти модели были основаны на вычислениях для идеального газа, представляющего собой стехиометрическую смесь азота и кислорода, разбавленную 70%-ным гелием, истекающую со сверхзвуковой скоростью из источника диаметром 10 (в единицах толщины зоны реакции при стационарной плоской детонации). Газ расширяется сначала без химических реакций и ускоряется до тех пор, пока не переходит в детонационную ударную волну, после чего начинает гореть. Процесс горения является неравномерным и приводит к характеристической многомерной зоне реакции с поперечными ударными волнами, распространяющимися вдоль основного скачка уплотнения, как показано на обоих упомянутых чертежах. На фиг.3 показано поле давлений в барах. Давление, которое сначала уменьшается во время расширения из источника, испытывает значительный рост по детонационной ударной волне, после чего уменьшается во внешних областях потока, когда газообразные продукты сгорания выбрасываются радиально с высокой скоростью. На фиг.4 показана температура потока в единицах 395 K.
Продукты сгорания в возможном детонационном двигателе могут взаимодействовать с вращающимися лопатками. Это взаимодействие может способствовать достижению нескольких вещей. Оно может обеспечивать необходимую тягу для совершения полезной работы. Взаимодействие может стабилизировать зону реакции детонации за счет снижения радиального расширения. Детонацию можно стабилизировать, помещая препятствия в потоке за детонационной ударной волной. Чтобы смоделировать этот эффект стабилизации посредством вращающихся лопаток, можно разместить некоторое количество малых жестких круговых препятствий по кольцу определенного радиуса. Эти препятствия могут быть ясно видны на графике температуры как малые белые пятна там, где видны рывки вихрей, сбрасываемых с препятствий, иными словами, в головных частях вихревых дорожек. В возможном варианте осуществления вращающиеся лопатки с не такой геометрией, как на упомянутых чертежах, могут способствовать достижению стабилизации в двигателе. Такие лопатки могли бы обеспечить и средство для преобразования кинетической энергии детонации в механическую энергию двигателя, и средство для стабилизации детонации. Положение препятствий может повлиять на радиус круговой детонации в установившемся состоянии, но можно предотвратить неограниченное расширение детонационной волны за счет присутствия этих препятствий. Достичь детонационного горения можно как при этой геометрии, так и при других геометриях.
Подробности одного или нескольких вариантов осуществления приведены на прилагаемых чертежах и в описании. Другие признаки, задачи и преимущества станут очевидными из описания, чертежей и формулы изобретения. Хотя описано некоторое количество вариантов осуществления изобретения, следует понять, что в рамках существа и объема притязаний изобретения возможно внесение различных модификаций. Также следует понять, что прилагаемые чертежи не обязательно сделаны в масштабе, давая несколько упрощенное представление о различных признаках и основных принципах изобретения.
ЛИТЕРАТУРА
Нижеследующее во всей его полноте включено сюда посредством ссылки.
F.A. Bykovskii, S.A. Zhdan, and E.F. Vedernikov. Continuous spin detonations. Journal of Propulsion and Power, 22(6):1204-1216, 2006.
F.A. Bykovskii, V.V. Mitrofanov, and E.F. Vedernikov. Continuous detonation combustion of fuel-air mixtures. Combustion, Explosion and Shock Waves, 33(3):344-353, 1997.
A. Dadone. Symmetry techniques for the numerical solution of the 2D Euler equations at impermeable boundaries. International Journal for Numerical Methods in Fluids, 28(7):1093-1108, 1998.
W. Doring. Uber den detonationvorgang in gasen. Annalen der Physik, 43(6/7):421-428, 1943. W. Fickett and W.C. Davis. Detonation: theory and experiment. Dover Publications, 2011.
S. Gottlieb and C.W. Shu. Total variation diminishing runge-kutta schemes. Mathematics of Computation, 67(221):73-85, 1998.
K. Kailasanath. Review of propulsion applications of detonation waves. AIAA journal, 38(9):1698-1708, 2000.
J.H.S. Lee. The Detonation Phenomenon. Cambridge University Press, 2008.
X.-D. Liu, S. Osher, and T. Chan. Weighted essentially non-oscillatory schemes. Journal of Computational Physics, 115(1):200-212, 1994.
J.A. Nicholls and E.K. Dabora. Recent results on standing detonation waves. In Symposium (International) on Combustion, volume 8, pages 644-655. Elsevier, 1961.
G.D. Roy, S.M. Frolov, A.A. Borisov, and D.W. Netzer. Pulse detonation propulsion: challenges, current status, and future prospects. Progress in Energy and Combustion Science, 30(6):545-672, 2004.
P.M. Rubins and R.C. Bauer. Review of shock-induced supersonic combustion research and hypersonic applications. Journal of Propulsion and Power, 10(5):593-601, 1994.
R.I. Soloukhin. Shock waves and detonations in gases. Mono Book Corporation, 1966.
B.D. Taylor, A.R. Kasimov, and D.S. Stewart. Mode selection in unstable two-dimensional detonations. Combust. Theory Model, 13(6):973-992, 2009.
A.A. Vasil'ev, V.I. Zvegintsev, and D.G. Nalivaichenko. Detonation waves in a reactive supersonic flow. Combustion, Explosion and Shock Waves, 42(5):568-581, 2006.
B.V. Voitsekhovskii, V.V. Mitrofanov, and M.Y. Topchian. The Structure of Detonation Front in Gases. Report FTD-MTD-64-527. Foreign Technology Division, Wright Patterson Air Force Base, OH(AD 633-821)., 1966.
J. von Neumann. Theory of detonation waves. Office of Scientific Research and Development, Report 549. Technical report, National Defense Research Committee Div. B, 1942.
P. Wolanski. Detonative propulsion. Proceedings of the Combustion Institute, 2012.
Y.B. Zel'dovich. On the theory of propagation of detonation in gaseous systems. J. Exp. Theor. Phys., 10(5):542-569, 1940.
F. Zhang, editor. Shock Waves Science and Technology Library, Vol. 6: Detonation Dynamics, volume 6. Springer, 2012.
T.A. Zhuravskaya and V.A. Levin. Investigation of certain techniques for stabilizing detonation waves in a supersonic flow. Fluid Dynamics, 47(6):793-801, 2012.
Реферат
Детонационный двигатель содержит первый и второй впуски, первое и второе сопла и сепаратор. Первый впуск имеет первый конец, соединенный по текучей среде с первой емкостью, и второй конец, соединенный по текучей среде с детонационным двигателем. Второй впуск имеет первый конец, соединенный по текучей среде со второй емкостью, и второй конец, соединенный по текучей среде с детонационным двигателем, напротив первого впуска. Первый и второй впуски выровнены по общей оси. Первое сопло соединено с первым впуском. Второе сопло соединено со вторым впуском. Сепаратор расположен между вторым концом первого впуска и вторым концом второго впуска и вдоль упомянутой общей оси. Изобретение направлено на стабилизацию детонацию смеси. 2 н. и 17 з.п. ф-лы, 15 ил.

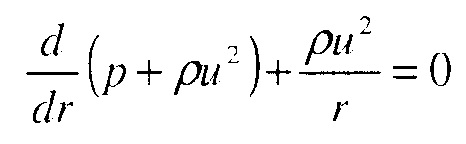
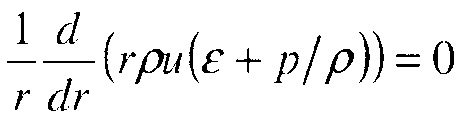
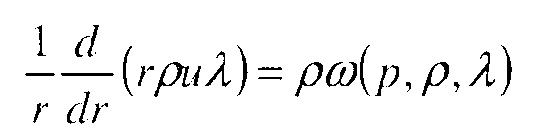
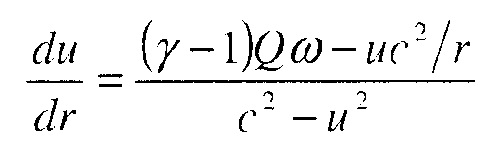


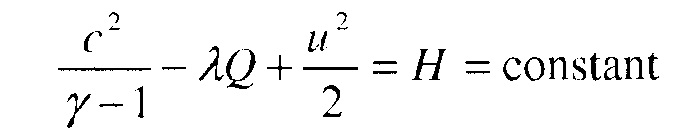
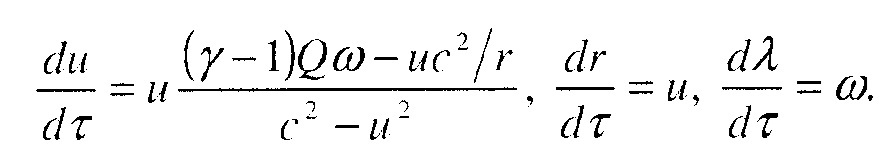

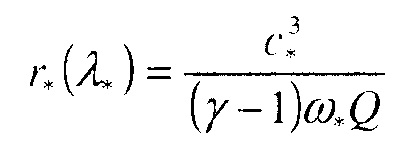
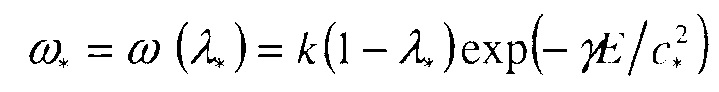
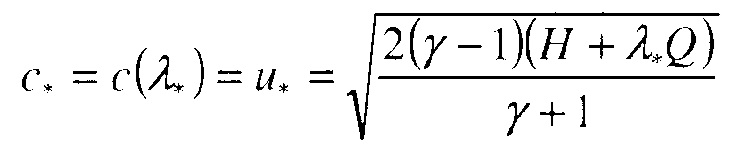

Комментарии