Способ томографической регистрации наклонной дальности и азимута положения надводных объектов и объектов над подстилающей поверхностью - RU2760976C1
Код документа: RU2760976C1
Чертежи
Описание
Изобретение относится к области радиолокационной техники, а именно к способам определения координат наклонной дальности и азимута:
- надводных объектов;
- объектов над подстилающей поверхностью.
В традиционной активной радиолокации с пассивным ответом существуют четыре варианта траектории, по которым отраженная от объекта и от иной поверхности электромагнитная волна возвращается к приемнику:
- непосредственно отраженный от объекта сигнал с траекторией «излучатель - объект - приемник»;
- сигнал с траекторией «излучатель - поверхность - объект - приемник»;
- сигнал с траекторией «излучатель - объект - поверхность - приемник», типа одиночного зеркального отражения;
- сигнал с траекторией «излучатель - объект - поверхность - приемник», описывающий диффузное рассеяние отраженного от объекта сигнала. Принято считать, что первые два варианта приведенного списка - есть полезный сигнал, из которого происходит определение координат; последние два варианта приведенного списка - есть ложный сигнал, который требует исключения.
Известен способ определения угломестной координаты низколетящей цели (НЛЦ), содержащий прием суммарного сигнала, отраженного от цели и одстилающей поверхности, на выходах четырех антенн, формирование дискриминационных характеристик (ДХ) измерителя координат в двух ортогональных плоскостях Sx и Sy и позиционирование максимума главного лепестка суммарной диаграммы направленности (ДН) антенной системы измерителя координат в направлении точки проекции цели на подстилающую поверхность, отличающийся тем, что центры четырех антенн измерителя координат располагаются попарно симметрично в горизонтальной и вертикальной плоскостях, на одном их выходов измерителя координат формируется дополнительный сигнал, представляющий собой разность суммарных сигналов пар элементов антенной системы, расположенных в горизонтальной и вертикальной плоскостях, который используется для формирования дополнительной ДХ, а угломестная координата и (при известной наклонной дальности) высота НЛЦ определяются из соотношений, использующих найденные таким образом ДХ. Достигаемый технический результат - повышение точности определения координат цели [1]. Известный способ не позволяет точно определить угловые координаты даже двух близко расположенных целей. Алгоритм, основанный на известном способе, достаточно чувствителен к расхождениям с реальной ситуацией и может давать значительные статистические ошибки даже в двухлучевой модели распространения электромагнитных волн.
Наиболее близким аналогом является способ измерений угловых координат группы N близко расположенных целей, возможно в условиях воздействия активных помех, заключающийся в том, что отраженные от целей истинные и ложные сигналы принимаются посредством цифровой линейной эквидистантной фазированной антенной решетки, представляющей собой матрицу, состоящую из 2N × 2N лучей, всего 4N2 лучей, и представляющую собой эквидистантную линейку диаграмм направленности, с одинаковыми суммарными диаграммами направленности и фазовыми центрами, расположенными на одинаковом расстоянии друг от друга, из полученных суммарных сигналов формируют вектор 2N сигналов строковых диаграмм
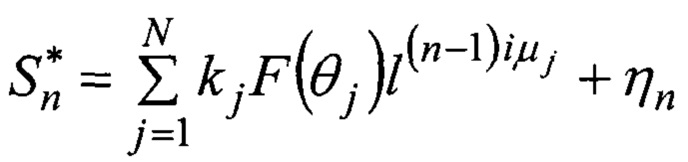
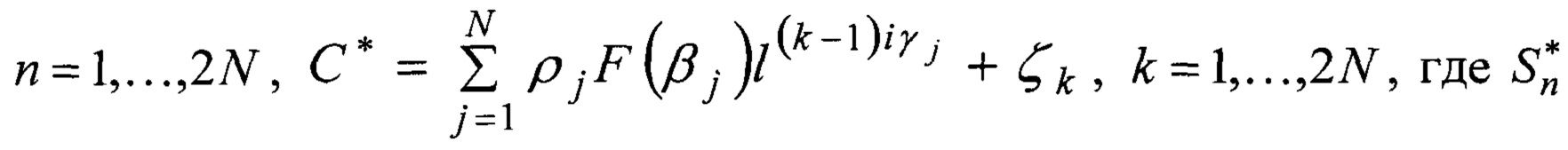
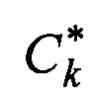
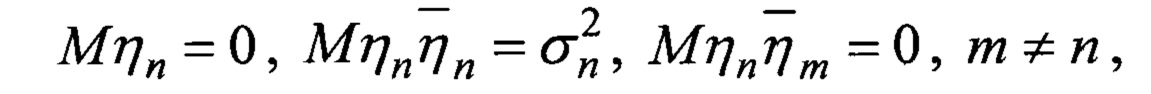
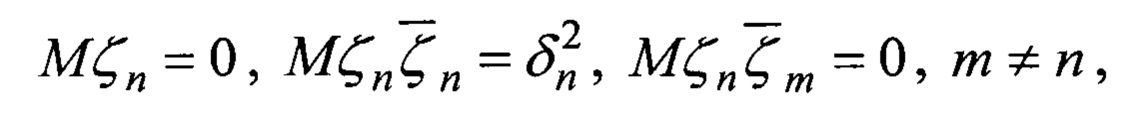
a F(θ) - функция амплитудно-фазового распределения суммарной диаграммы направленности, общая для всех строковых и столбцевых диаграмм, kj и ρj - комплексные коэффициенты отражения целей в вертикальной и горизонтальной плоскостях, μj и γj - обобщенные углы цели с номером j в горизонтальной и вертикальной плоскостях:
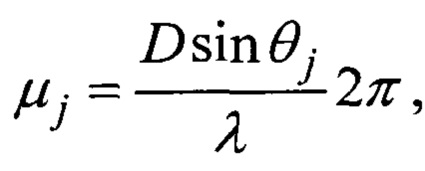
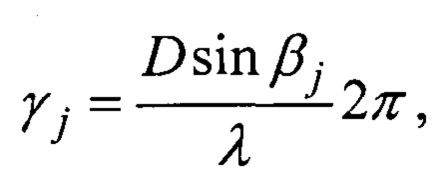
D - расстояние между фазовыми центрами приемных диаграмм, λ - длина волны, через
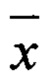
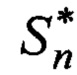
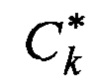
Задача состоит в разработке способа, позволяющего фиксировать координаты наклонной дальности и азимута положения рассеивающих объектов из множества объектов радиолокационной сцены, допускающего возможное отсутствие отраженного эхосигнала, характерного для традиционной активной моностатической радиолокации с пассивным ответом, но не исключающего возвращение радиоэха в результате многократного отражения сканирующего сигнала внутри Радиолокационной сцены, в том числе от других объектов и по другим азимутальным углом. Традиционным способом - активной радиолокацией с пассивным ответом - этого добиться невозможно.
Технический результат состоит в обнаружение скрытых объектов, находящихся вне прямой радиовидимости или в силу конструктивных особенностей не отражающих, а рассеивающих радиоволны.
Указанный результат достигается за счет того, что в способе томографической регистрации наклонной дальности
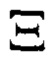
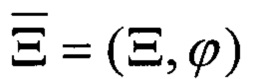
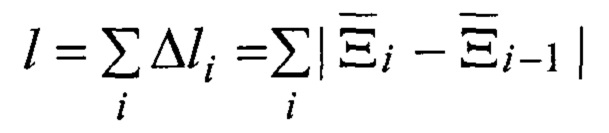
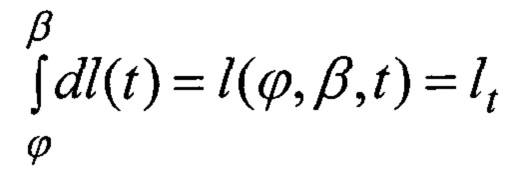
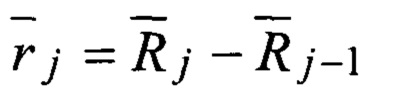
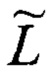
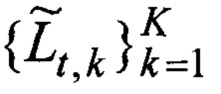
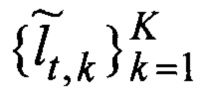
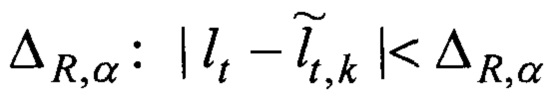

для каждого полученного (т.е. состоявшегося) или отсутствующего события lt наполнение функции P(lt) оценками исходной функцией
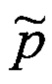
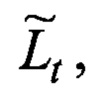
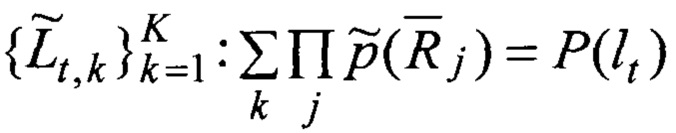
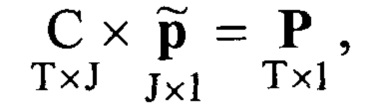
где вектор-столбец неизвестных
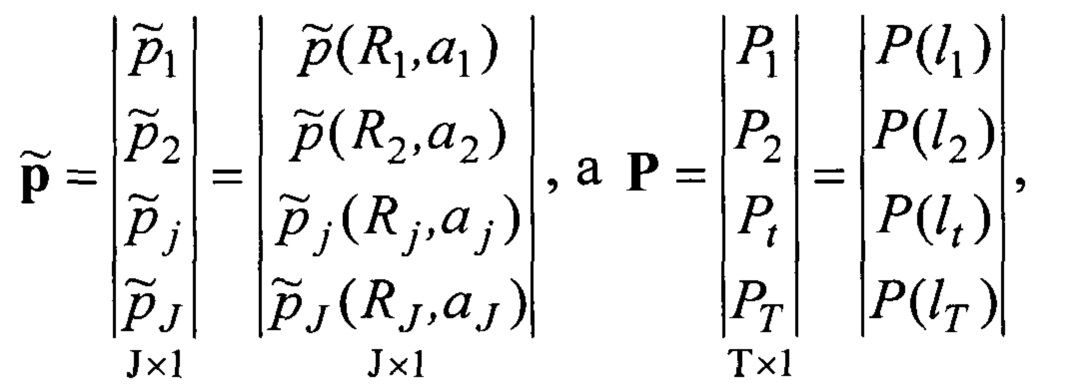
решением методом последовательных исключений Гаусса которой является вектор-столбец
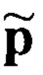
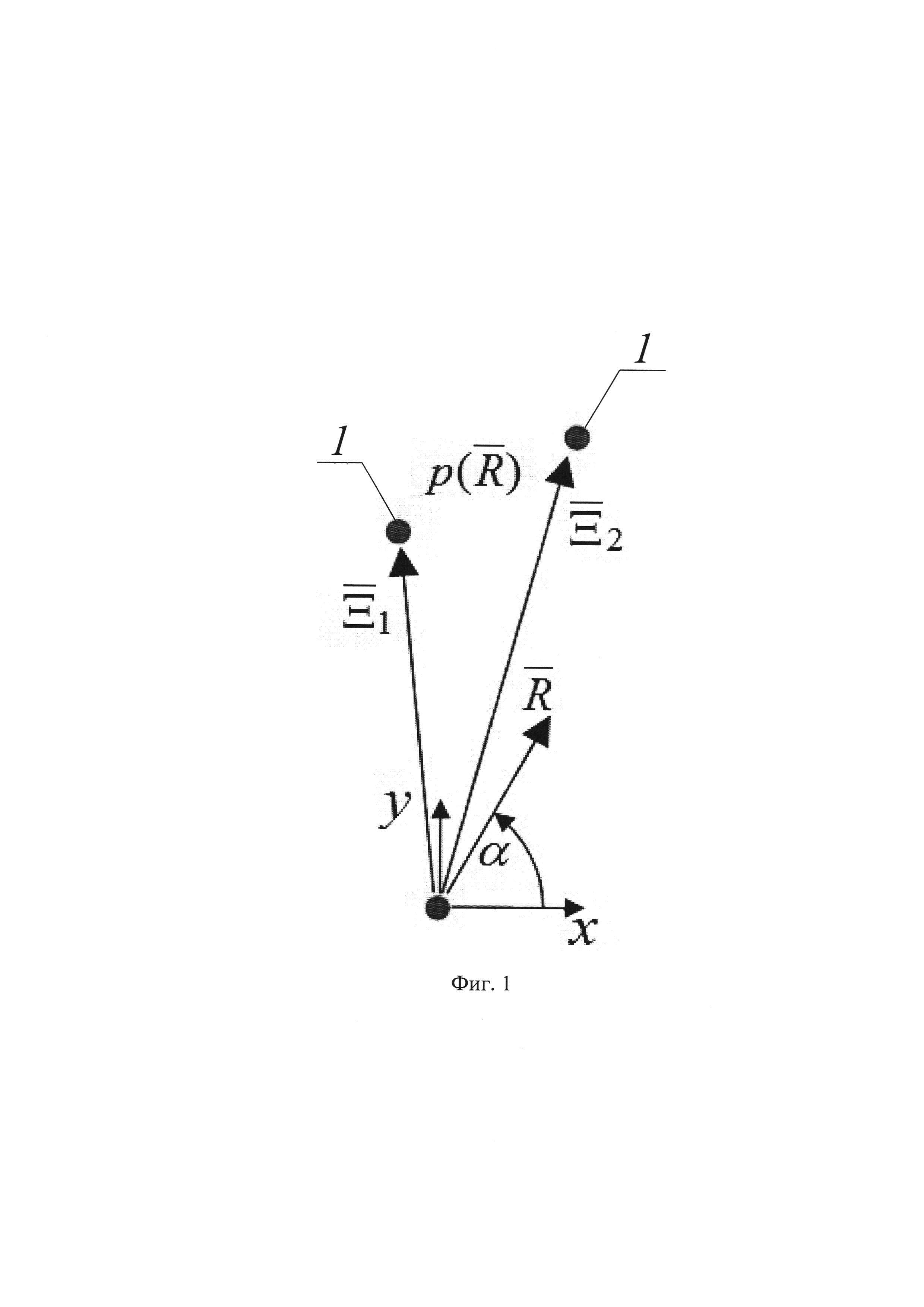
На фиг. 1 показана радиолокационная сцена.
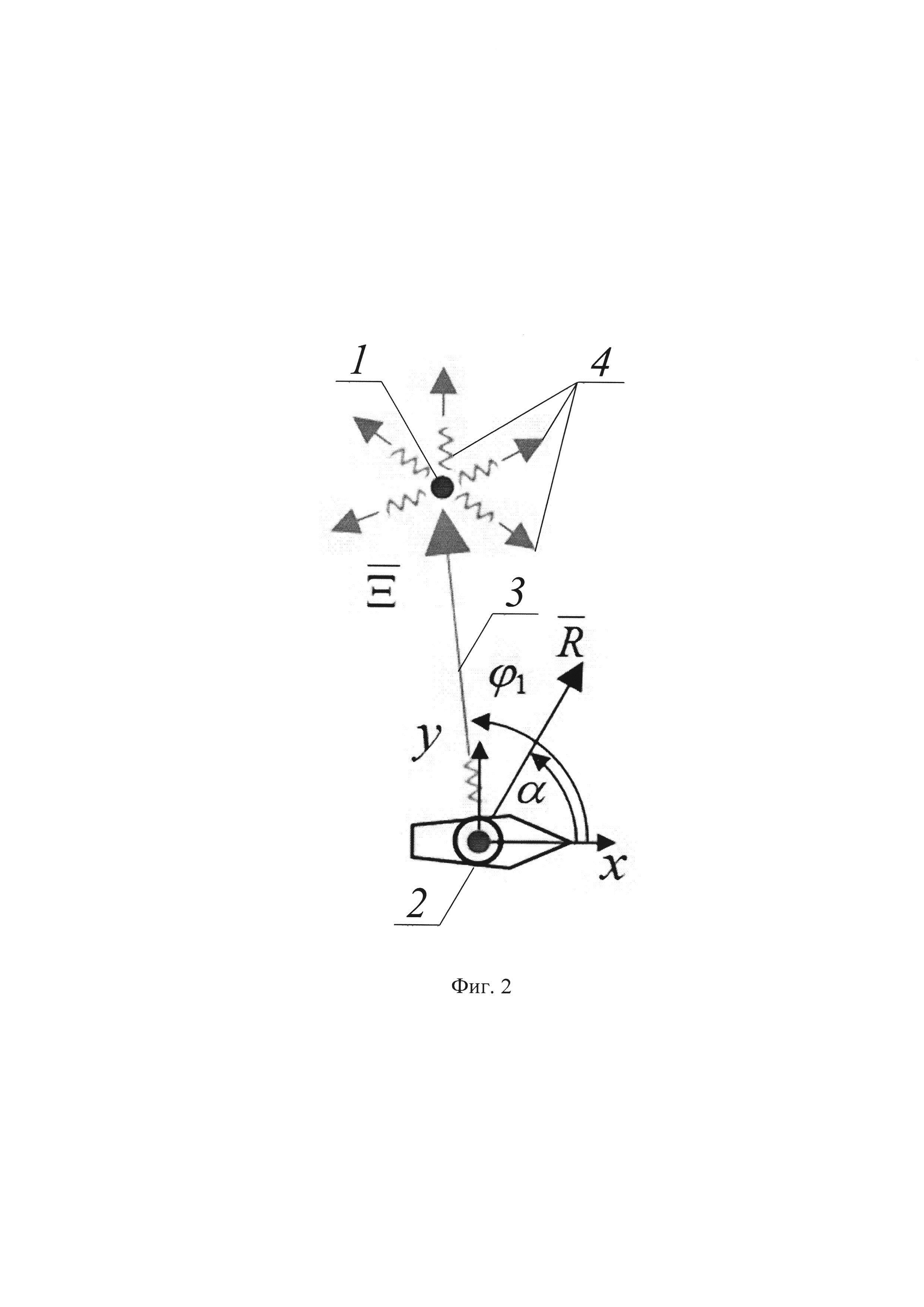
На фиг. 2 показаны принципы активной моностатической радиолокации с пассивным ответом.
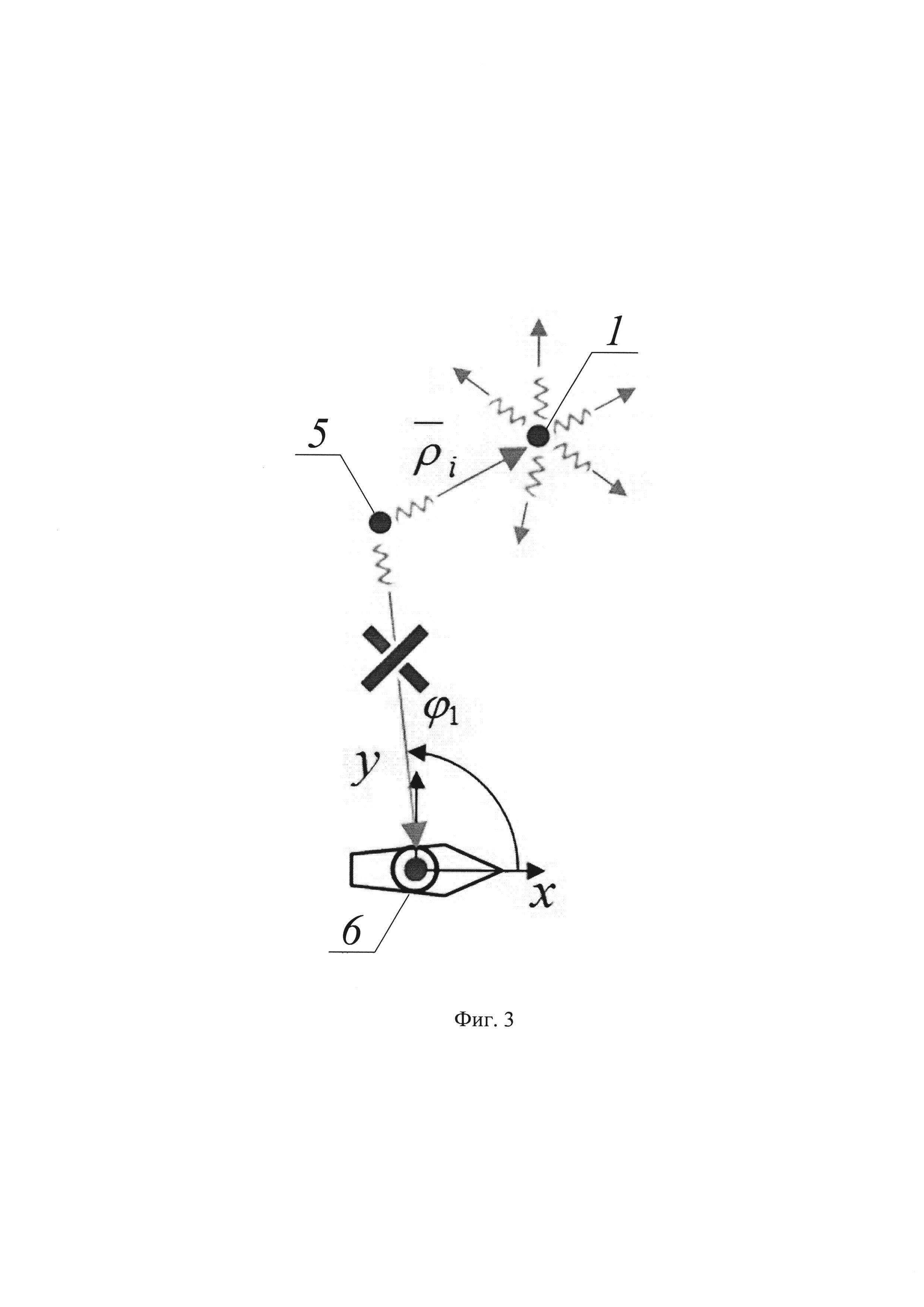
На фиг .3 показано зеркальное отражение и диффузное рассеяние отраженного от объекта сигнала.
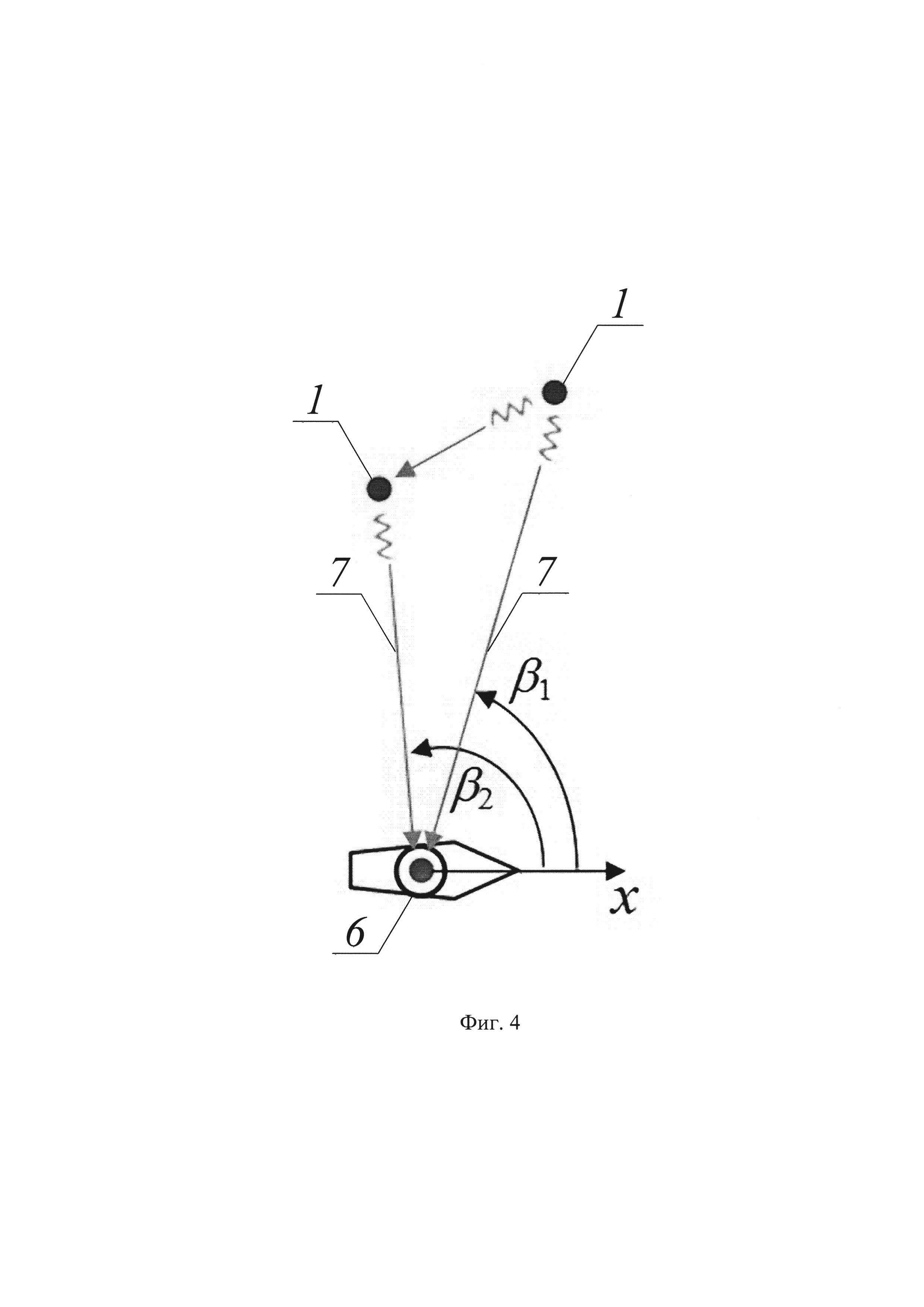
На фиг. 4 показаны трассы возвращения радиоэхо в результате многократного отражения зондирующего сигнала внутри радиолокационной сцены.
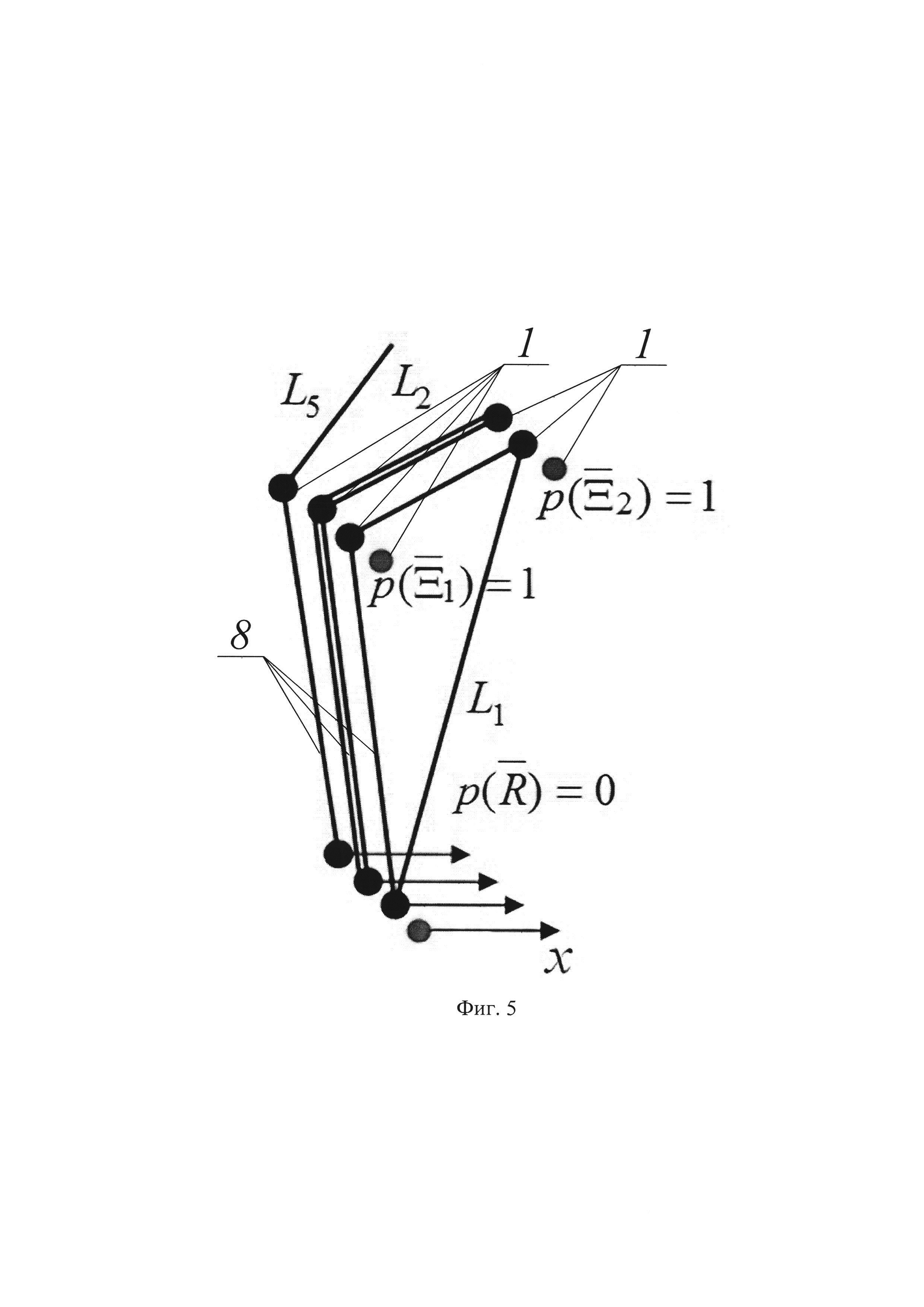
На фиг. 5 показаны траектории радиоэхо в результате многократного отражения зондирующего сигнала внутри радиолокационной сцены.
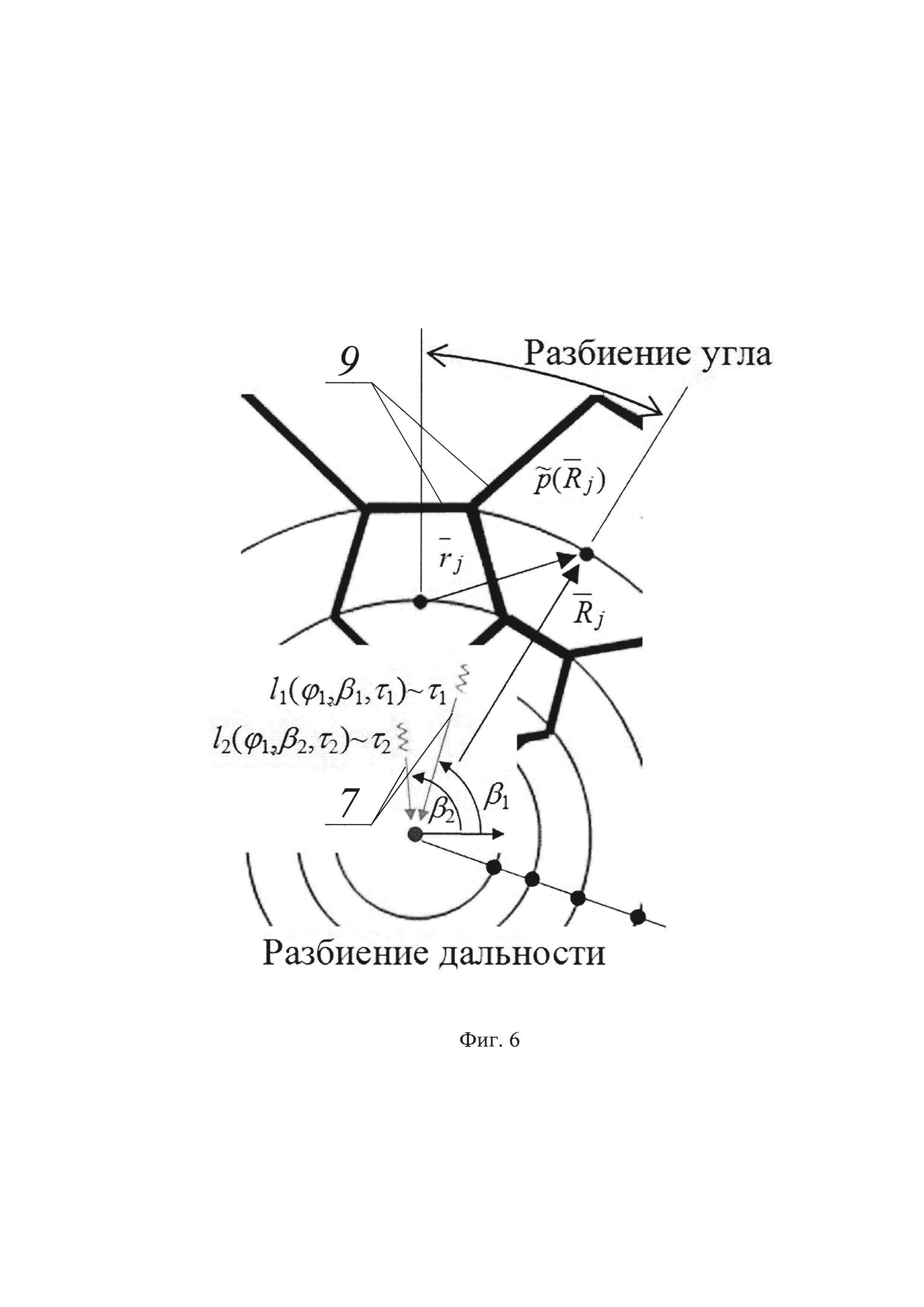
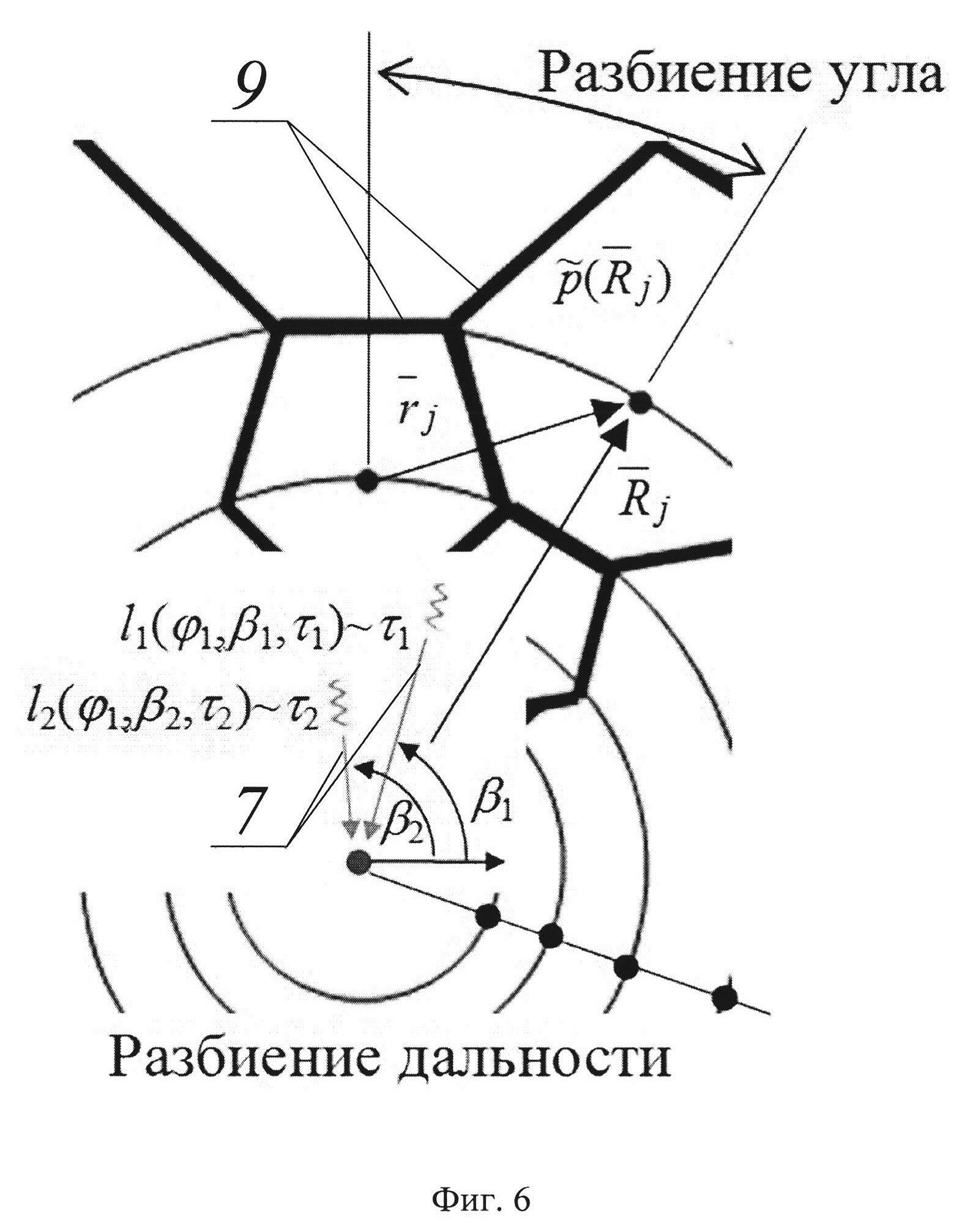
На фиг. 6. показана дискретизация пространства радиолокационной сцены сеткой.
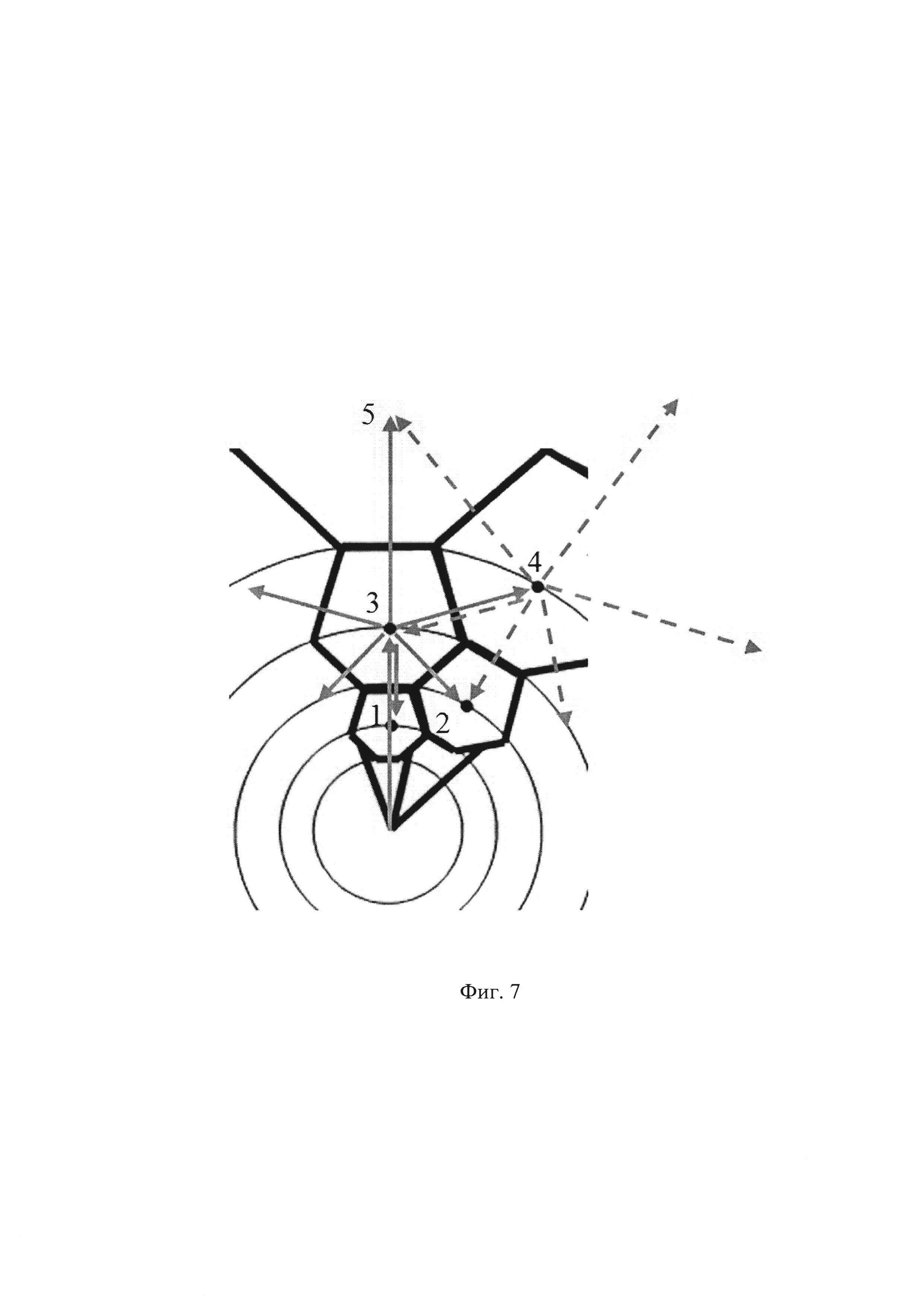
На фиг. 7. показано фрактальное построение звеньев оценок траектории на гексагональных элементах.
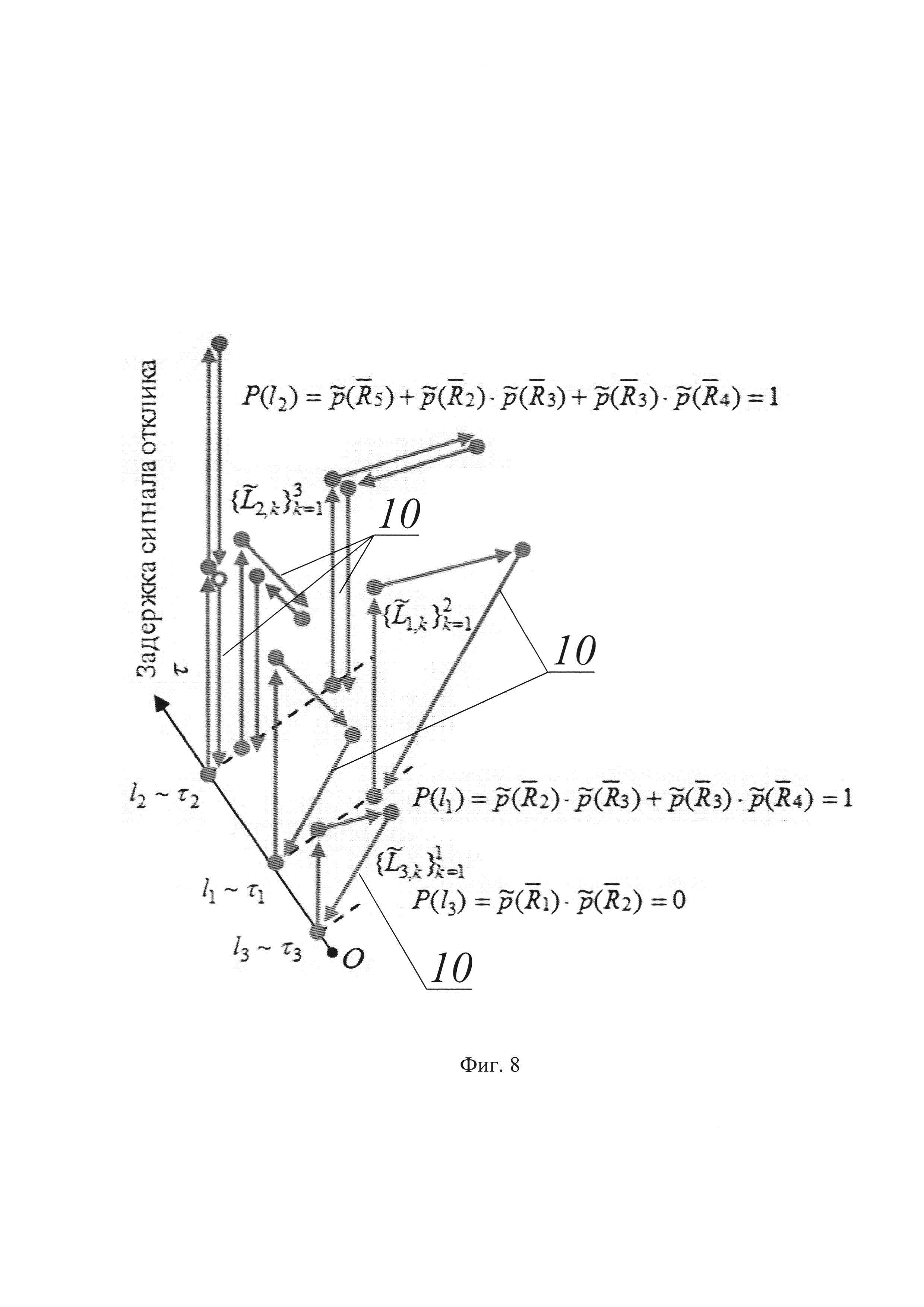
На фиг. 8. показано множество оценок траекторий по проекционным данным.
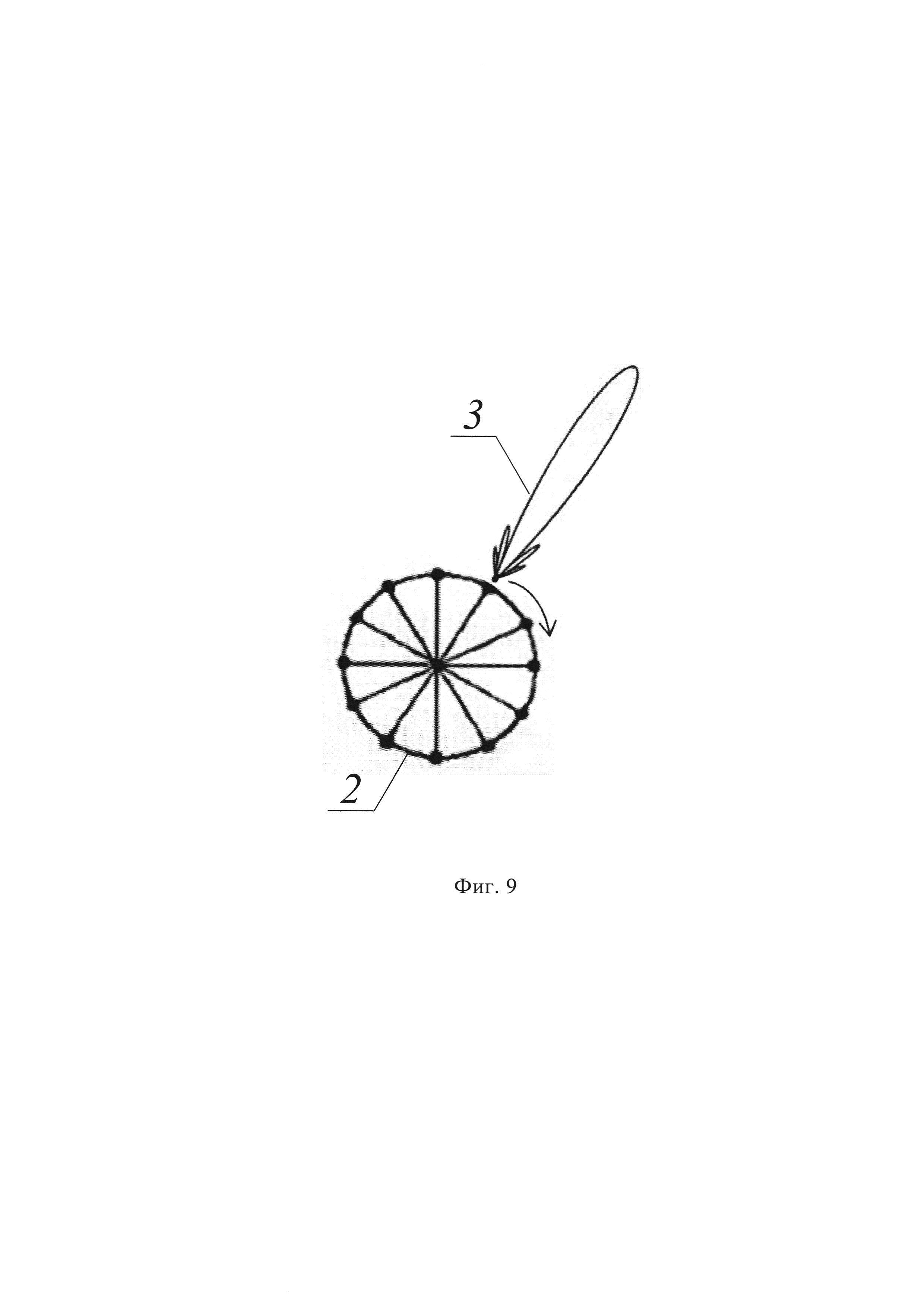
На фиг. 9. показана излучающая антенна и зондирующий остронаправленный луч.
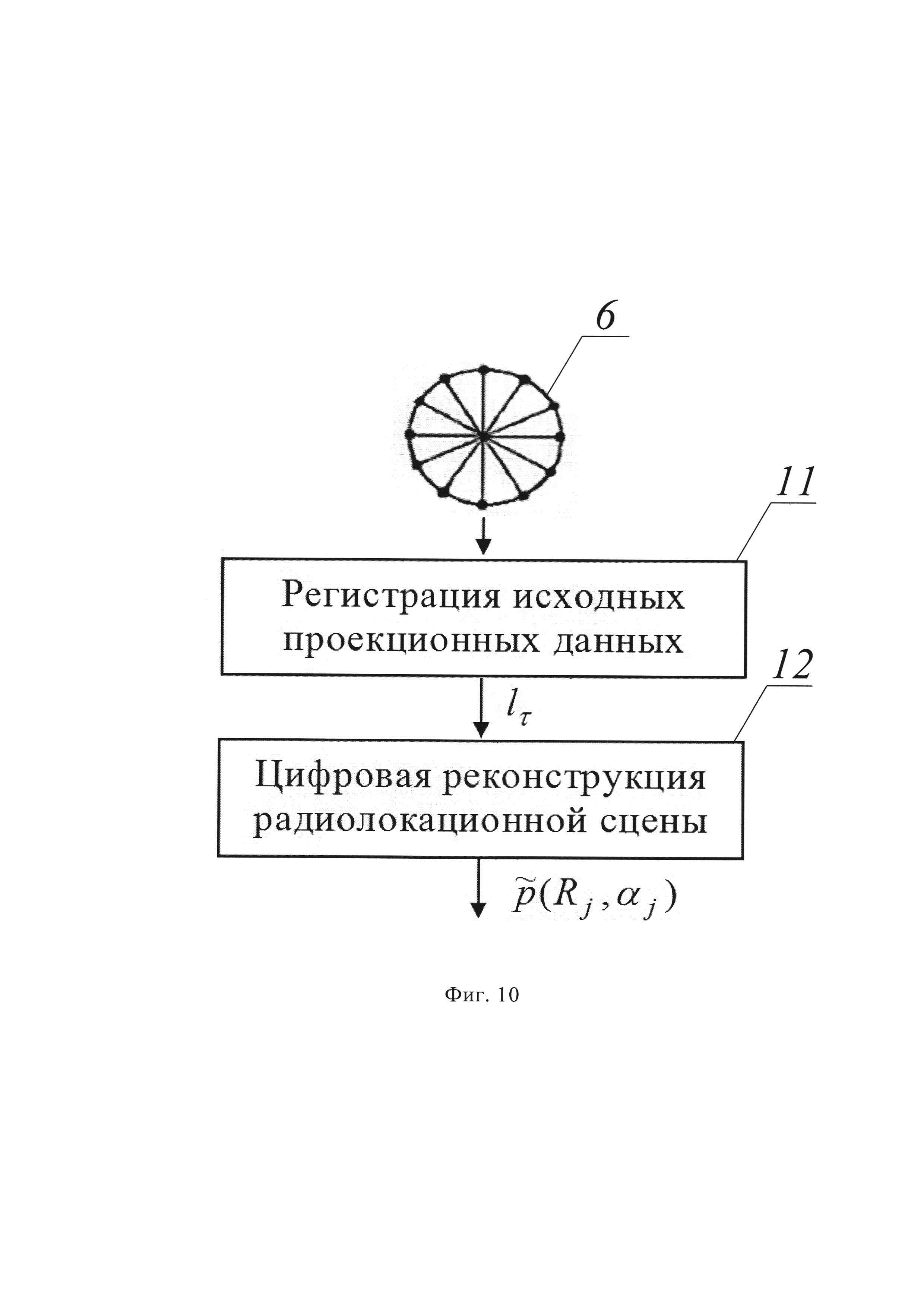
На фиг. 10. показана схема определения координат наклонной дальности и азимута надводных объектов и объектов над подстилающей поверхностью.
На фиг. 1-10 обозначены: 1 - надводные объекты и объекты, находящихся над подстилающей поверхностью, 2 - излучающая антенна, 3 - зондирующий остронаправленный луч, 4 - рассеяние отраженного от объекта сигнала, 5 - объект, не возвращающий отраженное радиоэхо в направлении принимающей антенны, 6 - принимающая антенна, 7 - трассы возвращения радиоэхо, 8 - траектории, 9 - гексагональные элементы, представленные в обратном (к центру) перспективном сокращении, 10 - оценки траектории, 11 - блок регистрации исходных проекционных данных, 12 - блок цифровой реконструкции радиолокационной сцены.
Предполагается, что в заданной системе координат имеет место быть радиолокационная сцена, содержащая надводные объекты и объекты, находящихся над подстилающей поверхностью (фиг. 1).
Широко известны принципы активной моностатической радиолокации, основанные на эффекте рассеивания излучаемой радиоволны на объектах, находящихся на трассе зондирующего сигнала, и последующей регистрации части энергии волны, отраженной в направлении излучателя (фиг. 2). При описании координат полярной системы радиус-вектором
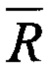
В настоящем изобретении к известным принципам радиолокации предлагается добавить регистрацию объектов, не возвращающих отраженное радио эхо в направлении излучателя (фиг. 3). Другими словами, учитывать, что, при фиксировании описываемых радиус-вектором
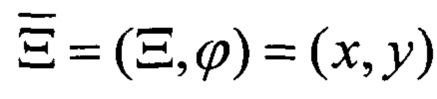

Для решения задачи формализации прямого томографического преобразования введена исходная функции
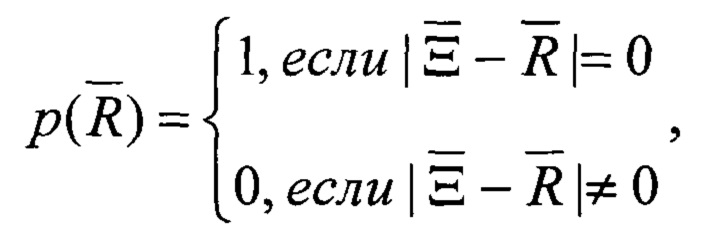
которая в точках пространства, где отражающий (рассеивающий) объект присутствует, принимает значение равное единице, а в остальных точках ноль.
Кроме того, введена некоторая траектория, по которой движется зондирующий и многократно отраженный от объектов сигнал. Траектория L одна из множества {L} траекторий - в общем случае ломаная линия (замкнутая с конечной длинной / или незамкнутая) в пространстве, обладающая изломами в точках присутствия объектов

В выбранной системе координат траектория представляет собой множество точек (фиг. 5). Пусть траектория L - ломаная задана параметрически:
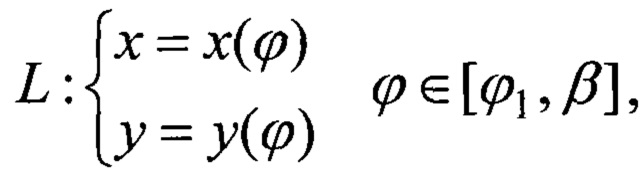
если
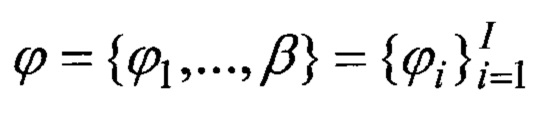
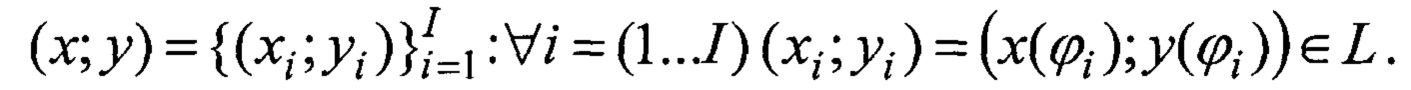
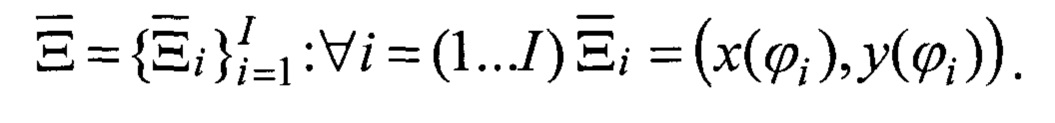
Замкнутые траектории повременной задержке сигнала отклика τ регистрируется приемником, так как имеют конечную длину l(ϕ, β, τ)=lt причем
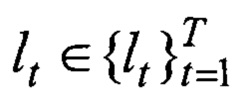
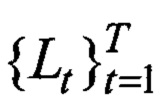
Связь ломаной траектории Lt с формирующими ее отражающими объектами, определена:
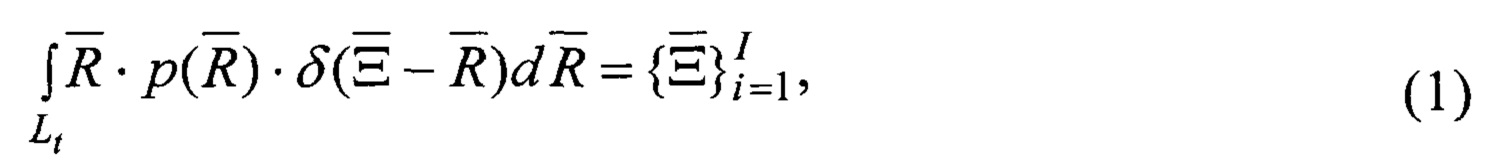
где δ - функция Дирака, а каждый вектор множества
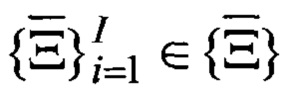
Аналогия предложенного метода с томографией требует наличия, так называемых, исходных проекционных данных, получаемых в ходе процедуры сканирования (зондирования) пространства. Исходными данными в предложенном методе томографии отражений является длина lt пропорциональная времени задержки τt, затраченному сигналом на прохождение ломаной траектории Lt.
Так как прямое томографическое преобразование - есть процедура получения исходных проекционных данных или как их еще называют интегральных сумм (траекторий-сумм), то исходные проекционные данные, являющие собой процедуру суммирования вдоль замкнутой ломаной линии траектории, описываются выражением:

численно равным
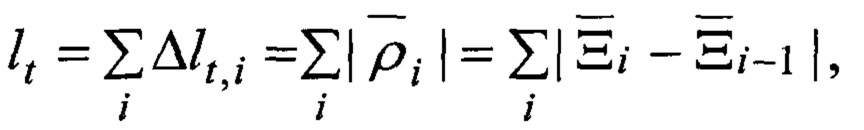
где разностный вектор координат объектов, участвующих в отражении,
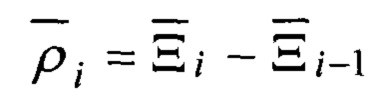
Для решения задачи обратного томографического преобразования осуществлены предварительные построения. Подвергнуто дискретизации оригинальное исследуемое пространство радиолокационной сцены сеткой, состоящей из гексагональных элементов. В полярных координатах сетка представлена в обратном (к центру) перспективном сокращении (фиг. 6). При этом, если
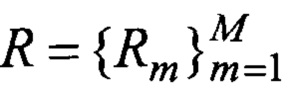
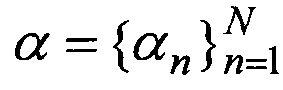
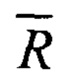

где индекс j=(1…J) -уникален и указывает на комбинацию аргументов (m, n), соответственно мелкость разбиения отрезка параметризации полного азимутального угла
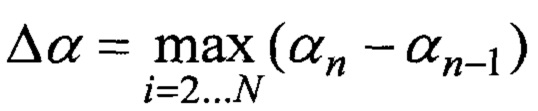
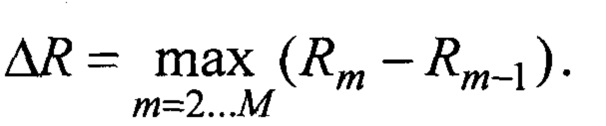
Известно, что задача обратного томографического преобразования заключается в поиске по исходным проекционным данным {lt} из (2) множества отражающих объектов

Заявленный поиск потребовал введения понятия оценки положения объекта, т.е. оценки радиус-вектора
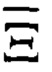
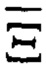
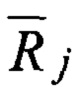
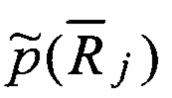
Следует обратить внимание, что рассчитываемая стохастическая функция
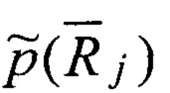
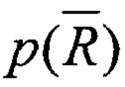
Таким образом, в ходе реконструкции детерминированного исходного оригинала
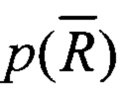
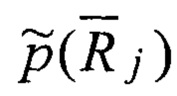
Оценка конкретной траектории Lt длинной lt представляет собой множество
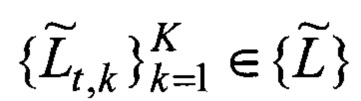
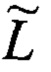
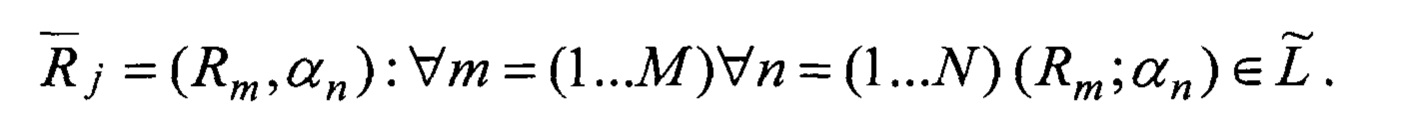
Указанные построения представлены на фиг. 7.
Длина замкнутой ломаной линии оценки траектории
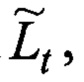
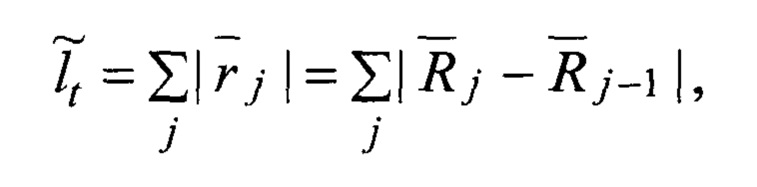
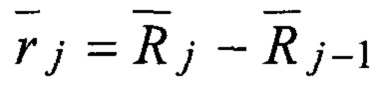
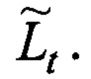
Поиск начинается с подбора (фиг. 8). Для каждой неизвестной исходной траектории Lt, но с известной длинной lt ~ τ пропорциональной времени задержки отклика сигнала τ, подбирается оценка в виде множества K всех возможных оценок траекторий
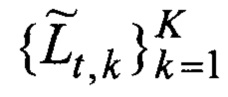
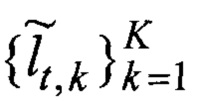

где Δ - систематическая погрешность дискретизации пространства, заданная мелкостью разбиения гексагональной сеткой.
Проекционным данным (2), если отклик получен, присваивается статус достоверных событий с вероятностью равной единице, если отклик отсутствует, - невозможных событий с вероятностью равной нулю:

Для каждого полученного (т.е. состоявшегося) или отсутствующего события lt наполнение функции P(lt) оценками
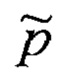
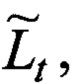
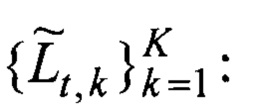

где
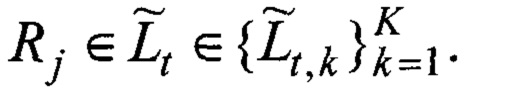
Пусть проекционные данные (2) представлены множеством:
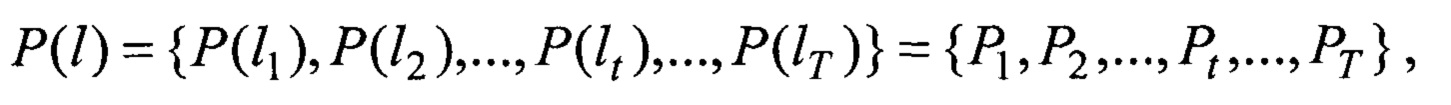
где
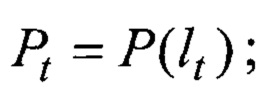
тогда вероятности нахождения объекта (хотя бы одного) в дискретных гексагональных элементах сетки радиолокационной сцены представлены множеством:
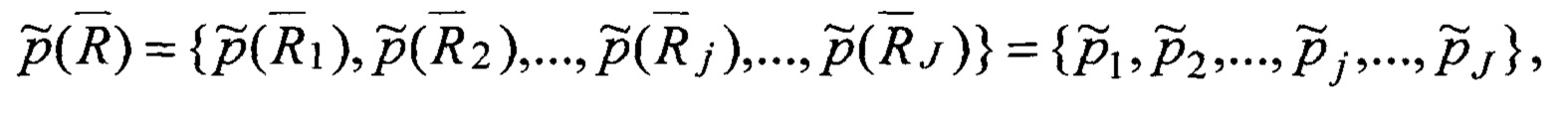
где
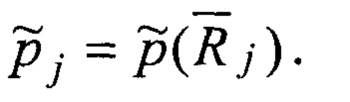
Из (5) формируется система T нелинейных уравнений с J неизвестными, записываемая в матричном виде:

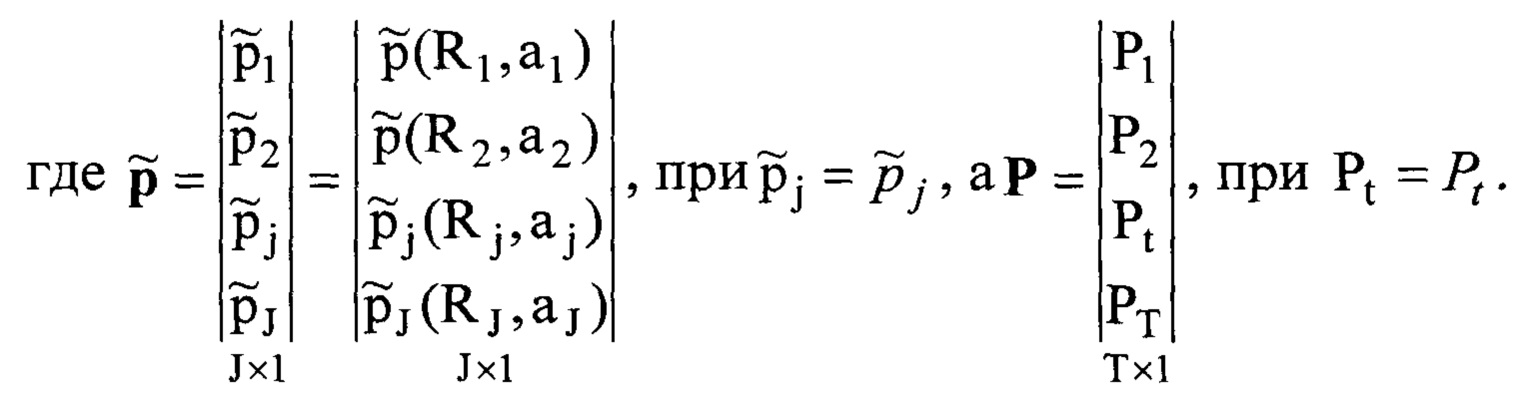
Поиск вектор-столбца
Литература
1. Патент №2444750 РФ, МПК G01S 5/08. Способ определения угломестной координаты низколетящей цели / Балагуровский В.А., Кондратьев А.С., Полищук Н.П. - Опубл. 10.03.2012.
2. Патент №2649899 РФ, МПК G01S 13/20. Способ измерения угловых координат групповых низколетящих целей / Коробочкин Ю.Б. - Опубл. 05.04.2018.
Реферат
Изобретение относится к области радиолокационной техники, а именно к способам определения координат наклонной дальности и азимута надводных объектов и объектов над подстилающей поверхностью. Достигаемый технический результат - обнаружение скрытых объектов, находящихся вне прямой радиовидимости или в силу конструктивных особенностей не отражающих, а рассеивающих радиоволны. В заявленном способе используется цифровая кольцевая многоэлементная эквидистантная фазированная антенная решетка. Благодаря использованию решетки, последовательно генерирующей одинаковые диаграммы направленности, осуществляется круговое зондирование радиолокационной сцены остронаправленным лучом. С задержкой по времени, пропорциональной длине образованной многократными отражениями от объектов внутри радиолокационной сцены траектории, регистрируются возвращенные под разными углами сигналы отклика, так называемые траектории-суммы, представляющие собой исходные проекционные данные томографического метода. По проекционным данным в результате цифровой реконструкции на дискретной гексагональной сетке осуществляется подбор оценки траектории. Для каждой неизвестной исходной траектории подбирается множество всех возможных ее оценок с соответствующими длинами, удовлетворяющими условию сравнения модуля разности длин с систематической погрешностью дискретизации. Кроме того, проекционным данным, если отклик получен, присваивается статус достоверных событий с вероятностью, равной единице, если отклик отсутствует – невозможных событий с вероятностью, равной нулю. Для каждого полученного (т.е. состоявшегося) или отсутствующего события восстановление исходной функции радиолокационной сцены осуществляется с помощью теорем умножения вероятностей независимых событий - нахождения отражающих объектов в вершинах оценки траектории, и последующего сложения всех удовлетворяющих условию оценок траекторий, из которых формируется система нелинейных уравнений с неизвестными. Решением методом последовательных исключений Гаусса системы нелинейных уравнений является вектор-столбец неизвестных восстановленной вероятностной оценки радиолокационной сцены с оценкой наклонной дальности и оценкой азимута положения объектов внутри сцены. 10 ил.
Формула
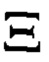
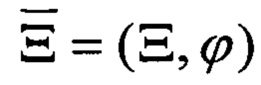
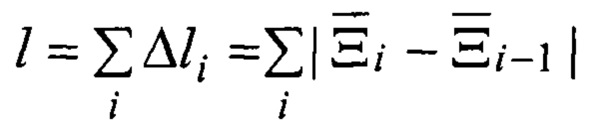
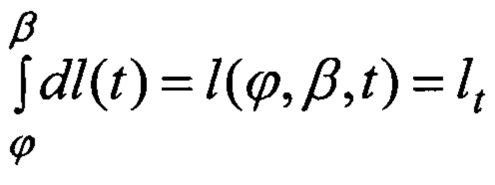
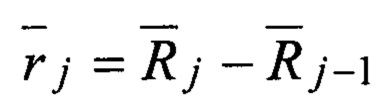
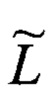
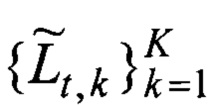
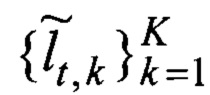
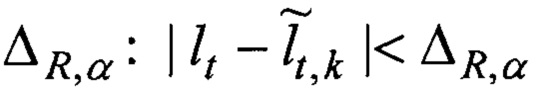

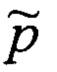
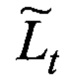
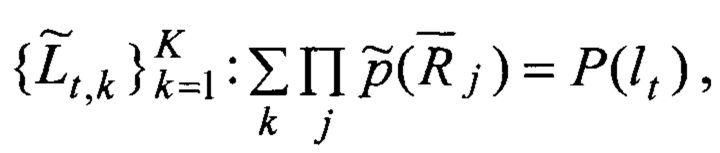
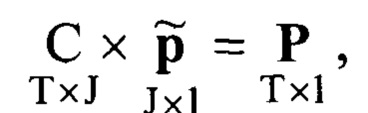
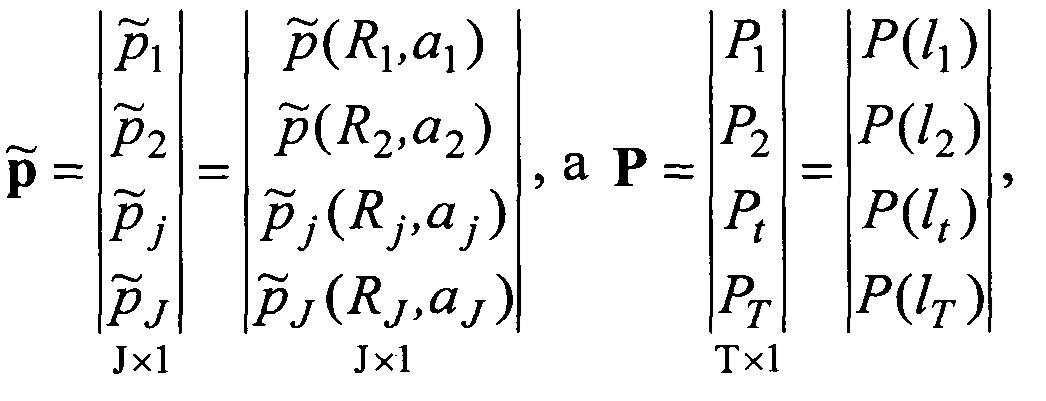
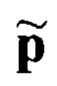
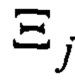
Документы, цитированные в отчёте о поиске
Способ измерения угловых координат групповых низколетящих целей
Способ однопозиционного определения координат источников радиоизлучений коротковолнового диапазона радиоволн при ионосферном распространении
Способ радиолокационной съёмки земли и околоземного пространства радиолокатором с синтезированной апертурой антенны в неоднозначной по дальности полосе с селекцией движущихся целей на фоне отражений от подстилающей поверхности и радиолокатор с синтезирова
Патенты аналоги
Способ измерения угловых координат групповых низколетящих целей

Комментарии