Способ определения пространственных угловых координат радиосигнала в амплитудных моноимпульсных пеленгационных системах - RU2625349C1

Чертежи

Показать все 13 чертежа(ей)

Описание

Изобретение относится к радиотехнике и может быть использовано при определении угловых координат источника радиоизлучения (ИРИ) одновременно в двух координатных плоскостях амплитудными моноимпульсными пеленгаторами.

Известные способы определения пространственных угловых координат амплитудными моноимпульсными пеленгаторами (аналоги предлагаемого), в соответствии с классификацией принятой в [1, 2, 3], основаны на применении в качестве антенной системы (АС) углового датчика, который формирует систему из различно ориентированных по направлению в двух координатных плоскостях лучей диаграмм направленности (ДН), обнаруживает сигналы, принятые лучами ДН, измеряет их амплитуды, формирует функции отношения амплитуд сигналов отдельно в каждой из двух координатных плоскостей, определяющие зависимость угловых координат: углов азимута и места соответственно от указанных параметров сигналов. Эти функции обычно называют пеленгационными характеристиками (ПХ) [1, 2, 3]. С помощью функций, обратных ПХ, определяют оценки угловых координат. В качестве угловых координат обычно используется система, где направление в пространстве определяют в виде углов азимута и места [1, 2, 3].

Для определения пространственных угловых координат обычно используется пара взаимно ортогональных излучателей, являющихся, например, облучателем зеркальной антенны [1, 2, 3]. Очевидно, что число лучей ДН, обеспечивающих двухкоординатную пеленгацию должно быть не менее трех[4].

Недостатком известных способов является отсутствие возможности беспоисковой по направлению пеленгации в широких угловых секторах обзора, так как для обеспечения необходимой точности пеленгования, как правило, используются достаточно узкие ДН, ширина которых несопоставима с необходимой областью обзора пространства. Для преодоления этого недостатка обычно используются те или иные методы сканирования ДН АС, как механические, в случае зеркальных АС, так и электронные - для АС в виде фазированных антенных решеток (ФАР). Однако это не обеспечивает в строгой формулировке мгновенного беспоискового по направлению формирования оценок угловых координат, которое требуется в ряде перспективных комплексах радиомониторинга.

Наиболее близким по технической сущности (прототипом) является способ амплитудного моноимпульсного пеленгования, в котором формируют две пары парциальных (перекрещивающихся в одной плоскости и разнесенных на угол ±θ₀ относительно равносигнального направления (РСН)) лучей ДН соответственно в азимутальной и угломестной плоскостях, осуществляют обнаружение и измерение амплитуды сигналов, принимаемых каждой парой парциальных лучей и вычисляют их отношения, которые являются ПХ для каждой из координатных плоскостей, а для формирования оценок угловых координат по углу места и азимута используют функции, обратные ПХ (см. например §1.5 рис. 1.14, стр. 30 в [1] и [3] или рис. 4.8 в [2] - блок схема амплитудно-амплитудной моноимпульсной системы для пеленгации в двух плоскостях).

Способ-прототип обладает указанным выше недостатком - отсутствием возможности беспоисковой по направлению пеленгации в широких угловых секторах обзора. При этом при использовании наиболее быстродействующих АС в виде ФАР, которые могли в некоторой степени уменьшить влияние этого недостатка при высокой скорости сканирования, возникают дополнительные проблемы при поиске в широких угловых секторах обзора. Так, при классическом методе фазирования в виде независимого управления по строкам и столбцам решетки излучателей ФАР при двухкоординатном сканировании наблюдается искажение формы луча ДН. Этот недостаток еще более проявляется при управлении группой лучей ДН при моноимпульсном пеленговании («скручивание» координат при широкоугольном сканировании, сопровождаемом разворотом плоскостей РСН направлений, что не позволяет реализовать прямоотсчетный съем координат азимута и угла места по ПХ [5]).

Целью изобретения является обеспечение беспоискового по направлению определения пространственных угловых координат сигнала в заданной области зоны обзора, характеризуемой границами углов азимута и места или значением телесного угла, соответствующего указанной области, амплитудными моноимпульсными пеленгационными системами в условиях противоречия между угловыми размерами зоны обзора и шириной лучей ДН АС, необходимой для обеспечения заданной точности пеленгования.

Поставленная цель достигается за счет того, что в известном способе амплитудного моноимпульсного пеленгования, при котором формируют взаимно пересекающиеся ДН АС, обеспечивающие зависимости уровней принимаемых сигналов от углов азимута и места, производят обнаружение, измеряют амплитуды сигналов и определяют их отношения, в предлагаемом способе в АС формируют N лучей ДН таким образом, что они одновременно накрывают всю область зоны обзора, последнюю разбивают в пределах ее границ на дискретные элементы, каждый из которых характеризуется аргументами l, m функции разбиения и соответствующими им значениями углов азимута α_AЗ(l) и места α_УМ(m) и максимальным значением нормированной функции луча ДН, номер которого k_max(l, m) фиксируют, определяют отношения R_kт(l, m) значений функций остальных лучей ДН АС к максимальному, из l×m дискретных элементов образуют множество азимутально-угломестных значений (МАУЗ) указанных отношений, которое состоит из N подмножеств k_max(l, m) в соответствии с числом лучей ДН, при этом для измеренных амплитуд принимаемых сигналов аналогично находят максимальную с фиксацией номера луча k_иmax и отношения R_k амплитуд других лучей к максимальной, а оценки угловых координат формируют с помощью метода наименьших квадратов (МНК) [8], где в качестве невязок используют разности одноименных по номерам лучей отношений амплитуд принимаемых сигналов и элементов подмножества МАУЗ, соответствующего равенству номеров лучей ДН с максимальной амплитудой принимаемых сигналов и подмножества МАУЗ, а оценки угловых координат согласно МНК определяют как значения углов азимута и места для элемента указанного подмножества МАУЗ, обращающего в минимум сумму квадратов невязок.

Таким образом, технический эффект предлагаемого способа заключается в возможности обеспечения беспоискового по направлению пеленгования в заданном секторе обзора с помощью АС в виде многолучевой антенны (МЛА), ДН которой охватывают всю область наблюдения. Последняя может быть задана как интервалами по углам азимута и места, так и значением телесного угла в зависимости от поставленной задачи. Важным преимуществом при этом является то, что при формировании лучей ДН здесь не накладывается жестких ограничений на взаимное угловое положение и конфигурацию лучей ДН АС, что позволяет использовать предлагаемый способ при различных принципах построения многолучевых АС.

Сочетание отличительных признаков из литературы неизвестно, поэтому способ соответствует критериям новизны и изобретательского уровня.

Реализация предлагаемого способа иллюстрируется с помощью приложенных фигур.

Фиг. 1 - функциональная схема варианта устройства амплитудного моноимпульсного пеленгатора для измерения пространственных угловых координат.

Фиг. 2 - пример пространственного расположения лучей ДН МЛА [6].

Фиг. 3 - варианты задания зоны обзора при использовании способа.

Фиг. 4 - сечение лучей ДН в плоскости, параллельной поверхности земли для рассматриваемого примера использования способа.

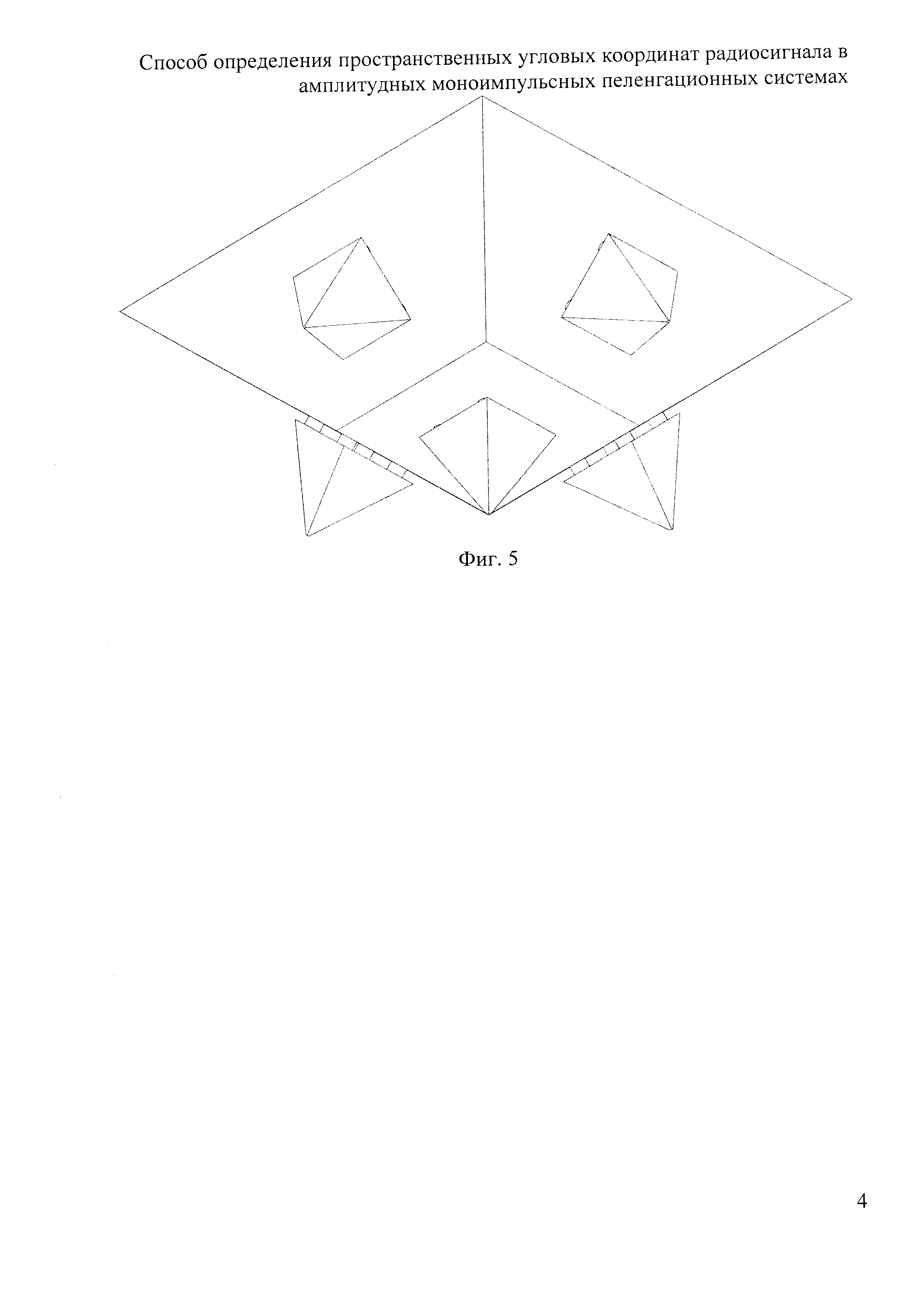
Фиг. 5 - опорная конструкция АС для примера реализации способа.

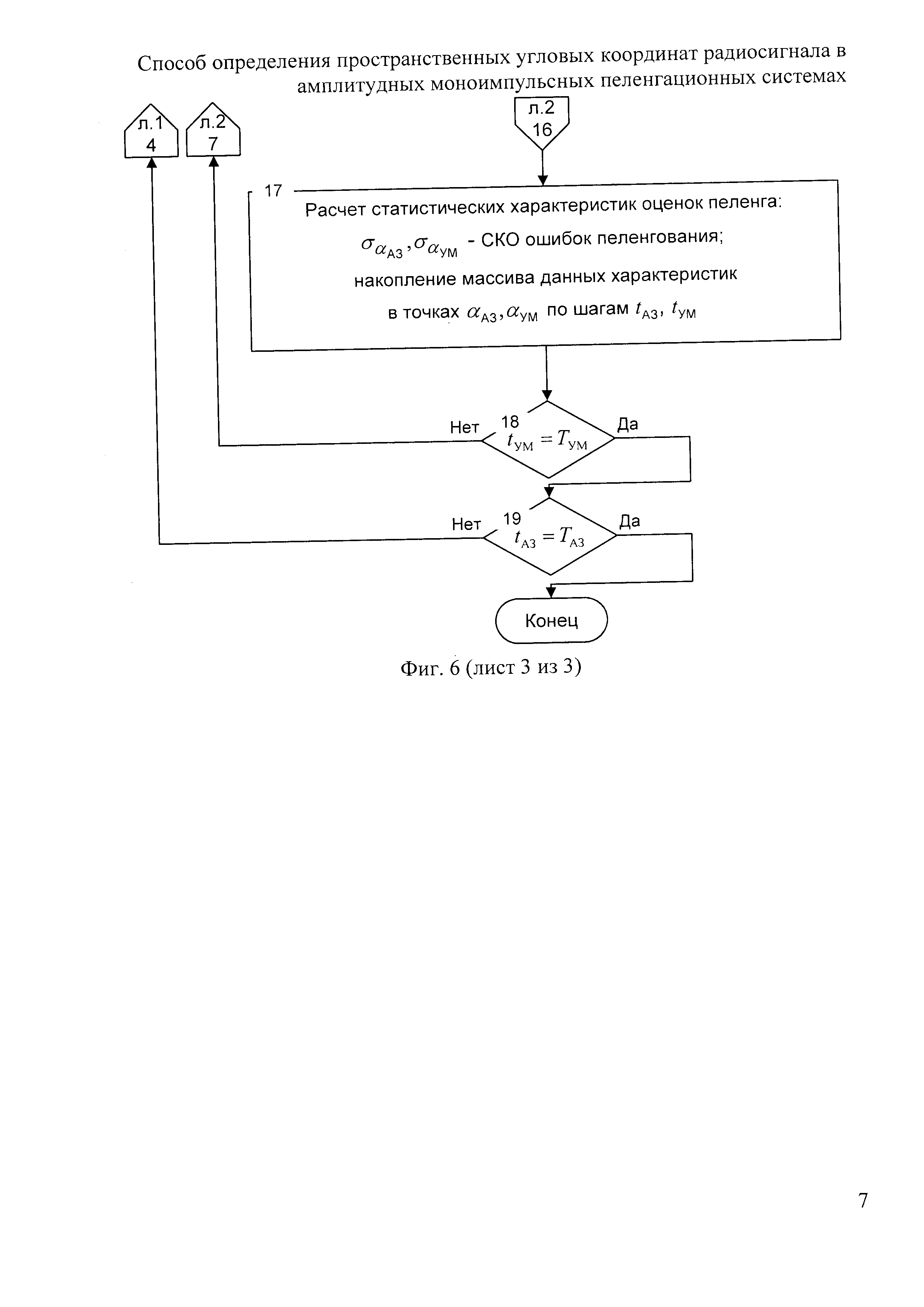
Фиг. 6 - обобщенный алгоритм математической модели для примера реализации способа.

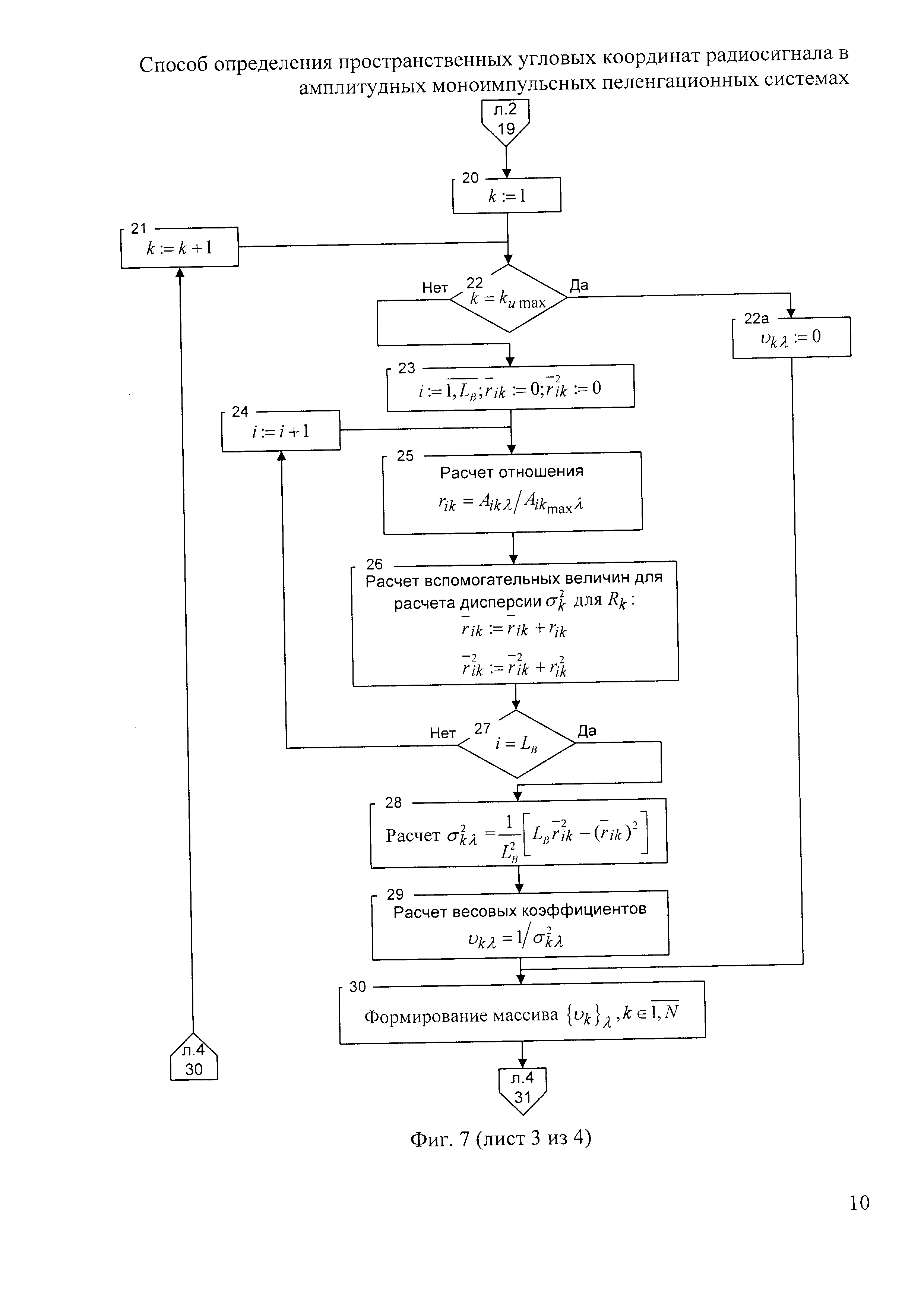
Фиг. 7 - алгоритм формирования данных измерения.

Фиг. 8 - результаты моделирования для примера реализации способа.

Функциональная схема устройства, реализующего предлагаемый способ содержит МЛА, формирующую N лучей ДН, блок высокой частоты (БВЧ), содержащий генератор контрольного сигнала (ГКС) и блок из N коммутаторов, первые входы которых подсоединены к выходам МЛА, а вторые к выходам ГКС. Выходы ГКС соединены с входами N-канального радиоприемного тракта (РПТ), выходы которого в свою очередь подключены ко входам блока цифровой обработки (БЦО), а его выходы к устройству управления и отображения.

Приведенная на фиг. 1 схема соответствует построению многоканальной амплитудно-амплитудной [1-3] системы пеленгования. В качестве МЛА возможно использование как отдельных АЭ, так и специализированных зеркальных антенн с многоэлементными облучателями, а также многолучевых антенных решеток (MAP). Пример расположения лучей ДН, представленных в виде сечений (контуров) функций ДН на уровне равного усиления в плоскости углов места и азимута, сформированных в многолучевой зеркальной антенне [6] приведен на фиг. 2. При построении МЛА на основе отдельных АЭ необходимая ориентация максимумов лучей может быть получена, например, при установке на гранях усеченной пирамиды (см. рис. 3 [7]). Число граней пирамиды, как правило будет равно числу лучей такой МЛА.

Сигналы, принятые МЛА поступают в БВЧ, который обеспечивает последовательную подачу на вход РПТ либо принимаемых сигналов, либо сигналов от ГКС с помощью коммутаторов K₁…K_N. Подача сигналов от ГКС соответствует режиму калибровки трактов, что обеспечивает уменьшение ошибок в измерении амплитуд сигналов и их отношений в режиме пеленгования за счет неидентичности коэффициентов передачи с_k,

БЦО обеспечивает оцифровку и цифровую фильтрацию входных сигналов в субблоке DDC. В качестве БЦО на фиг. 1 приведена структура реального блока, поставляемого ЗАО СКАН Инжиниринг Телеком г. Воронеж на основе плат установленных в конструктив Micro ТСА 10 19'' фирмы ELMA (для числа каналов N=8). В сигнальном процессоре БЦО (DSP) реализуются функции обнаружения и измерения амплитуд сигналов, так что образуется массив данных

где А_k - амплитуда сигнала в k-м канале,

p_k - признак обнаружения,

р_k=0 - нет обнаружения, р_k=1 - сигнал обнаружен

Массив (1) можно также представить состоящим из элементов р_kА_k, где амплитуды умножены на признак обнаружения.

Если в массиве (1) менее трех сигналов с р_k=1 (или

Данные массива (1) подаются в процессорный модуль БЦО (HOST) в котором выполняются все дальнейшие операции по вычислению оценок угловых координат. В соответствии с приведенным в раскрытии предлагаемого способа описанием выполняемых операций при использовании полученного массива данных измерения необходимо определить максимальную амплитуду сигнала с фиксацией номера луча ДН, ей соответствующего k_иmax.

А₀=max{р_kА_k}, k:=k_иmax

Тогда достаточно нормировать все элементы полученной последовательности на А₀ и получим массив отношений, удовлетворяющий условию:

{p_k,R_k)=(p₁R₁…p_NR_N),

где R_k=А_k/А₀, один из элементов массива k=k_иmax равен 1.

Для формирования множества МАУЗ необходимо для каждого дискретного элемента пространства, каждый из которых характеризуется аргументами

Таким образом, для каждого

где

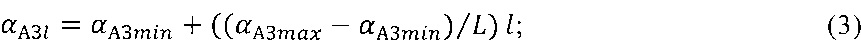
α_УМm= - α_УМmin+((α_УМmax-α_УМmin)/M)m

Далее, аналогично описанной выше процедуре определения отношений для амплитуд принимаемых сигналов, в каждой

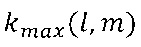
где

Здесь в последовательность введен множитель р_kт. При этом р_kт - 1, для

п, р_nт=0. В определенном смысле этот множитель эквивалентен признаку обнаружения р_k в (2).

В соответствии с (3) множество МАУЗ состоит из

элементов:

Для обеспечения взаимно однозначного соответствия по номерам лучей ДН АС массива данных измерений (2) с элементами МАУЗ в соответствии с изложенным из общего множества элементов МАУЗ:

,

,

необходимо выделить N подмножеств В⊂А, которые идентифицируются по номерам лучей

,

В соответствии с МНК для случая нескольких неизвестных (в нашем случае двух α_АЗ, α_УМ) в качестве их оценок принимают такие величины

,

для которых сумма квадратов равна [8]:

где результаты измерений отношения амплитуд R_k связаны с искомыми оценками

,

функциональной зависимостью, а минимум суммы квадратов определяется из области зоны обзора, задаваемой интервалами α_AЗ∈[α_AЗmin,α_АЗmax], α_УМ∈[α_УMmin,α_УМmax];

- весовой коэффициент,

, σ_k - среднее квадратичное отклонение (СКО) ошибки измерения R_k, зависящее от погрешности измерения отношения амплитуд А_k/А₀, входящих в массив данных (2)

С учетом полученных выше выражений для функциональной зависимости α_АЗ, α_УМ в виде множеств отношений амплитуд в точках разбиения зоны обзора

, m (4) и разбиения множества А на подмножества В (5) выражение (6) можно переписать в виде, удобном для вычислений оценок:

Оценки углов азимута

и места

определяются с помощью выражений (3) для значений

, m, соответствующих наименьшему значению суммы квадратов в формуле из подмножества

, в котором k_max=k_иmax. Поиск минимума осуществляется численным методом (согласно описанию структуры пеленгатора на фиг. 1 в HOST процессоре). В формуле (7) обеспечивается перебор всех дискретных элементов из подмножества В⊂А при

. Весовые коэффициенты

можно рассчитать в процессоре DSP БЦО фиг. 1 при проведении процедуры обнаружения и измерения амплитуд на основе статистической обработки отсчетов выборок принимаемых сигналов. Весовой коэффициент

, k=k_иmax приравнивается к нулю для исключения из состава данных отношений R_k, R_kт=1, как неинформативных.

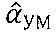
Дополнительно, в зависимости от решаемой задачи пеленгования, определяемой местом установки пеленгатора и способом представления зоны обзора, необходимо пояснить возможные варианты задания зоны обзора, возникающие при использовании способа.

Возможно три основных варианта задач (фиг. 3):

- Пеленгация в условиях зоны обзора, прилегающей к земной поверхности, когда измеряются углы азимута и места (пеленгатор установлен на поверхности земли) - фиг. 3а.

При этом в соответствии с принятыми обозначениями для сферической системы координат в математической литературе [9] угол азимута равен:

α_АЗ=ϕ, где ϕ - долгота

α_УМ=π/2-θ, где θ - полярное расстояние

Зона обзора при этом задается границами интервалов по углу места и азимута [α_AЗmin, α_АЗmax], [α_УМmin, α_УМmax].

- Пеленгация в верхней полусфере, когда зона обзора характеризуется максимальным значением телесного угла (угла при вершине кругового конуса, ось которого перпендикулярна поверхности земли θ_max (фиг. 3б)). В этом случае:

α_АЗ=ϕ,

α_УМ=θ

и границы зоны обзора будут определяться следующими интервалами:

α_AЗ∈[α_AЗmin, α_АЗmax],

α_УМ∈[0, θ_max]=[0, α_УМmax]

в частности, при круговом обзоре α_АЗ⊂[0,2π].

- Пеленгация с борта воздушно-космического носителя (в нижней относительно носителя полусфере), где зона обзора, аналогично предыдущему варианту, характеризуется максимальным значением телесного угла θ_max, отсчитываемого от вертикали к поверхности земли (фиг. 3в). Здесь α_АЗ=ϕ, α_УМ=θ и границы зоны обзора аналогичны предыдущему случаю:

α_AЗ∈[α_AЗmin, α_АЗmax], наиболее часто α_АЗ∈[0,2π]

и α_УМ∈[0, θ_max]=[0, α_УМmax]

Указанные границы зоны обзора используются при разбиении зоны обзора в соответствии с соотношениями (3).

Для иллюстрации применения предлагаемого способа было проведено математическое моделирование конкретной системы пеленгования для следующих условий:

- зона обзора представляет собой прямой круговой конус с углом при вершине θ_max=70° (телесный угол зоны обзора - 140°), что соответствует варианту расположения АС на фиг. 3в.

- для пеленгации предлагается использовать пучок из 5-ти лучей ДН, сечения которых по уровню -3 дБ и в плоскости, параллельной поверхности земли (X0Y) и -6 дБ показаны на фиг. 4. Здесь же нанесена граница зоны обзора (ГЗ).

- ширина ДН лучей ~ 55-58°.

- максимумы лучей ДН АЭ1, АЭ5 и АЭ2, АЭ4 отклонены от вертикали на 45° соответственно в координатных плоскостях X0Z и Y0X, максимум АЭЗ направлен вертикально вниз (вдоль отрицательного направления оси Z - фиг. 3в). Разбиение зоны обзора в соответствии с пояснениями к фиг. 3в на фиг. 4 будет представлять собой сектора по α_АЗ, угол при вершине которых равен шагу разбиения по α_АЗ, а по углу места в виде концентрических окружностей, радиусы которых пропорциональны

, где Δα_УМ - шаг по углу места в соответствии с (3) при α_АЗmax=θ_max. Указанная ширина лучей ДН характерна для логопериодических антенн. Описанное положение лучей соответствует расположению антенн на усеченной четырехгранной пирамиде с углом при вершине 90° - фиг. 5. Как видно из фиг. 4 при уровне ДН равном -6 дБ обеспечивается достаточно полное накрытие зоны обзора. Для работы АС при указанном расположении лучей антенны должны обеспечивать прием круговой поляризации сигнала.

На фиг. 6 приведен обобщенный алгоритм математической модели, соответствующий реализации предлагаемого способа. Модель построена на основе использования классического метода статистического моделирования Монте-Карло [10].

Исходные данные, используемые в модели приведены в оп. 1. В большинстве возможных на практике случаев в аналитическом представлении функции ДН лучей одинаковы, т.е. F_k(α_AЗ, α_УМ)=F(α_AЗ, α_УМ). Для случая осесимметричной ДН F(α_AЗ, α_УМ)=F(α). При измеренных функциях ДН они для каждого k-го луча различны, то есть необходимо использование функций F_k, которая в этом случае задается численно. Настоящая модель соответствует последнему случаю, что и определено в п. 4 оп. 1.

Для расчета МАУЗ (оп. 2, фиг. 6) необходимо первоначально определить направления максимумов лучей ДН АС в соответствии с фиг.4, которые в пространстве характеризуются координатами единичного вектора - направляющими косинусами (НК) [9]. Используя фиг. 4 и фиг. 3в можно определить значения НК, которые представим в виде матрицы М_АС. Ее строками будут являться НК для каждого k-го луча с нумерацией по фиг. 4 в координатной системе X, Y, Z (фиг. 3в). Число столбцов соответствует числу НК трехмерного пространства. Вместо углов места α_УМ здесь запишем равные им значения углов θ₀ для отличия переменных, соответствующих параметрам АС от угловых координат пеленгуемой цели. Индекс «0» также означает принадлежность к АС.

С учетом принятых значений углов отклонения лучей по фиг. 3 (45°) в числовом виде матрица (7) имеет вид:

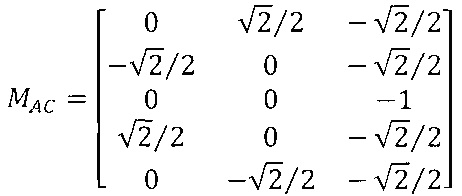
Для расчета функций ДН

необходимо определить углы

,

(3). Направление в пространстве, как и в случае максимумов лучей ДН, также задается в виде единичного вектора с координатами в виде НК. Используем известные выражения для сдвига фаз в фазовом пеленгаторе [11, рис. 1.4.2, стр. 30], где множитель в правой части выражения для сдвига фаз и есть НК направления относительно соответствующей оси. Одновременно учитывая, что рис. 1.4.2 в [11] соответствует по условию работы пеленгатора фиг. 3а, выражение для НК относительно всех координатных осей для фиг. 3в, в нашем случае можно для направления на цель в

-й, m-й точке разбиения зоны обзора определить единичным вектором

:

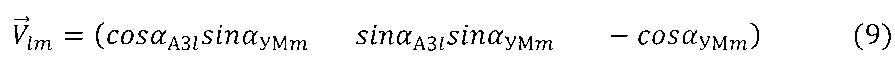
Известное соотношение для угла между двумя заданными направлениями с НК [9] позволяет определить массив

косинусов углов между максимумами лучей ДН и каждым

, m-м направлением, определяемым углами

,

в виде k-х элементов матрицы - строки произведения

.

где

- k-я строка матрицы М_АС (7), Т - знак транспонирования для вектора

(9).

Элементы матрицы (10) при известной осесимметричной функции луча ДН F_k(α) позволяют рассчитать значение уровня ДН в точке разбиения

m, то есть

:

Далее для формирования МАУЗ необходимо для каждого l, m-го элемента выполнить операции, определяемые выражением (4) настоящего описания.

С целью выделения из общего множества МАУЗ подмножеств

необходимо для каждого

отселектировать из МАУЗ

, m-ые элементы, соответствующие данному k_max, который по-существу является на ряду с

, m третьим аргументом подмножества.

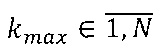
В оп. 4-8 алгоритма модели (фиг. 6) устанавливаются циклы по шагам α_AЗ(t_AЗ) и α_УМ(t_УМ) в модели с числом шагов T_АЗ, T_УМ. В отличие от шагов по переменным

, m данные шаги определяют только число точек, в которых рассчитываются характеристики пеленгования (число точек в графиках, иллюстрирующих работу системы пеленгования). Очевидно, что Т_АЗ, T_УМ<

Далее в оп. 9, 11, 14 устанавливаются циклы по числу статистических испытаний Λ, которые позволяют рассчитать точностные характеристики пеленга (оп. 15).

Для каждого из шагов по λ: в оп. 11 формируются данные измерения в точке с координатами α_АЗ(t_АЗ), α_УМ(t_УМ) с учетом уровня сигнала U₀ (оп. 11) и выполнения процедур обнаружения и измерения его амплитуды в каждом из N каналов пеленгатора: р_λ=1,0 - вероятность пеленгования или пропуска сигнала соответственно, массив весовых коэффициентов {

} и массив{p_k, R_k}.

- в оп. 13 осуществляется расчет оценок угловых координат с помощью выражения (7) с учетом поясняющих соотношений (8)-(11), формирующих МАУЗ. При р_λ=0 оценки координат не формируются, одновременно подсчитывается число таких ситуаций t для данной координатной точки.

В результате расчета статистических характеристик оценок пеленга в оп. 17 в циклах по переменным t_AЗ, t_УM формируется массив указанных характеристик для совокупности направлений в зоне обзора с координатами α_AЗ(t_АЗ), α_УМ(t_УМ). Расчет характеристик произведен с помощью выражений, вытекающих из формул для расчета СКО, применяемых в методах статистического анализа угловых наблюдений [14], при котором используются комплексные представления для угловых направлений: Для угла места:

, arg - аргумент комплексного числа

Для угла азимута:

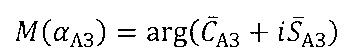
где

- средние значения аргументов комплексной функции, определяющие направление (вектора); r_УМ, r_АЗ - модули векторов направлений по α_УМ, α_АЗ; М(α_УМ), М(α_АЗ) - средние значения углов α_УМ, α_АЗ; σ_αУМ; σ_αАЗ, - СКО погрешностей α_УМ, α_АЗ.

Для более полного раскрытия работы математической модели на фиг. 7 приведен алгоритм формирования данных измерения (оп. 11 фиг. 6).

В исходные данные алгоритма (оп. 1) входят:

- текущие значения α_AЗ(t_AЗ), α_УM(t_УM), полученные в oп. 5 и 8 общего алгоритма фиг. 6;

- уровень сигнала U₀ в условных единицах, который при расчете отсчета амплитуды сигнала с использованием нормального распределения с СКО выборки σ=1 представляет собой величину, пропорциональную отношению сигнал/шум;

- положение максимумов лучей ДН МЛА соответствует матрице М_АС определенной выше - формула (8);

- функции ДН F_k(α) в модели использованы в виде данных массива измерения реальных ДН логопериодических антенн;

- порог обнаружения U_ПО устанавливается для реализации алгоритма обнаружения и измерения амплитуды сигналов;

- число статистических испытаний Λ определяет возможность расчета точностных характеристик пеленгатора;

- число отсчетов в выборке сигнала используется для реализации в модели алгоритма обнаружения и также для оценки дисперсии отношения сигналов R_k, что требуется для расчета весовых коэффициентов

в формуле (7).

Формирование вектора

соответствует формуле (9).

Для расчета массива амплитуд {р_kА_k} устанавливается цикл по номеру луча ДН оп. 3, 4, 15. В оп. 3 одновременно устанавливается начальное состояние переменной t_kλ - счетчика числа лучей ДН, в которых обнаружен сигнал. Оп. 5, 6 соответствуют выполнению вычислений по формулам (9)-(11) настоящего описания; в оп. 6 введено масштабирование с учетом уровня сигнала U₀.

Для реализации статистического моделирования и процедуры обнаружения и оценки амплитуды сигнала введен цикл формирования отсчетов амплитуды (оп. 7, 9, 11) в пределах длины выборки L_B. ОП. 8 обеспечивает расчет амплитуды i-го отсчета

на основе известного представления для формирования амплитуды сигнала для смеси узкополосного сигнала и шума [12].

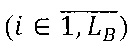
В результате в оп. 10 для каждой i-й амплитуды формируется массив выборок {А_ik}.

Оп. 12 реализует процедуру работы обнаружителя, одновременно определяющую оценки амплитуды и признака достоверности р_kА_k. В результате в оп. 14 формируется после выполнения цикла по k массив [р_kА_k], соответствующий результатам выполнения процедуры обнаружения и измерения амплитуды для сигналов, принимаемых лучами ДН АС. Одновременно определяется состояние переменной t_kλ.

Процедура обнаружения в настоящей работе моделировалась для цифрового обнаружителя с бинарным квантованием последовательности отсчетов сигнала в пределах выборки [13]. В пределах выборки формируется скользящее временное окно с числом анализируемых отсчетов n=4 и принятием или отсутствием решения о наличии или отсутствии сигнала в окне в соответствии с правилом:

где Р_c - скользящий признак обнаружения (Р_с=1,0 соответственно при обнаружении и необнаружении сигнала в окне). Логическая обработка последовательности признаков Р_c в пределах выборки реализует решающее правило об обнаружении (р_k=1) или (р_k=0) отсутствии сигнала в пределах выборки. Одновременно, как отмечалось, формируется оценка амплитуды А_k, пропорциональная среднему значению A_ik.

При наличии менее 3-х лучей ДН, в которых обнаружен сигнал (t_kλ<3), дальнейшие операции по формированию данных измерения, как указывалось выше (см. комментарии к (1)), не производятся, при этом р_λ=0, в противном случае р_λ=1 (оп. 16…18).

Оп. 19 алгоритма реализует описанные выше действия над массивом {р_kА_k} в соответствии с выражением (2) для получения массива отношений {p_kR_k}. Оп. 20-26 алгоритма фиг. 7 обеспечивают получение массива данных весовых коэффициентов

используемых для вычислений оценок углов места

и азимута

путем расчетов с помощью формулы (7). При этом при использовании массива отсчетов {A_ik}, полученного в оп. 10 формируются для каждого -го отсчета отношения:

r_ik=A_ik/A_ikmax(A_ikmax=A_i0),

дисперсии которых соответствуют дисперсиям отношений R_k oп. 25. Расчет дисперсий (оп. 26 - оп. 28) позволяет определить массив весовых коэффициентов (оп. 29). При k=k_иmax с учетом оп. 22, 22а

. Выходные данные процедуры измерения (оп. 32) используются в общем алгоритме модели (фиг. 6, оп. 11).

Результаты моделирования представлены на фиг. 8: 8а, 8б - для погрешностей измерения угла азимута (СКО σ_АЗ); 8в, 8г - для погрешностей угла места (СКО σ_УМ). Значения СКО представлены в виде областей в зоне обзора, где они принадлежат интервалам, выделенным различными видами штриховки. Соответствие видов штриховки значениям СКО приведены в столбце справа от графического отображения указанных областей. Фиг. 8а и 8в соответствуют отношению сигнал/шум (U₀=5)-14 дБ. При этом СКО σ_АЗ лежит в пределах 0,9°-5,5° (здесь взяты средние значения из интервалов, приведенных в столбцах). Причем, в подавляющей части направлений области обзора СКО лежит в пределах интервала 0,9°-4°. Аналогично, СКО σ_УМ во всей зоне заключено в интервале 0,55°-3,2°, а практически в 70% ее части - в интервале 0,55°-2,25°.

Фиг. 8б и 8г соответствуют отношению сигнал\шум (U₀=10)-20 дБ с естественным уменьшением ошибок пеленгования: для σ_АЗ интервал значений в основной области зоны обзора не более 0,5°-1,9°, для α_УМ - не более 0,3°-1,45°.

Имеющаяся несимметрия областей, соответствующих равным СКО пеленгования на фиг. 8а-8г определяется в первую очередь использованием при моделировании реальных ДН отдельных АЭ с их естественными различиями, а также интервальным представлением для значений СКО, без которого невозможно получить наглядную картину распределения ошибок в зоне обзора.

Полученные результаты вполне соответствуют предполагаемым точностям пеленгования для АЭ в АС с шириной 55°-58°. Моделирование подтверждает достижение основной цели предлагаемого способа - возможности беспоискового по направлению определения пространственных угловых координат с помощью МЛА, накрывающих заданную зону обзора.

Источники информации

1. А.И. Леонов, К.И. Фомичев «Моноимпульсная радиолокация» М. изд. «Советское радио», 1970

2. А.И. Леонов «Моноимпульсная радиолокация» М изд. «Рипол Классик», 2013 г

3. Леонов А.И., Фомичев К.И. «Моноимпульсная радиолокация» М. Радио и связь, 1984 г.

4. Анцев Г.В., Турнецкий Л.С, Павлов В.С, Турнецкая Е.Д., Французов А.Д., патент №2361230 G01S 3/14 «Моноимпульсный пеленгатор», опубликовано 10.07.2009.

5. Журавлев А.К., Бакшеева Ю.В., Коменко А.А., «Модификация алгоритмов управления лучами плоских фазированных решеток в моноимпульсных измерителях», «Успехи современной радиоэлектроники», №2, 2013 г., стр. 39-42.

6. Пономарев Л.В., Вечтомов В.А., Милосердов. «Крупноапертурный излучатель для многолучевой антенны системы спутниковой связи», электронный журнал «Труды МАИ», выпуск №52.

7. Кашин В.А., Голубцов Е.А., Кормилицын А.С, Попов В.М., Шумилов В.Ф., «Особенности создания активной фазированной антенной решетки сантиметрового диапазона с купольной линзой для РЛС ближнего радиуса действия», Антенны, вып. 2 (213), 2015 г, стр. 3-7 (рис. 3, стр. 4).

8. Математическая энциклопедия: гл. ред. И.М. Виноградов, Т3, стр. 877-882: Советская энциклопедия, 1982.

9. Бронштейн И.Н., Семендяев К.А., Справочник по математике для инженеров и учащихся втузов, Наука, 1986.

10. Пугачев В.С., Теория вероятностей и математическая статистика, М. Наука, Главная редакция физико-математической литературы, 1979.

11. Пестряков В.Б. Фазовые радиотехнические системы (основы статистической теории), М «Советское радио», 1968.

12. Зиновьев А.Л., Филиппов Л.И., Введение в теорию сигналов и цепей, М. Высшая школа, 1975.

13. Теоретические основы радиолокации: Учебное пособие для ВУЗов, Коростелев В.В., Клюев Н. Ф., Мельник Ю.А. и др., под ред. Дулевича В.Е., М. Сов. Радио, 1978.

14. Мардиа К. Статистический анализ угловых наблюдений, перевод с англ. Главная редакция физико-математической литературы, М. «Наука», 1978.

Реферат

Изобретение относится к радиопеленгации в двух координатных плоскостях. Достигаемый технический результат - обеспечение беспоискового по направлению определения пространственных угловых координат сигнала в условиях противоречия между угловыми размерами зоны обзора и шириной лучей диаграмм направленности (ДН) антенной системы (АС), необходимой для обеспечения заданной точности пеленгования. Сущность способа состоит в приеме сигнала N лучевой ДН АС, ориентация и число N лучей которой позволяет одновременное накрытие их ДН всей области зоны обзора, обнаружении сигналов и измерении их амплитуд для всех N каналов приема, среди которых находят максимальную и запоминают соответствующий ей номер луча, относительно которого определяют отношения амплитуд сигналов других лучей. Для формирования оценок угловых координат сигнала зону обзора предварительно разбивают на дискретные элементы, каждый из которых характеризуется парой угловых координат и соответствующих им значений отношений амплитуд сигналов для всех N лучей ДН по отношению к максимальной для данной пары. Для полученного множества отношений для каждого из дискретных элементов зоны обзора определяют наилучшее совпадение отношений с измеренными их значениями при одинаковых номерах лучей с максимальными амплитудами с помощью метода наименьших квадратов, при котором оценками координат являются соответствующие этому случаю координаты дискретного элемента. 8 ил.

Формула