Устройство управления силовым агрегатом - RU2660679C1

Чертежи

Показать все 10 чертежа(ей)

Описание

Уровень техники

1. Область техники, к которой относится изобретение

[0001] Изобретение относится к устройству управления силовым агрегатом.

2. Описание предшествующего уровня техники

[0002] Когда обычному устройству управления силовым агрегатом предоставляется целевое значение, связанное с выходным управляющим воздействием силового агрегата, устройство управления силовым агрегатом определяет входное управляющее воздействие для силового агрегата посредством управления с обратной связью, которое вынуждает выходное управляющее воздействие следовать целевому значению. При фактическом управлении силовым агрегатом могут существовать различные ограничения в отношении аппаратных средств или управления относительно количественного параметра состояния силового агрегата. Когда такие ограничения не удовлетворяются, может формироваться повреждение аппаратных средств или снижение характеристики управления. Удовлетворение ограничения является одним типом важной рабочей характеристики, требуемой для управления силовым агрегатом, аналогично инструктированию выходному управляющему воздействию следовать целевому значению.

[0003] Одно эффективное средство для удовлетворения ограничений приводится в пример посредством эталонного регулятора. Эталонный регулятор включает в себя прогностическую модель в качестве конфигурации, которая корректирует целевое значение для выходного управляющего воздействия, которое должно быть введено в контроллер обратной связи. Прогностическая модель моделирует систему с замкнутым контуром, которая включает в себя силовой агрегат и контроллер обратной связи. Эталонный регулятор прогнозирует будущее значение количественного параметра состояния силового агрегата посредством прогностической модели. Эталонный регулятор корректирует целевое значение для выходного управляющего воздействия на основе спрогнозированного будущего значения и ограничения, наложенного на будущее значение.

[0004] В публикации японской нерассмотренной патентной заявки № 2016-61188 (JP 2016-61188 A) раскрывается устройство управления силовым агрегатом, которое применяет эталонный регулятор, чтобы управлять дизельным двигателем, который является установленным на транспортное средство силовым агрегатом. Эталонный регулятор включает в себя прогностическую модель, которая моделирует, как "время простоя+вторичную колебательную систему", динамическую характеристику системы с замкнутым контуром, относящуюся к управлению с обратной связью, которое инструктирует следование температуры корпуса дизельного сажевого фильтра (DPF) целевому значению. В эталонном регуляторе значение, которое получается сложением текущего значения температуры корпуса DPF с переменной (например, 2ζβ/ω_n), представленной с помощью коэффициента затухания ζ и собственной угловой частоты ω_n колебаний прогностической модели и верхнего предельного ограничения β, вычисляется в качестве возможного значения для целевого значения температуры корпуса. Кроме того, в эталонном регуляторе, целевое значение температуры корпуса корректируется на основе вычисленного возможного значения.

[0005] В обычном эталонном регуляторе целевое значение для выходного управляющего воздействия силового агрегата корректируется посредством сужения круга возможных значений для целевого значения количественного параметра состояния через итеративное вычисление, которое использует будущее значение количественного параметра состояния, полученное с помощью прогностической модели и ограничения. Между тем, в эталонном регуляторе, возможные значения для целевого значения температуры корпуса вычисляются посредством сложения текущего значения температуры корпуса DPF с переменной, включающей в себя коэффициент затухания ζ прогностической модели и верхнее предельное ограничение β. Т.е., итеративное вычисление не выполняется в эталонном регуляторе во время корректировки целевого значения. Соответственно, устройство управления силовым агрегатом может уменьшать вычислительную нагрузку по корректировке целевого значения в эталонном регуляторе.

Сущность изобретения

[0006] Устройство управления силовым агрегатом предполагает прогностическую модель, которая моделирует динамическую характеристику системы с замкнутым контуром, связанной с управлением с обратной связью, как "время простоя+вторичная колебательная система". Таким образом, когда прогностическая модель не может быть представлена посредством "времени простоя+вторичной колебательной системы", целевое значение может не быть скорректировано. Кроме того, в устройстве управления силовым агрегатом, верхнее предельное ограничение β задается для величины изменения температуры корпуса DPF в единицу времени, и ограничение не накладывается на температуру корпуса DPF. Таким образом, когда ограничение накладывается на температуру корпуса DPF, необходимо итеративное вычисление, тем самым, приводя к неизбежному увеличению в вычислительной нагрузке по корректировке целевого значения. Соответственно, желательно улучшение, чтобы добиваться высокой универсальности для прогностической модели и иметь возможность легко корректировать целевое значение количественного параметра состояния силового агрегата с ограничением, наложенным на количественный параметр состояния.

[0007] Изобретение предоставляет устройство управления силовым агрегатом, которое может добиваться высокой универсальности для прогностической модели и снижать вычислительную нагрузку по корректировке целевого значения количественного параметра состояния силового агрегата с ограничением, наложенным на количественный параметр состояния.

[0008] Первый аспект изобретения относится к устройству управления силовым агрегатом, включающему в себя контроллер обратной связи, выполненный с возможностью определять входное управляющее воздействие для силового агрегата во время ввода целевого значения предварительно определенного количественного параметра состояния силового агрегата, так что количественный параметр состояния следует целевому значению, и эталонный регулятор, выполненный с возможностью корректировать первоначальное целевое значение количественного параметра состояния во время ввода первоначального целевого значения, так что верхнее предельное ограничение, накладываемое на количественный параметр состояния, удовлетворяется, и выводить скорректированное первоначальное целевое значение в контроллер обратной связи. Эталонный регулятор выполнен с возможностью устанавливать целевое значение, удовлетворяющее верхнему предельному ограничению, равным возможному целевому значению, которое выбирается из возможных целевых значений, включающих в себя первоначальное целевое значение, и которое минимизирует значение предварительно определенной функции оценки. Функция оценки представляется с помощью первого члена и второго члена, причем первый член выполнен с возможностью иметь большее значение в пропорции к квадрату расстояния между возможным целевым значением и первоначальным целевым значением, а второй член выполнен с возможностью иметь большее значение в пропорции к величине нарушения верхнего предельного ограничения будущим значением количественного параметра состояния. Будущее значение количественного параметра состояния прогнозируется с помощью модели функции n-го порядка, принимающей возможное целевое значение в качестве переменной, где n - это натуральное число. Эталонный регулятор выполнен с возможностью устанавливать целевое значение, удовлетворяющее верхнему предельному ограничению, равным значению верхнего предельного ограничения, когда значение, полученное посредством замены переменной дифференциальной функции, полученной посредством дифференцирования функции оценки относительно возможного целевого значения, значением верхнего предельного ограничения, больше или равно нулю во время нарушения верхнего предельного ограничения первоначальным целевым значением.

[0009] В первом аспекте модель функции n-го порядка может быть моделью функции пятого или более низкого порядка, а эталонный регулятор может быть выполнен с возможностью устанавливать целевое значение, удовлетворяющее верхнему предельному ограничению, равным значению пересечения горизонтальной оси дифференциальной функции, начерченной на плоскости, имеющей дифференциальную функцию в качестве вертикальной оси и возможное целевое значение в качестве горизонтальной оси, когда значение, полученное посредством замены переменной дифференциальной функции значением верхнего предельного ограничения, меньше нуля во время нарушения верхнего предельного ограничения первоначальным целевым значением.

[0010] Второй аспект изобретения относится к устройству управления силовым агрегатом, включающему в себя контроллер обратной связи, выполненный с возможностью определять входное управляющее воздействие для силового агрегата во время ввода целевого значения предварительно определенного количественного параметра состояния силового агрегата, так что количественный параметр состояния следует целевому значению, и эталонный регулятор, выполненный с возможностью корректировать первоначальное целевое значение количественного параметра состояния во время ввода первоначального целевого значения, так что нижнее предельное ограничение, накладываемое на количественный параметр состояния, удовлетворяется, и выводить скорректированное первоначальное целевое значение в контроллер обратной связи. Эталонный регулятор выполнен с возможностью устанавливать целевое значение, удовлетворяющее нижнему предельному ограничению, равным возможному целевому значению, которое выбирается из возможных целевых значений, включающих в себя первоначальное целевое значение, и которое минимизирует значение предварительно определенной функции оценки. Функция оценки представляется с помощью первого члена и второго члена, первый член выполнен с возможностью иметь большее значение в пропорции к квадрату расстояния между возможным целевым значением и первоначальным целевым значением, а второй член выполнен с возможностью иметь большее значение в пропорции к величине нарушения нижнего предельного ограничения будущим значением количественного параметра состояния. Будущее значение количественного параметра состояния прогнозируется с помощью модели функции n-го порядка, принимающей возможное целевое значение в качестве переменной, где n - это натуральное число. Эталонный регулятор выполнен с возможностью устанавливать целевое значение, удовлетворяющее нижнему предельному ограничению, равным значению нижнего предельного ограничения, когда значение, полученное посредством замены, значением нижнего предельного ограничения, переменной дифференциальной функции, полученной посредством дифференцирования функции оценки относительно возможного целевого значения, меньше или равно нулю во время нарушения нижнего предельного ограничения первоначальным целевым значением.

[0011] Во втором аспекте модель функции n-го порядка может быть моделью функции пятого или более низкого порядка, а эталонный регулятор может быть выполнен с возможностью устанавливать целевое значение, удовлетворяющее нижнему предельному ограничению, равным значению пересечения горизонтальной оси дифференциальной функции, начерченной на плоскости, имеющей дифференциальную функцию в качестве вертикальной оси и возможное целевое значение в качестве горизонтальной оси, когда значение, полученное посредством замены переменной дифференциальной функции значением нижнего предельного ограничения, больше нуля во время нарушения нижнего предельного ограничения первоначальным целевым значением.

[0012] Первый аспект может прогнозировать прогнозируемое значение количественного параметра состояния с помощью модели функции n-го порядка, принимающей возможное целевое значение в качестве переменной, и, таким образом, может увеличивать универсальность для прогностической модели. Кроме того, первый аспект может определять целевое значение, удовлетворяющее верхнему предельному ограничению, как значение верхнего предельного ограничения, когда значение, полученное посредством замены, значением верхнего предельного ограничения, переменной дифференциальной функции, полученной посредством дифференцирования функции оценки относительно возможного целевого значения, больше или равно нулю во время нарушения верхнего предельного ограничения первоначальным целевым значением, введенным в эталонный регулятор. Т.е., первый аспект может не использовать итеративное вычисление при определении целевого значения. Соответственно, вычислительная нагрузка по определению целевого значения в эталонном регуляторе может быть уменьшена.

[0013] Первый аспект может определять целевое значение, удовлетворяющее верхнему предельному ограничению, как значение пересечения горизонтальной оси дифференциальной функции, когда значение меньше нуля во время модели функции n-го порядка, являющейся моделью функции пятого или более низкого порядка. Т.е., первый аспект может не использовать итеративное вычисление при определении целевого значения. Соответственно, вычислительная нагрузка по определению целевого значения в эталонном регуляторе может быть уменьшена.

[0014] Второй аспект может прогнозировать прогнозируемое значение количественного параметра состояния с помощью модели функции n-го порядка, принимающей возможное целевое значение в качестве переменной, и, таким образом, может увеличивать универсальность для прогностической модели. Кроме того, второй аспект может определять целевое значение, удовлетворяющее нижнему предельному ограничению, как значение нижнего предельного ограничения, когда значение, полученное посредством замены, значением нижнего предельного ограничения, переменной дифференциальной функции, полученной посредством дифференцирования функции оценки относительно возможного целевого значения, меньше или равно нулю во время нарушения нижнего предельного ограничения первоначальным целевым значением, введенным в эталонный регулятор. Т.е., второй аспект может не использовать итеративное вычисление при определении целевого значения. Соответственно, вычислительная нагрузка по определению целевого значения в эталонном регуляторе может быть уменьшена.

[0015] Второй аспект может определять целевое значение, удовлетворяющее нижнему предельному ограничению, как значение пересечения горизонтальной оси дифференциальной функции, когда значение больше нуля во время модели функции n-го порядка, являющейся моделью функции пятого или более низкого порядка. Т.е., второй аспект может не использовать итеративное вычисление при определении целевого значения. Соответственно, вычислительная нагрузка по определению целевого значения в эталонном регуляторе может быть уменьшена.

Краткое описание чертежей

[0016] Признаки, преимущества и техническое и промышленное значение примерных вариантов осуществления изобретения будут описаны ниже со ссылкой на сопровождающие чертежи, на которых аналогичные номера обозначают аналогичные элементы, и на которых:

Фиг. 1 - это схема, иллюстрирующая пример конфигурации системы турбонагнетателя, к которой применяется устройство управления силовым агрегатом согласно первому варианту осуществления изобретения;

Фиг. 2 - это схема, иллюстрирующая структуру управления с обратной связью для ECU 40, иллюстрированного на фиг. 1;

Фиг. 3 - это схема, иллюстрирующая структуру управления с прямой связью, полученную посредством эквивалентного преобразования структуры управления с обратной связью, иллюстрированной на фиг. 2;

Фиг. 4 - это схема, иллюстрирующая алгоритм обычного эталонного регулятора и его проблему;

Фиг. 5 - это схема, схематично иллюстрирующая функцию J(w) оценки, представленную в общей формуле (2) на плоскости xy, имеющей скорректированное целевое значение w в качестве оси x и функцию J(w) оценки в качестве оси y, с функцией J(w) оценки, разложенной на первый член с правой стороны и второй член с правой стороны;

Фиг. 6 - это схема, иллюстрирующая один пример (случай (A)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны к градиенту первого члена (i) с правой стороны, иллюстрированному на фиг. 5;

Фиг. 7 - это схема, иллюстрирующая один пример (случай (B)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны, иллюстрированного на фиг. 5, к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 5;

Фиг. 8 - это схема, иллюстрирующая пример алгоритма эталонного регулятора первого варианта осуществления изобретения;

Фиг. 9 - это схема, схематично иллюстрирующая функцию J(w) оценки, представленную в общей формуле (2) на плоскости xy, имеющей скорректированное целевое значение w в качестве оси x и функцию J(w) оценки в качестве оси y, с функцией J(w) оценки, разложенной на первый член с правой стороны и второй член с правой стороны;

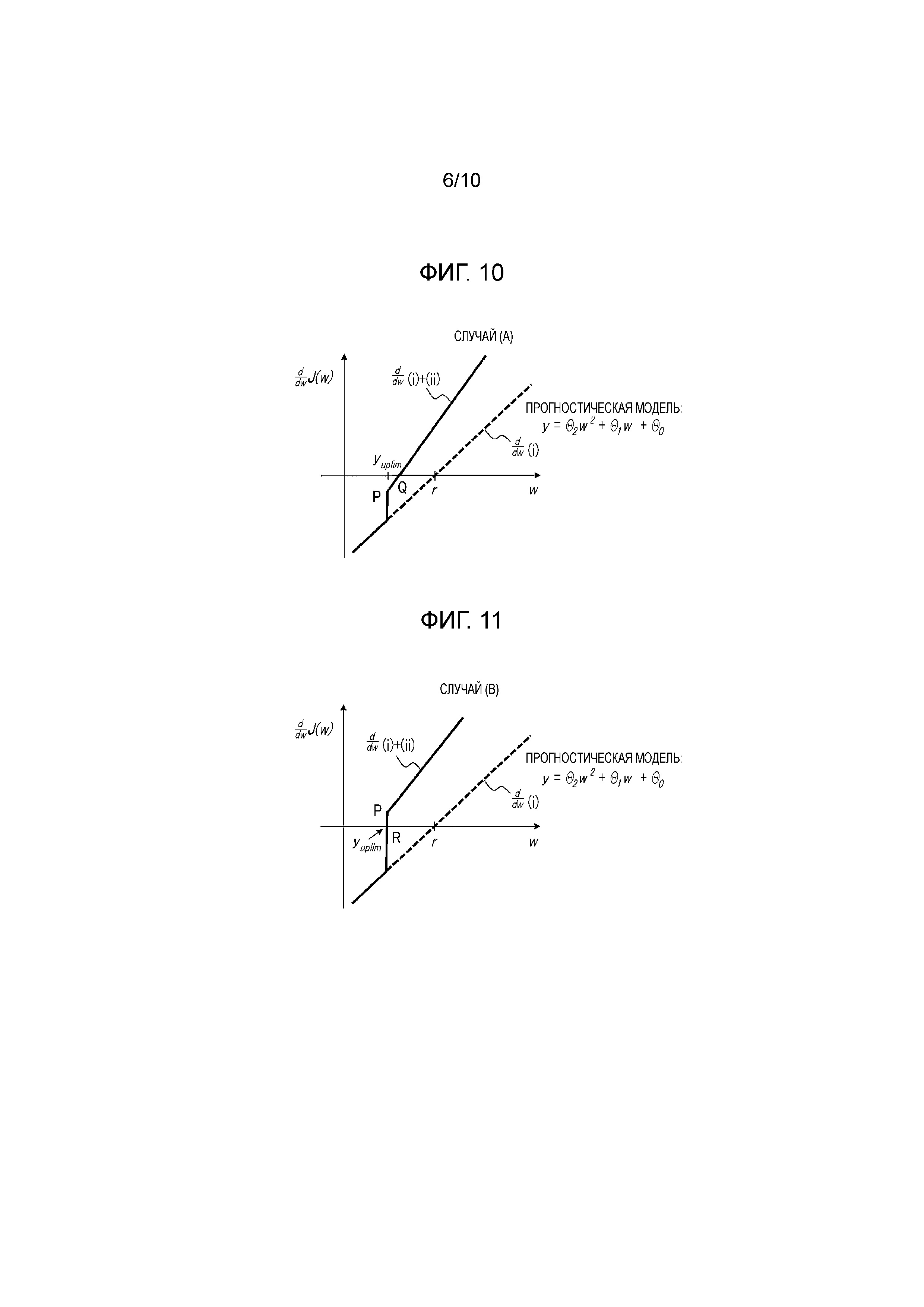
Фиг. 10 - это схема, иллюстрирующая один пример (случай (A)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 9;

Фиг. 11 - это схема, иллюстрирующая один пример (случай (B)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны, иллюстрированного на фиг. 9, к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 9;

Фиг. 12 - это схема, иллюстрирующая один пример алгоритма эталонного регулятора второго варианта осуществления изобретения;

Фиг. 13 - это схема, схематично иллюстрирующая функцию J(w) оценки, представленную в общей формуле (4) на плоскости xy, имеющей скорректированное целевое значение w в качестве оси x и функцию J(w) оценки в качестве оси y, с функцией J(w) оценки, разложенной на первый член с правой стороны и второй член с правой стороны;

Фиг. 14 - это схема, иллюстрирующая один пример (случай (C)) градиента, полученного добавлением градиента второго члена (iv) с правой стороны к градиенту первого члена (iii) с правой стороны, иллюстрированного на фиг. 13;

Фиг. 15 - это схема, иллюстрирующая один пример (случай (D)) градиента, полученного добавлением градиента второго члена (iv) с правой стороны, иллюстрированного на фиг. 13, к градиенту первого члена (iii) с правой стороны, иллюстрированного на фиг. 13;

Фиг. 16 - это схема, иллюстрирующая один пример алгоритма эталонного регулятора третьего варианта осуществления изобретения;

Фиг. 17 - это схема, иллюстрирующая один пример алгоритма эталонного регулятора четвертого варианта осуществления изобретения; и

Фиг. 18 - это схема, иллюстрирующая силовой агрегат, к которому может быть применена структура управления с обратной связью, иллюстрированная на фиг. 2, выходное управляющее воздействие, на которое накладывается ограничение, и пример сочетания количественного параметра состояния силового агрегата и ограничения.

Подробное описание вариантов осуществления

[0017] Далее в данном документе варианты осуществления изобретения будут описаны на основе чертежей. Общие элементы на чертежах будут обозначены одинаковыми ссылочными знаками и будут описаны один раз. Изобретение не ограничивается последующими вариантами осуществления.

Первый вариант осуществления

[0018] Сначала, первый вариант осуществления изобретения будет описан со ссылкой на фиг. 1-8.

Описание конфигурации системы, к которой применяется устройство управления силовым агрегатом

[0019] Устройство управления силовым агрегатом первого варианта осуществления изобретения применяется к системе турбонагнетателя дизельного двигателя, который является установленным на транспортном средстве силовым агрегатом. Фиг. 1 является схемой, иллюстрирующей пример конфигурации системы турбонагнетателя, к которой применяется устройство управления силовым агрегатом согласно первому варианту осуществления. Система турбонагнетателя, иллюстрированная на фиг. 1, включает в себя основной корпус 2 рядного четырехцилиндрового дизельного двигателя. Впускной коллектор 4 и выпускной коллектор 6 присоединяются к основному корпусу 2. Топливо под высоким давлением впрыскивается в каждый из цилиндров основного корпуса 2 через инжектор, соединенный с аккумуляторной топливной системой 8 высокого давления.

[0020] Впускной канал 10, по которому протекает воздух, забираемый из воздушного фильтра 20, соединяется с впускным коллектором 4. Компрессор 14a турбонагнетателя 14 соединяется с впускным каналом 10. Промежуточный охладитель 22 располагается ниже по потоку от компрессора 14a. Дизельный дроссель 24 располагается ниже по потоку от промежуточного охладителя 22. Выпускной канал 12, в котором протекает отработавший газ из основного корпуса 2, соединяется с выпускным коллектором 6. Турбина 14b турбонагнетателя 14 соединяется с выпускным каналом 12. Турбонагнетатель 14 является турбонагнетателем переменной геометрии. Регулируемое сопло 16 располагается в турбине 14b.

[0021] Система турбонагнетателя, иллюстрированная на фиг. 1, включает в себя устройство рециркуляции отработавшего газа (EGR), которое осуществляет рециркуляцию отработавшего газа из выхлопной системы в систему впуска. EGR-устройство является EGR-устройством контура высокого давления, которое соединяет впускной канал 10 на стороне ниже по потоку от дизельного дросселя 24 и выпускной коллектор 6 с EGR-каналом 30. EGR-клапан 32 располагается в EGR-канале 30. EGR-устройство может быть EGR-устройством контура низкого давления, которое соединяет впускной канал 10 на стороне выше по потоку от компрессора 14a и выпускной канал 12 на стороне ниже по потоку от турбины 14b с EGR-каналом, отличным от EGR-канала 30.

Описание конфигурации устройства управления силовым агрегатом

[0022] Электронный блок управления (ECU) 40, иллюстрированный на фиг. 1, соответствует устройству управления силовым агрегатом согласно первому варианту осуществления. ECU 40 включает в себя оперативное запоминающее устройство (RAM), постоянное запоминающее устройство (ROM), CPU (микропроцессор) и т.п. ECU 40 получает сигналы различных датчиков, установленных в транспортном средстве. Различные датчики включают в себя датчик 42 скорости вращения, который измеряет скорость вращения двигателя, датчик 44 величины срабатывания педали акселератора, который выводит сигнал, соответствующей величине срабатывания педали акселератора, и т.п. ECU 40 обрабатывает полученные сигналы различных датчиков. ECU 40 задействует актуатор, инструктируя CPU исполнять предварительно определенную управляющую программу, сохраненную в RAM или ROM. Актуатор, задействуемый посредством ECU 40, включает в себя, по меньшей мере, регулируемое сопло 16. Предварительно определенная управляющая программа включает в себя, по меньшей мере, алгоритм, иллюстрированный на фиг. 8.

[0023] В первом варианте осуществления ECU 40 исполняет управление с обратной связью (управление для следования целевому значению) для давления наддува дизельного двигателя. Входное управляющее воздействие u для управления с обратной связью является степенью открытия регулируемого сопла. Предварительно определенный количественный параметр x состояния дизельного двигателя, используемый в управлении с обратной связью, является фактическим давлением наддува. "Фактическое давление наддува" является, например, давлением на впуске впускного канала 10 непосредственно ниже по потоку от промежуточного охладителя 22. Ограничение в отношении аппаратных средств или управления накладывается на давление наддува, т.е., выходное управляющее воздействие y для управления с обратной связью. Ограничение не задается как предельное значение, которое давление наддува строго не должно превышать, а задается заранее как менее строгое значение, чем предельное значение.

[0024] В управлении с обратной связью первого варианта осуществления степень открытия регулируемого сопла определяется так, что давление наддува в качестве выходного управляющего воздействия y удовлетворяет верхнему предельному ограничению y_uplim, и что фактическое давление наддува как количественный параметр x состояния следует его целевому значению. Подробности управления с обратной связью будут описаны со ссылкой на фиг. 2 и фиг. 3. Для удобства описания, далее в данном документе, "давление наддува в качестве выходного управляющего воздействия y, на которое накладывается ограничение", может быть представлено как "давление y наддува", а "фактическое давление наддува в качестве количественного параметра x состояния" может быть представлено как "фактическое давление x наддува".

Описание структуры управления с обратной связью

[0025] Фиг. 2 - это схема, иллюстрирующая структуру управления с обратной связью для ECU 40, иллюстрированного на фиг. 1. Структура управления с обратной связью, иллюстрированная на фиг. 2, является конфигурацией, которая практически реализуется посредством инструктирования CPU работать в соответствии с управляющей программой, сохраненной в ROM ECU 40. Структура управления с обратной связью включает в себя карту (MAP) 50 целевых значений, эталонный регулятор (RG) 52, контроллер (FBC) 54 обратной связи и силовой агрегат 56.

[0026] Когда MAP 50 снабжается внешним входным сигналом d, который указывает рабочее состояние дизельного двигателя, MAP 50 выводит первоначальное целевое значение r давления наддува в RG 52. Внешний входной сигнал d включает в себя скорость вращения двигателя и объем впрыска топлива. Эти физические величины, включенные во внешний входной сигнал d, могут быть измеренными значениями или оцененными значениями.

[0027] Когда RG 52 снабжается первоначальным целевым значением r давления y наддува из MAP 50, RG 52 корректирует первоначальное целевое значение r так, что верхнее предельное ограничение y_uplim, относящееся к давлению y наддува, удовлетворяется, и выводит скорректированное первоначальное целевое значение r в качестве скорректированного целевого значения w в FBC 54. Подробности конфигурации RG 52 будут описаны позже.

[0028] Когда FBC 54 снабжается скорректированным целевым значением w от RG 52, FBC 54 определяет входное управляющее воздействие u, так что фактическое давление x наддува следует скорректированному целевому значению w. Спецификации FBC 54 не ограничиваются, и может быть использован известный контроллер обратной связи.

[0029] Фиг. 3 - это схема, иллюстрирующая структуру управления с прямой связью, полученную посредством эквивалентного преобразования структуры управления с обратной связью, иллюстрированной на фиг. 2. Система 58 с замкнутым контуром, окруженная прерывистой линией на фиг. 2, предварительно назначается и описывается в качестве одной модели в структуре с прямой связью, иллюстрированной на фиг. 3. Первый вариант осуществления предполагает, что модель системы с замкнутым контуром (далее в данном документе называемая "прогностической моделью") представляется посредством линейной модели. Тогда, прогностическая модель описывается общей формулой (1) с помощью давления y наддува, скорректированного целевого давления w и коэффициента Θ модели (Θ > 0).

y=Θw... (1)

Проблема итеративного вычисления посредством алгоритма эталонного регулятора

[0030] Фиг. 4 - это схема, иллюстрирующая алгоритм обычного эталонного регулятора и его проблему. В алгоритме, иллюстрированном на фиг. 4, прогнозирование будущего значения y^ входного управляющего воздействия y, вычисление функции J(w) оценки, переход к следующему возможному значению для скорректированного целевого значения w повторяются конечное число раз для возможного значения для скорректированного целевого значения w. Прогнозирование будущего значения y^ выполняется с помощью, например, прогностической модели, которая назначена заранее тем же образом, что и модель, описанная в общей формуле (1). Вычисление функции J(w) оценки выполняется с помощью, например, общей формулы (2).

[0031] Первый член с правой стороны общей формулы (2) является функцией, которая принимает возможное скорректированное целевое значение w в качестве переменной. Функция имеет большее значение, когда интервал между первоначальным целевым значением r, введенным в RG 52 из MAP 50, иллюстрированной на фиг. 2, и возможным скорректированным целевым значением w является большим. Второй член с правой стороны общей формулы (2) является функцией, которая принимает будущее значение y^ в качестве переменной. Функция добавляет штрафной коэффициент к целевой функции, когда будущее значение y^ нарушает верхнее предельное ограничение y_uplim. Функция принимает нулевое значение, когда будущее значение y^ не превышает верхнее предельное ограничение y_uplim, и имеет большее значение, когда величина нарушения верхнего предельного ограничения y_uplim будущим значением y^ является большей. Весовая константа ρ (ρ > 0), которая взвешивает штрафной коэффициент, задается для функции.

[0032] Алгоритм, иллюстрированный на фиг. 4, будет описан подробно, предполагая, что число итераций для последовательности операций, иллюстрированных на фиг. 4, равно трем. В этом случае, сначала, вычисление будущего значения y₁^ с помощью прогностической модели и вычисление функции J(w₁) оценки с помощью функции J(w) оценки, как описано в общей формуле (2), выполняются для возможного значения w₁ для скорректированного целевого значения w (первое вычисление). Возможное значение w₁ является первоначальным целевым значением r. Когда первое вычисление заканчивается, выполняется переход к следующему возможному значению w₂ для скорректированного целевого значения w. Вычисление будущего значения y₂^ и вычисление функции J(w₂) оценки выполняются для возможного значения w₂ (второе вычисление). Когда второе вычисление заканчивается, выполняется переход к следующему возможному значению w₃ для скорректированного целевого значения w. Вычисление будущего значения y₃^ и вычисление функции J(w₃) оценки выполняются для возможного значения w₃ (третье вычисление).

[0033] В алгоритме, иллюстрированном на фиг. 4, окончательное определение скорректированного целевого значения w выполняется на стадии, когда число итераций для последовательности операций достигает конечного числа. Например, когда число итераций равно трем, как описано ниже, выбирается минимальное значение из трех функций J(w₁), J(w₂) и J(w₃) оценки, вычисленных в итерациях. Далее, скорректированное целевое значение w, которое используется в вычислении минимального значения, окончательно определяется как скорректированное целевое значение w. Определенное скорректированное целевое значение w используется в управлении с обратной связью. Способ поиска минимального значения функции типа функции J(w) оценки широко известен в качестве оптимального поиска решения методом градиента.

[0034] Число итераций для последовательности операций ставит проблему. Может быть задано любое число итераций последовательности. В целом, когда число итераций является более значительным, возможность выбора более оптимального скорректированного целевое значение w, является более высокой. Однако, когда число итераций последовательности является большим, объем вычислений для выбора скорректированного целевого значения w увеличивается. Кроме того, возможности обработки CPU в ECU 40, иллюстрированном на фиг. 1, являются ограниченными.

Отличительные признаки первого варианта осуществления

[0035] Первый вариант осуществления выполняет поиск оптимального решения с помощью геометрической структуры градиентов (значений производных) каждого члена функции J(w) оценки для того, чтобы уменьшать объем вычислений для выбора скорректированного целевого значения w. Фиг. 5 - это схема, схематично иллюстрирующая функцию J(w) оценки, представленную в общей формуле (2), на плоскости xy, имеющей скорректированное целевое значение w в качестве оси x и функцию J(w) оценки в качестве оси y, с функцией J(w) оценки, разложенной на первый член с правой стороны и второй член с правой стороны. Часть (i) на фиг. 5 соответствует первому члену с правой стороны, а часть (ii) на фиг. 5 соответствует второму члену с правой стороны. Как иллюстрировано на фиг. 5, первый член (i) с правой стороны представляется как квадратическая кривая с J(w)=0, когда скорректированное целевое значение w равно первоначальному целевому значению r. Второй член (ii) с правой стороны представляется как J(w)=0, когда скорректированное целевое значение w меньше верхнего предельного ограничения y_uplim, и представляется как J(w)=ρΘw - ρΘy_uplim, когда скорректированное целевое значение w больше верхнего предельного ограничения y_uplim.

[0036] На фиг. 5 первоначальное целевое значение r имеет значение, больше верхнего предельного ограничения y_uplim. Первоначальное целевое значение r, большее, чем верхнее предельное ограничение y_uplim, означает, что первоначальное целевое значение r заранее выше верхнего предельного ограничения y_uplim на стадии, когда первоначальное целевое значение r вводится в RG 52 из MAP 50, иллюстрированной на фиг. 2.

[0037] Фиг. 6 - это схема, иллюстрирующая один пример (случай (A)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 5. Фиг. 7 - это схема, иллюстрирующая один пример (случай (B)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны, иллюстрированного на фиг. 5, к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 5. Фиг. 6 и фиг. 7 начерчены как плоскость xy, имеющая скорректированное целевое значение w в качестве оси x и градиент dJ(w)/dw функции J(w) оценки в качестве оси y. Прерывистые линии, иллюстрированные на фиг. 6 и фиг. 7, представляют соотношение между скорректированным целевым значением w и градиентом d(i)/dw первого члена (i) с правой стороны. Сплошные линии, иллюстрированные на фиг. 6 и фиг. 7, представляют соотношение между скорректированным целевым значением w и градиентом d{(i)+(ii)}/dw, полученным посредством добавления градиента d(ii)/dw второго члена (ii) с правой стороны к градиенту d(i)/dw.

[0038] Как описано выше, прогностическая модель описывается как линейная модель в первом варианте осуществления. В этом случае градиент d(ii)/dw является следующим.

(1) скорректированное целевое значение w < верхнего предельного ограничения y_uplim: ноль

(2) скорректированное целевое значение w > верхнего предельного ограничения y_uplim: ρΘ

[0039] Соответственно, как иллюстрировано на фиг. 6 и фиг. 7, траектория градиента d{(i)+(ii)}/dw делится следующим образом.

(1) В области скорректированного целевого значения w < верхнего предельного ограничения y_uplim: прямая линия, соответствующая градиенту d(i)/dw

(2) скорректированного целевого значения w=верхнему предельному ограничению y_uplim: отрезок линии, параллельный оси y

(3) В области скорректированного целевого значения w > верхнего предельного ограничения y_uplim: прямая линия, параллельная градиенту d(i)/dw

[0040] Длина отрезка линии, когда траектория градиента d{(i)+(ii)}/dw параллельна оси y, равна ρΘ. Когда длина отрезка линии является небольшой, координата P(y_uplim, 2y_uplim- 2r + ρΘ) располагается ниже оси x, как иллюстрировано на фиг. 6. Наоборот, когда длина отрезка линии является большой, координата P(y_uplim, 2y_uplim- 2r + ρΘ) располагается выше оси x, как иллюстрировано на фиг. 7. Так или иначе, случаи делятся на "случай (A)" на фиг. 6 и "случай (B)" на фиг. 7 по позиции координаты P(y_uplim, 2y_uplim- 2r + ρΘ) с осью x в качестве ориентира, и другие случаи не существуют. y-координата для координаты P получается на основе того факта, что градиент d(i)/dw представляется посредством J(w) = 2w - 2r, и что длина отрезка линии равна ρΘ.

[0041] Функция J(w) оценки имеет минимальное значение, когда градиент dJ(w)/dw функции J(w) оценки равен нулю. Т.е., функция J(w) оценки имеет минимальное значение, когда градиент d{(i)+(ii)}/dw, иллюстрированный на фиг. 6 или фиг. 7, равен нулю, т.е., когда скорректированное целевое значение w является пересечением x-оси для градиента d{(i)+(ii)}/dw. Более конкретно, в "случае (A)" на фиг. 6, функция J(w) оценки имеет минимальное значение, когда скорректированное целевое значение w равно значению x-координаты для координаты Q(r - ρΘ/2,0). В "случае (B)" на фиг. 7, функция J(w) оценки имеет минимальное значение, когда скорректированное целевое значение w равно значению x-координаты для координаты R(верхнее предельное ограничение y_uplim, 0). x-координата для координаты Q получается как пересечение x-оси для линейной прямой линии, имеющей уклон, равный 2, и проходящей через координату P(y_uplim, 2y_uplim - 2r + ρΘ).

[0042] Первый вариант осуществления может получать скорректированное целевое значение w, когда функция J(w) оценки имеет минимальное значение, посредством разделения случаев по позиции координаты P(y_uplim, 2y_uplim - 2r + ρΘ) с помощью оси x в качестве ориентира. Т.е., оптимальное решение для скорректированного целевого значения w может быть найдено без выполнения итеративного вычисления, как описано на фиг. 4. Таким образом, объем вычислений для выбора скорректированного целевого значения w уменьшается, и вычислительная нагрузка на CPU может быть уменьшена.

[0043] Фиг. 8 является схемой, иллюстрирующей один пример алгоритма эталонного регулятора первого варианта осуществления. Этот алгоритм выполняется, когда первоначальное целевое значение r, вычисляемое для каждого предварительно определенного цикла управления (например, для каждого цикла сгорания каждого цилиндра), определяется как большее или равное верхнему предельному ограничению y_uplim.

[0044] В алгоритме, иллюстрированном на фиг. 8, сначала, выполняется определение относительного того, устанавливается или нет отношение 2y_uplim - 2r + ρΘ ≥ 0 (этап S10). Процесс этапа является определением относительно того, располагается или нет y-координата для координаты P, иллюстрированной на фиг. 6 и фиг. 7, выше оси x. Когда результат определения на этапе S10 является положительным, оптимальное решение для скорректированного целевого значения w определяется как верхнее предельное ограничение y_uplim (этап S12). Процесс этапа S12 определяет x-координату для координаты R, иллюстрированной на фиг. 7, как оптимальное решение для скорректированного целевого значения w. Между тем, когда результат определения этапа S10 является отрицательным, оптимальное решение для скорректированного целевого значения w определяется как r - ρΘ/2 (этап S14). Процесс этапа S14 определяет x-координату для координаты Q, иллюстрированной на фиг. 6, как оптимальное решение для скорректированного целевого значения w. Оптимальное решение для скорректированного целевого значения w, определенное на этапе S12 или этапе S14, вводится в FBC 54, иллюстрированный на фиг. 2.

[0045] Алгоритм, иллюстрированный на фиг. 8, может получать оптимальное решение для скорректированного целевого значения w посредством простой инструкции "если-то-иначе" и вычисления пересечения. Соответственно, вычислительная нагрузка для CPU, когда ECU 40 функционирует в качестве эталонного регулятора, минимизируется, и вычислительные ресурсы могут быть сэкономлены.

Второй вариант осуществления

[0046] Далее, вариант осуществления изобретения будет описан со ссылкой на фиг. 9-12. Конфигурация устройства управления силовым агрегатом второго варианта осуществления, в основном, является такой же, что и в первом варианте осуществления. Таким образом, конфигурация устройства управления силовым агрегатом и структура управления с обратной связью описываются с соответствующей ссылкой на фиг. 2 и фиг. 3.

[0047] Во втором варианте осуществления модель системы с замкнутым контуром, иллюстрированной на фиг. 3, описывается, например, как модель квадратической функции, представленная в общей формуле (3) с помощью давления y наддува, скорректированного целевого значения w и коэффициента Θ₂ модели (Θ₂ > 0), Θ₁ и Θ₀.

y=Θ₂w²+ Θ₁w + Θ₀... (3)

Отличительные признаки второго варианта осуществления

[0048] Как и в первом варианте осуществления, второй вариант осуществления выполняет поиск оптимального решения с помощью геометрической структуры градиента функции J(w) оценки. Фиг. 9 - это схема, схематично иллюстрирующая функцию J(w) оценки, представленную в общей формуле (2), на плоскости xy, имеющей скорректированное целевое значение w в качестве оси x и функцию J(w) оценки в качестве оси y, с функцией J(w) оценки, разложенной на первый член с правой стороны и второй член с правой стороны. Часть (i) на фиг. 9 соответствует первому члену с правой стороны, а часть (ii) на фиг. 9 соответствует второму члену с правой стороны. Как иллюстрировано на фиг. 9, первый член (i) с правой стороны представляется как квадратическая кривая с J(w)=0, когда скорректированное целевое значение w равно первоначальному целевому значению r. Часть до сих пор является такой же, что и в первом варианте осуществления. Отличием от первого варианта осуществления является второй член (ii) с правой стороны. Т.е., второй член (ii) с правой стороны представляется как J(w)=0, когда скорректированное целевое значение w меньше верхнего предельного ограничения y_uplim, и представляется как J(w)=Θ₂w²+ Θ₁w + Θ₀ - ρΘy_uplim, когда скорректированное целевое значение w больше верхнего предельного ограничения y_uplim.

[0049] Фиг. 10 - это схема, иллюстрирующая один пример (случай (A)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 9. Фиг. 11 - это схема, иллюстрирующая один пример (случай (B)) градиента, полученного добавлением градиента второго члена (ii) с правой стороны, иллюстрированного на фиг. 9, к градиенту первого члена (i) с правой стороны, иллюстрированного на фиг. 9. Типы линий, иллюстрированных на фиг. 10 и фиг. 11, в основном, являются такими же, что и на фиг. 6 и фиг. 7. Т.е., прерывистые линии, иллюстрированные на фиг. 10 и фиг. 11, представляют соотношение между скорректированным целевым значением w и градиентом d(i)/dw первого члена (i) с правой стороны. Сплошные линии, иллюстрированные на фиг. 10 и фиг. 11, представляют соотношение между скорректированным целевым значением w и градиентом d{(i)+(ii)}/dw, полученным посредством добавления градиента d(ii)/dw второго члена (ii) с правой стороны к градиенту d(i)/dw.

[0050] Как описано выше, прогностическая модель описывается как модель квадратической функции во втором варианте осуществления. В этом случае градиент d(ii)/dw является следующим.

(1) скорректированное целевое значение w < верхнего предельного ограничения y_uplim: ноль

(2) скорректированное целевое значение w > верхнего предельного ограничения y_uplim: ρ(2Θ₂w+Θ₁)

[0051] Соответственно, как иллюстрировано на фиг. 10 и фиг. 11, траектория градиента d{(i)+(ii)}/dw делится следующим образом.

(1) В области скорректированного целевого значения w < верхнего предельного ограничения y_uplim: прямая линия, соответствующая градиенту d(i)/dw

(2) скорректированного целевого значения w=верхнему предельному ограничению y_uplim: отрезок линии, параллельный оси y

(3) В области скорректированного целевого значения w > верхнего предельного ограничения y_uplim: прямая линия, имеющая градиент, больше градиента d(i)/dw.

[0052] Длина отрезка линии, когда траектория градиента d{(i)+(ii)}/dw параллельна оси y, равна ρ(2Θ₂y_uplim+ Θ₁). Когда длина отрезка линии является небольшой, координата P(y_uplim, 2y_uplim(1 + ρΘ₂) - 2r + ρΘ₁) располагается ниже оси x, как иллюстрировано на фиг. 10. Наоборот, когда длина отрезка линии является большой, координата P(y_uplim, 2y_uplim(1 + ρΘ₂) - 2r + ρΘ₁) располагается выше оси x, как иллюстрировано на фиг. 11. Так или иначе, случаи делятся на "случай (A)" на фиг. 10 и "случай (B)" на фиг. 11 по позиции координаты P(y_uplim, 2y_uplim(1 + ρΘ₂) - 2r + ρΘ₁) с осью x в качестве ориентира, и другие случаи не существуют. y-координата для координаты P получается на основе того факта, что градиент d(i)/dw представляется посредством J(w)=2w - 2r, и что длина отрезка линии равна 2ρΘ₂y_uplim+ ρΘ₁.

[0053] Как описано в первом варианте осуществления, функция J(w) оценки имеет минимальное значение, когда градиент dJ(w)/dw функции J(w) оценки равен нулю. Более конкретно, в "случае (A)" на фиг. 10, функция J(w) оценки имеет минимальное значение, когда скорректированное целевое значение w равно значению x-координаты для координаты Q((2r - ρΘ₁)/2(1 + ρΘ₂),0). В "случае (B)" на фиг. 11, функция J(w) оценки имеет минимальное значение, когда скорректированное целевое значение w равно значению x-координаты для координаты R(верхнее предельное ограничение y_uplim, 0). x-координата для координаты Q получается как пересечение оси x для линейной прямой линии, имеющей уклон 2(1+ρΘ₂) и проходящей через координату P(y_uplim,2y_uplim(1 + ρΘ₂) - 2r + ρΘ₁).

[0054] Второй вариант осуществления может получать скорректированное целевое значение w, когда функция J(w) оценки имеет минимальное значение, как в первом варианте осуществления, даже когда прогностическая модель описывается как модель квадратической функции. Таким образом, как и в первом варианте осуществления, объем вычислений для выбора скорректированного целевого значения w уменьшается, и вычислительная нагрузка для CPU может быть уменьшена.

[0055] Фиг. 12 является схемой, иллюстрирующей один пример алгоритма эталонного регулятора второго варианта осуществления. Этот алгоритм выполняется, когда первоначальное целевое значение r, вычисляемое для каждого предварительно определенного цикла управления, определяется как большее или равное верхнему предельному ограничению y_uplim.

[0056] В алгоритме, иллюстрированном на фиг. 12, сначала, выполняется определение относительно того, устанавливается ли отношение 2y_uplim(1 + ρΘ₂) - 2r + ρΘ₁ ≥ 0 (этап S20). Процесс этапа является определением относительно того, располагается или нет y-координата для координаты P, иллюстрированной на фиг. 10 и фиг. 11, выше оси x. Когда результат определения на этапе S20 является положительным, оптимальное решение для скорректированного целевого значения w определяется как верхнее предельное ограничение y_uplim (этап S22). Процесс этапа S22 определяет x-координату для координаты R, иллюстрированной на фиг. 11, как оптимальное решение для скорректированного целевого значения w. Между тем, когда результат определения на этапе S20 является отрицательным, оптимальное решение для скорректированного целевого значения w определяется как (2r - ρΘ₁)/2(1 + ρΘ₂) (этап S24). Процесс этапа S24 определяет x-координату для координаты Q, иллюстрированной на фиг. 10, как оптимальное решение для скорректированного целевого значения w. Оптимальное решение для скорректированного целевого значения w, определенное на этапе S22 или этапе S24, вводится в FBC 54, иллюстрированный на фиг. 2.

[0057] Алгоритм, иллюстрированный на фиг. 12, может получать оптимальное решение для скорректированного целевого значения w посредством простой инструкции "если-то-иначе" и вычисления пересечения, даже когда прогностическая модель описывается как модель квадратической функции.

Третий вариант осуществления

[0058] Далее, третий вариант осуществления изобретения будет описан со ссылкой на фиг. 13-16. Конфигурация устройства управления силовым агрегатом третьего варианта осуществления, в основном, является такой же, что и в первом варианте осуществления. Таким образом, конфигурация устройства управления силовым агрегатом и структура управления с обратной связью описываются с соответствующей ссылкой на фиг. 2 и фиг. 3.

[0059] Как и в первом варианте осуществления, модель системы с замкнутым контуром, иллюстрированная на фиг. 3, описывается посредством линейной модели, представленной в общей формуле (1), в третьем варианте осуществления.

Отличительные признаки третьего варианта осуществления

[0060] В первом варианте осуществления верхнее предельное ограничение в отношении аппаратных средств или управления накладывается на давление наддува. Между тем, в третьем варианте осуществления, нижнее предельное ограничение в отношении аппаратных средств или управления накладывается на давление наддува. Функция J(w) оценки, когда нижнее предельное ограничение задается, описывается, например, общей формулой (4).

[0061] Первый член с правой стороны общей формулы (4) является такой же функцией, что и первый член с правой стороны общей формулы (2). Второй член с правой стороны общей формулы (4) является функцией, которая принимает будущее значение y^ в качестве переменной. Функция добавляет штрафной коэффициент к целевой функции, когда будущее значение y^ нарушает нижнее предельное ограничение y_lolim. Функция принимает нулевое значение, когда будущее значение y^ не превышает нижнее предельное ограничение y_lolim, и имеет большее значение, когда величина нарушения нижнего предельного ограничения y_lolim будущим значением y^ является большей. Весовая константа ρ (ρ > 0), которая взвешивает штрафной коэффициент, задается для функции.

[0062] Фиг. 13 - это схема, схематично иллюстрирующая функцию J(w) оценки, представленную в общей формуле (4), на плоскости xy, имеющей скорректированное целевое значение w в качестве оси x и функцию J(w) оценки в качестве оси y, с функцией J(w) оценки, разложенной на первый член с правой стороны и второй член с правой стороны. Часть (iii) на фиг. 13 соответствует первому члену с правой стороны, а часть (iv) на фиг. 13 соответствует второму члену с правой стороны. Как иллюстрировано на фиг. 13, первый член (iii) с правой стороны представляется как квадратическая кривая с J(w)=0, когда скорректированное целевое значение w равно первоначальному целевому значению r. Часть до сих пор является такой же, что и в первом варианте осуществления. Отличием от первого варианта осуществления является второй член (iv) с правой стороны. Т.е., второй член (iv) с правой стороны представляется как J(w)=0, когда скорректированное целевое значение w больше нижнего предельного ограничения y_lolim, и представляется как J(w)=ρΘy_lolim - ρΘw, когда скорректированное целевое значение w меньше нижнего предельного ограничения y_lolim.

[0063] На фиг. 13 первоначальное целевое значение r имеет значение меньше нижнего предельного ограничения y_lolim. Первоначальное целевое значение r, меньшее, чем нижнее предельное ограничение y_lolim, означает, что первоначальное целевое значение r заранее ниже нижнего предельного ограничения y_lolim на стадии, когда первоначальное целевое значение r вводится в RG 52 из MAP 50, иллюстрированной на фиг. 2.

[0064] Фиг. 14 - это схема, иллюстрирующая один пример (случай (C)) градиента, полученного добавлением градиента второго члена (iv) с правой стороны к градиенту первого члена (iii) с правой стороны, иллюстрированного на фиг. 13. Фиг. 15 - это схема, иллюстрирующая один пример (случай (D)) градиента, полученного добавлением градиента второго члена (iv) с правой стороны, иллюстрированного на фиг. 13, к градиенту первого члена (iii) с правой стороны, иллюстрированного на фиг. 13. Фиг. 14 и фиг. 15 начерчены как плоскость xy, имеющая скорректированное целевое значение w в качестве оси x и градиент dJ(w)/dw функции J(w) оценки в качестве оси y. Прерывистые линии, иллюстрированные на фиг. 14 и фиг. 15, представляют соотношение между скорректированным целевым значением w и градиентом d(iii)/dw первого члена (i) с правой стороны. Сплошные линии, иллюстрированные на фиг. 14 и фиг. 15, представляют соотношение между скорректированным целевым значением w и градиентом d{(iii)+(iv)}/dw, полученным посредством добавления градиента d(iv)/dw второго члена (iv) с правой стороны к градиенту d(iii)/dw.

[0065] Как описано выше, прогностическая модель описывается как линейная модель в третьем варианте осуществления. В этом случае градиент d(iv)/dw является следующим.

(1) скорректированное целевое значение w < нижнего предельного ограничения y_lolim: -ρΘ

(2) скорректированное целевое значение w > нижнего предельного ограничения y_lolim: ноль

[0066] Соответственно, как иллюстрировано на фиг. 14 и фиг. 15, траектория градиента d{(iii)+(iv)}/dw делится следующим образом.

(1) В области скорректированного целевого значения w > нижнего предельного ограничения y_lolim: прямая линия, соответствующая градиенту d(iii)/dw

(2) скорректированного целевого значения w=нижнему предельному ограничению y_lolim: отрезок линии, параллельный оси y

(3) В области скорректированного целевого значения w < нижнего предельного ограничения y_lolim: прямая линия, параллельная градиенту d(iii)/dw

[0067] Длина отрезка линии, когда траектория градиента d{(iii)+(iv)}/dw параллельна оси y, равна ρΘ. Когда длина отрезка линии является небольшой, координата P(y_lolim, 2y_lolim - 2r - ρΘ) располагается выше оси x, как иллюстрировано на фиг. 14. Наоборот, когда длина отрезка линии является большой, координата P(y_lolim, 2y_lolim - 2r - ρΘ) располагается ниже оси x, как иллюстрировано на фиг. 15. y-координата для координаты P получается на основе того факта, что градиент d(iii)/dw представляется посредством J(w)=2w - 2r, и что длина отрезка линии равна ρΘ.

[0068] Как описано в первом варианте осуществления, функция J(w) оценки имеет минимальное значение, когда градиент dJ(w)/dw функции J(w) оценки равен нулю. Т.е., функция J(w) оценки имеет минимальное значение, когда градиент d{(iii)+(iv)}/dw, иллюстрированный на фиг. 14 или фиг. 15, равен нулю, т.е., когда скорректированное целевое значение w является пересечением x-оси для градиента d{(iii)+(iv)}/dw. Более конкретно, в "случае (C)" на фиг. 14, функция J(w) оценки имеет минимальное значение, когда скорректированное целевое значение w равно значению x-координаты для координаты Q(r+ρΘ/2,0). В "случае (D)" на фиг. 15, функция J(w) оценки имеет минимальное значение, когда скорректированное целевое значение w равно значению x-координаты для координаты R(нижнее предельное ограничение y_lolim, 0). x-координата для координаты Q получается как пересечение x-оси для линейной прямой линии, имеющей уклон, равный 2, и проходящей через координату P(y_lolim, 2y_lolim - 2r - ρΘ).

[0069] Третий вариант осуществления может получать скорректированное целевое значение w, когда функция J(w) оценки имеет минимальное значение как в первом варианте осуществления, даже когда нижнее предельное ограничение накладывается на давление наддува. Таким образом, как и в первом варианте осуществления, объем вычислений для выбора скорректированного целевого значения w уменьшается, и вычислительная нагрузка для CPU может быть уменьшена.

[0070] Фиг. 16 является схемой, иллюстрирующей один пример алгоритма эталонного регулятора третьего варианта осуществления. Этот алгоритм выполняется, когда первоначальное целевое значение r, вычисляемое для каждого предварительно определенного цикла управления, определяется как меньшее или равное нижнему предельному ограничению y_lolim.

[0071] В алгоритме, иллюстрированном на фиг. 16, сначала, выполняется определение относительно того, устанавливается или нет отношение 2y_lolim - 2r - ρΘ ≤ 0 (этап S30). Процесс этапа является определением относительно того, располагается или нет y-координата для координаты P, иллюстрированной на фиг. 14 и фиг. 15, выше оси x. Когда результат определения на этапе S30 является положительным, оптимальное решение для скорректированного целевого значения w определяется как нижнее предельное ограничение y_lolim (этап S32). Процесс этапа S32 определяет x-координату для координаты R, иллюстрированной на фиг. 15, как оптимальное решение для скорректированного целевого значения w. Между тем, когда результат определения этапа S30 является отрицательным, оптимальное решение для скорректированного целевого значения w определяется как r+ρΘ/2 (этап S34). Процесс этапа S34 определяет x-координату для координаты Q, иллюстрированной на фиг. 14, как оптимальное решение для скорректированного целевого значения w. Оптимальное решение для скорректированного целевого значения w, определенное на этапе S32 или этапе S34, вводится в FBC 54, иллюстрированный на фиг. 2.

[0072] Алгоритм, иллюстрированный на фиг. 16, может получать оптимальное решение для скорректированного целевого значения w посредством простой инструкции "если-то-иначе", даже когда нижнее предельное ограничение y_lolim накладывается на давление y наддува.

Четвертый вариант осуществления

[0073] Далее, четвертый вариант осуществления изобретения будет описан со ссылкой на фиг. 17. Конфигурация устройства управления силовым агрегатом четвертого варианта осуществления, в основном, является такой же, что и в первом варианте осуществления. Таким образом, конфигурация устройства управления силовым агрегатом и структура управления с обратной связью описываются с соответствующей ссылкой на фиг. 2 и фиг. 3.

[0074] Как и во втором варианте осуществления, модель системы с замкнутым контуром, иллюстрированной на фиг. 3, описывается, например, посредством модели квадратической функции, представленной в общей формуле (3) в четвертом варианте осуществления. Кроме того, как и в третьем варианте осуществления, нижнее предельное ограничение y_lolim в отношении аппаратных средств или управления накладывается на давление y наддува в четвертом варианте осуществления.

Отличительные признаки четвертого варианта осуществления

[0075] Как описано во втором варианте осуществления, скорректированное целевое значение w, когда функция J(w) оценки имеет минимальное значение, может быть получено, даже когда прогностическая модель описывается посредством модели квадратической функции. Кроме того, как описано в третьем варианте осуществления, скорректированное целевое значение w, когда функция J(w) оценки имеет минимальное значение, может быть получено, даже когда нижнее предельное ограничение y_lolim накладывается на давление y наддува. Таким образом, даже когда прогностическая модель описывается посредством модели квадратической функции с нижним ограничением y_lolim, наложенным на давление y наддува, как в четвертом варианте осуществления, скорректированное целевое значение w, когда функция J(w) оценки имеет минимальное значение, может быть получено.

[0076] Фиг. 17 является схемой, иллюстрирующей один пример алгоритма эталонного регулятора четвертого варианта осуществления. Этот алгоритм выполняется, когда первоначальное целевое значение r, вычисляемое для каждого предварительно определенного цикла управления, определяется как меньшее или равное нижнему предельному ограничению y_lolim.

[0077] В алгоритме, иллюстрированном на фиг. 17, сначала, выполняется определение относительно того, установлено или нет отношение 2y_lolim(1 - ρΘ₂) - 2r - ρΘ₁≤ 0 (этап S40). Когда результат определения на этапе S40 является положительным, оптимальное решение для скорректированного целевого значения w определяется как нижнее предельное ограничение y_lolim (этап S42). Между тем, когда результат определения на этапе S40 является отрицательным, оптимальное решение для скорректированного целевого значения w определяется как (2r + ρΘ₁)/2(1 - ρΘ₂) (этап S44). Оптимальное решение для скорректированного целевого значения w, определенное на этапе S42 или этапе S44, вводится в FBC 54, иллюстрированный на фиг. 2.

[0078] Алгоритм, иллюстрированный на фиг. 17, может получать оптимальное решение для скорректированного целевого значения w посредством простой инструкции "если-то-иначе" и вычисления пересечения, даже когда прогностическая модель описывается посредством модели квадратической функции с нижним предельным ограничением y_lolim, наложенным на давление y наддува.

Другие варианты

[0079] Первый и третий варианты осуществления описывают прогностическую модель как линейную модель (т.е., модель линейной функции), а второй и четвертый варианты осуществления описывают прогностическую модель как модель квадратической функции. Однако, прогностическая модель может быть описана посредством модели функции третьего или более высокого порядка. Как понятно из использования координаты P во время получения значения x-координаты для координаты Q, иллюстрированной на фиг. 6, фиг. 10 и фиг. 14, и использования градиента d(ii)/dw во время получения координат для координаты Q, получение значения x-координаты для координаты Q использует формулу для решения дифференциальной функции, полученной посредством дифференцирования прогностической модели относительно скорректированного целевого значения w. Так как формула для решения уравнения пятого порядка не существует, прогностическая модель желательно описывается посредством модели функции пятого или более низкого порядка для того, чтобы дифференциальная функция была функцией четвертого или более низкого порядка, если предполагается вычисление значения x-координаты для координаты Q.

[0080] Значение x-координаты для координаты R, иллюстрированной на фиг. 7, фиг. 11 и фиг. 15, может быть определено посредством простой инструкции "если-то-иначе", даже когда прогностическая модель описывается посредством модели функции шестого или более высокого порядка. В этом случае итеративное вычисление в соответствии с алгоритмом обычного эталонного регулятора, описанным на фиг. 4, используется во время получения значения x-координаты для координаты Q. Т.е., если значение y-координаты для координаты P больше или равно нулю, когда задается верхнее предельное ограничение y_uplim, значение x-координаты для координаты R, т.е., верхнее предельное ограничение y_uplim, определяется как оптимальное решение скорректированного целевого значения w. Иначе, значение x-координаты для координаты Q может быть определено посредством итеративного вычисления. Т.е., если значение y-координаты для координаты P меньше или равно нулю, когда задается нижнее предельное ограничение y_lolim, значение x-координаты для координаты R, т.е., нижнее предельное ограничение y_lolim, определяется как оптимальное решение скорректированного целевого значения w. Иначе, значение x-координаты для координаты Q может быть определено посредством итеративного вычисления. С этой точки зрения, модель функции шестого или более высокого порядка может быть применена в качестве прогностической модели изобретения.

[0081] В то время как первый-четвертый варианты осуществления описывают систему турбонагнетателя дизельного двигателя в качестве цели применения, управление с обратной связью может быть выполнено как в первом-четвертом вариантах осуществления для любого силового агрегата, предварительно определенный количественный параметр состояния которого может быть спрогнозирован с помощью модели функции n-го порядка (n является натуральным числом), принимающей возможное целевое значение в качестве переменной. Фиг. 18 - это схема, иллюстрирующая силовой агрегат, к которому может быть применена структура управления с обратной связью, иллюстрированная на фиг. 2, выходное управляющее воздействие, на которое накладывается ограничение, и пример сочетания предварительно определенного количественного параметра состояния силового агрегата и ограничения. В первом примере на фиг. 18 силовой агрегат является EGR-системой дизельного двигателя, выходное управляющее воздействие, на которое накладывается верхнее предельное ограничение или нижнее предельное ограничение, является коэффициентом EGR, и предварительно определенный количественный параметр состояния является фактическим коэффициентом EGR. Во втором примере силовой агрегат является системой постобработки для дизельного двигателя, выходное управляющее воздействие, на которое накладывается верхнее предельное ограничение, является температурой DPF, а предварительно определенный количественный параметр состояния является фактической температурой DPF. В третьем примере силовой агрегат является системой турбонагнетателя двигателя, выходное управляющее воздействие, на которое накладывается верхнее предельное ограничение или нижнее предельное ограничение, является степенью открытия VN (степенью открытия регулируемого сопла), а предварительно определенный количественный параметр состояния является фактической степенью открытия VN. В четвертом примере силовой агрегат является EGR-системой двигателя, выходное управляющее воздействие, на которое накладывается верхнее предельное ограничение или нижнее предельное ограничение, является степенью открытия EGR-клапана, а предварительно определенный количественный параметр состояния является фактической степенью открытия EGR-клапана. В пятом примере силовой агрегат является системой впуска двигателя, выходное управляющее воздействие, на которое накладывается верхнее предельное ограничение или нижнее предельное ограничение, является степенью открытия дроссельной заслонки, а предварительно определенный количественный параметр состояния является фактической степенью открытия дроссельного клапана. В шестом примере силовой агрегат является аккумуляторной топливной системой высокого давления, выходное управляющее воздействие, на которое накладывается верхнее предельное ограничение или нижнее предельное ограничение, является магистральным давлением впрыска, а предварительно определенный количественный параметр состояния является фактическим магистральным давлением впрыска.

Реферат

Изобретение относится к машиностроению, а именно к устройствам управления силовым агрегатом. Устройство управления силовым агрегатом содержит контроллер обратной связи, выполненный с возможностью определять входное управляющее воздействие для силового агрегата во время ввода целевого значения предварительно определенного количественного параметра состояния силового агрегата, так что количественный параметр состояния следует целевому значению. Эталонный регулятор выполнен с возможностью корректировать первоначальное целевое значение количественного параметра состояния во время ввода первоначального целевого значения, так что верхнее предельное ограничение, наложенное на количественный параметр состояния, удовлетворяется, и выводить скорректированное первоначальное целевое значение в контроллер обратной связи. Эталонный регулятор также выполнен с возможностью устанавливать целевое значение, удовлетворяющее верхнему предельному ограничению, равному возможному целевому значению, которое выбирается из возможных целевых значений, включающих в себя первоначальное целевое значение, и которое минимизирует значение предварительно определенной функции оценки. Также эталонный регулятор выполнен с возможностью устанавливать целевое значение, удовлетворяющее верхнему предельному ограничению, равным значению верхнего предельного ограничения, когда значение, полученное посредством замены переменной дифференциальной функции, полученной посредством дифференцирования функции оценки относительно возможного целевого значения, значением верхнего предельного ограничения, больше или равно нулю во время нарушения верхнего предельного ограничения первоначальным целевым значением. Упомянутая функция оценки представляется с помощью первого члена и второго члена. Причем первый член выполнен с возможностью иметь большее значение в пропорции к квадрату интервала между возможным целевым значением и первоначальным целевым значением, а второй член выполнен с возможностью иметь большее значение в пропорции к величине нарушения верхнего предельного ограничения будущим значением количественного параметра состояния. Будущее значение количественного параметра состояния прогнозируется с помощью модели функции n-го порядка, принимающей возможное целевое значение в качестве переменной, где n - это натуральное число. Также раскрыт вариант устройства управления силовым агрегатом. Технический результат заключается в снижении вычислительной нагрузки по корректировке целевого значения количественного параметра состояния силового агрегата с ограничением, наложенным на количественный параметр состояния. 2 н. и 2 з.п. ф-лы, 18 ил.

Формула