Способ возбуждения колебаний - RU2716862C1

Чертежи

Показать все 7 чертежа(ей)

Описание

Настоящее изобретение относится к вибрационной технике и может быть использовано в вибрационных машинах, применяемых в строительстве, транспорте, медицине, металлообработке, сельском хозяйстве, станкостроении, пищевой, горной и других отраслях промышленности, где используется вибрация.

Известен способ возбуждения колебаний [RU 2441714 С1, «СПОСОБ ВОЗБУЖДЕНИЯ РЕЗОНАНСНЫХ МЕХАНИЧЕСКИХ КОЛЕБАНИЙ», МПК B06B 1/10, опубл. 10.02.2012], согласно которому возбуждение резонансных механических колебаний производят путем согласованной синхронной работы двух или более параметрических вибровозбудителей, установленных на общем рабочем органе (несущем теле), связанном с основанием упругими связями, с достижением эффекта самосинхронизации без вмешательства извне. Резонансные колебания возбуждают путем периодического принудительного изменения инерционных параметров колебательной системы.

Недостатком данного способа является ограниченность вынуждающей силы, невозможность получения колебаний сложной формы, а также, малые возможности регулирования параметров.

Известен способ возбуждения колебаний [RU 2533743 С1, «СПОСОБ ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ», МПК B06B 1/00, опубл. 20.11.2014], при котором вращаемое тело и контртело сопрягают с тарированной силой прижима и обкатывают его по замкнутой траектории, имеющей поворотную симметрию вокруг оси симметрии траектории и одновременно воздействуют на них неуравновешенной радиальной силой, постоянно меняя ее направление с частотой вращения тела, при этом суммарной амплитудой колебаний управляют по соотношению равенства амплитуды колебаний А в левой части и квадратного корня из суммы трех слагаемых в правой части. Первое слагаемое является квадратом частного радиуса вращаемого тела и частоты колебаний вращаемого тела в числителе к частоте вращения в знаменателе. Второе слагаемое является квадратом частного неуравновешенной радиальной силы в числителе к суммарной массе тел и квадрата частоты вращения в знаменателе. Третье слагаемое является произведением двух радиусов вращаемого тела на неуравновешенную радиальную силу, частного от частоты колебания вращаемого тела в знаменателе к частоте вращения в числителе, частного от единицы в знаменателе, деленной на суммарную массу тел и квадрата частоты вращения в знаменателе, и все это умноженное на косинус суммы частоты колебания вращаемого тела и частоты вращения по времени.

где

Δω = ω₁ + ω₂;

F₂ - неуравновешенная радиальная сила;

ω₁ - частота колебаний вращаемого тела;

ω₂ - частота вращения;

r₁ - радиус вращаемого тела;

М - суммарная масса тел;

t - время.

Недостатками данного способа являются ограниченность вынуждающей силы, значительное увеличение инерционного момента, в случае создания колебаний большей амплитуды и энергозатратность.

Известен способ возбуждения колебаний и устройство для его осуществления [RU 2347627 С1, «СПОСОБ ВОЗБУЖДЕНИЯ КОЛЕБАНИЙ И УСТРОЙСТВО ДЛЯ ЕГО ОСУЩЕСТВЛЕНИЯ», МПК B06B 1/16, опубл. 27.02.2009], взятый за прототип, согласно которому по крайней мере два тела вращения сопрягают с контртелом тарированной силой прижима и посредством жесткой кинематической связи с одинаковыми угловыми скоростями одновременно обкатывают по их собственным замкнутым траекториям, каждая из которых имеет поворотную симметрию вокруг оси симметрии своей траектории.

Недостатком прототипа является сложность регулирования параметров и настройки требуемой формы возбуждаемых колебаний, а также ограниченность рабочего частотного диапазона.

Технической задачей изобретения является устранение указанных недостатков, а именно, повышение эффективности и универсальности способа возбуждения колебаний, которые заключаются в обеспечении возможности управления формой траектории колебательного движения и возможности одновременного получения синхронных высокочастотной и низкочастотной составляющей колебаний, расширение функциональных возможностей виброприводов, посредством возбуждения механических колебаний на резонансных частотах, а так же, вследствие полного уравновешивания сил инерции, возможность разгрузить привод от действия динамических давлений, что, в свою очередь, позволяет уменьшить его размеры, повысить долговечность, и уменьшить затраты энергии на преодоление сопротивлений вращению.

Поставленная техническая задача достигается тем, что в способе возбуждения колебаний по крайней мере два тела вращения сопрягают с контртелом, затем эти тела посредством жесткой кинематической связи с одинаковыми угловыми скоростями одновременно обкатывают по их собственным замкнутым траекториям, каждая из которых имеет поворотную симметрию вокруг оси симметрии своей траектории, отличающийся тем, что одновременно на них воздействуют неуравновешенной радиальной силой и постоянно меняют ее направление с частотой вращения этих тел.

Сравнение заявленного способа возбуждения колебаний с известными позволяет сделать вывод о достижении нового эффекта, выразившегося в расширении функциональных возможностей, а именно регулирования формы и параметров возбуждаемых колебаний и обеспечении условий для самосинхронизации колебаний вращаемых тел.

Сущность изобретения поясняется чертежами,

где на фиг. 1 показана схема возбуждения колебаний при принудительном воздействии радиальной неуравновешенной силы на вращаемые тела;

на фиг. 2 показана схема формирования траектории вибрационных перемещении для схемы фиг. 1 при несинхронном режиме работы;

на фиг. 3 показана схема формирования траектории вибрационных перемещении для схемы фиг. 1 при синхронном режиме работы;

на фиг. 4а) показана форма колебаний и временная диаграмма колебаний роторно-дебалансного (x1;y1) и бироторно-дебалансного (х2;у2) виброприводов, при частоте вращения роторов - 100 об/мин, частоте вращения дебаланса - 200 об/мин;

на фиг. 4б) показана форма колебаний и временная диаграмма колебаний роторно-дебалансного (x1;y1) и бироторно-дебалансного (х2;у2) виброприводов, при частоте вращения роторов - 100 об/мин, частоте вращения дебаланса - 300 об/мин;

на фиг. 4в) показана форма колебаний и временная диаграмма колебаний роторно-дебалансного (x1;y1) и бироторно-дебалансного (х2;у2) виброприводов, при частоте вращения роторов - 200 об/мин, частоте вращения дебаланса -100 об/мин

на фиг. 5а) показаны формы колебаний: дебалансного (1), роторно-дебалансного (2) и предлагаемого способа (3), при ω₁ = ω₂ = 2ω₃;

на фиг. 5б) показаны формы колебаний: дебалансного (1), роторно-дебалансного (2) и предлагаемого способа (3), при ω₁ = ω₂ = ω₃.

Способ возбуждения колебаний заключается в том, что по крайней мере два тела вращения 1 и 2 сопрягают с контртелом 4 с тарированной силой прижима Р_ос (см. фиг. 1). Затем тела вращения 1 и 2 посредством жестких кинематических связей 5, 6 и 7 с одинаковыми угловыми скоростями ω_ВР1 и ω_ВР2 одновременно обкатывают по их собственным замкнутым траекториям, каждая из которых имеет поворотную симметрию вокруг оси симметрии своей траектории. При этом, образуются центры мгновенного качения, а вращаемые тела 1 и 2 совершают круговые высокочастотные колебания ω₁ и ω₂ соответственно, обкатываясь периферией торцев по поверхности контртела 4. Вместе с тем, когда на синхронно вращаемые тела воздействуют неуравновешенной радиальной силой F₃ и постоянно меняют ее направление с частотой вращения ω₃, колебания всей системы обретают модулирующие свойства.

Для пояснения сущности способа рассмотрим изменение радиус-вектора суммарной амплитуды колебаний (см. фиг. 2) при несинхронном режиме работы, для определения траектории виброперемещений и формы колебаний, создаваемых при заявляемом способе. Для общего случая действия трех колебаний с разными амплитудами и частотами рассмотрим движение радиус-вектора суммарной амплитуды А колебаний с углом поворота α.

где

Система уравнений проекций колебаний системы

где

Тогда система уравнений (2) примет вид:

где

ω₁, ω₂ - частоты колебаний вращаемых тел;

A_1X, A_2X, A_1Y, A_2Y - проекции радиус-векторов амплитуд колебаний вращаемых тел, соответственно на оси ОХ и OY;

ω₃ - частота вращения неуравновешенной радиальной силы;

A_3X, A_3Y - проекция радиус-вектора амплитуды колебаний неуравновешенной радиальной силы F₃ соответственно на оси ОХ и OY.

Полученная система уравнений является общим случаем для трех тел, генерирующих колебания отличных друг от друга значений. Наибольший интерес в вибрационной механике представляет частный случай рассматриваемого явления, при котором два тела работают синхронно (см. фиг. 3), т.е. согласование частот, фаз или других характеристик колебаний, генерируемых взаимодействующими системами.

Так как условием существования синхронных гармонических колебаний является, как известно [Блехман И.И. Синхронизация динамических систем. - М., 1972. - 894 с.,] равенство частот и амплитуд этих колебаний, то в рассматриваемом способе должны выполняться тождества ω₁ = ω₂ и А₁ = А₂. Поэтому, обозначив в системе уравнений (3) A₁ = А₂ = А' и ω₁ = ω₂ = ω', получим:

С целью дальнейших преобразований уравнений системы (4), обозначим ω' + ω₃ = Δω и в уравнениях системы (4) заменим ω' на Δω - ω₃, система уравнений примет вид:

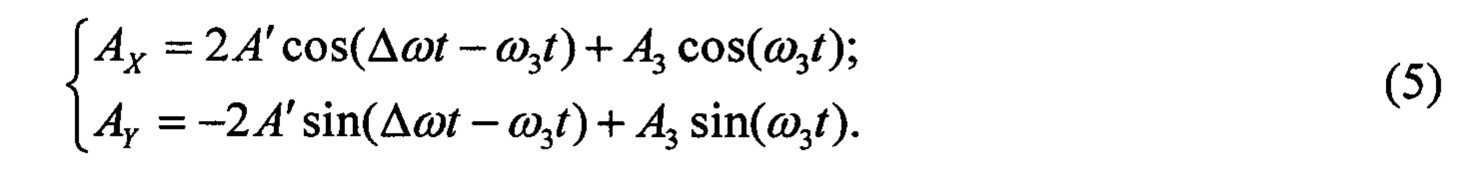
Используя формулы синуса суммы углов и косинуса суммы углов (6), преобразуя систему уравнений (5) получим систему уравнений:

С целью дальнейшего упрощения уравнений системы (7), вынесем общие множители за скобки и получим систему уравнений:

Для упрощения системы уравнений (8), введем обозначения:

Система уравнений (8) примет вид:

Для упрощения системы уравнений (10), используя формулы обратные формулам синуса суммы углов и косинуса суммы углов (6), выполним преобразования и получим систему уравнений:

Из уравнения (9) находим сдвиг фаз угла поворота радиус-вектора колебаний А, разделив одно уравнение на другое:

Для перехода от системы уравнений вида (9) к одному общему уравнению, возведем уравнения системы (9) в квадрат и сложим:

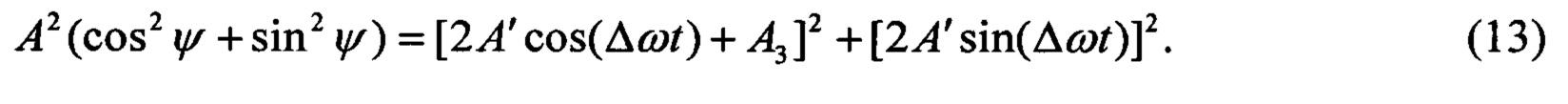
С целью упрощения полученного уравнения, используя формулы квадрата суммы и квадрата разности и основного тригонометрического тождества, упростим уравнение (13), и получим:

В правой части уравнения (14) вынесем общий множитель за скобки и получим уравнение:

Упростим выражение (15), используя основное тригонометрическое тождество, и получим:

Из уравнения (16) находим результирующую амплитуду радиуса-вектора колебаний А:

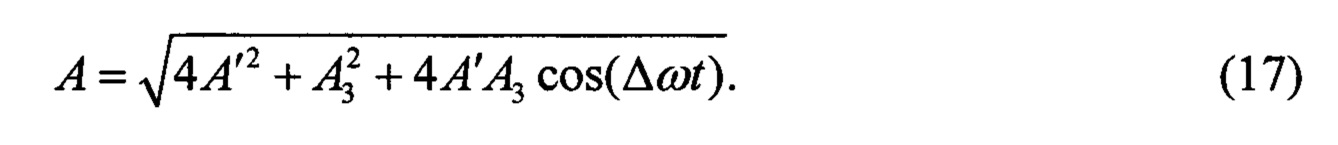
Из системы уравнений (11) видно, что угол поворота α радиуса-вектора колебаний А равен:

Возведем уравнения (11) в квадрат и сложим:

Из приведенных уравнений видно, что полученное каноническое уравнение движения радиуса-вектора колебаний А в конечном счете зависит от частот колебаний вращаемых тел и частоты вращения неуравновешенной радиальной силы, а также от значений амплитуд колебаний этих тел и неуравновешенной радиальной силы, а траектория может меняться от квазикруговой до линейной.

Для определения амплитуды радиуса-вектора колебаний А воспользуемся уравнением (17), при этом амплитуда высокочастоных колебаний А₁ = А₂ = А' равна:

где r = r₁ = r₂ - радиусы вращаемых тел.

Амплитуда низкочастотных колебаний А₃ равна:

где

F₃ - неуравновешенная радиальная сила;

ω₃ - частота вращения неуравновешенной радиальной силы;

М - суммарная масса тел.

Подставив выражения (20) и (21) в (17), получим:

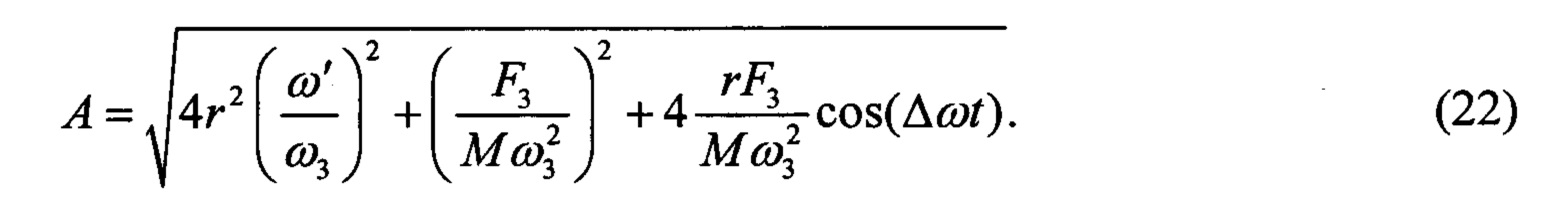
Введем коэффициенты

и подставив их в уравнение (22) получим:

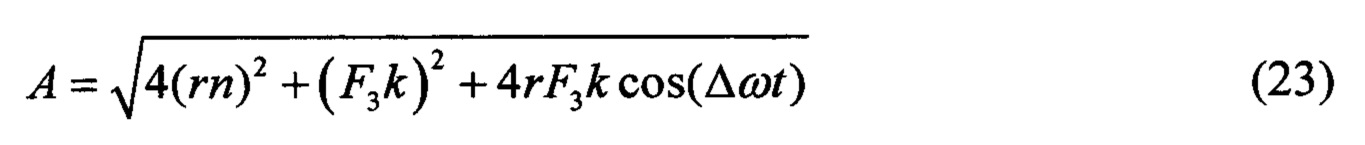
В этом выражении первое слагаемое под корнем 4(rn)² - частотная составляющая или «высокочастотная составляющая», второе слагаемое (F₃k)² - составляющая, зависящая от массы или «низкочастотная» составляющая, а третье слагаемое 4rF₃kcos(Δωt) - составляющая разности фаз колебаний Δωt. Используя зависимость (23), управляют величиной амплитуды А, изменяя параметры этих составляющих. Параметры колебаний неуравновешенной силы задают посредством изменения скорости вращения ω₃ и самой силы F₃. Параметрами колебаний вращаемого тела управляют посредством изменения осевой силы Р_ос в соответствии с зависимостями, приведенными в [А.с. 1664412 А1, 23.07.91]. В результате формой траектории колебательных перемещений управляют посредством изменения частот и амплитуд колебаний вращаемых тел и неуравновешенной радиальной силы. Для сравнения, выполним математическое моделирование амплитудно-частотных характеристик роторно-дебалансного [RU 2533743 С1, 20.11.2014] и предлагаемого способа возбуждения колебаний в зависимости от разных частот вращения роторов и дебаланса. Результаты моделирования при частоте вращения роторов - 100 об/мин, частоте вращения дебаланса - 200 об/мин представлены на фиг. 4а). Результаты моделирования при частоте вращения роторов - 100 об/мин, частоте вращения дебаланса - 300 об/мин представлены на фиг. 4б). Результаты моделирования при частоте вращения роторов - 200 об/мин, частоте вращения дебаланса - 100 об/мин; представлены на фиг. 4в). Из полученных графиков видно, что с изменением частот вращения роторов и дебаланса происходит изменение форм колебаний. В сравнении с существующим способом предлагаемый способ позволяет значительно повысить амплитудно-частотные характеристики колебаний за счет синхронизации высокочастных колебаний с низкочастотными. К тому же, более плавные формы колебаний, получаемых в предлагаемом способе, свидетельствуют о возможности более точного регулирования выходных параметров вибропривода.

В соответствии с предлагаемым способом была испытана в лабораторных условиях модель способа генерации колебаний сложной формы. Испытания показали работоспособность способа и его эффективность. Ожидается экономический эффект от внедрения и использования предлагаемого способа за счет возможности генерации управляемых сложных колебаний, требуемой формы одним вибровозбудителем. Промышленное применение предлагаемого способа может найти, например, в различных отраслях в виброприводах измельчителей для переработки отходов упруговязких материалов в качественное вторичное сырье в виде измельченных частиц с требуемыми формой и размерами.

Примеры реализации способа.

Для примера рассмотрим схему возбуждения колебаний, представленную на фиг. 1, имеющую следующие параметры:

m₁ = m₂ = 0,5 кг; m₃ = 0,3 кг; r = r₁ = r₂ = 0,02 м; ω₁ = ω₂ = 200 с^-1; ω₃ = 500 с^-1; F₃ = 75 Н; t=10 с.

Суммарная масса тел равна

М = m₁ + m₂ + m₃ = 1,3 кг.

Подставив в уравнение (23) заданные числовые значения, получим:

На плоскости, заданные параметры описывают траекторию, изображенную на фиг 5 а). В качестве сравнения возьмем известный способ возбуждения колебаний [RU 2533743 С1, 20.11.2014]. Из сравнительной диаграммы видно, что при одних и тех же условиях, формы колебаний рассматриваемых виброприводов различаются. Колебания дебалансного вибропривода представляют собой окружность, центр которой совпадает с началом системы координат, роторно-дебалансого вибропривода представляют собой дельтоиду, а колебания вибропривода, основанного на предлагаемом способе представлены в виде фигуры Лиссажу.

Аналогично произведем расчет для случая, когда частота колебания неуравновешенной радиальной силы 3 равна частотам колебаний синхронно вращаемых тел 1 и 2, со следующими параметрами:

m₁ = m₂ = 0,6 кг.; m₃ = 0,3 кг.; r = r₁ = r₂ = 0,03 м.; ω₁ = ω₂ = 600 с^-1; ω₃ = 900 с^-1; F₃ = 2400 Н.; t=10 c.

Суммарная масса тел равна

М = m₁ + m₂ + m₃ = 1,5 кг.

Подставив в уравнение (23) заданные числовые значения, получим:

На плоскости, заданные параметры описывают траекторию, изображенную на фиг. 5б). На сравнительной диаграмме видно, что также, как и в предыдущем случае, колебания дебалансного вибропривода являются круговыми. Колебания роторно-дебалансного вибропривода представлены в виде прямой линии, а форма колебаний, получаемых предлагаемым способом представляет собой полумесяц. К тому же, в предлагаемом способе, в сравнении с существующими, прослеживается увеличение амплитуды колебаний в обоих направлениях практически в два раза при одних и тех же параметрах.

На ряду с получением различных форм колебаний, предлагаемый способ позволяет осуществлять «тонкую» регулировку геометрии траектории в пределах требуемой ее формы. Наиболее характерно это можно наблюдать на траекториях сложных форм, например фигур Лиссажу или многоугольников.

Реферат

Изобретение относится к вибрационной технике и может быть использовано в вибрационных машинах, применяемых в строительстве, транспорте, медицине, металлообработке, сельском хозяйстве, станкостроении, пищевой, горной и других отраслях промышленности, где используется вибрация. Технический эффект, заключающийся в повышении эффективности и универсальности способа возбуждения колебаний, в расширении функциональных возможностей виброприводов, а также в возможности разгрузки привода от действий динамических давлений, достигается за счёт того, что на два тела вращения одновременно воздействуют неуравновешенной радиальной силой и постоянно меняют ее направление с частотой вращения этих тел, при этом суммарной амплитудой колебаний управляют по соотношению, гдеF- неуравновешенная радиальная сила; Δω = ω' + ωω' = ω= ω- частоты колебаний вращаемых тел при синхронном режиме работы; ω- частота вращения неуравновешенной радиальной силы; М - суммарная масса тел; r = r= r- радиусы вращаемых тел; t - время. 8 ил.

Формула

,