Оценка пластов с использованием каротажных измерений методом магнитного резонанса - RU2229594C2

Чертежи

Описание

Область техники

Изобретение относится к способам ядерно-магнитного резонанса и более точно к способу оценки пласта с использованием измерений ядерно-магнитного резонанса (ЯМР).

Предшествующий уровень техники

Известные способы оценки пластов для обнаружения углеводородов полагались в большей степени на электрические каротажные измерения либо сопротивления пласта, либо электропроводности пласта, а также на измерения пористости пластов, полученные путем нейтронных, плотностных и ультразвуковых измерений. Практичность электрических каротажных измерений для обнаружения углеводородов, а также для количественной оценки нефтегазонасыщенности, зависит от эмпирических уравнений насыщенности, таких как хорошо известное уравнение Арчи (Archie) или другие, включая модели Waxman-Smits и Dual-Water. Во многих средах этот традиционный подход к оценке пластов обеспечивает точные прогнозы продуктивности пластов. Тем не менее, нередки случаи, когда случаются пропуски рентабельных зон, неточные оценки углеводородов на месте и дорогостоящая разведка зон, которые оказались некоммерческими. Такие случаи включают пластовые воды неизвестной или переменной солености, пластовые пресные воды, влияние электропроводности глины на измеряемое удельное сопротивление, неточная инверсия данных удельного сопротивления и пласты, которые имеют аномальные значения параметров Арчи.

Оценка углеводородных продуктивных пластов с использованием ЯМР импульсных каротажных приборов предлагает потенциальную возможность решения проблемы оценки пластов, исходя из того факта, что многие углеводородные продуктивные пласты могут быть неверно истолкованы или даже совершенно пропущены при использовании известных способов оценки, основанных на измерении удельного сопротивления.

ЯМР подход, который использует ″ дифференциальную методологию″ , был предложен в публикациях Akkurt и др. (NMR Logging оf Natural Gas Reservoirs, стр. N, представленную на 36^th ежегодной конференции Society of Professional Well Log Analysts, 1995). Эта методология включает выполнение двух измерений спинового эхо-сигнала ЯМР с различными временами ожидания, т.е. различными временами для поляризации и деполяризации спинов. Исходные измерения (детектированные спиновые эхо-сигналы) или T₂-распределения, вычисленные из этих измерений, вычитаются, чтобы получить "дифференциальный сигнал" (либо дифференциальный Т₂-спектр, либо последовательность эхо-сигналов), которые в дальнейшем могут обрабатываться для оценки пористости пласта, заполненного углеводородами. В литературе по каротажу скважин методом ЯМР некоторые из дифференциальных методов называются метод дифференциального спектра (DSM) и метод анализа временных выборок (TDA). Времена ожидания методов выбираются таким образом, чтобы дифференциальный сигнал содержал малые вклады от рапы, находящейся в пласте. Чтобы выбрать надлежащее время ожидания, чтобы исключить вклад рапы, требуется знание ЯМР свойств пластовых флюидов. Этот фактор ограничивает методы каротажа нефтеразведки. Кроме того, интерпретация метода требует, чтобы T₁-распределение рапной фазы не перекрылось с T₁-спектрами углеводородных фаз. В карбонатных продуктивных пластах и в продуктивных пластах, содержащих нефть со значениями вязкости от низких до промежуточных значений (например, 1-50 сантипуаз), T₁-распределения рапы и углеводородов могут перекрываться. Это ограничивает применимость дифференциальных методов к сланцеватым пескам, содержащим нефть и газ с очень низкими значениями вязкости. Недавняя публикация (Akkurt и др., "Enhanced Diffusion: Expanding the Range of NMR Direct Hydrocarbon-Typing Methods", стр. GG, представлена на the 36^th ежегодной конференции of the Society of Professional Well Log Analysts, 1998) отмечает ограничения методов дифференциального спектра (DSM) и анализа временных выборок (TDA) для нефти с промежуточными значениями вязкости и предлагает метод, названный метод повышенной диффузии (EDM), который пытается использовать тот факт, что рапная фаза является более диффузионной, чем нефть с промежуточными значениями вязкости. Увеличивая временное разнесение эхо-сигналов таким образом, чтобы диффузия доминировала над временем релаксации Т₂ рапы, можно достичь верхнего предела (T_2DW) на кажущемся времени Т₂. Чтобы получить пористость пласта, заполненного нефтью, в публикации Akkurt и др. 1998 года предлагается интегрировать кажущееся T₂-распределение для времен релаксации больших, чем T_2DW. Хотя предполагается, что базовая концепция метода повышенной диффузии (EDM) жизнеспособна, имеются практические сложности, которые ограничивают надежность обнаружения нефти, поскольку (1) кажущиеся Т₂-распределения расширяются посредством регуляризации (сглаживания), которая используется при обработке для снижения шумовых артефактов, таким образом, интегрирование кажущихся Т₂-распределений из крутого заднего фронта рапы может привести к прогнозам нефти в водных зонах; (2) сигнал нефти может иметь хвост с коротким временем релаксации, который переходит в сигнал рапы; (3) в поисково-разведочных скважинах не может быть принято предположение, что диффузные свойства пластов нефти оказываются меньшими, чем для воды; и (4) в скважинах, пробуренных с буровым раствором на углеводородной основе, используя концепцию метода повышенной диффузии (EDM), трудно отделить сигнал фильтрата от сигнала природной нефти.

Недавняя статья Chen и др. "Estimation of Hydrocarbon Viscosity With Multiple ТЕ Dual Wait-Time MRIL Logs", стр.49009, в трудах "Transactions of the 1998 SPE Annual Technical Conference and Exhibition, 1998", предлагает способ для объединения двойного времени ожидания и многочисленных данных временного разнесения эхо-сигналов для оценки вязкости нефти. Дифференциальная методология используется для объединения различных измерений. Последовательности спиновых эхо-сигналов из данных о длительных и коротких временах ожидания, собранных с одинаковым временным разнесением эхо-сигналов, вычитаются для исключения сигнала водной рапы. Этот способ имеет ограничения, обсуждаемые выше. Более того, вычитание дифференциального сигнала увеличивает шум в 1,4 раза, что тоже является одним из недостатков способа анализа временных выборок (TDA).

Основополагающий недостаток вышеупомянутых способов инверсии состоит в том, что разделение измеренных данных на сигналы рапы и углеводородов выполнимо только для данного конкретного случая в аппроксимации дифференциального сигнала. Подход, который делает это разделение на начальном этапе, раскрывается автором Looyestijn в публикации "Determination of Oil Saturation from Diffusion NMR Logs", стр. SS, представленная на 37^th ежегодной конференции of the Society of Professional Well Log Analysts, 1996, который использует "диффузионную обработку" для вычисления нефтенасыщенности из ЯМР данных, собранных с различным временным разнесением эхо-сигналов. Looyestijn аппроксимирует измеренные данные к модели, которая явно включает сигналы рапы и нефти.

Модель использовала пять простых экспонент для рапной фазы и затянутую экспоненту для нефтяной фазы и применялась к ЯМР каротажным данным из эксплуатационной скважины, пробуренной с буровым раствором на водной основе. Время релаксации нефти было известно из лабораторных измерений на произведенных образцах, а пористость пластов, заполненных нефтью и рапой, вычислялись из каротажных диаграмм.

В публикации РСТ-заявки WO 97/34166 of R.Bonnie, M.Johannes, P.Hofetra, W.Looyestijn, R.Sandor and J.Karl раскрывается способ определения фракции флюида, выбранного по меньшей мере из двух пластовых флюидов, который включает следующие шаги: выбор зависимости между ЯМР эхо-откликом от флюидов, фракций флюидов и по меньшей мере одной переменной, которая воздействует на ЯМР эхо-отклик способом, зависящим от фракций флюидов, посредством варьирования по меньшей мере одной переменной, такой как время ожидания или временное разнесение импульсов в ходе ЯМР измерения, чтобы воздействовать на ЯМР эхо-отклик способом, зависящим от фракций флюидов, и определения фракции выбранного флюида посредством аппроксимации ЯМР эхо-отклика к выбранному соотношению. Пример, приведенный в описании, включает определение водонасыщенности в грунтовом пласте, содержащем нефть средней плотности и воду, посредством ЯМР измерений с приложением постепенно изменяющегося магнитного поля на образец грунтового пласта. Вода была смоделирована с двумя временами поперечной релаксации и двумя соответствующими объемными фракциями, компонентой с коротким временем релаксации, представляющей связанную воду, и компонентой с длительным временем релаксации, представляющей подвижную воду. Нефть была смоделирована с одним временем поперечной релаксации и с одной соответствующей объемной фракцией. В описании утверждается, что посредством повторения способа для диапазона практических значений для параметров воды и нефти было обнаружено, что способ весьма слабо зависит от фактических значений параметров нефти. Утверждается также, что если недоступна никакая информация относительно этих параметров, то ошибки оцененной водонасыщенности могут составлять до 0.1. Также указано, что если вязкость нефти оценивается с точностью до двух десятичных знаков, то результирующая ошибка водонасыщенности пренебрежимо мала по сравнению с полной точностью измерения. Таким образом, в этом способе, который моделирует нефть с одним временем поперечной релаксации и с соответствующей объемной фракцией, очевидно, чтобы получить адекватную точность, необходимо априорно знать вязкость нефти. В практике каротажа скважин априорное знание истинной вязкости нефти обычно невозможно. Указанный способ требует входных данных отношения T₁/T₂ для рапы. Эта величина является переменной и неизвестна, так что надлежащее значение в основном не может быть введено. Результат неточностей во входном отношении T₁/T₂ может привести к ошибкам амплитуд флюида, оцененных этим методом. Подводя итог, можно сделать вывод, что известным способам недостает согласованного теоретического и практического подхода, необходимого для того, чтобы обеспечить точную и завершенную оценку пластов на основе метода ЯМР. Задачей настоящего изобретения является создание улучшенного способа оценки параметров пласта по сравнению с известными способами.

Сущность изобретения

Отличительный признак настоящего изобретения состоит во введении в инверсионный способ обработки модели, имеющей сырую нефть с распределением составляющих вязкостей. Составляющие вязкости могут быть непосредственно отнесены к распределению времен ЯМР релаксации, измеренных на объемных образцах сырой нефти, и могут отражать сложный состав сырой нефти как смеси многих различных типов молекул углеводорода. Составляющие вязкости упрощают инверсию, обеспечивая единый набор параметров для характеристики распределений времен объемной релаксации и коэффициентов диффузии для сырой нефти. Показано, что макроскопическая вязкость сырой нефти может быть выражена как логарифмическое среднее значение распределения составляющих вязкостей. Также в приложении Б показано, почему в сырой нефти также существует распределение коэффициентов диффузии. Кроме того, прогнозируется, что распределение коэффициентов диффузии и времен релаксации в сырой нефти имеет подобный характер.

Согласно изобретению предлагается способ определения свойств земных пластов, окружающих ствол скважины, содержащий следующие шаги: (а) размещение каротажного прибора, который способен перемещаться по стволу скважины; (б) передача энергии электромагнитного поля от каротажного прибора в пласты и прием спиновых эхо сигналов ядерно-магнитного резонанса в каротажном приборе; (в) выполнение шага (б) много раз с соответствующим множеством различных условий передачи и приема для получения множества измерений; (г) создание модели пласта, которая включает множество модельных составляющих для рапной фазы и множество модельных составляющих для фазы природной нефти; (д) модификация модельных составляющих для оптимизации модели относительно сигналов измерения; (е) выведение модельных составляющих оптимизированной модели.

В зависимости от обстоятельств шаг (г) создания модели пласта может включать создание модели, которая дополнительно включает составляющую фильтрата бурового раствора на углеводородной основе и/или может включать составляющую газа.

В варианте воплощения изобретения шаг передачи энергии электромагнитного поля от каротажного прибора и приема спиновых эхо-сигналов ядерно-магнитного резонанса в каротажном приборе включает создание постоянного магнитного поля в области исследования и генерацию последовательностей импульсов радиочастотного магнитного поля в области исследования, а также прием последовательностей спиновых эхо-сигналов ядерно-магнитного резонанса. В этом варианте воплощения градиент приложенного постоянного магнитного поля в области исследования обозначен как G_p, время ожидания между последовательностями - W_р, временное разнесение эхо-сигналов - ТЕ_р, число принятых спиновых эхо-сигналов последовательности - J_p. Вышеупомянутый шаг (в) содержит выполнение шага (б) много раз с соответствующими различными значениями по меньшей мере одного условия, выбранного из группы, состоящей из G_p, W_p, TE_p и J_p. Также в этом варианте воплощения шаг (в) содержит выполнение шага (б) N раз для получения серии N измерений, а измерения р выполняются на множестве соответственно разделенных слоев области измерения в пласте. Отдельные исследуемые слои могут выбираться по частоте каротажным прибором.

В варианте воплощения изобретения шаг (г) создания модели пласта включает создание набора модельных амплитудных составляющих, которые определяют распределение времен поперечной релаксации для рапной фазы, и еще набора амплитудных модельных составляющих, которые определяют распределение времен поперечной релаксации для фазы природной нефти, а также набора модельных составляющих, которые определяют составляющие вязкости природной нефти.

Настоящее изобретение обеспечивает усовершенствования во всех стандартных результатах ЯМР откликов, включая ЯМР оценки общей пористости, пористости свободных флюидов и связанных флюидов, Т₂-распределения и проницаемость в сланцеватых песках. Дополнительно он может обеспечить оценки насыщенностей и пористости пласта, заполненного водой, нефтью, фильтратом бурового раствора на углеводородной основе (OBMF) и газом, вязкости нефти, T₁-распределений для нефти, коэффициентов диффузии нефти и отношений T₁/T₂ для рапы. Также могут быть получены профили насыщенности пластов флюидами.

Настоящее изобретение также может использоваться для измерений, выполняемых на поверхности земли на кернах земных пластов. В таком случае керн может быть помещен в ЯМР лабораторное оборудование (или непосредственно в каротажный прибор), и могут быть осуществлены соответствующая последовательность импульсов и сбор эхо-сигналов. Могут быть определены объемы флюидов в колонке породы и другие параметры оценки пластов.

Краткое описание чертежей

В дальнейшем изобретение поясняется описанием конкретных вариантов его воплощения со ссылками на сопровождающие чертежи, на которых:

фиг.1 изображает схему устройства, которое может быть использовано в практическом применении варианта воплощения настоящего изобретения;

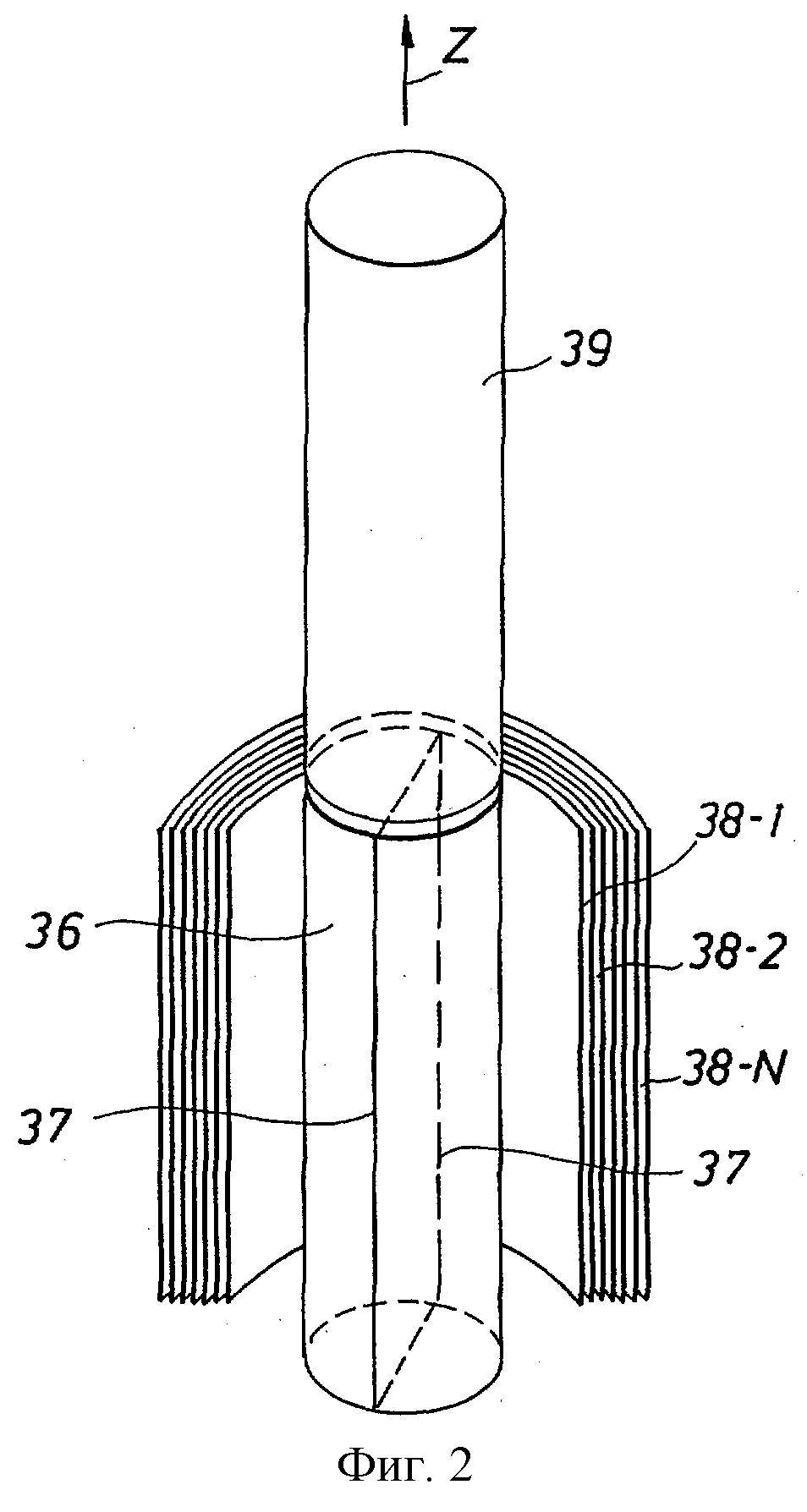
фиг.2 изображает схему типичного образца каротажного прибора, который может использоваться для получения измерений согласно изобретению.

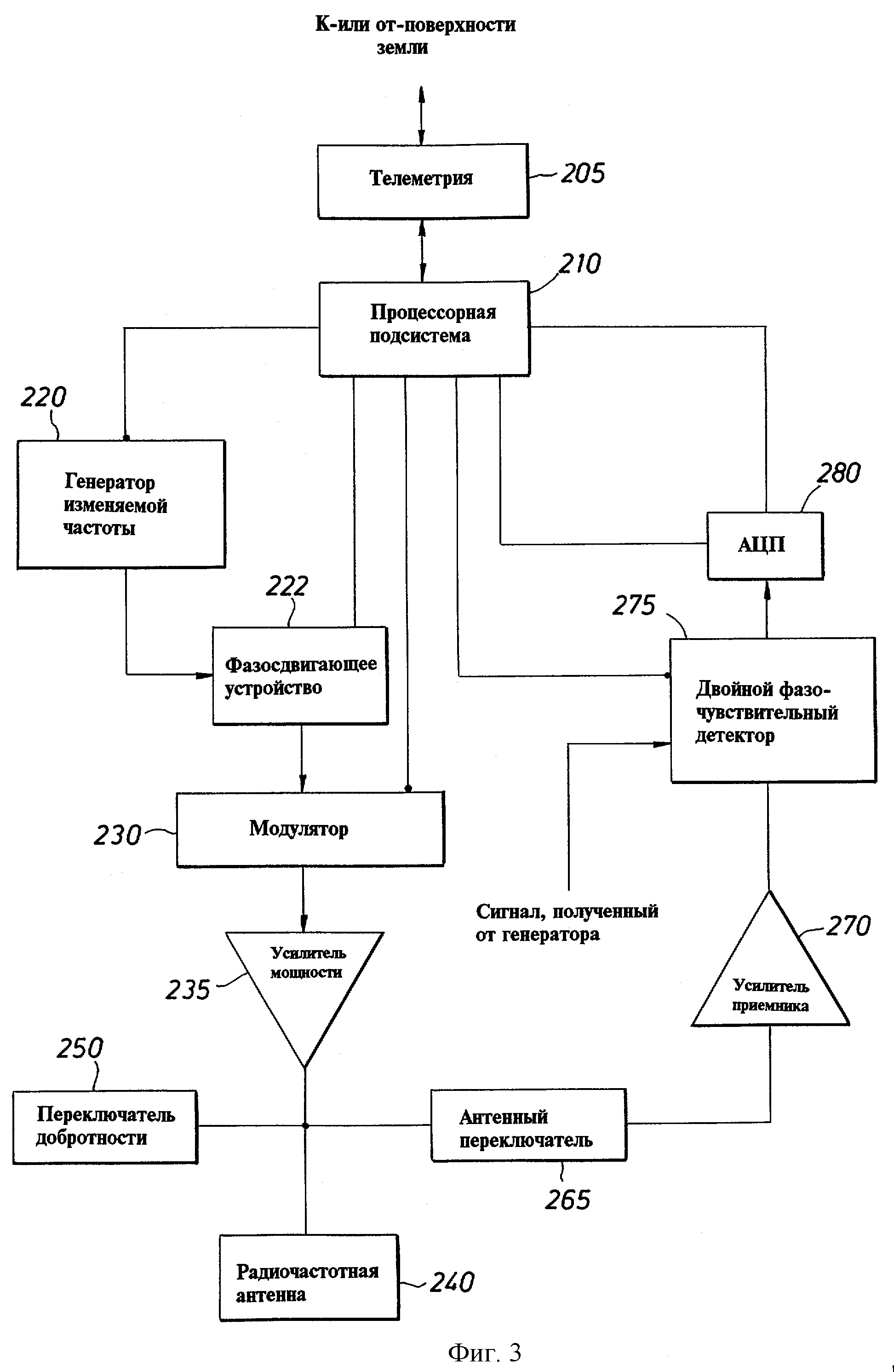
фиг.3 изображает схему для генерации радиочастотных импульсов и для приема и запоминания спиновых эхо-сигналов согласно изобретению;

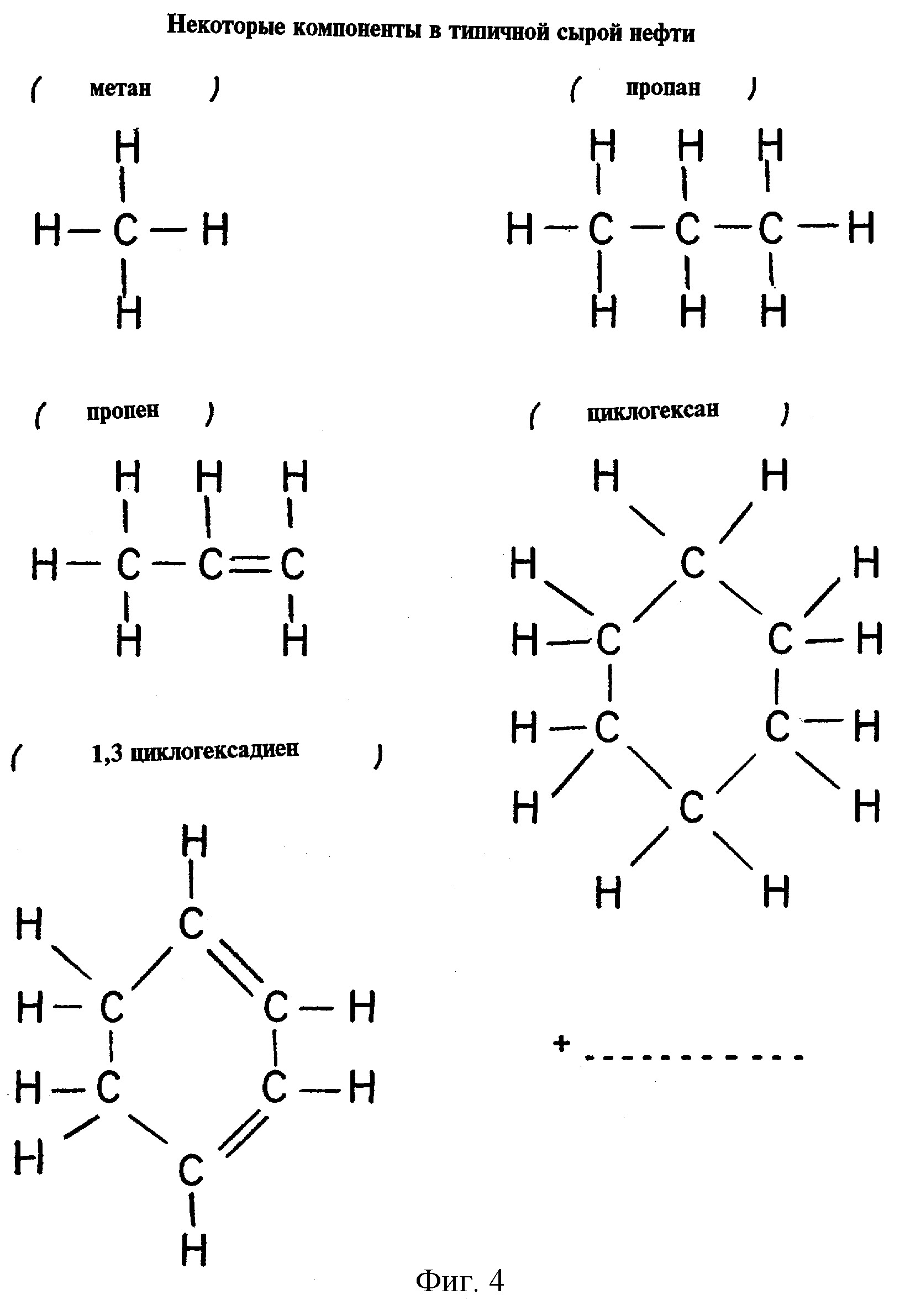
фиг.4 изображает диаграмму, иллюстрирующую молекулярную структуру некоторых составляющих типичной сырой нефти;

фиг.5А, 5В, 5В, 5Г, 5Д и 5Е изображают алгоритмы для управления способом согласно изобретению;

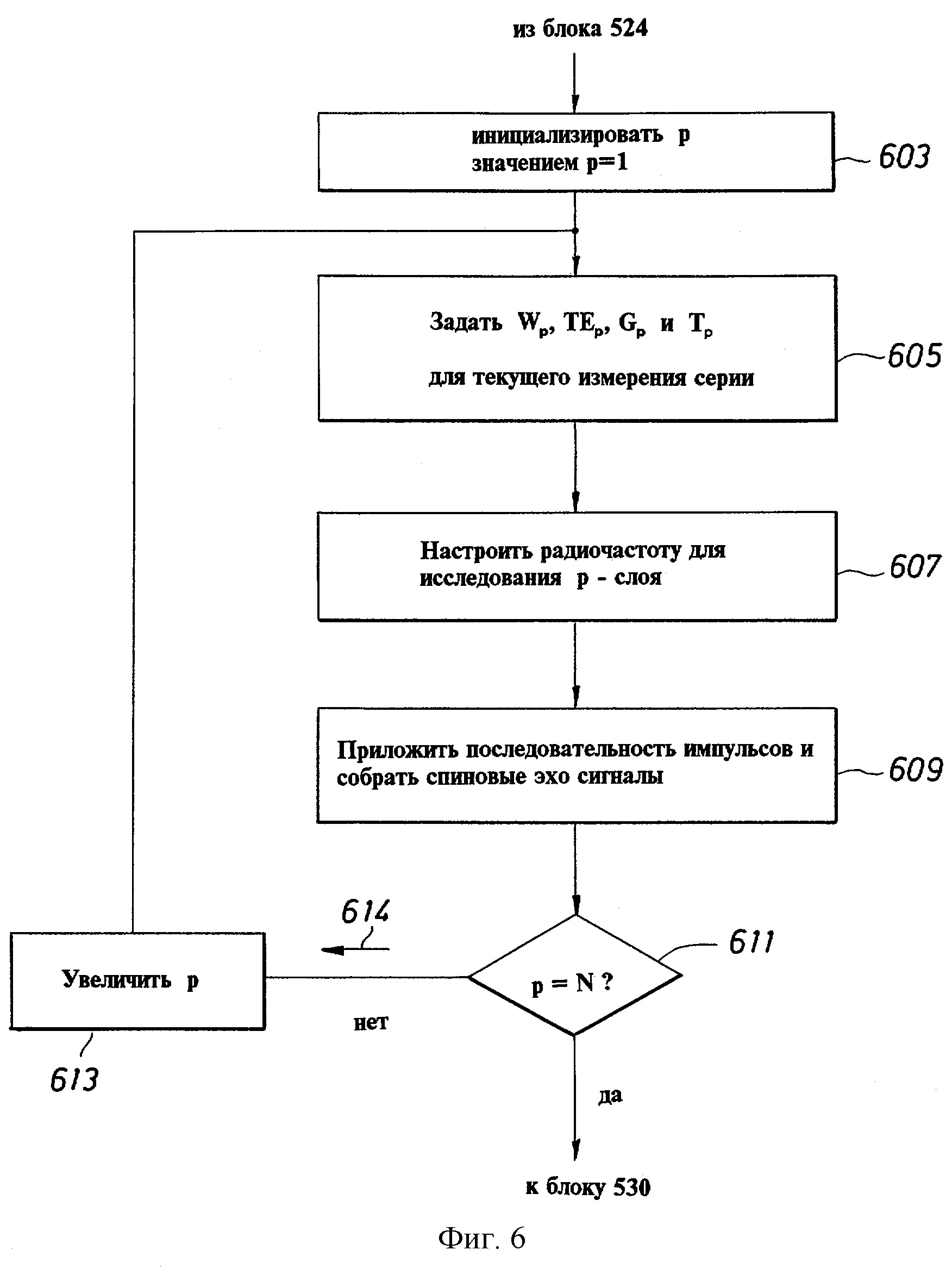
фиг.6 изображает блок-схему алгоритма сбора данных, которая представлена блоком 527 на фиг.5;

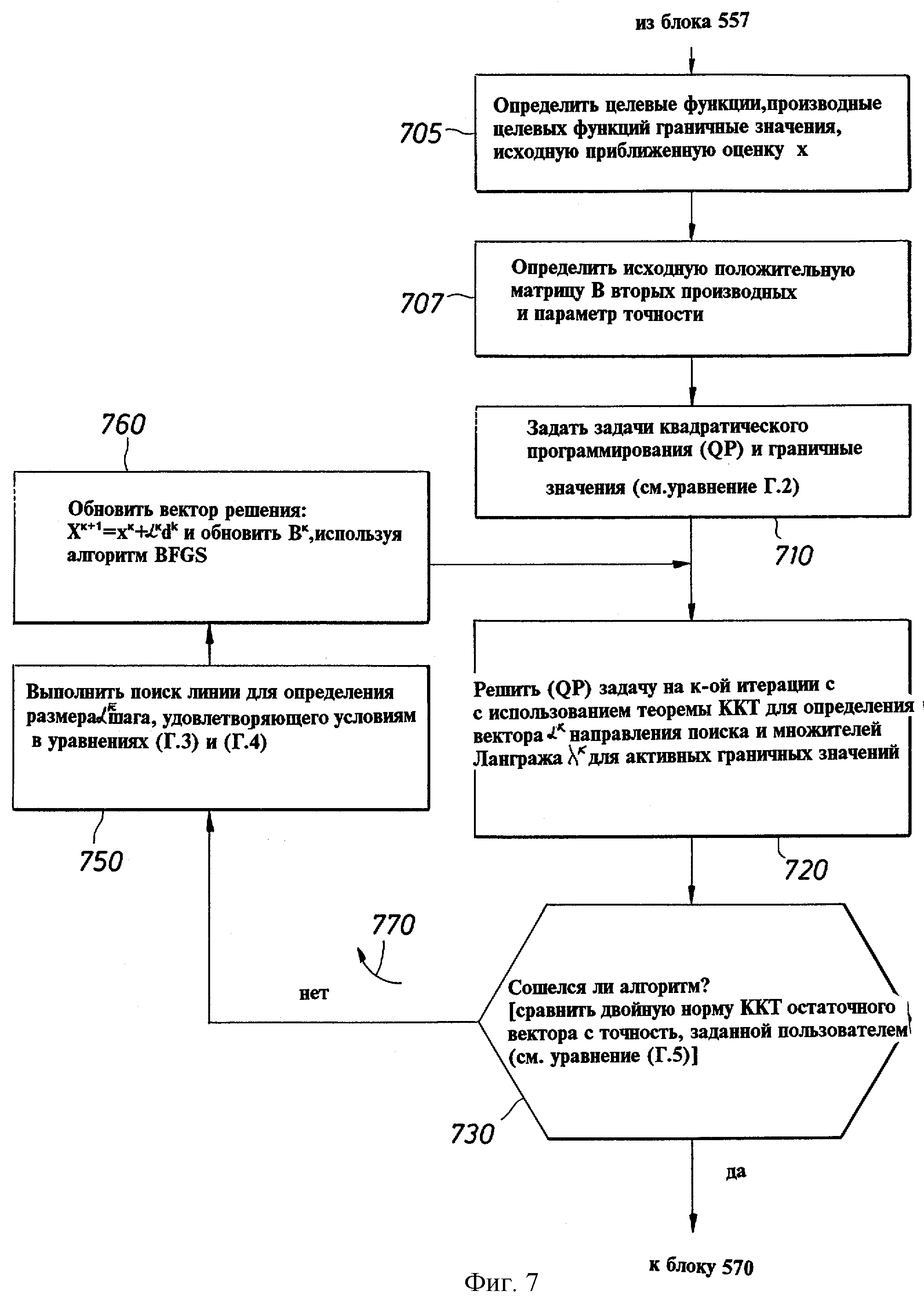
фиг.7 изображает блок-схему алгоритма оптимизации модели, как представлено блоком 560 на фиг.5;

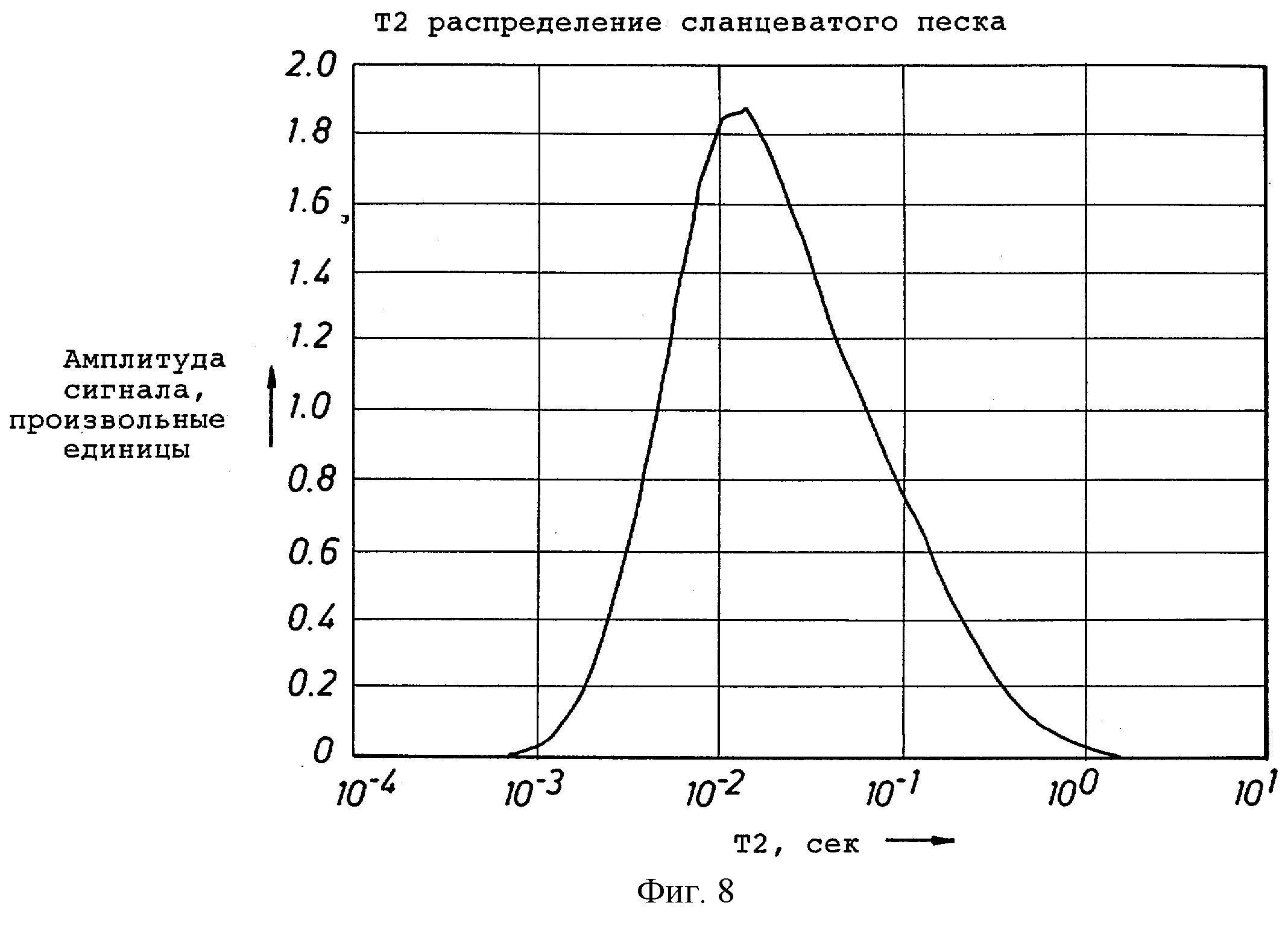
фиг.8 изображает диаграмму Т₂-распределения для рапы в пласте песчаника, как в примере инверсии, согласно изобретению;

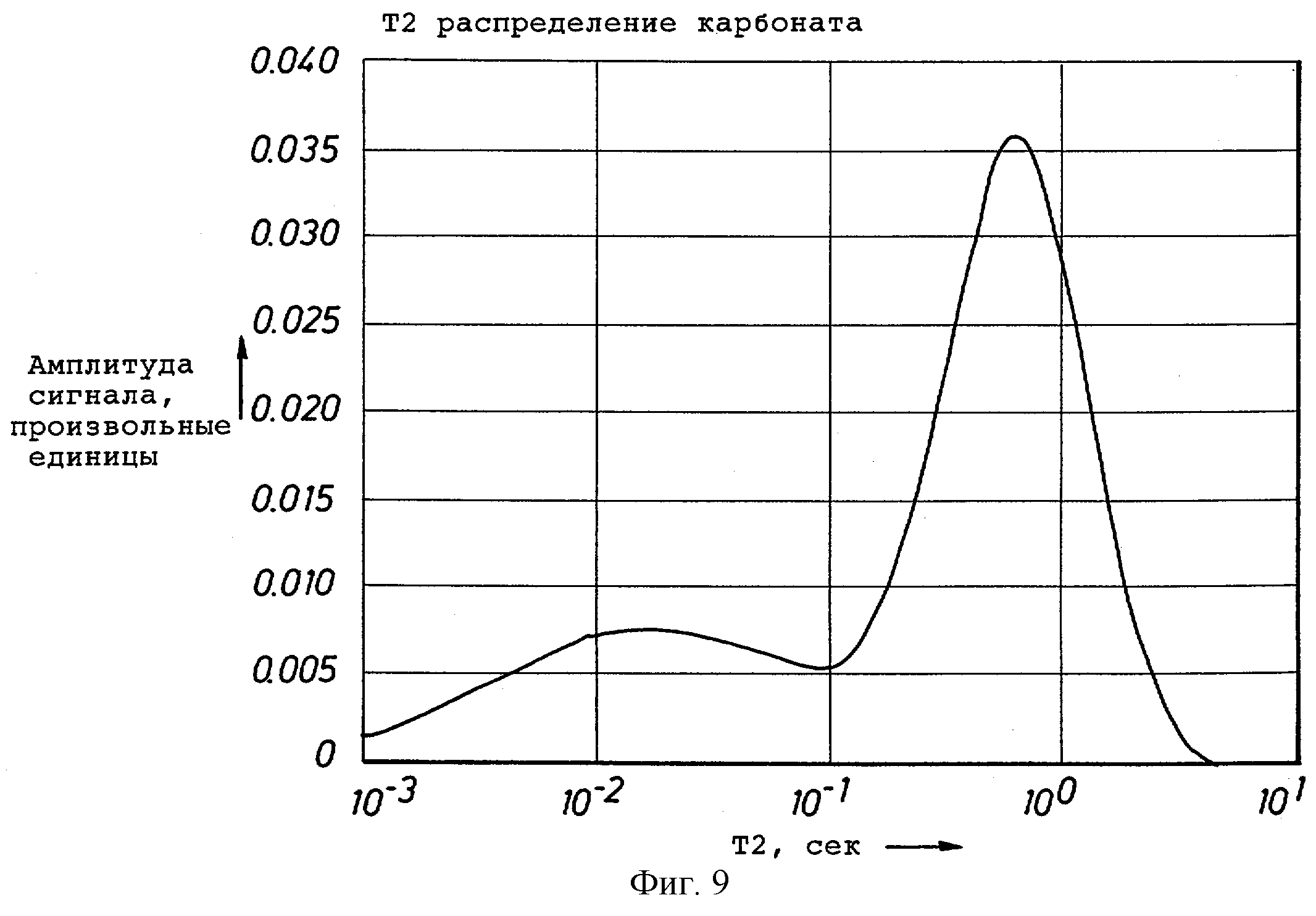
фиг.9 изображает диаграмму Т₂-распределения для рапы в карбонатном пласте, который используется в другом примере инверсии настоящего изобретения,

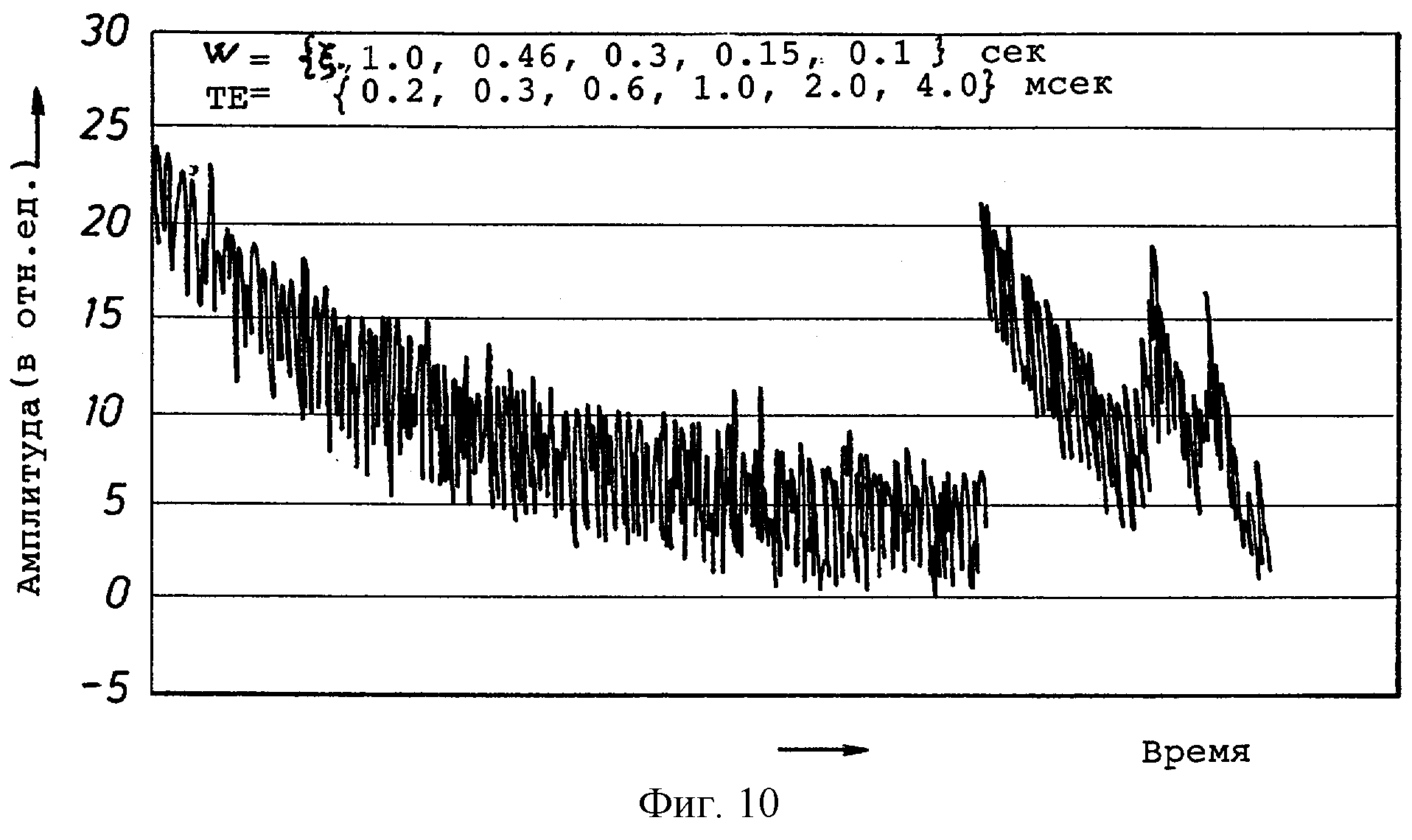
фиг.10 изображает диаграмму зависимости амплитуды эхо-сигналов как функции от времени для серии измерений используемой в примере инверсии, согласно изобретению;

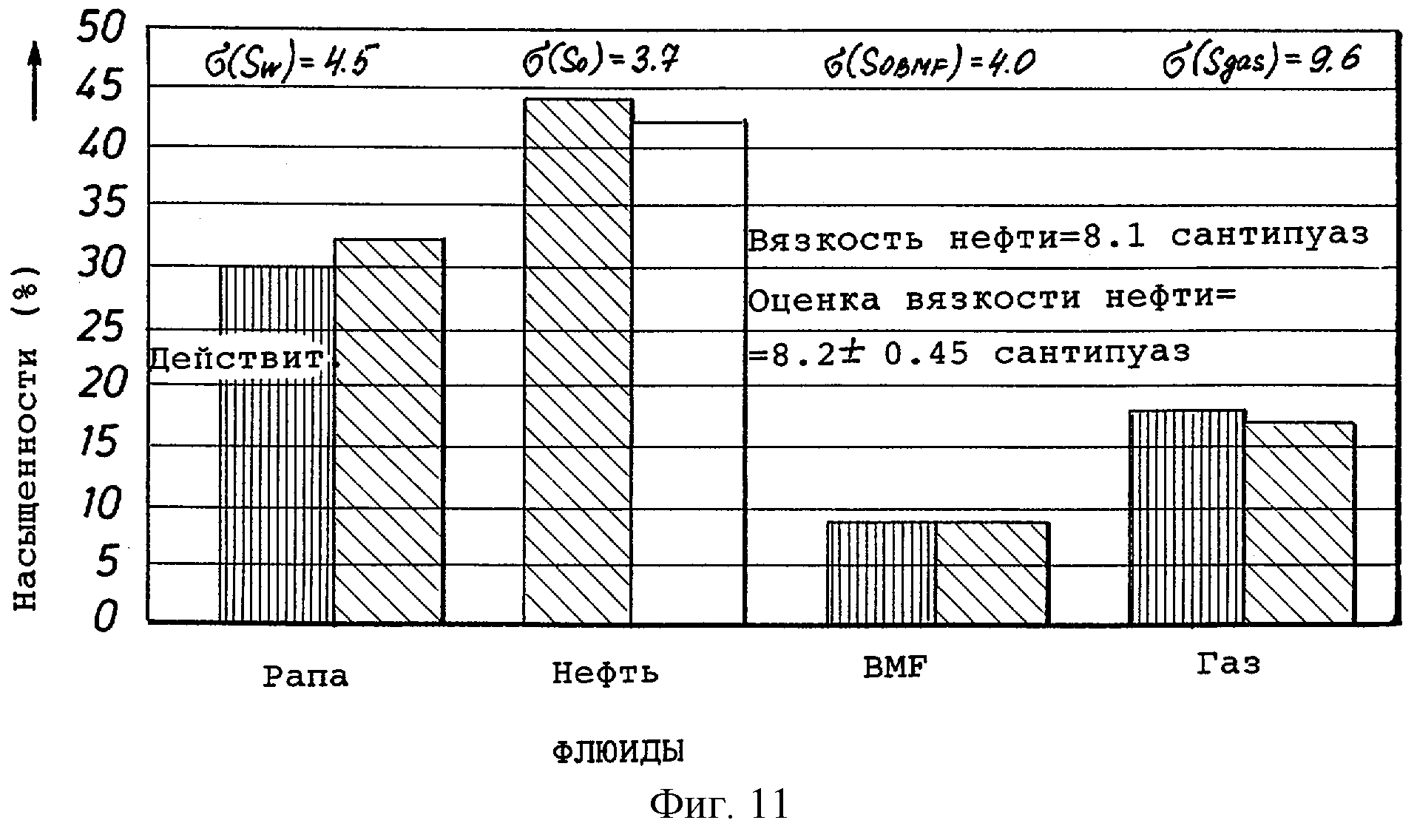
фиг.11 изображает диаграмму в виде столбцов для рапы, нефти, фильтрата бурового раствора на углеводородной основе (OBMF) и газа, сравнивающую истинные (входные) значения насыщенности с теми, которые получены способом согласно изобретению в моделировании методом Монте Карло с использованием измерений на фиг.10;

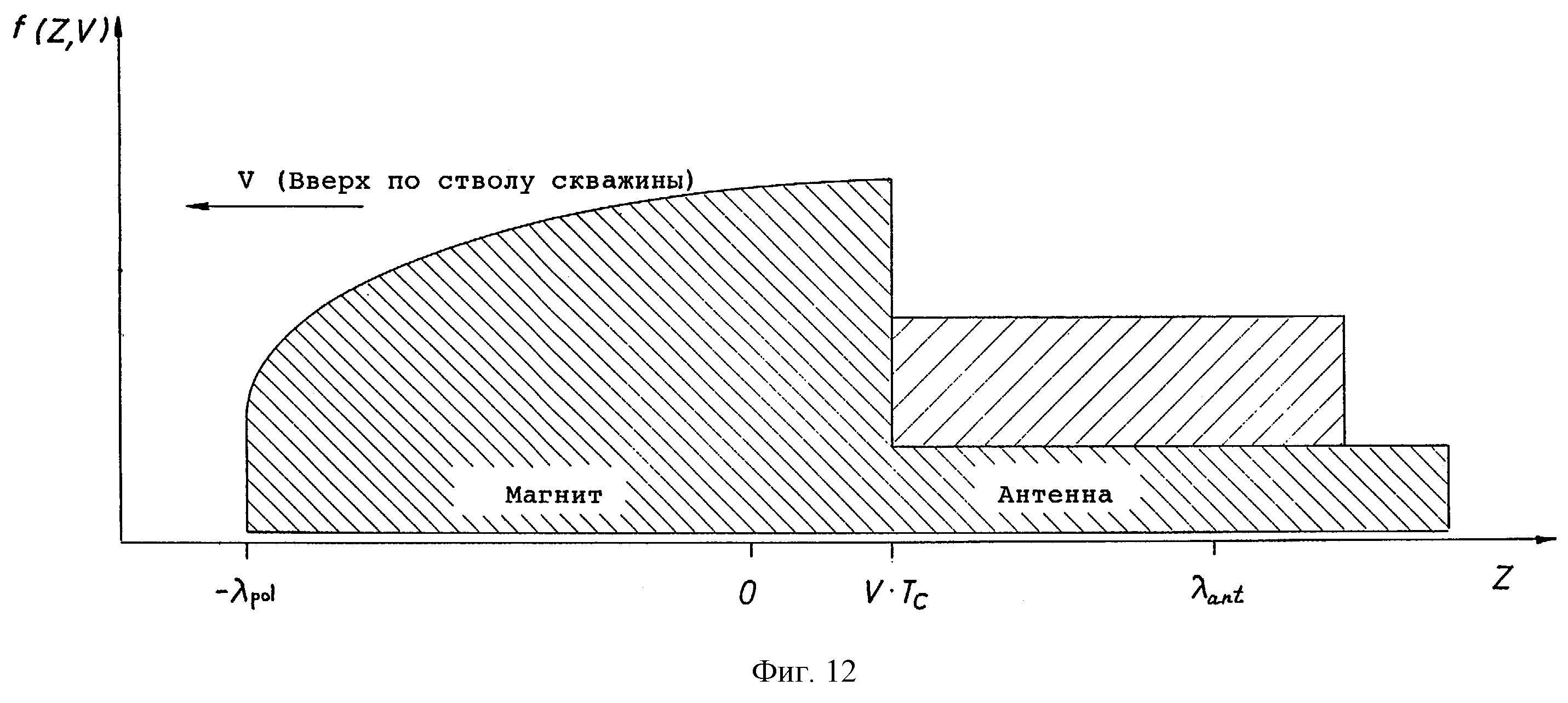
фиг.12 изображает диаграмму, показывающую профиль поляризации, произведенной в пласте перемещающимся каротажным прибором, имеющим область предварительной поляризации, который может использоваться для получения измерений, компенсированных с учетом скорости перемещения каротажного прибора согласно изобретению;

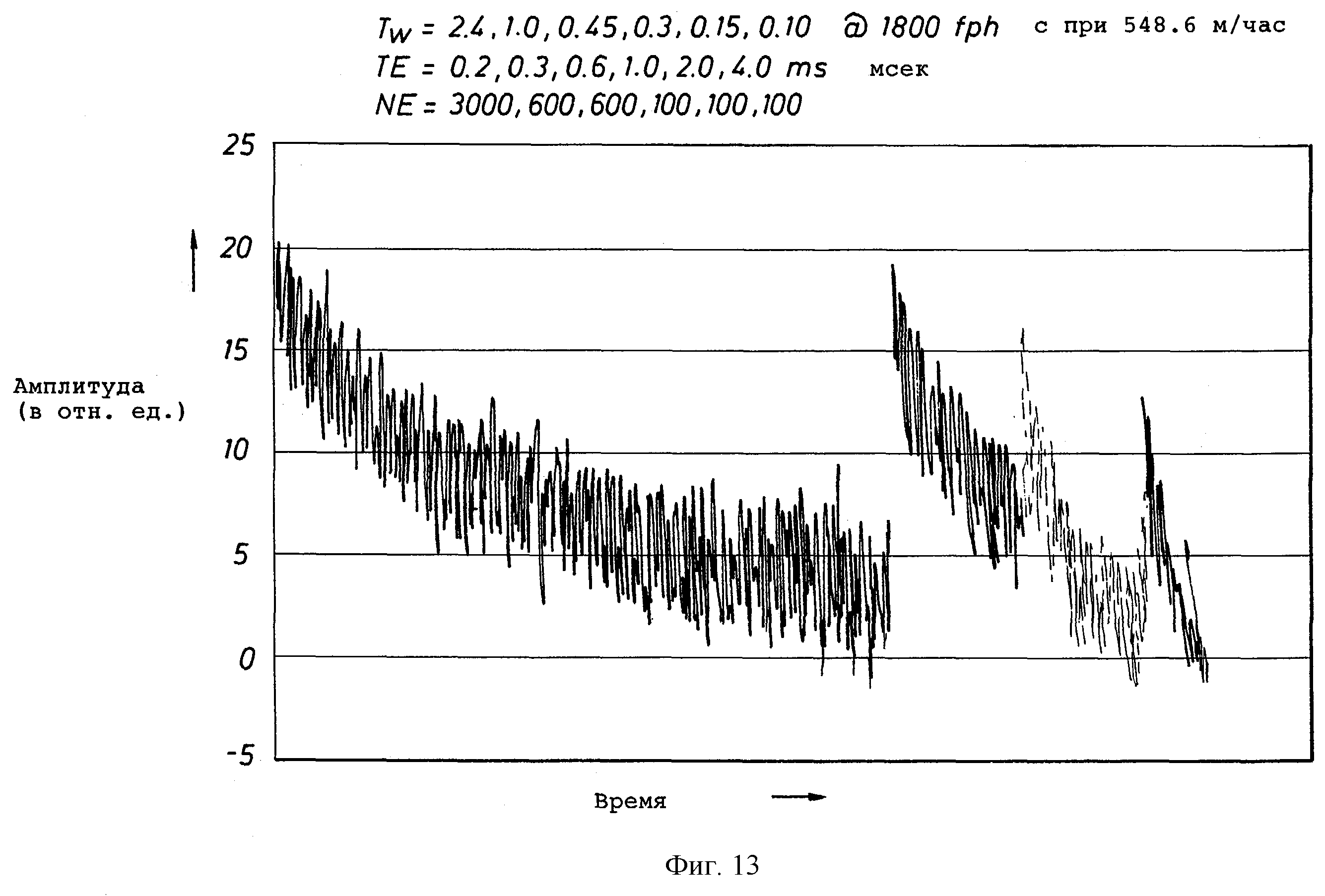
фиг.13 изображает диаграмму зависимости амплитуды эхо-сигнала как функцию от времени для серии измерений, используемой в другом примере инверсии;

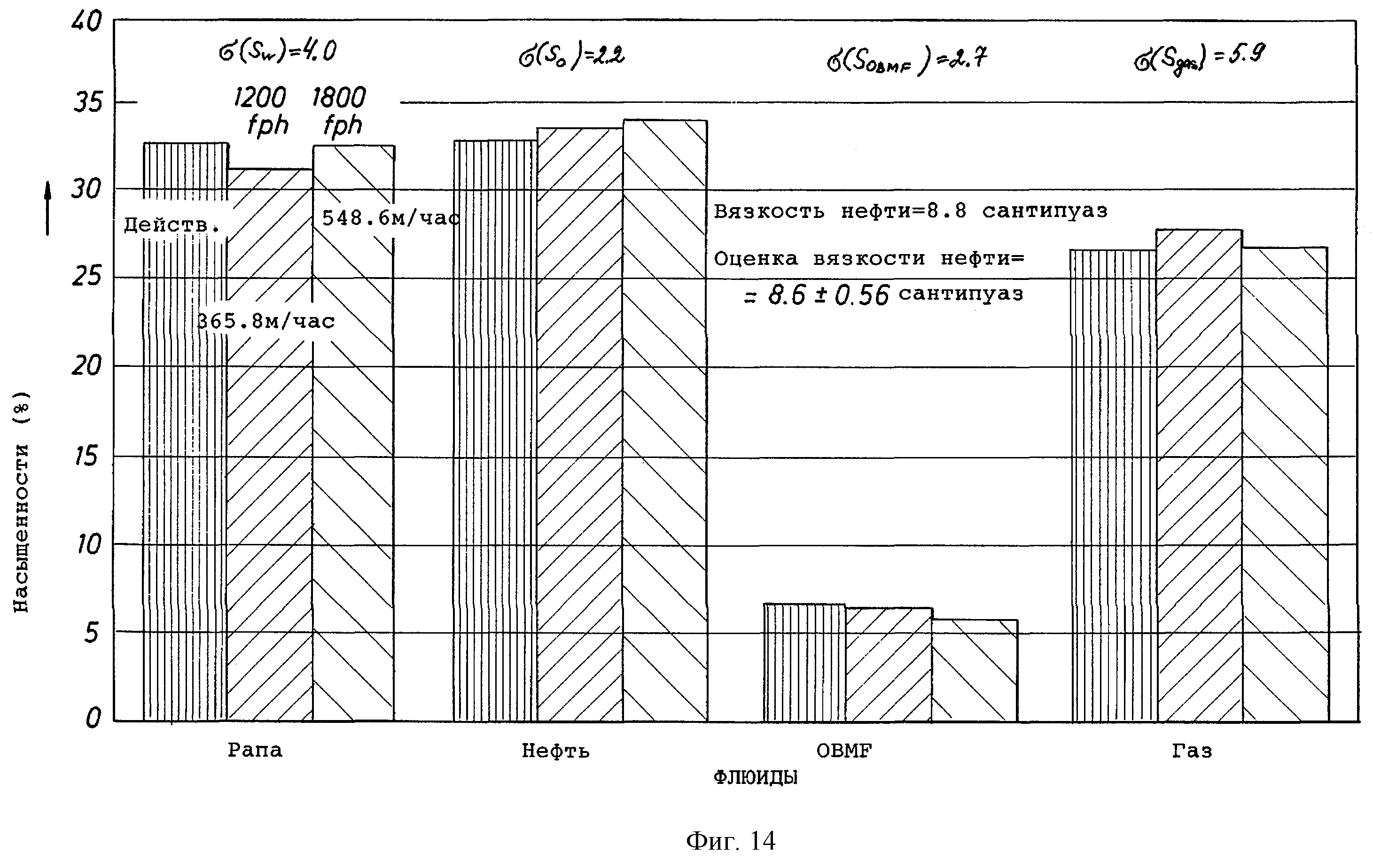
фиг.14 изображает диаграмму в виде столбцов для рапы, нефти, фильтрата бурового раствора на углеводородной основе (OBMF) и газа, сравнивающую истинные (входные) значения насыщенности с теми, которые получены способом согласно изобретению в моделировании методом Монте Карло с использованием измерений на фиг.13.

Подробное описание предпочтительных вариантов воплощения изобретения

На фиг.1 показано устройство для исследования подповерхностных пластов 31, пересеченных стволом 32 скважины, которое может использоваться для воплощения способа настоящего изобретения.

Каротажный прибор 30 подвешивается в стволе 32 скважины на армированном кабеле 33, длина которого по существу определяет относительную глубину погружения прибора 30. Длина кабеля управляется подходящим средством, находящимся на поверхности, таким как барабан или лебедочный механизм (не показан). Наземное оборудование может включать процессорную подсистему и связываться со скважинным оборудованием.

Каротажный прибор 30, который выполняет измерения, может быть любым подходящим каротажным прибором на основе ядерно-магнитного резонанса для проводного каротажа (как показано) или может быть такого типа, который применяется в измерениях во время бурения. Прибор 30 включает средство для создания постоянного магнитного поля в пластах и радиочастотную антенну для генерации импульсов радиочастотного магнитного поля в пластах, а также для приема спиновых эхо-сигналов из пластов. Средство для создания постоянного магнитного поля может содержать постоянный магнит или набор магнитов, а также радиочастотную антенну для генерации импульсов радиочастотного магнитного поля и для приема спиновых эхо-сигналов из пластов, которое может содержать, например, одну или более радиочастотных антенн. Вариант воплощения настоящего изобретения использует серию измерений от ЯМР каротажного прибора такого типа, который может эксплуатироваться для получения отдельных измерений от множества близко расположенных тонкослойных областей в окружающих пластах.

На фиг.2 иллюстрируется упрощенный вид некоторых элементов каротажного прибора 30, который содержит первый центральный магнит или набор магнитов 36, а также радиочастотную антенну 37, которая может представлять собой соответствующим образом ориентированную катушку или катушки.

Также показан общий вид близко расположенных цилиндрических тонких слоев 38-1, 38-2,...38-N, которые могут выбираться по частоте, используя упомянутый тип многочастотного каротажного прибора. Как известно из уровня техники, например из патента США №4710713, каротажный прибор может выбирать исследуемую область слоя посредством надлежащего выбора частоты радиочастотной энергии в передаваемых импульсах. Дополнительный магнит 39, набор магнитов может использоваться для приложения предварительно поляризованного постоянного магнитного поля к тем пластам, к которым приближается область исследования каротажного прибора по мере того, как он поднимается в стволе скважины в направлении стрелки Z.

Фиг.3 изображает схему известного типа для генерации радиочастотных импульсов и для приема и запоминания спиновых эхо-сигналов. Для практического осуществления способа настоящего изобретения могут использоваться любые другие подходящие схемы.

Скважинная процессорная подсистема 210 имеет подключенную память, синхронизацию, интерфейсы и периферийные устройства (отдельно не показанные), как хорошо известно из уровня техники. Процессорная подсистема обычно соединяется с телеметрическими схемами 205 для связи с поверхностью земли. Схемы формирования импульсов включают генератор 220 изменяемой частоты, который генерирует радиочастотные сигналы на желаемых частотах под управлением процессора. Выход генератора присоединен к фазосдвигающему устройству 222 и затем к модулятору 230, которые управляются процессорной подсистемой 210. Фазосдвигающее устройство и модулятор могут управляться способом, известным из уровня техники, чтобы генерировать желаемые импульсы радиочастотного поля, например 90-градусные и 180-градусные импульсы для CPMG типов последовательностей или любых других желательных последовательностей ЯМР импульсов. Выход модулятора 230 присоединен через усилитель 235 мощности к радиочастотной антенне 240. Переключатель 250 добротности может быть использован для критического демпфирования системы радиочастотной антенны для снижения осцилляции антенны. Также антенна соединена с приемным устройством через антенный переключатель 265, выход которого соединен с усилителем 270 приемного устройства. Антенный переключатель 265 предохраняет усилитель 270 приемного устройства от импульсов высокой мощности, которые проходят к радиочастотной антенне 240 во время режимов передачи и демпфирования. Во время режима передачи антенный переключатель 265 является только низкоимпедансным соединением от антенны к усилителю 270 приемного устройства. Выход усилителя 270 приемного устройства присоединен к сдвоенному фазочувствительному детектору 275, который также принимает опорный сигнал от генератора сигналов. Продетектированный выходной сигнал подается в аналого-цифровой преобразователь 280, выходные данные которого являются цифровой версией принятого сигнала ядерно-магнитного резонанса. Каротажный прибор 30 показан на фиг.1 как единый предмет, он альтернативно может содержать отдельные компоненты и может комбинироваться с другими каротажными инструментами. Также могут быть использованы альтернативные виды физической связи, например в системе измерений во время бурения может быть использована линия телекоммуникаций.

В описанном варианте воплощения слои в пределах прослойка расположены близко (например, на расстоянии порядка 10 миллиметров) так, чтобы насыщенность флюидов можно было считать постоянной на протяжении всего прослойка. N измерений. выполняется в пределах прослойка. Каждое измерение характеризуется набором параметров {G_p, W_p, ТЕ_р, J_p} для р=1...N, где W_p - времена ожидания, ТЕ_р - временное разнесение эхо-сигналов (сек), G_p-градиент приложенного постоянного магнитного поля (Гаусс/см), J_p - число принятых спиновых эхо-сигналов. Предполагается, что каждое измерение отличается от другого. Если измерение повторяется, то оно "объединяется" (усредняется аналогичным измерением для уменьшения шума). С таким допущением не должно быть двух идентичных наборов параметров измерений.

Модель ЯМР релаксации для многих флюидов

Рассмотрим общую модель релаксации спинового эхо сигнала для пласта, содержащего рапу и природную нефть. Из-за того что многие скважины бурят с буровыми растворами на углеводородной основе, модель также учитывает присутствие в пласте фильтрата бурового раствора на углеводородной основе (OBMF). В приложении А модель распространяется еще и на газ. Допустим A представляет амплитуду j-ого эха, полученного во время измерения р. Рассмотрим следующую общую модель релаксации.

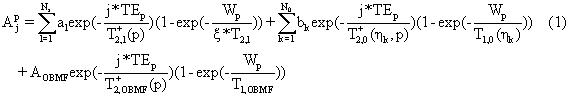
где первый, второй и третий члены представляют сигналы рапы, природной нефти и фильтрата бурового раствора на углеводородной основе (OBMF) соответственно. Модель точно учитывает экспериментально наблюдаемое распределение рапы и распределения времен релаксации сырой нефти. Измерения на фильтрах бурового раствора на углеводородной основе показывают, что распределения времен релаксации очень узкие и могут быть описаны единой экспонентой. Кажущиеся скорости поперечной релаксации включают самопроизвольную диффузию молекул флюида в градиенте G_p постоянного магнитного поля, которые для неограниченной диффузии в однородном градиенте могут быть записаны известным образом

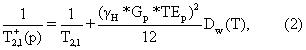
для рапной фазы. Параметр T₂,₁ представляет набор N_s логарифмически разнесенных времен релаксации, которые представляют сумму поверхностной и объемной релаксации рапной фазы. Второй член в правой части уравнения представляет вклад в скорость релаксации вследствие диффузии, где γ_H=2π · 4258G^-ls^-1представляет гиромагнитное отношение протона, a D_w(T) представляет температурно-зависимый коэффициент самопроизвольной диффузии воды, выраженный в единицах см²/сек. При необходимости могут применяться поправки для D_w(T), учитывающие эффекты ограниченной диффузии и для G_p, учитывающие внутренние градиенты скальных пород (см. приложение Д). Кажущаяся скорость релаксации природной нефти может быть записана в виде

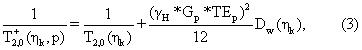
где T_2,0(η_k) - время объемной релаксации, связанное с амплитудой b_k в распределении времен релаксации природной нефти; D₀(η_k) - коэффициент диффузии, зависящий от вязкости. Обычно считается, что сырая нефть является несмачиваемой фазой, на которую не влияет поверхностная релаксация. Допускается, что в сырой нефти на молекулярном уровне существует распределение составляющих вязкостей (η_k), и этот постулат согласуется с экспериментальными данными, в которых существует распределение времен релаксации в сырой нефти. Morriss и др. "Hydrocarbon Saturation And Viscosity Estimation From NMR Logging In The Belridge Diatomite", стр. С, представленной на конференции 35^th Annual Meeting Of The Society Of Professional Well Logging Analysis, 1994 показали, что для набора разных видов сырой нефти существует сильная корреляция между логарифмическими средними временами релаксации их распределений и их измеренных вязкостей. Измеренная вязкость является свойством макроскопического переноса сырой нефти, которое определяет реологические свойства и является величиной, которая используется в уравнениях гидродинамического переноса, подобных уравнению Навье Стокса. Параметры η_k в уравнении 3 представляют феноменологические микроскопические переменные, которые отражают сложный состав сырой нефти. Сырая нефть представляет собой смеси, состоящие из многих различных типов углеводородных молекул различающихся размеров, форм и молекулярных весов (McCain, W.D., The Properties Of Petroleum Fluids, опубликованной компанией Penn Well Publishing Co., Second Edition, Chapter 1, 1990). На фиг.4 показаны несколько составляющих, которые могли бы присутствовать в типичной сырой нефти.

Макроскопическая вязкость (η₀) сырой нефти эмпирически связывается с логарифмическим средним

распределения времен поперечной релаксации посредством уравнения следующего вида

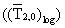
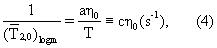
где а≅ 250 является эмпирически определенным составным коэффициентом, раскрытым Looyestijn "Determination Of Oil Saturation From Diffusion NMR Logs", стр. SS, представленной на 37^th Annual Meeting of the Society of Professional Well Log Analysts, 1996, Т - температура в градусах Кельвина, с≅ Аt^-1. По аналогии с вышеупомянутым уравнением предположим, что составляющие вязкости связаны с составляющими в распределении времен релаксации одним и тем же уравнением:

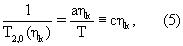
Зависимость времен релаксации в уравнениях (4) и (5) от вязкости и температуры согласуется с экспериментами и теоретическими прогнозами работ Bloembergen, Purcell and Pound "Relaxation Effects In Nuclear Magnetic Resonance Absorption", Physical Review, том 73, №7, стр. 679-712, 1948, используя определения логарифмического среднего времени релаксации;

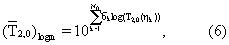
c

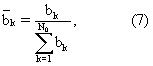
где b_k представляет N₀ амплитуды в распределении времен объемной релаксации сырой нефти. Если (4) и (5) подставить в (6), то можно обнаружить, что макроскопическая вязкость сырой нефти представляет собой логарифмическое среднее параметра η_k

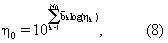
что подобно высокотемпературному пределу "правила смешения Аррениуса" для вязкости смеси (см. Bondi "Physical Properties Of Molecular Crystals, Liquids, And Glasses", опубликованной компанией John Wiley & Sons, стр. 348-349, 1968), где

- "концентрация" составной части смеси с вязкостью η_k. Важная разница между правилом смешения вязкостей в уравнении (8) и правилом смешения Аррениуса состоит в том, что параметры η_k в уравнении (8) являются вязкостями составных частей в смеси и они не равны вязкостям чистых компонентов. Таким образом, постулат о том, что "эмпирически наблюдаемое распределение времен поперечной релаксации подразумевает распределение составляющих вязкостей на молекулярном уровне" при объединении с эмпирически установленной корреляцией в уравнении (4), приводит к правилу смешения типа правила Аррениуса для вязкости смеси сырой нефти. Распределение составляющих вязкостей обеспечивает информацию о составах и молекулярных весах составных частей сырой нефти. Макроскопическая вязкость сырой нефти в дополнение к определению реологических свойств нефти может быть отнесена к ее API плотности (плотность нефтепродуктов в градусах Американского нефтяного института).

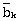
Кажущаяся скорость поперечной релаксации фильтрата бурового раствора на углеводородной основе (OBMF) в уравнении (1) может быть записана в виде

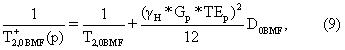
где T₂,_OBMF и D_OBMF - время объемной релаксации и коэффициент самопроизвольной диффузии фильтрата бурового раствора на углеводородной основе (OBMF).

В опубликованной литературе обычно заявляется, что времена поперечной и продольной релаксации объемной сырой нефти и фильтрата бурового раствора на углеводородной основе (OBMF) (то есть при нулевом градиенте магнитного поля) могут быть приняты равными так, чтобы в уравнениях (1) и (3), T_1,0(η_k)=T_2,0(η_k) для природной нефти и уравнениях (1) и (9), T_1,OBMF=Т_2,OBMF для фильтрата. Заметим, что предположение, что T₁ и Т₂ распределения сырой нефти равны, не является существенным элементом, поскольку модель релаксации может быть приспособлена так, чтобы учитывать неравные распределения. Фактически, недавно полученные данные для сырой нефти говорят о том, что T₁ и Т₂ распределения некоторых видов сырой нефти могут значительно отличаться, и в этих случаях отношения T₁/Т₂, по-видимому, должны быть коррелированны с битумным содержанием нефти.

Для удобства описания

определяется как отношение вязкости к абсолютной температуре. Зависимость от времен объемной релаксации многих жидкостей, задаваемая уравнениями (4) и (5), была экспериментально проверена посредством многих экспериментов в разнообразных системах (см. Abragam A. "The Principles Of Nuclear Magnetism", published by Oxford Univ. Press, стр. 324-325, 1961; Zhang Q., Lo, S-W., Huang C.C., Hirasaki G.J., Kobayashi, R., and House W.V. "Some Ex-ceptions To Default NMR Rock And Fluid Properties", Paper FF presented at the 39^th Annual Meeting of the Society of Professional Well Log Analysts, 1998). Зависимость среднего времени релаксации от , построенная в двойном логарифмическом масштабе (т.е. ( )_{log m}) от ), для многих жидкостей, включая сырую нефть продуктивного пласта, может быть аппроксимирована прямой линией с наклоном, равным -1. Zhang и др. показали, что время релаксации в чистом метане имеет обратно пропорциональную зависимость (наклон равен 1) от , которая наблюдается в жидкостях, и утверждают, что это происходит потому, что релаксация вызывается преимущественно посредством механизма вращения спинов в газе, в противоположность диполь-дипольной релаксации в жидкостях. Zhang и др. далее утверждают, что времена релаксации сырой нефти в продуктивных пластах, содержащей растворенный метан, могли бы отклоняться от зависимости ^-1 в уравнениях (4) и (5). Они доказывают, что для того, чтобы охарактеризовать времена релаксации нефти, содержащей газообразные пластовые флюиды, потребуется отличная функциональная зависимость. Времена релаксации нефти, содержащей газообразные пластовые флюиды как функции газового фактора (GOR), температуры и вязкости, в настоящее время не установлены и существует необходимость аргументировать или возможно даже заменить соотношения, принятые в уравнениях (4) - (5). Общая релаксационная модель в уравнении (1) остается в силе, и можно было бы модифицировать только функциональную зависимость времени релаксации от вязкости и температуры. Недавняя публикация Ло и др. "Relaxation Time And Diffusion Measurements of Methane And N-Decane Mixtures" The Log Analyst, стр. 43-46, November-December, 1998, показывает, что в смесях метана и n-декана график зависимости T₁ от , построенной в двойном логарифмическом масштабе, отличается от прямой линии (т.е. простой зависимости степенного закона) при возрастании молярной доли газа в смеси. Предполагается, что для залежей сырой нефти, имеющей высокие газовые факторы, требуется более общая функциональная зависимость времени релаксации от вязкости и температуры, чем выраженная в уравнениях (4) и (5). Результаты Ло и др. показывают, что газовый фактор (то есть GOR) - важный параметр в определении зависимости времени релаксации от вязкости и температуры. Функциональная зависимость времени релаксации от для нефти, содержащей газообразные пластовые флюиды, также отклонится от простого соотношения степенного закона и будет иметь явную зависимость от газового фактора - GOR.

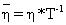
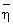
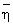
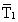
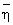
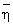
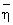
Далее принимается, что коэффициенты самопроизвольной диффузии D₀ (η_k) составных частей сырой нефти в уравнении (3) имеют ту же самую зависимость от η_k*T^-1, что и времена релаксации в уравнении (5). Эта зависимость предсказывается теорией диффузии Стокса-Эйнштейна и была проверена экспериментально для многих типов жидкостей (Abragam, 1961, см. выше).

Для сырой нефти

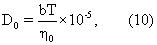
где D₀ является измеренным коэффициентом диффузии сырой нефти, выраженным в см²/сек, а Т - температура в градусах Кельвина. Эмпирически установленная константа b≅ 25/300=8,33× 10^-3 дается в публикации Looyestijn (1996, см. выше). По аналогии с уравнением (5) установленные коэффициенты диффузии составных частей смесей сырой нефти связываются с составляющими вязкостями посредством уравнений

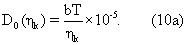
Уравнение (10а) подразумевает, что в смеси сырой нефти на молекулярном уровне существует распределение коэффициентов диффузии, аналогичное распределению времен релаксации. Метод ЯМР представляет собой локальное измерение, которое может зондировать систему в молекулярном масштабе, и импульсные ЯМР измерения с градиентом поля использовались Ло и др. (1998, см. выше) для того, чтобы измерить распределение коэффициентов диффузии в смесях метана и n-декана. Распределение коэффициентов диффузии, установленное Ло и др., показывает два раздельных пика, как ожидалось для бинарной смеси газа и жидкости. Приложение Б теоретически показывает, почему имеется распределение коэффициентов диффузии в сырой нефти, а также устанавливает связь между η_k в уравнении (10а) и силой трения, которая противодействует движению k-ой составляющей в смеси сырой нефти. Приложение В представляет некоторые альтернативные параметризации релаксационной модели.

Параметры в релаксационной модели, которые должны быть определены посредством инверсии

Релаксационная модель в уравнении (1) определяет первую модель, которая будет инвертирована, используя данные из набора близко расположенных измерений в прослойке слоев. Заметим, что слои в основном близко расположены, чтобы минимизировать разницу насыщенности от слоя к слою, которая могла бы быть вызвана проникновением бурового раствора. Если бы не было такого фактора, как проникновение (например, для глубинных ЯМР измерений), то можно было бы использовать более широко разнесенные слои. Неизвестные параметры, которые должны быть определены в результате инверсии в настоящем варианте воплощения, следующие:

(1) набор N_s амплитуд {а₁}, которые определяют Т₂-распределение рапной фазы; (2) ξ , кажущееся отношение T₁/Т₂ для рапной фазы; (3) набор N₀ амплитуд {b_k}, которые определяют Т₂-распределение природной сырой нефти; (4) набор N₀ составляющих вязкостей {η_k} природной нефти, (5) A_OBMF, амплитуда сигнала фильтрата бурового раствора на углеводородной основе (OBMF). Имеется полное количество N_s+2* N₀+2 неизвестных. Время релаксации и вязкость фильтрата бурового раствора на углеводородной основе (OBMF) известны из лабораторных измерений перед каротажем, но если эти данные недоступны, то вязкость фильтрата OBMF может рассматриваться как дополнительный неизвестный параметр в релаксационной модели. Практически, даже если доступны лабораторные измерения свойств фильтратов (OBMF), в них будут существовать неопределенности и будет важно изучить устойчивость инверсии, когда варьируются предполагаемые свойства фильтратов (OBMF). В скважинах, пробуренных с буровым раствором на водной основе, модель и проблема инверсии упрощается, потому что сигнал фильтрата может быть включен в сигнал рапы, и член, представляющий сигнал фильтрата OBMF в уравнении (1), может быть выброшен из модели.

Параметры оценки пласта и информации, полученной из инверсии

Следующие параметры оценки пласта могут быть вычислены из инверсии релаксационной модели в настоящем варианте воплощения. Пористость φ_w пласта, заполненного рапой, вычисляется путем суммирования

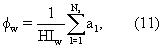
где без потери общности принимается, что амплитуды в релаксационной модели, заданной уравнением (1), имеют размерность единиц пористости. Водородный индекс (HI_w) рапы может быть оценен, исходя из солености пластовых вод (Kleinberg, R.L. and Vinegar, H.J., NMR Properties Of Reservoir Fluids, The Log Analyst, стр. 20-32, November - December, 1996). Пористость φ_o пласта, заполненного нефтью, задается выражением

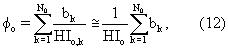
и пористость φ_obmf пласта, заполненного фильтратом OBMF, просто равна

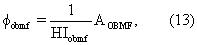
где HI₀ и HI_obmf - водородные индексы сырой нефти и фильтрата OBMF соответственно. Заметим, что в уравнении (12) было принято допущение, что распределение водородных индексов составных частей сырой нефти является узким, так что НI₀,_k ≅ НI₀, где HI₀ - макроскопический или измеренный водородный индекс смеси.

Водородный индекс свободной от газа сырой нефти может быть оценен из API плотности и близок к водородному индексу для нефти с API плотностями, большими чем 25 (Kleinberg and Vinegar, 1996, см. выше). Водородный индекс фильтрата бурового раствора на углеводородной основе (OBMF) может быть либо измерен, используя ЯМР метод, либо вычислен по известной химической формуле, массовой плотности, молекулярного веса и числа ядер водорода в химической формуле. Формулы для водородного индекса нефти, содержащей газообразные пластовые флюиды как функции температуры, давления и газового фактора (GOR), были опубликованы Zhang и др. (1998, см. выше). Нефтенасыщенность, S_o(r), на глубине исследования (DOI) в прослойке слоев, где собираются измерения, задается выражением

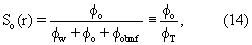
где заданная общая пористость пласта, заполненного флюидом, равна φ_T.

″ Профиль нефтенасыщенности″ может быть рассчитан посредством выполнения измерений в нескольких прослойках на различных глубинах исследования (DOI) близко расположенных слоев. Связь близко расположенных слоев на каждой глубине исследования (DOI) позволяет объединять измерения в различных слоях с тем допущением, что насыщенности флюидов (и, следовательно, амплитуды рапы, сырой нефти и фильтрата OBMF в уравнении (1)) не изменяются значительно для измерений, выполняемых в разных слоях в пределах прослойки.

Макроскопическая вязкость η₀ сырой нефти может быть вычислена из логарифмического среднего значения N₀ составляющих вязкостей {η_k}, используя уравнение (8). Т₂-распределение объемной нефти может быть вычислено из {η_k}, используя уравнение (5).

Т₂ - распределение рапы, график зависимости N_s амплитуд {а₁} от логарифмически разнесенных времен T_2,1 в уравнении (2) обеспечивает информацию относительно распределения размеров пор в пластах, где объемная релаксация рапы незначительна по сравнению с поверхностной релаксацией. Этот случай включает почти все пласты сланцеватого песка. Пористость связанного флюида может быть вычислена путем интегрирования Т₂-распределения рапы от предела Т₂-чувствительности (минимальное детектируемое время Т₂) до заднего фронта связанного флюида, например значения 33 мс, обычно используемого в сланцевых песках. Пористость связанного флюида важна для прогнозирования продуктивности продуктивных пластов и для оценки проницаемости. Привлекательность релаксационной модели в уравнении (1) состоит в том, что сигналы флюидов явно разделяются (даже, когда они накладываются на временном промежутке – T₂), тогда как в используемых моделях имелась единая функция распределения. Инверсия релаксационных моделей, которые используют единое распределение в зоне углеводородов, может приводить к вычислению ошибочно высоких оценок связанных флюидов для вязкой нефти (например, Т_2,0 меньше 33 мс), а также для легких углеводородов, когда их кажущиеся времена релаксации уменьшаются за счет диффузии до значений, меньших заднего фронта связанного флюида. Использование релаксационной модели, которая явно разделяет флюиды, позволяет отслеживать связанный флюид, который нормально должен появляться только как часть распределения рапы.

Кажущееся отношение T₁/T₂, ξ , рапной фазы является важным компонентом в инверсии. Оно выполняет автоматическую ″ поляризационную коррекцию″ амплитуд рапы. Это особенно важно для наборов параметров измерения, которые используют последовательности импульсов, получаемые с короткими временами ожидания. Эта особенность инверсии необходима для того, чтобы гарантировать, что вычисляются точные значения общей пористости (φ_T). Использование измерений с короткими временами ожидания необходимо для того, чтобы обеспечить: (1) максимальную T₁-чувствительность в продуктивных пластах с нефтью, имеющей вязкость от средней до высокой, и (2) увеличенное соотношение сигнал/шум за счет объединения многих быстрых измерений.

Инверсия модели

В описываемом варианте воплощения инверсия релаксационной модели в уравнении (1) основана на способе оконной обработки (WP), раскрытом в патенте США №5291137. Этот способ показал себя как устойчивый, гибкий и быстрый способ инверсии, который идеально приспособлен для инверсии нелинейной релаксационной модели в уравнении (1). В способе оконной обработки (WP) выводится функционал максимального правдоподобия неизвестных параметров в модели. Отрицательный логарифм функционала правдоподобия может быть записан в виде

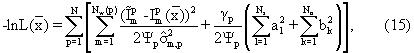
где элементы вектора x являются неизвестными параметрами в релаксационной модели.

Внешнее суммирование по индексу p распространяется на все измерения в пределах прослойка слоев и применятся ко всем членам в скобках. Для каждого p-измерения внутренняя сумма берется по набору N_w(p) предопределенных окон остатков во временной выборке. Число окон N_w(p) зависит от показателя p набора параметров измерений, потому что число окон зависит от числа спиновых эхо-сигналов (J_p). Остатки в m-ом окне представляют собой разности между измеренными оконными суммами (I) и модельными оконными суммами (I(

)), вычисленными из релаксационной модели. Оконные суммы представляют собой суммы амплитуд эхо-сигналов по временным окнам с ранними временными эхо-сигналами, которые отдельно оформляются в окна, чтобы сохранить чувствительность к быстрым временам релаксации. Остатки для p- измерения взвешиваются обратными дисперсиями измерений, т.е. ψ_p - шумовая дисперсия на отдельном эхо-сигнале, а σ =N_m+1,p-N_{m, p}+δ_m,1 - число эхо-сигналов в m-окне, где целые числа N_m,р и N_m+1,p представляют собой левую и правую конечные точки (числа сигналов) окон. Дельта функция δ_m,1 используется для того, чтобы удовлетворить принятому условию оконной обработки, что первое окно содержит его левую конечную точку. Два последних суммирования по квадратам амплитуд Т₂-распределений рапы и сырой нефти являются минимальными членами нормирующей регуляризации или сглаживания, используемых для предотвращения шумовых артефактов в инвертированных распределениях. Параметры (γ_p) регуляризации определяются из данных для каждого измерения. Модельные оконные суммы представляют собой суммирования по временным окнам амплитуд эхо сигналов в уравнении (1) и могут быть записаны в виде

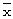
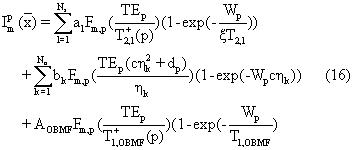
где были введены функции F_m,p(y) чувствительности, которые определяются суммированием эхо по окнам

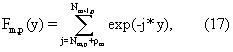
Бинарная функция ρ_m=1-δ_m,1 используется для того, чтобы удовлетворить принятому условию оконной обработки, при котором только первое окно содержит его левую конечную точку.

Геометрические ряды в уравнении (17) могут быть суммированы для получения замкнутой формы для F_m,p(y), т.е.

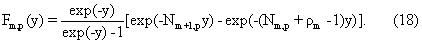
Аргументы функций чувствительности в уравнении (16) представляют собой отношения временного разнесения эхо-сигналов к кажущимся временам поперечной релаксации. Заметим, что уравнения (3), (5) и (10) использовались для того, чтобы записать кажущееся время релаксации сырой нефти в терминах составляющих вязкостей, т.е.

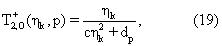
где было задано ^

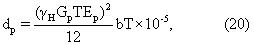
Аналитические производные для инверсии

Устойчивость ограниченной минимизации уравнения (15) улучшается посредством использования аналитических производных для всех параметров. Ограничения на оценки параметров представляют собой верхние и нижние границы. Минимизация должна выполняться с использованием двойной точности. В минимуме эти производные численно должны быть равны нулю за исключением граничных решений. Аналитические выражения для производных даются ниже. Производные по спектральным амплитудам рапы задаются выражением

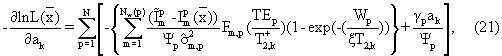
для k=1,..., N_s. Производная по параметру ξ , кажущемуся отношению T₁/T₂, равна

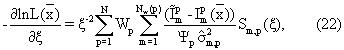
где матричная функция S_m,р (ξ ) задается выражением

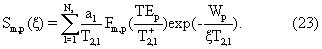
Производные по спектральным амплитудам сырой нефти даются выражением

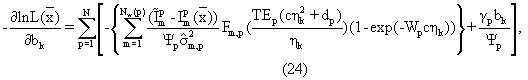
для k=1,..., N_o. Производные по составляющим вязкостям сырой нефти даются выражением

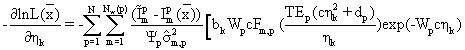
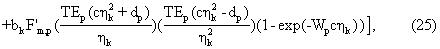
для k=1,..., N_o. В вышестоящем уравнении F’_m,p(y) представляет собой производную функции F_m,p (у) чувствительности в уравнении (18) по ее аргументу, то есть в точности,

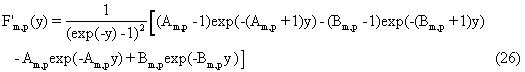
где было определено

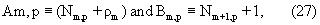
и где ρ_m=1-δ_m,1 представляет собой ранее определенную бинарную функцию.

Производная по амплитуде фильтрата бурового раствора на углеводородной основе (OBMF) дается выражением,

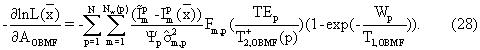
Производные общей зависимости времени релаксации и коэффициента диффузии по вязкости для подвижной нефти, содержащей газообразные пластовые флюиды.

Производные функции правдоподобия по составляющим вязкостям в уравнении (25) справедливы для конкретной зависимости T_2,0(η_k) и D_о(η_k) от вязкости, что задается в уравнениях (5) и (10). Как отмечалось выше, имеется неопределенность в отношении времени релаксации и коэффициентов диффузии для сырой нефти, содержащей газообразные пластовые флюиды, содержащие растворенный метан, неопределенность, которая может иметь зависимость от вязкости, отличную от той, что выражена уравнениями (5) и (10). Поэтому для возможного будущего использования полезно сформулировать общую форму производных по составляющим вязкостям.

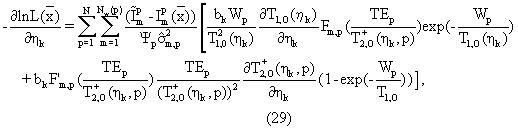
где кажущиеся времена Т (η_k,p) поперечной релаксации заданы в уравнении (3).

Расчет ковариационной матрицы параметров

Ковариационная матрица оценок параметров полезна для оценки неопределенностей в оценках параметров. Способ расчета, вкратце описанный ниже, аналогичен способу, использованному авторами Freedman и Rouault (Remaining - Oil Determination Using Nuclear Magnetism Logging SPE Formation Evaluation Journal, pp. 121-130, June, 1989). Ковариационная или корреляционная матрица оценок параметров может быть определена выражением,

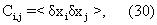
где скобки обозначают статистическое среднее или среднее по множеству и δ x_i=x_i-i> представляет собой отклонение параметра x_i от значения математического ожидания. Диагональные элементы представляет собой дисперсии в оцененных параметрах. Можно показать (Stuart and Ord, Kendall’s Advanced Theory Of Statistics, Oxford Univ. Press, vol. 2, pp. 675-676, 1991), что ковариационная матрица для оценок максимального правдоподобия дается инверсией симметричной матрицы, например,

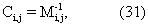
где

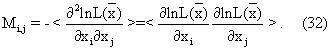
Stuart и Ord (1991, см. выше) показали, что если функция правдоподобия подчиняется условиям достаточности и регулярности, которые принимаются такими, которые удовлетворяются функционалом в уравнении (15), тогда,

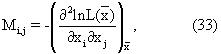
где производные оцениваются при оценках (

* ) максимального правдоподобия параметров. Форма в уравнении (33) удобна потому, что она устраняет необходимость вычислить значения математического ожидания. Элементы матрицы M_i,j могут быть вычислены аналитически.

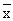
Рассмотрим фиг.5, на которой изображается блок-схема процедуры в соответствии с вариантом воплощения изобретения для программирования одного или более процессоров для воплощения метода согласно настоящему изобретению. В настоящем варианте воплощения изобретения процессор наверху скважины (например, в оборудовании 7) может осуществлять большую часть процедуры, а процессор в нижней части скважины может быть привлечен для выполнения по меньшей мере части функций сбора, запоминания и передачи данных на поверхность земли. Также должно быть понятно, что при желании часть процедуры может быть выполнена автономно, например, отдаленным процессором, расположенным в другом местоположении.

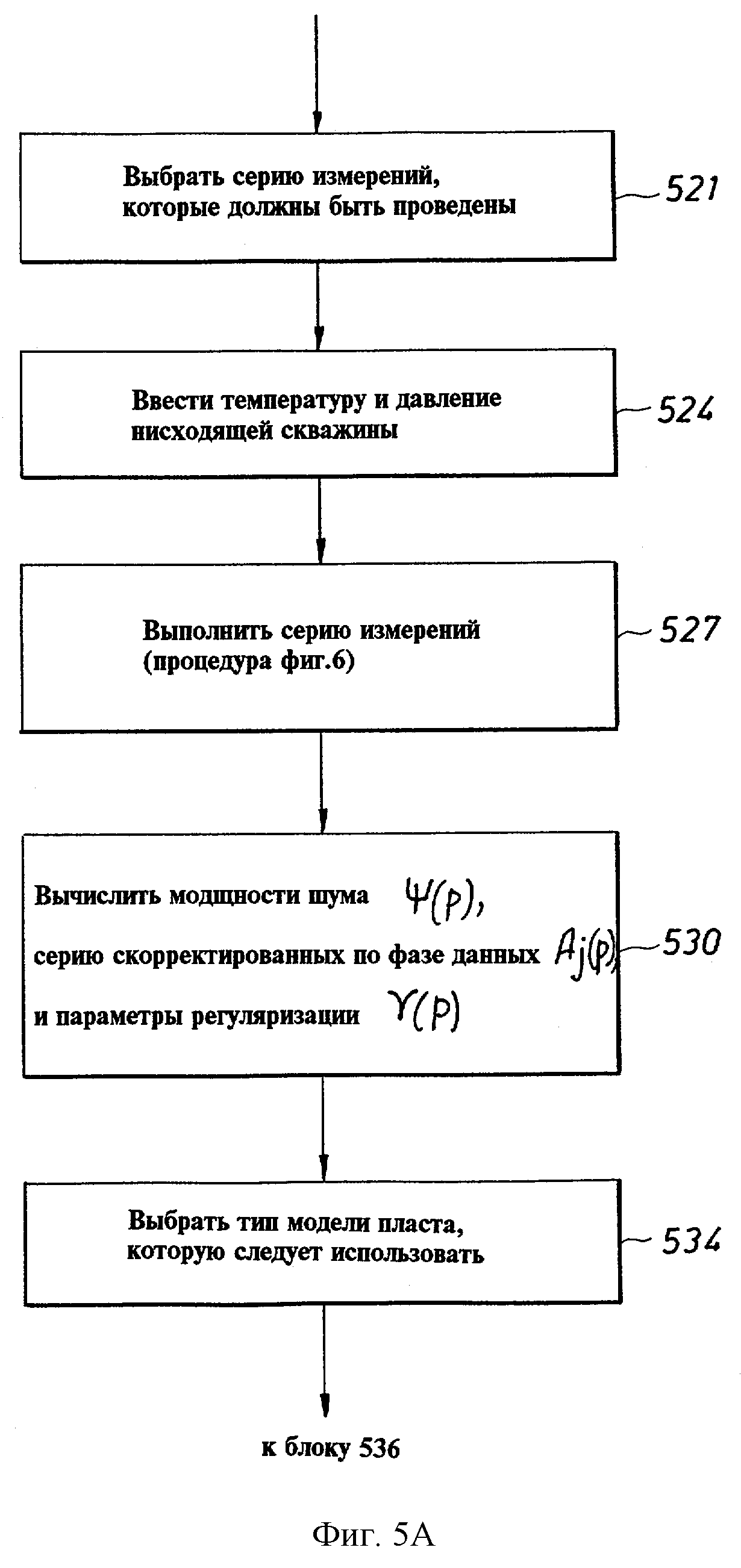
Блок 521 представляет выбор серии измерений, которые должны быть выполнены. Например, серия измерений может соответствовать типам выборов, показанных в таблицах последующих примеров. В этих примерах, для каждого из N измерений в серии (с р=1,2...N, и N=6 для этих случаев) будет иметься различная комбинация параметров: W_p (время ожидания или время поляризации), ТЕ_р (временное разнесение эхо-сигналов), G_p (градиент приложенного постоянного магнитного поля) и/или J_p (число принятых спиновых эхо-сигналов). Для каждого измерения, p, в серии измерений может быть множество повторений, имеется ввиду, что должен быть компромисс между скоростью каротажа (которая, вообще говоря, уменьшается за счет повторений) и помехоустойчивостью (которая, вообще говоря, увеличивается при объединении данных от повторений). Должно быть также понятно, что могли бы изменяться другие параметры. Блок 524 представляет ввод температуры и давления в нижней части скважины. Измерение температуры может выполняться в каротажном приборе обычными средствами как периодически, так и непрерывно, а давление на данной глубине может быть оценено, исходя из плотности бурового раствора и/или знания места, или могло бы быть измерено в нижней части скважины соответствующим оборудованием. Затем выполняется серия измерений, которая представлена блоком 527.

Блок 527 представляет управление стадией сбора данных описываемого варианта воплощения, и подпрограмма этого блока описывается подробно далее в сочетании с блок-схемой на фиг.6. Индекс p первоначально берется равным 1 (блок 603). Затем условия измерения W, ТЕ, G и J устанавливаются равными W_p, ТЕ_р, G_p и J_p, что представлено блоком 605. W_p - время ожидания для p измерения (время ожидания является временем между окончанием последовательности импульсов и началом следующей последовательности импульсов, в течение которого может возникнуть поляризация). ТЕ_р представляет разнесение эхо сигнала для p измерения (то есть время между последовательно принимаемыми импульсами в течение последовательности импульсов). G_p - градиент приложенного постоянного магнитного поля для р измерения. J_p - число спиновых эхо сигналов, полученных для р измерения. В настоящем варианте воплощения используется CPMG последовательность импульсов с обычными R и Х каналами приемника, но должно быть понятно, что могли бы использоваться модифицированные CPMG последовательности импульсов или другие подходящие типы последовательностей импульсов или каналов приемников. Затем, как представлено блоком 607, радиочастота магнитных импульсов, которые должны быть использованы для измерений, устанавливается на частоту, которую нужно использовать для изучения р слоя (например, посредством управления генератором 220 перестраиваемой частоты 220, фиг.3).

Как описано выше, в предпочтительном варианте воплощения изобретения используются смежные или близко расположенные тонкие слои зоны исследования, чтобы ускорить измерения, поскольку времена ожидания (в течение которых устанавливается продольная поляризация спинов в постоянном магнитном поле) могут быть уменьшены посредством разделения слоев и, чтобы поляризация в заданном слое не подвергалась существенному влиянию действия импульсного эхо сигнала в другом слое.

Данные получаются в близко расположенных тонких слоях в зоне исследования пластов, разделение позволяет проводить последовательное накопление без необходимости в чрезмерных временах ожидания (для поляризации), причем слои расположены настолько близко друг к другу, чтобы выполнялось предположение о том, что в большинстве случаев пласты не будут существенно изменяться по характеру в радиальном направлении исследуемой многослойной зоны. (Если время каротажа или скорость каротажа не имеют значения, серия измерений могла бы вся быть выполнена в одной и той же зоне. исследования). Затем, как представлено блоком 609, прикладывается последовательность импульсов, например CPMG последовательность импульсов, и спиновые эхо-сигналы детектируются и запоминаются. Затем делается запрос (блок 611 принятия решения) - выполняется ли условие р=N, то есть были ли выполнены измерения для каждого слоя (и, таким образом, для каждого набора условий). Если нет, то р увеличивают (блок 613), блок 605 повторно запускается, чтобы условия были установлены для следующего значения р, и замкнутый цикл 614 продолжается до тех пор, пока не будет получена полная серия измерений.

Схема фиг.6 для простоты понимания изображает простой случай. В действие может быть введено несколько дополнительных условий при выборе последовательности слоев, числа повторений и времен ожидания поляризации, учитывая специфическую желательную скорость каротажа и любые временные пределы, которые наложили бы эти условия. Например, несмотря на то, что тонкие слои могут быть относительно изолированы (в зависимости от конструкции прибора, геометрии и разнесения слоев), может быть полезен скачкообразный переход от одного слоя к другому, когда это возможно, между далеко отстоящими слоями, а не между смежными слоями, чтобы минимизировать эффекты типа взаимного влияния между слоями. Должно быть также понятно, что временная эффективность может быть усилена посредством выбора маршрута скачкообразного перехода от одного слоя к другому, который преднамеренно обеспечивает большее время ожидания (для поляризации или деполяризации) слоям с более длительными параметрами W_p. Как известно в уровне техники, при необходимости может использоваться "запирающий импульс" (например, соответственно сфазированный 90-градусный импульс), например, когда скачкообразный переход от одного слоя к другому возвращается к тому слою для повторения измерения, где требуется короткое время ожидания. Таким образом, должно быть понятно, что могут подходить многие разные маршруты скачкообразного перехода от одного слоя к другому в зависимости от обстоятельств.

Вернемся опять к схеме на фиг.5, на которой блок 530 представляет вычисление мощностей шума ψ (р) для данных, вычисление параметров регуляризации γ (р) для данных и вычисление серии скорректированных по фазе данных A_j (p). Для заданного измерения известно, что скорректированные по фазе данные могут быть определены подходящей комбинацией канальных фаз. Мощности шума ψ (p) и параметры регуляризации γ (р) полезны в инверсии, которая в описываемом варианте воплощения использует коммерчески доступный алгоритм минимизации Powell’i (нелинейный ограниченный алгоритм минимизации, Powell’s Nonlinear Constrained Minimization Algorithm) и метод оконной обработки. Далее, как представлено блоком 534, оператор выбирает тип используемой модели пласта: например модель, которая включает рапную фазу, фазу сырой нефти, фазу фильтрата бурового раствора на углеводородной основе (OBMF). Должно быть понятно, что модель пласта может дополнительно или альтернативно включать фазы, которые представляют газ, а также учитывает внутренние градиенты. Тип выбранной модели (или первоначально выбранной, поскольку могут быть обработаны последующие типы моделей) может зависеть от локальных данных, или от других доступных входных данных, или от первоначального отсеивания данных, и/или других доступных данных. В последующем описании блок-схемы будет понятно, что представление конкретной фазы может быть или не может быть применимо к конкретной используемой модели пласта.

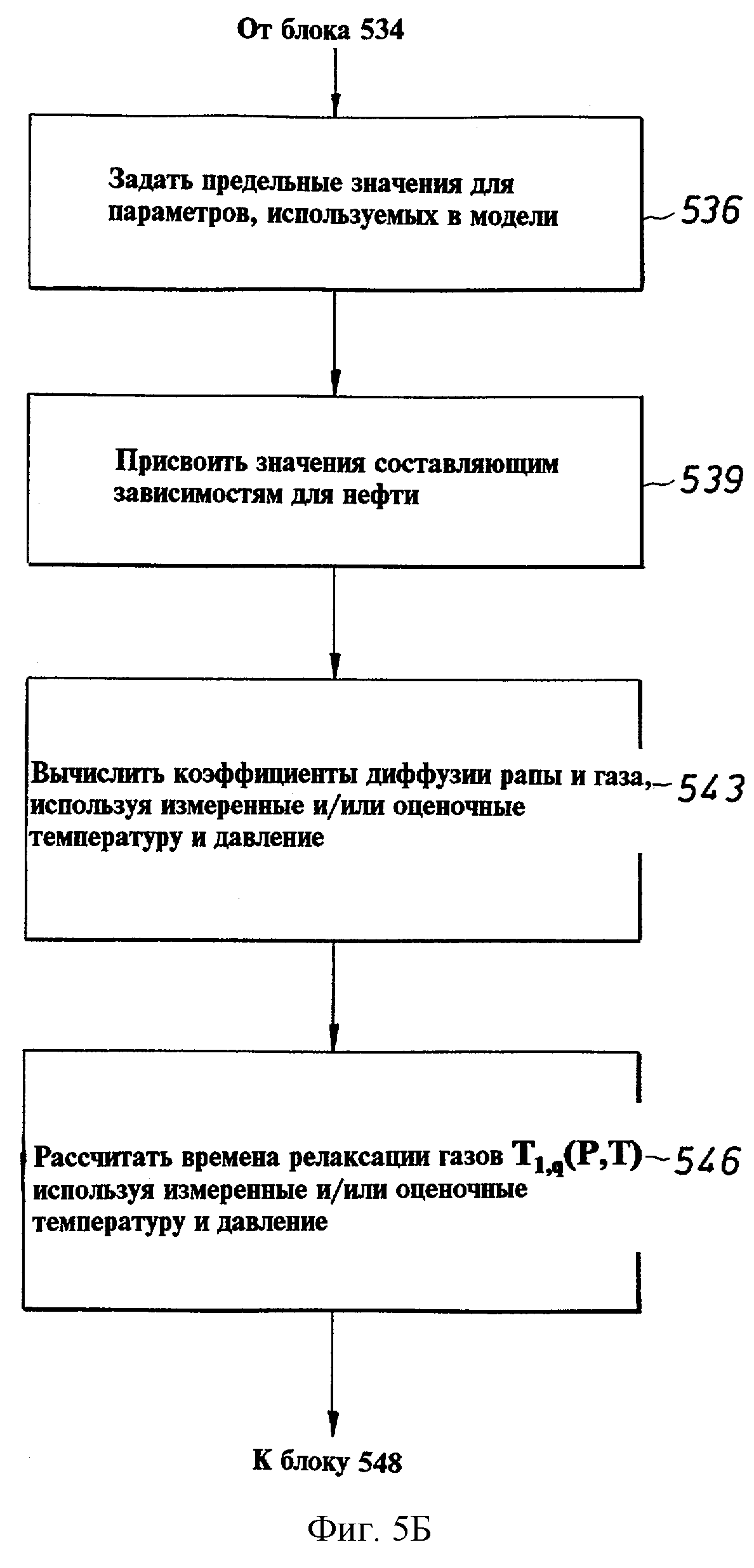
Блок 536 выполняет определение предельных значений (включая диапазоны, приращения и соотношения) для параметров, которые должны быть использованы в модели. Как показано выше, параметры модели включают, ссылаясь на релаксационную модель уравнения (1), N_s амплитуды {a₁}, которые определяют T₂-распределение рапной фазы; ξ , кажущееся отношение T₁/T₂рапной фазы; набор N_o амплитуд {b_k}, которые определяют Т₂-распределение природной сырой нефти; набор N_o составляющих вязкостей {η_k} сырой нефти; А_OBMF- амплитуду сигнала фильтрата OBMF. Для модели, которая включает газовую фазу, параметры дополнительно включают (ссылаясь на уравнение (2) в приложении А) амплитуду сигнала газа, A_s. Термины, описывающие параметры фильтрата OBMF и газа, включены далее в блок-схемы, хотя должно быть понятно, что в зависимости от обстоятельств конкретная используемая модель может включать, а может не включать эти составляющие.

Блок 539 выполняет присвоение значении материальным уравнениям для сырой нефти, т.е. материальные уравнения, которые устанавливают зависимость составляющих вязкостей с временами релаксации и коэффициентами диффузии. Как описано выше, значение коэффициента а составной части (см. уравнения (4) и (5)) может быть приблизительно 250, и значение коэффициента b составной части (см. уравнение (10а)) может быть приблизительно 8,33× 10^-3. Для нефти, содержащей газообразные пластовые флюиды, материальные уравнения и коэффициенты будут изменяться согласно газовому фактору.

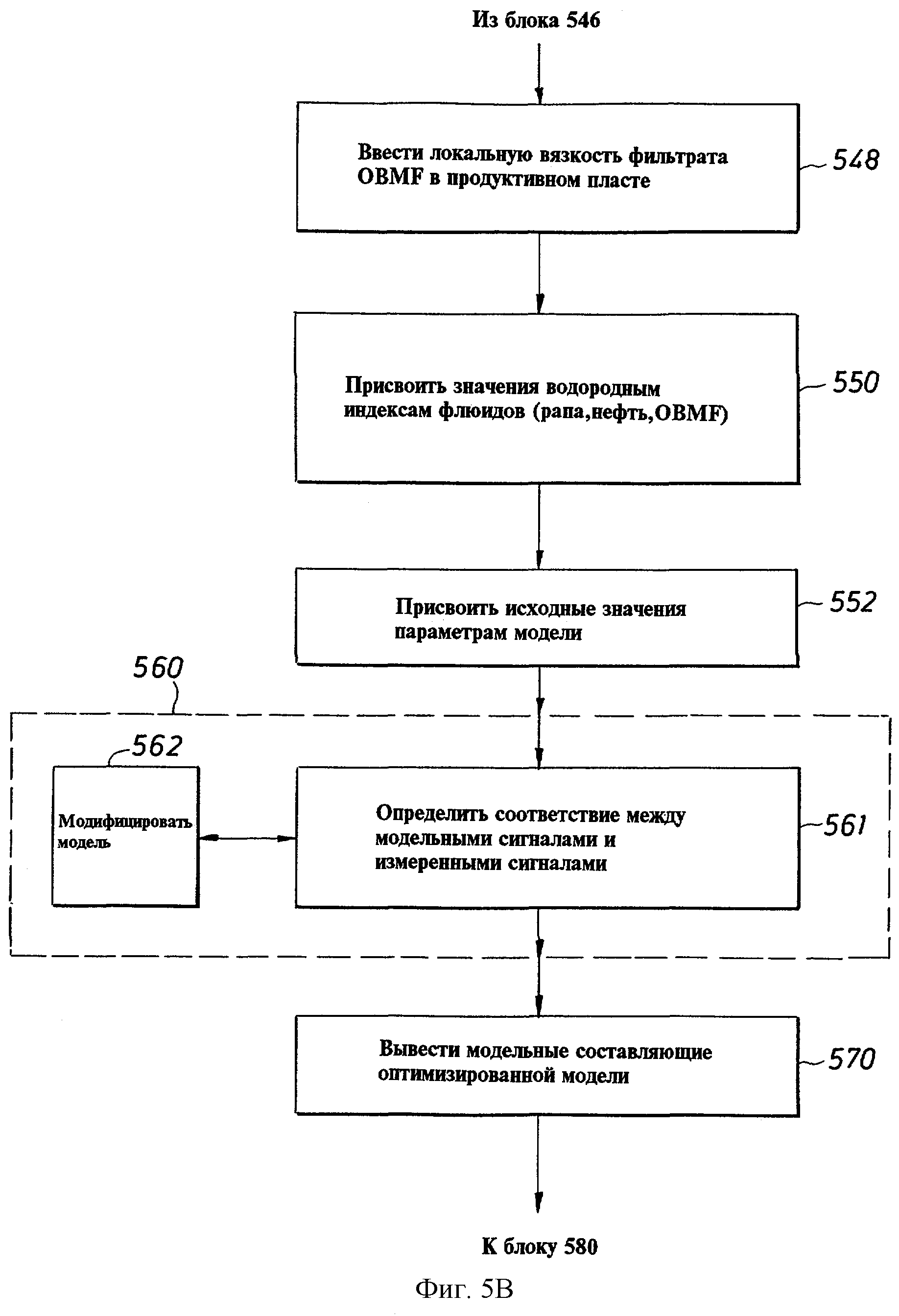
Блок 543 выполняет вычисление коэффициентов диффузии рапы и газа из известных зависимостей, используя измеренную температуру и оцененное или измеренное давление, т.е. D_w(T) согласно уравнению (2) и D_g(P,T) согласно уравнению (А.2) приложения А. Далее, блок 546 представляет вычисление времен релаксации газа T_{1, g}(P,T) с использованием измеренных температуры и давления (см, например, Kleinberg выше). Затем, блок 548 представляет ввод оценки локальной вязкости фильтрата бурового раствора на углеводородной основе (OBMF) (полученный, например, от поставщика бурового раствора или посредством измерения) и вычисление коэффициента диффузии фильтрата OBMF, для которого может использоваться уравнение (10).

Блок 550 выполняет ввод значений водородного индекса каждого из флюидов. Как отмечалось выше, водородный индекс свободной от газа сырой нефти может быть оценен из API плотности и близок к водородному индексу для нефти с API плотностями, большими чем 25 (Kleinberg and Vinegar, см. выше). Водородный индекс фильтрата бурового раствора на углеводородной основе (OBMF) может быть либо измерен, используя ЯМР метод, либо вычислен из известных химических формул, массовой плотности, молекулярного веса и числа ядер водорода в химической формуле. Формулы для водородного индекса нефти, содержащей газообразные пластовые флюиды как функции температуры, давления и газового фактора (GOR), были опубликованы Zhang и др. (1998, см. выше). Далее, как представлено блоком 552, параметрам модели присваиваются начальные значения. Затем, как представлено пунктирным блоком 560, выполняется процедура оптимизации модели, которая подробно описана в связи с блок схемой фиг.7, Как представлено в упрощенном виде в блоке 560, блок 561 определяет соответствия между сигналами, полученными из модели, и сигналами измерения, и блок 562 представляет модифицирование модели. Подробности варианта воплощения оптимизации формулируются в связи с блок схемой на фиг.7. Затем параметры модели считываются, как представлено блоком 570.

Фиг.7 изображает блок-схему процедуры выполнения нелинейного ограниченного алгоритма минимизации Powell (Powell’s Nonlinear Constrained Minimization Algorithm). Также можно сослаться на приложение Г. Блок 705 выполняет определение целевой функции, производных целевой функции и предельных значений, а также выбор исходной приближенной оценки х⁰. Исходная приближенная оценка х⁰ может быть определена, если не была уже выполнена ранее (см. блок 552). Также определяется исходная положительная определенная матрица В⁰ вторых производных и параметр точности (блок 707). Далее, как представлено блоком 710, задаются задача квадратического программирования (QP) и предельные значения. Можно сослаться на уравнение (Г.2) приложения Г. Далее, как представлено блоком 720, задача квадратического программирования (QP) решается на k-ой итерации с использованием теоремы ККТ (Karush-Kuhn-Tucker) для определения вектора d^k направления поиска и множителей Лагранжа λ^k для активных предельных значений. Затем делается запрос (блок 730 принятия решения) - сошелся ли алгоритм, путем сравнения по теореме ККТ остаточного вектора с двойной нормой с точностью, заданной пользователем (см. уравнение (Г.5) приложения Г). Если алгоритм сошелся, то начинает действовать блок 579 (фиг.5) и могут быть выведены определенные значения параметров модели. Если нет, то соответственно начинают действовать блоки 750 и 760, т.е. блок 750, представляющий выполнение линии поиска для определения размера α^k шага, удовлетворяющего условиям в уравнениях (Г.3) и (Г. 4) приложения Г, и блок 760, представляющий обновление вектора решения и обновление В^k используя алгоритм базисного возможного решения (BFGS). Затем снова запускается блок 770 и цикл продолжается до тех пор, пока не будет достигнута сходимость.

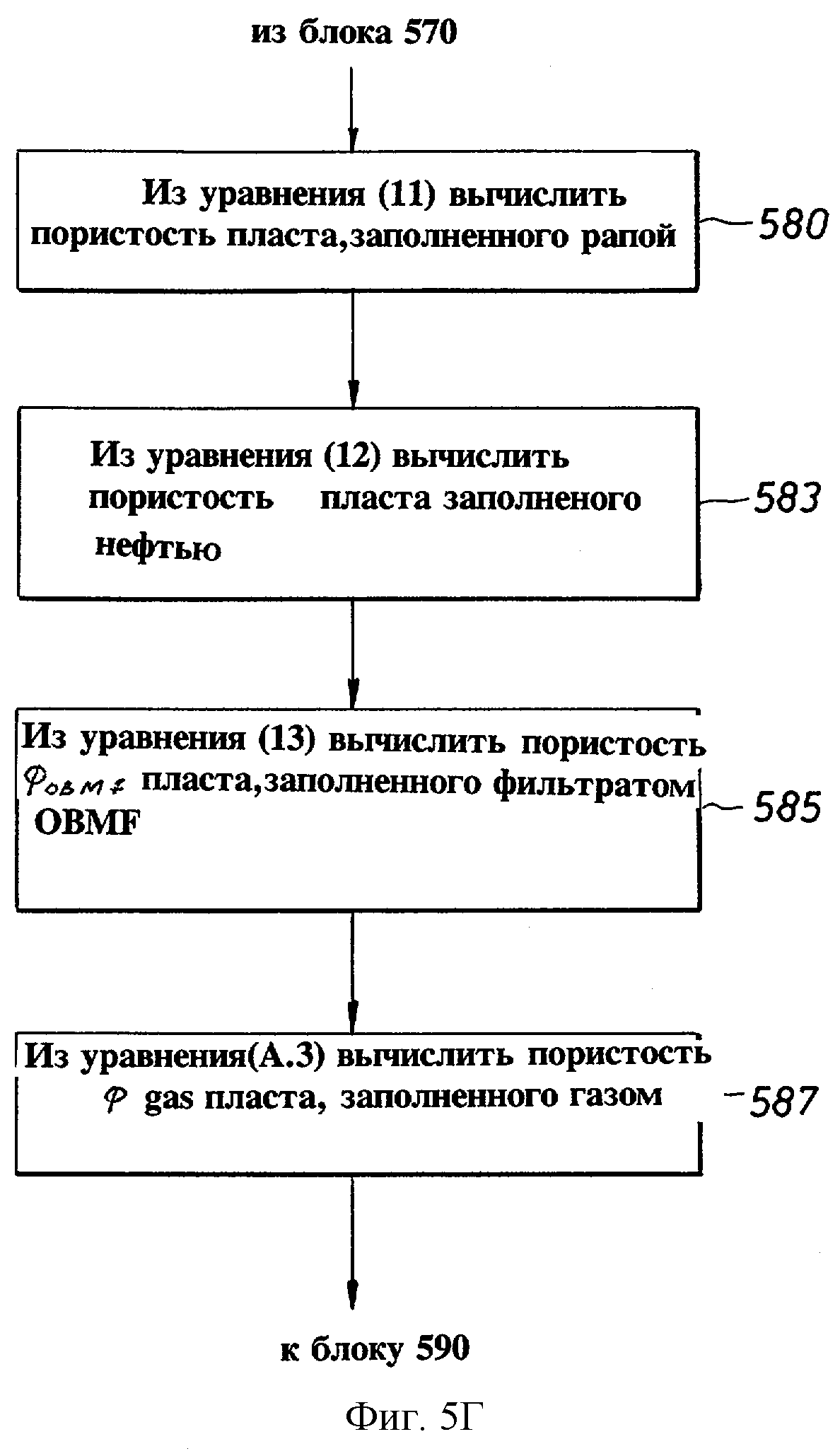
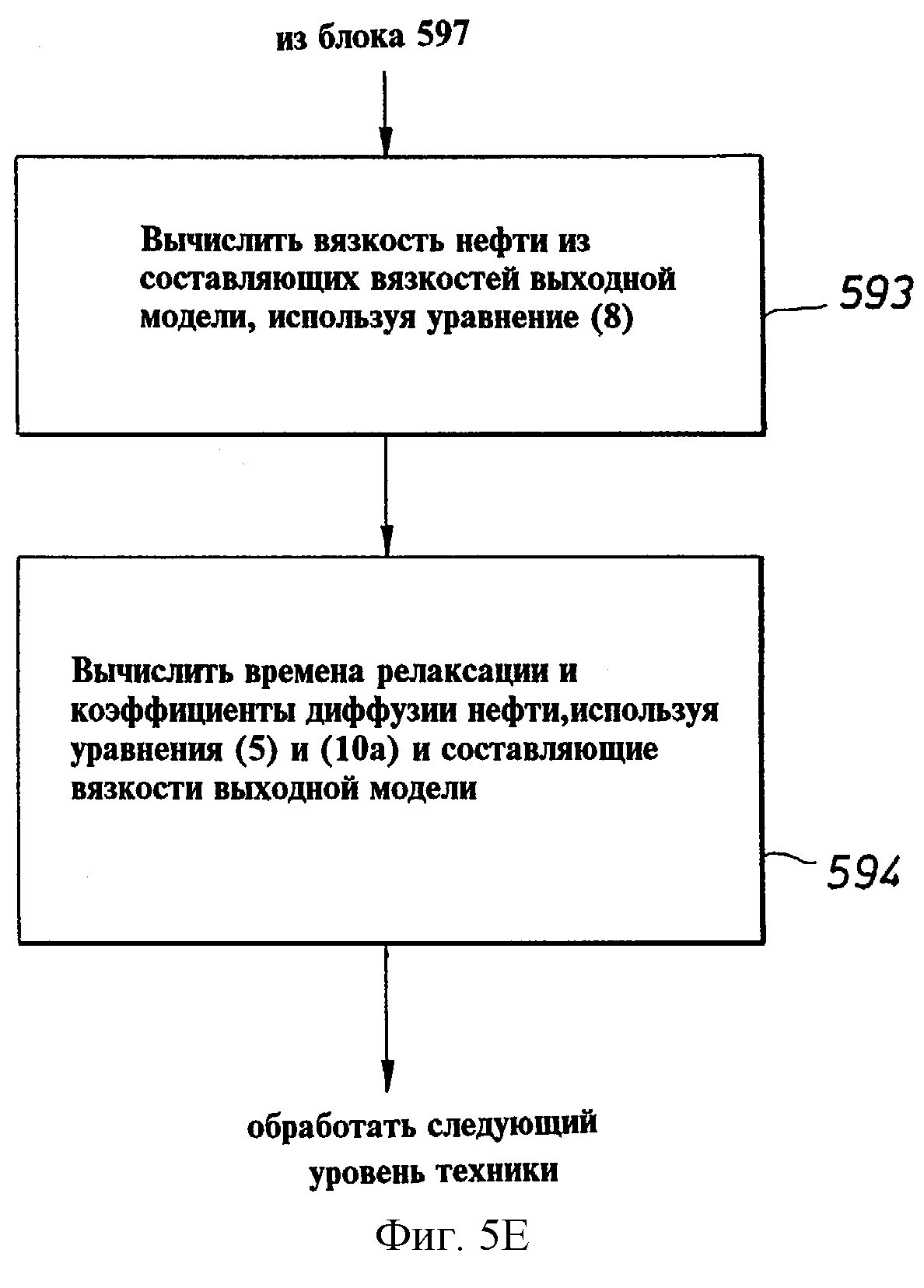
Вернемся опять к фиг.5. После выведения параметров оптимизированной модели запускается блок 580, представляющий вычисление пористости φ_w пласта, заполненного рапой, которая может быть получена с использованием уравнения (11). Также может быть вычислена пористость φ_о пласта, заполненного природной нефтью, с использованием уравнения (12) (блок 583). Далее, в зависимости от ситуации, может быть вычислена пористость φ_OBMF пласта, заполненного фильтратом бурового раствора на углеводородной основе (OBMF), с использованием уравнения (13) (блок 585), а также может быть вычислена пористость φ_gas пласта, заполненного газом, с использованием уравнения (А.З) приложения А (блок 587). Затем может быть вычислена общая пористость φ_T пласта, заполненного флюидом, с использованием уравнения (14) или, когда в модели присутствует газ, уравнения (А.4) приложения А. Затем, с использованием вычисленной пористости φ_T пласта, заполненного флюидом, могут быть вычислены различные насыщенности в зоне исследования (т.е. в радиусе r от центра зоны исследования, заданном N цилиндрическими тонкими слоями), как показано в блоке 592. Нефтенасыщенность S_o(r) вычисляется с использованием уравнения (14) или (А.4), а насыщенность рапы S_w(r) и насыщенность S_OBMF(r) фильтрата бурового раствора на углеводородной основе (OBMF) могут быть вычислены с использованием соотношений, показанных на фиг.5. Далее вязкость нефти может быть вычислена (блок 593) из составляющих вязкостей с использованием уравнения (8), и коэффициенты могут быть вычислены (блок 594) с использованием уравнений (5) и (10а) составляющих вязкостей выходной модели. Затем может быть обработан следующий уровень глубины.

Настоящий способ может также применяться к измерениям, выполняемым на поверхности земли на кернах земных пластов. В таком случае керн может быть помещен в лабораторное ЯМР оборудование и могут быть осуществлены соответствующая последовательность импульсов и прием эхо-сигналов. Описанным способом могут быть определены объемы флюидов в керне и другие параметры оценки пласта (см. приложение Е).

Примеры инверсии

Могут иметь практический интерес следующие примеры. Вычисления были выполнены с помощью программы прототипа, которая осуществляет вышеописанный способ инверсии. Данные генерировались посредством программы, которая генерирует шумящие последовательности спиновых эхо сигналов, с использованием релаксационной модели в уравнении (1). Все примеры в этом разделе были вычислены, используя последовательность импульсов, состоящую из одинаковых шести измерений, хотя оказалось, что эта последовательность обеспечивает хорошие результаты по широкому диапазону насыщенностей флюидов и свойств нефти, должно быть понятно, что эта конкретная последовательность или использование шести измерений необязательно являются оптимальными для любой заданной ситуации. Примеры демонстрируют эффективность способа. Чтобы установить прецизионность и точность инверсии, а также определить наилучшие последовательности измерения, вычисления могут быть выполнены методом Монте Карло. Примеры также показывают, что этот способ может использоваться для того, чтобы идентифицировать и оценивать влажные зоны.

Измерения и параметры, использованные для примеров

Параметры импульсов для шести измерений, используемых для этих примеров, показаны в таблице 1. Измерения с короткими временами ожидания необходимы для того, чтобы обеспечить чувствительность к вязкой нефти с короткими временами релаксации. Широкий диапазон разнесений эхо-сигналов обеспечивает максимальную чувствительность к различным диффузионным способностям флюидов и фильтратов OBMF. Градиент прибора фактически может варьироваться до некоторой степени в пределах прослойки близко расположенных слоев, но для удобства принимается постоянным. Исходя из уравнений (2), (3) и (9), заметим, что на кажущиеся времена релаксации влияет произведение градиента прибора и разнесения эхо-сигналов. Таким образом любые ошибки в градиенте прибора, принятые в инверсии, эквивалентны изменению в разнесениях эхо сигналов настолько, насколько затрагиваются явления диффузии. В частности, в пластах с внутренними градиентами, допускающими некорректный градиент для инверсии, инверсия необязательно будет деградировать в зависимости от устойчивости к ошибкам последовательности измерений к изменениям в разнесении эхо-сигналов и величине ошибок градиента.

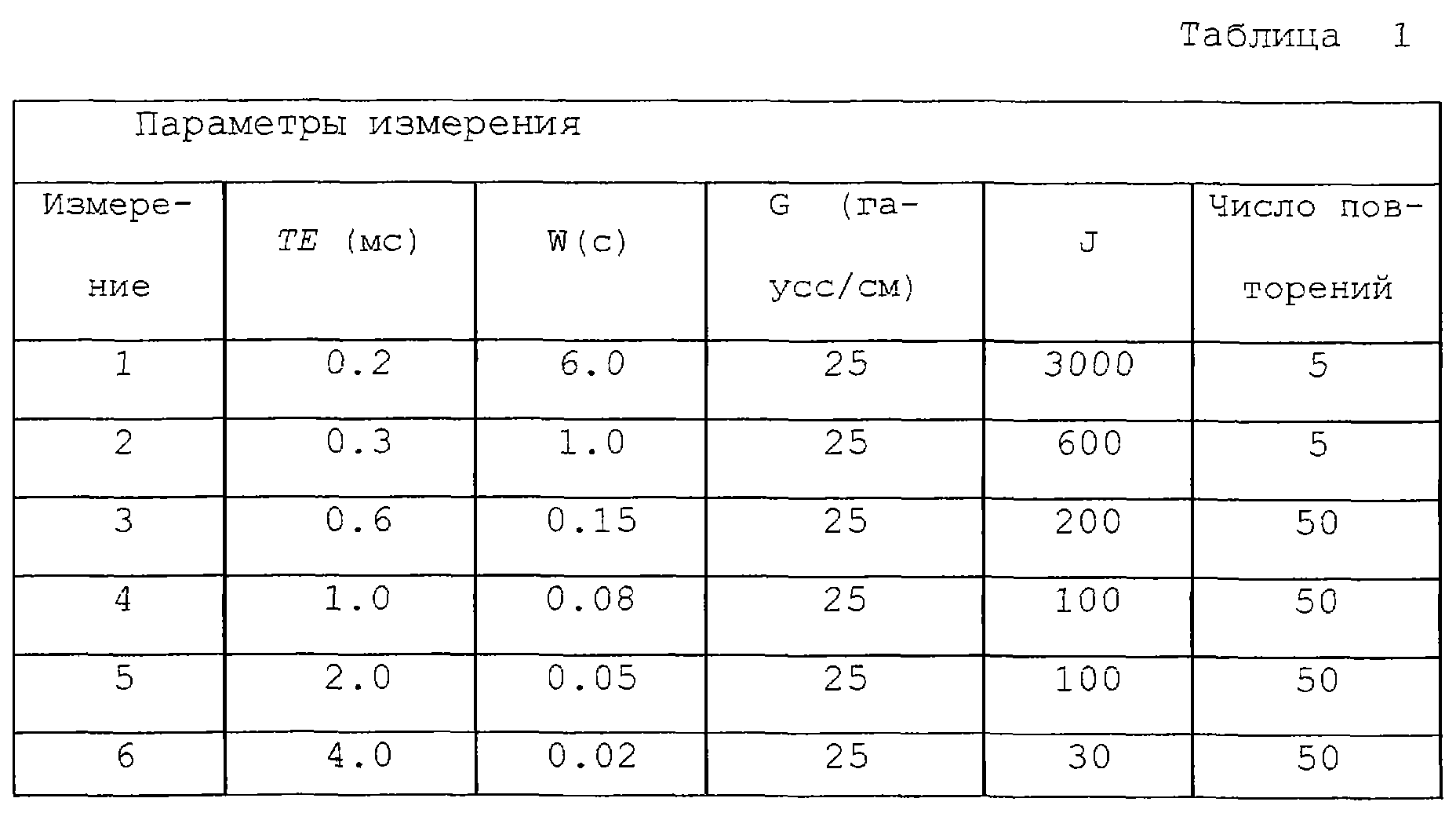
Для всех вычислений используется температура пласта 100° С. Коэффициент диффузии для рапной фазы при температуре пласта вычисляется, используя полином, аппроксимированный к опубликованным данным для коэффициента диффузии воды в зависимости от температуры. Уравнение для параметра D_w(T), который использовался для вычислений, имеет вид,

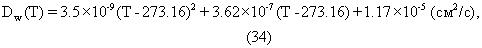
где Т - температура пласта в градусах Кельвина. Для приведенных здесь примеров температура пласта принималось равной 100 градусов по шкале Цельсия, так чтобы коэффициент диффузии рапы, вычисленный из последнего уравнения, был равен 8,29× 10^-5 см²/с.

T₂ - распределение рапы, которое использовалось для всех вычислений в примерах, было выбрано (например, на одной конкретной глубине) из серии 30 распределений, которые были использованы ранее для моделирования методом Монте Карло. Это Т₂- распределение рапы показано на фиг.8.

Синтетические данные относительно спиновых эхо-сигналов генерируются с использованием времен релаксации спина фильтрата OBMF, T₁,_OBMF=Т₂,_OBMF=3 сек, и вязкости фильтрата OBMF, равной η =2 сантипуаз. Также в генерации синтетических данных коэффициенты составных частей, используемые в уравнениях (4), (5) и (10), были такими, которые даны Looyestijn (см. выше), например, а=250 и b=8.33× 10^-3. Для удобства и без потери общности водородные индексы жидкостей рапы, сырой нефти и фильтрата OBMF были приняты равными для всех примеров.

Во всех вычислениях число спектральных составляющих рапы N_w=41, а число спектральных составляющих сырой нефти, N_o=8. Общее число неизвестных параметров было, следовательно, равно 59 во всех вычислениях (за исключением примеров газа в приложении А, для которого имеются 60 неизвестных параметров).

Пример №1. Пласт, заполненный рапой

Первый пример дается для пласта, заполненного на 100% рапой. Входные параметры пласта и результаты инверсии показаны в таблице 2. "Галочки" над параметрами используются для того, чтобы показать, что это оценки, полученные от инверсии. Первый набор оценок был получен посредством инверсии синтетических данных относительно спиновых эхо-сигналов в предположении, что для генерации спиновых эхо-сигналов использовались такие же свойства фильтрата бурового раствора на углеводородной основе (OBMF) и составляющие коэффициенты уравнений. Чтобы прочувствовать действие таких ошибок, инверсии повторялись в предположении, что свойства фильтрата (OBMF) и составляющие коэффициенты уравнений отличались от тех, которые использовались для генерации данных спиновых эхо-сигналов. Предполагаемые свойства фильтрата (OBMF) для повторных инверсий были: T₁,_OBMF=Т₂,_OBMF=2 сек, и η_OBMF=1 сантипуаз, что на 50% отличается от значений, используемых для генерации спиновых эхо-сигналов. Постоянные коэффициенты, принятые для повторных инверсий, отличались на 30% от их входных значений, например, значения, принятые в повторных инверсиях, были а=300 и b=1.0× 10^-2. Результаты повторных инверсий представлены в таблицах числами в круглых скобках.

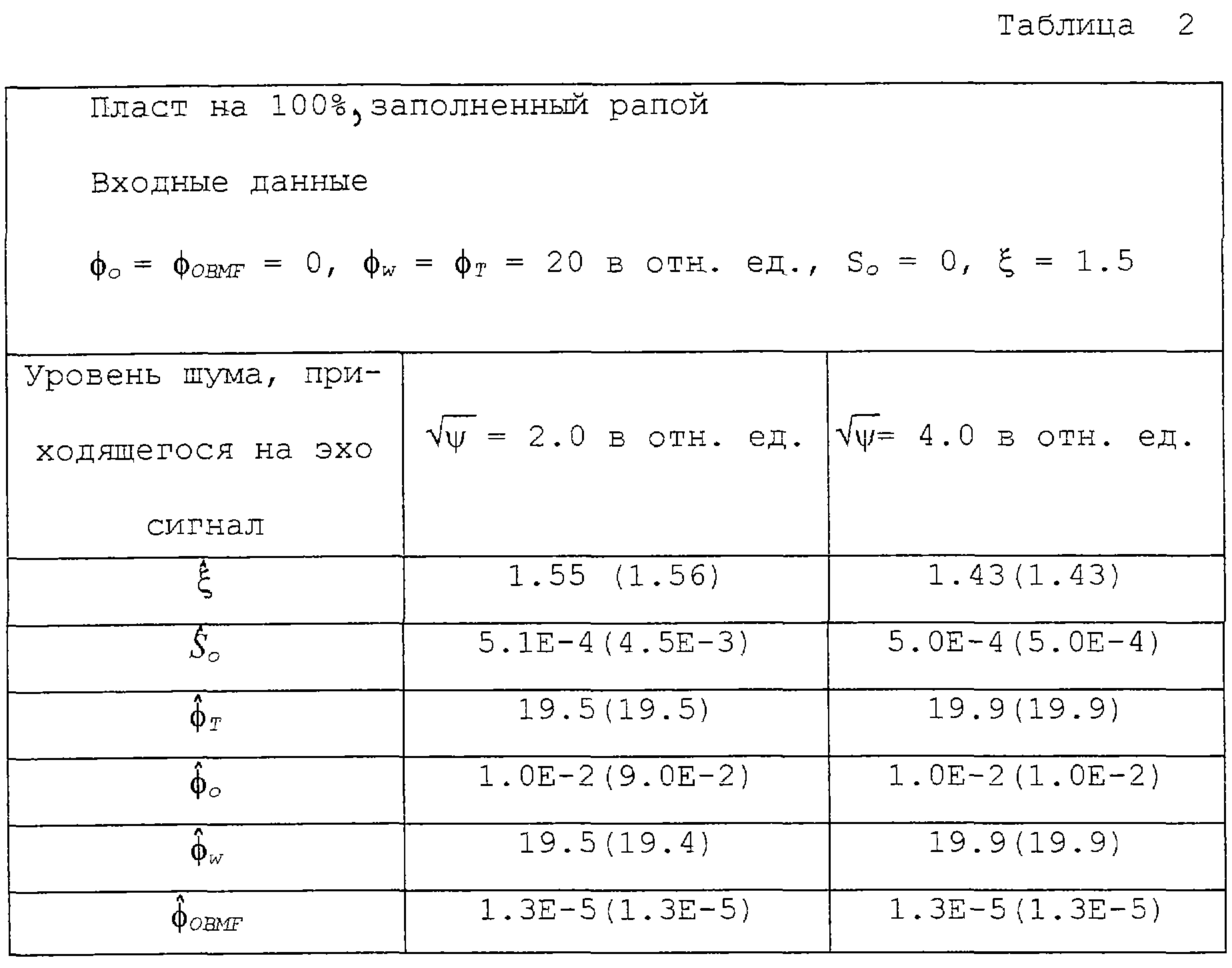
Заметим, что инверсия данных устойчива к ошибкам и, в частности, при принятии некорректных значений для свойств фильтрата (OBMF) для составляющих коэффициентов в уравнениях (4), (5) и (10) никакой нефти не предсказывается, и никаких изменений в оценках параметров не произошло.

Пример №2. Пласт, заполненный рапой и фильтратом OBMF

Входные параметры пласта и результаты инверсии показаны в таблице 3. Заметим, что инверсия зашумленных данных устойчива к ошибкам и что только непромышленные количества (то есть насыщенность нефтью 1.5% и 4.7%) сырой нефти прогнозируются для отношения шум/эхо, равного 2.0 в относительных единицах. Для более высокого уровня шума, 4.0 в отн. ед. на эхо, прогнозируемые насыщенности нефти (например, 4.7% и 9.6%) увеличиваются, но коммерчески несущественны. То есть прогнозируется, что пласт должен быть насыщен рапой на 90% и мог бы при оценке параметров пласта справедливо рассматриваться как "влажная" зона. Заметим, что общая пористость пласта, заполненного флюидом и заполненного рапой, прогнозируются правильно, при этом прогнозируемая сырая нефть обусловлена оцениваемой пористостью пласта, заполненного фильтратом OBMF и рапой.

Пример №3. Пласт, заполненный рапой, фильтратом OBMF и нефтью

Этот пример дается для пласта, который содержат рапу, природную нефть и фильтрат OBMF. Инверсия выполняется для нефти низкой вязкости (η₀=5.7 сантипуаз), нефти высокой вязкости (η₀=71.7 сантипуаз} и "нефти очень низкой вязкости" (η₀=1.65 сантипуаз). Нефть очень низкой вязкости имеет такую вязкость, которая сопоставима с принятой для OBMF (то есть 1.0 и 2.0 сантипуаз). Входные параметры пласта и результаты инверсии для нефти низкой вязкости показы в таблице 4.

Заметим хорошую идентификацию всех трех флюидов для обоих соотношений шум, эхо сигнал, равных 2 и 4 в отн. ед., а также, что объемная вязкость нефти вычислялась точно для широкого распределения составляющих вязкостей. Также заметим, что относительно меньшие изменения (например, числа в круглых скобках) в оценках параметров были вызваны принятием неправильных свойств фильтрата OBMF и составляющих постоянных коэффициентов в инверсии.

Таблица 4а содержит входные данные и результаты инверсии для нефти высокой вязкости. Заметим, что все другие входные данные кроме вязкостей идентичны данным таблицы 4.

Точные насыщенности флюидов получены для уровня шума 2.0 в отн. ед. Числа в круглых скобках показывают, что для уровня шума 2.0 в отн. ед. и 4.0 в отн. ед. продуктивный нефтеносный пласт все еще остается идентифицированным, даже если имеются ошибки в принятых OBMF свойствах и в материальных уравнениях. Последние ошибки приводят к тому, что вязкость нефти оказывается недооцененной и объемы рапы и фильтраты OBMF оказываются переоцененным и недооцененным соответственно.

Для данных с уровнем шума 4.0 в отн. ед. водонасыщенность является значительно завышенной, а насыщенность нефтьюнедооцененной. Заметим, что общая пористость пласта, заполненного флюидом, точно выявляется с уровнем шума 4 в отн. ед.. Этот результат указывает на то, что для того, чтобы определить точные насыщенности в продуктивных пластах с нефтью высокой вязкости (то есть с короткими временами релаксации), вероятно требуются данные с высоким отношением сигнал/шум. Инверсия полностью не удается для экстремальных случаев (например, η₀=1000 сантипуаз), для которых времена объемной релаксации составляют порядка 1.5 мсек.

Таблица 4б содержит входные данные и результаты инверсии для нефти очень низкой вязкости. Заметим, что все другие входные данные кроме вязкостей идентичны данным таблиц 4 и 4а.

Нефть очень низкой вязкости затрудняет точное разделение рапы, нефти и фильтрата OBMF из-за того, что предельные значения вязкости очень малы. Это - не проблема соотношения сигнал/шум, а скорее вопрос различных флюидов, имеющих очень похожие отклики на измерения. Заметим, что инверсия путает природную нефть с рапой и с фильтратом OBMF. Недостаток контраста в свойствах флюидов составляет фундаментальную проблему и нельзя ожидать того, чтобы можно было изменить это обстоятельство либо улучшенным отношением сигнал/шум, либо путем выбора другой серии измерений.

Пример №4. Пласт, заполненный рапой и нефтью

Последний из этой группы примеров представляет пласт, заполненный рапой и нефтью, не содержащий фильтрата бурового раствора на углеводородной основе (OBMF) на заданной глубине исследования. Таблица 5 содержит входные данные и результаты инверсии для нефти низкой вязкости.

Инверсия точно выявляет истинную пористость пласта, заполненного фильтратом OBMF, и общую пористость пласта, заполненного флюидом. Хотя пористость пласта, заполненного нефтью, слегка недооценивается, результаты для нефтенасыщенности, вязкости нефти и общей пористости пласта, заполненного флюидом, являются превосходными. Заметим, что имеются относительно меньшие изменения в оценках в круглых скобках, например, когда инверсия использует некорректные значения свойств фильтрата OBMF и постоянных коэффициентов в материальных уравнениях.

Таблица 5а содержит входные данные и результаты инверсии для нефти высокой вязкости. Заметим, что все другие входные данные кроме вязкостей идентичны данным таблицы 5.

Результаты, представленные в таблице 5а для нефти высокой вязкости в пласте, заполненном рапой и нефтью, являются очень хорошими. Результаты для двух уровней шума удивительно близки.

Значения насыщенности нефти, полученные из инверсии, являются более точными, чем те, которые можно ожидать из вычислений, основанных на уравнениях насыщенности (например, Арчи (Archie) или Dual-Water) и на электрических каротажных измерениях. Заметим, что по существу нет изменений в оценках в круглых скобках, например, когда инверсия использует некорректные значения свойств фильтрата OBMF и постоянных коэффициентов в материальных уравнениях.

Таблица 5б содержит входные данные и результаты инверсии для нефти очень низкой вязкости. Заметим, что все другие входные данные кроме вязкостей идентичны данным таблицы 5 и 5а.

Инверсия путает нефть низкой вязкости с фильтратом OBMF и с рапой, как в случае, показанном в таблице 4б примера №3. Тем не менее, продуктивный нефтяной пласт мог бы быть идентифицирован инверсией с пессимистическими оценками насыщенности нефти из-за нефти очень низкой вязкости.

Результаты, полученные методом Монте Карло, для идентификации углеводородов в карбонатном пласте

Этот пример представляет результаты моделирования методом Монте Карло для модельного карбонатного пласта, который содержит нефть, газ, фильтрат OBMF и рапу. Т₂-распределение рапы, используемое для генерирования спиновых эхо-сигналов для моделирования, показано на фиг.9. Серия измерений для моделирования карбоната методом Монте Карло состояла из шести измерении, представленных в таблице 6. Короткие времена ожидания в серии увеличились по сравнению с временами в таблице 1. Причина состоит в разнице характера T₂-распределений. В распределении на фиг.8 большая часть амплитуды приходится на времена релаксации ниже 100 мсек, тогда как распределение на фиг.9 имеет очень низкую амплитуду в этом диапазоне. Моделирование карбоната выполнялось, используя T₂-распределение на фигуре 9, чтобы генерировать 25 последовательностей спиновых эхо сигналов, не имеющих шумов. Аддитивный случайный шум со среднеквадратичным отклонением 4.0 в отн.ед. на эхо-сигнал на измерение был добавлен к каждой CPMG последовательности в серии после начального снижения шума на квадратный корень от числа повторений, показанных в таблице 1. Импульсы CPMG для последовательности Монте Карло генерировались с использованием постоянного значения отношения T₁/T₂=1.8.

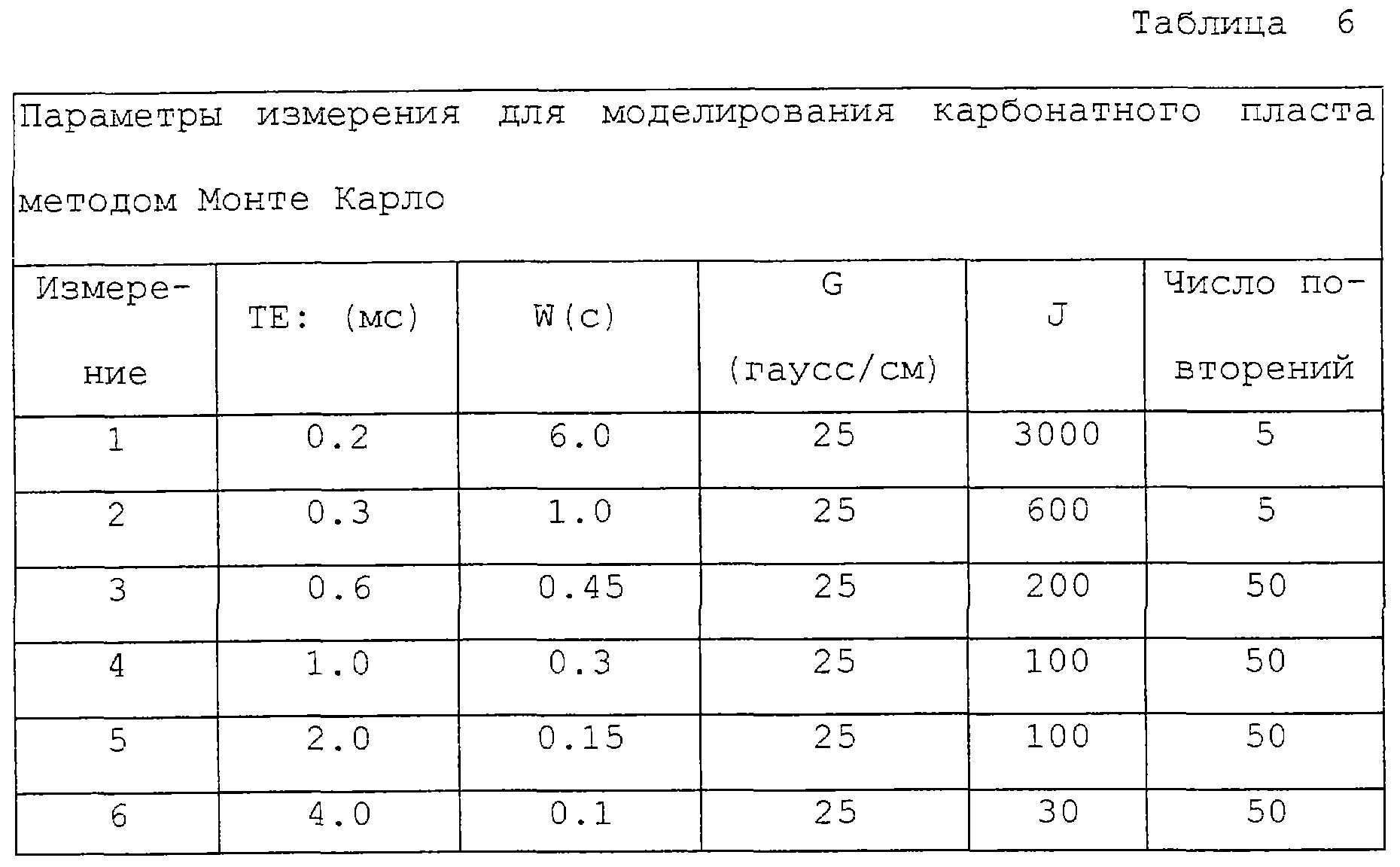
Фиг.10 изображает серию измерений. Фиг.11 изображает график входных (т.е. действительных) насыщенностей флюидов и средних оценочных насыщенностей из моделирования методом Монте Карло с использованием инверсионной модели. Также показаны среднеквадратичные отклонения в вычисленных значениях насыщенности. Показаны также истинная вязкость нефти, оцененная вязкость и ее среднеквадратичное отклонение.

Эффекты перемещения прибора

До этого пункта эффекты перемещения прибора не включаются в релаксационные модели. Поляризационные функции в уравнениях (1) и (A.1), которые описывают подход продольного намагничивания к равновесному значению, остаются в силе для стационарного прибора. В этом разделе выводится функция поляризации, зависящая от скорости для постоянной скорости прибора. Эта функция должным образом учитывает тот факт, что поляризация пласта варьируется по длине прибора. На фиг.12 изображен поляризационный профиль f(z,v) для каротажного прибора, перемещающегося вверх по стволу скважины с постоянной скоростью (v). Прибор имеет антенну длиной l_ant и магнит с длиной предварительной поляризации l_роl. Ось z является частью системы координат, заданной в пласте, и параллельна оси ствола скважины. Время цикла Т_c определяется как полное время измерения, то есть сумма времени получения эхо-сигнала и времени ожидания. Время ожидания является мертвым временем в промежутке после того, как заканчивается получение эхо-сигнала, и перед тем, как инициируется девяносто градусный (или в более общем случае α -градусный) импульс, чтобы начать следующий цикл измерения. Фиг. 12 изображает моментальный снимок прибора в момент перед тем, как инициируется новый цикл измерения посредством применения девяностоградусного импульса. Во время предыдущего измерения прибор переместился на расстояние vT_c. Заметим, что поляризационный профиль напротив антенны является прерывистым. Первая часть была поляризована заранее поляризованным магнитом, расположенным перед антенной. Вторая часть поляризуется в течение мертвого времени вслед за получением эхо сигнала.

Измерение, изображенное на фиг.12, является "перекрывающимся" измерением, потому что расстояние, на которое прибор перемещается в течение времени цикла измерения, меньше длины антенны. Если в течение времени цикла измерения прибор перемещается на расстояние, равное длине антенны, то измерение называется "неперекрывающимся". Неперекрывающиеся измерения вызывают частичную поляризацию флюидов в пласте и обеспечивают серию измерений с чувствительностью к различным временам T₁ релаксации пластовых флюидов. На фиг.12 можно видеть, что детали поляризационного профиля в пласте зависят от скорости каротажа. Поэтому неудавшаяся попытка учесть эффекты скорости каротажа может привести к ошибочным результатам. Неперекрывающиеся измерения обеспечивают полную поляризацию и возможность быстрого каротажа, пользуясь преимуществом длины предварительной поляризации магнита. Выводимые ниже функции поляризации, зависящие от скорости, используются для обоих типов измерений.

Функции поляризации, зависящие от скорости перемещения

Пусть f(z,v) обозначают профиль поляризации в зависимости от скорости. Поляризационный профиль задается выражением,

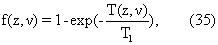
где T(z,v) - время восстановления для спинов в пласте, расположенном в положении z напротив антенны (см. фиг.12) и Т₁ - время продольной релаксации пласта. Вид уравнения (35) имеет силу при условии, что величина постоянного магнитного поля в области предварительной поляризации - фактически такая же, как поле напротив антенны (то есть не имеется никаких эффектов неравновесного перехода в продольном намагничивании). Время цикла измерения определяется уравнением

где W - время ожидания, J - полное число эхо-сигналов и ТЕ - разнесение эхо-сигналов. Время поляризации варьируется по длине антенны, а в области перекрытия постоянно и задается выражением

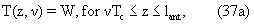
тогда как в неперекрывающейся области измерения

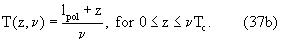
Зависящая от скорости функция f(v) поляризации получается путем умножения f(z,v) на функцию S_a(z) чувствительности антенны и интегрированием по длине антенны, т.е.

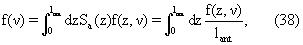
где при получении последнего равенства мы предположили, что чувствительность антенны равномерна по длине. Используя уравнения (35) и (37), можно найти при выполнении интегрирования

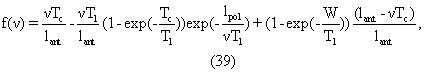
функция в уравнении (39) приводится к виду, используемому в уравнении (1) для стационарного измерения. Также наблюдается, что для неперекрывающегося измерения, то есть, если vT_c=l_ant, третий член исчезает. Чтобы включить эффекты скорости перемещения в релаксационные модели, поляризационные функции в уравнениях (1) и (A.1) заменяются на функцию f(v), что имеет место как для перекрывающегося, так и для неперекрывающегося измерений. Части пласта будут пропущены измерениями, если vT_c>l_ant.

Аналитические производные для инверсии с поправками на скорость перемещения

Минимизация целевого функционала в уравнении (15), включая функции поляризации, зависящие от скорости, может быть выполнена после той же самой процедуры, как обсуждалось для стационарного прибора. Минимизация выполняется более надежно и более дешево при помощи аналитически выведенных производных. Аналитические формы большинства производных, выведенных ранее для стационарного прибора, остаются в силе. Например, производные в уравнениях (21), (24) и (28) корректны для перемещающегося прибора, если просто заменить стационарные поляризационные функции на функции поляризации, зависящие от скорости. Однако производные в уравнениях (22) и (25) по кажущемуся отношению T₁/Т₂ для рапы (ξ ) и по составляющим вязкостям (η_k) сырой нефти модифицируются из-за более сложной зависимости T₁ от функции поляризации, зависящей от скорости. Производная по ξ для перемещающегося прибора задается выражением

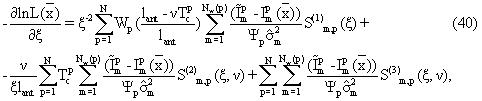
где Т=W_p+J_p ТЕ_р - время цикла измерения р. Первый член в уравнении (40) учитывает перекрывающуюся часть измерения. Заметим, что он уничтожается для неперекрывающихся измерений, т.е. когда vT=l_ant. В уравнении (40) могут быть заданы следующие выражения

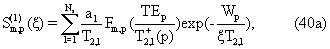
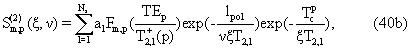
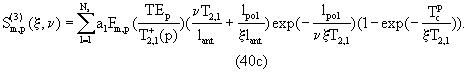
Заметим, что для предельного значения скорости v→ 0, суммы в уравнениях (40б) и (40в) исчезают, и производная в уравнении (40) приводится к выражению в уравнении (22) для стационарного прибора.

Производные по вязкостны η_k для k=1,... N_o для перемещающегося прибора задаются выражением

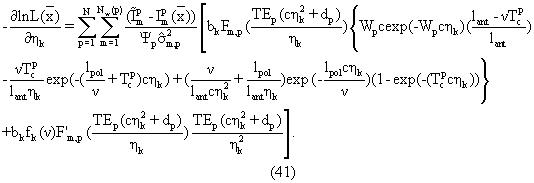
Для предельного значения скорости v→ 0 производные в уравнениях (41) упрощаются до выражения в уравнении (29) для стационарного прибора. Функция f_k(v) в последнем члене представляет собой поляризационную функцию, зависящую от скорости для составляющих вязкостей сырой нефти. Она получается путем замены T₁ на (cη_k)^-i в уравнении (39).

Моделирования методом Монте Карло для перемещающегося прибора

В инверсии релаксационной модели в уравнении (1) была осуществлена поляризационная коррекция, зависящая от скорости. Для проверки инверсии для модельного пласта проводились моделирования методом Монте Карло. Последовательность синтетических данных о спиновых эхо-сигналах генерировалась для модельного прибора с длиной антенны l_ant=45.7 см (18 дюймов), длиной предварительной поляризации магнита l_pol=91.44 см (36 дюймов) и для постоянных скоростей перемещения каротажного прибора, составляющих 365.8 и 548.6 м/час (1200 и 1800 футов/час). Данные генерировались с использованием полной релаксационной модели в уравнении (A.1) приложения А для пласта, содержащего рапу, природную нефть и фильтрат бурового раствора на углеводородной основе (OBMF). Т₂-распределение рапы, используемое для моделирования, показано на фиг.8. При моделировании температура пласта принимается равной 100 градусам Цельсия. Водородный индекс из жидкостей принимается равным 1, и водородный индекс для газа принимается равным 0.5. К каждому эхо сигналу был добавлен случайный шум со среднеквадратичным отклонением, равным 4.0 в отн. ед. Чтобы снизить шум и моделировать глубину накопления каротажных диаграмм по глубине, последовательности эхо сигналов были повторены и усреднены. Число повторений для каждого измерения показано в таблице 7. Два мертвых времени для измерения, которое является неперекрывающимся, были выбраны так, чтобы в течение времени цикла инструмент перемещался на одну длину антенны. Все другие измерения являются перекрывающимися. Фиг.11 изображает серию измерений, используемую для моделирования методом Монте Карло, и фиг.12 изображает сравнение действительных насыщенностей флюидов и вязкости нефти с оценками методом Монте Карло.

Влияние скорости каротажа на времена Т2 релаксации

В дополнение к влиянию перемещения прибора на поляризационные функции (влияние скорости на времена Т1) также имеется очевидная увеличенная скорость поперечной релаксации (влияние скорости на времена Т2), обусловленная перемещением прибора. Влияние скорости на времена Т2 возникает вследствие того, что имеется потеря поперечного намагничивания в течение CPMG, потому что радиочастотная антенна перемещается от интервала пласта, который возбуждался девяностоградусным импульсом. Если влияние скорости на времена Т2 не учитывается, тогда более длинные времена Т2 релаксации, выявленные посредством инверсии, будут подавлены по сравнению с их действительными значениями.

Для учета этого влияния была принята следующая модель. Допустим Δ M_t - изменение поперечного намагничивания напротив радиочастотной антенны во временном интервале Δ t обусловлено перемещением прибора. Тогда

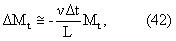
где L - длина антенны и v - скорость каротажа. Вышеупомянутое уравнение является приближением, потому что принимается, что поперечное намагничивание равномерно по антенне. Перестраивая уравнение (42) и переходя к пределу v→ 0, можно определить, что

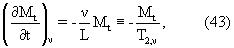
где была определена скорость релаксации, обусловленная перемещением прибора, т.е.

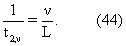
Скорости релаксации являются аддитивными, так что влияние скорости перемещения на времена Т2 легко включить в релаксационную модель. То есть можно просто добавить член, показанный в вышеупомянутом уравнении, ко всем уравнениям для скоростей поперечной релаксации. Влияние скорости на времена Т2 было включено в Т2-релаксационную модель (например, см. уравнение (1)). Главный результат состоит в модификации функций чувствительности, определенных в уравнениях (16)-(18).

Приложение А. Расширение способа для включения газа

Модель в уравнении (1) может быть легко модифицирована, чтобы включить сигнал газа, то есть

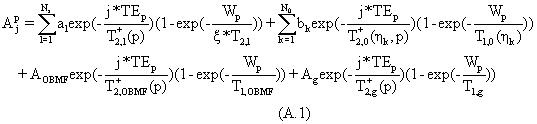
где A_s - амплитуда сигнала газа. Кажущаяся скорость релаксации газа равна

где скорости релаксации газа при нулевом градиенте, T_1,g(P,T)= Т_2,g(Р,Т), и газовый коэффициент диффузии - D_g(P,T) являются функциями температуры и давления пласта и могут быть оценены с учетом опубликованных данных (Kleinberg и другие, 1996, см. выше). Используя способ, разработанный в указанной публикации, можно выполнить инверсию серии данных с многими частотами посредством использования модели уравнения (A.1). Амплитуда сигнала (А_g) газа определяется, исходя из оценки максимального правдоподобия. Пористость пласта, заполненного газом, вычисляется, используя A_g. Водородный индекс HI_q(P,T) можно оценить из опубликованных корреляции. Газ может быть легче детектирован, чем сырая нефть, потому что коэффициент диффузии газа больше приблизительно на порядок, чем таковой для рапы, тогда как коэффициент диффузии сырой нефти в зависимости от вязкости может быть сопоставим с таковым для рапы. Использование полной модели с членом, учитывающим параметры газа, приводит к очевидным модификациям в уравнениях (11)-(14), т.е. пористость (φ_g) пласта, заполненного газом, определяется как

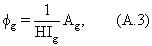
и нефтенасыщенность, и газонасыщенность вычисляются по аналогии с уравнением (14), например,

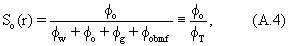
для нефтенасыщенности и

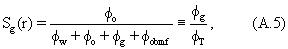
для газонасыщенности.

Два следующих примера демонстрируют применение способа к детектированию газа. Первый пример приведен для газового продуктивного пласта, пробуренного с фильтратом бурового раствора на углеводородной основе. Зашумленные данные спиновых эхо сигналов генерировались, используя шесть измерений таблицы 1 для обоих примеров. Первый пример приведен для пласта, содержащего только рапу и газ, то есть радиус проникновения фильтрата бурового раствора на углеводородной основе (OBMF) меньше, чем глубина исследования (DOI). Время релаксации газа, газовый водородный индекс и коэффициент диффузии газа, используемые для обоих примеров в этом приложении, соответственно равны T_1,g=4,5 сек, HI_g=0.5 и D_g=8.0Е-4 см²/сек. Входные данные и результаты инверсии для первого примера газа показаны в таблице A.1. Заметим, что результаты представляют один образец.

Результаты, приведенные в таблице A.1, показывают, что способ может использоваться для точной оценки газовых продуктивные пластов. Второй пример приведен для продуктивного пласта, содержащего три флюида, то есть рапу, фильтрат OBMF и газ. Входные данные и результаты инверсии показаны в таблице А. 2.

Результаты, приведенные в таблице А.2, показывают, что можно правильно оценивать газовый продуктивный пласт, загрязненный фильтратом OBMF. Поскольку пористость пласта, заполненного фильтратом OBMF, точно вычисляется, то газонасыщенность в неискаженной зоне может быть вычислена, если продуктивный пласт находится на остаточной водонасыщенности (то есть, если фильтрат OBMF замещает только газ).

Приложение Б. Почему сырая нефть имеет распределение коэффициентов диффузии

Это приложение показывает, используя простую модель, основанную на уравнении Ланжевена, почему существует распределение коэффициентов самопроизвольной диффузии в смеси сырой нефти. Показано, что предположение в уравнении (10а) о том, что коэффициенты самопроизвольной диффузии обратно пропорциональны составляющим вязкостям, естественно вытекает из решения уравнения Ланжевена.

Уравнение Ланжевена обычно используется для того, чтобы изучать броуновское движение частицы в гомогенной жидкости. Это - стохастическое классическое уравнение для "одной частицы" в системе многих частиц. Молекулярные взаимодействия со всеми остальными частицами в системе описываются двумя эффектами. Первый эффект - сила трения или вязкости действует как сопротивление движению. Он представляет собой среднее действие других частиц. На очень коротком промежутке времени по сравнению со средним временем столкновения существует также хаотически флуктуирующая сила, производимая посредством быстрых движений других частиц. Уравнение Ланжевена имеет прочный микроскопический базис и может быть выведено из уравнения Гамильтона, учитывающего движение многих частиц (Forster, 1975), которое включает эффекты молекулярных взаимодействий.

Пусть x_k(t) будет х-координата в момент t составляющей k в смеси сырой нефти. Составляющая - любая из углеводородных молекул, которые содержатся в смеси. На молекулярном уровне каждая составляющая, обусловленная различиями в размере, составе, форме и массе, будет иметь различные взаимодействия с другими составными частями. В результате каждая составляющая будет иметь отличающийся коэффициент самопроизвольной диффузии, который зависит от ее локальной окружающей среды. Постоянный коэффициент D_k самопроизвольной диффузии составляющей k может быть определен в терминах среднеквадратичного смещения частицы в момент t (для движения в одном измерении)

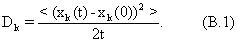
Угловые скобки в вышеупомянутом уравнении обозначают статистическое усреднение по множеству идентично приготовленных систем. Для простоты записи рассматривается одномерное движение. Обобщение результатов на случай трех измерений очевидно. Например, множитель 2 в знаменателе уравнения (Б.1) заменяется на множитель 6 в случае трех измерений, поскольку все направления равноправны, то есть в модели не имеется никакого предпочтительного направления для диффузии. Уравнение Ланжевена для движения может быть написано в виде

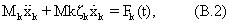
где M_k является массой частицы. Точки используются для обозначения производных по времени. Второй член - сила трения, которая учитывает усредненный эффект межмолекулярных взаимодействий на диффундирующую частицу. Для удобства в последующих вычислениях масса частицы была включена в силу трения. Заметим, что параметр ξ_k трения имеет размерность обратного времени. Функция F_k(t) представляет случайную силу с нулевым средним значением с автокорреляционной функцией, задаваемой выражением

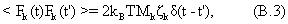
где k_B - постоянная Больцмана, Т - температура в градусах Кельвина и δ (t-t’) - дельта-функция. Константа, умножающая функцию Дирака, не является произвольной. Она выбирается так, чтобы гарантировать, что решение уравнения Ланжевена имеет корректные равновесные статистико-механические свойства, например теорема о равнораспределении требует, чтобы

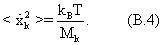
Уравнение (Б.3) иногда упоминается как флуктуационно-диссипационная теорема в области неравновесной статистической механики. Общее решение уравнения (Б.2) Ланжевена с начальными условиями X_k(0)=0 и

получается посредством двойного интегрирования

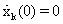
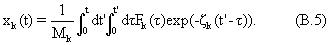
Двойной интеграл в (Б.5) может быть сокращен до обычного интеграла посредством выполнения интегрирования внешнего интеграла по частям. Тем самым находим, что

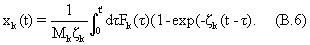
Действительно, дифференцирование уравнения (Б.6) показывает, что оно удовлетворяет и уравнению (Б.2), и начальным условиям. Среднеквадратичное смещение частицы рассчитывается посредством возведения в квадрат уравнения (Б.6) и выполнения статистических усреднений, т.е.

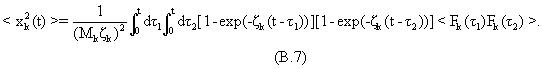
Интегралы в (Б.7) легко выполнить, возвращаясь к уравнению (Б.3) и используя свойства дельта-функции Дирака. Тем самым находим, что

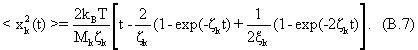
В пределе длительного времени, то есть для ζ_kt>>1 среднеквадратичное смещение в (Б.8) упрощается до равновесного решения, даваемого выражением

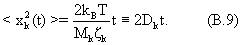
Следовательно, коэффициент самопроизвольной диффузии для k-ой составляющей в смеси задается

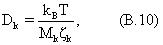
которое называется соотношением Эйнштейна. В сырой нефти имеется распределение коэффициентов диффузии из-за различных типов молекул в смеси. Измерение с помощью градиента импульсного поля для распределения коэффициентов диффузии в сырой нефти вероятно дало бы широкое распределение с немногими, если таковые есть, разнесенными пиками. Стокс показал, что для сферической частицы радиусом а, диффундирующей в гомогенной жидкости с вязкостью η , Мζ =6π аη . При объединении соотношения Стокса с соотношением Эйнштейна получается известный коэффициент диффузии Стокса-Эйнштейна

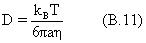
(Уравнение Эйнштейна - Стокса). (Б.11)

По аналогии с соотношением Стокса резонно принять, что для каждой составляющей в смеси сырой нефти M_kζ_k=Сη_k, где η_k - составляющие вязкости, введенные в уравнения (5) и (10а) и где С - коэффициент пропорциональности, который зависит от некоторого параметра среднего размера. То есть составляющие вязкости пропорциональны параметрам трения. При использовании (В.10) это непосредственно приводит к уравнению, которое имеет тот же самый функциональный вид, что и уравнение (10а).

Приложение В. Альтернативные параметры релаксационной модели

Для специфических применений возможны и могли бы быть желательными другие параметры релаксационной модели в уравнении (1). Например, времена поперечной релаксации (в нулевом градиенте поля) и коэффициенты диффузии в релаксационной модели сырой нефти в уравнении (1) могут по аналогии с членом релаксации рапы быть распределением логарифмически разнесенных времен релаксации (конечно, также возможны другие разнесения). То есть вводится набор времен релаксации сырой нефти

где

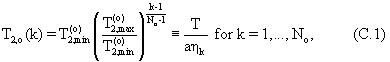
и - минимальные и максимальные значения соответственно распределения времен релаксации сырой нефти. В этом представлении параметры η_k задаются временами релаксации. Времена продольной релаксации сырой нефти могут быть таким же набором логарифмически разнесенных времен релаксации, т.е.

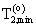
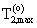
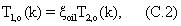
где ξ_oil ≥ 1 - параметр, который учитывает компоненты сырой нефти, которые имеют неравные времена поперечной и продольной релаксации. Для компонентов сырой нефти, характеристики которых были измерены, ξ_оil ≅ 1. Коэффициенты диффузии в уравнении (3) могут быть также представлены в терминах логарифмически разнесенных времен релаксации, поскольку объединяя уравнения (5) и (10а) и вышестоящие уравнения можно найти

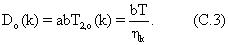
Вышеупомянутые представления снижают число неизвестных в члене релаксации сырой нефти в уравнении (1) с 2N₀ до N₀. Более того, задача является более линейной, поскольку неизвестные представляют собой набор амплитуд {b_k}. Сразу после определения амплитуд {b_k} посредством аппроксимации данных макроскопическая вязкость определяется из уравнения (8).

Введение составляющих вязкостей частично зависит от справедливости материальных соотношений в уравнениях (5) и (10). Подход к инверсии уравнения (1), который не зависит от материальных соотношений, состоит в том, чтобы рассматривать N₀ времен (T_2,0(η_k)) релаксации сырой нефти и N₀ диффузионных способностей (T_{2, 0}(η_k)) в качестве независимых параметров модели. Обратная сторона этого подхода двояка: (1) он увеличивает число неизвестных на N₀, и (2) параметры T_2,0 (η_k) и D_2,0(η_k) сами по себе без связи с вязкостью обеспечивают менее полезную информацию об оценке продуктивного пласта.

Приложение Г. Нелинейный ограниченный алгоритм минимизации Powell

Приложение Г представляет общий краткий обзор того, как алгоритм и подпрограмма, разработанные M.J.D. Powell, могут быть использованы для минимизации функции в уравнении (15). Функция, подлежащая минимизации, называется целевой функцией. Минимизация целевой функции попадает в общий класс, известный как линейно ограниченные задачи нелинейной оптимизации. В этом классе задач целевая функция нелинейно зависит от всех или некоторых переменных, и переменные подчинены линейному равенству и/или ограничениям неравенства. Последнее включает простые границы переменных, например верхние и нижние пределы, которые налагаются физической природой задачи. Минимизация уравнения (15) попадает в этот класс и задачу можно поставить следующим образом:

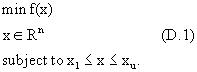
Верхние и нижние граничные значения представляет граничные значения параметров модели в релаксационных моделях в уравнениях (1) и (A.1), например составляющих вязкостей, флюидов и кажущегося отношения T₁/T₂ для рапы. Способ минимизации является итеративным и алгоритм, применяемый к сериям данных, которые использовались в примерах настоящего описания и обсуждались в этом приложении и в связи с фиг.7, был разработан M.J.D, Powell (1989 г.) (называемый здесь как алгоритм Powell) и является частью коммерчески доступной библиотеки IMSL подпрограмм, лицензированной корпорацией Visual Numerics Corp. (Хьюстон, штат Техас). Исполнение алгоритма Powell, используемого для описанных здесь вычислений, представляет собой версию двойной точности подпрограммы IMSL, называемой DLCONG, и использовалось для выполнения показанных здесь моделирований. Другие отличающиеся алгоритмы нелинейной оптимизации (см., например, Schittkowski, К., NLPQL "A Fortran Subroutine Solving Constrained Nonlinear Programming Problems", опуб. в Annals of Operations Research, том 5, стр. 485-500, 1985) могут также использоваться для осуществления минимизации нелинейной целевой функции.

Первый шаг должен установить верхние и нижние граничные и начальные значения (обозначенные в этом приложении векторами Х_u, X₁, X⁰) для всех переменных параметров в целевой функции. Алгоритм, как считают, является глобально сходящимся таким образом, что допустимое (то есть то, которое удовлетворяет предельным значениям) решение могло быть найдено независимо от стартового значения. Следует отметить, что если нелинейная целевая функция не является строго выпуклой, например имеет несколько локальных минимумов в допустимой области, то различные начальные значения для параметров могут приводить к решениям, которые не являются глобальным минимумом. В таких случаях одна из процедур для обнаружения глобального минимума состоит в том, чтобы применять сетку начальных значений, а затем выбирать глобальный минимум из семейства решений, то есть это - решение, которое соответствует наименьшему значению целевой функции.

В алгоритме Powell при каждой итерации целевая функция аппроксимируется квадратичной функцией, и направление поиска для следующей итерации находится путем решения задачи квадратического программирования (QP). Например, пусть х^k является k-ой итерацией и рассмотрим задачу квадратического программирования (QP)

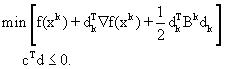
Вектор с выбирается так, чтобы он был вектором из единиц (е), которые должны удовлетворить верхнему граничному предельному значению x_i ≤ x_u, и (-е), которые должны удовлетворить нижнему граничному предельному значению - x_i ≤ x₁. Задача квадратического программирования (QP) решается с помощью теоремы ККТ (Karush-Kuhn-Tucker) (см., например, Peressini, A.L., Sullivan R.E. and Uhl "The Mathematics Of Nonlinear Programming", Springer Verlag Publishing Company, New York, Chapter 5, 1988) для определения вектора d_k направления поиска и вектора множителей Лагранжа λ_k ≤ 0 для активных предельных значений (например, для переменных на предельных границах). Матрица B^k является положительно определенным приближением к матрице вторых производных целевой функции на k-ой итерации. После того как найдено направление d_k поиска, выполняется поиск линии для определения размера α_k шага для следующей итерации. Новая точка x^k+l=х^k+α^kd^k требуется для того, чтобы удовлетворить следующим условиям

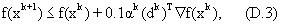
и

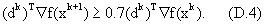
Матрица В^k вторых производных обновляется способом базисного возможного решения (BFGS) (см., например, Peressini, Sullivan and Uhl, 1988, см. выше). Итерации продолжаются до тех пор, пока двойная норма ККТ остаточного вектора не станет меньше, чем параметр сходимости, заданной пользователем, т.е.

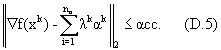
где а^k - единичные вектора в пространстве параметров для активных предельных значений на k-ой итерации и асc - параметр точности, заданный пользователем. Если последовательные итерации будут не в состоянии уменьшать целевую функцию, может также происходить завершение алгоритма.

Приложение Д. Влияние внутреннего градиента скальных пород на инверсию

В предшествующем описании предполагалось, что градиенты магнитного поля обусловлены исключительно пространственными вариациями приложенного магнитного поля. Известно, что в пористых скальных породах, содержащих флюиды, разности магнитной восприимчивости флюидов, заполняющих поры, и материнской скальной породы могут вызывать внутренние градиенты в скальной породе (Hurlimann, Martin D., Effective Gradients In Porous Media Due To Susceptibility Differences, Journal of Magnetic Resonance, 131, стр. 232-240, 1998). Внутренние градиенты вызываются приложенным магнитным полем и будут существовать, даже если приложенное магнитное поле будет совершенно однородным. Локальный внутренний градиент G_int(r) в положении r пропорционален напряженности В₀(r) приложенного магнитного поля, т.е.

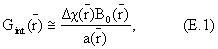
где: Δ χ - локальная разность восприимчивостей между магнитной восприимчивостью флюидов, заполняющих поры, и гранул скальной породы, и а(r) - средний локальный размер пор. Распределения внутреннего градиента внутри скальных пород неизвестно. Однако теоретические аргументы дают основание предполагать, что градиенты локализованы близко к поверхностям пор и самые сильные градиенты локализованы в меньших порах. Возможно, что влияние внутренних градиентов на определение насыщенности нефти и вязкости нефти будет небольшим, если вообще будет.

Тем не менее, полезно включать оценки таких эффектов, которые могут возникнуть при некоторых полевых условиях. В приложении показано, что эффективный внутренний градиент может быть оценен в каждом слое измерения их серий ЯМР данных и что его влияние может быть включено в инверсию. Идея способа состоит в том, что влияние внутреннего градиента может быть включено в T₂-релаксационную модель для многих флюидов (например, уравнение 1) путем замены приложенного приборного градиента эффективным полным градиентом. Допустим, что эффективный полный градиент задается как сумма приложенного приборного градиента и внутреннего градиента скальной породы, т.е.

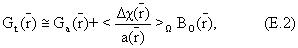
где угловые скобки обозначают объемное среднее по макроскопическому объему измерения (Ω ), например, объем набора близко расположенных слоев измерения, соответствующих серии данных. Величина в скобках имеет размерность обратной длины, которая обозначена параметром λ так, что верхнее уравнение можно записать

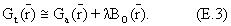
Средний внутренний градиент определяется путем оценки неизвестного параметра X из ЯМР данных, то есть

Чтобы оценить λ из серии ЯМР данных, заменим приборные градиенты (G_р) в T₂-релаксационной модели для многих флюидов (например, см. уравнения 1-3) на полный градиент

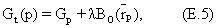
для р=1, N, где N - число измерений в серии ЯМР измерений, G_p и В₀(

_p) - полный градиент и приложенное магнитное поле для измерения р. Логарифм модифицированной функции максимального правдоподобия, аналогичный уравнению 15, может быть построен из Т₂-релаксационной модели для многих флюидов, содержащей полный градиент. Параметр λ внутреннего градиента становится дополнительным параметром в модели, которая должна быть определена посредством инверсии. Чтобы облегчить инверсию, были вычислены аналитические производные логарифма модифицированной функции правдоподобия по параметру λ . Главная идея состоит в том, что многочастотные ЯМР данные содержат информацию о внутренних градиентах, и поэтому сами данные могут использоваться для самостоятельной последовательной оценки градиентов. Более того, этот подход учитывает влияние градиентов на результаты инверсии. Хотя в этом приложении обсуждалась специфическая модель (уравнения Д.1-Д.5) для представления полного градиента, понятно, что любая другая физическая модель последнего может быть использована в Т₂-релаксационной модели для многих флюидов.

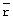
Приложение Е. Определение распределений насыщенностей флюидов в частично насыщенных лабораторных кернах

В лабораторных исследованиях физических свойств пористых скальных пород часто желательно насыщать скальные породы нефтью (или другими флюидами) и водой, чтобы моделировать природные условия в нефтяных продуктивных пластах. При определении физических свойств частично насыщенных образцов скальных пород ключевое значение имеет точное определение насыщенности нефтью. Обычно нефть должна вдавливаться в образец посредством центрифуги, начиная с состояния первоначального насыщения рапой. Задача определения точной конечной насыщенности нефтью хорошо известна. Имеются способы, используемые на практике, такие как "дифференциальные весовые измерения" (DWM), которые обычно используются для оценки насыщенности.

Насыщенность нефтью оценивается методом ″ дифференциальных весовых измерений″ (DWM), используя уравнение

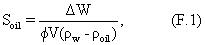
где Δ W - разность весов полностью насыщенного рапой образца и частично насыщенного образца; φ - пористость образца; V - объем образца; ρ_w - плотность рапы и ρ_oil - плотность нефти.

Метод дифференциальных весовых измерений (DWM) имеет ограничения и недостатки. Во-первых, он обеспечивает среднюю насыщенность для всего образца. На практике насыщенность будет варьироваться по всему образцу из-за неоднородности скальной породы и разности давления центрифуги в образце. Для оценки насыщенности флюидов могут использоваться другие методы, такие как развертка удельного сопротивления образца в сочетании с уравнением Арчи. Этот метод имеет ограниченную точность из-за приблизительного характера уравнения Арчи и его зависимости от экспонент насыщенности и факторов пласта, которые часто точно неизвестны.

Наземное применение настоящего метода обеспечивает ЯМР способ, который может использоваться для определения локальных насыщенностей флюидов в относительно тонких пластинках образца, предпочтительнее, чем средних насыщенностей (например, согласно резюмированному выше методу DWM). Он обеспечивает "представление насыщенности" по длине образца. Настоящий метод даже не требует знания пористости образца (то есть насыщенности, вычисленные методом ЯМР, определяются из отношений). Из-за того, что способ обеспечивает прямое измерение насыщенности, он не имеет проблем развертки удельного сопротивления, которые требуют использования приближенного вспомогательного уравнения.

Реферат

Изобретение касается способа определения свойств земных пластов, окружающих ствол скважины. Размещают каротажный прибор с возможностью перемещения по стволу скважины, передают энергию электромагнитного поля от каротажного прибора в пласты и принимают спиновые эхо-сигналы ядерно-магнитного резонанса в каротажном приборе много раз с соответствующим множеством различных условий передачи и приема для получения множества измерений. Создают модель пласта, которая включает в первом варианте множество модельных составляющих для рапной фазы и множество модельных составляющих для фазы природной нефти, а во втором варианте - множество модельных составляющих для рапной фазы и также включает множество времен релаксации природной нефти для фазы природной нефти. Модифицируют модельные составляющие для оптимизации модели относительно сигналов измерения, и выводят модельные составляющие для оптимизированной модели. При модификации модельных составляющих могут осуществлять итеративную модификацию. Модель пласта может дополнительно включать составляющую фильтрата бурового раствора на углеводородной основе и составляющую газа. Из выведенных составляющих могут получать характеристики пласта, в том числе пористость, нефтенасыщенность, водонасыщенность, вязкость, и коэффициент диффузии. Измерения могут осуществляться при перемещении каротажного прибора по стволу скважины с определенной скоростью. Изобретения направлены на повышение точности и снижение трудоемкости измерения. 2 c. и 40 з.п.ф-лы, 19 ил., 13 табл.

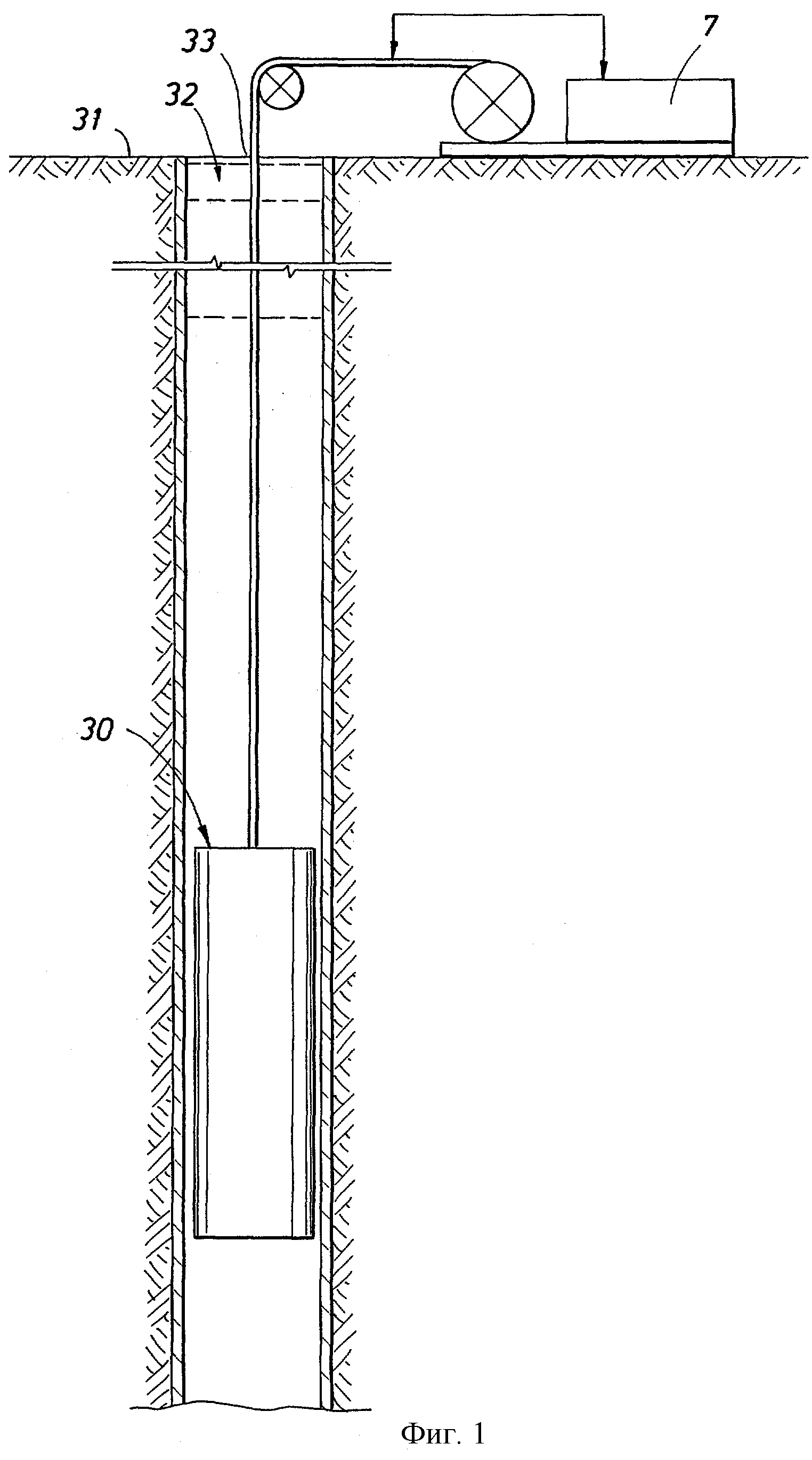
Формула