Моделирование взаимодействия трещин гидравлического разрыва в системах сложных трещин - RU2575947C2

Чертежи

Показать все 31 чертежа(ей)

Описание

В общем, настоящее раскрытие относится к способам и системам для выполнения работ на месте расположения скважины. Более конкретно, это раскрытие относится к способам и системам для выполнения работ по гидравлическому разрыву пласта, таких как исследование подземных пластов и определение характеристик систем трещин гидравлического разрыва в подземном пласте.

Для содействия добыче углеводородов из нефтегазовых скважин можно выполнять гидравлический разрыв подземных пластов, окружающих такие скважины. Гидравлический разрыв можно использовать для создания трещин в подземных пластах, чтобы обеспечивать возможность перемещения нефти или газа к скважине. Пласт разрывают путем введения специально разработанной жидкости (называемой в этой заявке «жидкостью для гидравлического разрыва» или «суспензией для гидравлического разрыва») под высоким давлением и при больших скоростях потока в пласт через одну или несколько буровых скважин. Трещины гидравлического разрыва могут распространяться от буровой скважины на расстояния сотен футов в двух различных направлениях в соответствии с естественными напряжениями в пласте. При определенных условиях они могут образовывать систему сложных трещин. Системы сложных трещин могут включать в себя искусственно образованные трещины гидравлического разрыва и естественные трещины, которые могут пересекаться или могут не пересекаться вдоль многочисленных азимутов, в многочисленных плоскостях и направлениях и в многочисленных областях.

Современными способами и системами мониторинга трещин гидравлического разрыва можно картировать места, где трещины возникают, и распространение трещин. В некоторых способах и системах микросейсмического мониторинга положения сейсмических событий могут обрабатываться путем преобразования времен вступления сейсмических волн и информации о поляризации в трехмерное пространство при использовании моделируемых времен пробега и/или траекторий лучей. Эти способы и системы можно использовать для прогнозирования развития трещин гидравлического разрыва с течением времени.

Картины трещин гидравлического разрыва, создаваемых при воздействии на пласт для образования трещин, могут быть сложными и могут составлять систему трещин, отображаемую распределением связанных микросейсмических событий. Для представления создаваемых трещин гидравлического разрыва разработаны модели систем сложных трещин гидравлического разрыва. Примеры моделей трещин представлены в патентах США №№6101447, 7363162, 7788074 и в заявках №№2008/0133186, 2010/0138196 и 2010/0250215 на патенты США.

КРАТКОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

По меньшей мере один аспект настоящего открытия относится к способам выполнения операции гидравлического разрыва на месте расположения скважины. Место расположения скважины находится в подземном пласте, имеющем тем самым буровую скважину и систему трещин. Система трещин имеет естественные трещины. Место расположения скважины можно возбуждать нагнетанием закачиваемой жидкости вместе с проппантом в систему трещин. Способ включает в себя получение данных о месте расположения скважины, содержащих параметры естественных трещин, и получение механической модели геологической среды для подземного пласта, и образование картины роста трещин гидравлического разрыва для системы трещин с течением времени. Образование включает в себя распространение трещин гидравлического разрыва от буровой скважины и в систему трещин подземного пласта для формирования системы трещин гидравлического разрыва, включающих в себя естественные трещины и трещины гидравлического разрыва, определение параметров трещин гидравлического разрыва после распространения, определение параметров переноса для проппанта, проходящего через систему трещин гидравлического разрыва, и определение размеров трещин гидравлического разрыва на основании определенных параметров трещин гидравлического разрыва, определенных параметров переноса и механической модели геологической среды. Кроме того, способ включает в себя осуществление затенения напряжения относительно трещин гидравлического разрыва для определения взаимного влияния напряжений между трещинами гидравлического разрыва и повторение образования на основании определенного взаимного влияния напряжений.

Если трещины гидравлического разрыва встречаются с естественной трещиной, способ может также включать в себя определение характера пересечения между трещинами гидравлического разрыва и встреченной трещиной на основании определенного взаимного влияния трещин, а повторение может включать в себя повторение образования на основании определенного взаимного влияния напряжений и характера пересечения. Кроме того, способ может включать в себя возбуждение места расположения скважины путем нагнетания закачиваемой жидкости вместе с проппантом в систему трещин.

Кроме того, способ может включать в себя, если трещина гидравлического пласта встречается с естественной трещиной, определение характера пересечения со встреченной естественной трещиной, и в способе повторение содержит повторение образования на основании определенного взаимного влияния напряжений и характера пересечения. Картина роста трещин может изменяться или не изменяться под влиянием характера пересечения. Давление гидравлического разрыва системы трещин гидравлического разрыва может быть больше, чем напряжение, действующее на встреченную трещину, и картина роста трещин может распространяться вдоль встреченной трещины. Картина роста трещин может продолжать распространяться вдоль встреченной трещины до тех пор, пока не достигает конца естественной трещины. Картина роста трещин может изменять направление на конце естественной трещины и картина роста трещин может продолжаться в направлении, перпендикулярном к минимальному напряжению на конце естественной трещины. Картина роста трещин может распространяться перпендикулярно к локальному главному напряжению в соответствии с затенением напряжения.

Затенение напряжения может включать в себя выполнение разрыва смещений для каждой из трещин гидравлического разрыва. Затенение напряжения может включать в себя осуществление затенений напряжений вокруг многочисленных буровых скважин на месте расположения скважин и повторение образования с использованием затенений напряжений, выполняемых относительно многочисленных буровых скважин. Затенение напряжения может включать в себя осуществление затенения напряжения на многочисленных этапах возбуждения в буровой скважине.

Кроме того, способ может включать в себя проверку достоверности картины роста трещин. Проверка достоверности может включать в себя сравнение картины роста трещин с по меньшей мере одним моделированием из моделирований системы трещин.

Распространение может включать в себя распространение трещин гидравлического разрыва на всем протяжении картины роста трещин на основании параметров естественных трещин и минимального напряжения и максимального напряжения, действующих на подземный пласт. Определение размеров трещин может включать в себя одно из оценивания сейсмических измерений, прослеживания движения муравьев, акустических измерений, геологических измерений и сочетаний их. Данные о месте расположения скважины могут включать в себя по меньшей мере одни из геологических, петрофизических, геомеханических данных, данных каротажных измерений, заканчивания скважины, исторических данных и сочетаний их. Параметры естественных трещин можно образовать одним из наблюдения скважинных каротажных изображений, оценивания размеров трещин на основании скважинных измерений, получения микросейсмических изображений и сочетаний их.

КРАТКОЕ ОПИСАНИЕ ЧЕРТЕЖЕЙ

Варианты осуществления системы и способа для определения характеристик скважинных напряжений будет описаны с обращением к сопровождающим чертежам. Для обозначения аналогичных признаков и компонентов на всех чертежах используются одни и те же позиции. На чертежах:

фиг. 1.1 - схематичная иллюстрация места гидравлического разрыва пласта с показом операции разрыва;

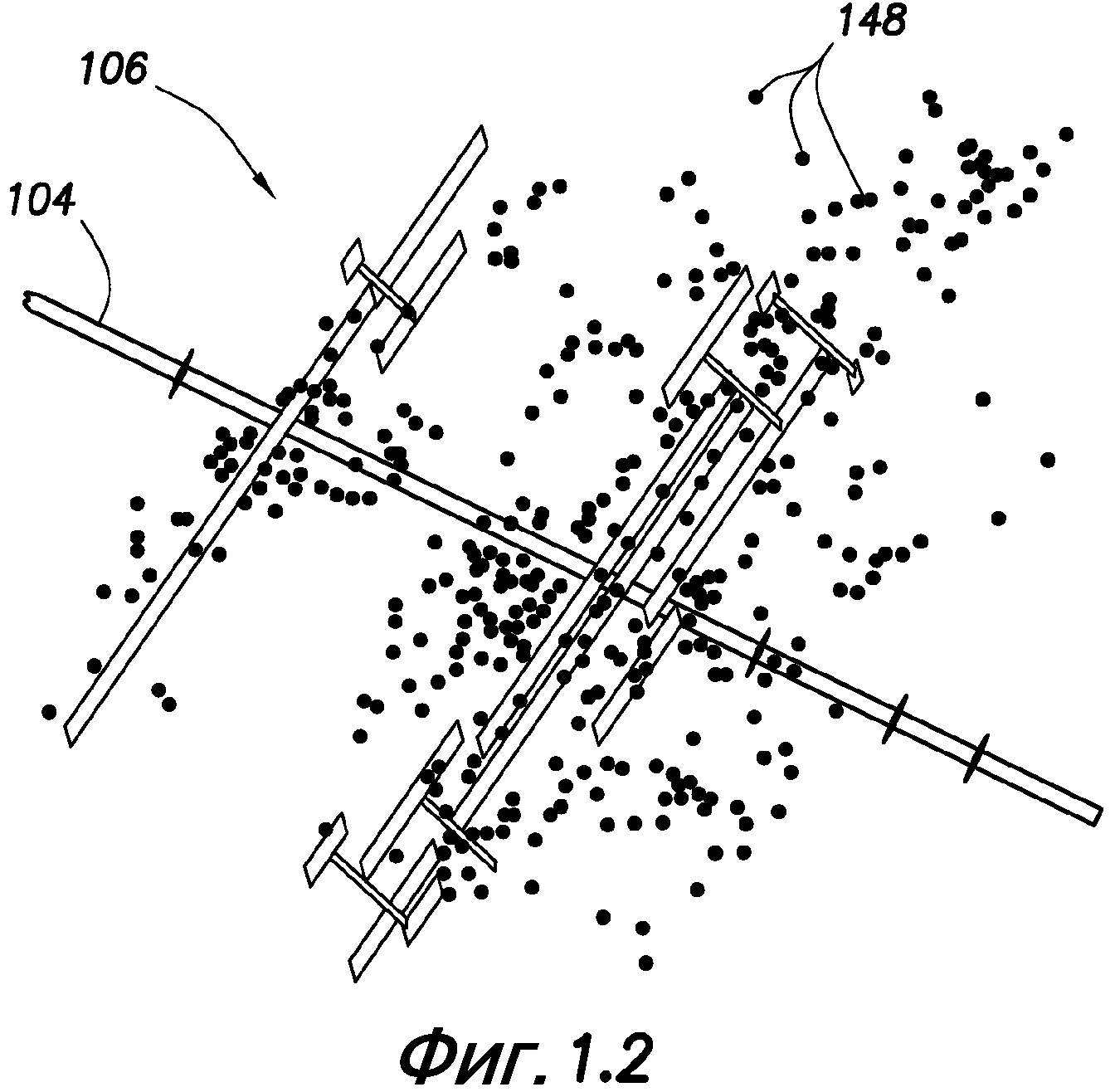
фиг. 1.2 - схематичная иллюстрация места гидравлического разрыва пласта с показом микросейсмических событий;

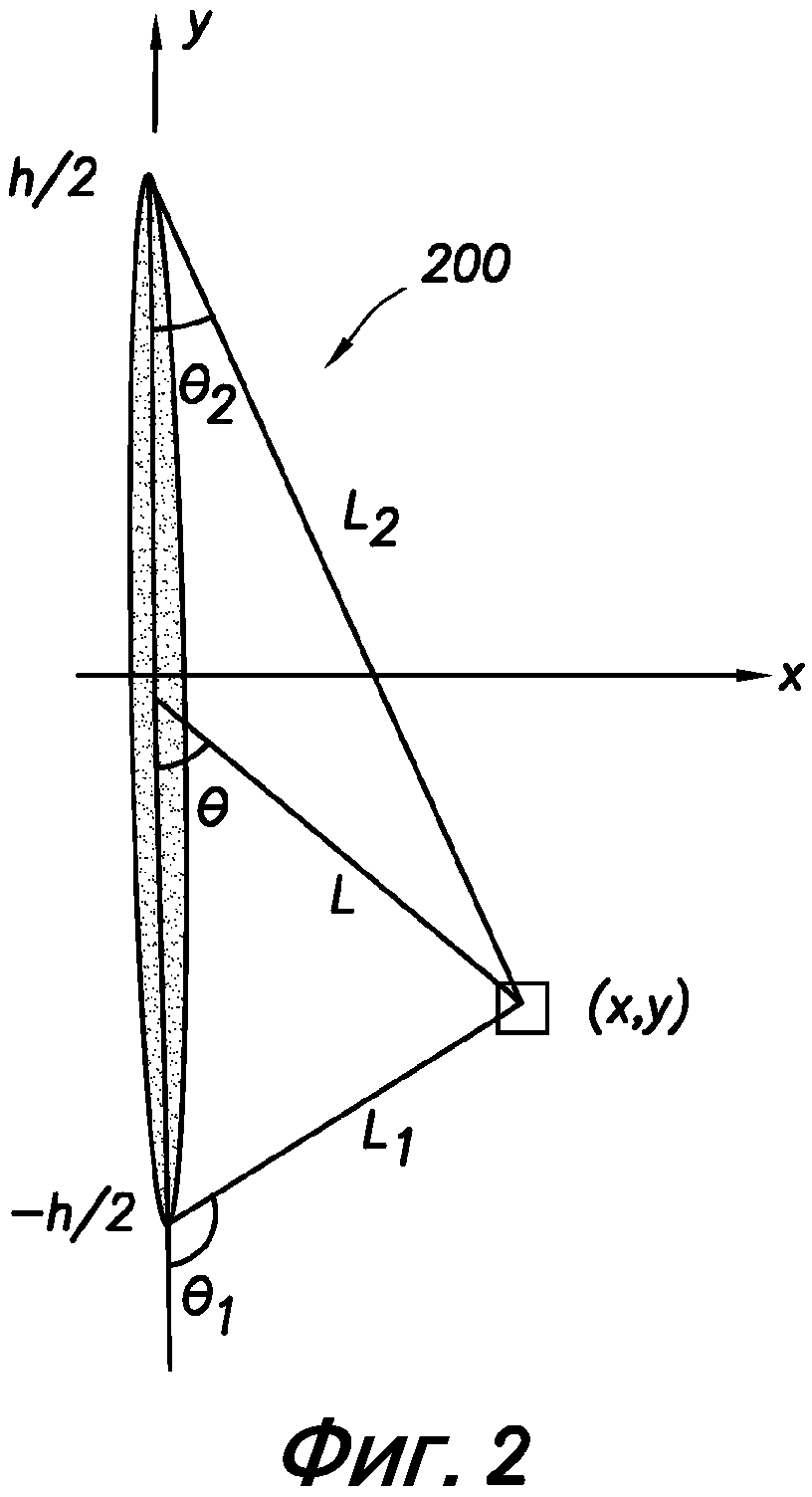
фиг. 2 - схематичный вид двумерной трещины;

фиг. 3.1 - схематичная иллюстрация эффекта тени напряжения;

фиг. 3.2 - схематичная иллюстрация разрывов Ds и Dn;

фиг. 4 - схематичный вид двух параллельных прямолинейных трещин для сравнения двумерного метода разрывных смещений и трехмерного быстрого анализа Лагранжа непрерывных сред;

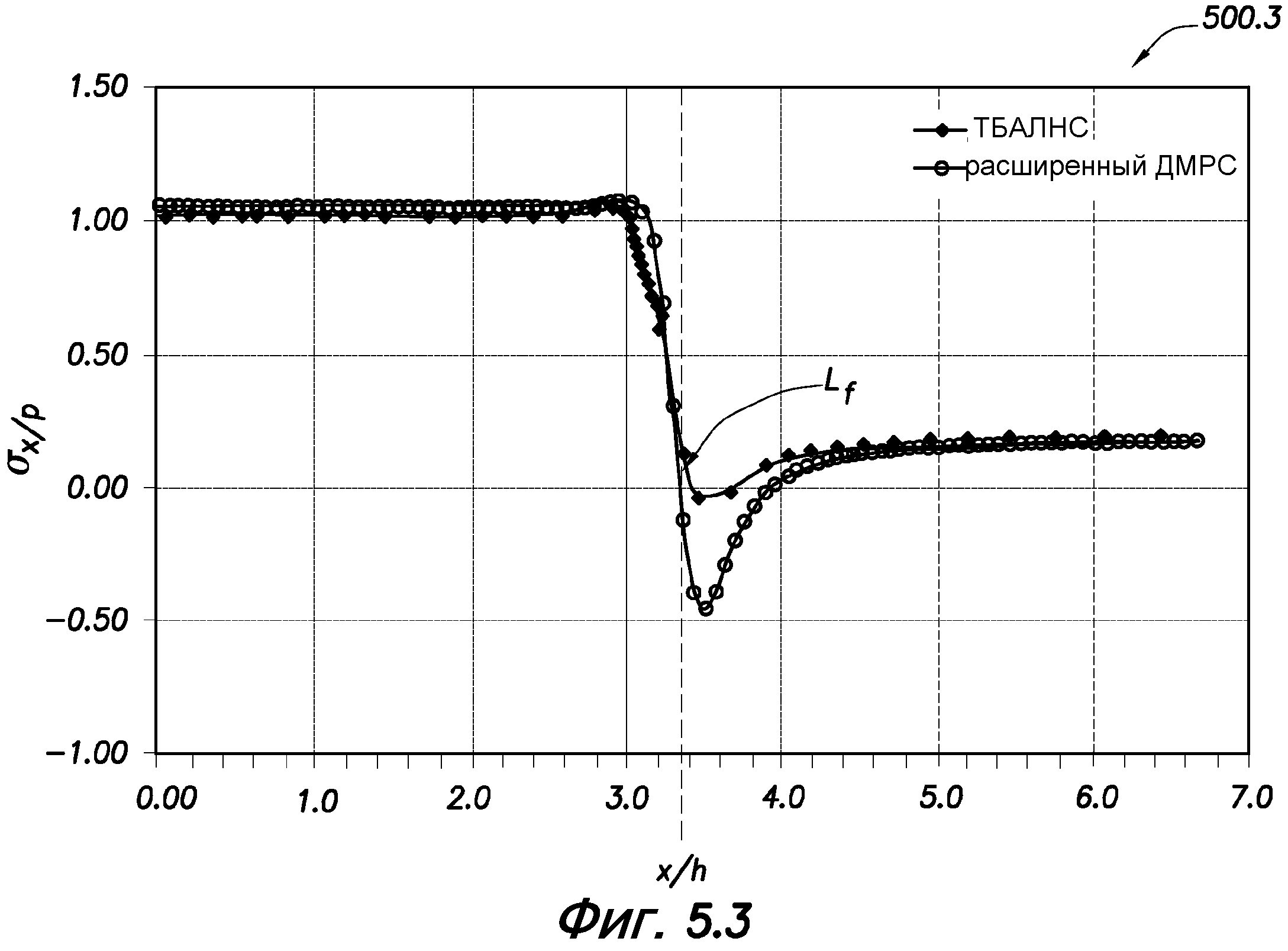
фиг. 5.1-5.3 - графики, иллюстрирующие напряжения на различных местах для продолженных трещин, полученные двумерным методом разрывных смещений и трехмерным быстрым анализом Лагранжа непрерывных сред;

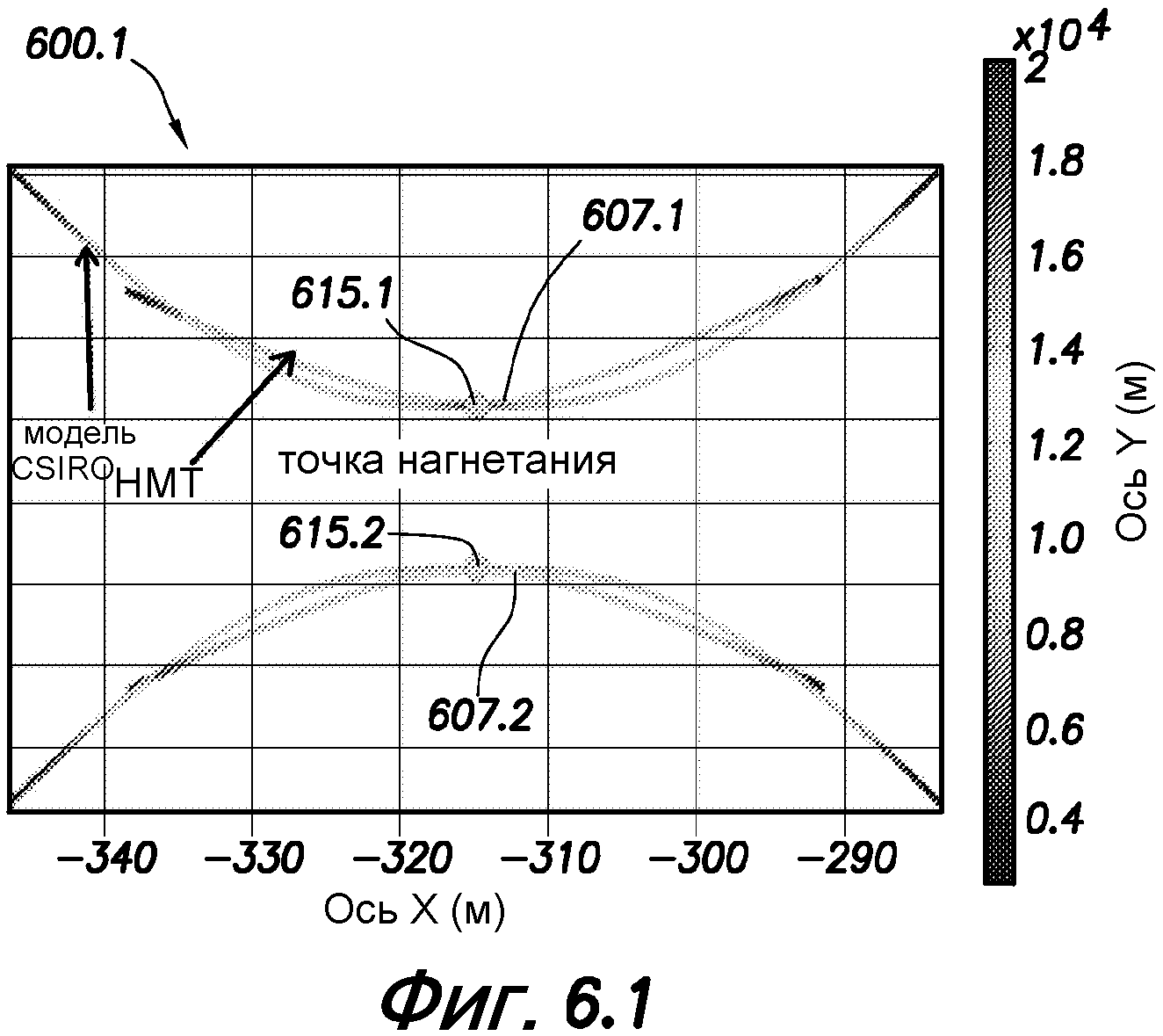
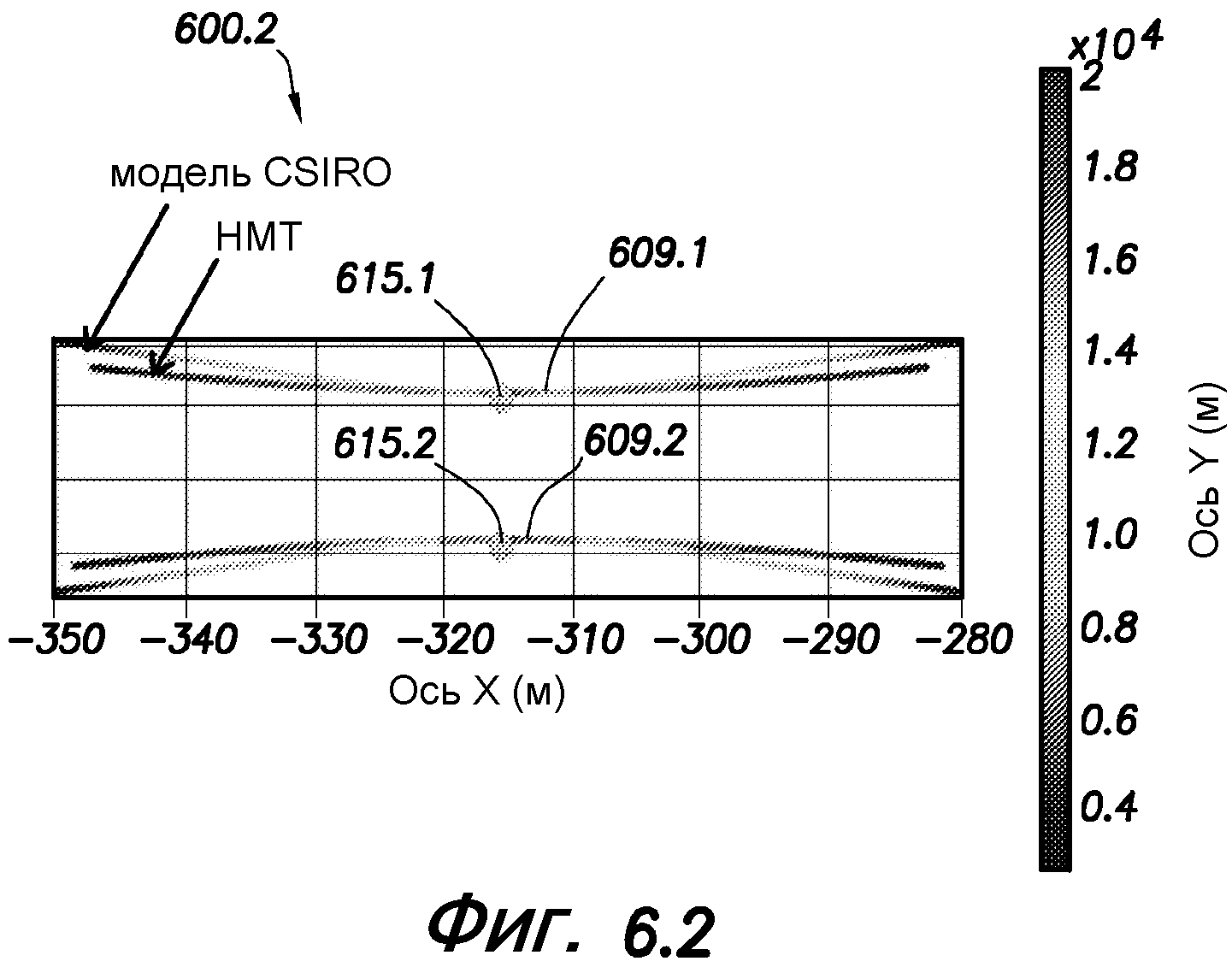
фиг. 6.1, 6.2 - графики, показывающие траектории развития двух первоначально параллельных трещин в изотропном и анизотропном поле напряжений, соответственно;

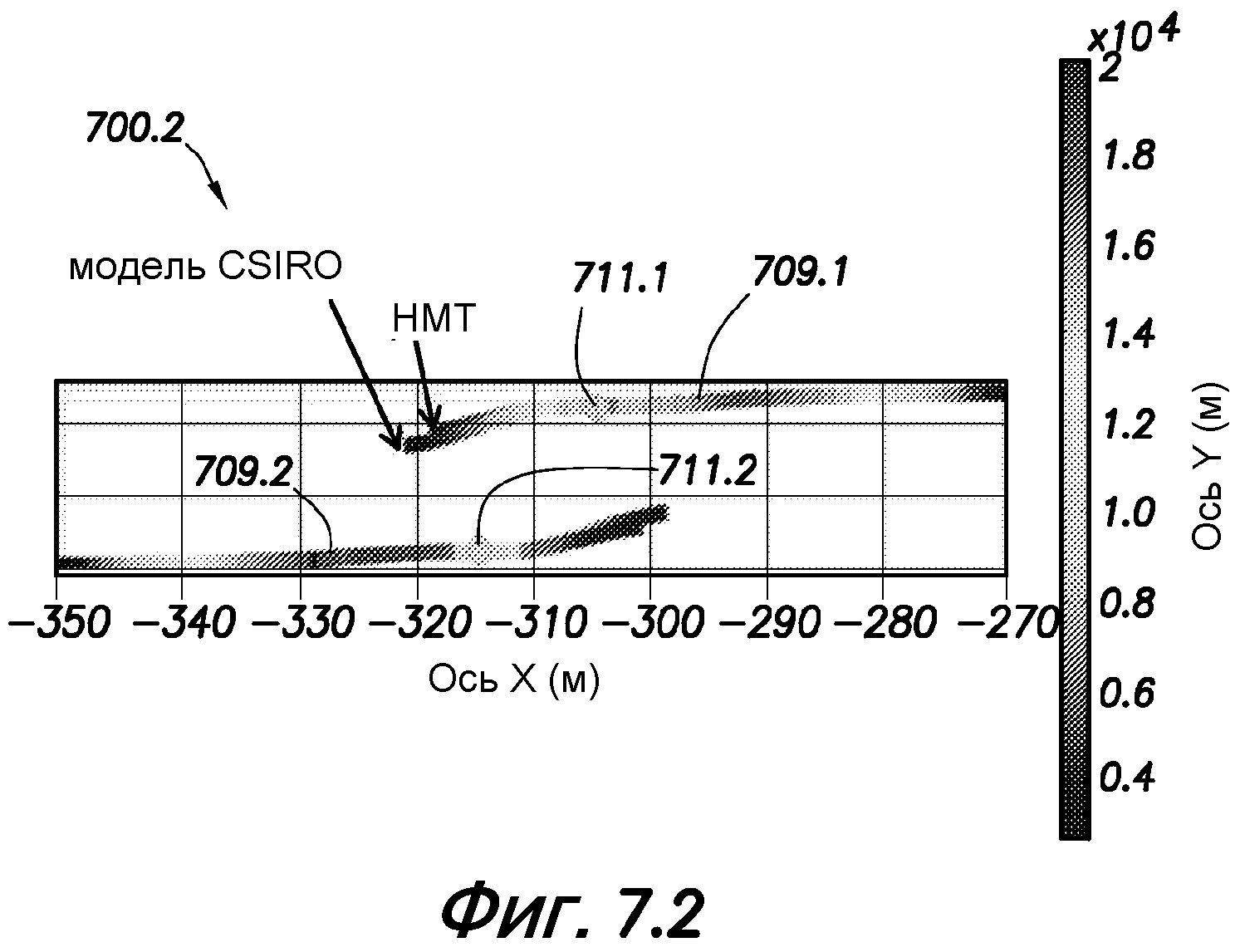
фиг. 7.1, 7.2 - графики, показывающие траектории развития двух первоначально разнесенных трещин в изотропном и анизотропном поле напряжений, соответственно;

фиг. 8 - схематичный вид поперечных параллельных трещин вдоль горизонтальной скважины;

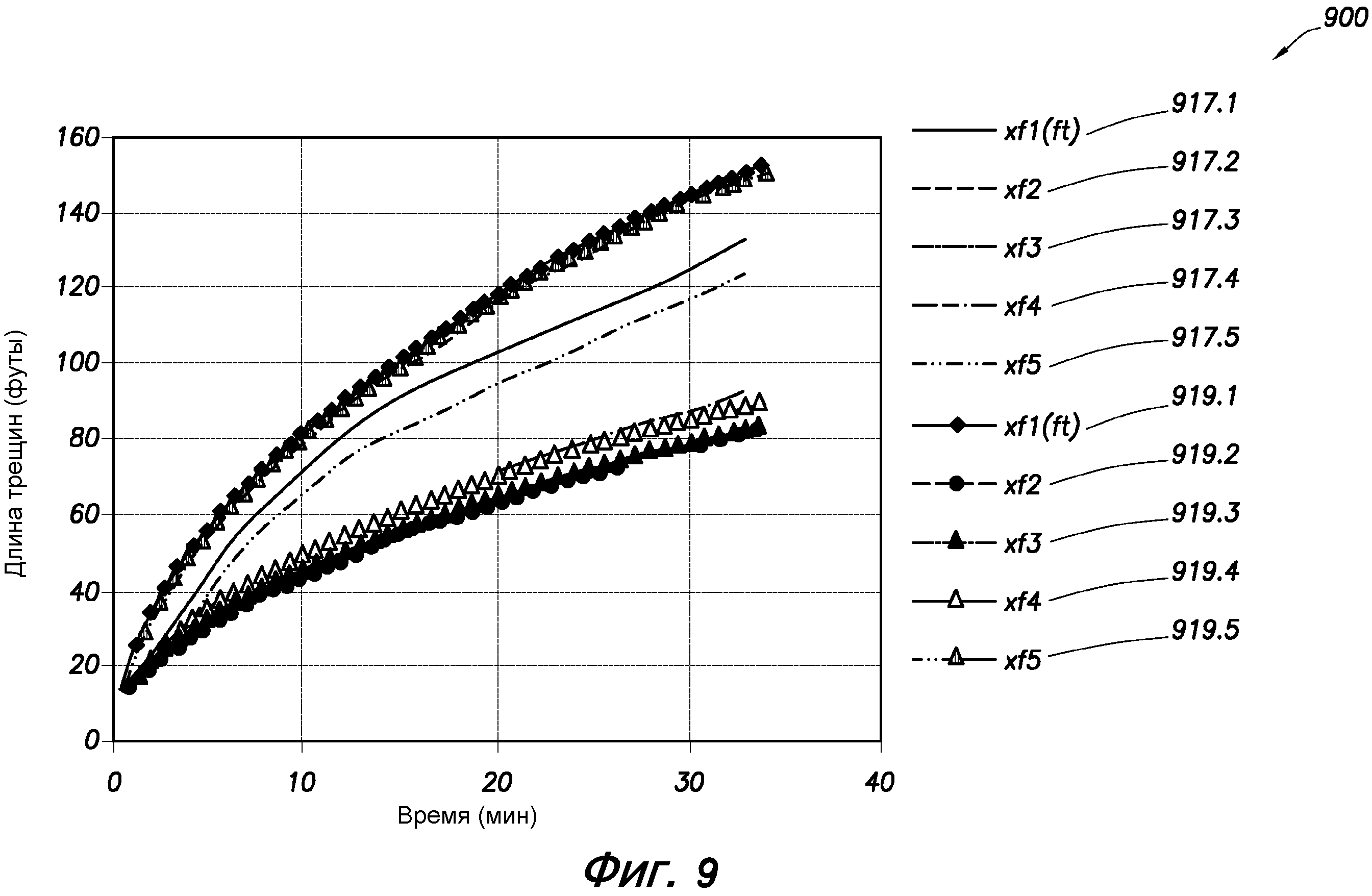
фиг. 9 - график, показывающий длину пяти параллельных трещин;

фиг. 10 - схематичный вид параллельных трещин из фиг. 9 с показом геометрии и ширины трещин в соответствии с нетрадиционной моделью трещин;

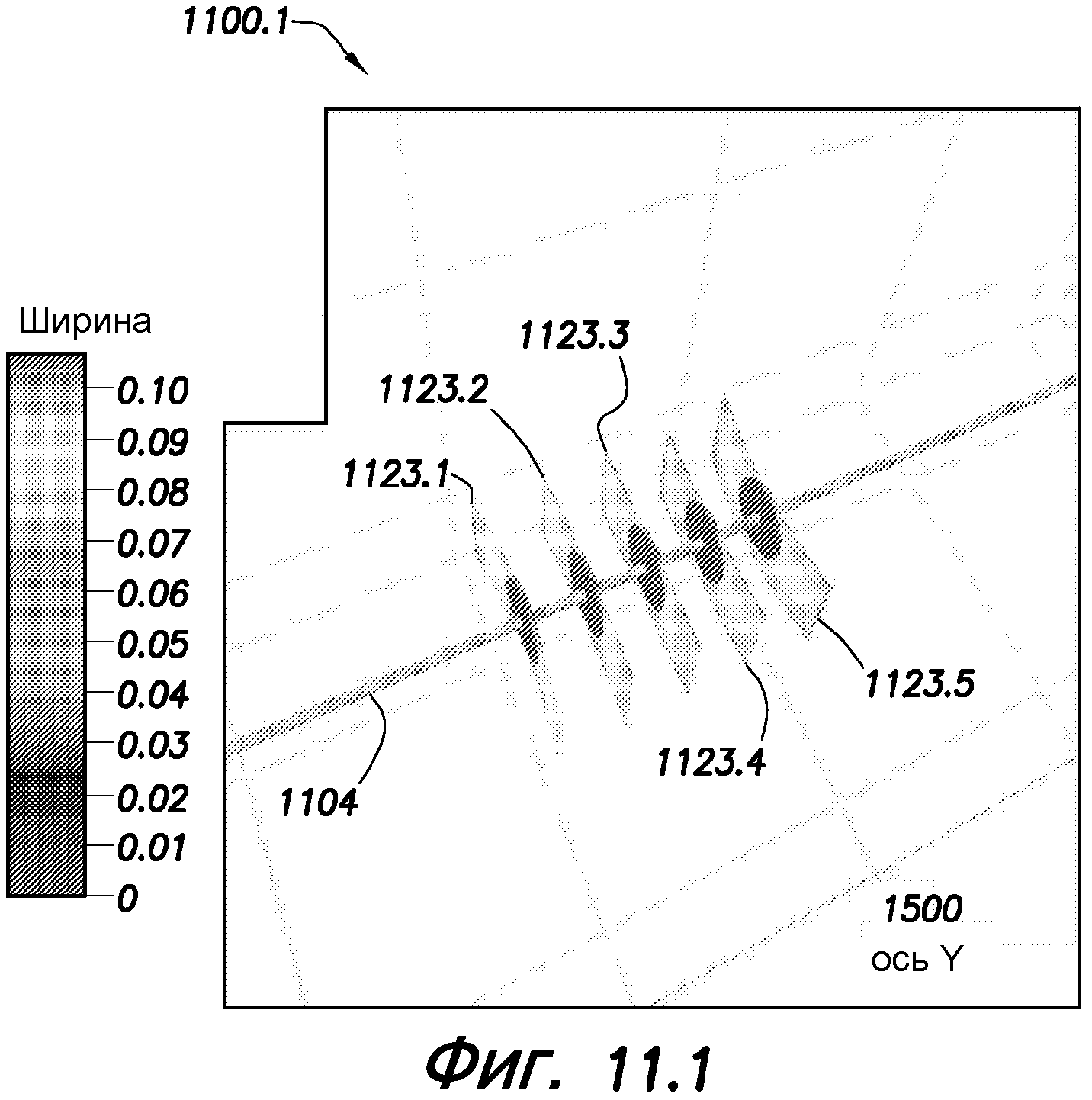
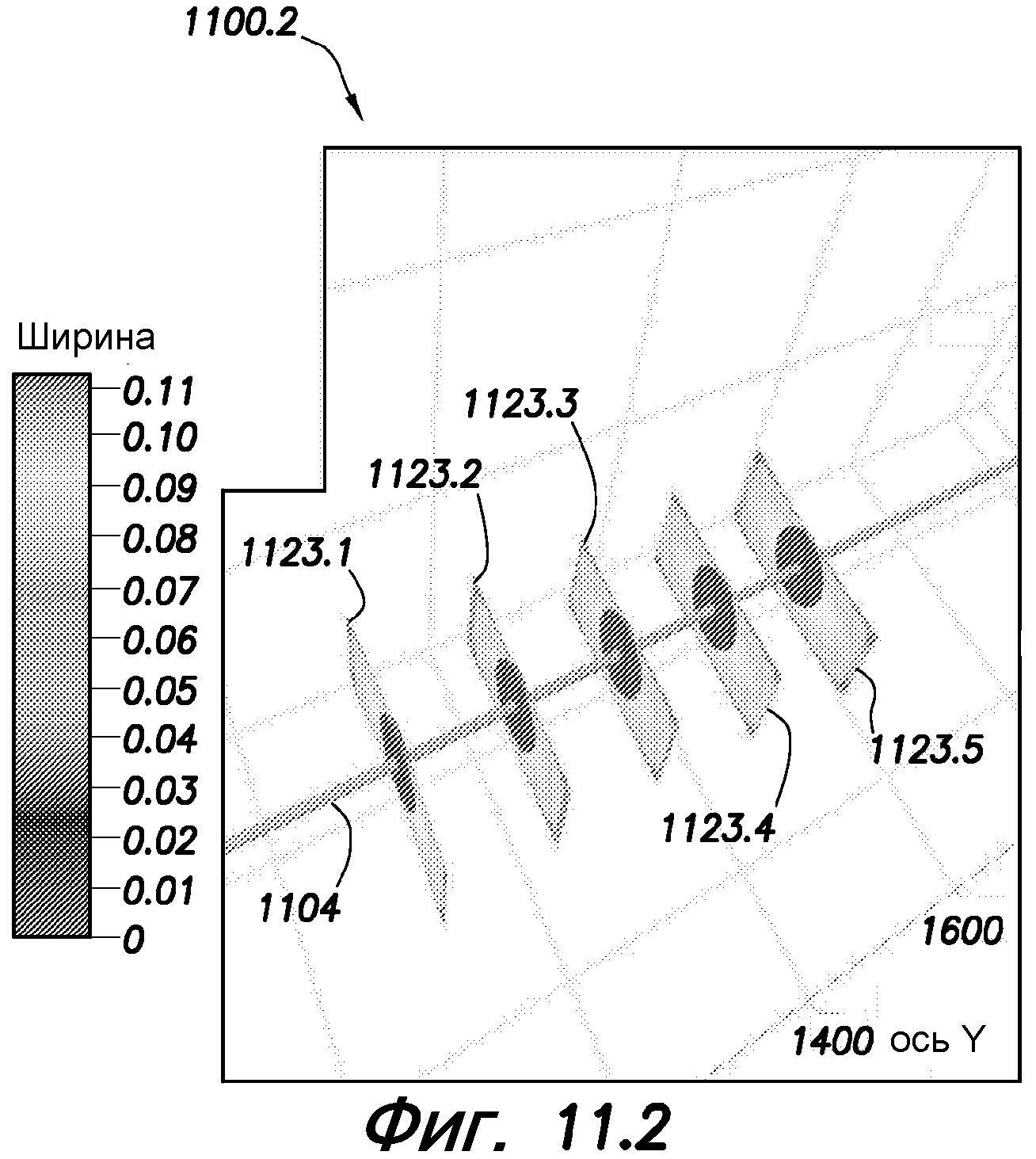
фиг. 11.1, 11.2 - схематичные представления, показывающие геометрию трещин для случая высокого перепада давления на перфорациях и случая большого разнесения трещин, соответственно;

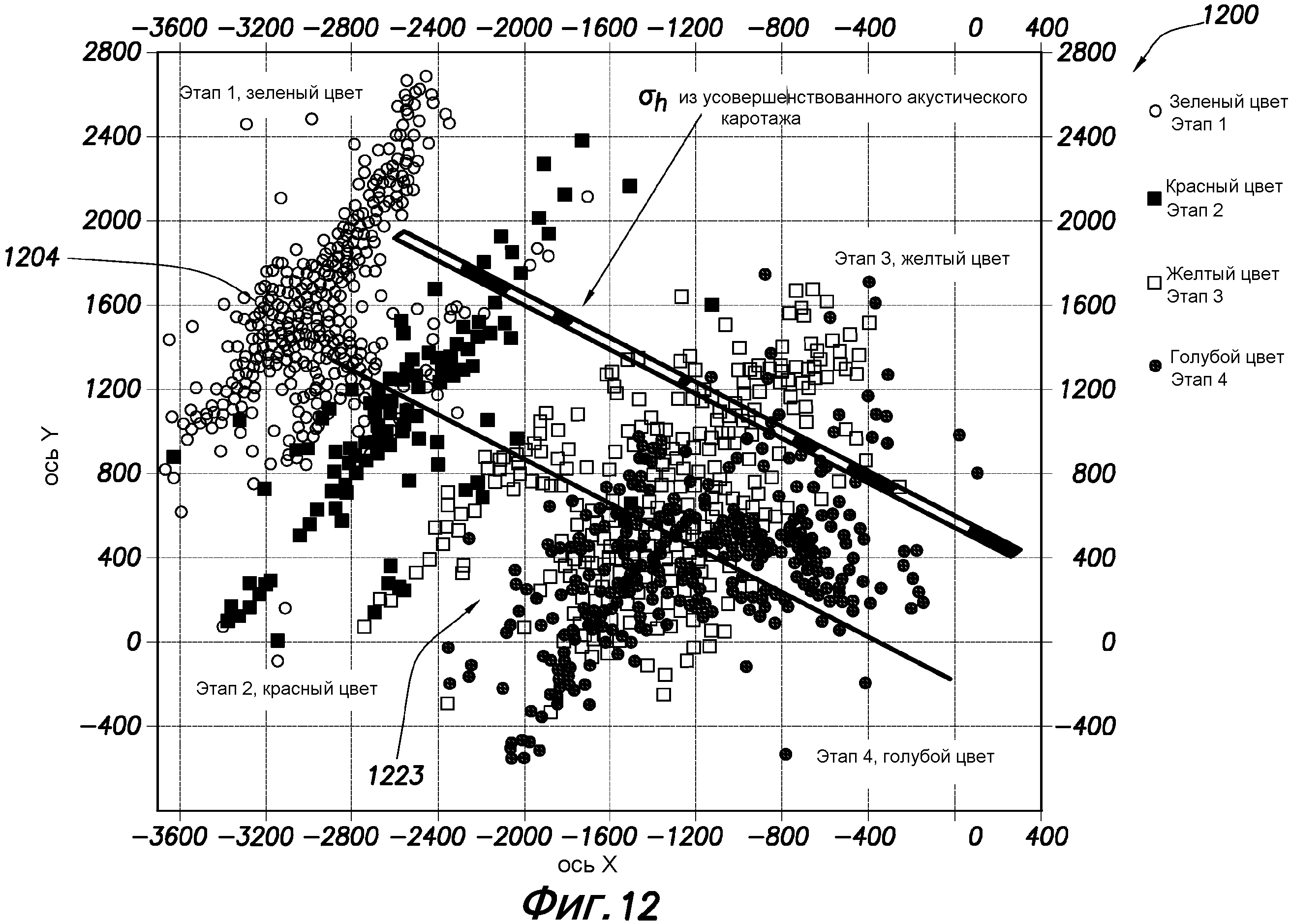
фиг. 12 - график, показывающий картирование микросейсмических событий;

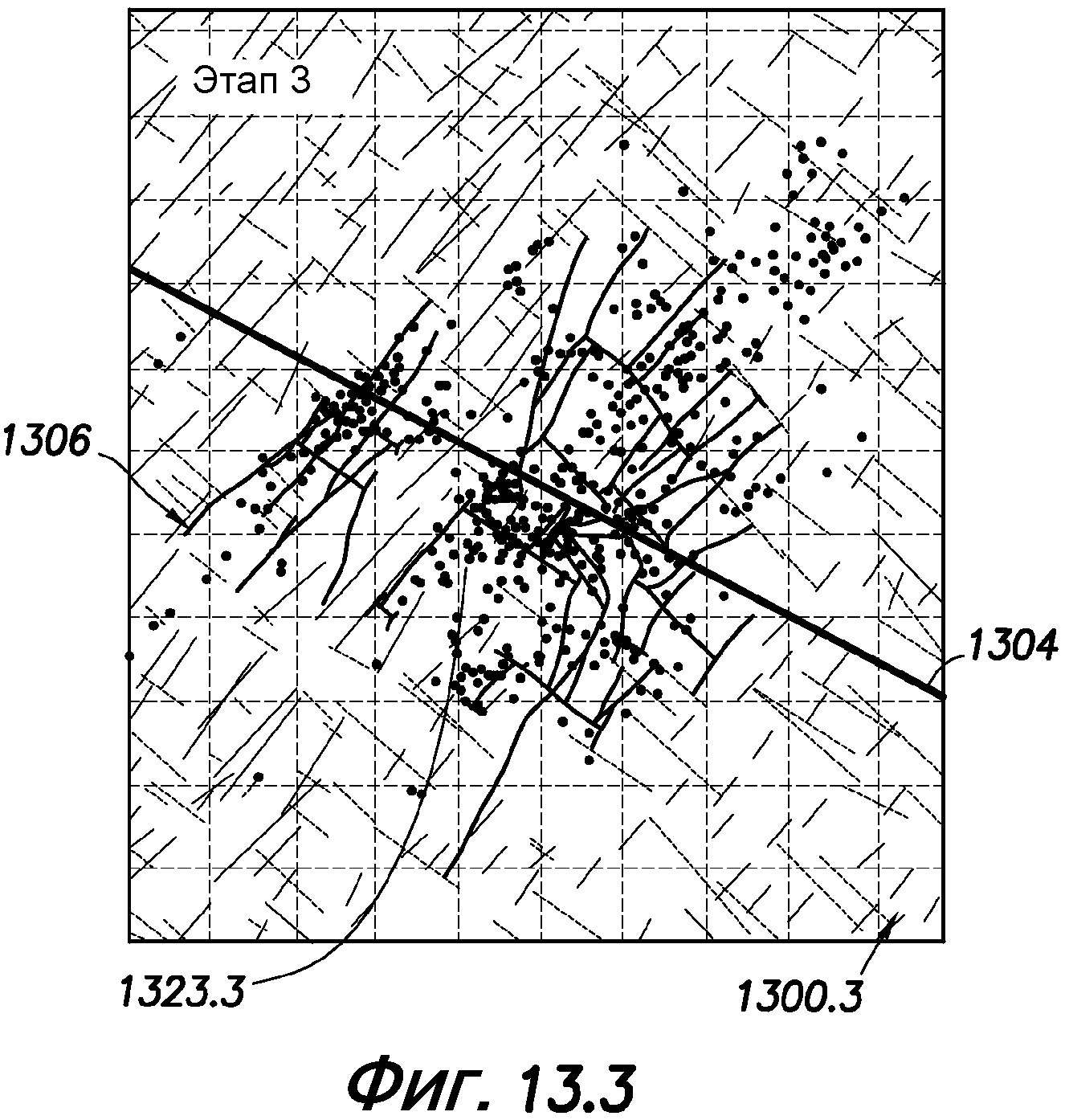
фиг. 13.1-13.4 - схематичные представления, иллюстрирующие моделированную систему трещин в сравнении с микросейсмическими измерениями на этапах 1-4, соответственно;

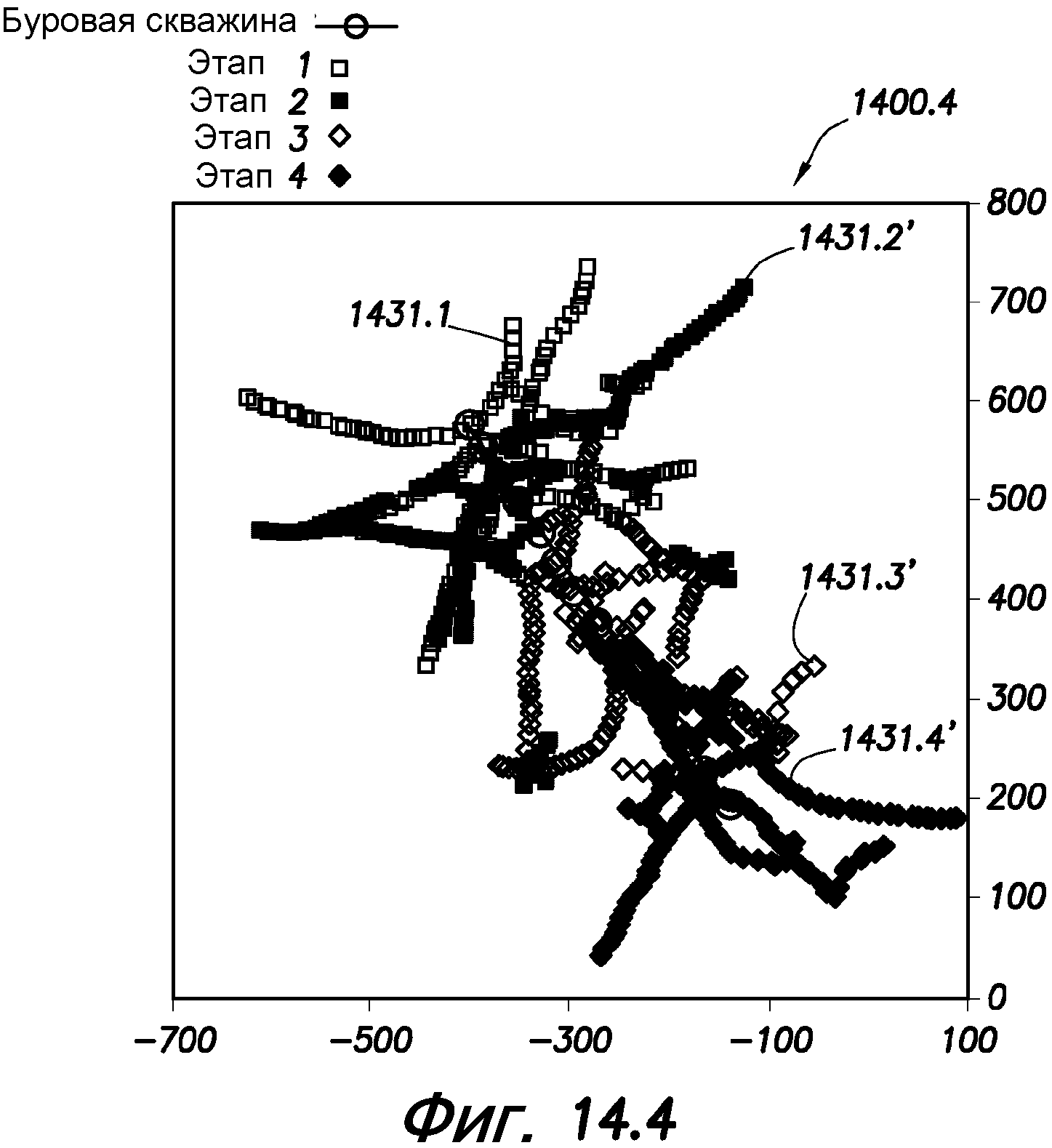
фиг. 14.1-14.4 - схематичные представления, показывающие систему распределенных трещин на различных этапах;

фиг. 15 - блок-схема последовательности действий, показывающих способ выполнения операции гидравлического разрыва; и

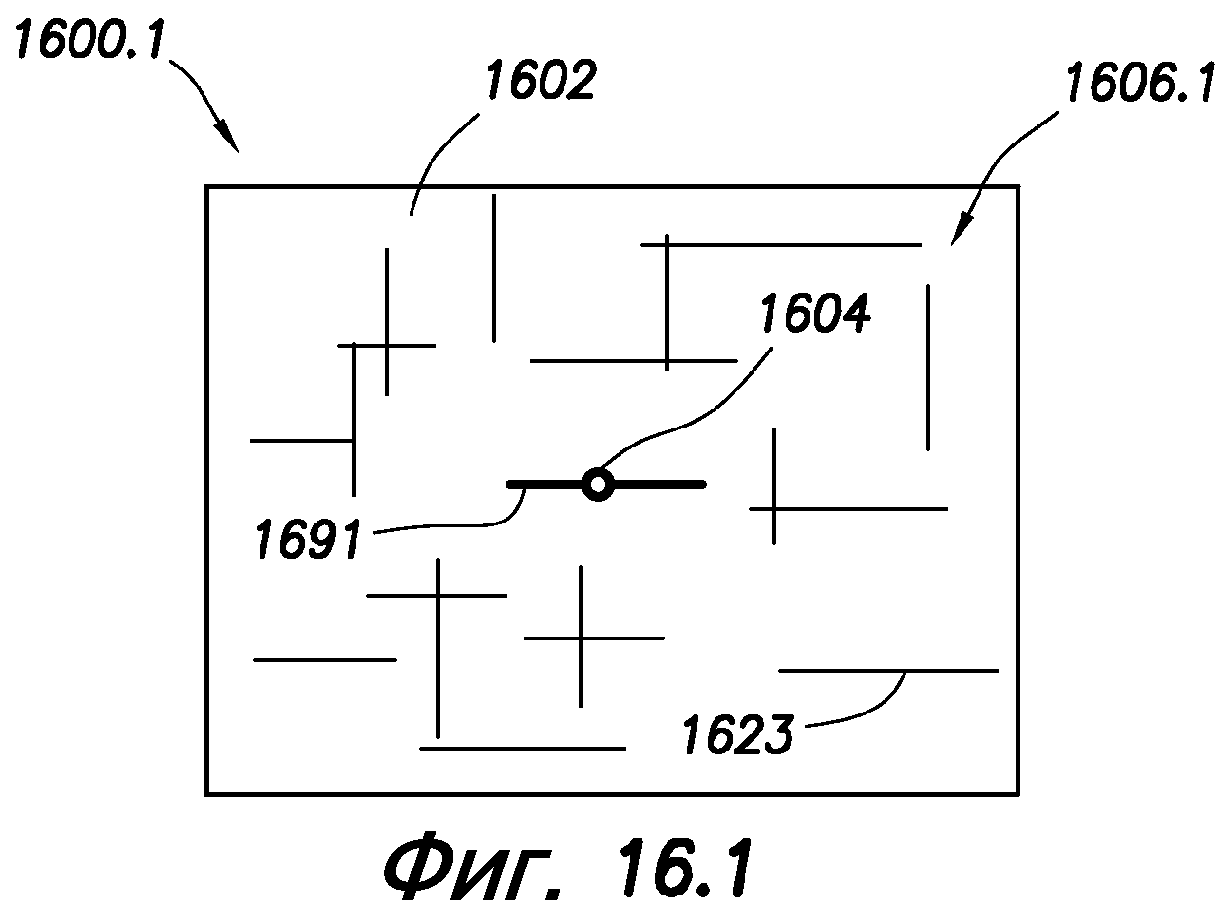
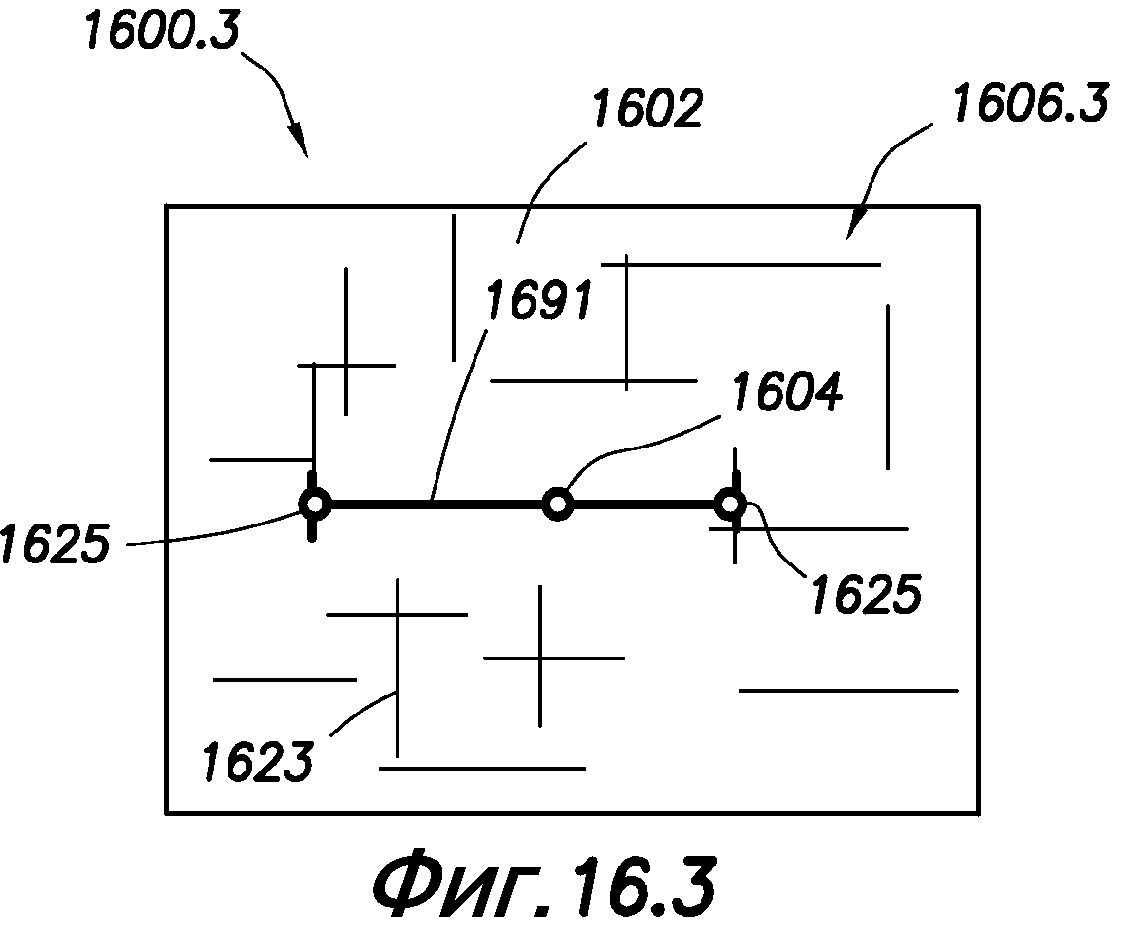
фиг. 16.1-16.4 - схематичные иллюстрации, показывающие рост трещин вокруг буровой скважины во время операции гидравлического разрыва.

ПОДРОБНОЕ ОПИСАНИЕ ИЗОБРЕТЕНИЯ

В описание, которое следует ниже, включены примеры устройств, способов, методик и последовательностей инструкций, которыми реализуются способы согласно предмету изобретения. Однако понятно, что описанные варианты осуществления могут быть применены на практике без этих конкретных подробностей.

Для получения представления о системах подземных трещин разрабатывают модели. В моделях могут приниматься во внимание различные факторы и/или данные, чтобы модели не могли быть связаны ограничениями благодаря учету количества закачиваемой жидкости или механических взаимодействий между трещинами и нагнетаемой жидкостью, а также между трещинами. Связанные ограничениями модели можно создавать для получения общего представления о вовлеченных механизмах, но математическое описание может быть сложным и/или могут требоваться компьютерные обрабатывающие ресурсы и время для выполнения точных моделирований развития трещин гидравлического разрыва. Связанную ограничениями модель можно конфигурировать для выполнения моделирований с учетом таких факторов, как взаимодействие между трещинами с течением времени и в соответствии с заданными условиями.

Нетрадиционную модель трещин (НМТ) (или сложную модель) можно использовать для моделирования развития системы сложных трещин в пласте с уже существующими естественными трещинами. Многочисленные ответвления трещин могут развиваться попутно и с перекрещиванием/пересечением друг друга. Каждая открытая трещина может вызывать дополнительные напряжения в окружающей породе и прилегающих трещинах, и это можно назвать эффектом «тени напряжения». Тень напряжения может быть причиной ограничения параметров трещин (например, ширины), что может приводить, например, к большей вероятности выпадения проппанта. Кроме того, тенью напряжения может изменяться траектория развития трещин и оказываться воздействие на картины системы трещин. Тень напряжения может влиять на моделирование взаимодействия трещин в сложной модели трещин.

Предложен способ вычисления тени напряжения в системе сложных трещин гидравлического разрыва. Способ можно выполнять на основании усовершенствованного двумерного метода разрывных смещений (ДМРС) с коррекцией за влияние конечной высоты трещин или трехмерного метода разрывных смещений (TMPC). Поле напряжений, вычисленное двумерным методом разрывных смещений, можно сравнивать с результатами трехмерного численного моделирования (трехмерным методом разрывных смещений или трехмерным методом быстрого анализа Лагранжа непрерывных сред), чтобы определять приближение для трехмерной задачи о трещинах. Это вычисление тени напряжения может быть включено в нетрадиционную модель трещин. Результаты для простых случаев двух трещин показывают, что трещины могут притягиваться или отталкиваться друг от друга в зависимости, например, от их первоначальных относительных положений, и эти результаты можно сравнивать с независимой двумерной моделью непланарных трещин гидравлического разрыва.

Представлены дополнительные примеры развития планарных и сложных трещин от кластеров перфораций, показывающие, что взаимодействие трещин может влиять на размер трещин и картину развития. В пласте с небольшой анизотропией напряжения взаимодействие трещин может приводить к значительному расхождению трещин, поскольку они могут стремиться отталкиваться друг от друга. Однако, даже когда анизотропия напряжения является большой и поворот трещины вследствие взаимодействия трещин ограничен, затенение напряжения может оказывать сильное влияние на ширину трещины, и это может влиять на распределение скоростей нагнетания в многочисленные кластеры перфораций и следовательно, на общую геометрию системы трещин и размещение проппанта.

На фиг. 1.1 и 1.2 показано развитие трещин вокруг места 100 расположения скважины. На месте расположения скважины имеется буровая скважина 104, продолжающаяся от устья 108 скважины на поверхности и ниже сквозь подземный пласт 102. Система 106 трещин распространяется вокруг буровой скважины 104. Насосная система 129 расположена возле устья 108 скважины для обеспечения протекания жидкости по насосно-компрессорной колонне 142.

Насосная система 12 9 показана управляемой промысловым оператором 127, регистрирующим эксплуатационные и рабочие промысловые данные и/или выполняющим работу в соответствии с установленным расписанием закачивания. Насосная система 129 закачивает жидкость с поверхности в буровую скважину 104 в продолжение операции гидравлического разрыва.

Насосная система 129 может включать в себя источник воды, такой как множество водяных цистерн 131, из которых вода подается в установку 133 гидратации геля. В установке 133 гидратации геля вода из цистерн 131 объединяется с гелеобразующим агентом для образования геля. Затем гель подается в смеситель 135, в котором он смешивается с проппантом из средства 137 транспортировки проппанта для образования жидкости для гидравлического разрыва. Гелеобразующий агент можно использовать, чтобы повышать вязкость жидкости для гидравлического разрыва и чтобы проппант имел возможность суспендироваться в жидкости для гидравлического разрыва. Кроме того, он может действовать как уменьшающий трение агент, позволяющий иметь более высокие скорости нагнетания при меньшей потере давления на трение.

Далее жидкость для гидравлического разрыва выкачивается из смесителя 135 в автоцистерны 120 для обработки, снабженные плунжерными насосами, показанные сплошными линиями 143. В каждой автоцистерне 120 для обработки жидкость для гидравлического разрыва принимается под низким давлением, а выпускается, что показано пунктирными линиями 141, из нее в общий манифольд 139 (иногда называемый «ракетным нагнетателем на трейлере» или «ракетным нагнетателем») под высоким давлением. Далее «ракетный нагнетатель» 139 направляет, что показано сплошной линией 115, жидкость для гидравлического разрыва из автоцистерн 120 для обработки в буровую скважину 104. Одну или несколько автоцистерн 120 для обработки можно использовать для подачи жидкости для гидравлического разрыва с заданной скоростью.

Каждая автоцистерна 120 для обработки обычно может работать с любой скоростью, например, с соответствующей максимальной рабочей производительностью. При работе автоцистерн 120 для обработки с рабочей производительностью можно допустить отказ одной и работу оставшихся с более высокой скоростью, чтобы компенсировать отсутствие отказавшего насоса. Компьютеризированную систему 149 управления можно использовать для управления всей насосной системой 129 во время операции гидравлического разрыва.

Различные жидкости, такие как обычные жидкости для воздействия на пласт вместе с проппантами, можно использовать для создания трещин. Другие жидкости, такие как вязкие гели, реагент на водной основе (который может иметь понизитель трения (полимер) и воду), также можно использовать для гидравлического разрыва в скважинах сланцевого газа. Такой реагент на водной основе может быть в жидкотекучей форме (например, с почти такой же вязкостью как у воды) и может использоваться для создания более сложных трещин, таких как многочисленные микросейсмические трещины, обнаруживаемые при мониторинге.

Как также показано на фиг. 1.1 и 1.2, система трещин включает в себя трещины, расположенные на различных местах вокруг буровой скважины 104. Различные трещины могут быть естественными трещинами 144, присутствовавшими до нагнетания жидкостей, или трещинами 146 гидравлического разрыва, образовавшимися в пласте 102 во время нагнетания. На фиг. 1.2 показана система 106 трещин, определенная по микросейсмическим событиям 14 8, собранным при использовании обычных средств.

Многоэтапное моделирование может быть нормой при разработке нетрадиционных коллекторов. Однако препятствие на пути оптимизации вскрытий в пластах глинистых коллекторов может заключаться в отсутствии моделей гидравлического разрыва, которыми надлежащим образом может моделироваться развитие сложных трещин, часто наблюдаемых в этих пластах. Была разработана модель системы сложных трещин (или нетрадиционная модель трещин) (см., например, Weng X., Kresse О., Wu R. and Gu H., "Modeling of hydraulic fracture propagation in a naturally fractured formation", Paper SPE 140253, presented at the SPE Hydraulic Fracturing Conference and Exhibition, Woodlands, Texas, USA, January 24-26 (2011) (в дальнейшем "Weng 2011"); Kresse О., Cohen С., Weng Χ., Wu R. and Gu H., 2011 (в дальнейшем "Kresse 2011"), "Numerical modeling of hydraulic fracturing in naturally fractured formations", 45th Rock Mechanics/Geomechanics Symposium, San Francisco, CA, June 26-29, полные содержания источников включены в эту заявку).

Существующие модели можно использовать для моделирования развития трещин, деформации породы и втекания жидкости в систему сложных трещин, создаваемую во время обработки. Кроме того, модель можно использовать для решения полносвязной задачи втекания жидкости в систему трещин и упругой деформации трещин, для которой можно иметь такие же предположения и определяющие уравнения, как в обычной псевдотрехмерной модели трещин. Уравнения переноса могут быть решены для каждого компонента закачиваемых жидкостей и проппантов.

С помощью обычных моделей планарных трещин можно моделировать различные аспекты системы трещин. Предложенная нетрадиционная модель трещин к тому же включает в себя возможность моделирования взаимодействия трещин гидравлического разрыва с уже существующими естественными трещинами, то есть позволяет определять, что трещина гидравлического разрыва развивается беспрепятственно или задерживается естественной трещиной, когда они пересекаются, и впоследствии развивается вдоль естественной трещины. Ответвление трещины гидравлического разрыва при пересечении с естественной трещиной может дать начало развитию системы сложных трещин.

Модель пересечений можно расширить на основании критерия Renshaw и Polland пересечения границы раздела (см., например, Renshaw СЕ. and Polland D.D., 1995, "An experimentally verified criterion for propagation across unbounded frictional interfaces in brittle, linear elastic materials", Int. J. Rock Mech. Min. Sci. and Geomech. Abstr., 32: 237-249 (1995), полное содержание источника включено в эту заявку), чтобы можно было применять к любому углу пересечения и усовершенствовать (см., например, Gu H. and Weng X., "Criterion for fractures crossing frictional interfaces at non-orthogonal angles", 44th US Rock symposium, Salt Lake City, Utah, June 27-30, 2010 (в дальнейшем "Gu и Weng 2010"), полное содержание источника включено в эту заявку путем ссылки), и подтверждать экспериментальными данными (см., например, Gu H., Weng X., Lund J., Mack M., Ganguly U. and Suarez-Rivera R., 2011, "Hydraulic fracture crossing natural fracture at non-orthogonal angles, A criterion, its validation and applications", Paper SPE 139984, presented at the SPE Hydraulic Fracturing Conference and Exhibition, Woodlands, Texas, January 24-26 (2011) (в дальнейшем "Gu и соавторы 2011"), полное содержание источника включено в эту заявку путем ссылки), и включать в нетрадиционную модель трещин.

Для надлежащего моделирования развития многочисленных или сложных трещин в модели трещин можно учитывать взаимодействие между прилегающими ответвлениями трещин гидравлического разрыва, часто называемое эффектом тени напряжения. Когда одна планарная трещина гидравлического разрыва раскрывается при конечном чистом давлении жидкости, к окружающей породе может прилагаться поле напряжений, которое пропорционально чистому давлению.

Для ограниченного случая вертикальной трещины бесконечной длины и постоянной конечной высоты можно получить аналитическое выражение для поля напряжений, вызываемое открытой трещиной. См., например, Warpinski N.F. and Teufel L.W., "Influence of geologic discontinuous on hydraulic fracture propagation", JPT, Feb., 209-220 (1987) (в дальнейшем "Warpinski и Teufel") и Warpinski N.R. and Branagan P.T., "Altered-stress fracturing", SPE JPT, September, 1989, 990-997 (1989), полные содержания источников включены в эту заявку путем ссылки). Чистое давление (или более точно, давление, при котором раскрывается данная трещина) может вызывать сжимающее напряжение в направлении, перпендикулярном к трещине, вдобавок к минимальному локальному напряжению, которое может быть равно чистому давлению на поверхности трещины, но быстро спадает с расстоянием от трещины.

На расстоянии сверх одной высоты трещины наведенное напряжение может быть всего лишь небольшой частью чистого давления. Поэтому термин «тень напряжения» можно использовать для описания этого возрастания напряжения в области, окружающей трещину. Если вторую трещину гидравлического разрыва создают параллельно существующей открытой трещине и если она попадает в тень напряжения (то есть расстояние до существующей трещине меньше, чем высота трещины), то в результате вторая трещина фактически будет воспринимать напряжение смыкания, превышающее исходное локальное напряжение. Вследствие этого более высокое давление может потребоваться для развития трещины и/или трещина может иметь меньшую ширину по сравнению с шириной соответствующей единственной трещины.

Одно применение анализа тени напряжения может включать в себя расчет и оптимизацию расстояний между многочисленными трещинами, одновременно развивающимися от горизонтальной буровой скважины. В глинистых пластах с очень низкой проницаемостью трещины можно располагать близко друг к другу для эффективного дренирования коллектора. Однако эффект тени напряжения может препятствовать развитию трещины в непосредственной близости от других трещин (см., например, Fisher M.К., Heinze J.R., Harris CD., Davidson Β.M., Wright С.A. and Dunn К.P., "Optimizing horizontal completion technique in the Barnett shale using microseismic fracture mapping", SPE 90051, presented at the SPE Annual Technical Conference and Exhibition, Houston, 26-29 September 2004, полное содержание источника включено в эту заявку путем ссылки).

Ранее выполнялись исследования взаимного влияния параллельных трещин (см., например, Warpinski и Teufel; Britt L.K. and Smith M.В., "Horizontal well completion, stimulation, optimization and risk mitigation", Paper SPE 125526, presented at the 2009 SPE Eastern Regional Meeting, Charleston, September 23-25, 2009; Cheng Y, 2009, "Boundary element analysis of the stress distribution around multiple fractures: Implications for the spacing of perforation clusters of hydraulically fractured horizontal wells", Paper SPE 125769, presented at the 2009 SPE Eastern Regional Meeting, Charleston, September 23-25, 2009; Meyer B.R. and Bazan L.W, "A discrete fracture network model for hydraulically induced fractures: Theory, parametric and case studies, Paper SPE 140514, presented at the SPE Hydraulic Fracturing Conference and Exhibition, Woodlands, Texas, USA, January 24-26, 2011; Roussel N.P. and Sharma M.M., "Optimizing fracture spacing and sequencing in horizontal-well fracturing", SPEPE, May, 2011, pp.173-184, полные содержания источников включены в эту заявку путем ссылки). Исследования охватывают параллельные трещины в статических состояниях.

Результатом действия тени напряжения может быть меньшая ширина трещин в средней области многочисленных параллельных трещин вследствие повышенных сжимающих напряжений от соседних трещин (см., например, Germanovich L.N. and Astakhov D., "Fracture closure in extension and mechanical interaction of parallel joints", J. Geophys. Res., 109, B02208, doi: 10.1029/2002, JB002131 (2004); Olson J.E., "Multi-fracture propagation modeling: Applications to hydraulic fracturing in shales and tight sands", 42nd US Rock Mechanics Symposium and 2nd US-Canada Rock Mechanics Symposium, San Francisco, CA, June 29 - July 2, 2008, полные содержания источников включены в эту заявку путем ссылки). Когда многочисленные трещины развиваются одновременно, распределение скоростей втекания в трещины может быть динамическим процессом и может находиться под влиянием чистого давления трещин. Чистое давление может сильно зависеть от ширины трещины и следовательно, влияние тени давления на распределение скоростей втекания и размеры трещин нуждаются в дальнейшем исследовании.

Кроме того, динамика одновременно развивающихся многочисленных трещин может зависеть от относительных положений первоначальных трещин. Если трещины параллельны, например в случае многочисленных трещин, которые ортогональны к горизонтальной буровой скважине, трещины могут отталкиваться друг от друга, в результате чего будет происходить искривление трещин наружу. Однако, если многочисленные трещины расположены эшелоном, например трещины, начинающиеся от горизонтальной буровой скважины, не перпендикулярные к плоскости разрыва, взаимодействие между соседними трещинами может быть таким, что их концы будут притягиваться друг к другу и даже соединяться (см., например, Olson J.Ε., "Fracture mechanics analysis of joints and veins", PhD dissertation, Stanford University, San Francisco, California (1990); Yew CH., Mear Μ. Ε., Chang С.С.and Zhang X.С, "On perforation and fracturing of deviated cased wellbores", Paper SPE 26514, presented at SPE 68th Annual Technical Conference and Exhibition, Houston, TX, Oct. 3-6 (1993); Weng X., "Fracture initiation and propagation from deviated wellbores", Paper SPE 26597, presented at SPE 68th Annual Technical Conference and Exhibition, Houston, TX, Oct. 3-6 (1993), полные содержания источников включены в эту заявку путем ссылки).

Когда трещина гидравлического разрыва пересекает вторичную трещину, ориентированную в другом направлении, она может вызывать дополнительное напряжение смыкания вторичной трещины, которое пропорционально чистому давлению. Это напряжение можно определять и учитывать в расчете давления раскрытия трещины при анализе зависимой от давления утечки в трещиноватом пласте (см., например, Nolte К., "Fracturing pressure analysis for nonideal behavior", JPT, Feb. 1991, 210-218 (SPE 20704) (1991) (в дальнейшем "Nolte 1991"), полное содержание источника включено в эту заявку путем ссылки).

Для более сложных трещин можно предложить сочетание взаимодействий различных трещин, рассмотренных выше. Для надлежащего учета этих взаимодействий и сохранения вычислительной эффективности с тем, чтобы их можно было включить в модель системы сложных трещин, можно создать соответствующую основу моделирования. Способ, основанный на усовершенствованном двумерном методе разрывных смещений (ДМРС), можно использовать для вычисления напряжений, наводимых на данную трещину и породу из остальной части системы сложных трещин (см., например, Olson J.Ε., "Predicting Fracture Swarms - The Influence of Sub critical Crack Growth and the Crack-Tip Process Zone on Joints Spacing in Rock. In The Initiation, Propagation and Arrest of Joints and Other Fractured, ed. J.W. Cosgrove and T. Engelder, Geological Soc. Special Publications, London, 231, 71-78 (2004) (в дальнейшем "Olson 2004"), полное содержание источника включено в эту заявку путем ссылки). Кроме того, поворот трещины можно моделировать на основании изменяющегося направления локального напряжения перед концом развивающейся трещины. Представлены результаты моделирования из нетрадиционной модели трещин, которые включают в себя моделирование взаимодействия.

Описание нетрадиционной модели трещин

Для моделирования развития системы сложных трещин, которая состоит из многих пересекающихся трещин, можно использовать уравнения, определяющие основополагающие физические свойства процесса образования трещин. Основные определяющие уравнения могут включать в себя, например, уравнения, определяющие втекание жидкости в систему трещин, уравнения, определяющие деформацию трещин, и критерий развития/взаимодействия трещин.

Для уравнения непрерывности предполагается, что поток жидкости проходит по системе трещин с сохранением массы в соответствии с:

где q - локальная скорость потока внутри трещины гидравлического разрыва вдоль длины,

Свойства рабочей жидкости можно определить показателем n′ степени (показателем движения жидкости) и показателем К′ консистенции. Поток жидкости через набивку проппанта может быть ламинарным, турбулентным или потоком Дарси и соответственно может описываться различными законами. Для общего случая одномерного ламинарного потока в любом данном ответвлении трещины можно использовать закон Пуазейля (см., например, Nolte, 1991):

где

В данном случае w(z) представляет ширину трещины как функцию глубины при текущем положении s, α - коэффициент, n′ показатель степени (показатель консистенции жидкости), ϕ - функция формы и dz - приращение интегрирования в формуле вдоль высоты трещины.

Ширину трещины можно связать с давлением жидкости через уравнение упругости. Упругие свойства породы (которую большей частью можно считать однородным, изотропным, линейным упругим материалом) можно определить через модуль Е Юнга и отношение v Пуассона. В случае вертикальной трещины в слоистой среде с переменным минимальным горизонтальным напряжением σ_h(x, y, z) и давлением р жидкости профиль (w) ширины можно определить из аналитического решения в виде:

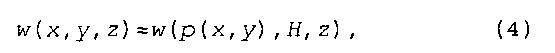
где w - ширина трещины в точке с пространственными координатами х, у, z (координатами центра элемента трещины); р(х, у) - давление жидкости, H - высота элемента трещины и z - вертикальная координата вдоль элемента трещины в точке (х, у).

Поскольку высота трещин может изменяться, в систему определяющих уравнений можно также включить вычисление прироста высоты, описанное, например, в Kresse 2011.

В дополнение к уравнениям, представленным выше, может удовлетворяться глобальное условие баланса объемов:

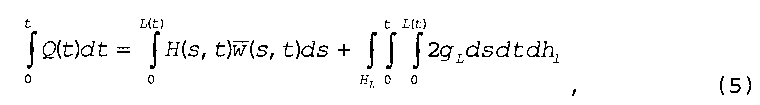
где g_L - скорость утечки жидкости, Q(t) - зависимая от времени скорость нагнетания, H(s, t) - высота трещины в точке s(x, y) пространства и в момент t времени, ds - приращение длины при интегрировании по длине трещины, dh₁ - приращение высоты утечки, H_L - высота утечки и s₀ - коэффициент струйных потерь. Уравнением (5) устанавливается, что общий объем жидкости, закачанной в течение времени t, равен объему жидкости в системе трещин и объему, вытекшему из трещин к моменту t времени. В данном случае L(t) представляет общую длину развившихся трещин гидравлического разрыва к моменту t времени и S₀ - коэффициент струйных потерь. Для граничных условий может потребоваться, чтобы скорость потока, чистое давление и ширина трещин были равны нулю на концах всех трещин.

Систему уравнений 1-5 вместе с начальными и граничными условиями можно использовать для представления системы определяющих уравнений. Объединение этих уравнений и дискретизация системы трещин на небольшие элементы может приводить к нелинейной системе уравнений с учетом давления р жидкости в каждом элементе, упрощающейся при f(р)=0, которую можно решить при использовании демпфированного метода Ньютона-Рафсона.

Взаимодействие трещин можно учитывать при моделировании развития трещин гидравлического разрыва в коллекторах с естественными трещинами. Оно включает в себя, например, взаимодействие между трещинами гидравлического разрыва и естественными трещинами, а также взаимодействие между трещинами гидравлического разрыва. Для взаимодействия между трещинами гидравлического разрыва и естественными трещинами в нетрадиционной модели трещин можно реализовать полуаналитический критерий пересечения при использовании, например, подхода, описанного в Gu и Weng 2010 и в Gu и соавторы 2011.

Моделирование тени напряжения

В случае параллельных трещин тень напряжения можно представить суперпозицией напряжений от соседних трещин. На фиг. 2 схематично показана двумерная трещина 200 в системе координат, имеющей ось х и ось у. Различные точки вдоль двумерной трещины, такие как первый конец в h/2, второй конец в -h/2 и средняя точка, соединены линиями с точкой (х, у) наблюдения. Линии L, L₁, L₂ проходят под углами θ, θ₁, θ₂ от точек вдоль двумерной трещины до точки наблюдения.

Поле напряжений вокруг двумерной трещины с внутренним давлением р можно вычислить при использовании, например, способов, описанных в Warpinski и Teufel. Напряжение σ_х, которое влияет на ширину, можно вычислить из:

где

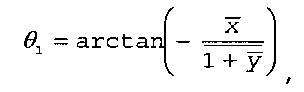
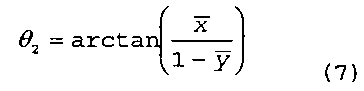
и где σ_х - напряжение в направлении х, р - внутреннее давление и

Аналитическое уравнение, приведенное выше, можно использовать при вычислении среднего эффективного напряжения одной трещины, действующего на соседнюю параллельную трещину, и его можно включать в эффективное напряжение смыкания, действующее на эту трещину.

Трещины могут быть ориентированы по различным направлениям и могут пересекаться друг с другом в системах более сложных трещин. На фиг. 3.1 показана система 300 сложных трещин с отображением эффектов тени напряжения. Система 300 трещин включает в себя трещины 303 гидравлического разрыва, продолжающиеся от буровой скважины 304 и взаимодействующие с другими трещинами 305 в системе 300 трещин.

Более общий способ можно использовать для вычисления эффективного напряжения, действующего на любое ответвление трещины от остальной части системы трещин. В нетрадиционной модели трещин механические взаимодействия между трещинами можно моделировать на основе двумерного метода разрывных смещений (ДМРС) (Olson 2004), чтобы вычислять наведенные напряжения (см., например, фиг. 3.1).

Двумерное решение разрывных смещений при плоской деформации (см., например, Crouch S.L. and Starfield A.M., Boundary element methods in solid mechanics, George Allen and Unwin Ltd, London, Fisher, M.K. (1983) (в дальнейшем Crouch и Starfield 1983), полное содержание источника включено в эту заявку путем ссылки) можно использовать для описания нормального и сдвигового напряжений (σ_n и σ_х), действующих на один элемент трещины, наводимых разрывными раскрывающими и сдвигающими смещениями (D_n и D_s) со всех элементов трещины. Для учета трехмерного эффекта, обусловленного конечной высотой трещин, можно использовать подход Olson 2004, чтобы получать трехмерный поправочный коэффициент для коэффициентов С^ij влияния в сочетании с модифицированными уравнениями упругости из двумерного метода разрывных смещений:

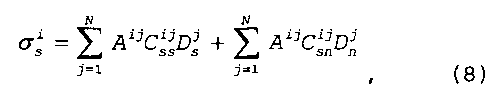
где А - матрица коэффициентов влияния, представленных в уравнении (9), N - суммарное число элементов в системе, взаимодействие которых учитывается, i - рассматриваемый элемент и j=1,N - другие элементы в системе, влияние которых на напряжения элемента i вычисляют; и где С^ij - двумерные коэффициенты влияния упругости при плоской деформации. Эти выражения можно найти в Crouch и Starfield 1983.

Элементами i и j на фиг. 3.1 схематично показаны переменные i и j из уравнения (8). Разрывы D_s и D_n, относящиеся к элементу j, также показаны на фиг. 3.2. D_n может быть таким же, как ширина щели, а напряжение s сдвига может быть равно 0, как показано. Разрыв смещения элемента j создает напряжение на элементе i, показанное как σ_s и σ_n.

Трехмерный поправочный коэффициент, предложенный в Olson 2004, можно представить в следующем виде:

где h - высота трещины, d_ij - расстояние между элементами i и j, α и β - подгоняемые параметры. Уравнение (9) показывает, что трехмерный поправочный коэффициент может приводить к ослаблению взаимодействия между любыми двумя элементами трещины при увеличении расстояния.

В нетрадиционной модели трещин на каждом временном шаге можно вычислять дополнительные наведенные напряжения, обусловленные эффектами тени напряжения. Можно предположить, что в любой момент времени ширина щели равна нормальным разрывам (D_n) смещений, а напряжение сдвига на поверхности трещины равно нулю, то есть

Влияния напряжений, наводимых тенью напряжения, на картину развития системы трещин можно описать в два приема. Во-первых, во время итерации давления и ширины исходные локальные напряжения на каждом элементе трещины можно модифицировать путем добавления нормального напряжения, обусловленного эффектом тени напряжения. Это может непосредственно влиять на давление разрыва и распределение ширины, что может привести к изменению роста трещин. Во-вторых, при включении напряжений, наведенных тенью напряжения (нормальных и сдвиговых напряжений), поля локальных напряжений перед развивающимися концами также могут изменяться, что может вызывать отклонение направления локального главного напряжения от исходного направления локального напряжения. Это изменяемое направление локального главного напряжения может приводить к повороту трещины из исходной плоскости развития и также может влиять на картину развития системы трещин.

Проверка достоверности модели тени напряжения

Проверка достоверности нетрадиционной модели трещин для случаев трещин с двумя крыльями можно выполнить при использовании, например, методики Weng 2011 или Kresse 2011. Кроме того, проверку достоверности можно выполнить при использовании способа моделирования тени напряжения. Как предложено, например, в Itasca Consulting Group Inc., 2002, FLAC3D (Fast Lagrangian Analysis if Continua in 3 Dimensions), Version 2.1, Minneapolis: ICG (2002) (в дальнейшем "Itasca 2002"), результаты двумерного метода разрывных смещений можно сравнивать с результатами трехмерного быстрого анализа Лагранжа непрерывных сред.

Сравнение усовершенствованного двумерного метода разрывных смещений с трехмерным быстрым анализом Лагранжа непрерывных сред

Трехмерные поправочные коэффициенты, предложенные в Olson 2004, содержат две эмпирические постоянные, α и β. Значения α и β можно калибровать путем сравнения напряжений, получаемых в результате численных решений (усовершенствованным двумерным методом разрывных смещений), с напряжениями из аналитического решения для плоско деформированной трещины с бесконечной длиной и бесконечной высотой. Достоверность модели можно дополнительно проверять сравнением результатов для двух параллельных прямолинейных трещин с конечной длиной и высотой из двумерной модели разрывных смещений с полными трехмерными численными решениями при использовании, например, трехмерного быстрого анализа Лагранжа непрерывных сред.

Задача проверки достоверности показана на фиг. 4. На фиг. 4 показано схематичное представление 400 для сравнения усовершенствованного двумерного метода разрывных смещений с трехмерным быстрым анализом Лагранжа непрерывных сред применительно к случаю двух параллельных прямолинейных трещин. Как показано на фиг. 4, две параллельные трещины 407.1, 407.2 подвергаются воздействию напряжений σ_х, σ_y вдоль осей х, у координат. Трещины имеют длину 2L_xf и давление p₁, р₂ разрыва, соответственно. Трещины находятся на расстоянии s друг от друга.

При трехмерном быстром анализе Лагранжа непрерывных сред трещину можно моделировать как две поверхности на одном и том же месте, но с не присоединенными точками сеток. Постоянное внутреннее давление жидкости может быть приложено к сеткам как нормальное напряжение. Кроме того, трещины могут подвергаться воздействию удаленных напряжений, σ_х и σ_y. Две трещины могут иметь одинаковые длину и высоту при отношении высоты к половине длины, равном 0,3.

Можно сравнить напряжения вдоль оси к (y=0) и оси у (х=0). Как показано для сравнения на фиг. 5.1-5.3, можно моделировать две близко расположенные трещины (s/h=0,5). Эти фигуры даны для сравнения усовершенствованного двумерного метода разрывных смещений и трехмерного быстрого анализа Лагранжа непрерывных сред: напряжений вдоль оси х (y=0) и оси у (х=0).

Эти фигуры включают в себя графики 500.1, 500.2, 550.3, соответственно, иллюстрирующие σ_y вдоль оси y, σ_х вдоль оси y и σ_y вдоль оси х, соответственно, для продолженных трещин, полученные двумерным методом разрывных смещений и трехмерным быстрым анализом Лагранжа непрерывных сред. На фиг. 5.1 показаны графики σ_x/р (по оси у) в зависимости от нормированного расстояния от трещины (по оси х), полученные при использовании двумерного метода разрывных смещений (ДМРС) и трехмерного быстрого анализа Лагранжа непрерывных сред (ТБАЛНС). На фиг. 5.2 показаны графики σ_х/р (по оси y) в зависимости от нормированного расстояния от трещины (по оси х), полученные при использовании двумерного метода разрывных смещений (ДМРС) и трехмерного быстрого анализа Лагранжа непрерывных сред (ТБАЛНС). На фиг. 5.3 показаны графики σ_y/р (по оси y) в зависимости от нормированного расстояния от трещины (по оси х), полученные при использовании двумерного метода разрывных смещений (ДМРС) и трехмерного быстрого анализа Лагранжа непрерывных сред (ТБАЛНС). Положение L_f конца трещины показано вдоль линии x/h.

Как показано на фиг. 5.1-5.3, напряжения, моделированные на основании усовершенствованного двумерного метода разрывных смещений при использовании трехмерного поправочного коэффициента, очень хорошо согласуются с напряжениями из результатов полной трехмерной имитационной модели, которые показывают, что поправочный коэффициент позволяет получать трехмерный эффект на основании высоты трещины в поле напряжений.

Сравнение с моделью CSIRO

Достоверность нетрадиционной модели трещин, которая включает в себя усовершенствованный двумерный метод разрывных смещений, можно проверить сравнением с полной двумерной имитационной моделью разрывных смещений от CSIRO (организация содружества по научным и промышленным исследованиям) (см., например, Zhang X., Jeffrey R.G. and Thiercelin M., 2007, "Deflection and propagation of fluid-driven fractures at frictional bedding interfaces: A numerical investigation", Journal of Structural Geology, 29: 396-410 (в дальнейшем "Zhang 2007"), полное содержание источника включено в эту заявку путем ссылки). Такой подход можно использовать, например, в ограниченном случае очень большой высоты трещины, поскольку в двумерном методе разрывных смещений не учитываются трехмерные эффекты высоты трещин.

Можно использовать сравнение влияния двух близко развивающихся трещин на другие траектории развития. Развитие двух трещин гидравлического разрыва, возникающих параллельно друг другу (развитие по направлению локального максимального напряжения), можно моделировать для таких конфигураций, как: 1) точки инициирования на вершинах друг друга и удаление друг от друга при изотропном напряжении; и 2) анизотропные напряжения в дальнем поле. Траекторию развития трещин и давление внутри каждой трещины при входных данных, приведенных в таблице 1, можно сравнивать для нетрадиционной модели трещин и кода CSIRO.

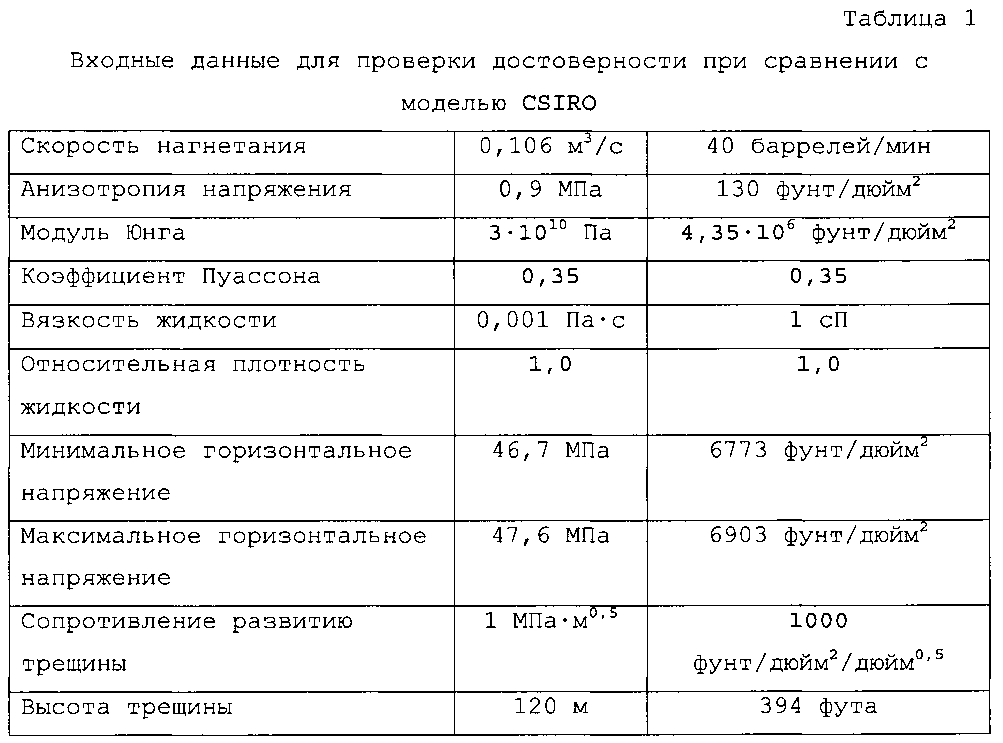
Когда две трещины инициируют параллельно друг другу при разнесении точек инициирования на dx=0, dy=33 фута (10,1 м) (максимальное горизонтальное поле напряжений ориентировано в направлении х), они могут отклоняться друг от друга вследствие эффекта тени напряжения.

Траектории развития в случае изотропных и анизотропных полей напряжений показаны на фиг. 6.1 и 6.2. Эти фигуры представляют собой графики 600.1 и 600.2, показывающие траектории развития двух первоначально параллельных трещин 609.1 и 609.2 в изотропном и анизотропном полях напряжений, соответственно. Трещины 609.1 и 609.2 сначала являются параллельными вблизи точек 615.1, 615.2 нагнетания, но расходятся по мере удаления от них. При сравнении с изотропным случаем видно, что кривизна трещин меньше в случае анизотропии напряжения. Это может быть обусловлено конкуренцией между эффектом тени напряжения, который стремится отклонить трещины друг от друга, и напряжениями в дальнем поле, которые продвигают трещины для развития в направлении максимального горизонтального напряжения (в направлении х). Влияние напряжения в дальнем поле становится доминирующим по мере повышения расстояния между трещинами, и в этом случае трещины могут стремиться развиваться параллельно в направлении максимального горизонтального напряжения.

На фиг. 7.1 и 7.2 представлены графики 700.1, 700.2, показывающие пару трещин, инициированных из двух различных точек 711.1, 711.2 нагнетания, соответственно. На этих фигурах показано для сравнения инициирование трещин из точек, разнесенных на расстояние dx=dy=10,1 м, для изотропного и анизотропного полей напряжений, соответственно. На этих фигурах для трещин 709.1 и 709.2 имеется тенденция распространения друг к другу. Примеры поведения подобного вида наблюдались при лабораторных экспериментах (см., например, Zhang 2007).

Как показано выше, усовершенствованным двумерным методом разрывных смещений, реализованным в нетрадиционной модели трещин, можно захватывать трехмерные эффекты конечной высоты трещин из картины взаимодействия и развития трещин, и в то же время метод является эффективным в вычислительном отношении. Можно получать хорошую оценку поля напряжений для системы вертикальных трещин гидравлического разрыва и (картины) направления развития трещин.

Примеры случаев

Случай №1, параллельные трещины в горизонтальных скважинах

На фиг. 8 представлено графическое изображение 800 параллельных поперечных трещин 811.1, 811.2, 811.3, развивающихся одновременно от многочисленных кластеров 815.1, 815.2, 815.3 перфораций, соответственно, вокруг горизонтальной буровой скважины 804. В каждой из трещин 811.1, 811.2, 811.3 создаются отличающиеся скорости q₁, q₂, q₃ потока, которые являются частью суммарного потока q_t при давлении р₀.

Когда пластовые условия и перфорации являются одинаковыми для всех трещин, трещины могут иметь приблизительно одинаковые размеры, если потери давления на трение в буровой скважине между кластерами перфораций являются соразмерно малыми. Это можно предполагать, когда трещины разнесены на достаточно большие расстояния и эффекты тени напряжения являются пренебрежимо малыми. Когда расстояния между трещинами находятся в области влияния тени напряжения, она может влиять не только на ширину трещин, но также и на другую размерность трещин. Для иллюстрации этого можно рассмотреть простой пример пяти параллельных трещин.

В этом примере трещины предполагаются имеющими постоянную высоту 100 футов (30,5 м). Расстояние между трещинами составляет 65 футов (19,8 м). Другие входные параметры приведены в таблице 2.

В этом простом случае обычную модель Перкинса-Керна-Нордгрена (ПКН) (см., например, Mack M.G. and Warpinski N.R., "Mechanical of Hydraulic Fracturing", Chapter 6, "Reservoir Stimulation", 3rd Ed., eds. Economides M.J. and Nolte K.G., John Willey and Sons (2000)) для многочисленных трещин можно модифицировать путем включения вычисления тени напряжения, взятого из уравнения (6). Повышение напряжения смыкания может быть аппроксимировано путем усреднения вычисленного на основании уравнения (6) напряжения по всей трещине. Заметим, что в этой упрощенной модели Перкинса-Керна-Нордгрена нельзя моделировать поворот трещин, обусловленный эффектом тени напряжения. Результаты из этой простой модели можно сравнить с результатами из нетрадиционной модели трещин, в которую включено поточечное вычисление тени напряжения вдоль всех траекторий трещин, а также поворота трещин.

На фиг. 9 показаны результаты моделирования длины пяти трещин, вычисленных на основании обеих моделей. На фиг. 9 представлен график 900, показывающий длину (по оси у) в зависимости от времени (t) пяти параллельных трещин во время нагнетания. Линии 917.1-917.5 получены на основании нетрадиционной модели трещин. Линии 919.1-919.5 получены на основании упрощенной модели Перкинса-Керна-Нордгрена.

Геометрия трещин и контуры ширины из нетрадиционной модели трещин для пяти трещин из фиг. 9 показаны на фиг. 10. На фиг. 10 дано схематичное представление 1000, показывающее трещины 1021.1-1021.5 около буровой скважины 1004.

Трещина 1021.3 является средней трещиной из числа пяти трещин, а трещины 1021.1 и 1021.5 являются самыми крайними трещинами. Поскольку трещины 1021.2, 1023.3 и 1021.4 имеют меньшую ширину по сравнению с шириной крайних трещин, то вследствие эффекта тени напряжения, они могут оказывать большее сопротивление потоку, воспринимать меньшую скорость потока и иметь меньшие длины. Следовательно, в динамическом режиме тень напряжения может влиять не только на ширину трещин, но также на длину трещин.

Влияние тени напряжения на геометрию трещины может находиться под воздействием многих параметров. Для иллюстрации действия некоторых из этих параметров вычисленные длины трещин для различных разнесений трещин, перепадов давления на перфорациях и анизотропиях напряжения показаны в таблице 3.

На фиг. 11.1 и 11.2 показана геометрия трещин, полученная прогнозированием с помощью нетрадиционной модели трещин для случая большого падения давления на перфорациях и случая большого разнесения трещин (например, около 120 футов (36,6 м)). На фиг. 11.1 и 11.2 даны схематичные представления 1100.1 и 1100.2, показывающие пять трещин 1123.1-1123.5 около буровой скважины 1104. Когда падение давления на перфорациях большое, может создаваться большая отклоняющая сила, вследствие которой скорость потока будет неравномерно распределяться по всем кластерах перфораций. Следовательно, тень напряжения может ослабляться, а результирующие длины трещин могут становиться приблизительно равными показанным на фиг. 11.1. Когда разнесение трещин большое, эффект тени напряжения может рассеиваться и трещины могут иметь приблизительно одинаковые размеры, показанные на фиг. 11.2.

Случай №2, сложные трещины

В примере из фиг. 12 нетрадиционная модель трещин использовалась для моделирования 4-этапной операции гидравлического разрыва пласта в горизонтальной скважине в глинистом пласте. См., например, Cipolla С, Weng X., Mack М., Ganguly U., Kresse O., Gu H., Cohen С.and Wu R., "Integrating microseismic mapping and complex fracture modeling to characterize fracture complexity", Paper SPE 140185, presented at the SPE Hydraulic Fracturing Conference and Exhibition, Woodlands, Texas, USA, January 24-26, 2011 (в дальнейшем "Cipolla 2011"), полное содержание источника включено в эту заявку путем ссылки. Скважина может быть обсаженной и цементированной и каждый этап закачивания осуществляется через три или четыре кластера перфораций. На каждом из четырех этапов может быть приблизительно 25000 баррелей (4000 м³) жидкости и 440000 фунтов (2·10⁶ кг) проппанта. Исчерпывающие данные можно получать в скважине, в том числе высококачественные диаграммы акустического каротажа, которые обеспечивают оценку минимального и максимального горизонтального напряжения. Микросейсмические картированные данные можно получать на всех этапах. См., например, Daniels J., Waters G., LeCalvez J., Lassek J. and Bentley D., "Contacting more of the Barnett shale through an integration of real-time microseismic monitoring, petrophysics and hydraulic fracture design", Paper SPE 110562, presented at the 2007 SPE Annual Technical Conference and Exhibition, Anaheim, California, USA, October 12-14, 2007. Этот пример показан на фиг. 12. На фиг. 12 представлен график, показывающий микросейсмическое картирование микросейсмических событий 1223 около буровой скважины 1204 на различных этапах.

Анизотропия напряжения из высококачественной диаграммы акустического каротажа проявляется как более высокая анизотропия напряжения в нижней секции скважины по сравнению с устьем скважины. Усовершенствованная трехмерная интерпретация

сейсмических данных показывает, что преобладающее направление естественных трещин в нижней секции ориентировано от северо-востока к юго-западу, а в устье изменяется и ориентировано от северо-запада к юго-востоку. См., например, Rich J.P. and Ammerraan М., "Unconventional geophysics for unconventional plays", Paper SPE 131779, presented at the Unconventional Gas Conference, Pittsburg, Pennsylvania, USA, February 23-25, 2010, полное содержание источника включено в эту заявку путем ссылки.

Результаты моделирования могут быть основаны на нетрадиционной модели трещин без полного расчета тени напряжения (см., например, Cipolla 2011), в том числе без напряжения сдвига и поворота трещин (см., например, Weng 2011). Как предложено в этой заявке, модель можно обновлять при использовании полной модели напряжения. На фиг. 13.1-13.4 показан вид в плане моделированной системы 1306 трещин возле буровой скважины 1304 для всех четырех этапов, соответственно, и для сравнения показаны соответствующие микросейсмические измерения 1323.1-1323.4.

Из результатов моделирования на фиг. 13.1-13.4 можно видеть, что на этапах 1 и 2 близко расположенные трещины не расходятся значительно. Это может быть следствием высокой анизотропии напряжения в нижней секции буровой скважины. На этапах 3 и 4, на которых анизотропия напряжения меньше, можно видеть большее расхождение трещин, являющееся результатом эффекта тени напряжения.

Случай №3, многоэтапный пример

Случай №3 является примером, показывающим, каким образом тень напряжения из предшествующих этапов может влиять на картину развития системы трещин гидравлического разрыва на следующих этапах воздействия на пласт, приводя к изменению общей картины образованной системы трещин гидравлического разрыва в случае четырехэтапного воздействия на пласт.

Этот случай включает в себя четыре этапа операции гидравлического разрыва. Скважина является обсаженной и цементированной. На этапах 1 и 2 осуществляют закачивание через три перфорированных кластера, а на этапах 3 и 4 осуществляют закачивание через четыре перфорированных кластера. Структура породы является изотропной. Входные параметры перечислены в таблице 4, приведенной ниже. Виды сверху полной системы трещин гидравлического разрыва с учетом и без учета тени напряжения из предшествующих этапов показаны на фиг. 13.1-13.4.

На фиг. 14.1-14-4 даны схематичные представления 1400.1-14 00.4, показывающие систему 1429 трещин на различных этапах во время операции гидравлического разрыва. На фиг. 14.1 показана система 1429 дискретных трещин (СДТ) до воздействия на пласт. На фиг. 14.2 показана моделированная система 1429 дискретных трещин после первого этапа воздействия на пласт. Вследствие первого этапа воздействия на пласт система 1429 дискретных трещин имеет развившиеся трещины 1431 гидравлического разрыва (ТГР), продолжающиеся от нее. На фиг. 14.3 показана система дискретных трещин с моделированными трещинами 1431.1-1431.4 гидравлического разрыва, развившимися в течение соответствующих четырех этапов, но без учета влияния предшествующих этапов. На фиг. 14.4 показана система дискретных трещин с изображением трещин 1431.1, 1431.2′-1431.4′ гидравлического разрыва, развившихся в течение четырех этапов, но без учета влияния на трещины теней напряжения и трещин гидравлического разрыва из предшествующих этапов.

Когда этапы выполняют отдельно, то, как показано на фиг. 14.3, их можно не представлять себе относительно друг друга. Когда тень напряжения и трещины гидравлического разрыва из предшествующих этапов учитывают, как на фиг. 14.4, картина развития может изменяться. Трещины 1431.1 гидравлического разрыва, образуемые на первом этапе, являются одинаковыми в обоих вариантах, показанных на фиг. 14.3 и 14.4. На картину развития на втором этапе 1431.2 может влиять первый этап через посредство тени напряжения, а также через посредство новой системы дискретных трещин (в том числе через посредство трещины 1431.1 гидравлического разрыва из этапа 1), что приводит к изменению картин развития трещин 1431.2′ гидравлического разрыва. Трещина 14 31.1′ гидравлического разрыва может начать повторять трещину 1431.1 гидравлического разрыва, образованную на этапе 1, когда его принимают во внимание. На третьем этапе 1431.3 может повторять трещину гидравлического разрыва, образованную в течение второго этапа 1432.2, 1431.2′ воздействия на пласт, и может отсутствовать развитие на очень большое расстояние вследствие эффекта тени напряжения из второго этапа, как показано при помощи 1431.3 в сопоставлении с 1431.3′. Для четвертого этапа (1431.4) может иметься тенденция поворота по сравнению с третьим этапом, когда это возможно, но может быть повторение трещины 1431.3′ гидравлического разрыва из предшествующих этапов, когда происходит столкновение, и это отображено трещиной 1431.4′ гидравлического разрыва на фиг. 14.4.

Предложен способ вычисления тени напряжения в системе сложных трещин гидравлического разрыва. Способ может включать в себя усовершенствованный двумерный или трехмерный метод разрывных смещений с коррекцией за влияние конечной высоты трещин. Способ можно использовать для аппроксимирования взаимодействия между различными ответвлениями трещин в системе сложных трещин для фундаментального решения трехмерной задачи о трещинах. Это вычисление тени напряжения можно включать в нетрадиционную модель трещин, сложную модель системы трещин. Результаты для простых случаев двух трещин показывают, что в зависимости от первоначальных относительных положений трещины могут притягиваться или отталкиваться друг от друга, и результаты являются вполне сравнимыми с результатами из независимой двумерной модели непланарных трещин гидравлического разрыва.

Имитационные модели многочисленных параллельных трещин от горизонтальной трещины можно использовать для подтверждения свойств двух самых крайних трещин, которые могут быть более определяющими, в то время как внутренние трещины имеют меньшую длину и ширину вследствие эффекта тени напряжения. Кроме того, эти свойства могут зависеть от других параметров, таких как перепад давления на перфорациях и расстояние между трещинами. Когда расстояние между трещинами больше высоты трещин, эффект тени напряжения может ослабляться и могут быть незначительные различия между многочисленными трещинами. Когда падение давления на перфорациях большое, может создаваться значительное отклонение от равномерного распределения потока по кластерам перфораций и размеры трещин могут становиться приблизительно равными независимо от эффекта тени напряжения.

Если при создании сложных трещин пласты имеют небольшую анизотропию напряжения, взаимодействие трещин может приводить к сильной расходимости трещин, когда они стремятся оттолкнуться друг от друга. С другой стороны, при большой анизотропии напряжения может быть ограниченная расходимость трещин, когда анизотропия напряжения ослабляет явление поворота трещин, обусловленное тенью напряжения, и трещина может принуждаться к прохождению в направлении максимального напряжения. Независимо от степени расходимости трещин затенение напряжения может оказывать влияние на ширину трещины, что может влиять на распределение скоростей нагнетания по многочисленных кластерам перфораций, общую площадь, занимаемую системой трещин, и размещение проппанта.

На фиг. 15 представлена блок-схема последовательности действий способа 1500 выполнения операций гидравлического разрыва пласта на месте расположения скважины, таком как место 100 расположения скважины из фиг. 1.1. Место расположения скважины находится в подземном пласте, имеющем буровую скважину, проходящую через него, и систему трещин. Система трещин имеет естественные трещины, показанные на фиг. 1.1 и 1.2. Способ (1500) может включать в себя выполнение (1580) операции возбуждения скважины путем возбуждения места расположения скважины нагнетанием жидкости вместе с проппантом в систему трещин для образования системы трещин гидравлического разрыва. В некоторых случаях возбуждение может выполняться на месте расположения скважины или путем моделирования.

Способ включает в себя получение (1582) данных о месте расположения скважины и механической модели геологической среды для подземного пласта. Данные о месте расположения скважины могут включать в себя любые данные относительно места расположения скважины, которые могут быть полезными при моделировании, такие как параметры естественных трещин, изображения системы трещин и т.д. Параметры естественных трещин могут включать в себя, например, ориентацию, распределение плотности и механические свойства (например, коэффициенты трения, связность, сопротивление развитию трещины и т.д. Параметры трещин можно получать на основании непосредственных наблюдений скважинных каротажных изображений, оценивания трехмерных сейсмических исследований, алгоритма прослеживания движения муравьев, оценивания анизотропии звуковых волн, кривизны геологического слоя, микросейсмических событий или изображений и т.д. Примеры способов получения параметров трещин представлены в заявках PCT/US 2012/48871 и US 2008/0183451, полные содержания которых включены в эту заявку путем ссылки.

Изображения можно получать, например, при наблюдении скважинных каротажных изображений, оценивании размеров трещин на основании скважинных измерений, формировании микросейсмических изображений и/или аналогичным образом. Размеры трещин можно оценивать путем анализа сейсмических измерений, с помощью алгоритма прослеживания движения муравьев, и оценивания акустических измерений, геологических измерений и/или аналогичных. Кроме того, другие данные о месте расположения скважины можно получать из различных источников, таких как измерения на месте расположения скважины, исторические данные, предположения и т.д. Такие данные могут включать в себя, например, данные о заканчивании скважины, геологической структуре, петрофизические, геомеханические, каротажные измерения и данные других видов. Механическую модель геологической среды можно получать при использовании обычных способов.

Способ (1500) также включает в себя образование (1584) картины роста трещин гидравлического разрыва с течением времени, например, во время операции возбуждения скважины. На фиг. 16.1-16.4 показан пример образования (1584) картины роста трещин гидравлического разрыва. Как показано на фиг. 16.1, в начальном состоянии система 1606.1 естественных трещин 1623 расположена в подземном пласте 1602 с буровой скважиной 1604 в нем. Когда проппант нагнетают в подземный пласт 1602 из буровой скважины 1604, давлением проппанта создаются трещины 1691 гидравлического разрыва вокруг буровой скважины 1604. Трещины 1691 гидравлического разрыва распространяются в подземный пласт вдоль L₁ и L₂ (фиг. 16.2) и, как показано на фиг. 16.2-16 - 3, с течением встречаются с другими трещинами в системе 1606.1 трещин. Точки контакта с другими трещинами представляют собой пересечения 1625.

Образование (158 4) может включать в себя распространение (158 6) трещин гидравлического разрыва от буровой скважины и в систему трещин подземного пласта для формирования системы трещин гидравлического разрыва, включающей в себя естественные трещины и трещины гидравлического разрыва, показанные на фиг. 16.2. Картина роста трещин основана на параметрах естественных трещин и минимальном напряжении и максимальном напряжении, действующих на подземный пласт. Образование также может включать в себя определение (1588) параметров трещин гидравлического разрыва (например, давления р, ширины w, скорости q потока и т.д.), определение (1590) параметров переноса для проппанта, проходящего через систему трещин гидравлического разрыва, и определение (1592) размеров (например, высоты) трещин гидравлического разрыва на основании, например, определенных параметров трещин гидравлического разрыва, определенных параметров переноса и механической модели геологической среды. Параметры трещин гидравлического разрыва можно определять после распространения. Кроме того, определение (1592) можно выполнять на основании параметров переноса проппанта, параметров места расположения скважины и других элементов данных.

Образование (1584) может включать в себя моделирование свойств породы на основании механической модели геологической среды, описанной, например, в Koutsabeloulis and Zhang, "3D reservoir geomechanics modeling in oil/gas field production", SPE Paper 126095, 2009 SPE Saudi Arabia Section Technical Symposium and Exhibition held in Al Khobar, Saudi Arabia, 9-11 May, 2009. Кроме того, образование может включать в себя моделирование операции гидравлического разрыва с использованием данных о месте расположения скважины, параметров трещин и/или изображений в качестве входных данных программного обеспечения для модели, такой как нетрадиционная модель трещин, чтобы получать последовательные изображения наведенных трещин гидравлического разрыва в системе трещин.

Кроме того, способ (1500) может включать в себя осуществление (1594) затенения напряжения относительно трещин гидравлического разрыва для определения взаимного влияния трещин гидравлического разрыва (или влияния на другие трещины) и повторение (1598) образования (1584) на основе затенения напряжения и/или определенного взаимного влияния трещин гидравлического разрыва. Повторение можно выполнять для учета взаимного влияния трещин, которое может сказываться на росте трещин. Осуществление затенения напряжения может включать в себя, например, выполнение двумерного или трехмерного метода разрывных смещений для каждой из трещин гидравлического разрыва и обновление картины роста трещин с течением времени. Картина роста трещин может распространяться перпендикулярно к локальному главному направлению напряжения в соответствии с затенением напряжения. Картина роста трещин может включать в себя влияния естественных трещин и трещин гидравлического разрыва на систему трещин (см. фиг. 16.3).

Затенение напряжения можно осуществлять для многочисленных буровых скважин на месте расположения скважин. Затенения напряжения от различных буровых скважин можно объединять, чтобы определять взаимодействие трещин для каждой из буровых скважин. Образование можно повторять для каждого из затенений напряжения, осуществляемых для одной или нескольких из многочисленных буровых скважин. Кроме того, образование можно повторять для затенения напряжения, осуществляемого при выполнении моделирования с учетом многочисленных буровых скважин. Кроме того, многократные моделирования можно выполнять относительно одной и той буровой скважины при различных сочетаниях данных и сравнивать при желании. Исторические и другие данные также можно вводить в этап образования, чтобы получать многочисленные источники информации для учета в окончательных результатах.

Кроме того, способ включает в себя определение (1596) характера пересечения трещин гидравлического разрыва и встречающейся трещины, если трещина гидравлического разрыва встречается с другой трещиной, и повторение (1598) образования (1584) на основании характера пересечения, если трещина гидравлического разрыва встречается с трещиной (см., например, фиг. 16.3). Характер пересечения можно определять при использовании, например, способов из заявки PCT/US 2012/059774, полное содержание которой включено в эту заявку путем ссылки.

Определение характера пересечения может включать в себя осуществление затенения напряжения. В зависимости от скважинных условий картина роста трещин может изменяться или не изменяться, когда трещина гидравлического разрыва встречается с трещиной. Когда давление гидравлического разрыва больше, чем напряжение, действующее на встреченную трещину, картина роста трещин может распространяться вдоль встреченной трещины. Картина роста трещин может распространяться вдоль встреченной трещины до тех пор, пока не будет достигнут конец естественной трещины. Направление картины роста трещин может изменяться на конце естественной трещины, при этом, как показано на фиг. 16.4, картина роста трещин будет продолжаться в направлении, перпендикулярном к минимальному напряжению, на конце естественной трещины. Как показано на фиг. 16.4, трещина гидравлического разрыва распространяется по новой траектории 1627 в соответствии с локальными напряжениями σ₁и σ₂.

По желанию, способ (1500) может включать в себя проверку (1599) достоверности картины роста трещин. Проверку достоверности можно выполнять путем сравнения результирующей картины роста с другими данными, такими как микросейсмические изображения, показанные, например, на фиг. 7.1 и 7.2.

Способ можно выполнять в любом порядке и при необходимости повторять. Например, этапы образования (1584)-(1599) можно повторять с течением времени, например, в соответствии с итерацией, когда система трещин изменяется. Образование (1584) можно выполнять для обновления итерированного моделирования, выполненного во время образования, для учета взаимодействия и влияний многочисленных трещин, когда систему трещин моделируют с течением времени.

Хотя настоящее раскрытие описано применительно к примерам вариантов осуществлений и реализациям осуществлений, настоящее раскрытие не ограничено такими примерами вариантов осуществления и/или реализациями. Точнее, в системах и способах настоящего раскрытия допускаются различные модификации, изменения и/или улучшения без отступления от сущности или объема настоящего раскрытия. В соответствии с этим объемом настоящего раскрытия безусловно охватываются все такие модификации, изменения и улучшения.

Следует заметить, что при разработке любого такого актуального варианта осуществления или многочисленных реализаций должны приниматься специфические решения для достижения конкретных намерений разработчика, такие как согласование с ограничениями, связанными с системой и связанными с деловой деятельностью, которые изменяются от одной реализации к другой. Кроме того, следует понимать, что такие разработки могут быть сложными и требующими много времени, но тем не менее должны быть обычным делом для специалистов в данной области техники, имеющих выгоду от этого раскрытия. В дополнение к этому используемые варианты осуществления, раскрытые в этой заявке, могут также включать в себя некоторые компоненты, отличающиеся от перечисленных.

В описании каждое численное значение следует читать один раз как модифицированное термином «около» (за исключением случаев, когда оно уже определенно модифицировано таким образом) и затем читать еще раз как не модифицированное, если не указан иной смысл. Кроме того, следует понимать, что в описании для любого диапазона, приведенного или указанного как используемого, пригодного или аналогичного, предполагается, что любое или каждое значение в диапазоне, в том числе начальная точка и конечная точка, считается точно определенным. Например, «диапазон от 1 до 10» следует читать как показывающий каждое и любое возможное число на всем протяжении континуума между около 1 и около 10. Таким образом, даже если конкретные точки данных в диапазоне или же точки данных вне диапазона явным образом идентифицированы или отнесены к нескольким специфическим точкам, то следует полагать и понимать, что любая и все точки данных в диапазоне считаются точно определенными и что имеются сведения о всем диапазоне и всех точках в диапазоне.

Положения, изложенные в этой заявке, всего лишь обеспечивают информацию, относящуюся к настоящему раскрытию, и не могут представлять предшествующий уровень техники, а могут характеризовать некоторые варианты осуществления, иллюстрирующие изобретения. Все источники, цитированные в этой заявке, полностью включены в настоящую заявку путем ссылки.

Хотя выше были подробно описаны всего лишь несколько примеров вариантов осуществления, специалисты в данной области техники без труда поймут, что в примерах вариантов осуществления возможны многочисленные модификации без существенного отклонения от системы и способа для выполнения работ по возбуждению скважины. В соответствии с этим все такие модификации предполагаются включенными в объем этого раскрытия, определенный в нижеследующей формуле изобретения. В формуле изобретения фразы «средство плюс функция» предполагаются охватывающими структуры, описанные в этой заявке, в момент выполнения описанной функции, и не только структурные эквиваленты, но также и эквивалентные структуры. Таким образом, хотя гвоздь и винт не могут быть структурными эквивалентами по той причине, что в гвозде цилиндрическая поверхность используется для скрепления деревянных деталей друг с другом, тогда как в винте используется винтовая поверхность, но в ситуации скрепления деревянных деталей гвоздь и винт могут быть эквивалентными структурами. Ясно выраженной целью заявителя является отсутствие ссылки на раздел 35 кодекса законов США, §112, пункт 6, для любых ограничений любого из пунктов формулы изобретения за исключением тех, в которых определенно используются слова «средство для» вместе с соответствующей функцией.

Реферат

Предложен способ выполнения операции гидравлического разрыва на месте расположения скважины с системой трещин. Способ включает в себя получение данных о месте расположения скважины и механической модели геологической среды и образование картины роста трещин гидравлического разрыва в системе трещин с течением времени. Образование включает в себя распространение трещин гидравлического разрыва от буровой скважины и в систему трещин подземного пласта для формирования системы трещин гидравлического разрыва, определение параметров трещин гидравлического разрыва после распространения, определение параметров переноса для проппанта, проходящего через систему трещин гидравлического разрыва, и определение размеров трещин гидравлического разрыва на основании параметров трещин гидравлического разрыва и механической модели геологической среды. Кроме того, способ включает в себя осуществление затенения напряжения относительно трещин гидравлического разрыва для определения взаимного влияния напряжений между трещинами и повторение образования на основании определенного взаимного влияния трещин. Кроме того, способ может включать в себя определение характера пересечения. Технический результат заключается в повышении эффективности моделирования взаимодействия трещин гидравлического разрыва в системах сложных трещин. 16 з.п. ф-лы, 32 ил., 4 табл.

Формула