Способ высокоточного позиционирования аппарата на поверхности луны и устройство для его осуществления - RU2692350C1

Чертежи

Описание

Изобретение относится к космической навигационной технике и может быть использовано для автономного (пассивного) определения селенографических координат работающих на поверхности Луны аппаратов, включая обратную сторону Луны.

Целью изобретения является разработка способа глобального позиционирования аппаратов на поверхности Луны с высокой точностью и высокой оперативностью координатных измерений при обеспечении полной скрытности измерений.

Проведение исследований на поверхности Луны должно опираться на высокоточную систему позиционирования находящихся на Луне объектов, особенно луноходов и пилотируемых аппаратов. При этом повторение методов позиционирования, отработанных на Земле, оказывается невозможным или экономически и организационно нецелесообразным.

Известен астрономический способ определения географических координат точки на земной поверхности, заключающийся в прокладывании меридиана, проходящего через точку позиционирования, и измерении высоты звезды над местным горизонтом и времени в момент ее кульминации. Астрономические измерения координат являются самыми точными, но требуют развертывания астропунктов в точке измерения. Трудности настройки наблюдательной техники и сложность проведения самих наблюдений требует участия квалифицированных специалистов, поэтому астропункты использовались только в узлах Геодезической Сети I класса. Недостатком Астрономического способа в условиях Луны является необходимость доставки на Луну специальных телескопов и участия астронавтов в наблюдениях в каждой точке измерений, а также системы определения звездного времени на нулевом меридиане и транслирования его в позиционируемый пункт [1-2].

Известен способ позиционирования на Земле, заключающийся в измерении расстояний от точки измерения до нескольких космических аппаратов, передающих специальные навигационные сигналы. Если пространственное положение каждого космического аппарата известно с высокой точностью, то измеренные расстояния до них позволяют вычислить пространственное положение измеряемой точки и определить ее географические координаты. Системы глобального позиционирования GPS, Galileo, ГЛОНАСС и др. [3-5], использующие этот способ, позволяют обеспечить измерение координат скрытных объектов. Недостатком этого способа является необходимость использования большой группировки навигационных спутников (от 18 до 24), необходимость постоянного контроля орбитальных параметров всех спутников наземными средствами, и большая уязвимость системы от внешних воздействий. Применение этого способа на Луне с целью позиционирования небольшого числа работающих на Луне аппаратов нецелесообразно.

Известен способ создания триангуляционной селенодезической сети, состоящей из одного селенодезического спутника (СДС) и нескольких селенодезических пунктов (СДП) [6-7]. Этот способ состоит в размещении на поверхности Луны нескольких пассивных отражателей радиоволн, которые облучаются передатчиком на спутнике. Промежуток времени между посылкой сигнала и получением его отражения определяет расстояние между спутником и отражателем. Наличие измеренных значений дальности позволит решить прямую задачу координатной привязки СДП при известных параметрах орбиты СДС и обратную задачу - самоопределение параметров орбиты СДС при известных координатах СДП. Однако во всех случаях необходимо привлекать наземные радиотехнические средства для определения параметров орбиты СДС (на видимых с Земли участках орбиты) и координат СДП, размещенных на видимой с Земли стороны Луны. Кроме того, недостатком способа является необходимость перманентного проведения измерений орбитальным аппаратом с ограниченным сроком функционирования, то есть плановой замены СДС.

Известен также способ позиционирования аппаратов на Луне, снабженных автономными световыми маяками, угловое положение которых относительно звезд измеряется угломерным инструментом, размещаемым на борту полярного спутника Луны [8-10]. При этом топоцентрические углы между спутником и навигационной звездой являются дополнительными к измеряемым углам между звездой и маяком. Тем самым световой маяк выполняет роль астропункта на поверхности Луны в астрономическом способе позиционирования. Этот способ позволяет определять координаты маяка с точностью в единицы метров. Способ можно считать скрытным, так как маяк включается только на время измерений кооперируемым аппаратом, что позволяет исключить случайное обнаружение позиционируемого объекта из космоса по его излучению. Недостатком способа является необходимость проведения измерений орбитальным аппаратом, а также гарантированная периодичность измерения координат раз в четырнадцать суток.

Задача, на решение которой направлено заявленное изобретение, заключается в разработке способа глобального позиционирования аппаратов на поверхности Луны, сочетающего с высокую точность (единицы метров) с высокой оперативностью (частотой) координатных измерений при обеспечении скрытности измерений и без использования постоянно действующей группировки СДС.

Эта задача решается за счет предложенного способа высокоточного позиционирования аппарата на поверхности Луны, состоящего в измерении ориентации местной вертикали в точке позиционирования в аппаратной системе координат с помощью бортового датчика вертикали, в измерении положений двух навигационных звезд в аппаратной системе координат с помощью бортовых звездных датчиков, при фиксации момента проведения измерений в шкале всемирного времени бортовой службой времени, в вычислении положения местного меридиана в системе лунных небесных координат с помощью бортового вычислительного устройства по данным проведенных измерений и с использованием известных экваториальных координат навигационных звезд и экваториальных координат полюса Луны. При этом в вычислении положения нулевого меридиана системы селенодезических координат для момента времени измерений используются параметры математической модели движения Луны, в результате чего широта позиционируемой точки вычисляется как высота полюса Луны над местным горизонтом, а долгота позиционируемой точки определяется как разность прямых восхождений местного и нулевого меридианов, вычисленных для момента проведения измерений. Устройство для реализации такого способа состоит из двух бортовых звездных датчиков, бортового датчика вертикали, бортовой службы времени и бортового вычислительного устройства, причем выходы службы времени, звездных датчиков и датчика вертикали соединены со входами вычислительного устройства, в котором заложены значения экваториальных координат навигационных звезд, положение полюса Луны и математическая модель движения Луны.

Поставленная цель достигается тем, что находящийся на Луне аппарат снабжен звездными датчиками, датчиком вертикали, бортовым вычислительным комплексом и системой точного времени, необходимыми для проведения работ по целевому назначению аппарата, а в бортовой вычислительный комплекс дополнительно загружена математическая модель движения Луны, т.е. теоретически заданное положение полюса Луны и нулевого меридиана на небесной сфере в любой момент времени, а также производится фиксация момента проведения измерений. В результате измерений широта точки позиционирования вычисляется как высота лунного полюса над местным горизонтом, а долгота - как разность прямых восхождений (в системе экваториальных небесных координат) нулевого и местного меридианов, вычисленных для момента проведения измерений.

Сочетание модельных характеристик ориентации тела Луны относительно звезд и результатов измерений положений позиционируемого аппарата относительно звезд и направления на центр масс Луны позволяет однозначно определить широту и долготу аппарата в селеноцентрической системе координат с точностью, определяемой точностью проводимых измерений. При использовании штатных звездных датчиков и датчика вертикали, применяемых в запускаемых космических аппаратах, точность позиционирования предложенным способом будет не ниже единиц метров, но может быть повышена при применении более точных звездных датчиков и датчика вертикали.

Техническим результатом, обеспечиваемым приведенной совокупностью признаков, является обеспечение высокоточного позиционирования космического аппарата на поверхности Луны в любой требуемый момент времени при частоте измерений до 10 Гц, с сохранением скрытности измерений, причем метод не требует использования устройств, расположенных вне позиционируемого аппарата, что позволяет определять его селенографические координаты без возможности его обнаружения.

Применение предлагаемого способа происходит следующим образом. Находящийся на поверхности Луны аппарат производит измерение в бортовой (приборной) системе координат положений точки местного зенита с помощью датчика вертикали и положений двух навигационных звезд с известными экваториальными координатами, при этом фиксируется момент проведения измерений. На основании результатов измерений в бортовом вычислительном комплексе вычисляются положение проекции полюса Луны на небесную сферу, а также часовой угол точки весеннего равноденствия. Далее, на основании параметров модели движений Луны, заложенных в бортовое вычислительное устройство, вычисляется часовой угол нулевого меридиана Луны в момент проведения измерений. Искомые широта и долгота позиционируемой точки определяются как высота полюса Луны над местным горизонтом и как разность часового угла точки весеннего равноденствия и часового угла нулевого меридиана, соответственно.

Устройство работает следующим образом. Находящийся на поверхности Луны аппарат ориентирован произвольным образом по углу наклона и в азимутальном направлении. В момент времени Т происходит опрос бортовых датчиков, в результате которого в бортовое вычислительное устройство поступают измеренные значения координат точки местного зенита и двух навигационных звезд, которые определены в аппаратной (приборной) системе координат. На основании результатов измерений в бортовом вычислительном устройстве определяется пространственная ориентация приборной системы координат и вычисляются величины высоты полюса Луны над местным горизонтом (широта позиционируемой точки) и положение местного меридиана (часовой угол точки его пересечения с лунным небесным экватором). Далее на основании заложенных в БВУ параметров математической модели движений Луны вычисляется для момента времени Т часовой угол нулевого меридиана селенодезической системы координат и вычисляется разность между ним и часовым углом точки пересечения местного меридиана с небесным экватором (долгота позиционируемой точки).

Сущность изобретения поясняется чертежами, на которых изображены точки на небесной сфере, координаты которых измеряются на борту позиционируемого аппарата:

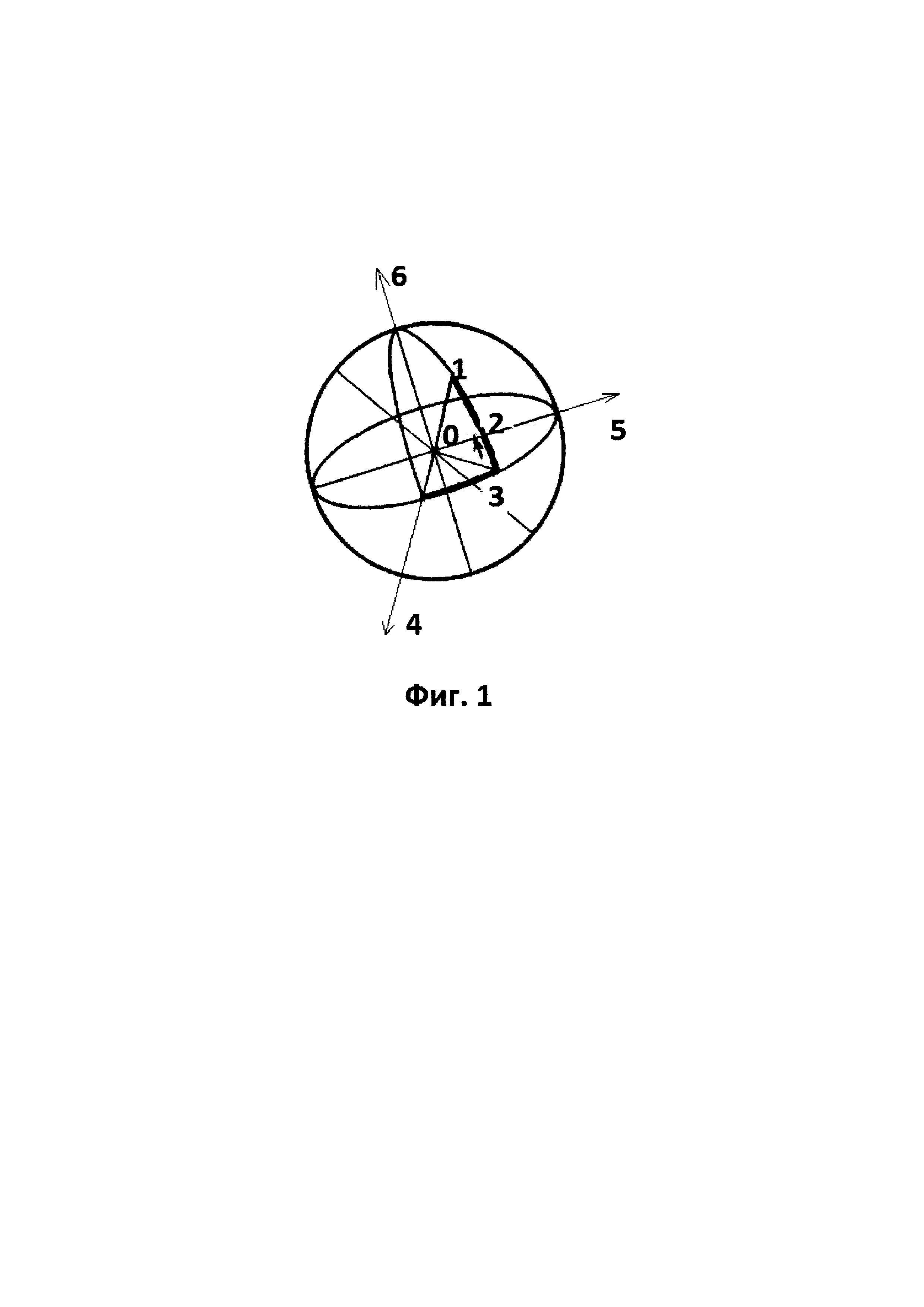
Фиг. 1 - Определение бортовым датчиком вертикали положения точки зенита в системе аппаратных координат.

Фиг. 2 - Схема взаимного расположения точек, для которых в приборной системе координат измерены координаты.

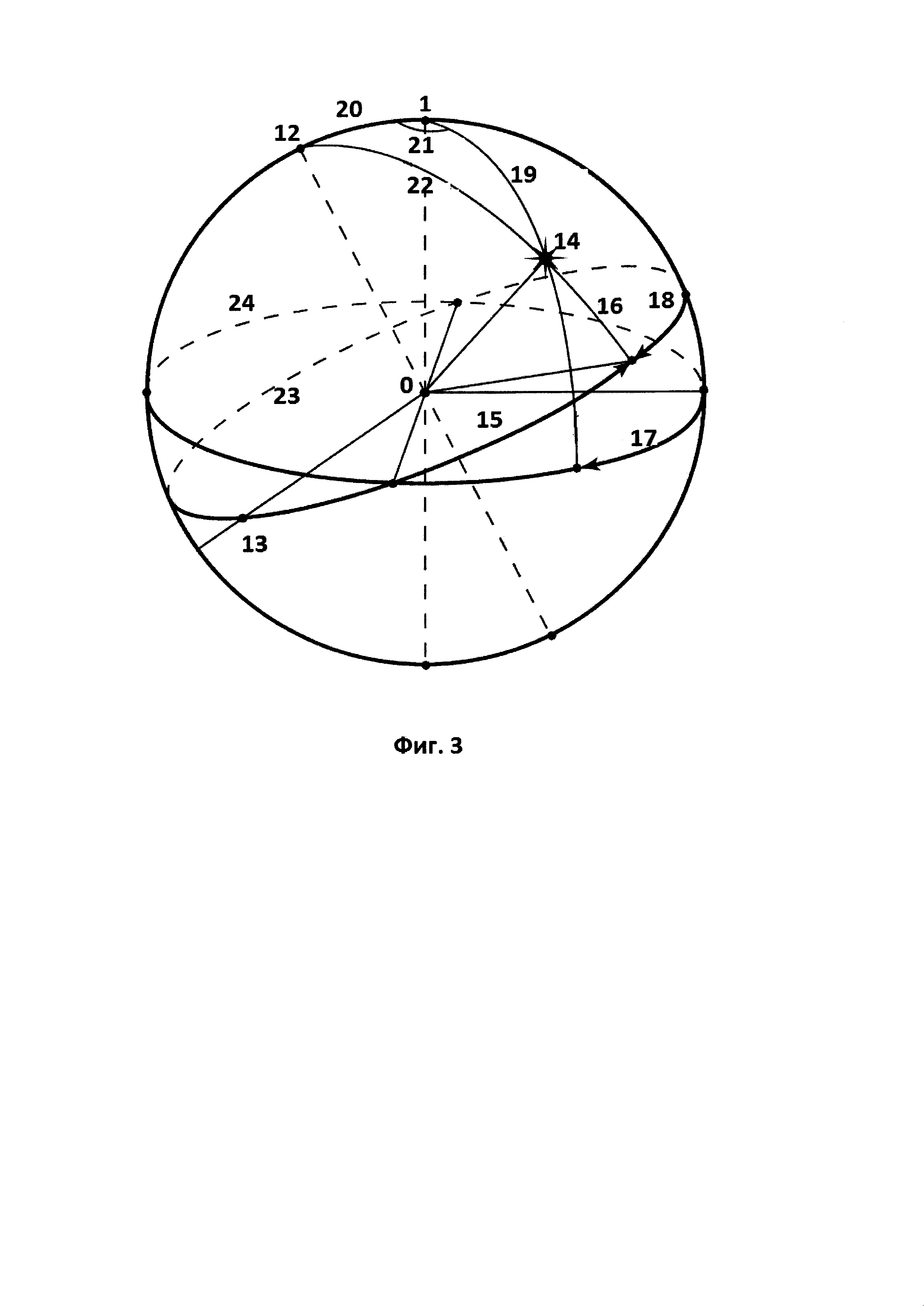
Фиг. 3 - Координаты звезды в экваториальной и топоцентрической азимутальной системах координат.

На Фиг. 1 изображена схема, в соответствии с которой 0 - центр системы координат, координаты точки зенита 1 - Z{2 - h_Z, 3 - A_Z} определяются датчиком вертикали в системе аппаратных координат {4 - X', 5 - Y', 6 - Z'}, где h_Z - высота точки зенита и A_Z - азимут точки зенита в аппаратной системе координат.

На Фиг. 2 показано взаимное расположение координат точек (точки местного зенита 1 - Z, и двух звезд 7 - S1 и 8 - S2), измеряемых в аппаратной системе координат. Бортовой звездный датчик отождествляет звездный узор в своем поле зрения и измеряет видимые координаты звезд {9 - h_s1, 10 - A_s1} и {11 - h_s2, 12 - A_s2} в системе аппаратных координат {4 - X', 5 - Y', 6 - Z'} (ориентация осей – вдоль конструктивных осей аппарата). В системе топоцентрических азимутальных координат места посадки азимуты звезд S1 и S2 можно вычислить из решения сферических треугольников (Z, Z′, S1) и (Z, Z′, S2) соответственно, в которых:

сторона (Z′, S1) является частью дуги большого круга, равной (90° - h_S1);

сторона (Z, Z′) является частью дуги большого круга, равной (90° - h_Z);

сторона (Z, S1) является частью дуги большого круга, равной (90° - H_S1);

угол ∠Z′ZS1 равен азимуту звезды S1 в системе местных азимутальных координат, отсчитываемому от меридиана точки Z′, то есть (А_S1-Ao)

сторона (Z′, S2) является частью дуги большого круга, равной (90° - h_S2);

сторона (Z, S2) является частью дуги большого круга, равной (90° - H_S2);

угол ∠Z′ZS2 равен азимуту звезды S2 в системе местных азимутальных координат, отсчитываемому от меридиана точки Z′, то есть (А_S2-Ao)

Решение сферических треугольников дает:

cos(90° - H_S1) = cos(90° - h_S1)cos(90° - h_Z) + sin(90° - h_S1)sin(90° - h_Z)cos(А_S1-A_Z)

cos(90° - h_S1) = cos(90° - H_S1)cos(90° - h_Z) + sin(90° - H_S1)sin(90° - h_Z)cos(А_S1-A₀)

и

cos(90° - H_S2) = cos(90° - h_S2)cos(90° - h_Z) + sin(90° - h_S2)sin(90° - h_Z)cos(А_S2-A_Z)

cos(90° - h_S2) = cos(90° - H_S2)cos(90° - h_Z) + sin(90° - H_S2)sin(90º - h_Z)cos(А_S2-A₀)

Здесь:

h_S1 - высота звезды S1 в системе приборных (аппаратных) координат;

h_S2 - высота звезды S2 в системе приборных (аппаратных) координат;

h_Z - высота точки зенита в системе приборных (аппаратных) координат;

A_Z - азимут точки зенита в системе приборных (аппаратных) координат.

H_S1 - высота звезды S1 в системе топоцентрических азимутальных координат;

H_S2 - высота звезды S2 в системе топоцентрических азимутальных координат;

А_S1 - азимут звезды S1 в системе топоцентрических азимутальных координат;

А_S2 - азимут звезды S2 в системе топоцентрических азимутальных координат;

Ao - азимут полюса мира в системе топоцентрических азимутальных координат.

Эта система независимых уравнений позволяет однозначно вычислить азимутальные координаты звезд S1 и S2 в системе топоцентрических координат по результатам измерений положений точки местного зенита и положений звезд в приборной (аппаратной) системе координат.

На Фиг. 3 показаны координаты звезды в экваториальной и топоцентрической азимутальной системах координат.

Для каждой звезды известны ее экваториальные координаты {α_i, δ_i} в системе небесных координат. Экваториальные координаты в земной системе небесных координат отличаются от лунных небесных координат, поскольку полюс Луны не совпадает с полюсом мира. Эти две системы координат отличаются только положением полюсов, поэтому координаты навигационных звезд легко пересчитываются в систему лунных небесных координат, поскольку положение полюса Луны в экваториальной системе координат известно с высокой точностью. Поэтому ниже все указания на систему небесных координат относятся к системе лунных экваториальных небесных координат.

Взаимная ориентация аппаратной системы координат и системой небесных координат задается положением полюса мира 12 - P{h_P, A_P} и направлением на точку весеннего равноденствия 13 - γ{h_γ, A_γ} в аппаратной системе координат. 14 - произвольная звезда S с экваториальными координатами {15 - α_s, 16 - δ_s}. 17 - ее азимут А_S в системе топоцентрических азимутальных координат, 18 - t_S - часовой угол звезды. Hs - высота звезды S в системе топоцентрических азимутальных координат, на Фиг. 3 угол (90°-H_S) обозначен числом 19. ϕ - широта позиционируемой точки в селеноцентрической системе координат, на Фиг. 3 угол (90° - ϕ) обозначен числом 20. 21 - угол (180° -As), 22 - угол (90° - δ_s), 23 - экватор, 24 - горизонт.

Из решения треугольника PZS имеем:

cosδ_S⋅cost_S =cos(90° - H_S)·cosϕ +sin(90° - H_S)·sinϕ·cosA_S,

cosδ_S⋅sint_S =sin(90° - H_S)·sinA_S,

sinδ_S =cos(90° - H_S)·sinϕ - sin(90° - H_S)⋅cosϕ⋅cosA_S.

Часовой угол звезды равен сумме значений звездного времени (выраженного в угловой мере) и прямого восхождения звезды По этим уравнениям на основании измеренных в момент времени T положений точки зенита и двух навигационных звезд должен быть вычислен часовой угол точки весеннего равноденствия t_γ :

t_γ = t_S1 + α_S1 = t_S2 + α_S2

который равен значению местного звездного времени в точке позиционирования на момент Т, и равен прямому восхождению местного меридиана α_М(Т).

Далее по параметрам модели движения Луны для того же момента Т вычисляется величина прямого восхождения нулевого меридиана α_Мо(Т).

Искомое значение долготы позиционируемой точки λ вычисляется как разность

λ = α_М(Т) - α_Мо(Т).

Таким образом, на основании одновременных измерений в аппаратной (приборной) системе координат точки местного зенита датчиком вертикали и координат двух звезд (с известными экваториальными координатами) в той же системе координат бортовыми звездными датчиками, измерению момента времени проведения измерений и вычислению на этот момент времени величины прямого восхождения проекции нулевого меридиана селенодезической системы координат исключительно на основе параметров модели движения Луны в бортовом вычислительном устройстве могут быть вычислены селенодезические координаты позиционируемой точки без использования обмена информацией с внешними источниками.

Точность позиционирования по описанному способу определяется точностью измерений положений звезд и местной вертикали. Если на борту посадочного аппарата будут применяться 6-секундные звездные датчики и датчик вертикали аналогичной точности, то точность вычисления широты позиционируемой точки будет близка к 6'', что соответствует ошибке положения по меридиану 35 метров. Ошибка позиционирования в широтном направлении (по долготе), в силу медленного осевого вращения Луны, будет зависеть от широты точки и склонений измеряемых навигационных звезд, и составит от 7 до 15 метров. Если же на борту посадочной станции будут применены односекундные датчики, то точность позиционирования по каждой координате возрастет в 6 раз.

ЛИТЕРАТУРА.

1. Подобед В.В., Нестеров В.В. Общая астрометрия . - М.: Наука. Главная редакция физико-математической литературы, 1982. - 576с.

2. В.Е. Жаров. Сферическая астрономия. Фрязино, 2006.

3. GPS tracking system (US Patent 5379224A).

4. Positioning System and Method Thereof (US Patent 12827239).

5. Satellite-based vehicle position determining system (US Patent 4359733A).

6. Глонасс. Принципы построения и функционирования [Р.В. Бакитько и др.]; под ред. А.И. Перова, В.Н. Харисова. Москва, 2005. (Изд. 3-е, перераб.).

7. Чеботарев В.Е., Кудымов В.И., Звонарь В.Д., Внуков А.А., Владимиров А.В. Концепция окололунной навигации, Исследования наукограда. 2014. № 4 (10). С. 14-20.

8. Чеботарев В.Е., Звонарь В.Д., Грицан О.Б., Внуков А.А. Концепция построения триангуляционной селенодезической сети, Исследования наукограда. 2014. № 2 (8). С. 4-9.

9. Багров А.В., Дмитриев А.О., Леонов В.А., Москатиньев И.В., Сысоев В.К., Ширшаков А.Е., Юдин А.Д. Система глобального позиционирования для Луны на основе активных световых маяков. 2017, Вестник НПО им. Лавочкина 38, №4, с.5-10.

10. Багров А.В. Установление селенодезических координат высокой точности на системе размещенных на Луне реперов. Избранные проблемы астрономии // Материалы III Всерос. астроном. конф. “Небо и Земля”. Иркутск. 22-24 ноября 2011 г. Иркутск: Изд-во ИГУ, 2011. С. 295-305.

11. Bagrov A.V. Establishing of fine co-ordinate frame for Mars and atmosphereless bodies // The First Moscow Solar System Symposium. 11-15 October 2010. Space Research Institute. М.: ИКИ РАН, 2010. P. 90.

12. Ширенин А.М., Мазурова Е.М., Багров А.В. Построение высокоточной селенодезической системы координат на физической поверхности Луны с помощью светодиодных маяков, расположенных на ее поверхности // Космические исследования. 2016. Т. 54, № 6. С. 493-498.

Реферат

Группа изобретений относится к автономной космической навигации космических аппаратов (КА), в частности, на обеих сторонах поверхности Луны. Способ включает измерения в аппаратной системе координат ориентации местной вертикали в точке позиционирования КА бортовым датчиком вертикали, а также положений двух навигационных звезд бортовыми звездными датчиками. Момент измерений фиксируют в шкале всемирного времени бортовой службой точного времени. В бортовое вычислительное устройство КА загружена математическая модель движения Луны. По данным измерений оно вычисляет положение местного меридиана на лунной небесной сфере, используя экваториальные координаты навигационных звезд и полюса Луны. При этом широта позиционирования КА вычисляется как высота полюса Луны над местным горизонтом, а долгота - как разность прямых восхождений нулевого и местного меридианов. Техническим результатом является достижение высоких точности, оперативности и скрытности измерений координат КА в любом месте на поверхности Луны. 2 н.п. ф-лы, 3 ил.

Формула