Диск для отсчетных устройств - SU645022A1

Код документа: SU645022A1

Чертежи

Описание

Изобретение относится к области приборостроения и может быть использовано для отсчетных устройств в прецизионных измерительных приборах.

Известны циферблаты отсчетных устройств , выполненные из стекла .

Известен также диск для отсчетных устройств , выполненный из прозрачного материала , преимущественно из стекла, на одной из плоскостей которого нанесена круговая шкала ,{2.

В указанных дисках наряду с изгибными деформациями могут возникать так называемые эллиптические деформации, действующие в плоскости диска и снижающие точность щкалы, особенно при монтаже диска в корпусе прибора. Вторичные ошибки градуировки, вызываемые эллиптическими деформациями градуированного круга. Не могут быть исключены оптической компенсацией , например диаметральным двойным считыванием. Эти эллиптические деформации не могут быть устранены в известных градуированных дисках в случае, когда градуированный диск установлен в - корпусе жестко, с помощью склеивания или посредством скоб, так как от этих мест закрепления на диск действуют радиально направленные силы.

Целью изобретения является повышение

точности щкалы диска отсчетного устройства .

Указанная цель достигается тем, что круговая щкала в предлагаемом устройстве

выполнена на расстоянии Гу 1,52

от оси диска, .;

где г -радиус средней линии шкалы; Га - внешний радиус диска; Гг - радиус отверстия в диске, при этом диск имеет поперечное сечение, составленное из двух прямоугольников, отношение длин которых равно

. л-1

-26 ,Ь

Д2

f iW L/iLV JL

2 «-1 И

п V-r)+ 2(6 )- 2

где ai - длина первого прямоугольника;

а2. - длина второго прямоугольника;

b - высота диска;

&1 - ширина первого прямоугольника;

п - показатель преломления материала диска.

Такое решение позволяет исключить вторичпые ошибки градуировки шкалы, обусловленные изгибом и эллиптическими деформациями , и повысить ее точность.

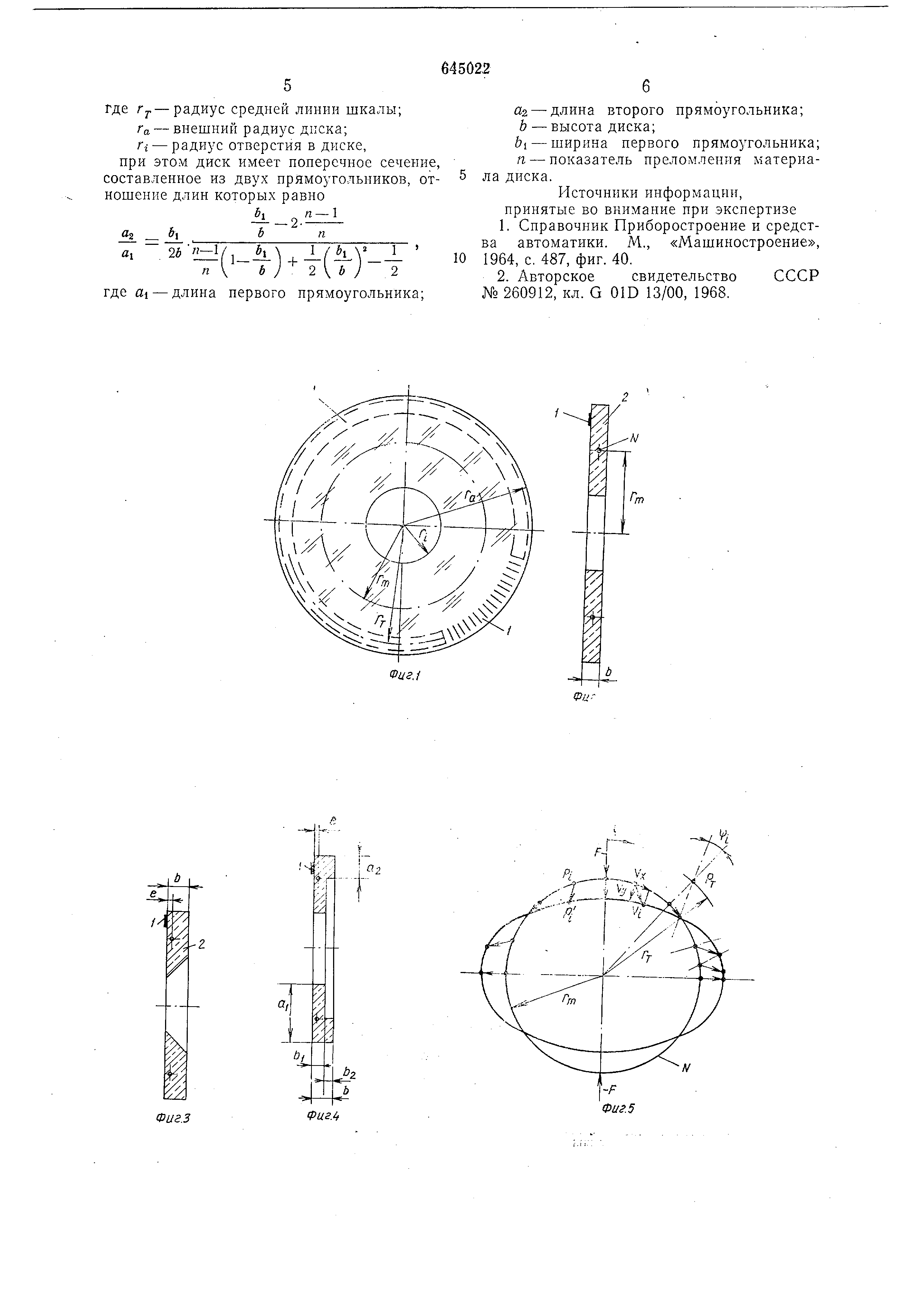
На фиг. 1 схематично показан стеклянный градуированный диск, вид сверху; на фиг. 2 - диск прямоугольного поперечного сечения в разрез е; на фиг. 3 - диск трапециевиднтзтй поперечногй сечения в разрезе; на фиг/ с поперечным сечением, составленггый йз нескольких прямоугольников; на фиг. 5 дано схематическое изображение соотношений деформации в градуированном диске. С помощью фиг. 5 поясняются соотношения , возникающие при эллиптической деформации градуированного диска под действием сил F и -F. Для упрощения на этой фигуре изображено только нейтральное волокно Л диска, принимающее эллиптическую форму под действием сил F и -F. При деформации точки Р; градуировки на недеформированном диске смещаются на составляющую Vi и принимают положение точек Pi на деформированном диске. Поперечные сечения диска испытывают при деформации тангенциальные смещения Vx и радиальные смещения Vy, и дополнительно еще происходит скручивание поперечного сечения на угол -фг. Указанные вторичные ошибки градуировки вызываются тангенциальными смещениями Vx и скручиванием поперечного сечения на угол фг- Воздействие обоих эффектов на градуировку 1 диска 2 могут усиливаться или ослабляться в зависимости от выбора расстояния г. градуировки от оси диска. Как следует из фиг. 5, точки Р находятся на расстоянии г 1,52 ---, при котором оба эффекта компенсируются. Здесь Га+ - наружный и внутренний радиусы диска (фиг. 2). Это происходит при ( и, исходя из соображений симметрии, также при Ф zi: - IT - It; - It. Т 4 3 4 Благодаря этому делительный щтрих градуировки , расположенный в точке , остается безощибочным как на недеформированном , так и эллиптически деформированном диске. Градуировка, расположенная на расстоянии гг -1,52 ° - от оси диска 2, является независимой от эллиптических деформаций . На фиг. 1 показан стеклянный диск с градуировкой , расположенной снаружи нейтрального волокна N на расстоянии г.. Разрез на фиг. 2 показывает градуированный диск с прямоугольным сечением, в котором нейтральное волокно N расположено на расстоянии г - от оси круга. Исходя из геометрических соотношений , плоскость, в которой расположено нейтральное волокно Л, находится на расстоянии 6/2, где 6 -высота диска. Градуировка предусмотрена снаружи плоскости нейтрального волокна Л на поверхности диска. Если смотреть на градуировку с нижней стороны сквозь градуированный диск, то происходит воображаемое смещение плоскости градуировки 1. Наблюдаемая воображаемая плоскость градуировки расположена внутри диска 2. Чтобы избежать нарушения градуировки вследствие изгиба диска , воображаемая плоскость градуировки при наблюдении должна лежать в плоскости нейтрального волокна /V. Для определения положения воображаемой плоскости градуировки имеется соотношение Ь, где п - показатель преломления материала диска; b - толщина диска; е - расстояние градуировки от плоскости нейтрального волокна N. Для прямоугольного поперечного сечения согласно фиг. 2 это условие выполняется тогда, когда . В этом случае , Ьсли показатель преломления материала диска меньше двух, что соответствует практике, то с помощью трапециевидного поперечного диска 2 или поперечного сечения, составленного из двух различных прямоугольников (фиг. 3 и 4) необходимо добиться согласования воображаемой плоскости градуировки с плоскостью нейтрального волокна V. Градуировка должна также в этих случаях находиться на расстоянии ГУ 1,52 от оси 2 дуированного диска, чтобы избежать ощибок градуировки, обусловленных эллиптическими деформациями. Таким образом, благодаря не чувствительной к изгибу и короблению конструкции стеклянного градуированного диска наряду с компенсацией ошибок градуировки, связанных с изгибом, компенсируются ошибки градуировки, связанные с эффектами поперечного смещения и скручивания поперечного сечения диска при эл;я1Гптической деформации . Благодаря этому в первую очередь возможно получить градуированный круг высокой точности. Кроме того, применение предлагаемого диска в измерительных приборах позволяет исключить дорогостоящие оправки и крепления , лищь частично устраняющие коробление диска. Формула изобретения Диск для отсчетных устройств, выполненный из прозрачного материала, преимущественно из стекла, на одной из плоскостей которого нанесена круговая шкала, (Этличаю щийся тем, что, с целью повышения точности шкалы, она выполнена на расстоя ./а rj.,52 от оси диска.

где Гу,- радиус средней линии шкалы; Га - внешний радиус диска; Гг - радиус отверстия в диске, при этом диск имеет поперечное сечеиие, составленное из двух прямоугольников, отношение длин которых равно

2«--2

ai Ь

+ Т

( ) 2 л где ui - длина первого прямоугольника;

uz - длина второго прямоугольника; b - высота диска;

6i - ширина первого прямоугольника; п - показатель преломления материала диска.

Источники информации, принятые во внимание при экспертизе

1.Справочник Приборостроение и средства автоматики. М., «Машиностроение,

1964, с. 487, фиг. 40.

2.Авторское свидетельство СССР № 260912, кл. G 01D 13/00, 1968.