Способ определения размерных параметров газотурбинного двигателя - RU2694693C2
Код документа: RU2694693C2
Чертежи

Описание
Общая область техники
Настоящее изобретение относится к системам автоматизированного проектирования. Более конкретно оно касается способа определения размерных параметров газотурбинного двигателя, в частности, турбореактивного двигателя летательного аппарата.
Уровень техники
Рабочие характеристики газотурбинного двигателя, такого как авиационный турбореактивный двигатель, в значительной степени зависят от расстояния между вращающимися частями и неподвижными частями газотурбинного двигателя. Уменьшение этого расстояния до минимума, например, между лопатками газотурбинного двигателя и его корпусом, позволяет ограничить утечки и, следовательно, в целом максимизировать характеристики газотурбинного двигателя с точки зрения гидравлики. Однако, если это расстояние является небольшим, между лопатками и корпусом газотурбинного двигателя могут происходить контакты. Такие контакты, если они создают слишком большие силы реакции или вибрации на ненадлежащих частотах, могут привести к повреждению газотурбинного двигателя. Такие риски существуют, в частности, в современных газотурбинных двигателях, в которых как для подвижных, так и для неподвижных частей применяют легкие, но гибкие материалы, которые могут подвергаться деформации и вибрации.
Следовательно, необходимо как можно точнее определять размеры этого зазора, чтобы обеспечивать хорошие характеристики, но в тоже время избежать риска повреждения газотурбинного двигателя или ухудшения его характеристик по причине контакта между его неподвижными и вращающимися частями.
Первая категория моделей, используемых для такого определения размерных параметров, объединяет модели лопаточных колес. Эти модели учитывают гибкость лопаток и поддерживающего их диска и позволяют анализировать вибрационное поведение этих элементов. В частности, применяют трехмерные модели конечных элементов для точного отображения геометрии лопаток и корпуса вокруг концов лопаток и для оценки контактного поведения между лопатками и корпусом. Однако такие модели являются локальными и не учитывают динамическое механическое поведение приводного вала газотурбинного двигателя и других его элементов. Кроме того, вычисления с применением таких моделей требуют расхода большого объема вычислительных ресурсов.
Вторая категория моделей, используемых для определения размерных параметров турбореактивных двигателей, объединяет модели динамики роторов. Такие модели включают в себя моделирование всех элементов газотурбинного двигателя, позволяя анализировать вибрационное поведение ротора газотурбинного двигателя. Для таких моделей не применяют дискретизацию геометрии, чтобы ограничить количество вычислительных ресурсов, расходуемых при вычислении. Однако, как правило, такие модели используют упрощенное и жесткое моделирование лопаток и корпуса газотурбинного двигателя и не позволяют точно рассчитывать контактные взаимодействия между лопатками и корпусом при определении размерных параметров газотурбинного двигателя.
Поэтому существует потребность в способе определения размерных параметров газотурбинного двигателя, позволяющем точно вычислять контактные взаимодействия между лопатками и корпусом, учитывая механическое поведение ротора и вибрации и деформации лопаток, диска и корпуса, при ограниченной стоимости вычислительных ресурсов.
Сущность изобретения
Первым объектом настоящего изобретения является способ определения размерных параметров газотурбинного двигателя, содержащего корпус и диск, на котором закреплена по меньшей мере одна лопатка, при этом указанный корпус окружает диск и указанную по меньшей мере одну лопатку, указанный диск приводится во вращение валом вокруг оси, называемой осью z газотурбинного двигателя, и указанная лопатка содержит переднюю кромку ВА и заднюю кромку BF,
при этом указанный способ включает в себя следующие этапы, осуществляемые средствами обработки данных:
получение предварительно определенных координат Р концов передней кромки и задней кромки лопатки в системе координат, связанной с диском (Xb,Yb,Zb);
на основании указанных полученных координат выражение координат Р’ верхних концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc);
вычисление расстояния g между корпусом и концами передней кромки и задней кромки лопатки на основании координат Р’ концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc);
вычисление нормальных и тангенциальных контактных давлений между лопаткой и корпусом вдоль конца лопатки на основании вычисленного расстояния g;
вычисление нормальной и тангенциальной сил реакции и нормального и тангенциального моментов реакции, появляющихся в результате контакта между лопаткой и корпусом, на основании вычисленных давлений;
определение размерных параметров газотурбинного двигателя в зависимости от вычисленных расстояний, давлений, сил и моментов.
Такой способ позволяет определять размерные параметры газотурбинного двигателя при помощи точного вычисления возможностей контактов и соответствующих реакций, не прибегая к тонкому и дорогому локальному моделированию, такому как трехмерное моделирование с применением метода конечных элементов.
Координаты концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc), можно выразить в виде функции от степеней свободы диска, корпуса и лопатки.
Эти степени свободы можно выбрать среди поступательного и вращательного перемещения диска и корпуса, прогиба лопатки на вершине и радиальной деформации корпуса.
В частности, эти степени свободы можно выбрать из группы, в которую входят:
поступательные перемещения диска на первую длину xd(t) и вторую длину yd(t) вдоль двух осей (х,у), поперечных к оси z газотурбинного двигателя, при этом две поперечные оси (х,у) и ось z газотурбинного двигателя образуют первую систему координат (x,y,z), связанную с валом;
поворот диска на первый угол ϕxd(t) вокруг первой оси первой системы координат х, при этом вторую систему координат (x1,y1,z1) получают посредством поворота первой системы координат (x,y,z) на первый угол ϕxd(t) вокруг первой оси первой системы координат х;
поворот диска на второй угол ϕyd(t) вокруг второй оси второй системы координат y1 при этом третью систему координат (x2,y2,z2) получают посредством поворота второй системы координат (x1,y1,z1) на второй угол ϕyd(t) вокруг второй оси второй системы координат у1;
угловое позиционирование лопатки относительно второй оси третьей системы координат у2, при этом указанное угловое позиционирование соответствует повороту на третий угол αj вокруг третьей оси третьей системы координат z2, при этом система координат, связанная с диском (Xb,Yb,Zb), образует четвертую систему координат, получаемую посредством поворота третьей системы координат (x2,у2,z2) на третий угол αj вокруг третьей оси третьей системы координат z2,;
прогиб лопатки на ее вершине на третью длину хb(t) вдоль первой оси хb пятой системы координат (хb,уb,zcb), полученной посредством поворота четвертой системы координат (Xb,Yb,Zb) на четвертый угол β вокруг второй оси четвертой системы координат Yb;
поступательное перемещение корпуса на четвертую длину xc(t) и пятую длину yc(t) вдоль первых осей первой системы координат (х,у);
поворот корпуса на пятый угол ϕxc(t) вокруг первой оси первой системы координат х, при этом шестую систему координат (xc1,yc1,zc1) получают посредством поворота первой системы координат (x,y,z) на пятый угол ϕxc(t) вокруг первой оси первой системы координат х;
поворот корпуса на шестой угол ϕyc(t) вокруг второй оси первой системы координат у, при этом систему координат (xc,yc,zc), связанную с корпусом, получают посредством поворота шестой системы координат (xc1,yc1,zc1) на шестой угол ϕyc(t) вокруг второй оси первой системы координат у;
радиальная деформация корпуса на шестую длину u(α,t) по отношению к радиусу корпуса Rc.
Таким образом, для точного вычисления возможностей контакта между каждой лопаткой и корпусом можно учитывать кинематику в трех измерениях (3D) всех элементов газотурбинного двигателя.
Координаты Р’ концов передней кромки и задней кромки лопатки, выраженные в системе координат, связанной с корпусом (xc,yc,zc), можно выразить при помощи следующей формулы:
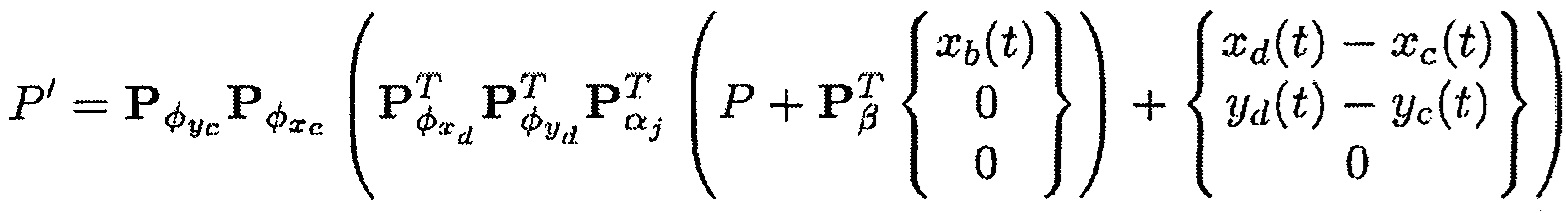
где:
Pϕxd - матрица перехода от первой системы координат (x,y,z) к второй системе координат (x1,y1,z1), Pϕyd - матрица перехода от второй системы координат (x1,y1,z1) к третьей системе координат (x2,у2,z2), Pϕхс - матрица перехода от первой системы координат (x,y,z) к шестой системе координат (xc1,yc1,zc1) и Рϕус - матрица перехода от шестой системы координат (xc1,yc1,zc1) к системе координат (xc,yc,zc), связанной с корпусом,
Pαj - матрица перехода, связанная с угловым позиционированием лопатки на диске,
Рβ - матрица перехода, связанная с ориентацией прогиба лопатки на ее вершине,
и
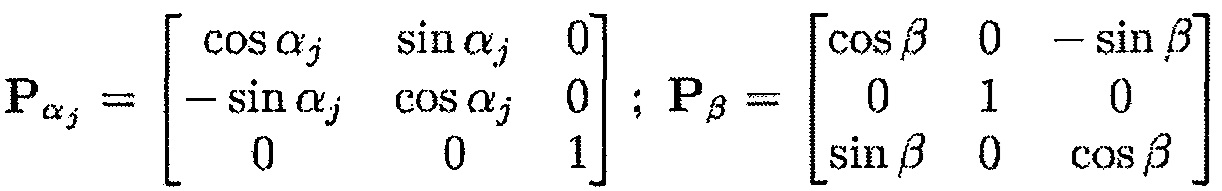


Это позволяет получить прямое отношение между положением конца лопатки, задаваемое ее 3D-геометрией, и положением этого же конца в системе координат, связанной с корпусом. Таким образом, вычисление зазора между корпусом и концом лопатки сводится к вычислению минимального расстояния между точкой и внутренней поверхностью корпуса, образованной в этой же системе координат.
Учитывая, что внутренняя поверхность корпуса образует круговой конус с углом θ, радиусом основания Rb и высотой h, можно вычислить расстояние g между корпусом и концами передней кромки и задней кромки лопатки при помощи следующей формулы:

где

Таким образом, вычисление зазора между корпусом и концом лопатки сводится к вычислению минимального расстояния между точкой и конусом в системе координат, связанной с корпусом. Выражение этого расстояния напрямую зависит от координат концов каждой лопатки Р, выведенных из 3D-геометрии газотурбинного двигателя, и его вычисление не требует решения дополнительного промежуточного уравнения. Это позволяет сократить время вычисления, необходимое для определения этого расстояния.
Вычисление давлений может потребовать применения функции, имеющей форму, адаптированную для конца лопатки и для профиля первоначального зазора. Такой вариант позволяет учитывать трехмерную геометрию конца контактной зоны, не прибегая к дискретизации.
Контактное давление можно вычислять вдоль хорды, которая предполагается прямолинейной и имеющей длину Iс и которая образует конец лопатки, посредством линейной интерполяции на основании вычисленных расстояний между корпусом и верхними концами передней кромки и задней кромки лопатки.
Нормальное pN и тангенциальное рT контактные давления в любой точке указанной хорды можно вычислить при помощи следующих формул:

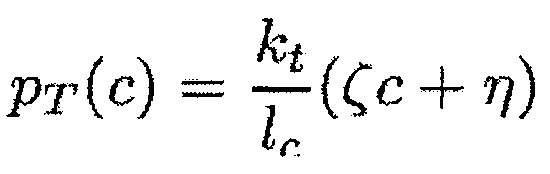
где
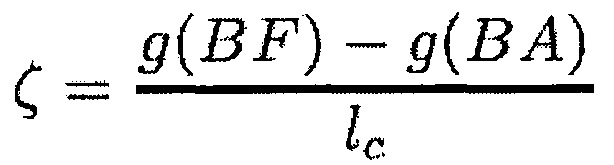
и
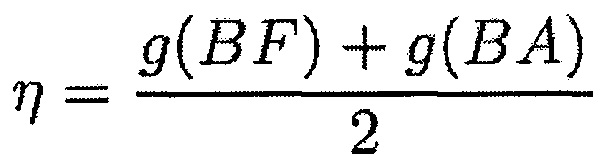
при этом с обозначает абсциссу положения вдоль указанной хорды, изменяющуюся между -1с/2 и +1с/2, и kr и kt обозначают нормальную и тангенциальную жесткость при контакте.
Нормальную FN и тангенциальную FT силы реакции и нормальный MN и тангенциальный МT моменты реакции, появляющиеся в результате контакта между лопаткой и корпусом, можно вычислить при помощи следующих формул:

где
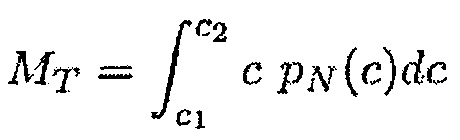
при этом c1 и с2 обозначают минимальную и максимальную абсциссы совокупности положений хорды лопатки, входящей в контакт с корпусом.
Это позволяет вычислить контактные реакции: силы и моменты, на основании распределения давления на вершине лопатки и, следовательно, учитывать изменение зоны контакта между лопаткой и корпусом.
Вторым объектом изобретения является компьютерный программный продукт, содержащий командные коды для осуществления заявленного способа определения размерных параметров, когда эту программу исполняет процессор.
Третьим объектом изобретения является устройство определения размерных параметров газотурбинного двигателя, которое содержит средства обработки данных, включающие в себя:
модуль для получения предварительно определенных координат Р концов передней кромки ВА и задней кромки BF лопатки газотурбинного двигателя в системе координат, связанной с диском газотурбинного двигателя (Xb,Yb,Zb), при этом указанный газотурбинный двигатель содержит корпус и указанный диск, на котором закреплена по меньшей мере указанная лопатка, указанный корпус окружает диск и указанную по меньшей мере одну лопатку, указанный диск приводится во вращение валом вокруг оси, называемой осью z газотурбинного двигателя;
модуль для выражения координат Р’ верхних концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc), на основании указанных полученных координат;
модуль вычисления расстояния g между корпусом и концами передней кромки и задней кромки лопатки на основании координат Р’ концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc);
модуль вычисления нормального и тангенциального контактного давления между лопаткой и корпусом вдоль конца лопатки на основании вычисленного расстояния g;
модуль вычисления нормальной и тангенциальной сил реакции и нормального и тангенциального моментов реакции, появляющихся в результате контакта между лопаткой и корпусом, на основании вычисленных давлений;
модуль определения размерных параметров газотурбинного двигателя в зависимости от вычисленных расстояний, давлений, сил и моментов.
Компьютерный программный продукт и средства обработки имеют те же преимущества, которые были указаны выше для способа согласно первому объекту.
Краткое описание чертежей
Другие признаки и преимущества настоящего изобретения будут более очевидны из нижеследующего описания предпочтительного варианта осуществления. Это описание представлено со ссылками на прилагаемые чертежи, на которых:
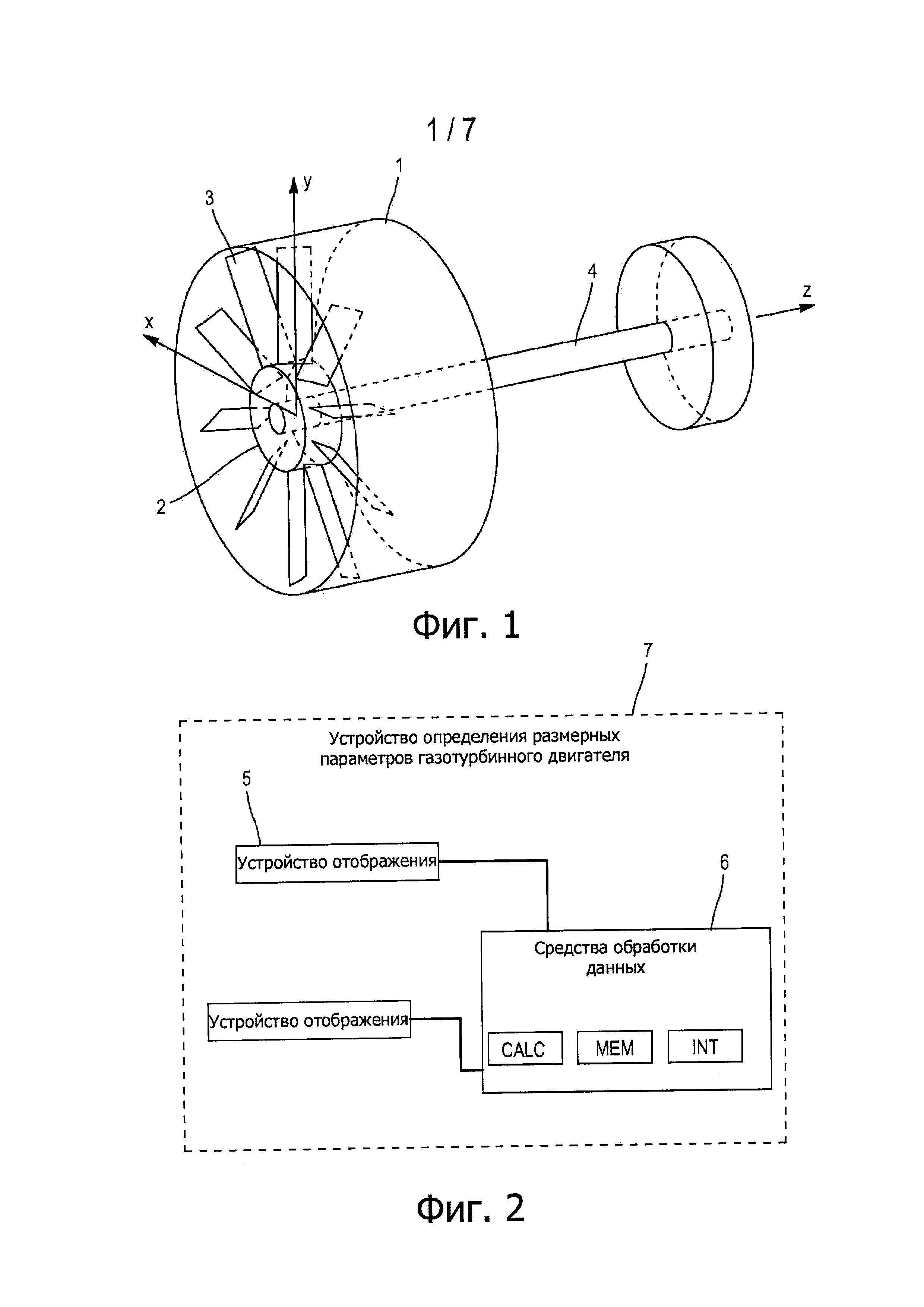
фиг. 1 - пример газотурбинного двигателя, для которого можно применять заявленный способ;
фиг. 2 - средства обработки данных для осуществления заявленного способа;
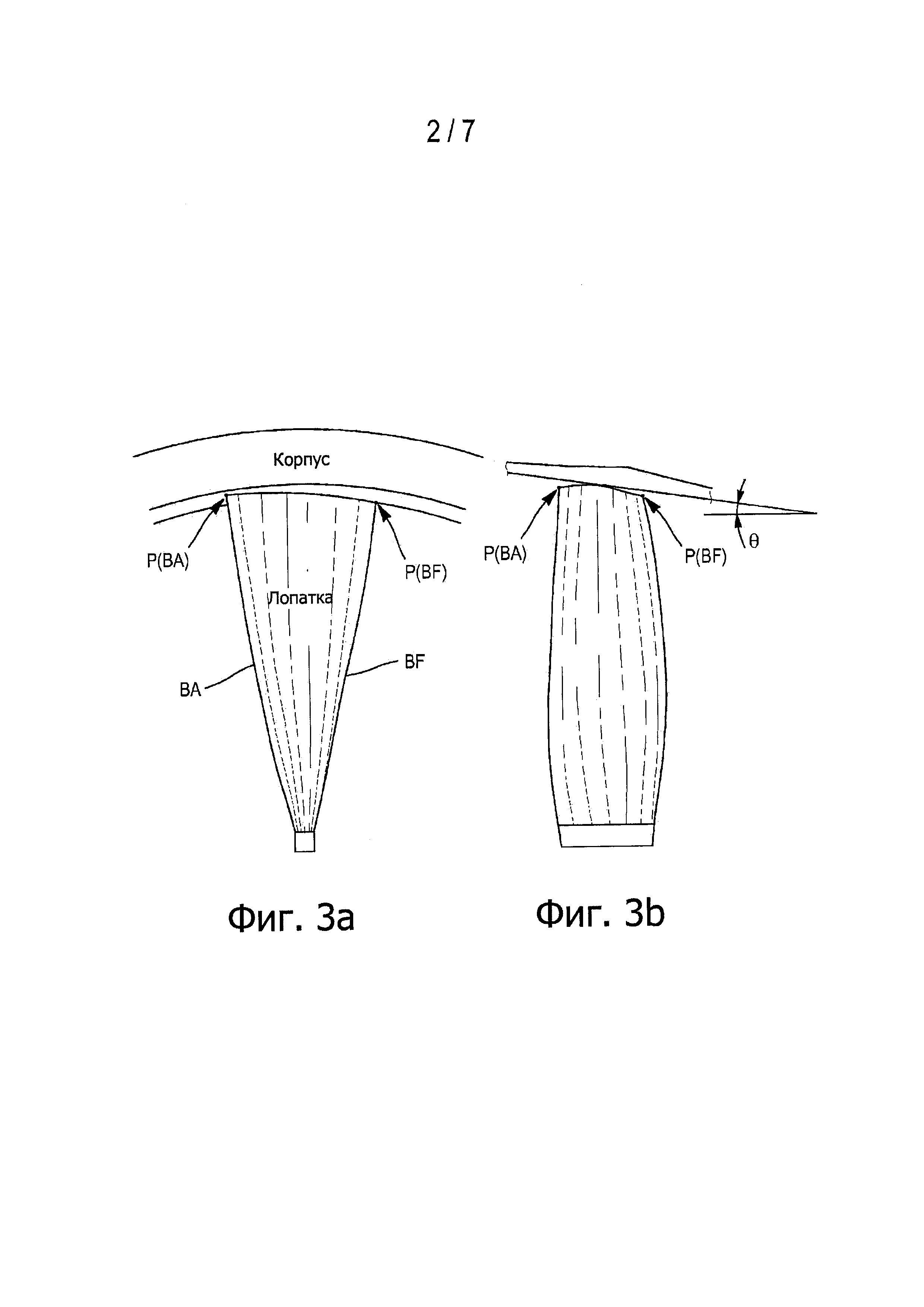
фиг. 3а и 3b - пример лопатки газотурбинного двигателя, показанной соответственно спереди и сбоку, для которой можно применять заявленный способ;
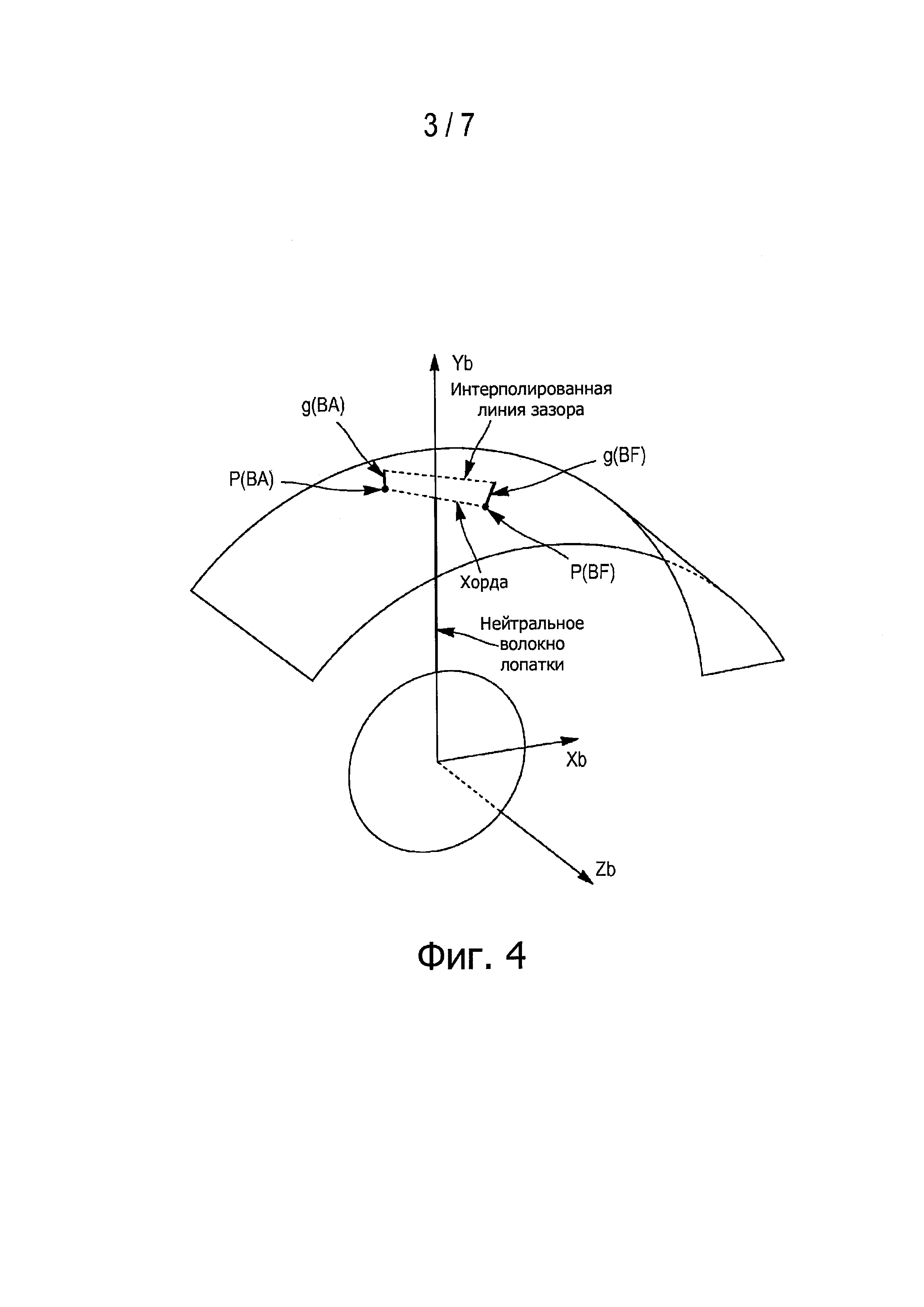
фиг. 4 - пример схематичного отображения лопатки газотурбинного двигателя, для которой можно применять заявленный способ, в системе координат (Xb,Yb,Zb), связанной с диском;
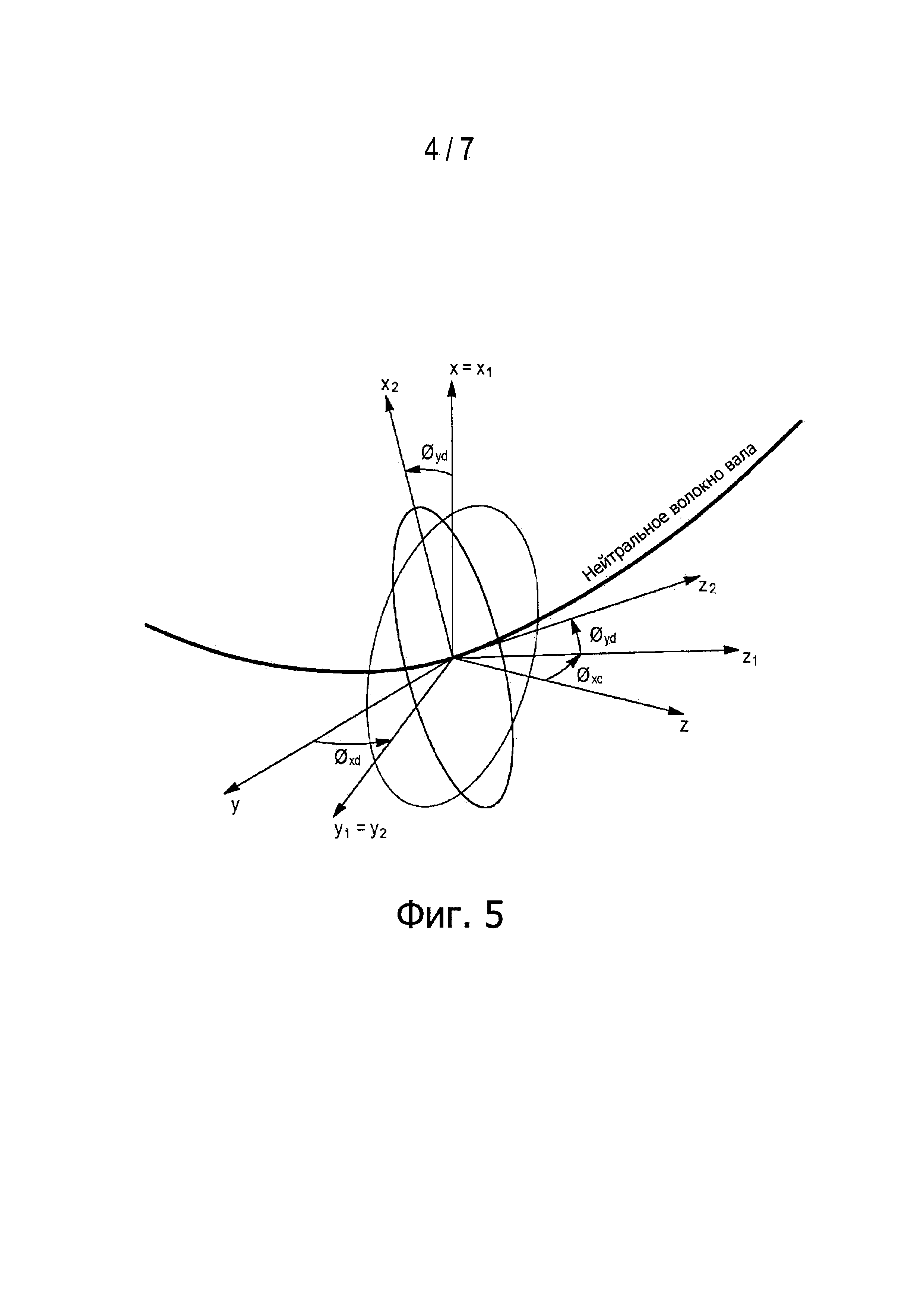
фиг. 5-9 иллюстрируют движения различных элементов газотурбинного двигателя, учитываемые для выражения координат Р’ концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом, с показом различных используемых соответствующих систем координат;
фиг. 10а и 10b иллюстрируют вычисление расстояний между концом лопатки и корпусом, а также давлений в любой точке прямолинейной хорды, образующей конец лопатки, посредством линейной интерполяции;
фиг. 11 - блок-схема заявленного способа определения размерных параметров.
Осуществление изобретения
Настоящее изобретение относится к способу определения размерных параметров газотурбинного двигателя, показанного на фиг. 1, содержащего корпус 1 и диск 2, на котором закреплена по меньшей мере одна лопатка 3, при этом корпус окружает диск и лопатки. Диск и лопатки приводятся во вращение вокруг оси z, называемой осью газотурбинного двигателя, при помощи вала 4, проходящего в продольном направлении вдоль оси z. Первая система координат (x,y,z), показанная на фиг. 1, в которой первые оси х и у являются поперечными к оси z газотурбинного двигателя, является вращающейся системой координат, связанной с валом 4.
Предпочтительно настоящий способ предназначен для определения размерных параметров авиационного турбореактивного двигателя, но он не ограничен ни этим типом газотурбинного двигателя, ни областью реактивных двигателей. Этот способ можно применять для определения размерных параметров любой вращающейся машины, содержащей вращающиеся лопатки внутри корпуса, такой как водяные, газовые, паровые турбины для производства электричества, вентиляторы и т.д.
Кроме того, он предназначен для осуществления при помощи устройства 7 определения размерных параметров газотурбинного двигателя, содержащего средства 6 обработки данных, показанные на фиг. 2, включающие в себя средства вычисления CALC (вычислительное устройство), средства запоминания MEM (память), интерфейс ввода INT и по меньшей мере одно устройство 5 отображения. Такими средствами обработки управляет оператор.
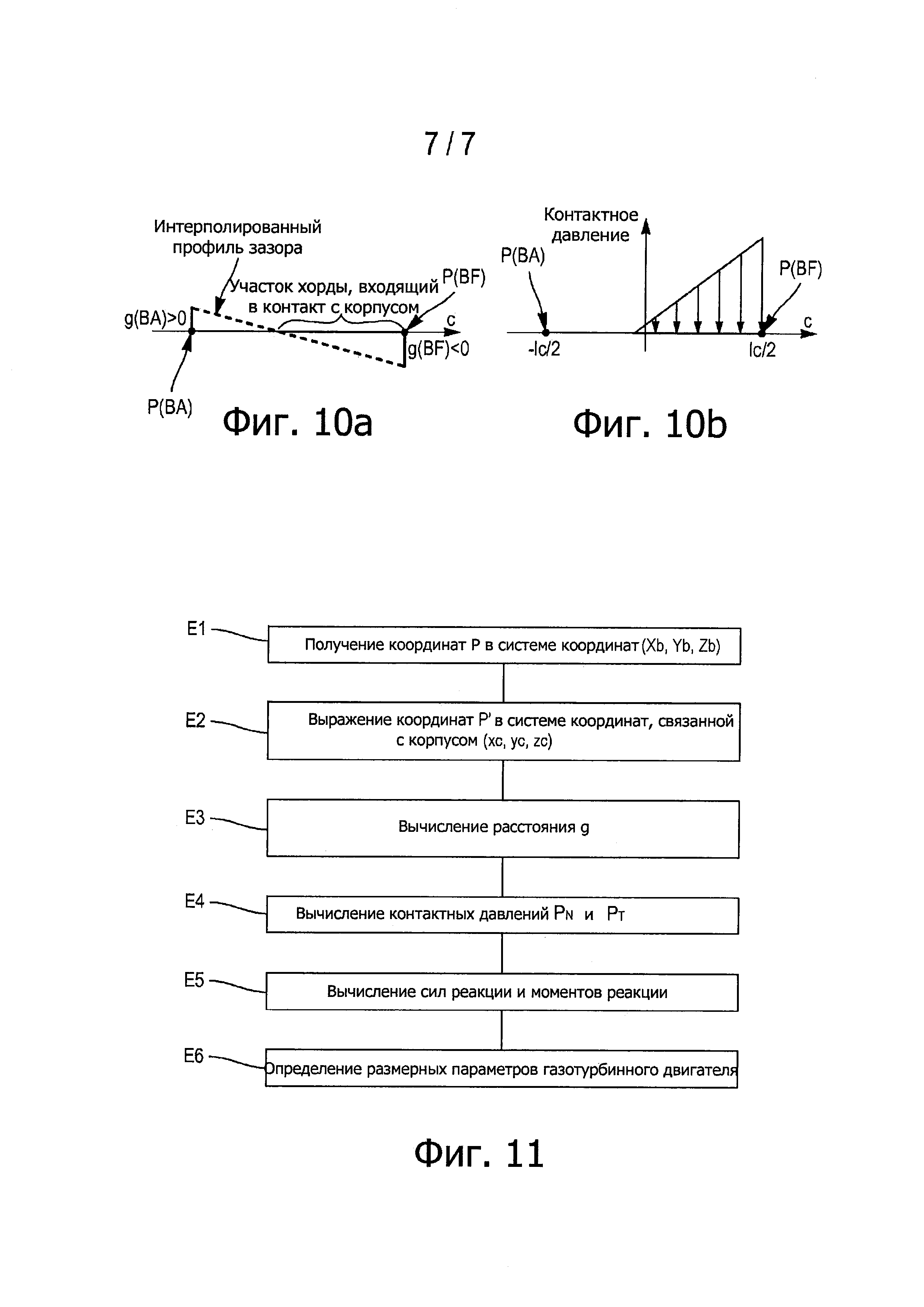
Лопатка газотурбинного двигателя, показанная спереди на фиг. 3а и сбоку на фиг. 3b, имеет переднюю кромку ВА и заднюю кромку BF. Если обозначить (Xb,Yb,Zb) систему координат, связанную с диском, в которой эта лопатка является по существу вертикальной, то есть нейтральное волокно лопатки совмещено с осью Yb, как показано на фиг. 4, можно обозначить РBA и PBF координаты концов на вершине лопатки передней кромки и задней кромки лопатки в этой системе координат. В следующих абзацах обозначение Р будет относиться соответственно к РBA и к PBF, если рассматриваемой точкой соответственно является конец передней кромки и конец задней кромки. Эти координаты получают средства 6 обработки данных после их предварительного определения на основании трехмерной (3D) геометрии газотурбинного двигателя на первом этапе считывания координат Е1, как показано на фиг. 11.
Согласно варианту осуществления изобретения, после этого в рамках способа предложено:
- на основании полученных координат Р концов выражать координаты Р’ верхних концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc);
- вычислять расстояние g между корпусом и концами передней кромки и задней, кромки лопатки на основании координат Р’BA и P’BF концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc);
- вычислять нормальные рN и тангенциальные рT контактные давления между лопаткой и корпусом вдоль конца лопатки на основании вычисленного расстояния g;
- вычислять нормальную FN и тангенциальную FT силы реакции и нормальный MN и тангенциальный МT моменты реакции, появляющиеся в результате контакта между лопаткой и корпусом, на основании вычисленных давлений pN и рT;
- определять размерные параметры газотурбинного двигателя в зависимости от вычисленных расстояний, давлений, сил и моментов.
Координаты концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc), можно выразить в виде функции от большого числа степеней свободы элементов газотурбинного двигателя, в частности, диска, корпуса или лопатки, по отношению к вращающейся системе координат (x,y,z), показанной на фиг. 1. Эти степени свободы можно выбрать среди поступательного и вращательных перемещений диска и корпуса, прогиба лопатки на ее вершине и радиальной деформации корпуса.
Таким образом, можно определить размерные параметры вращающейся машины с точным вычислением зазора между концами лопатки и корпусом, а также взаимодействий в случае контакта, учитывая 3D-кинематику всех элементов газотурбинного двигателя, не прибегая к точному и дорогому локальному моделированию, такому как 3D-моделирование по конечным элементам.
В частности, во время второго этапа выражения координат Е2 координаты Р’ концов передней кромки и задней кромки лопатки выражают в системе координат, связанной с корпусом (xc,yc,zc), учитывая заданные перемещения элементов газотурбинного двигателя, исходя из следующих степеней свободы элементов газотурбинного двигателя:
- поступательное перемещение диска на первую длину xd(t) и вторую длину уd(t) вдоль двух первых осей х и у первой системы координат (x,y,z);
- поворот диска на первый угол ϕxd(t) вокруг первой оси первой системы координат х, при этом вторую систему координат (x1,y1,z1) получают посредством поворота первой системы координат (x,y,z) на первый угол ϕxd(t) вокруг первой оси первой системы координат х, как показано на фиг. 5;
- поворот диска на второй угол ϕyd(t) вокруг второй оси второй системы координат y1 при этом третью систему координат (x2,у2,z2) получают посредством поворота второй системы координат (x1,y1,z1) на второй угол ϕyd(t) вокруг второй оси второй системы координат у1 как показано на фиг. 5;
- угловое позиционирование лопатки относительно второй оси третьей системы координат у2, при этом указанное угловое позиционирование соответствует повороту на третий угол αj вокруг третьей оси третьей системы координат z2, при этом система координат, связанная с диском (Xb,Yb,Zb), образует четвертую систему координат, получаемую посредством поворота третьей системы координат (x2,y2,z2) на третий угол αj вокруг третьей оси третьей системы координат z2, как показано на фиг. 6;
- прогиб лопатки на ее вершине на третью длину xb(t) вдоль первой оси хb пятой системы координат (хb,уb,zсb), полученной посредством поворота четвертой системы координат (Xb,Yb,Zb) на четвертый угол β вокруг второй оси четвертой системы координат Yb, как показано на фиг. 7;
- поступательное перемещение корпуса на четвертую длину xc(t) и пятую длину yc(t) вдоль двух первых осей первой системы координат (х,у);
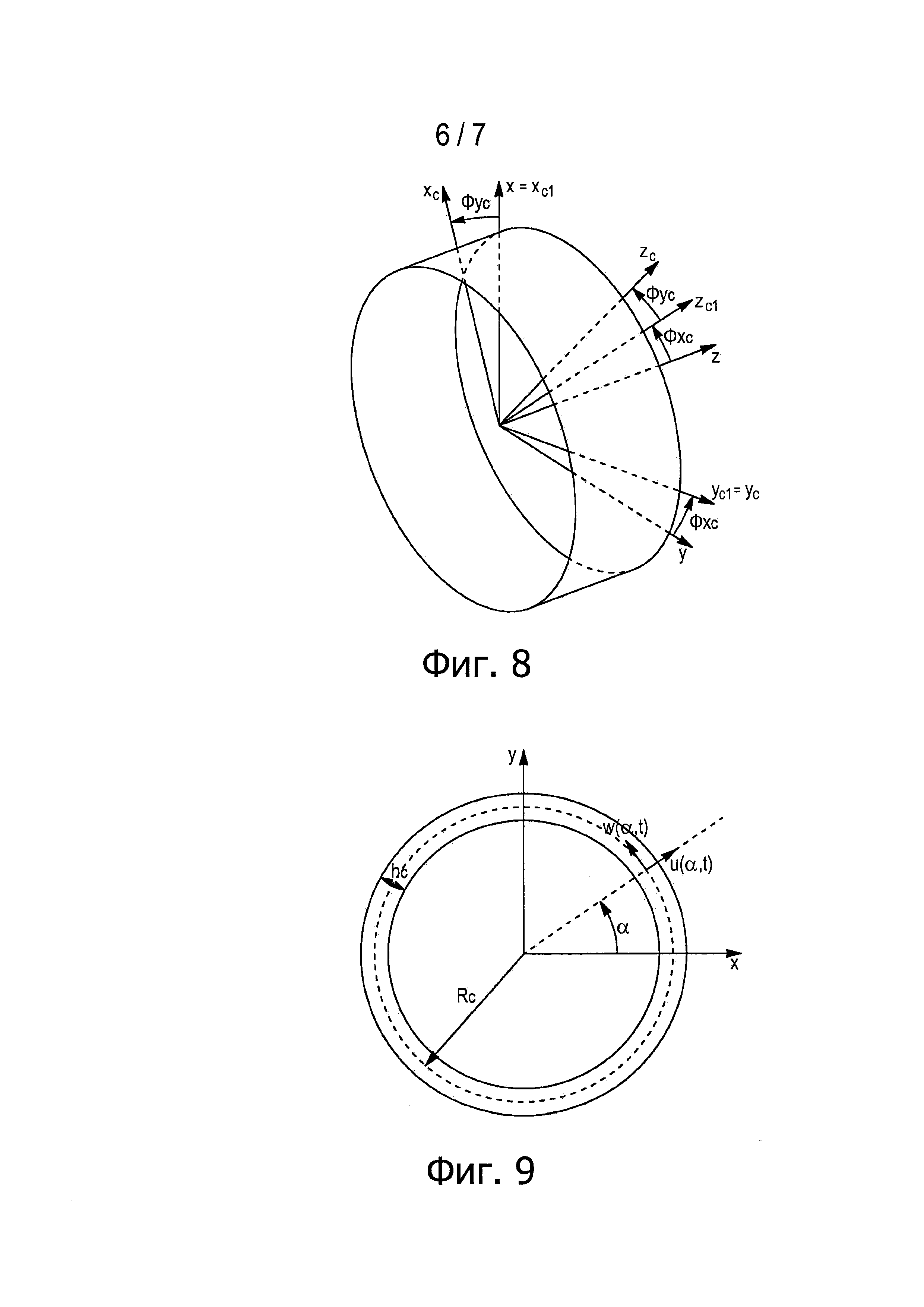
- поворот корпуса на пятый угол ϕxc(t) вокруг первой оси первой системы координат х, при этом шестую систему координат (xc1,yc1,zc1) получают посредством поворота первой системы координат (x,y,z) на пятый угол ϕxc(t) вокруг первой оси первой системы координат х, как показано на фиг. 8;
- поворот корпуса на шестой угол ϕyc(t) вокруг второй оси первой системы координат у, при этом систему координат (xc,yc,zc), связанную с корпусом, получают посредством поворота шестой системы координат (xc1,yc1,zc1) на шестой угол ϕyc(t) вокруг второй оси первой системы координат у, как показано на фиг. 8;
- радиальная деформация корпуса на шестую длину u(α,t) относительно радиуса корпуса Rc, как показано на фиг. 9.
Тангенциальной деформацией корпуса w(α,t) можно пренебречь. Кроме того, корпус рассматривают в его сечении как упругое нерастяжимое кольцо. Влиянием толщины корпуса hc на деформацию его внутренней поверхности можно пренебречь.
Таким образом, координаты Р’ концов передней кромки и задней кромки лопатки можно выразить в системе координат, связанной с корпусом (xc,yc,zc), при помощи следующей формулы:
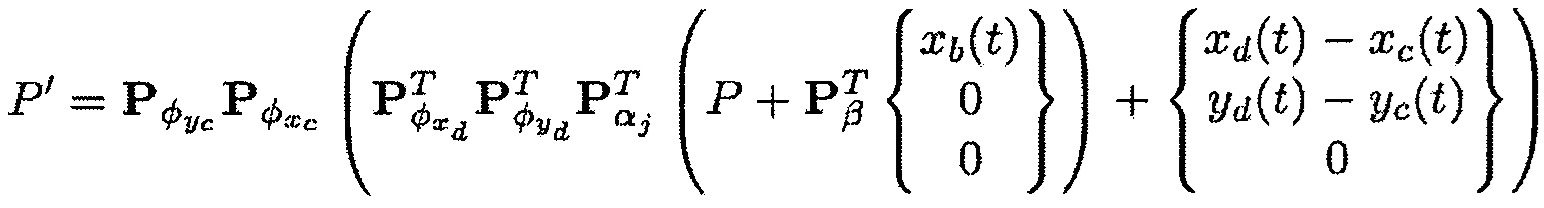
где:
Pϕxd - матрица перехода от первой системы координат (x,y,z) к второй системе координат (x1,y1,z1), Pϕyd - матрица перехода от второй системы координат (x1,y1,z1) к третьей системе координат (x2,у2,z2), Рϕхс - матрица перехода от первой системы координат (x,y,z) к шестой системе координат (xc1,yc1,zc1) и Рϕус - матрица перехода от шестой системы координат (xc1,yc1,zc1) к системе координат (xc,yc,zc), связанной с корпусом,
Рαj - матрица перехода, связанная с угловым позиционированием лопатки на диске,
Рβ - матрица перехода, связанная с ориентацией прогиба лопатки на ее вершине.
Матрицы перехода можно определить следующим образом:
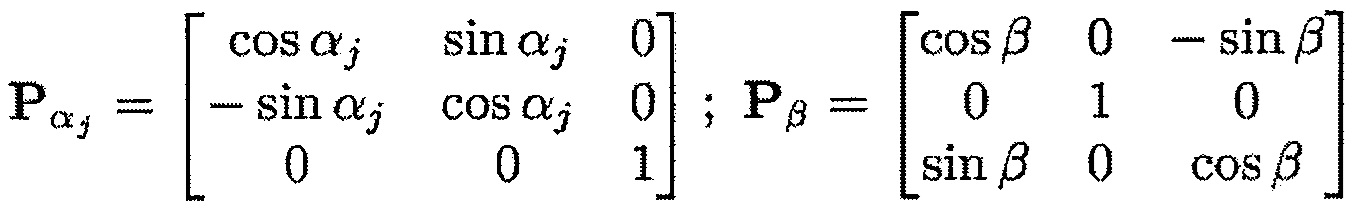
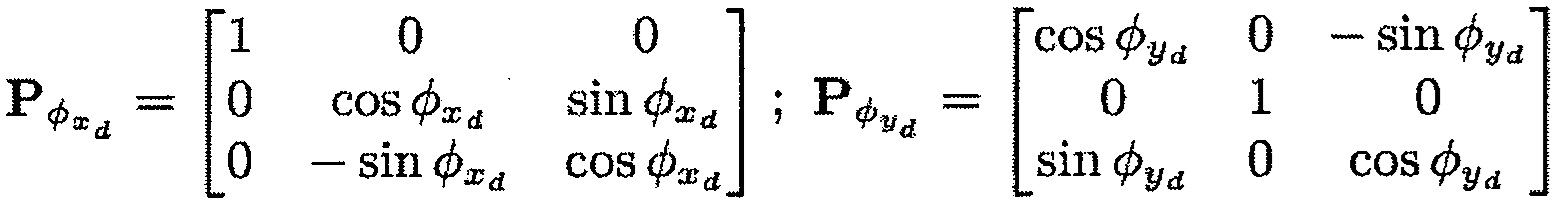
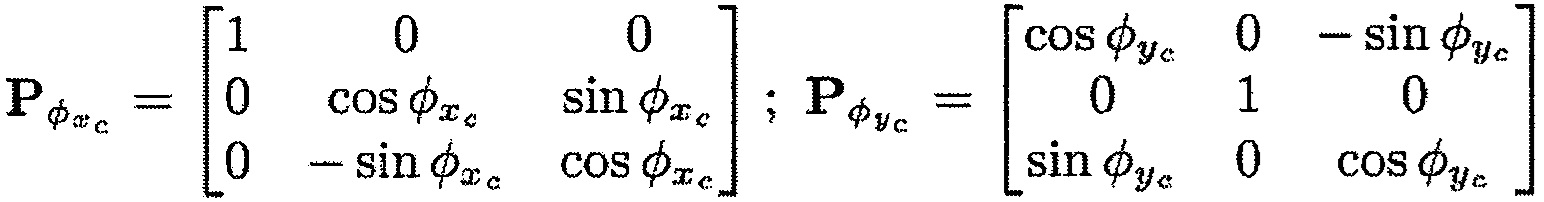
Во время первого этапа вычисления Е3 вычисляют расстояние между корпусом и концами передней кромки и задней кромки лопатки. С учетом того, что внутренняя поверхность корпуса образует показанный на фиг. 3 круговой конус с углом θ, радиусом основания Rb и высотой h, полученными во время считывания координат Р концов передней кромки, это расстояние можно выразить на основании координат Р при помощи следующей формулы:
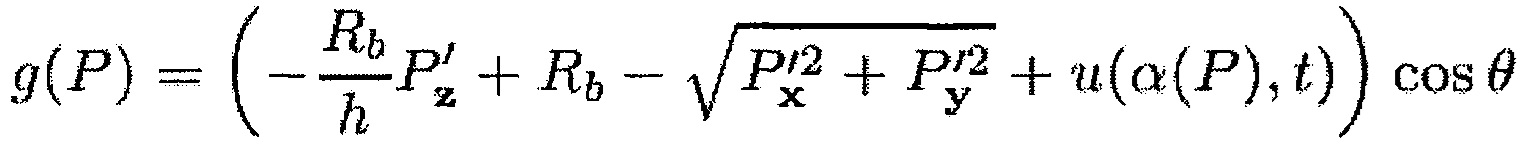
где
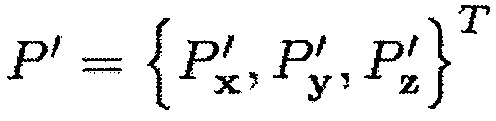
Выражение координат концов передней кромки и задней кромки лопатки в системе координат (xc,yc,zc), связанной с корпусом, показанной на фиг. 8, позволяет трансформировать вычисление зазора между лопаткой и корпусом в простое вычисление расстояния между точкой и конусом в системе координат.
Таким образом, применяемое моделирование позволяет точно вычислить расстояние между концами каждой лопатки и корпусом, учитывая большое количество степеней свободы всех элементов газотурбинного двигателя, не прибегая при этом к дорогой дискретизации, такой как модель конечных элементов. Выражение этого расстояния напрямую зависит от координат концов каждой лопатки Р, выведенных из 3D-геометрии газотурбинного двигателя, и его вычисление не требует решения дополнительного промежуточного уравнения. Это позволяет сократить время вычисления для определения этого расстояния.
Во время второго этапа вычисления Е4 в случае контакта между лопаткой и корпусом, можно вычислить нормальное и тангенциальное контактные давления вдоль конца лопатки на основании расстояний, вычисленных во время первого этапа вычисления Е3.
Можно использовать функцию формы, адаптированную к концу лопатки и к профилю первоначального зазора, чтобы точно определить расстояние между лопаткой и корпусом в любой точке хорды лопатки, а также соответствующие контактные давления. Этот профиль первоначального зазора можно определить на основании формы конца лопатки и формы внутренней поверхности корпуса напротив этого конца во время первого этапа Е1 получения данных на основании трехмерной (3D) геометрии газотурбинного двигателя.
В первом варианте используемая функция формы может быть линейной. Расстояние между концом лопатки и корпусом можно получить в любой точке прямолинейной хорды длиной 1с, образующей верхний конец лопатки, посредством линейной интерполяции на основании вычисленных расстояний на передней кромке и задней кромке, как показано на фиг. 10а, и нормальное рN и тангенциальное рT давления в любой точке этой хорды можно выразить при помощи следующих формул:
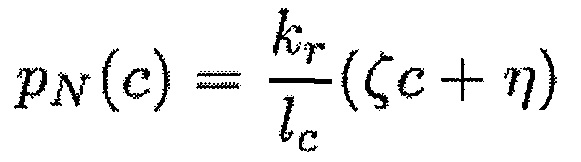

где
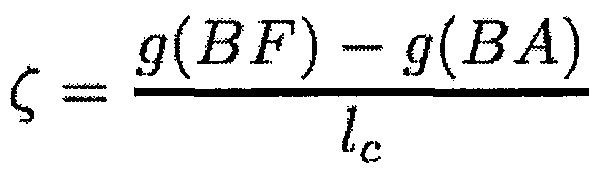
и
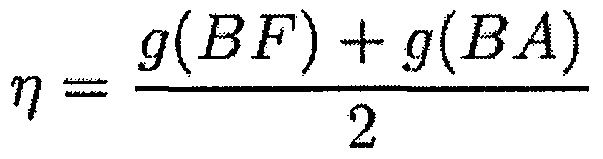
где «с» меняется вдоль хорды от -1с/2 до +1с/2, при этом kr и kt являются нормальной и тангенциальной жесткостями при контакте, η обозначает среднее расстояние между лопаткой и корпусом, и ζc+η является расстоянием между лопаткой и корпусом в положении «с» хорды, полученным путем линейной интерполяции.
В положениях, при которых расстояние между лопаткой и корпусом является положительным, что соответствует отсутствию контакта, учитываемые нормальное и тангенциальное давления являются нулевыми, как показано на фиг. 10b.
В альтернативном варианте можно использовать функцию формы, более реалистично отображающую форму конца лопатки и профиля первоначального зазора, чтобы точно определить расстояния между лопаткой и корпусом в любой точке хорды лопатки, в которой конец и профиль первоначального зазора не являются прямолинейными, а также соответствующие контактные давления. Например, можно применить полиномиальную функцию формы, например, 2-го порядка в виде W(c)=(a2*c2+a1*c+a0) или 3-го порядка в виде W(c)=(a3*c3+a2*c2+a1*c+a0), при этом коэффициенты а0, a1, а2 и а3 зависят от вычисленных зазоров на концах передней кромки и задней кромки лопатки и от профиля первоначального зазора, определенного на первом этапе Е1 получения данных. При этом нормальное и тангенциальное контактные давления между лопаткой и корпусом можно выразить в зависимости от такой функции формы при помощи следующих выражений:
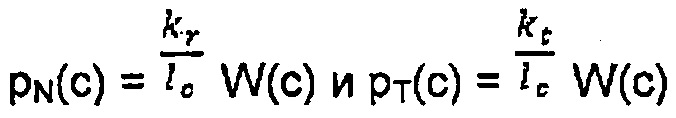
Таким образом, контактные давления можно вычислить в любой точке конца лопатки в случае контакта с корпусом, учитывая 3D-геометрию зоны контакта, не прибегая к дискретизации геометрии лопатки и к слишком упрощенной геометрии, не отображающей реальную геометрию лопатки.
Во время третьего этапа вычисления Е5 вычисляют нормальную FN и тангенциальную FT силы реакции и нормальный MN и тангенциальный МT моменты реакции, появляющиеся в результате контакта между лопаткой и корпусом. Их можно выразить при помощи следующих формул:
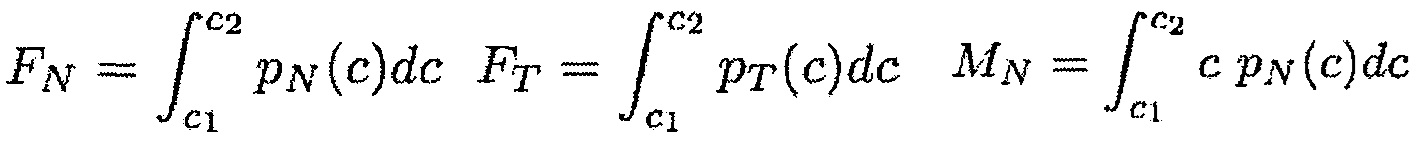
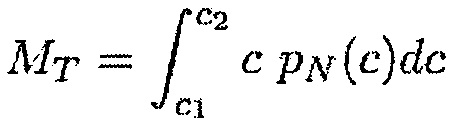
где c1 и с2 определяют границы контакта между лопаткой и корпусом:
- c1 = -1с/2 и с2 = 1с/2, если расстояния между лопаткой и корпусом являются отрицательными для передней кромки и задней кромки. В этом случае происходит контакт вдоль всей хорды.
- c1 = -1с/2 и с2 = -η/ζ, если расстояние между лопаткой и корпусом является отрицательным на передней кромке, но положительным на задней кромке. В этом случае происходит контакт на части хорды лопатки со стороны передней кромки.
- c1 = η/ζ и с2 = 1с/2, если расстояние между лопаткой и корпусом является отрицательным на задней кромке, но положительным на передней кромке. В этом случае происходит контакт на части хорды лопатки со стороны задней кромки.
В представленных формулах нормальные силы пропорциональны взаимному проникновению между твердыми телами, и силы трения получают при помощи закона Кулона.
Таким образом, силы и моменты реакции можно вычислить в любой точке конца лопатки в случае контакта с корпусом, не применяя дискретизации геометрии лопатки и не используя упрощенную геометрию, не отображающую реальную геометрию лопатки. Такая модель позволяет учитывать изменение распределения контактного давления на хорде. Контакт может начаться на одном из концов хорды, затем зона контакта может увеличиваться, пока лопатка не соприкоснется с корпусом по всей хорде. Описанные выше этапы позволяют вычислять реалистичное распределение сил с учетом развития зоны контакта.
Во время этапа Е6 определения размерных параметров используют результаты предыдущих этапов для определения размерных параметров газотурбинного двигателя.
Согласно первому примеру, результаты первого этапа вычисления Е3 используют для обнаружения контакта. Результаты таких вычислений для разных скоростей вращения и с предположением некоторой разбалансировки газотурбинного двигателя можно использовать для определения максимальных перемещений конца лопатки во время работы двигателя. Все диапазоны скоростей вращения, при которых первоначальное расстояние, в состоянии покоя между лопаткой и корпусом, меньше вычисленного максимального смещения, будут представлять собой риск контакта между лопаткой и корпусом газотурбинного двигателя.
Согласно второму примеру, результаты вычислений сил и моментов реакции во время третьего этапа вычисления Е5 можно проецировать на степени свободы модели для введения в систему уравнений, описывающую движения газотурбинного двигателя. Решение этого уравнения с контактом может позволить сделать вывод о силах, действующих на газотурбинный двигатель, и о появлении нестабильного режима работы, потенциально опасного для газотурбинного двигателя.
Уравнение движения с контактом можно решать несколькими способами. Анализ стабильности газотурбинного двигателя можно осуществлять, предполагая постоянный контакт по меньшей мере одной лопатки с корпусом газотурбинного двигателя. При этом контактные силы, вычисленные на этапе Е5 и проецированные на степени свободы модели, подвергают линеаризации и применяют постоянно к системе уравнений, описывающей движение элементов газотурбинного двигателя. Анализ стабильности можно производить, чтобы предсказать для разных скоростей вращения, может ли введение возмущения привести к появлению нестабильного режима работы, потенциально опасного для газотурбинного двигателя.
Наконец, согласно третьему примеру, результаты вычислений расстояний, сил и моментов, полученные во время различных предыдущих этапов, можно применять в рамках переходного вычисления, чтобы определять на каждом временном шаге вычислений риск контакта между лопаткой и корпусом и, в случае необходимости, соответствующие силы и моменты реакции. Такое вычисление можно осуществлять, например, при помощи метода интегрирования по времени, называемого методом центральных конечных разностей. Так, можно осуществлять вычисление переходного режима, появляющегося в результате возмущения, учитывая в каждый момент перехода возможность контакта и реакций в результате такого контакта. Изменение сил реакции во время переходного режима позволяет определять силы, которые должны выдержать газотурбинный двигатель и нестабильность рабочего режима в результате возмущения, являющегося причиной переходного режима.
Если один из анализов выявляет недопустимый риск для газотурбинного двигателя, оператор, осуществляющий такой способ при помощи средств обработки, может изменить характеристику газотурбинного двигателя, чтобы улучшить его параметры и сделать его более стойким, например, к возмущению. Например, оператор может изменить геометрические характеристики лопаток, диска или корпуса газотурбинного двигателя, не допускать определенный диапазон скоростей вращения, чреватый слишком большим риском повреждения, изменить материал, используемый для одного из элементов газотурбинного двигателя с целью уменьшения гибкости этого элемента и т.д.
Таким образом, можно оптимизировать параметры газотурбинного двигателя, чтобы ограничить риски повреждения в случае контакта между лопатками и корпусом газотурбинного двигателя, сводя к минимуму влияние на его характеристики, благодаря точному моделированию геометрии и динамики элементов газотурбинного двигателя, без увеличения количества потребляемых вычислительных ресурсов.
Устройство определения размерных параметров газотурбинного двигателя, показанное на фиг. 2, для осуществления способа определения размерных параметров содержит средства 6 обработки данные, включающие в себя:
- модуль для получения предварительно определенных координат Р концов передней кромки ВА и задней кромки BF лопатки газотурбинного двигателя в системе координат, связанной с диском газотурбинного двигателя (Xb,Yb,Zb), при этом указанный газотурбинный двигатель содержит корпус и указанный диск, на котором закреплена по меньшей мере одна указанная лопатка, указанный корпус окружает диск и указанную по меньшей мере одну лопатку, и указанный диск приводится во вращение валом вокруг оси, называемой осью z газотурбинного двигателя;
- модуль для выражения координат Р’ концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (хс,ус,zс), на основании указанных полученных координат;
- модуль вычисления расстояния g между корпусом и концами передней кромки и задней кромки лопатки на основании координат Р’ концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом (xc,yc,zc);
- модуль вычисления нормального и тангенциального контактных давлений между лопаткой и корпусом вдоль конца лопатки на основании вычисленного расстояния g;
- модуль вычисления нормальной и тангенциальной сил реакции и нормального и тангенциального моментов реакции, появляющихся в результате контакта между лопаткой и корпусом на основании вычисленных давлений;
- модуль определения размерных параметров газотурбинного двигателя в зависимости от вычисленных расстояний, давлений, сил и моментов.
Реферат
Изобретение относится к способу определения размерных параметров газотурбинного двигателя, содержащего корпус и диск, на котором закреплена по меньшей мере одна лопатка, при этом указанный корпус окружает диск и указанную по меньшей мере одну лопатку, указанный диск приводится во вращение валом вокруг оси, называемой осью z газотурбинного двигателя. Способ включает: получение (Е1) координат (Р) концов передней кромки и задней кромки лопатки в системе координат, связанной с диском; выражение (Е2) координат (Р’) концов передней кромки и задней кромки лопатки в системе координат, связанной с корпусом; вычисление (Е3) расстояния (g) между корпусом и концами передней кромки и задней кромки лопатки на основании координат (Р’), выраженных в системе координат, связанной с корпусом; вычисление (Е4) контактных давлений между лопаткой и корпусом вдоль конца лопатки на основании вычисленного расстояния (g); вычисление (Е5) сил и моментов реакции, появляющихся в результате контакта между лопаткой и корпусом, на основании вычисленных давлений; определение размерных параметров (Е6) газотурбинного двигателя в зависимости от вычисленных расстояний, давлений, сил и моментов. Изобретение позволяет определять размерные параметры газотурбинного двигателя при помощи точного вычисления возможностей контактов и соответствующих реакций, не прибегая к тонкому и дорогому локальному моделированию, такому как трехмерное моделирование с применением метода конечных элементов. Также представлено устройство для определения размерных параметров газотурбинного двигателя, содержащее средства обработки данных. 2 н. и 9 з.п. ф-лы, 13 ил.
Формула

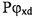
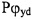


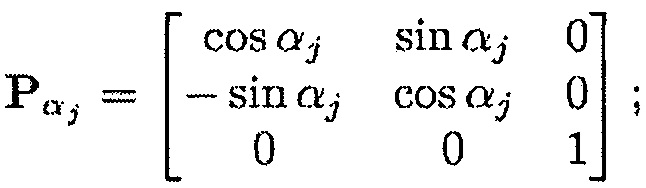


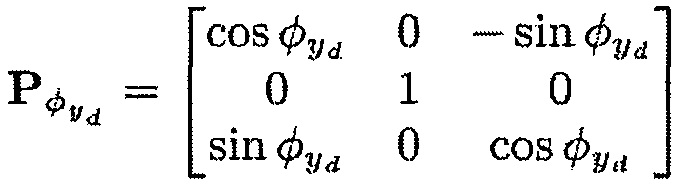
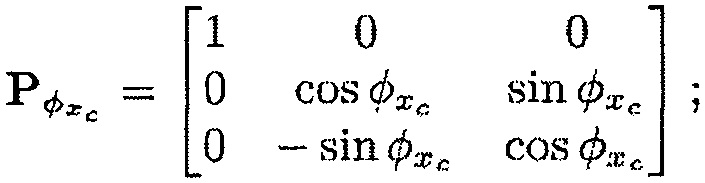
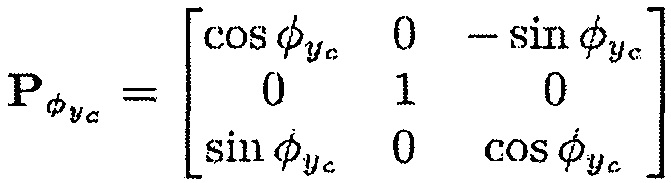
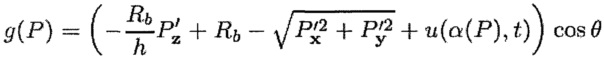
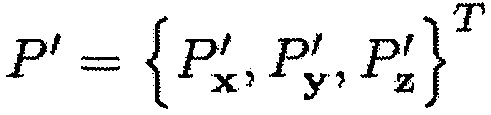
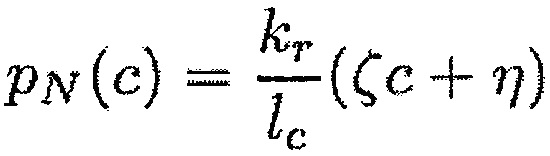


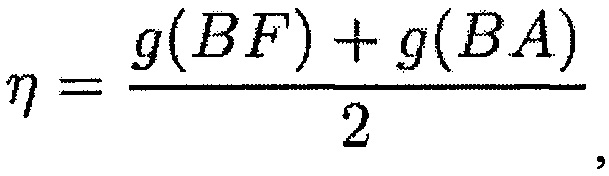
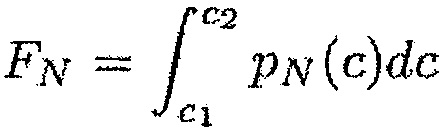
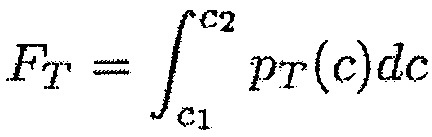

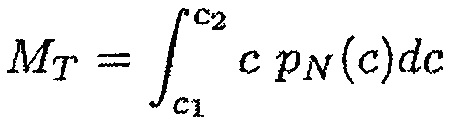

Комментарии