Способ восстановления формы асферической поверхности оптической детали по параметрам отраженного волнового фронта, получаемым приборами с датчиками волнового фронта (двф) - RU2715434C1
Код документа: RU2715434C1
Описание
1. Область техники, к которой относится изобретение
Предлагаемое изобретение относится к разработкам в области измерительных оптических систем и может применяться в системах контроля качества и других областях оптической промышленности.
2. Уровень техники
Задача восстановления формы асферической поверхности оптической детали является достаточно важной и актуальной, особенно в области высокоточных и астрономических оптических систем.
Существует способ контроля формы асферических поверхностей второго порядка с использованием анаберрационных точек, описанный в патенте RU №2396513, использующий сложную оптическую систему и достаточно трудоемкий с точки зрения юстировочных операций. Также известны способы контроля качества асферической поверхности с помощью интерферометра, которые предполагают наличие в измерительной ветви оптического корректора хода лучей для измерения отклонений формы поверхности от эталонной (Д.Т. Пуряев «Методы контроля оптических асферических поверхностей», Москва: Машиностроение, 1976 г.). В настоящее время линзовые оптические корректоры заменяются на голографические, называемые дифракционными оптическими элементами (ДОЭ), используемыми в интерферометрах, сделанных по различным схемам (авторское свидетельство SU 1017923, патент на изобретение RU №2534435).
Однако все эти способы не позволяют получить уравнение формы асферической поверхности в явном виде и требуют для своего осуществления изготовления дорогостоящего оптического корректора. В силу выше изложенного, в качестве прототипа выбран способ измерения радиуса кривизны поверхности оптической детали, описанный в патенте RU 2667323 (Способ и устройство дифференциального определения радиуса кривизны крупногабаритных оптических деталей с использованием датчика волнового фронта).
В прототипном способе измеряют радиус кривизны сферической поверхности Rз дифференциальной методикой, вычисляя его по формуле
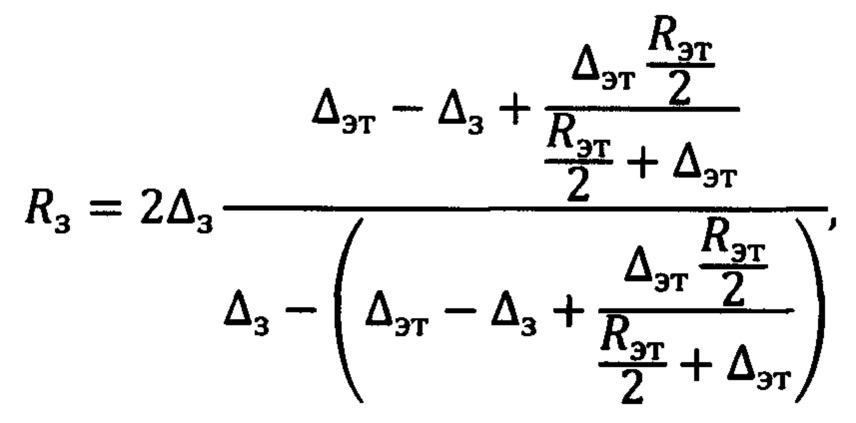
где Δз и Δэт - смещения прибора относительно точки автоколлимации для измеряемого и эталонного зеркала, соответственно, дающие одинаковую величину радиуса кривизны волнового фронта, регистрируемого ДВФ, а Rэт - радиус эталонного зеркала.
В самом деле, для получения уравнения формы асферической поверхности такого измерения недостаточно, поскольку при установке в прибор асферической оптической детали такие измерения дадут лишь радиус ближайшей сферы. В результате ограничением такого способа будет невозможность контроля несферических поверхностей. Тем не менее, для получения уравнения асферической поверхности необходимо знать радиус ближайшей сферы, поэтому в качестве прототипа выбран способ, позволяющий это сделать.
3. Раскрытие изобретения
Для решения поставленной задачи был разработан новый способ, в котором после измерения радиуса ближайшей сферы Rз (отклонение от которой у асферической поверхности минимально) необходимо зафиксировать отклонение волнового фронта Was от ближайшего сферического волнового фронта Ws с радиусом Rз в положении начальной установки для измеряемой асферической оптической детали (когда совпадение центра кривизны ближайшей сферы и фокуса насадки прибора обеспечат автоколлимационный ход лучей, контролируемый по получению плоского волнового фронта на ДВФ). Затем, учитывая, что Was это удвоенная величина отклонения самой измеряемой поверхности, необходимо сложить полученный сферический волновой фронт Ws с величиной Was/2, т.е получить сумму

Эта сумма будет полностью соответствовать форме измеряемой асферической поверхности. Для того, чтобы получить уравнение поверхности в каноническом виде достаточно любым математическим способом (например, методом наименьших квадратов) подобрать коэффициенты этого канонического уравнения формы асферической поверхности, приравняв его указанной выше сумме:
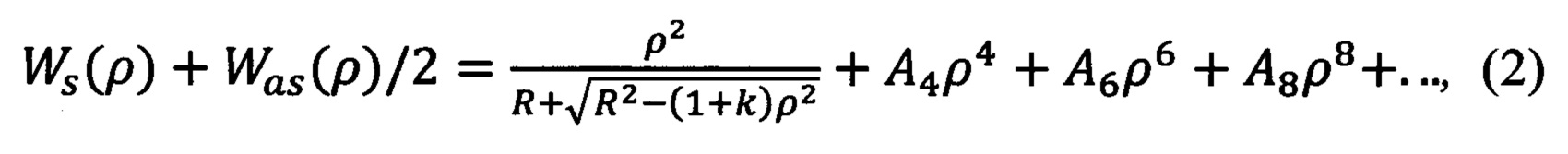
где А4, А6, A8, … - коэффициенты соответствующего порядка асферики, k - коническая константа, ρ - радиальная координата на зрачке, R - радиус вершинной сферы, который в случае асферики второго порядка соотносится с измеренным радиусом Rз ближайшей сферы соотношением:
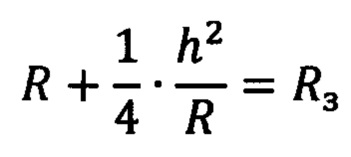
и, соответственно,

где h - половина светового диаметра исследуемой поверхности. Для асферики более высоких порядков выражение будет в первом приближении таким же, однако, численными методами все неизвестные коэффициенты в выражении (2) подбираются достаточно просто.
Таким образом, предлагаемый способ восстановления формы асферической поверхности оптической детали по параметрам отраженного волнового фронта, получаемым приборами с ДВФ позволяет получить уравнение формы исследуемой асферической поверхности и определить величину отклонения формы ΔS изготовленной поверхности от заданной путем вычисления разницы выражения (2) и заданного уравнения асферики
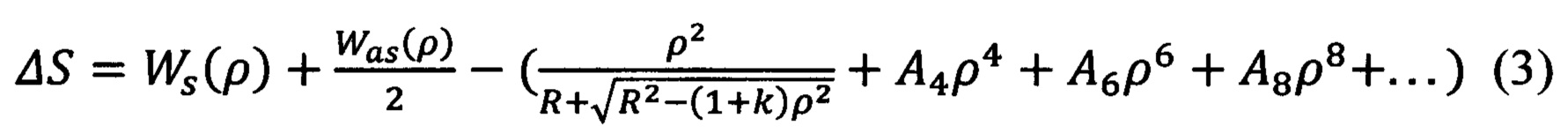
Принципиальным отличием является возможность восстановления формы асферической поверхности контролируемой детали.
3. Осуществление изобретения.
Пример осуществления изобретения
Для проверки работоспособности предлагаемого к патентованию способа восстановления формы асферической поверхности оптической детали по параметрам волнового фронта, получаемым приборами с ДВФ, в МГТУ им. Н.Э. Баумана в рамках НИР были проведены измерения на изготовленном авторами приборе (RU 2667323).
В качестве исследуемой оптической детали было взято параболическое зеркало (k=-1) с радиусом вершинной сферы 1736 мм и ошибкой формы PV=λ/8 (соответственно ошибка rms ~ λ/40) по паспорту.
Волновой фронт Was датчиком волнового фронта определялся как набор полиномов Цернике, а сферический волновой фронт Ws в этой системе координат характеризовался коэффициентом С21, называемым дефокусировка:
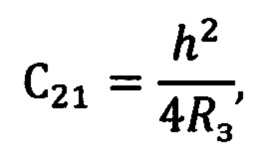
где h - половина диаметра измеряемой детали, а Rз - радиус ближайшей сферы, измеренный способом, приведенным в RU 2667323.
В результате восстановления поверхности получились следующие параметры уравнения параболической поверхности:
- вычисленный радиус вершинной сферы 1736,36 мм,
- коническая константа k=-0,9898,
- отличие восстановленного уравнения формы от исходного (ошибка rms) составило ~ λ/44.
Реферат
Способ восстановления формы асферической поверхности оптической детали по параметрам отраженного волнового фронта содержит получение радиуса ближайшей сферы Rи волнового фронта сферической формы W(ρ). В положении начальной установки для измеряемой асферической оптической детали, характеризующейся получением автоколлимационного хода лучей, контролируемого по получению плоского волнового фронта на датчике волнового фронта (ДВФ), фиксируют отличия волнового фронта от ближайшей сферы W(ρ) для вычисления коэффициентов уравнения асферической поверхности заданного порядка путем минимизации разницы этого уравнения и суммы сферического волнового фронта W(ρ) и половины величины W(ρ), т.е.где А, А, A, … - коэффициенты соответствующего порядка асферики, k - коническая константа, ρ - радиальная координата на зрачке, R - радиус вершинной сферы. Технический результат - возможность восстановления формы асферической поверхности оптической детали по параметрам отраженного волнового фронта.
Формула
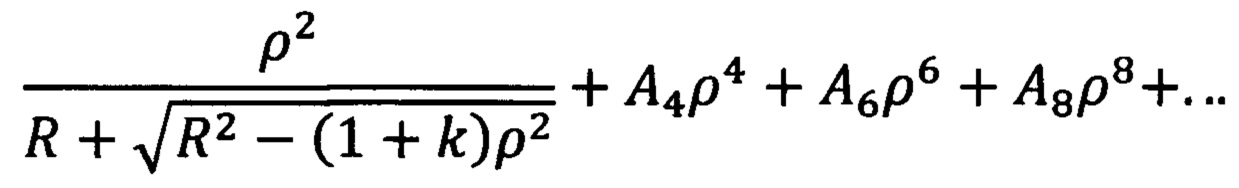

Документы, цитированные в отчёте о поиске
Способ и устройство дифференциального определения радиуса кривизны крупногабаритных оптических деталей с использованием датчика волнового фронта

Комментарии